2. 集美大学 轮机工程学院,福建 厦门 361021
2. School of Marine Engineering, College of Marine Engineering, Jimei University, Xiamen 361021, China
在全球范围内,二氧化碳、氮氧化物、颗粒物等作为主要污染物对空气造成了严重的污染[1]。以我国为例,2017年全国内燃机车的排放量达到了4548万吨,其中颗粒物为57万吨,氮氧化物为628万吨,碳氢为428万吨。在所有的排放当中,柴油机的排放占了很大比例,其中氮氧化物占了近70%。尽管众多学者在提高柴油机工作效率和降低柴油机排放方面开展了很多研究,但对柴油机的改善还存在一定的不足,不能满足日益严格的排放法规[2]。近年来,选取合适的替代燃料解决大气污染和石化燃料短缺的问题为我们提供了一种解决问题的新思路。由于生物柴油可再生、无毒、可降解、可持续等优点,被越来越多的专家认为是替代传统柴油最理想的燃料之一[3]。
生物柴油可以作为燃料只需要对柴油机进行小的改造或者直接就可以在柴油机缸内进行燃烧[4]。Zhang等[5]研究了不同组分生物柴油对柴油机排放特性的影响,研究发现生物柴油可以很大程度地减少碳氢、CO和颗粒物的排放,但NOx的排放略有增加。实验法是研究生物柴油的主要方法之一,但是会花费很多的时间和精力。而模拟仿真法不仅可以节省时间,而且可以很大程度节省实验成本,因此,模拟仿真法越来越得到了人们的认可。在计算过程中,3D-CFD法不仅可以得到燃烧室内流场、压力、组分、温度和湍流变化的情况,而且比热力学模型更接近柴油机缸内燃烧的实际过程。然而,CFD仿真模型的精度更依赖于计算代码中的子模型。
在早期生物柴油化学燃烧方面,Fisher等[6]把丁酸甲酯作为生物柴油替代物,但是由于其碳链长度远小于典型16-18的生物柴油甲酯,导致其化学动力特性难以实现。Brakora等[7]开发了一个简化的包含丁酸甲酯和正庚烷的化学反应机理,并模拟了柴油机缸内燃烧情况。其研究结果表明,仿真的缸压曲线和放热曲线与实验结果吻合较好,但是对低负荷柴油机的NOx的预测还有待改进。Ng等[8]在考虑生物柴油饱和度的前提下建立了生物柴油多组分化学反应机理。其研究发现,生物柴油的不饱和度越高燃烧时产生的碳烟就越多。Luo等[3]建立了一种由癸酸甲酯、癸酸甲酯和正庚烷组成包含115种物质和460个化学反应的三组分生物柴油化学反应机制。研究发现该机理可以准确预测不同环境条件下柴油机的着火延时、火焰长度和当量比。
综上所述,由于生物柴油热物理性质的不同,它的喷射、雾化和蒸发特性也不同于柴油。本文主要目的是通过建立的仿真模型详细分析生物柴油的特性和其在柴油机缸内燃烧过程,研究喷油策略对柴油机燃烧和排放特性的影响。
1 仿真模型的建立 1.1 数学模型1)燃烧、排放和传热模型
由于生物柴油是由多种碳氢化合物组成的,而各种碳氢化合物因各自的分子结构不同而具有不同的物理、化学和热力学性质。每一种碳氢化合物燃烧还会产生许多的中间产物,而且都会对柴油机的燃烧和排放特性产生影响。因此,生物柴油在柴油机缸内燃烧是一个非常复杂的过程。为了提高仿真模型的预测精度,本文采用ChemkinⅡ代码与三维AVL-Fire相耦合的方法进行计算,采用威斯康星麦迪逊大学开发的生物柴油的机理仿真柴油机中生物柴油的燃烧过程。该机理主要考虑了生物柴油饱和度的69种产物和204种化学反应。同时,在计算的过程中采用多组分燃烧模型,在化学的动力学预测过程中考虑化学物种的形成和破裂,并采用Zeldovich机理对氮氧化物的生成进行预测。
在传热的计算过程中,本文选用修正的Han and Reitz模型进行计算。该模型可以充分考虑湍流普朗特数和气体组分密度的变化情况。详细的传热公式可以从文献[9]得到。其壁面热通量的预测可以利用下面的公式计算得到:
| ${q_w} = \frac{{\rho {c_{p,F}}{u^ * }T\ln (\frac{T}{{{T_W}}}) - (2.1{y^ + } + 33.4)Gv/{u^ * }}}{{2.1\ln ({y^ + }) + 2.5}}\text{,}$ | (1) |
| ${y^ + } = \frac{{{u^ * } \times y}}{v}\text{,}$ | (2) |
| ${u^ * } = \sqrt {\frac{{{\tau _w}}}{\rho }} \text{。}$ | (3) |
式中:ρ为燃油液滴密度;u*为摩擦速度;cp为燃油液滴比热;τw为壁面应力;y+无量纲壁距离;其中G(G=Qc)为能源源相。
为了减少计算量,节省计算时间,忽略近壁计算单元源相的放热量,式(1)可以简化为:
| ${q_w} = \frac{{\rho {c_{p,F}}{u^ * }T\ln (\frac{T}{{{T_W}}})}}{{2.1\ln ({y^ + }) + 2.5}}\text{。}$ | (4) |
2)临界参数
采用Ambrose的方法对临界压力和临界温度进行预测,其表达式如下:
| ${p_c} = M(0.339 + \sum {{\Delta _p}{)^{ - 2}}}\text{,} $ | (5) |
| ${T_c} = {T_b}\left[ {1 + {{\left( {1.242 + \sum {{\Delta _T}} } \right)}^{ - 1}}} \right]\text{。}$ | (6) |
式中:Δp和ΔT分别通过各原子或分子间的相互贡献来计算得到,具体可以根据文献[10]得到;M为摩尔分子量;Tb为标准大气压下工质沸腾温度。
采用Jobac法计算临界压力[11],其表达式如下:
| ${V_c} = 17.5 + \sum {{\Delta _V}}\text {,} $ | (7) |
式中,ΔV通过各原子或分子间相互贡献计算得到,详细如文献[11]所示。
3)蒸汽压
采用Lee-Kesler法计算工质的蒸气压,其公式如下:
| ${p_{vp}}_r = {p_c}{e^{[{f^{(0)}}(T) + w{f^{(1)}}(T)]}}\text{,}$ | (8) |
| $\begin{split} {f^{(0)}}(T) = & 5.927\;14 - 6.096\;48\frac{{{T_c}}}{T} - \\ & 1.288\;62\ln \left( {\frac{T}{{{T_c}}}} \right) + 0.169\;347{\left( {\frac{T}{{{T_c}}}} \right)^6} \text{,} \end{split} $ | (9) |
| $\begin{split} {f^{(1)}}(T) = & 15.251\;8 - 15.687\;5\frac{{{T_c}}}{T} - \\ & 13.472\;1\ln \left( {\frac{T}{{{T_c}}}} \right) + 0.435\;77{\left( {\frac{T}{{{T_c}}}} \right)^6} \text{。} \end{split} $ | (10) |
式中,w为变心因子。
4)液相密度
液相密度的计算公式如下:
| $\phi = {(1 - T/{T_c})^{2/7}} - {(1 - {T_{r - R}})^{2/7}}\text{,}$ | (11) |
| ${V_s} = {V_{S - R}}Z_{RA}^\phi\text{,} $ | (12) |
式中:Tr-R和VS-R分别为相对温度TR时减小的温度和压力;ZRA可以从文献[11]中得到。
液相密度可以通过下面的公式得到:
| $\rho = \frac{{{\rho _R}}}{{Z_{RA}^\phi }}\text{,}$ | (13) |
式中,ρR为实测密度值。
5)汽化潜热
工质的汽化潜热计算公式如下:
| $\Delta L = R{T_c}[7.08{(1 - \frac{{{T_c}}}{T})^{0.354}} + 10.95w{(1 - \frac{{{T_c}}}{T})^{0.456}}]\text{,}$ | (14) |
式中,R为理想气体常数。
6)液相粘度
液相粘度ηL的计算公式如下[11]:
| $\ln \frac{{{\eta _L}}}{{{\rho _{20}}M}} = A + \frac{B}{T}\text{。}$ | (15) |
式中:ρ20为20 ℃度时液体密度;A和B为计算常数,可以从文献[8]中得到。
7)液相导热系数
稳态时,液相导热系数可以由下面公式计算得到:
| ${A_x} = \frac{{{A^*}T_b^\alpha }}{{{M^\beta }T_c^\gamma }}\text{,}$ | (16) |
| ${\lambda _L} = \displaystyle\frac{{{A_x}{{\left( {1 - \frac{{{T_c}}}{T}} \right)}^{0.38}}}}{{\left( {\displaystyle\frac{{{T_c}}}{T}} \right)_{}^{1/6}}}\text{。}$ | (17) |
式中:Tb为工质标准沸点温度;A*,α,β和γ为计算常数;λL为液相导热系数。
8)气体扩散系数
气体扩散系数为一个反映气体扩散强弱的物理量,即气体单位时间通过单位横截面积的多少。可以根据下面的公式计算得到:
| ${D_A} = A + B + C{T^2}\text{。}$ | (18) |
式中:DA为气体扩散系数;A,B和C为常数。
9)表面张力
表面张力σ是液体任意两相邻间垂直于它们表面的单位长度分界线间互相作用的拉力,张力的大小与液体表面薄层中分子特殊受力状态密切相关。表面张力可以通过下面的公式计算得到:
| $\frac{\sigma }{{p_c^{2/3}T_c^{1/3}}} = \left( {0.132{\alpha _c} - 0.279} \right){(1 - {T_c}/T)^{11/9}}\text{,}$ | (19) |
| ${\alpha _c} = 0.907\;6\left[ {1 + \frac{{{T_{br}}\ln \left( {{p_c}/1.013\;25} \right)}}{{1 - {T_{br}}}}} \right]\text{。}$ | (20) |
式中:σ为表面张力;αc为里德尔数。
1.2 AVL-Fire仿真模型与热力学模型相比,三维CFD仿真模型可以考虑湍流流动对流体流动的影响。然而,在三维CFD模拟中需要充分考虑计算精度和计算时间的折中。比如,如果化学反应机理太详细,就会增加模拟时间;如果机理太简单,则计算精度不够。目前,KIVA,AVL-Fire等软件广泛被用于多维度的CFD模拟计算。因此,本文选取AVL-Fire仿真软件进行模拟。考虑到柴油机喷孔数为8个,为了节省计算时间,根据柴油机燃烧室对称的原理,选取1/8个燃烧室作为研究的对象,其上止点时燃烧室的网格如图1所示。同时,为了保证燃油液滴破碎、蒸发和燃烧的精确性,对喷油器附近和喷射路径区域进行网格细化。
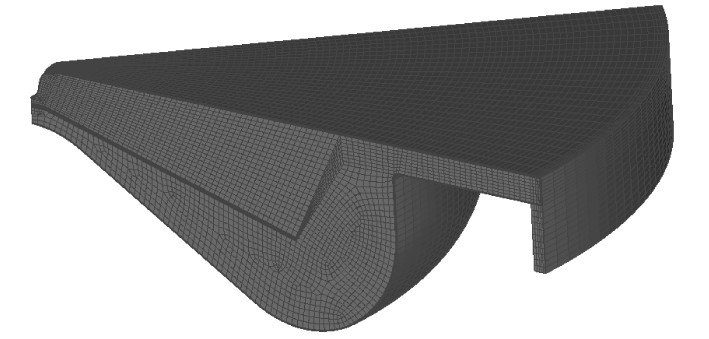
|
图 1 上止点时45°燃烧室网格 Fig. 1 The 45° sector grid shown at TDC |
选用1台船用船四冲程直喷式中速单体泵电控柴油机作为研究对象,其主要参数如表1所示。采用燃烧分析仪对柴油机的燃烧进行分析,采用FCMM-2燃油耗测量仪计算燃油消耗量。分析仪采样频率为500 ms,精度为±1%,不同的温度、流量、压力分别采用相应的传感器进行测量。柴油机的实验简图如图2所示。采用燃烧分析仪对柴油机的燃烧进行分析,采用FCMM-2燃油耗测量仪计算燃油消耗量。分析仪采样频率为500 ms,精度为±1%,不同的温度、流量、压力分别采用相应的传感器进行测量。柴油机的实验简图如图2所示。
|
|
表 1 柴油机主要参数 Tab.1 Main parameters of diesel engine |
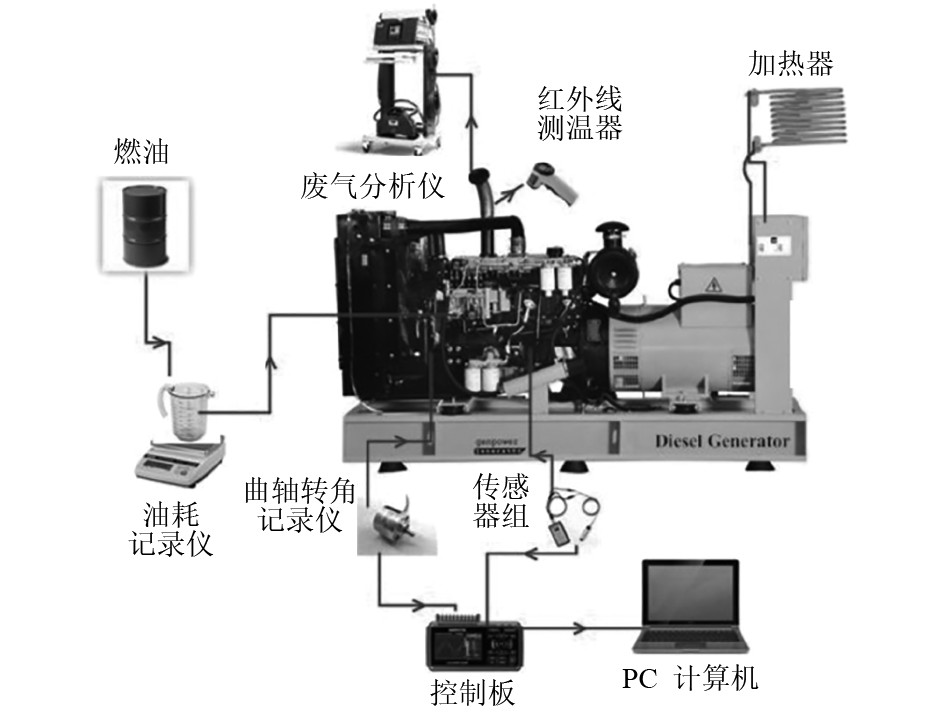
|
图 2 柴油机实验装置简图 Fig. 2 Schematics of experimental device |
为了考虑模型应用的广泛性,选取2个工况对该模型进行试验验证。工况1转速为799 r/min,负荷为50%负荷;工况2转速为1000 r/min,负荷为75%负荷。在实验的测试过程中,为了确保实验数据的准确性,等柴油运行20min后再进行测量,每个工况点测量3次,并取其平均值。
由于AVL-Fire中缺少相关物质的热力学参数,不能很准确地反映燃料的性能。因此,本文采用ChemkinⅡ代码与三维AVL-Fire相耦合的方法进行计算。该机理主要考虑了生物柴油饱和度的69种产物和204种化学反应。2种工况下柴油机缸压曲线和放热率变化情况如图3所示。
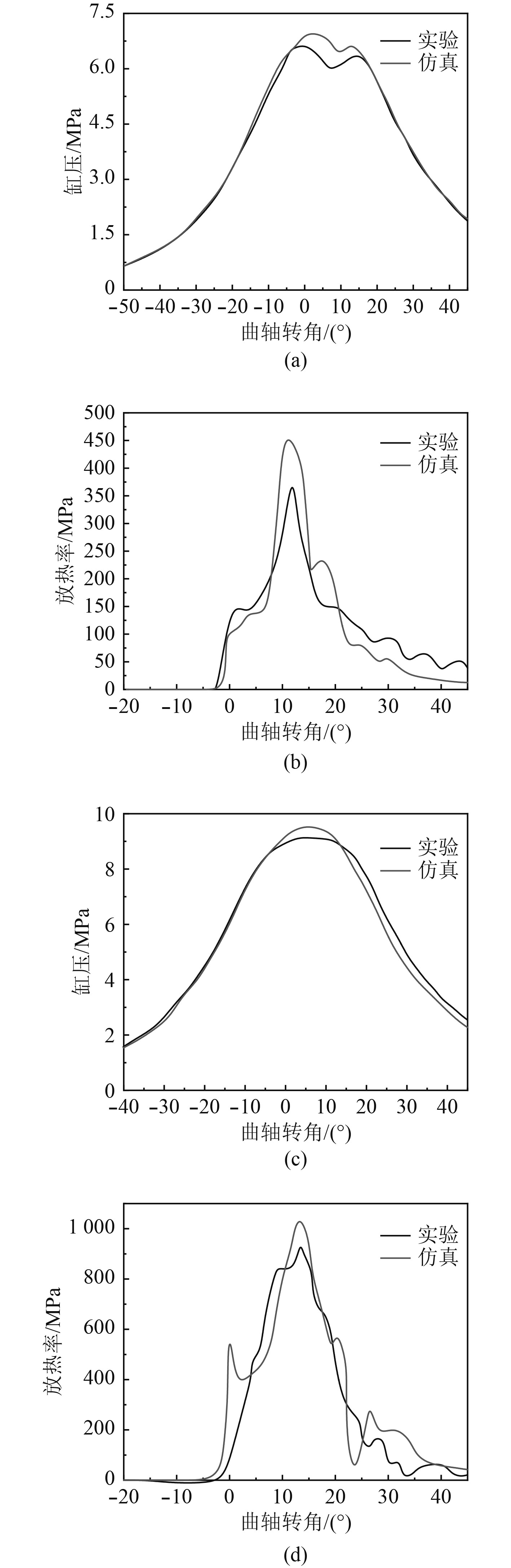
|
图 3 仿真和实验结果对比 Fig. 3 Comparisons of simulation and experiment results |
由图3可知,与实验结果相比,仿真的缸压曲线稍高一点,但最大误差都在7%以内。该机理采用多组分燃料的燃烧模型,从多组分的角度对饱和脂肪酸甲酯和不饱和脂肪酸甲酯进行了化学预测,因而可以比较准确地预测缸内生物柴油的蒸发和氧化过程。
2 仿真结果分析 2.1 柴油机燃烧特性燃油的喷油测量是影响柴油机动力特性和排放特性的重要因素之一。为了研究不同喷油策略对柴油机性能的影响。在以上2种工况下选取了3种不同喷油策略进行研究。具体的喷油速率和曲轴转角如图4所示。假定三次燃油喷射总量相等,其中单次喷射的开始时间为上止点前7°;双次喷射和三次喷射的开始时间为上止点前11°。
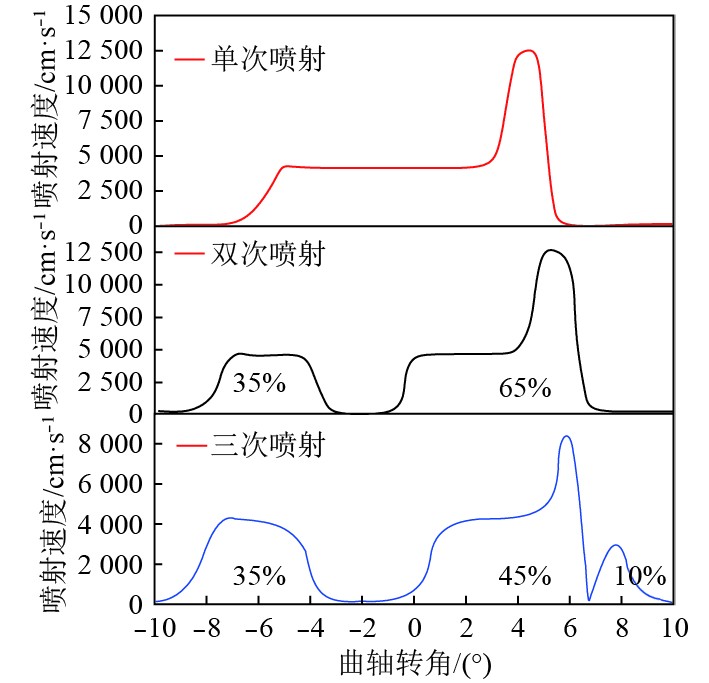
|
图 4 柴油机燃油喷射方案 Fig. 4 Injection profile and injected mass percentages |
1)缸压
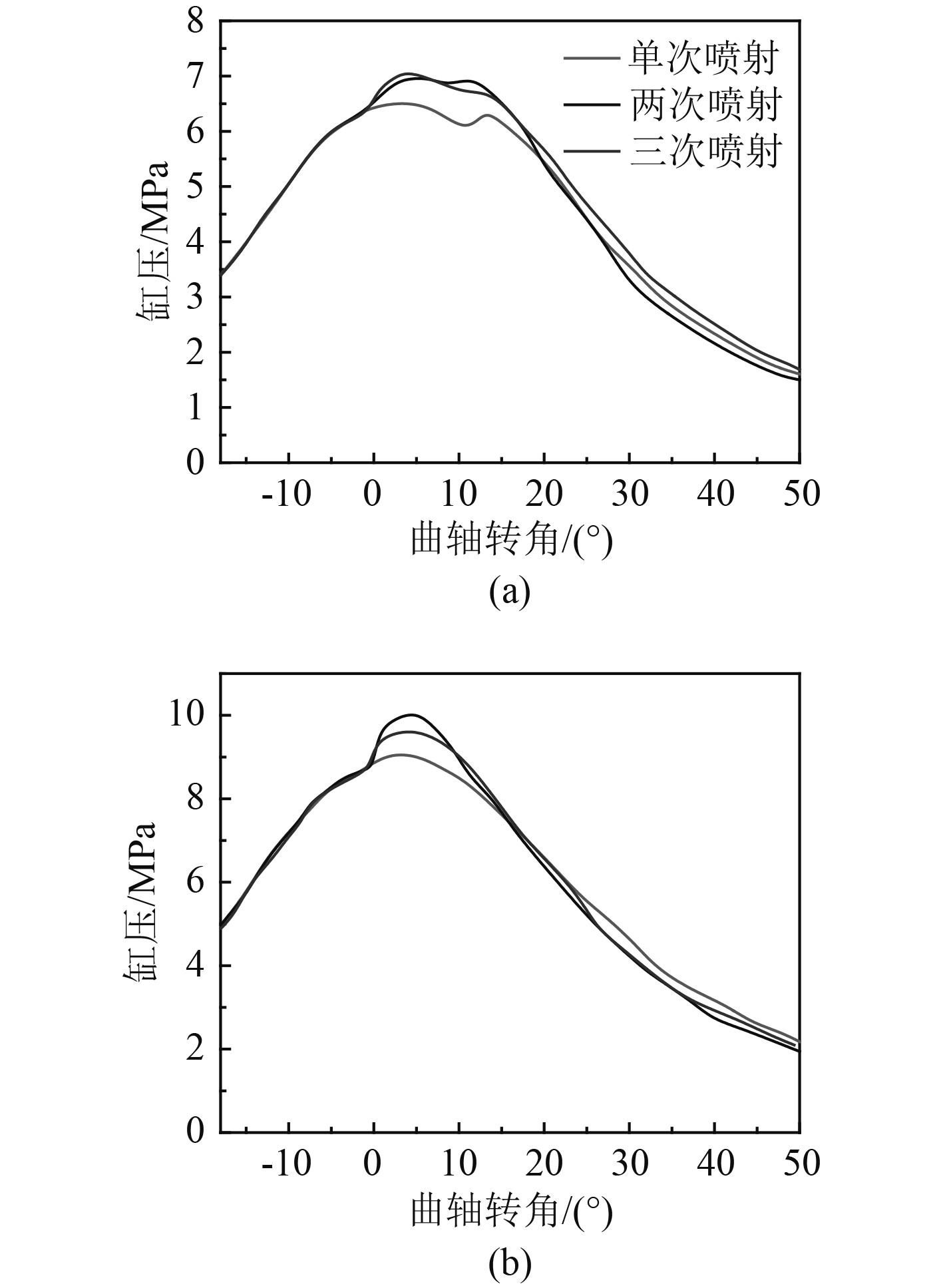
2种工况下,3种喷油速率仿真的缸压变化如图5所示。从图5(a)可以看出,在柴油机低负荷下,柴油机的缸压出现了2个波峰。虽然缸内燃烧在上止点前就开始了,但是燃烧释放的热量不足以克服由于膨胀减小的压力,即在上止点后,产生了第1个波峰。然而,当剧烈燃烧时,更多释放的热量导致了第2个波峰的出现。因此,可以发现燃油喷射量和喷油持续时间是非常关键的2个因素,如果不能精确地控制两者,还可能会导致发火失败。从图5(b)可以看出,在高负荷时,柴油机的缸压曲线并没有出现2个波峰,而是在上止点10°后出现了一个波峰。这主要是由于高负荷时喷入了较多的燃料,缸内初期燃烧时释放了较多能量。
|
图 5 不同工况柴油机缸压变化情况 Fig. 5 Cylinder pressure under different conditions |
同时还可以发现,在2种工况下两次和三次燃油喷油策略在一定程度上都增加了柴油机的气缸压力峰值,其中两次喷射策略的气缸压力峰值最大。这主要是因为在缸内燃烧初期两次和三次喷射有着更多的预混合燃料,柴油机的缸内燃烧在一定程度上得到了改善。
2)放热率
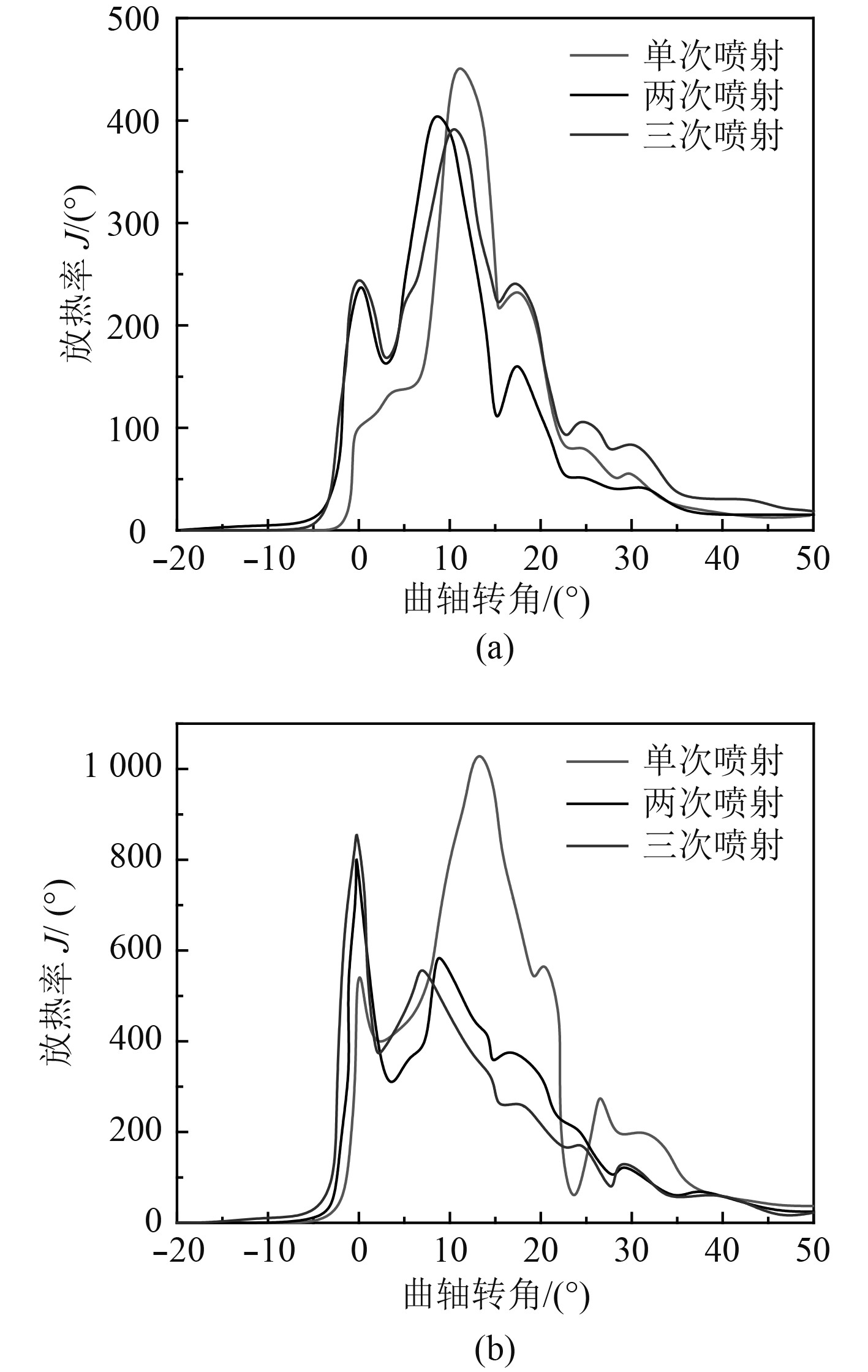
2种工况下,3种喷油速率仿真的放热率如图6所示。可以清楚地发现,低转速时柴油机的燃烧时刻明显比高转速的燃烧时刻更早。这主要是由于转速较低时燃油和空气的预混合时间和点火延时变长导致。
|
图 6 不同工况柴油机放热率变化情况 Fig. 6 Heat release rate under different conditions |
同时,从放热率也可以明看出,两次燃油喷射在燃烧初期放出的热量最多,其次为三次燃油喷射。即两次喷射和三次喷射提供了更多的预混燃料和空气混合,从而改善了预混燃烧阶段的燃烧。与单次喷射相比,在燃烧开始后两次喷射和三次喷射的放热速率值更大。然而,单次喷射具有最大的放热速率峰值,其中工况2更为明显,该值远大于两次和三次喷射的放热率峰值。在低速时,柴油机为燃料和空气的混合提供了充分的时间。因此,低速时柴油机的着火延时明显早于高速时的着火延时。
3)缸内温度
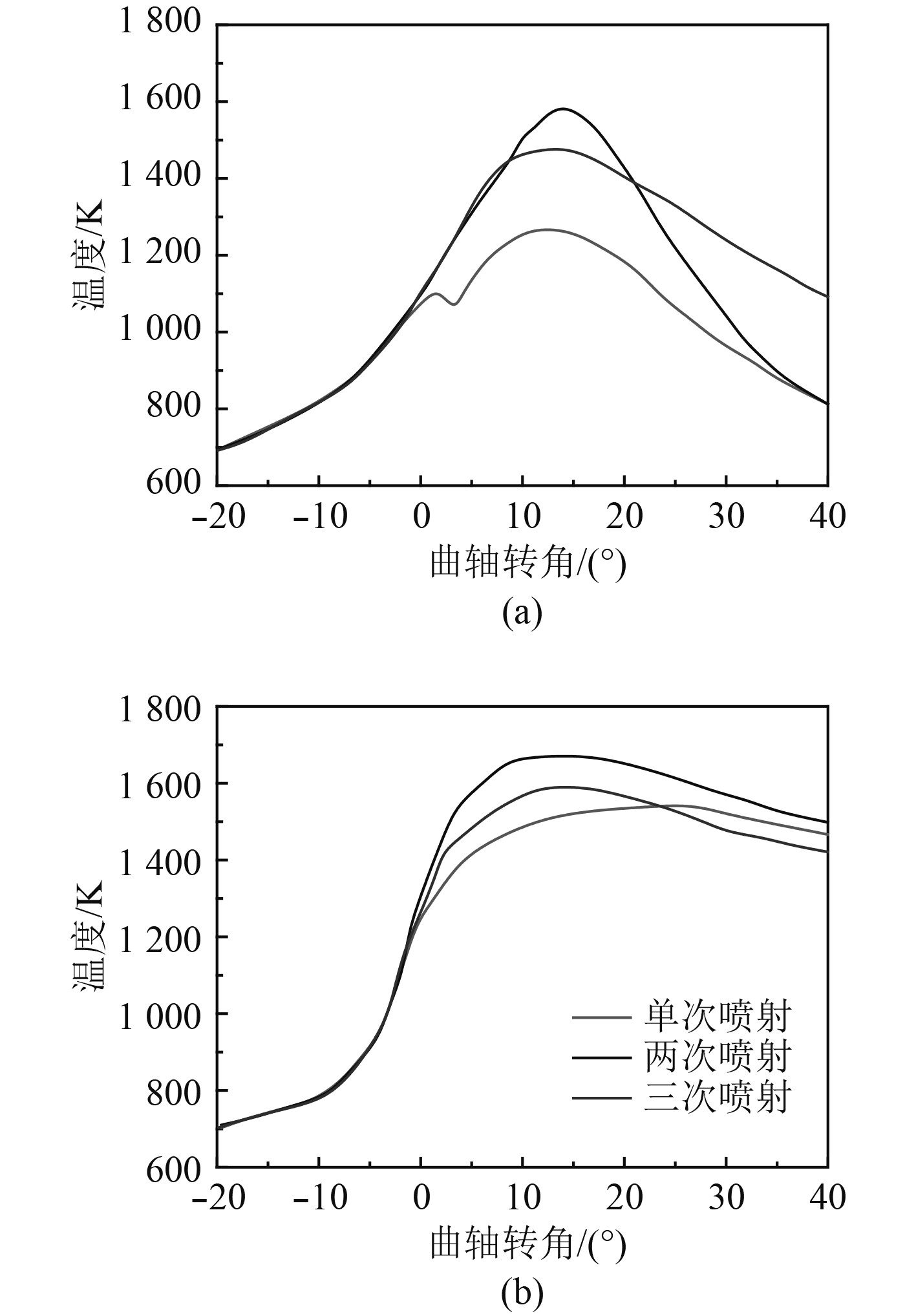
2种工况下,3种喷油速率仿真的缸内温度如图7所示。从图7(a)可以清楚地发现,在低转速时单次喷射的缸内温度明显低于两次和三次喷射的温度。这主要是由于两次喷射和三次喷射的燃烧时刻早于一次喷射的燃烧,且从图6可得其燃烧明显早于一次喷射。从图7(b)可以看出,高速时,三次喷射的缸内温度最高,其次为两次喷射和三次喷射。这主要是两次和三次喷射的时刻在上止点11°,而一次喷射在上止点9°,其燃烧早于单次喷射。
|
图 7 不同工况柴油机缸内温度变化情况 Fig. 7 Cylinder temperature under different conditions |
1)CO排放
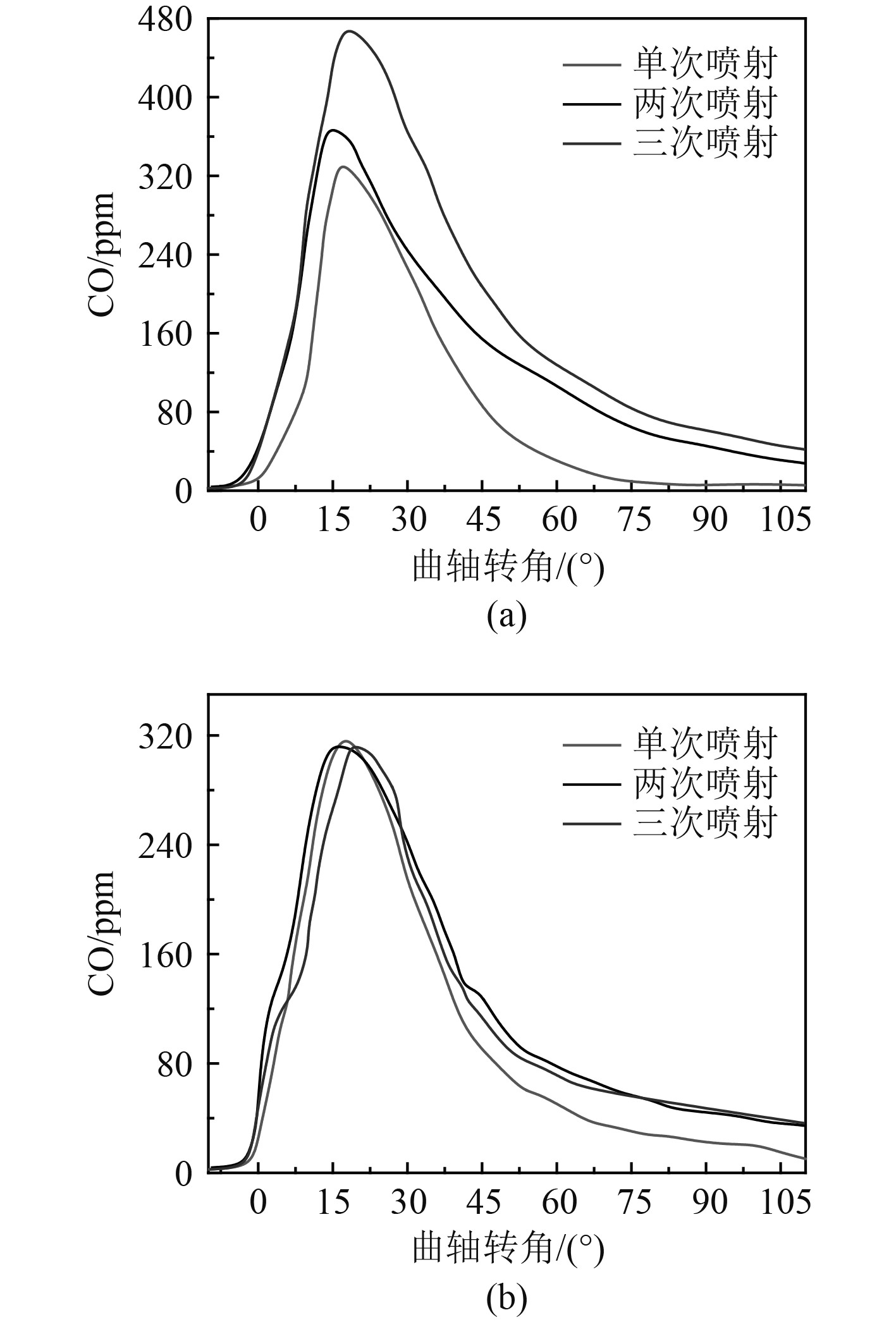
CO的生成主要受到混合气体和缸内燃烧温度的影响。2种工况下,3种喷油速率仿真计算的CO排放如图8所示。
|
图 8 不同工况柴油机CO排放情况 Fig. 8 CO emission under different conditions |
从图8可以看出,在燃烧初期生成了大量的CO,随后迅速被氧化,低转速时柴油机生成的CO明显高于高转速生成的CO。这主要是燃烧初期缸内温度比较低和燃油较多所致。随着缸内温度的增加,CO不断被进一步氧化为CO2。同时,在低转速时虽然缸内燃油和空气混合更好,但是由于较低的柴油机缸内燃烧温度不利于CO的氧化为CO2。因此,CO的排放受温度的影响非常明显。因为高的缸内温度,三次喷射和两次喷射的氧化速率明显高于单次喷射的氧化速率。在2种工况下,燃烧开始后单次喷射的放热率最大,单次喷射的CO排放量低于两次和三次喷射的CO排放。
2)NOx排放
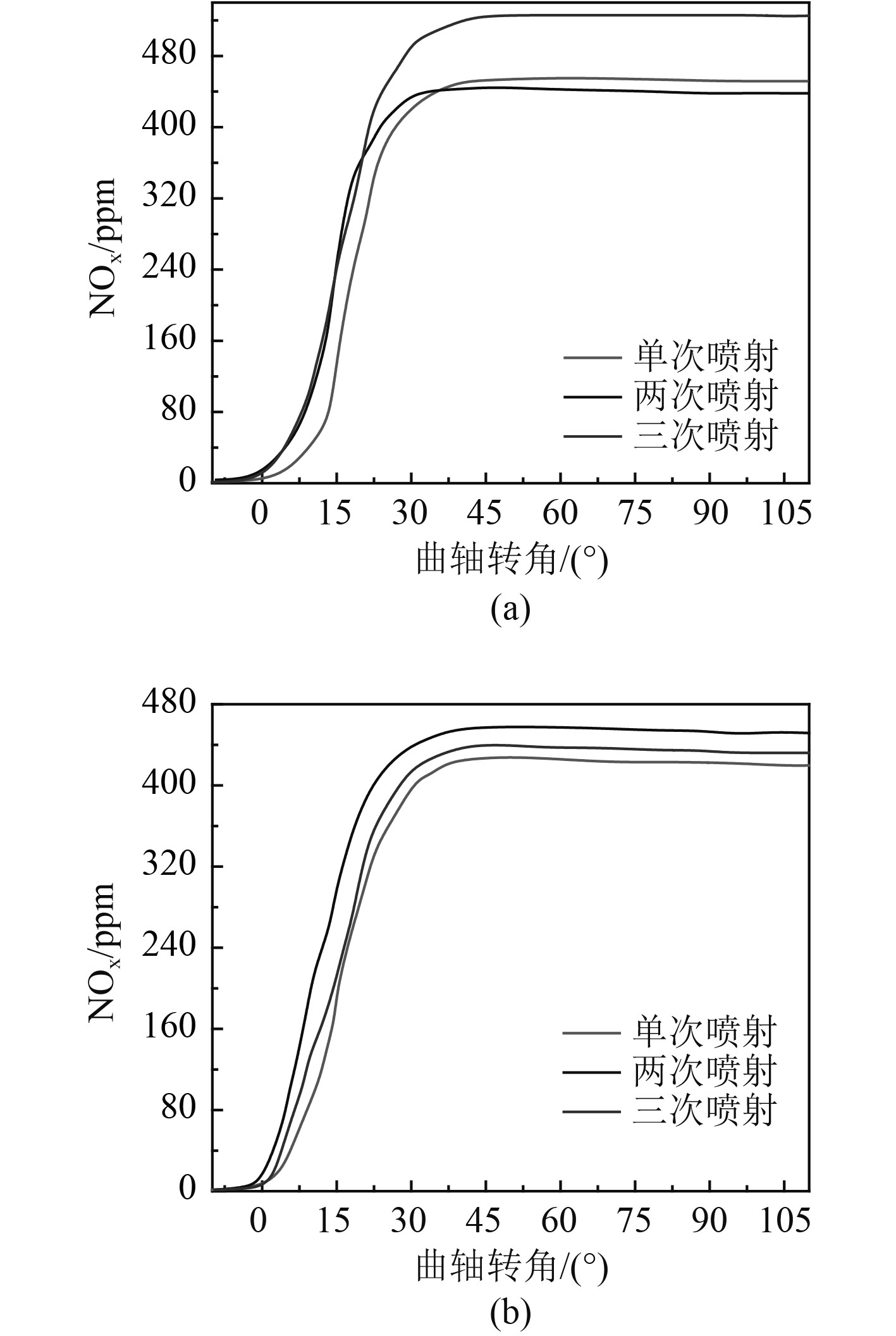
在柴油机燃烧过程中氧浓度、反应时间和温度是生成NOx的3个重要因素。其中任意一个因素发生变化都会影响其生成。在2种工况下,3种喷油速率仿真计算的NOx排放如图9所示。
|
图 9 不同工况柴油机NOx排放情况 Fig. 9 NOx emission under different conditions |
从图9可看出,NOx的生成主要在曲轴转角的0°~40°;在低转速时三次喷射产生的NOx最多,其次为一次喷射和二次喷射;在高转速时二次喷射产生的NOx最多,其次为三次喷射和一次喷射。这主要是由于相对于二次喷射三次喷射策略在前期喷射的燃油较少,燃烧前期空燃比较大有利于NOx的生成;而相对于一次喷射,三次喷射的着火延时较短,高的缸内温度促进了NOx的生成。因此,低转速时三次喷射产生的NOx最多。在高转速时,柴油机减小了着火延时的时间,缸内燃烧温度成为影响NOx生成的主要原因,即二次喷射生成的NOx最多,其次为三次喷射和一次喷射。
3 结 语减少柴油机对石化燃料的依赖,开发利用新的能源来取而代之具有非常重要的战略意义。因此,生物柴油成为研究的焦点。为了精确预测不同喷油策略对燃烧生物柴油柴油机排放特性和动力特性的影响,本文采用ChemkinⅡ代码与三维AVL-Fire相耦合的方法研究了2种工况下3种不同喷油策略对柴油机性能影响,得到的结果如下:在柴油机低速运行时,由于燃料和空气混合的时间较长柴油机预混燃烧阶段较剧烈;2种工况下两次和三次喷射在一定程度增加了柴油机CO和NOx的排放;柴油机转速较低时,两次和三次喷射增加了柴油机缸压、放热率和功率的输出,在高转速时喷射策略对柴油机的影响较小。
| [1] |
王存磊, 殷承良, 王磊. BOOST发动机建模及其在混合动力仿真中的应用[J]. 上海交通大学学报, 2011, 45(6): 875-879. |
| [2] |
朱益梁, 何勇灵. 可变压缩比对增压中冷柴油机性能影响的模拟分析[J]. 农业工程学报, 2012, 28(4): 27-32. DOI:10.3969/j.issn.1002-6819.2012.04.005 |
| [3] |
LUO ZY, PLOMER M, LU TF, SOM S,et al. A reduced mechanism for biodiesel surrogates for compression ignition engine appli-cations[J]. Fuel, 2012, 99: 143-153. DOI:10.1016/j.fuel.2012.04.028 |
| [4] |
BIRTAS A, CHIRIAC R. A study of injection timing for a diesel engine operating with gasoil and HRG gas[J]. UPB Scientific Bulletin, Bucharest, 2011. |
| [5] |
ZHANG ZQ, E JQ, DENG YW, etal. Effect of fatty acid methyl esters proportion on combustion and emission characteristics of a biodiesel fueled marine diesel engine[J]. Energy Conversion and Management, 2018, 159: 244-253. DOI:10.1016/j.enconman.2017.12.098 |
| [6] |
FISHER EM, PITZ WJ, CURRAN HJ, etal. Detailed chemical kinetic mechanisms for combustion of oxygenated fuels[J]. Proceeding of the Combustion Institute, 2000, 28: 1579-1586. DOI:10.1016/S0082-0784(00)80555-X |
| [7] |
BRAKORA JL, R RD. Investigation of NOx predictions from biodiesel-fueled HCCI engine simulations using a reduced kinetic mechanism[J]. SAE paper, 201001-0577. |
| [8] |
NG HK, GAN SY, NG JH,etal. Development and validation of a reduced combined biodiesel-diesel reaction mechanism[J]. Fuel, 2013, 104: 620-634. DOI:10.1016/j.fuel.2012.07.033 |
| [9] |
SCHWAB AW, BAGBY MO, FREEMAN B. Preparation and properties of diesel fuels from vegetable oils[J]. Fuel, 1987, 66(10): 1372-1378. DOI:10.1016/0016-2361(87)90184-0 |
| [10] |
KUMAR MS, BELLETTRE J, TAZEROUT M. Investigations on a CI engine using animal fat and its emulsions with water and methanol as fuel[J]SAE Technical Paper, 2005-01-1729.
|
| [11] |
ZHOU DZ, YANG WM, AN H, etal. A numerical study on RCCI engine fueled by biodiesel/methanol[J]. Energy Conversion and Management, 2015, 89: 798-807. DOI:10.1016/j.enconman.2014.10.054 |
 2020, Vol. 42
2020, Vol. 42
