2. 广东海洋大学 海运学院,广东 湛江 524088
2. Maritime College, Guangdong Ocean University, Zhanjiang 524088, China
船舶电力推进系统具有良好的控制和操纵性能,动力装置在机舱中布置灵活,同时在振动、噪声以及排放控制方面具有独特的优势,被广泛应用在船舶推进系统中[1-2]。采用电力推进的船舶,一般选择多台中速柴油机作为动力源,同时加入储能系统构成混合电力推进结构[3-5]。国内外学者对混合电力推进船舶的功率分配优化进行了大量研究,Zahedi等[6]利用非线性平均方法,对低压直流混合动力全电推船舶进行了建模和仿真研究。Soleymani等[7]采用带约束条件的粒子群算法解决混合动力船舶中各设备的最优输出功率组合。Kanellos等[8]提出一种优化需求侧管理和发电调度的方法,通过调整船舶推进电机的功率消耗,提出了一种动态规划算法,能够保证船舶电力系统运行的成本和温室气体排放最小化的目标。袁裕鹏[9]设计了船舶能量管理系统的逻辑门限值控制策略,在满足船舶的功率需求的基础上,提高系统的稳定性。王凯[10]通过小波神经网络确定了最优能量效率下的最佳发动机转速,以此改善船舶动力系统的经济性并减少二氧化碳排放。
船舶能量管理系统(Power Management System,PMS)在船舶航行过程中对发电机组、负载变化、储能系统的状态进行监测和控制,以保证船舶的安全、高效运行。目前针对船舶混合电力推进的研究主要集中在运用智能算法优化功率的分配问题上,鲜有通过混合电力推进系统控制策略对柴油发电机组油耗进行优化问题的研究。制定合理的能量管理策略,可以确保船舶运行的安全性和可靠性,并能够提高混合电力推进船舶的能效,减少燃料消耗,达到节能减排的目的。
本文拟对混合电力推进船舶的柴油发电机组油耗和储能系统的功率损耗进行建模,根据船舶航行负载功率需求,结合锂电池组在船舶直流组网下的工作特点,提出一种基于等效燃油消耗量分析的能量控制策略。通过仿真计算,得出在设定负载功率下,船舶发电机组和锂电池组的最佳工作区间,并与传统的电力推进船舶油耗量进行对比,验证控制策略的有效性。
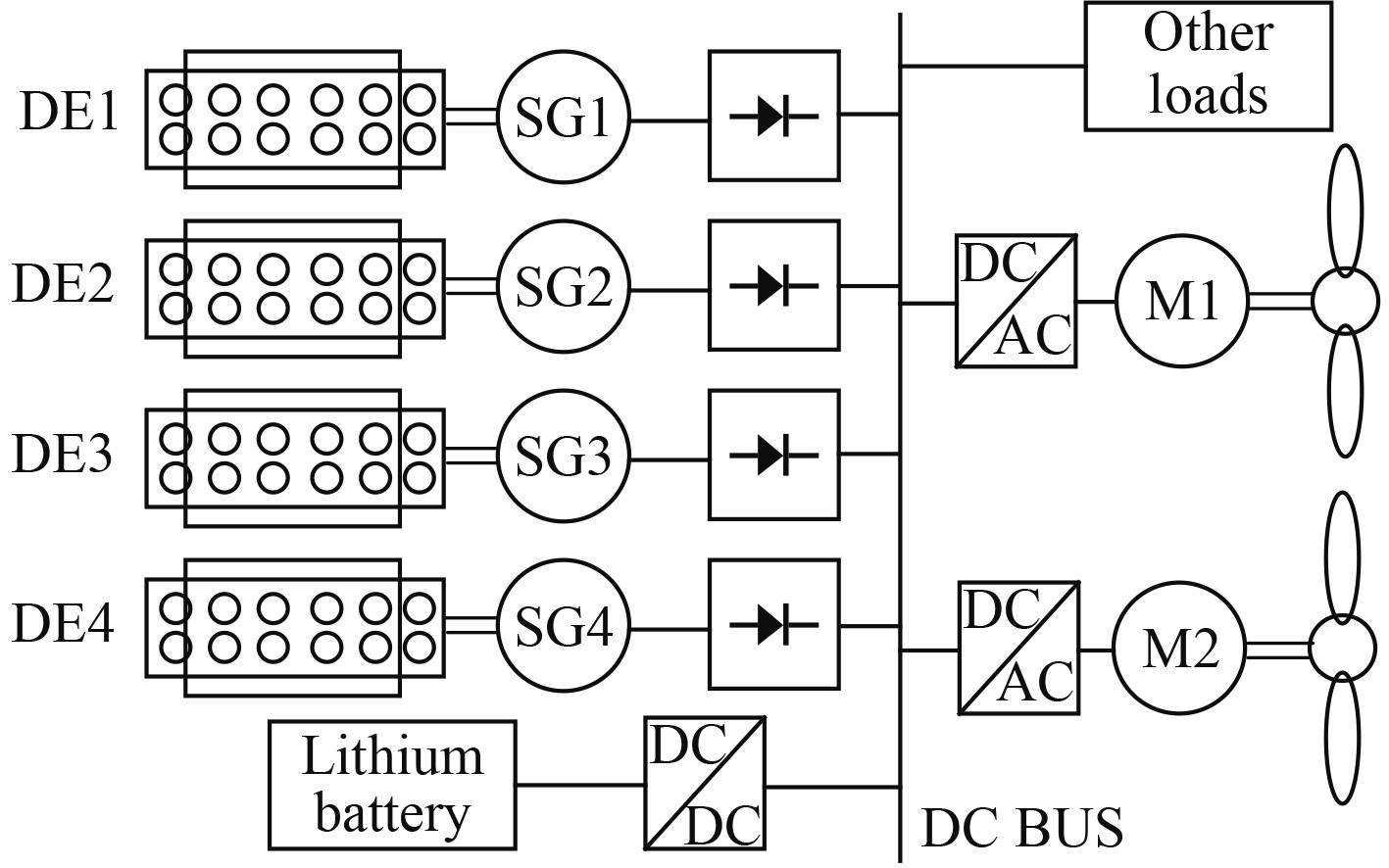
1 模型建立船舶混合电力推进系统结构如图1所示。
|
图 1 船舶混合电力推进结构图 Fig. 1 Hybrid electric propulsion ship structure |
在船舶混合电力推进系统中,主要动力源仍然是由船用柴油机驱动的同步发电机组,船用柴油机的燃料通常为柴油或重质燃料油。
传统的电力推进船舶一般采用交流组网技术,在网发电机组须以相同的固定频率同步工作,以保证船舶电网的稳定性和安全性。相比交流组网技术,直流组网下的各台柴油机可以独立工作,不需要频率和电压的同步控制,更便于机组之间的配合,各发电柴油机可工作在各自的最佳转速下。
1.1 柴油发电机组功率效率分析柴油机的每小时油耗量曲线可以用如下的二次函数拟合:
| $ {C_1} = {C_0} + a \times {P_m} + b \times {P_m}^2{\text{。}} $ | (1) |
其中:Pm为柴油机的机械功率;C0,a和b为拟合公式中二次多项式的系数。本文以300 kW柴油机为例,其中C0=8561,g·h–1;a=114.6,g·kWh–1,b=0.201;g·kW2h–1。
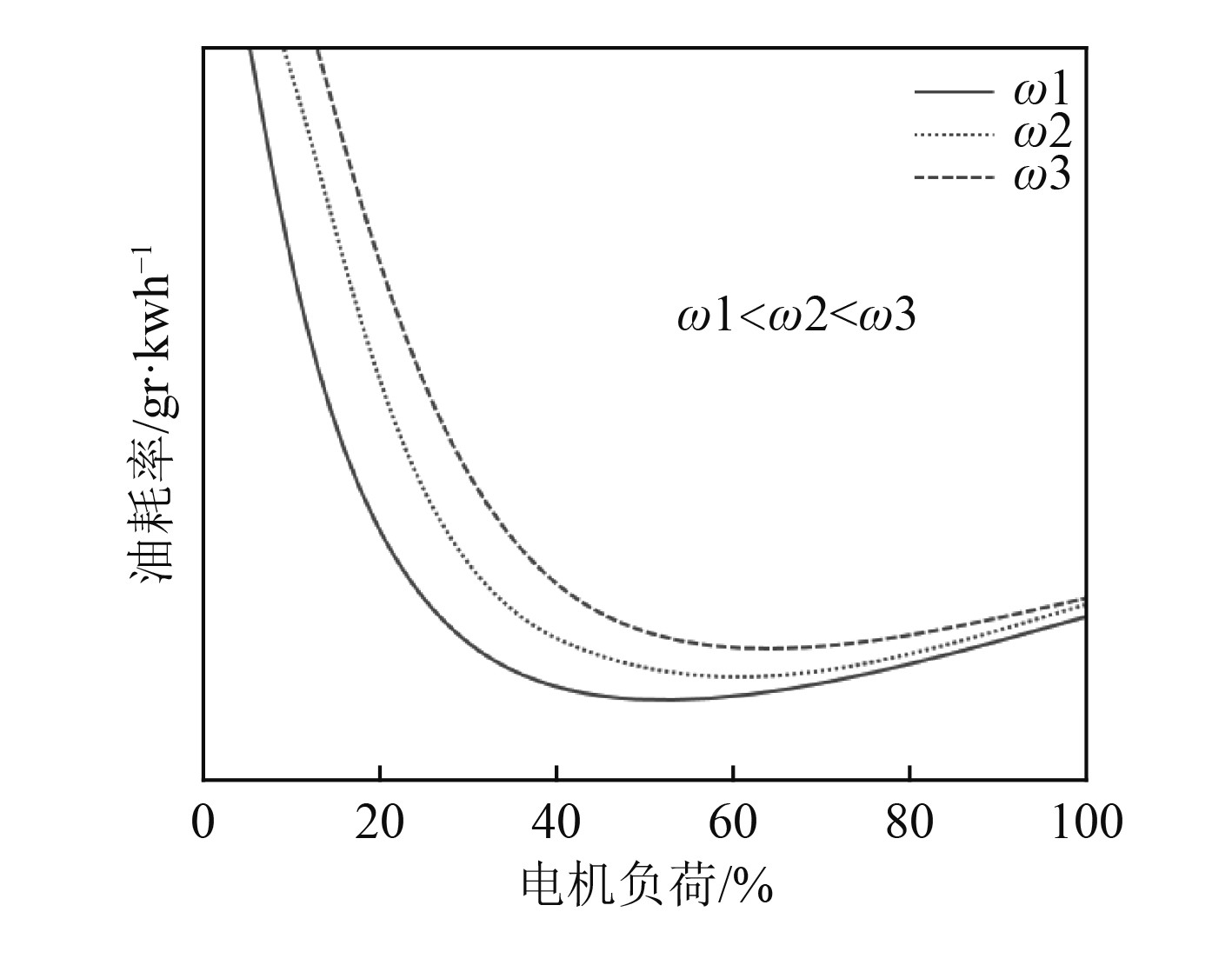
某型号同步发电机组柴油机的油耗率和其发电机负荷的关系如图2所示,最佳油耗率在50%~60%负荷区间。需要说明的是,最佳油耗区间和柴油机型号直接相关,不同柴油机有不同的最佳油耗率曲线。
|
图 2 柴油机油耗率与负荷关系图 Fig. 2 Diesel engine fuel consumption rate and load diagram |
锂电池组等储能设备需要通过DC/DC变换器接入电网,DC/DC变换器的作用是将船舶上的储能设备,如蓄电池组、超级电容等,变为可调控的直流电源,通过PWM技术控制的开关信号完成对直流电源的充放电控制。锂电池组和DC/DC变换器共同构成船舶的储能系统。
为了研究在充放电过程中电力系统的功率损耗,需对DC/DC变换器的功率损耗进行分析。主要包括晶体管的导通和开关损耗,二极管的导通损耗以及电感元件和电容元件的电阻损耗。
DC/DC变换器的工作模式分为升压变换器模式(Boost)和降压变换器模式(Buck),在这2种工作模式下,DC/DC变换器的工作效率几乎相同,均能以等效电阻的形式建立模型,开关损耗和电容、电感等损耗则忽略不计。为便于分析,按照高压侧电压导出损耗计算公式如下[11]:
| ${P_{{\rm{bid,l}}}}{\rm{ = }}{R_{{\rm{bid}}}}I_{{\rm{bid}}}^2 = {R_{{\rm{bid}}}}\frac{{P_{{\rm{bid,h}}}^2}}{{V_{{\rm{bid,h}}}^2}}{\text{。}}$ | (2) |
其中:Rbid为DC/DC的等效电阻;Vbid,h为变换器的高压侧电压。
在研究混合电力推进系统的控制策略时,对锂电池组的外特性表现精准程度需求较低,假定其在规定荷电状态区间工作时,电阻不受温度影响,呈线性变化。对锂电池组建立等效电阻模型。锂电池组的端电压计算公式由式(3)表示,SOC值计算由式(4)推导所得[12]:
| ${V_b}{\rm{ = }}{V_0}{\rm{ + }}{R_{\rm{b}}} \cdot {i_b} - K\frac{Q}{{Q + \int {i({\rm{t}})dt} }} + A \cdot \exp \left( {{\rm{B}}\int {i({\rm{t}})dt} } \right){\text{,}}$ | (3) |
| $SOC = 100\left( {SO{C_{ini}} - \frac{1}{Q}\int_0^t {i(t){\rm{d}}t} } \right){\text{。}}$ | (4) |
其中:Rb为锂电池组内阻;V0为锂电池组两端开路电压;i(t)为锂电池组的开路电流;K为极化电阻;Q为最大电池容量;A为电池电压指数;B为电池容量指数;SOCini为锂电池初始荷电量。
锂电池组的功率损耗可以用和式(2)一样的方法推导得出:
| ${P_{b,l}} = {R_b}I_b^2{\rm{ = }}{R_b}\frac{{P_b^2}}{{V_b^2}}{\text{。}}$ | (5) |
锂电池组和DC/DC变换器在同一支路,即Ib=Ibid,且忽略锂电池组上的压降,可以将公式(5)和公式(2)整理得到锂电池组和DC/DC变换器所在支路的整体功率损耗,即整个储能系统的功率损耗:
| ${P_{{\rm{ess,l}}}} = ({R_{\rm{b}}} + {R_{{\rm{bid}}}})I_{\rm{b}}^2{\rm{ = }}({R_{\rm{b}}} + {R_{{\rm{bid}}}})\frac{{P_{{\rm{bid,h}}}^2}}{{V_{{\rm{bid,h}}}^2}}{\text{。}}$ | (6) |
在整个混合电力系统中,柴油发电机组的功率记为Ps,负载功率为PL、锂电池组经DC/DC变换器吸收或发出功率Pbid,h和储能系统的功率损耗Pess,l,在锂电池组的充电和放电状态下满足的关系分别为:
| ${P_{\rm{s}}} = {P_{\rm{L}}} + {P_{{\rm{ess,l}}}} + {P_{{\rm{bid}}{\rm{.h}}}}{\text{,}}$ | (7) |
| ${P_{\rm{s}}} + {P_{{\rm{bid,h}}}} = {P_{\rm{L}}} + {P_{{\rm{ess,l}}}}{\text{。}}$ | (8) |
因此,将式(6)进行整理,可以得到:
| ${P_{ess,l}}{\rm{ = }}\frac{{({R_b} + {R_{bid}})}}{{V_{bid}^2}}{({P_s} - {P_L})^2}{\text{,}}$ | (9) |
| ${P_{ess,l}}{\rm{ = }}\frac{{({R_b} + {R_{bid}})}}{{V_{bid}^2}}{({P_L} - {P_s})^2}{\text{。}}$ | (10) |
船舶在海上航行时,随着海况发生变化,混合电力推进系统中发电机单元需要不断调整在网发电机组的功率或启停发电机组的数量。在电力系统中引入了储能设备与柴油发电机组配合工作,通过控制储能设备的充放电模式,合理的对船舶负载在储能设备和柴油发电机组间进行分配,即可以在保证系统动力输出的前提下,使发电柴油机一直工作在最佳油耗区间,进而实现降低柴油机油耗率的目的,这就是混合推进系统优化控制的目标。
控制策略设计以储能设备中锂电池组的荷电状态为状态参数,目标对象为船舶柴油发电机组的输出功率和锂电池组的充放电功率。
柴油发电机并网工况下的油耗率曲线如图3所示,n表示在网的柴油发电机总数量。可以看出,若相同型号的一组柴油机并网工作,在网发电机组数量一般由外界负载决定(需要考虑电站的裕度和安全性),但单台机组的输出功率,则需要由所设计的控制策略进行计算得出。

|
图 3 船舶柴油发电机组油耗率曲线 Fig. 3 Specific fuel consumption curve of marine diesel units |
船舶实际航行中,因海况变化,推进功率会发生一定的波动,甚至有时会出现瞬时较大幅度的增大或减小现象,这会引起船舶电站的瞬态调整动作。若控制动作不及时,则会导致船舶电网电压大幅度波动,严重时会危害到电网的安全性。同时,频繁的调整动作会造成船舶发电柴油机的工况不稳定现象,不但影响其运行经济性,而且对柴油机寿命也带来一定的损害。增加了锂电池组后,外界负载的功率变化可以由锂电池组承担,外界负载瞬时增高时,所增加的部分通过控制锂电池组发电来补充。同样,当外界负载瞬时减小时,通过控制锂电池组充电吸收发电机组所发出的剩余功率。
此外,锂电池组在和柴油发电机共同工作时,可以根据自身工作特点完成对柴油发电机工作点的优化,以达到降低燃料消耗的目的。因此需要对锂电池组的充放电模式进行合理控制,以使锂电池可以充分发挥自身在降低燃料消耗方面的作用。为了更合理地将船舶负载功率在锂电池组和柴油发电机组之间分配,船舶负载功率PL(t)分为负载功率平均值PLa和负载功率波动值
| $\alpha = \frac{{{P_{\rm{s}}}\left( t \right) - {P_{{\rm{s}}a}}}}{{({P_{\rm{L}}}\left( t \right) - {P_{{\rm{L}}a}})}}{\text{。}}$ | (11) |
其中,α =1时,此时锂电池组不工作,负载需求功率完全由发电机组提供。0
图4中,2条曲线分别为有n和n+1台柴油发电组在网工作时的油耗率曲线。假设在某一时刻,发电机组在点A的负载功率下工作,此时的负载功率为PL(t)。若此时检测到锂电池组的荷电状态SOC在90%以上,即可认为锂电池组电量充足,可以和柴油发电机组共同为船舶负载提供能量,通过控制DC/DC变换器将锂电池组调整为放电模式,将其接入电网,使柴油发电机组的工作点从A向B'点迁移。由对应纵坐标的SFC值可以看出,柴油发电机组的燃油消耗率较原先得到降低。

|
图 4 优化策略分析 Fig. 4 Optimization strategy analysis |
若检测到锂电池组的SOC值低于30%,则可认为其无法协助柴油发电机组共同为船舶负载提供能量,想要继续发挥锂电池组在优化油耗方面的作用,锂电池组则需进行充电,即从发电设备转换为负载设备。需要注意的是,此时的船舶需求负载功率应以原本的船舶负载功率加上锂电池充电功率之和计算,由船舶电站PMS决定是否另外启动一台柴油发电机进行并网供电。本文所用船舶模型中,在锂电池组的充电状态下,柴油发电机组在网台数为n+1。以柴油发电机组的工作点在燃油消耗率的最佳值附近为约束,确定n+1台柴油发电机组的工作点在图4的B点附近,此时柴油发电机组在最佳工况点附近工作,同时能够为锂电池组充电。控制策略程序设计流程图如图5所示,其中SOC_flag的初始值设为0。

|
图 5 控制策略流程图 Fig. 5 Control strategy process |
根据前面给出的各模块功率损耗模型,对船舶在运行过程中的油耗进行计算,研究船舶负载功率和油耗的关系。通过与未引入控制策略的油耗率对比探讨所研究控制策略的可行性和优化效果。
3.1 计算控制策略结果根据式(1),由于引入了控制策略之后,某一确定负载下的柴油发电机组的功率依据锂电池组的荷电状态被分为充电环节和放电环节,可以得到[13]:
| $\small\begin{split} SFC(t) =& {{\rm{C}}_{0,n + 1}}({{\rm{T}}_{{{ch}}}} + {{\rm{T}}_{{{dis}}}}) + {a_{n + 1}}(\int_{{T_{{\rm{ch}}}}} {{P_{s,n + 1}}(t){\rm{d}}t + \int_{{T_{{\rm{dis}}}}} {{P_{s,n}}(t){\rm{d}}t)} } + \\ &{{\rm{b}}_{n + 1}}(\int_{{T_{{\rm{ch}}}}} {{P^2}_{s,n + 1}(t){\rm{d}}t + \int_{{T_{{\rm{dis}}}}} {{P^2}_{s,n}(t){\rm{d}}t} }{\text{,}}\\[-15pt] \end{split} $ | (12) |
由第1节中混合电力推进系统各模块的功率损耗模型,可以将式(12)转换为:
| $\small\begin{split} &SFC({\rm{t}}) = {C_{0,n + 1}}{D_s} + {C_{0,n}}{{D'}_s} + a{P_{La}}+\\ & \quad a{D_{\rm{s}}}\frac{{({R_b} + {R_{bid}})}}{{V_{bid}^2}}[{({P_{sa,n + 1}} - {P_{La}})^2} + R_{eq}^2{(1 - {\alpha _{n + 1}})^2}]+\\ & \quad a{{D'}_s}\frac{{({R_b} + {R_{bid}})}}{{V_{bid}^2}}[{({P_{sa,n}} - {P_{La}})^2} + R_{eq}^2{(1 - {\alpha _n})^2}]+\\ & \quad {b_{n + 1}}{D_s}(P_{sa,n + 1}^2 + \alpha _{n + 1}^2R_{eq}^2) + {b_n}{{D'}_s}(P_{sa,n}^2 + \alpha _n^2R_{eq}^2){\text{,}} \end{split}$ | (13) |
其中,
| $ \begin{split} {{\rm{D}}_{\rm{s}}} =& \frac{{{P_{La}} - {P_{sa,n}} + \frac{{({R_b} + {R_{bid}})}}{{V_{bid}^2}}[{{({P_{sa,n}} - {P_{La}})}^2} + R_{eq}^2{{(1 - {\alpha _n})}^2}]}}{ {P_{sa,n + 1}} - {P_{sa,n}} - \frac{{({R_b} + {R_{bid}})}}{{V_{bid}^2}}[({P_{sa,n + 1}} - {P_{sa,n}})({P_{sa,n + 1}} + {P_{sa,n}} - {\rm{2}}PLa)}+\\ &R_{eq}^2({\alpha _{n + 1}} - {\alpha _n})({\alpha _{n + 1}} + {\alpha _n} - {\rm{2}})] {\text{。}}\\[-10pt] \end{split} $ | (14) |
其中,C0,n+1,C0,n,a,bn,bn+1分别为柴油机开启台数为n和n+1时的油耗曲线的各项系数,
一个充放电周期的总时间设定为T,为方便计算负载波动,用负载功率在总时间T上的均方差等效表示负载波动,PL(t)为船舶负载功率,PLa为负载功率平均值,定义等效负载波动Req如下:
| ${R_{\rm{eq}}} = \sqrt {\frac{1}{T}\int\limits_T {{{({P_L}({\rm{t}}) - {P_{La}})}^2}} {\rm{d}}t} {\text{。}}$ | (15) |
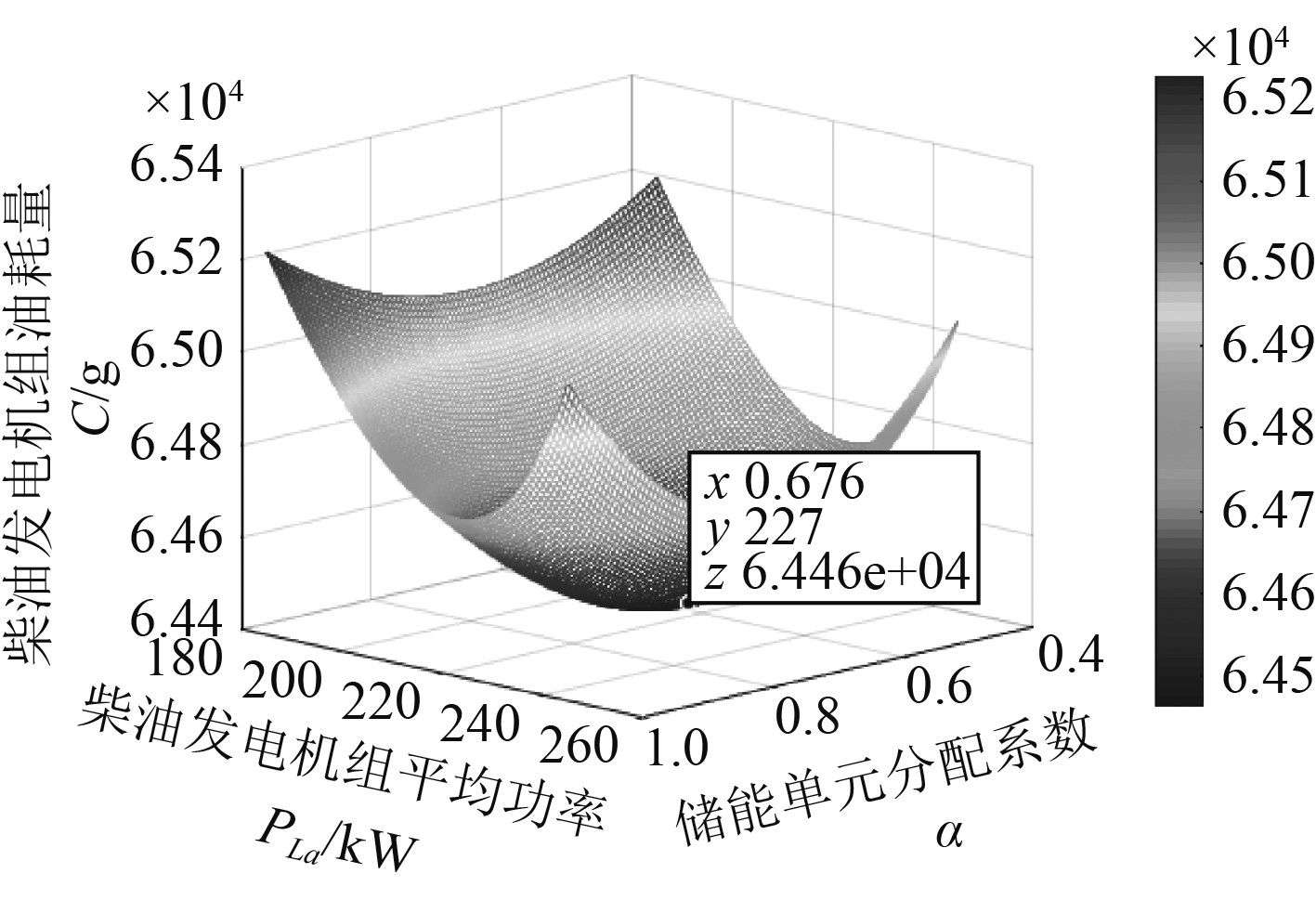
由第2节设计的控制策略,当船舶锂电池组满足辅助柴油发电机组工作条件时,在网工作的发电机组数为
|
图 6 n台在网柴油机燃油消耗关系图 Fig. 6 Fuel consumption relationship of multiple diesel engines. |
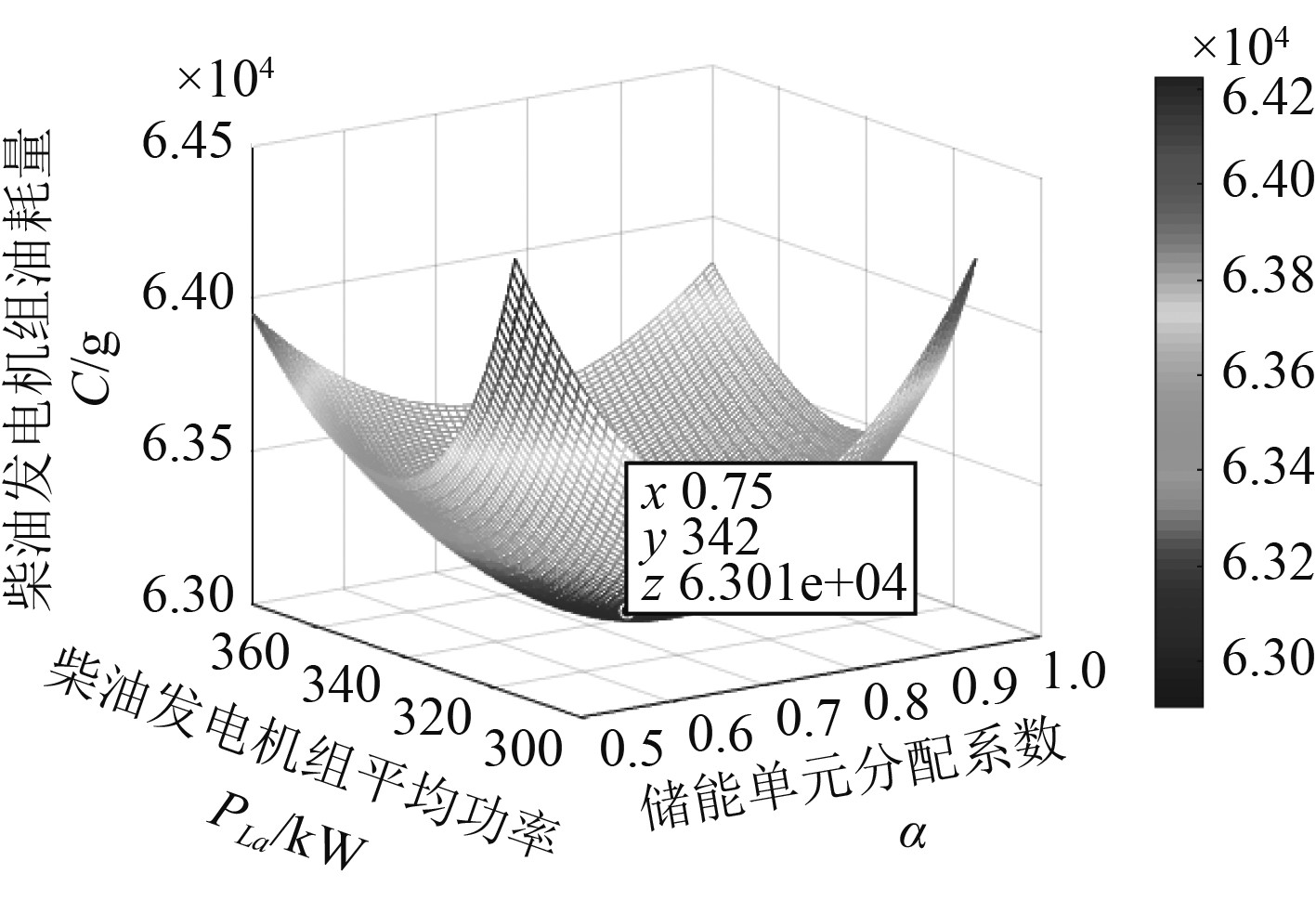
应用智能优化方法可以快速搜索到油耗的最小值SFCmin,n和其对应的Psa,n与αn。同样,可以得到锂电池组中的能量不能够满足辅助柴油发电机组工作时的计算结果,即需要增加1台在网柴油发电机的情况,计算结果如图7所示,求得此时油耗最小值SFCmin,n+1和其对应的Psa,n+1与αn+1。
|
图 7 n+1台在网柴油机燃油消耗关系图 Fig. 7 Fuel consumption relationship of multiple diesel engines |
应用Matlab进行优化控制策略结果的仿真验证。鉴于多数混合电力推进船舶为短途往返运输船,因此选择某海洋平台多功能支持船作为仿真对象,运输航行工况下的负载功率曲线如图8所示。
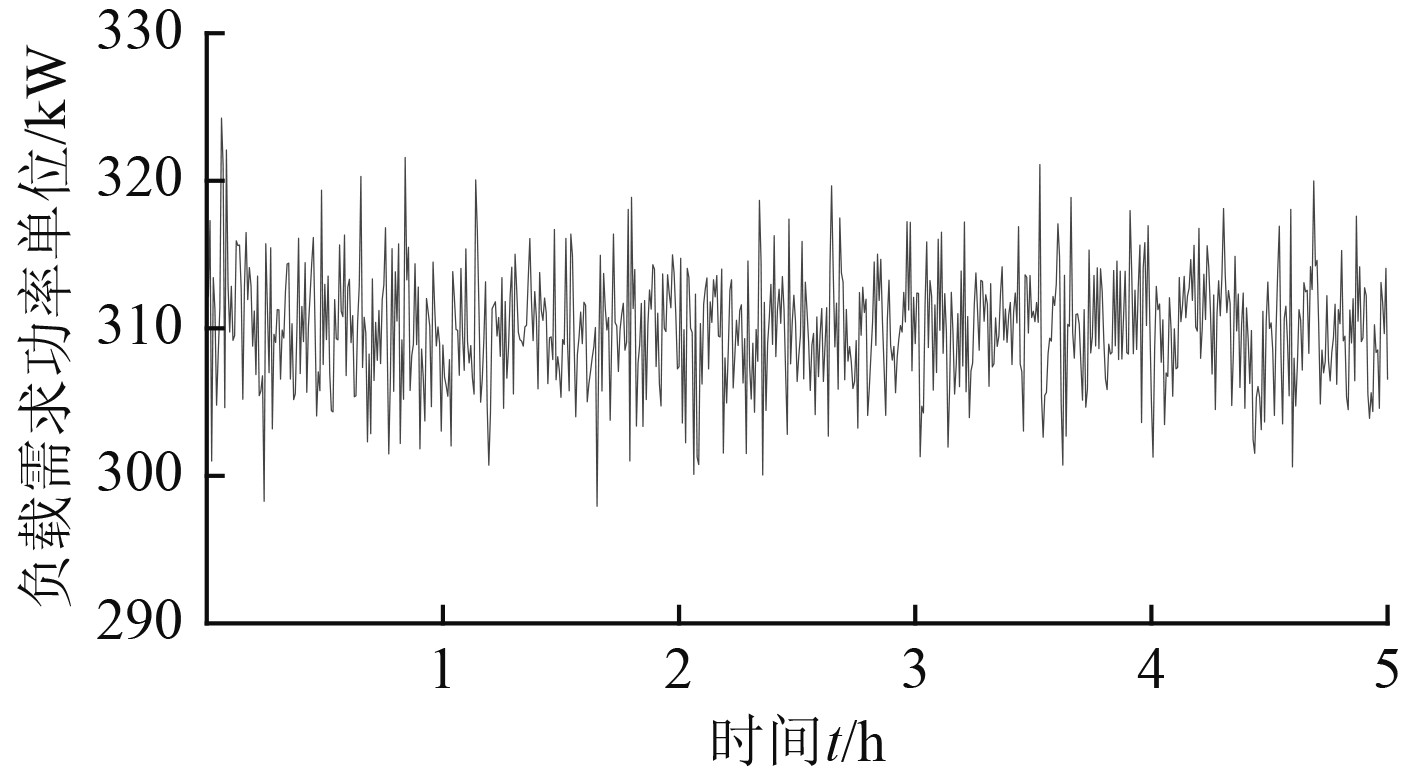
|
图 8 运输航行工况下负载功率曲线 Fig. 8 Load power curve under transport sailing conditions |
图9为加入本文所提出控制策略后的仿真结果。可以看出,随着对锂电池组的充放电控制,锂电池的荷电状态在设置的区间内变化。根据控制策略,对锂电池组充电时一般为多机并网供电模式,电池组放电时,和柴油发电机组共同为负载提供能量,在整个过程中,柴油发电机组都能够工作在其最佳工况点附近。
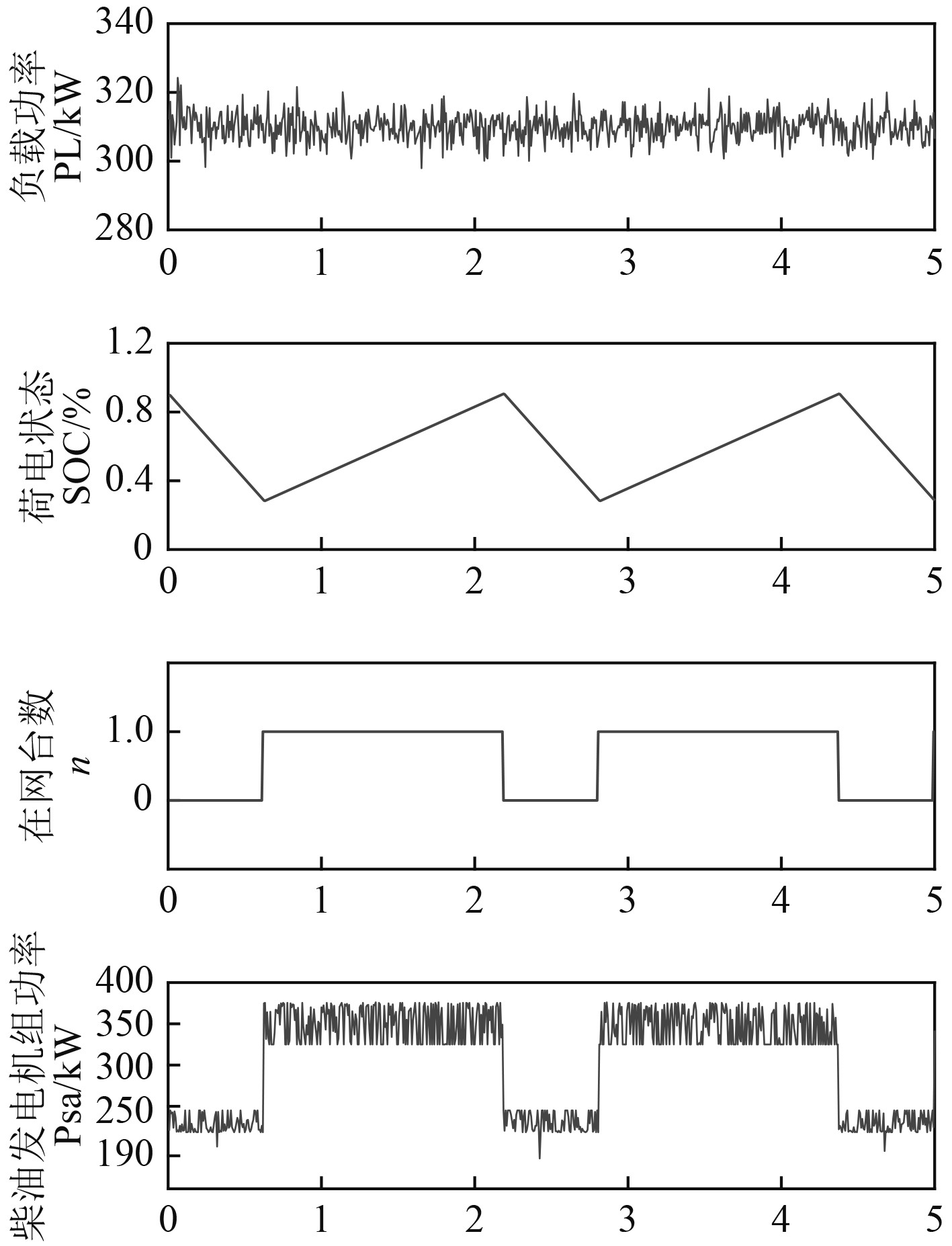
|
图 9 引入锂电池组与控制策略的仿真结果 Fig. 9 Simulation results of introducing lithium battery packs and control strategies |
图10为加入锂电池组并采用本文提出的控制策略与未引入锂电池组的燃油消耗率对比。由同一运行工况下的仿真对比可以看出,采用本文所提出方法,船舶动力系统的平均燃油消耗率在199 g/kWh附近,比不引入锂电池组的205 g/kWh有所降低。设定时长为5 h的仿真计算,总共节省的燃油量为119.37 kg,合计约为3%的节油量(见图11)。随着船舶运行时间的增长及海况变化,或者船舶电站输出功率的频繁变化,采用本文提出的方法在燃油消耗降低方面会有更明显的效果。
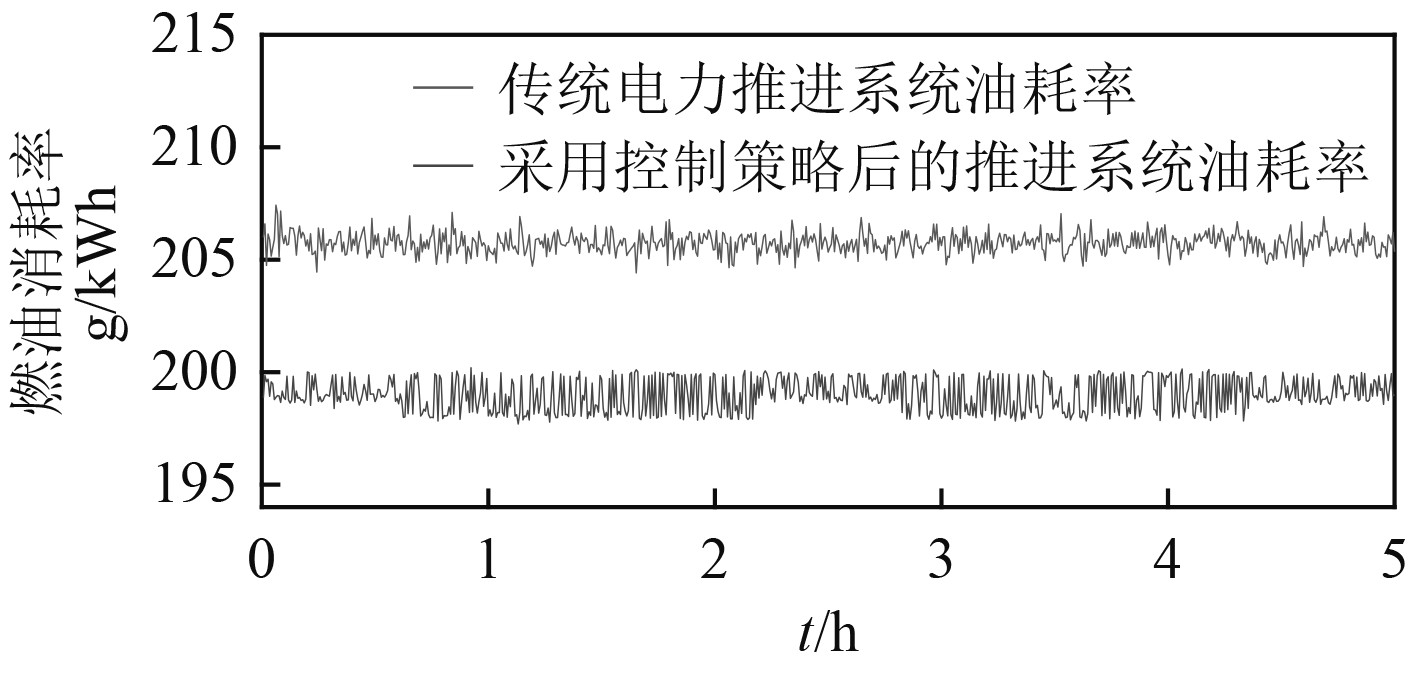
|
图 10 引入锂电池组与控制策略前后燃油消耗率对比 Fig. 10 Comparison of fuel consumption rate before and after introduction of lithium battery pack and control strategy |
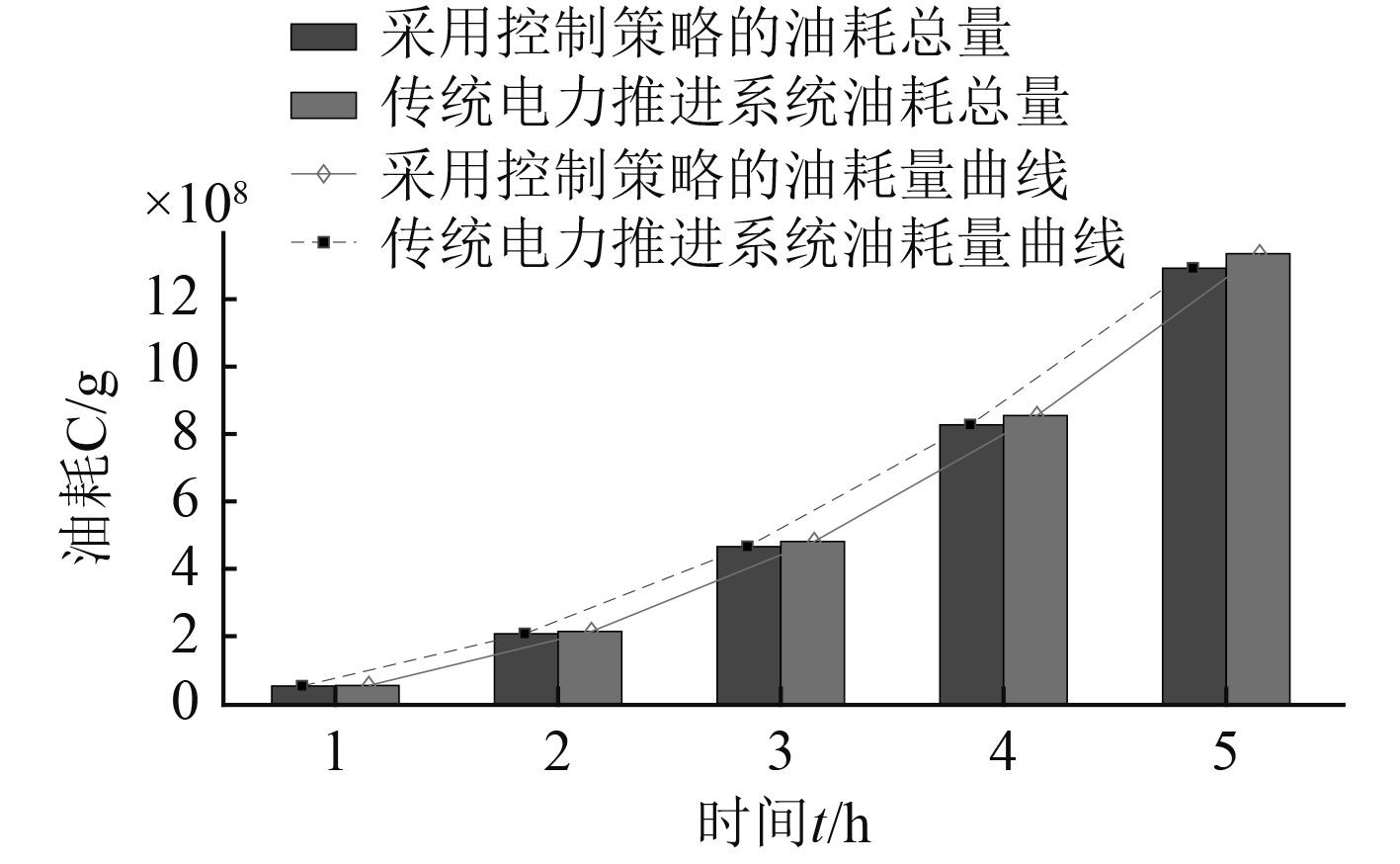
|
图 11 引入锂电池组与控制策略前后燃油消耗率总量对比 Fig. 11 Comparison of fuel consumption before and after introduction of lithium battery pack and control strategy |
本文通过将锂电池组引入传统电力推进船舶,构成一种新型混合电力推进船舶结构,通过DC/DC变换器将柴油发电机组发出的多余能量储存在锂电池组中。根据混合电力推进船舶的工作特性,提出一种锂电池组和柴油发电机组协调工作的优化控制策略,可以有效节省船舶运行期间的燃油消耗量,提高船舶能效。对海洋平台多功能支持船的仿真实验对比分析,验证了所提出的控制策略能够在运营期间节省约3%的燃料消耗。
| [1] |
GEERTSMA R D, NEGENBORN R R, VISSER K, et al. Design and control of hybrid power and propulsion systems for smart ships: A review of developments[J]. Applied Energy, 2017, 194: 30-54. DOI:10.1016/j.apenergy.2017.02.060 |
| [2] |
廖鹏飞, 周瑞平, 李江. 冰区船舶电力推进轴系瞬态扭振计算研究[J]. 推进技术, 2018, 39(8): 1889-1896. |
| [3] |
DEDES E K, HUDSON D A, TURNOCK S R. Assessing the potential of hybrid energy technology to reduce exhaust emissions from global shipping[J]. Energy Policy, 2012, 40(none): 204-218. |
| [4] |
HOU J, SUN J, HOFMANN H F. Mitigating power fluctuations in electric ship propulsion with hybrid energy storage system: design and analysis[J]. IEEE Journal of Oceanic Engineering, 2017, 1-15. |
| [5] |
杨祥国, 孙盼, 杨诚, 等. 电力推进船舶复合储能装置容量多目标优化[J]. 中国航海, 2018, 41(02): 9-14. DOI:10.3969/j.issn.1000-4653.2018.02.003 |
| [6] |
ZAHEDI B, NORUM L E. Modeling and simulation of all-electric ships with low-voltage DC hybrid power systems[J]. IEEE transactions on power electronics, 2013, 28(10): 4525-4537. DOI:10.1109/TPEL.2012.2231884 |
| [7] |
SOLEYMANI M, YOOSOFI A, KANDI-D M. Sizing and energy management of a medium hybrid electric boat[J]. Journal of marine science & technology, 2015, 20(4): 739-751. |
| [8] |
KANELLOS F D, TSEKOURAS G J, HATZIARGYRIOU N D. Optimal demand-side management and power generation scheduling in an all-electric ship[J]. Sustainable Energy, IEEE Transactions on, 2014, 5(4): 1166-1175. DOI:10.1109/TSTE.2014.2336973 |
| [9] |
袁裕鹏, 王凯, 严新平. 混合动力船舶能量管理控制策略设计与仿真[J]. 船海工程, 2015(02): 103-106. |
| [10] |
WANG K, YAN X, YUAN Y, et al. Real-time optimization of ship energy efficiency based on the prediction technology of working condition[J]. Transportation research part D: transport and environment, 2016, 46: 81-93. DOI:10.1016/j.trd.2016.03.014 |
| [11] |
KAZIMIERCZUK M K. Pulse-width modulated DC-DC power converters[M]. John Wiley & Sons, 2015.
|
| [12] |
OLIVIER T, LOUIS-A. D. Experimental validation of a battery dynamic model for EV applications[J]. World Electric Vehicle Journal, 2009, 3(2): 289-298. DOI:10.3390/wevj3020289 |
| [13] |
BARSALI S, MIULLI C, POSSENTI A. A control strategy to minimize fuel consumption of series hybrid electric vehicles[J]. IEEE transactions on energy conversion, 2004, 19(1): 187-195. DOI:10.1109/TEC.2003.821862 |
 2020, Vol. 42
2020, Vol. 42
