2. 上海交通大学 船舶海洋与建筑工程学院,上海 200240;
3. 阿哥德大学工程科学系,挪威
2. School of Naval Architecture, Ocean and Civil Engineering in Shanghai Jiaotong University, Shanghai 200240, China;
3. Department of Engineering Sciences in University of Agder, Norway
为了应对能源短缺和全球变暖,寻求可再生能源替代化石燃料已成为全球能源战略主要趋势。风能是目前能源市场发展的主要清洁可再生能源,海上风能更因其储量丰富,对陆上活动影响较小,正呈现蓬勃发展趋势。随着其由近岸逐步向深海开发发展,对各类大型浮式海上风机的关键问题研究已成为海上风电技术发展的重点关注领域
要设计包括海上风机(OWT)在内的任何类型海上结构,估算给定重现周期(例如50年或20年一遇)的结构长期极端响应或载荷是重要的一步[1-3]。完全长期分析法(FLTA)被认为是评估海洋结构物极端荷载下响应的最精确方法。但是,FLTA方法非常耗时,因为它考虑了所有的环境工况,而实际上只有少数几个环境工况对结构的响应有主要贡献。Sverre Haver[2]提出的环境等值线法(ECM),作为分析结构响应的一种简化方法被逐渐广泛用于确定海洋结构的最终设计载荷。该方法在预测包括波浪载荷在内的极值预报上被证明是相对准确的,同时可以节省大量的计算时间。环境等值线法基于反向一阶可靠度法(IFORM),该方法将环境变量与结构响应分离,响应通过所取的环境工况计算得到[4-6]。目前Monte Carlo模拟法也被提出并用来得到环境等值线[7]。ECM的第1步需要推导由环境变量(例如风速,波高和谱峰周期)所构成的环境等值面。只需要对等值表面上的选定点执行响应计算即可,从而提高了效率。
然而,在以往的环境等值线法的应用中并没有严格考虑湍流强度的影响,即没有将湍流强度作为环境变量进行考虑,或是直接将湍流强度假定为一个确定的值。通常在该方法的使用中,所考虑的环境变量只有风速(Uw),有义波高(
本文基于采用Spar浮式基础的NREL 5 MW风机模型,使用FAST v8[13]研究了风湍流对极限载荷的影响,该模型调用由Turbsim软件生成的各种湍流风文件[14]。以风的实测数据[9]为基础,根据风速的标准偏差将湍流强度作为随机环境变量加入环境等值线法中,该标准偏差由三参数威布尔概率密度函数拟合。采用概率方法得到将风速、有义波高、谱峰周期以及湍流强度考虑在内的环境等值线。通过考虑湍流强度变化的环境等值线法与未考虑湍流强度变化的环境等值线法对Spar型风机各极端响应的预报结果对比,探究湍流强度对极端响应的影响。
1 湍流强度的理论考虑湍流强度定义为风速的标准偏差除以平均风速。标准偏差
Larsen[9]通过拟合Vindeby和Gedser两个浅水点的近海风气候数据,选择使用三参数威布尔分布拟合2个浅站点的近海风气候测量数据表达式,并给出了3个参数值,如下式:
| $ f\left( {\sigma \text{,} k,\alpha ,\beta } \right) = \frac{k}{\beta }{\left( {\frac{{\sigma - \alpha }}{\beta }} \right)^{k - 1}}\text{,}{\rm{exp}}[ - {\left( {\frac{{\sigma - \alpha }}{\beta }} \right)^k}]\;\;\sigma \mathop = \limits^ {>} \alpha \text{。} $ | (1) |
其中:
表1给出了不同风速下3个参数的数值。其中
| $U\left(z\right)={U}_{C}\left(\frac{z}{30}\right)^{a}\text{。}$ | (2) |
环境等值线法的原理是在所求
| ${F_{1 - hr,N - yr}}\left( \xi \right) \approx F_{{X_{1 - hr|{\rm{Uw}},{\rm{TI}},{\rm{Hs}},{\rm{Tp}}}}}^{ST}\left( {\xi |{u_N},t{i_N},{h_N},{t_N}} \right)\text{。}$ | (3) |
其中,uN,tiN,hN,tN为导致在N年一遇的环境等值面上产生最大的极端响应的环境条件。
2.1 获取Li等[15]给出了欧洲5个近海点10 m高度(
| ${f_{{U_W}}}\left( u \right) = \frac{{{\alpha _U}}}{{{\beta _U}}}{\left( {\frac{u}{{{\beta _U}}}} \right)^{{\alpha _U} - 1}}{\rm{exp}}\left[ - {\left( {\frac{u}{{{\beta _U}}}} \right)^{{\alpha _U}}}\right]\text{。}$ | (4) |
其中:
| ${f_{{H_S}|{U_W}}}\left( {h|u} \right) = \frac{{{\alpha _{HC}}}}{{{\beta _{HC}}}}{\left( {\frac{h}{{{\beta _{HC}}}}} \right)^{{\alpha _{HC}} - 1}}{\rm{exp}}\left[ - {\left( {\frac{h}{{{\beta _H}}}} \right)^{{\alpha _{HC}}}}\right]\text{。}$ | (5) |
其中:
| $ \begin{split} &{\alpha _{HC}} = {a_1} + {a_2}{u^{{a_3}}}\text{,}\\ &{\beta _{HC}} = {b_1} + {b_2}{u^{{b_3}}}\text{。} \end{split} $ | (6) |
通过与原始数据拟合来获取其中的
| $ \begin{split} &{f_{{T_P}|{U_W},{H_S}}}\left( {t|u,h} \right) = \frac{1}{{\sqrt {2\pi } {\sigma _{{\rm{ln}}\left( {{T_P}} \right)}}t}}{\rm{exp}}\left( - \frac{1}{2}{\left( {\frac{{{\rm{ln}}\left( t \right) - {\mu _{{\rm{ln}}\left( {{T_P}} \right)}}}}{{{\sigma _{{\rm{ln}}\left( {{T_P}} \right)}}}}} \right)^2}\right)\text{,}\\ & {\mu _{{\rm{ln}}\left( {{T_P}} \right)}} = {\rm{ln}}\left[ {\frac{{{\mu _{{T_P}}}}}{{\sqrt {1 + \nu _{{T_P}}^2} }}} \right],\sigma _{{\rm{ln}}\left( {{T_P}} \right)}^2 = {\rm{ln}}\left[1 + \nu _{{T_P}}^2\right],{\nu _{{T_P}}} = \frac{{{\sigma _{{T_P}}}}}{{{\mu _{{T_P}}}}}\text{。} \end{split} $ | (7) |
其中:
| $ \begin{split} &\mathop {{T_P}}\limits^ - \left( h \right) = {e_1} + {e_2}{h^{{e_3}}}\text{,}\\ &\mathop u\limits^ - \left( h \right) = {f_1} + {f_2}{h^{{f_3}}}\text{。} \end{split} $ | (8) |
其中:
| $ {\nu }_{{T}_{P}}\left(h\right)={k}_{1}+{k}_{2}{exp}^{\left(h{k}_{3}\right)}\text{,} $ | (9) |
其中
| ${f}_{{U}_{W},{H}_{S},{T}_{P}}\left(u,h,t\right)\approx {f}_{{U}_{W}}\left(u\right) \cdot {f}_{{H}_{S}|{U}_{W}}\left(h|u\right) \cdot {f}_{{T}_{P}|{U}_{W},{H}_{S}}\left(t|u,h\right)\text{。}$ | (10) |
假设湍流强度独立于
| $\begin{split} &{f}_{{U}_{W},{TI, H}_{S},{T}_{P}}\left(u,ti,h,t\right)\approx {f}_{{U}_{W}}\left(u\right) \text{,} \\ & {f}_{{T}_{I}|{U}_{W}}\left(ti|u\right) \text{,}\\ & {f}_{{H}_{S}|{U}_{W}}\left(h|u\right) \text{,} \\ & {f}_{{T}_{P}|{U}_{W},{H}_{S}}\left(t|u,h\right)\text{。}\end{split}$ | (11) |
用Rosenblatt变换[16]将相关的环境变量
| $ \begin{split} &\varPhi \left( {{u_1}} \right) = {F_{{U_W}}}\left( u \right)\text{,}\\ &\varPhi\left( {{u_2}} \right) = {F_{{H_S}|{U_W}}}(h|u)\text{,}\\ &\varPhi\left( {{u_3}} \right) = {F_{{T_P}|{U_W},{H_S}}}\left( {t|u,h} \right)\text{,}\\ &\varPhi \left( {{u_4}} \right) = {F_{\sigma |{U_W}}}\left( {\sigma |u} \right)\text{。} \end{split} $ | (12) |
其中:
| $ \begin{split} & {F_{{U_W}}}\left( u \right) = \int {{f_{{U_W}}}} \left( u \right){\rm{d}}u \text{,}\\ & {F_{{H_S}|{U_W}}}\left( {h|u} \right) = \frac{{\int {{f_{{U_{W,{H_S}}}}}} \left( {u,h} \right){\rm{d}}h}}{{{f_{{U_W}}}\left( u \right)}} = \int {{f_{{H_S}|{U_W}}}} \left( {h|u} \right){\rm{d}}h\text{,}\\ & {F_{{T_P}|{U_W},{H_S}}}\left( {t|u,h} \right) = \frac{{\int {{f_{{U_{W,{H_S}}},{T_P}}}} \left( {u,h,t} \right){\rm{d}}t}}{{{f_{{U_W},{H_S}}}\left( {u,h} \right)}} = \\ & \int {{f_{{T_P}|{U_W},{H_S}}}} \left( {t|u,h} \right){\rm{d}}t\text{,}\\ & {F_{\sigma |{U_W}}}\left( {\sigma |u} \right) = \frac{{\int {{f_{{U_W},\sigma }}} \left( {u,\sigma } \right){\rm{d}}ti}}{{{f_{{U_W}}}\left( u \right)}} = \int {{f_{\sigma |{U_W}}}} \left( {\sigma |u} \right){\rm{d}}\sigma \text{。} \end{split} $ |
因此:
| $ \begin{split} & u = F_U^{ - 1}\left[ {\Phi \left( {{u_1}} \right)} \right]\text{,}\\ & h = F_h^{ - 1}[\Phi \left( {{u_2}} \right)|u]\text{,}\\ & t= F_t^{ - 1}[\Phi \left( {{u_3}} \right)|u,h]\text{,}\\ & ti = F_\sigma ^{ - 1}\left[ {\Phi \left( {{u_4}} \right)|u} \right]/u\text{。} \end{split} $ | (13) |
50年一遇的环境等值面可以通过解决一个可靠性问题得到。将每隔1 h时间间隔作为一个独立的单位,50年内1 h的数量为503 652 524个。失效概率为:
| $ {P}_{f}=\frac{1}{503\;652\;524}\text{。} $ | (14) |
对于标准正态变量,它们具有旋转对称性。由于可以显示的最大维度空间是三维的,因此应选择不同的环境变量组合以完全展示4个环境变量所对应的转换。对于考虑3个变量的等值表面,失效概率对应于半径为r的极限状态球面。图1为U空间中的极限状态面。
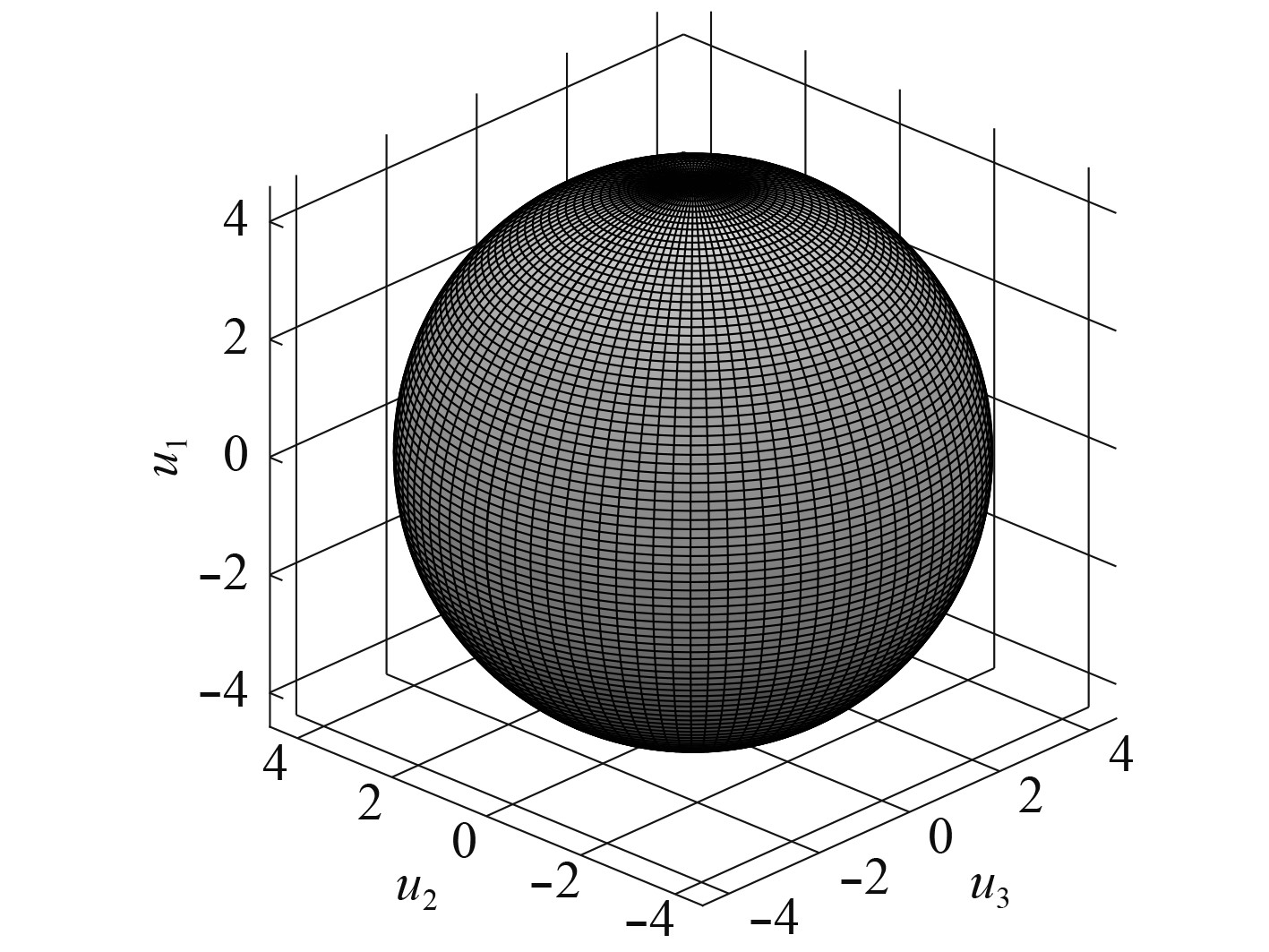
|
图 1 U空间中的极限面图 Fig. 1 Limit state surface in U space |
| $ \varPhi \left( {{r}} \right) = 1 - P_f\text{。} $ | (15) |
在U空间中半径为r的球体可以转换为物理空间中的极限状态曲面(见图2)。图2(a)表示物理空间中考虑到
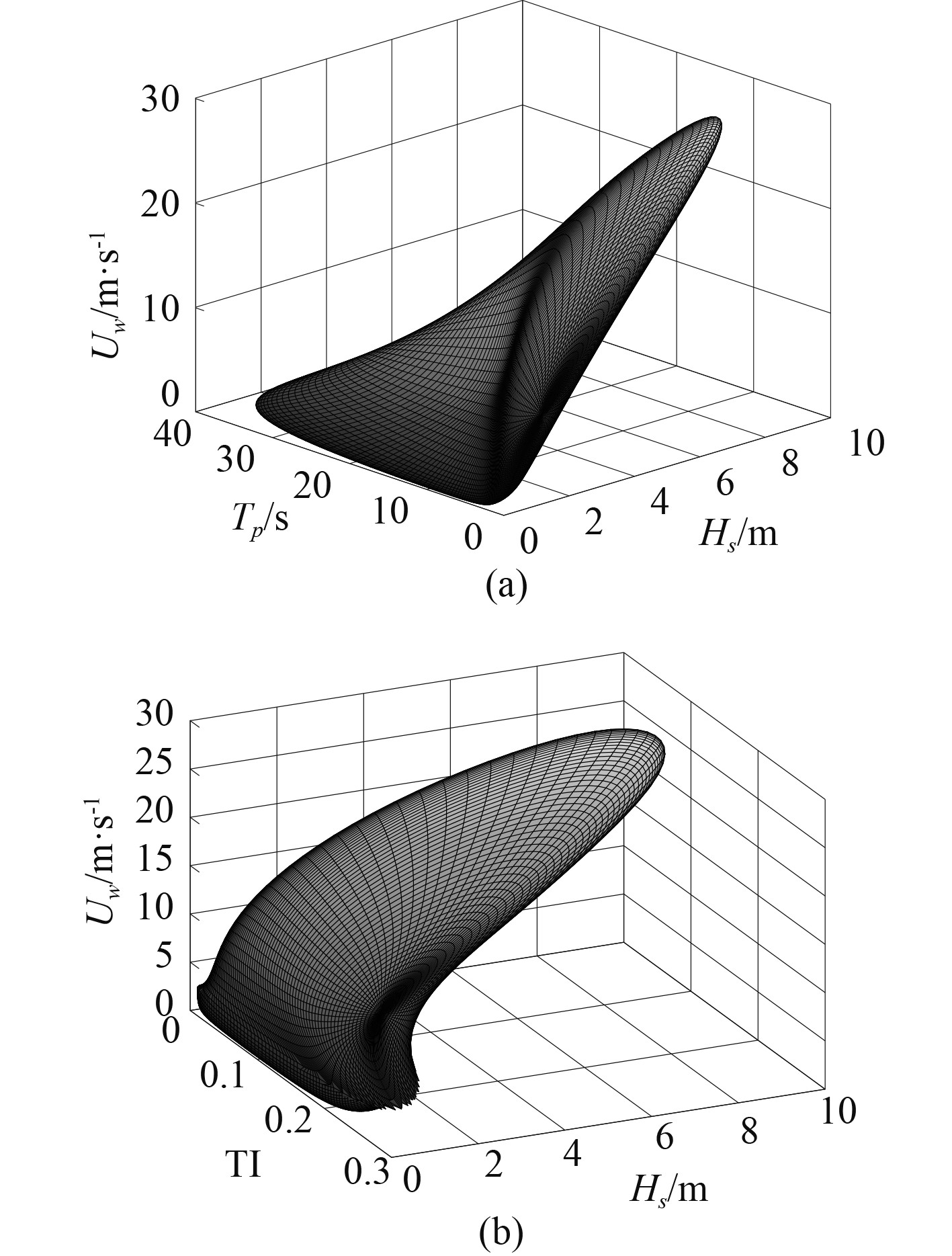
|
图 2 物理空间中的极限状态曲面 Fig. 2 Limit state surface in physical space |
本文选取由美国国家新能源实验室的Jonkman等开发的NREL 5MW基准风机[17]作为研究对象,在各种不同的子结构和基础形式中选择OC3-Hywind的Spar型浮体支撑结构,基本参数如表2所示。用该实验室开发的FAST程序对浮式风机的塔底,锚链等重要结构的载荷以及平台的纵摇角等整体响应进行研究分析。
|
|
表 2 基本参数 Tab.2 Basic parameters |
图3为2种工况下浮式风机4种响应的时历对比图。工况1为风浪联合工况,风速为21 m/s,海况取该风速下最可能出现的海况。工况2为仅在风速为21 m/s作用的工况。对于每种环境工况组合,都给20个随机种子进行4000 s模拟。在后处理过程中去除了前400 s的启动瞬变。假设对于每个环境工况下20个随机种子对应的20个极端响应服从于Gumbel分布,用Gumbel分布的最可能值μ表示此环境工况最可能的极端响应值。
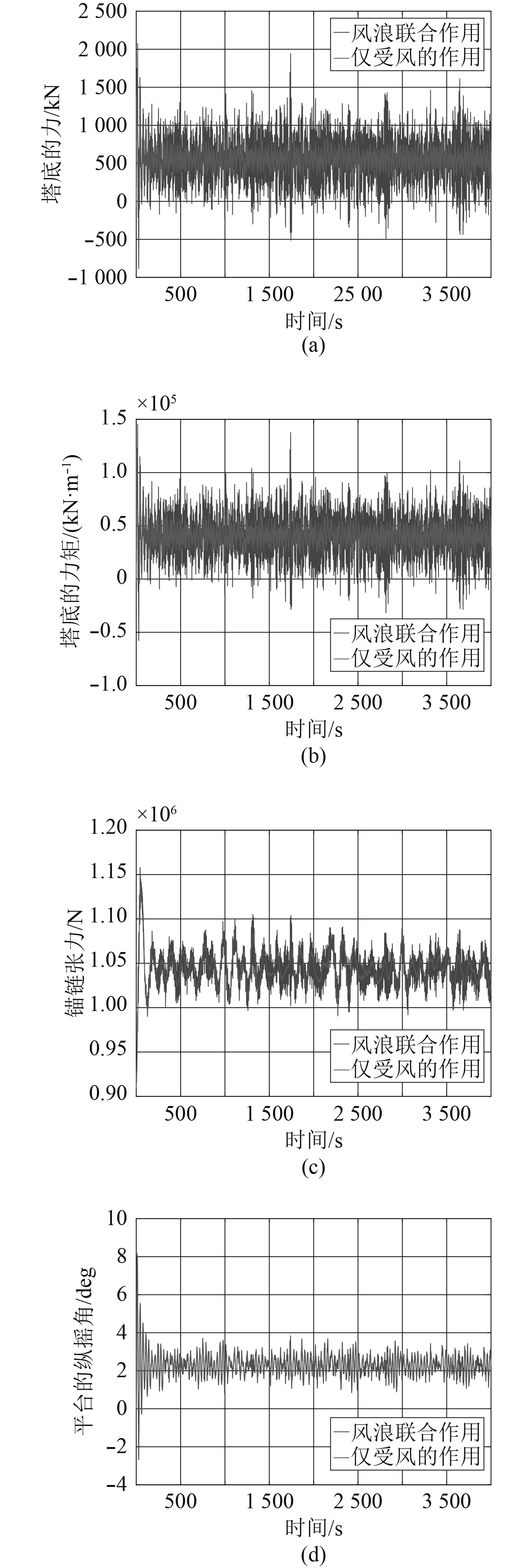
|
图 3 在风浪联合作用下与仅在风作用下各响应的时间历程对比图 Fig. 3 Comparison of the time history of each response |
| $F\left(x\right)={e}^{-{e}^{-(x-\mu )/\beta }}\text{。}$ | (16) |
从图3可以看出,对于塔底的力与力矩而言,波浪力占主导力。而风产生的作用力在锚链张力和平台纵摇角上占主导作用。
为了使ECM方法更准确高效地找到各响应的极值点,可以通过对各风速下选取最可能的湍流强度与波浪条件进行模拟得到各响应最有可能的1-h极值初步判断极值可能出现的位置,如图4所示。根据图4各响应的1-h极值分布中的峰值点,找到所对应的峰值风速,做出该风速下
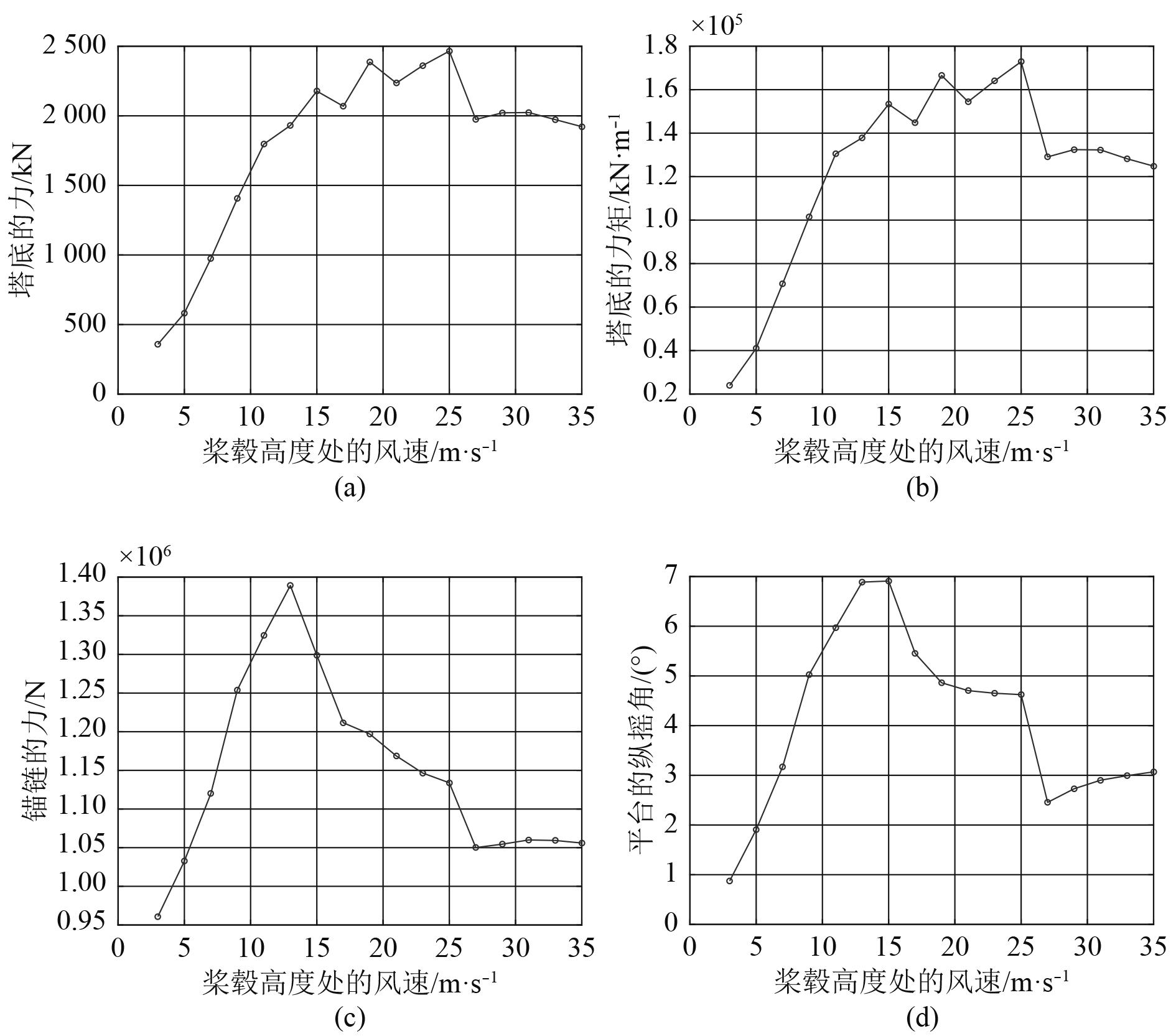
|
图 4 各响应最可能的1-h极值分布 Fig. 4 Most probable 1-h short-term extreme responses under different wind speeds |
本文用环境等值线法对Spar型浮式风机50年一遇的极端响应进行预报,并通过将考虑
由图4可以看出,对于塔底的力、力矩而言,其极端响应的极值出现在风速为15 m/s,19 m/s与25 m/s。平台纵摇角的极端响应极值出现在风速为13 m/s与15 m/s。对于锚链的力而言,其极端响应的极值出现在风速为13 m/s。因此对于这些可能会引起极端响应的极值点所对应的风速附近,绘制多条
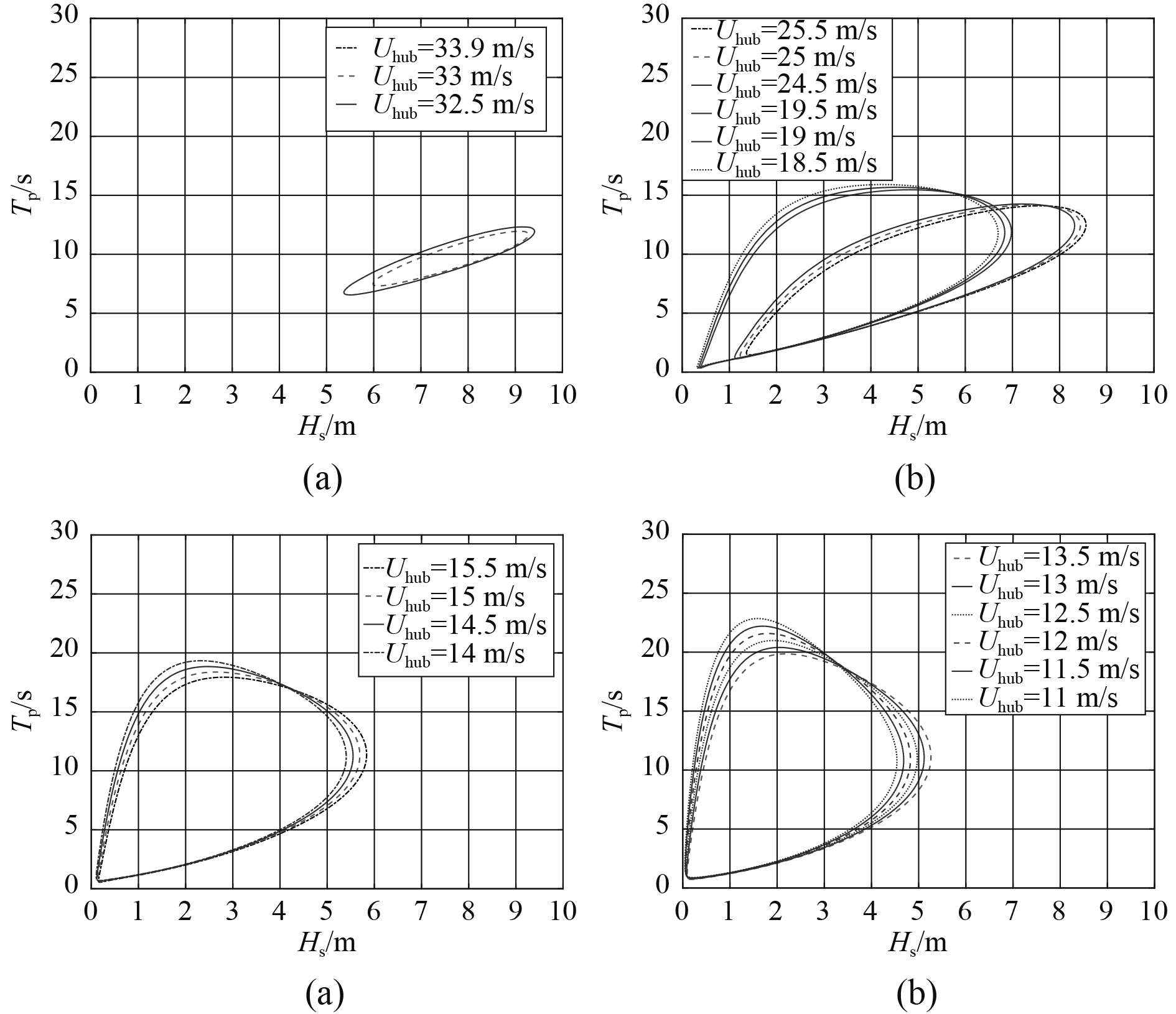
|
图 5 不同风速下HS与TP的二维等值线 Fig. 5 Contour lines of HS and TP under different wind speeds |
在仅考虑3个环境变量的环境等值线法中,
|
|
表 3 考虑Uw,HS,TP三个环境变量的环境等值线法预报极端响应 Tab.3 Extreme response predictions based on ECM with three variables |
由表3可以看出,塔底的力与力矩的极端响应出现在切出风速附近,这是由于波浪占主导因素,对于高风速,有义波高也就越大,波浪产生的响应就越大。而在超过切出风速时,风机处于停机状态,风载会迅速下降。因此其极端响应出现在切出风速。由于风对平台的纵摇角及锚链的力比波浪而言影响更大,故二者的极端响应出现在略高于额定风速附近。轮毂高度处的风速与10 m高度处的UW转换可以利用式(2)。
4.2 基于将
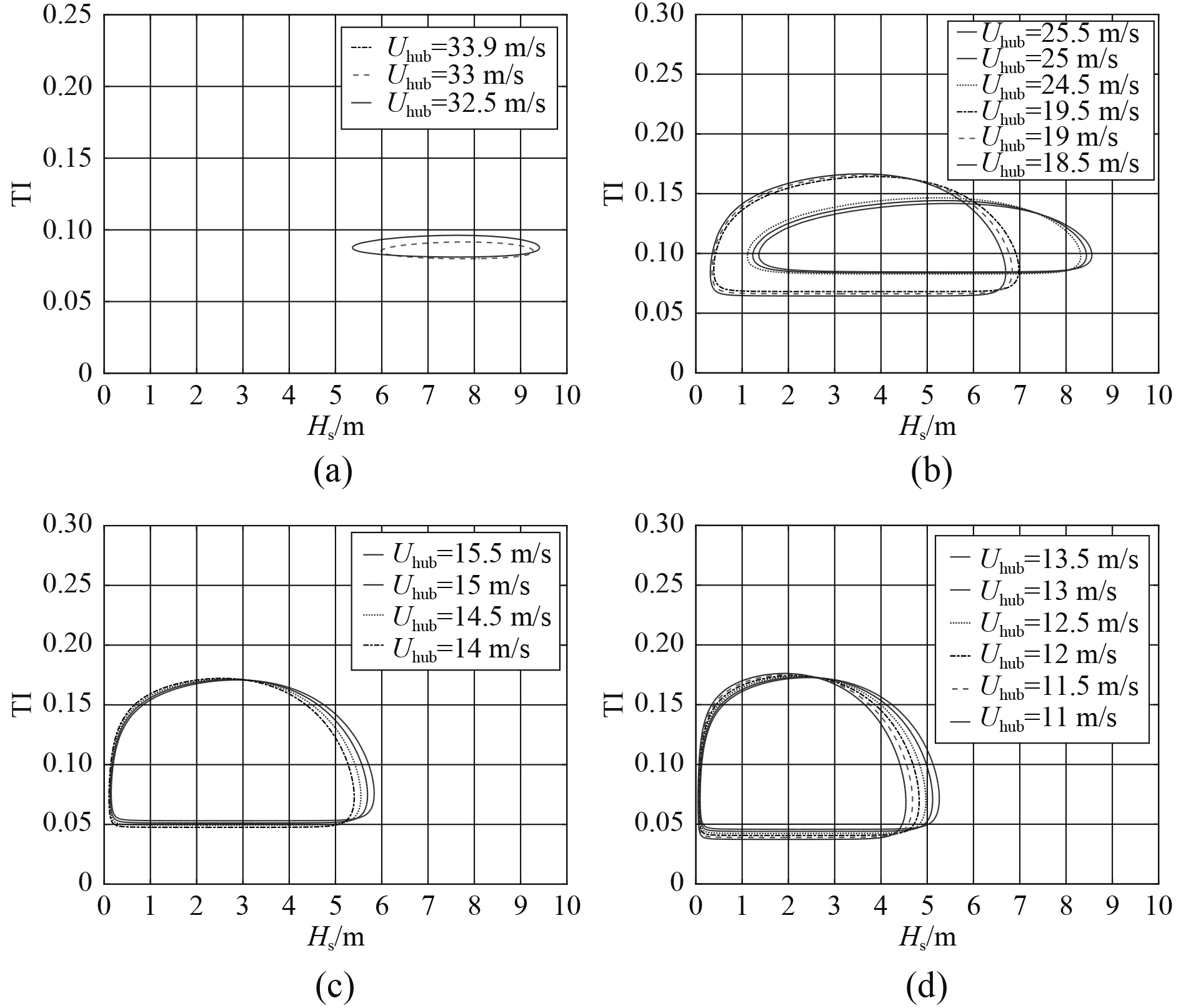
|
图 6
不同风速下
|
|
|
表 4 考虑
|
通过对比表3和表4可知,与
由于湍流强度是风的重要特性之一,为了更贴近真实风况,湍流强度需要被作为环境变量纳入环境等值线法中对海洋结构物的极端响应进行预报。本文通过使用NREL开发的Fast软件进行仿真,验证了各种
| [1] |
周帅, 王迎光, 李昕雪. 应用经典极值理论对风机极端载荷的预报[J]. 舰船科学技术, 2018, 40(19): 97-102. |
| [2] |
周帅, 王迎光, 李昕雪. Spar型海上浮式风机极端载荷预报[J]. 舰船科学技术, 2018, 40(17): 103-110. |
| [3] |
张毅, 马永亮, 曲先强, 等. 冰区海上风机的动力响应及疲劳分析[J]. 舰船科学技术, 2018, 40(1): 81-85. DOI:10.3404/j.issn.1672-7649.2018.01.014 |
| [4] |
HAVER S. On the joint distribution of heights and periods of sea waves[J]. Ocean Engineering, 1987, 14(5): 359-376. DOI:10.1016/0029-8018(87)90050-3 |
| [5] |
WINTERSTEIN S R, UDE T C, CORNELL C A, et al. Environmental parameters for extreme response: Inverse FORM with omission factors[J]. Proceedings of the ICOSSAR-93, Innsbruck, Austria, 1993, 551-557. |
| [6] |
SARANYASOONTORN K, MANUEL L. Efficient models for wind turbine extreme loads using inverse reliability[J]. Journal of wind engineering and industrial aerodynamics, 2004, 92(10): 789-804. DOI:10.1016/j.jweia.2004.04.002 |
| [7] |
HUSEBY A B, VANEM E, NATVIG B. Alternative environmental contours for structural reliability analysis[J]. Structural Safety, 2015, 54: 32-45. DOI:10.1016/j.strusafe.2014.12.003 |
| [8] |
LI Q, GAO Z, MOAN T. Modified environmental contour method for predicting long-term extreme responses of bottom-fixed offshore wind turbines[J]. Marine Structures, 2016, 48: 15-32. DOI:10.1016/j.marstruc.2016.03.003 |
| [9] |
CAMPUS Risø. Ultimate loading of wind turbines[J]. Campus Risø.
|
| [10] |
HANSEN K S, LARSEN G C. Characterising turbulence intensity for fatigue load analysis of wind turbines[J]. Wind Engineering, 2005, 29(4): 319-329. DOI:10.1260/030952405774857897 |
| [11] |
ERNST B, SEUME J R. Investigation of site-specific wind field parameters and their effect on loads of offshore wind turbines[J]. Energies, 2012, 5(10): 3835-3855. DOI:10.3390/en5103835 |
| [12] |
International Electrotechnical Commission. 61400-1: Wind turbines-part 1: Design requirements[J]. International Standard, 2005, 1-92. |
| [13] |
JONKMAN J M, BUHL Jr M L. FAST user’s guide[J]. National Renewable Energy Laboratory, Golden, CO, Technical Report No. NREL/EL-500-38230, 2005.
|
| [14] |
JONKMAN B J. TurbSim user's guide: Version 1.50[R]. National Renewable Energy Lab. (NREL), Golden, CO (United States), 2009.
|
| [15] |
LI L, GAO Z, MOAN T. Joint environmental data at five european offshore sites for design of combined wind and wave energy devices[C]//32nd International Conference on Ocean, Offshore and Arctic Engineering Volume 8: Ocean Renewable Energy. American Society of Mechanical Engineers (ASME), 2013.
|
| [16] |
ROSENBLATT M. Remarks on a multivariate transformation[J]. The annals of mathematical statistics, 1952, 23(3): 470-472. DOI:10.1214/aoms/1177729394 |
| [17] |
JONKMAN J. Definition of the Floating System for Phase IV of OC3[R]. National Renewable Energy Lab. (NREL), Golden, CO (United States), 2010.
|
 2020, Vol. 42
2020, Vol. 42
