0 引　言

电动力水下航行器在军民等领域均有广泛应用^[1]。其中电池舱段在航行过程中会产生较多热量，在狭小紧凑的结构空间中散热条件较差，温度的变化势必会对其他结构产生一定影响，影响航行器的正常工作。因此，在电动力航行器设计中，需对舱段进行热分析。

目前，对航行器电池舱的研究集中在电池结构布局^[2-3]、电池架导热系数对传热的影响^[4]，成组后的热分析等^[5]，侧重电池结构本身，对整个舱段的热分析研究较少。本文重点关注电池舱装配整体的热分析，研究电池放热过程对其他结构组件的影响，避免设计中存在缺陷。

1 数学模型 1.1 热传导

由能量守恒定律和傅里叶定律可以推导出适用于电池舱热传导分析的三维导热微分方程^[6]：

$ \rho c\frac{{\partial t}}{{\partial \tau }} = \frac{\partial }{{\partial x}}\left( {\lambda \frac{{\partial t}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\lambda \frac{{\partial t}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\lambda \frac{{\partial t}}{{\partial z}}} \right) + \dot \varPhi\text{。} $

(1)

式中： $\rho $ 为结构密度， ${\rm{kg}}/\rm{{m^3}}$ ， $c$ 为比热容， ${\rm{J}}/({\rm{kg}} \cdot {\rm{K}})$ ； $t$ 为结构温度， $\rm{K}$ ； $\tau $ 为时间， $\rm{s}$ ； $\dot \varPhi$ 为内热源生成热， $\rm{J}$ 。文中针对的是一个复杂电池舱段，装配关系不可避免，在此统一认为2个紧密接触面间接触关系不影响热量的正常传导。

1.2 热对流

舱段壳体外边面与海水存在对流散热关系，内部结构间存在的空隙也会产生热对流。对流通过牛顿冷却定律确定：

$ \varPhi = hA({T_S} - {T_F})\text{。} $

(2)

式中： $\varPhi$ 为对流换热量， $\rm{J}$ ； $h$ 为对流换热系数， ${\rm{ W}}/({{\rm{m}}^2} \cdot {\rm{K}})$ ； ${T_S}$ 为表面温度，℃； ${T_F}$ 为流体温度，℃。

对于在平均温度为20 ℃的海水中航行的航行器，取最低航速为3.2 $\rm{m}/\rm{s}$ 。将对流状态近似等效为流体外掠平板，则其雷诺数为：

$ Re = \frac{{ul}}{\nu } = 1.0 \times {10^6}\text{。} $

(3)

式中： $u$ 为流体平均速度; $l$ 为电池舱段的特征长度; $\nu $ 为海水运动黏度。雷诺数的值处于层流与湍流的边界区域，考虑到鱼雷外壳表面光滑，且存在更低航速的可能，此处认定其为层流对流状态。由层流状态下的努赛尔数为：

$ N{u_l} = 0.332{Re^{1/2}}{Pr^{1/3}} = 6.48 \times {10^2}({\rm{W}}/{{\rm{m}}^2} \cdot {\rm{K}}) \text{。} $

(4)

式中： $Pr$ 为普朗特数，查表可知为7.02。则雷体表面的对流换热系数为：

$ {h_l} = \frac{{N{u_l} \cdot \lambda }}{l} = 1\;200({\rm{W}}/{{\rm{m}}^2} \cdot {\rm{K}}) \text{。} $

(5)

式中： $\lambda $ 为水的导热系数。

1.3 辐射换热

电池表面的热量还会以热辐射的形式向壳体及其他结构组件辐射。由Stefan-Boltzmann定律定义, 从i面到j面辐射的热量：

$ Q = \sigma \varepsilon {A_i}{F_{ij}}(T_i^4 - T_j^4)\text{。} $

(6)

式中： $Q$ 为热流率， ${\rm{W}}$ ； $\sigma $ 为Stefan-Boltzmann常数，其值为 $5.67 \times {10^{{\rm{ - }}8}}{\rm{W}}/({{\rm{m}}^2} \cdot {{\rm{K}}^4})$ ； $\varepsilon $ 为发射率；为 $i$ 面的面积， ${{\rm{m}}^2}$ ； ${F_{ij}}$ 为 $i$ 面到 $j$ 面的形状因子； ${T_i}$ 为 $i$ 面的绝对温度， ${\rm{K}}$ ； ${T_j}$ 为 $j$ 面的绝对温度， ${\rm{K}}$ 。辐射率数据通过查找工程材料数据得到，辐射率大小与材料表面状态有很大的关系，铝合金的辐射率在0.5～0.8的范围内，本次分析取辐射率为0.8。

2 有限元仿真模型 2.1 物理模型

采用大型通用有限元软件Ansys构建舱段的热仿真有限元模型。首先对物理模型进行适当简化。

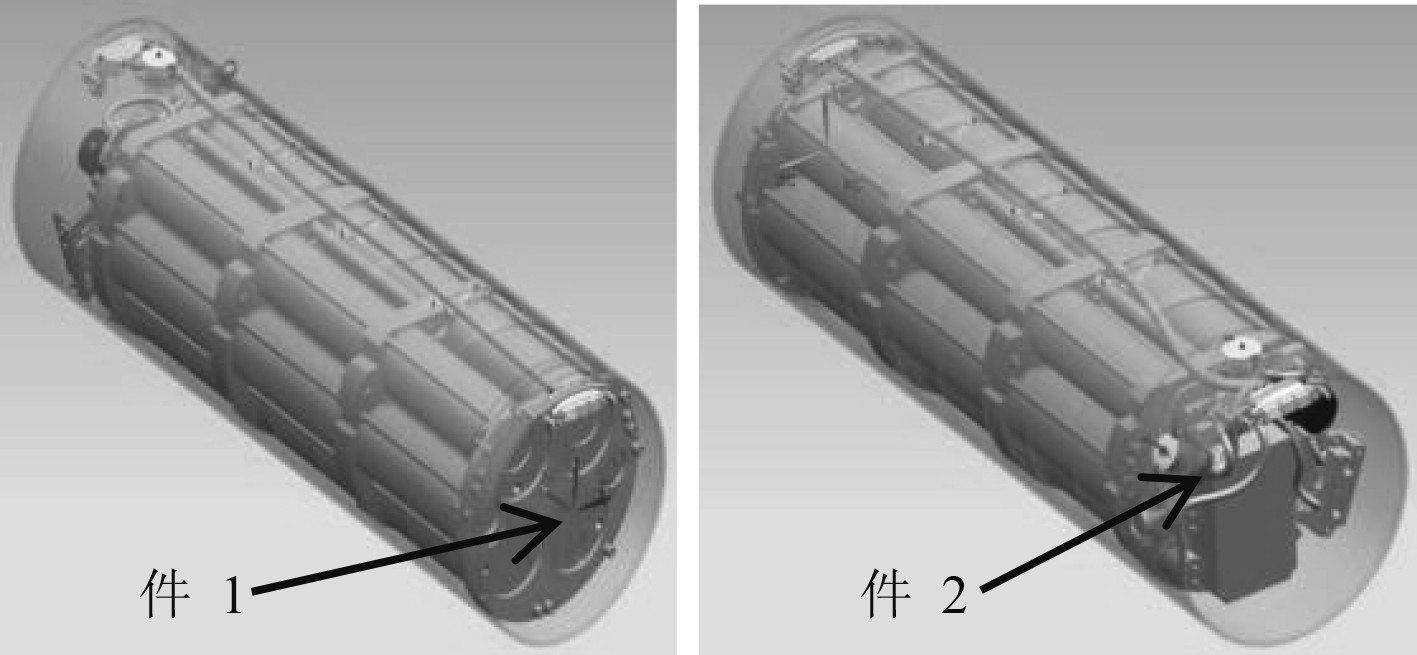
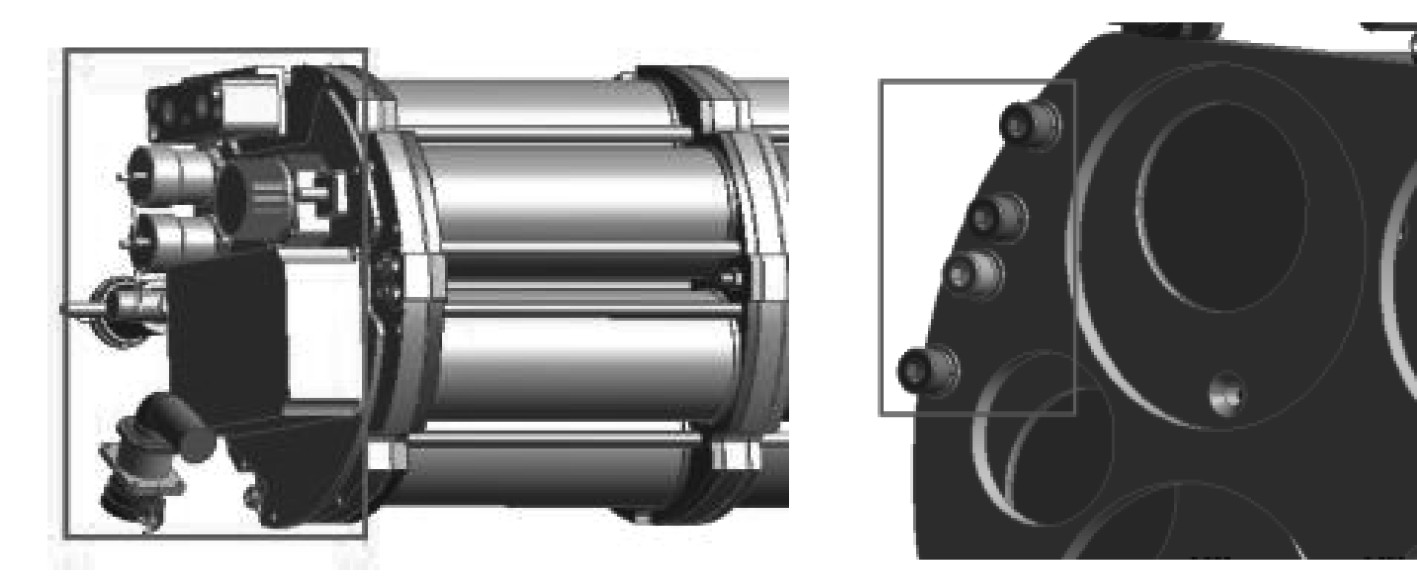
舱段模型主要由发热体（内部圆柱体）、壳体、后安装板(件1)、前安装板(件2)组成, 模型如图1所示。其中发热体通过件1及件2连接在壳体上，同时件1及件2上安装了一系列电子组件，为了快速散热，发热体与舱段壳体之间设计了供热传导用的接触面，为中间安装板。在尽量不影响壳体、前安装板、后安装板温度计算结果的前提下，对模型中的一些小部件进行删除，如前安装板上的一系列电子组件，不重要连接部位的螺栓，发热体之间板件的简化处理以及倒角等小特征的简化，如图2～图4所示。

2.2 网格划分

为保证关注区域的计算精度，壳体、前安装板、后安装板采用结构化网格进行划分，其他组件尽量也使用结构化网格进行划分，辅之以少量的四面体单元填充。对大尺寸部件单元尽可能粗一些以保证网格数量不致过多，对螺栓等小尺寸部件采用细小的单元进行划分以保证网格能够准确表征几何体的几何特征。整个模型主要采用实体单元SOLID186（六面体单元）和SOLID187（四面体）划分网格，且六面体网格占主导。模型共划分669818个单元，704597个节点，划分网格后的有限元模型如图5所示。

2.3 接触关系

接触关系的设定尽量反应各部件间真实的连接状态。在本次仿真中主要采用了不分离（No Separation）与绑定（Bonded）来模拟各个组件之间的连接关系。

2.4 材料属性

模型发热体及壳体组件的材料均按铝合金（919-AT62CB1191-1988）处理，后安装板为钛合金（TC4 GJB2218A-2008），螺钉材料为不锈钢（14Cr17Ni2 GB/T1220-2007），垫片为不锈钢材料（12Cr18Ni9 GB/T1220-2007）。热分析时，材料的物理性能和力学性能如表1～表4所示。应力分析时，材料的性能数据如表5所示。

2.5 边界条件及载荷设置

壳体外表面从初始时刻开始即与20 ℃水直接接触，故壳体外表面设置与水的对流边界条件，对流换热系数已在上文中得出，壳体对流边界条件施加如图7所示。

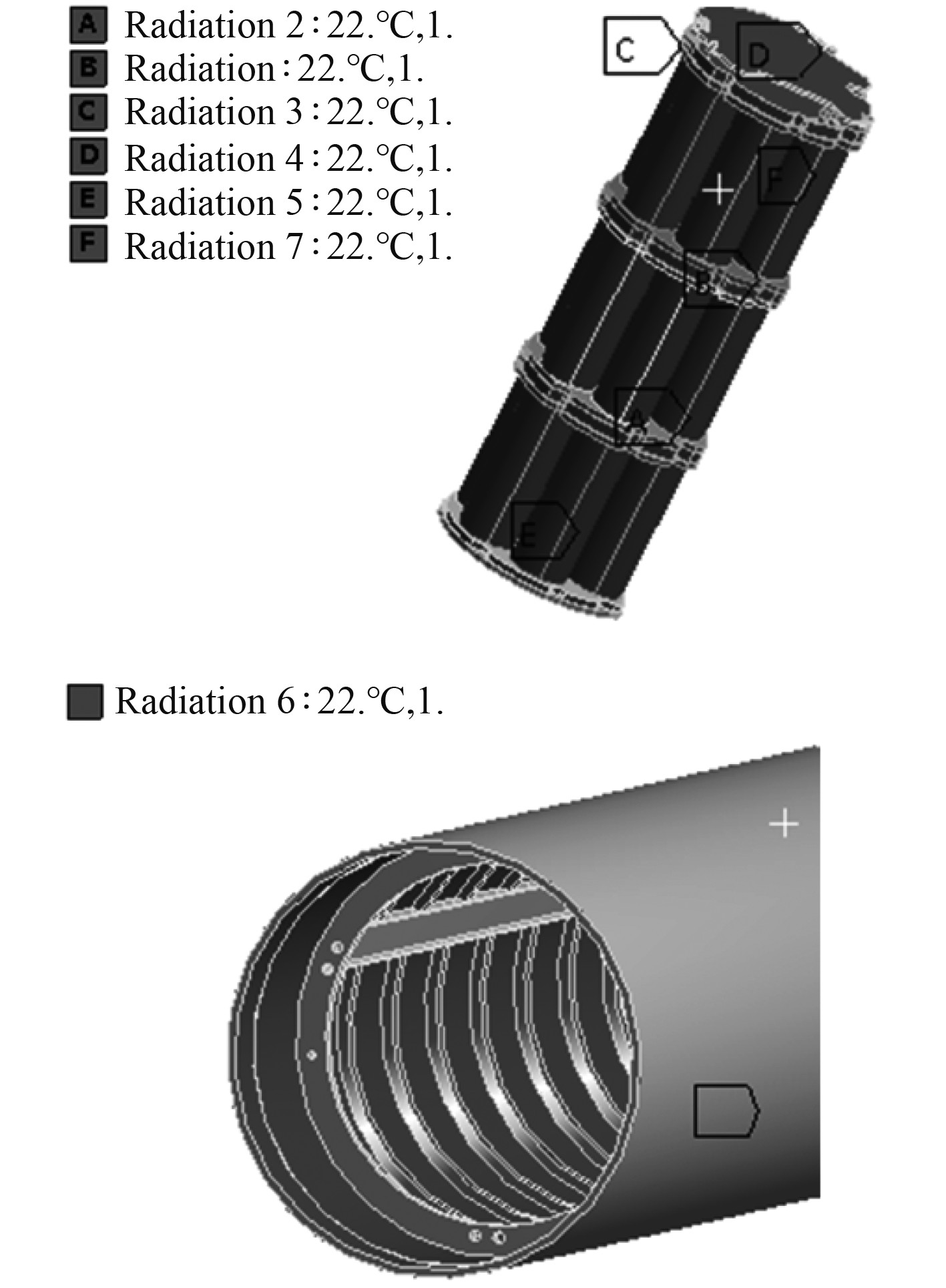
壳体内表面、发热体外表面及其他部件的外表面均施加辐射边界，辐射行为采用面对面（surface to surface）形式，辐射边界的施加情况如图8所示。

舱段应力场分析采用Static Structural模块进行计算，在Workbench中进行热应力间接耦合非常方便，利用搭建好的分析流程，热分析结果可以自动无缝传递到应力计算模块。应力计算时，载荷为瞬态热分析最后时刻的温度场数据。由于舱段在水中重力和浮力相平衡的条件下，不存在任何其他约束条件，理论上而言，应力分析时应不施加边界条件，但有限元计算时，由于舱段整体不是对称结构，在膨胀变形时会发生整体的刚体位移而导致计算失败，因此在本次仿真计算时需要对舱段施加位移约束，限制其刚体位移，从而使有限元计算能够得到收敛解。舱段壳体变形较小，边界条件为固定约束壳体一端的端部如图9所示。

舱段温度场仿真采用Mechanical中的Transient Thermal模块进行计算，其载荷条件为在发热体的外表面施加随时间变化的温度载荷。0～240 s，温度由20 ℃上升到270 ℃，240～400 s时，温度保持270 ℃不变，初始环境温度设为20 ℃，温度载荷的施加如图10所示。

3 仿真结果及分析 3.1 温度分析结果

图11为400 s时壳体的温度场分布。可以看出，模型的最高温度为172 ℃，壳体与发热体直接接触部位，由于热传导的作用，在壳体上相应部位的温度较高，壳体其余部分由于热辐射和传导作用，温度上升至25 ℃左右，可知辐射对传热的影响较小。

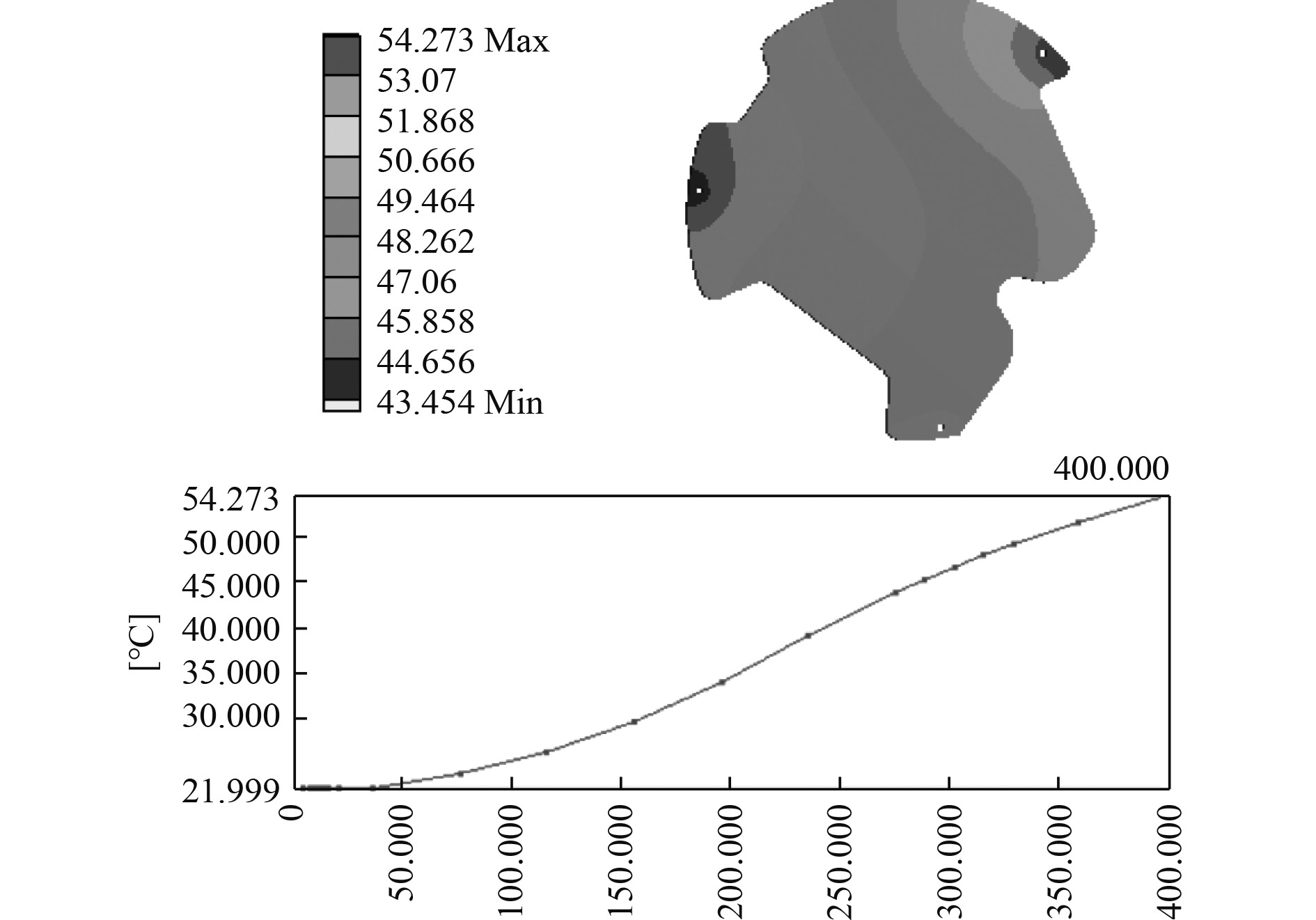
图12分别为前安装板400 s时的温度场分布云图及温升曲线。可以看出，前安装板在400 s时的最高温度为54 ℃，最低温度为43 ℃。整个温度分布的趋势是由于舱段模型的不对称性引起。从温度随时间变化曲线可以看出，0～400 s的时间内，温度是一个逐渐缓慢上升的过程。

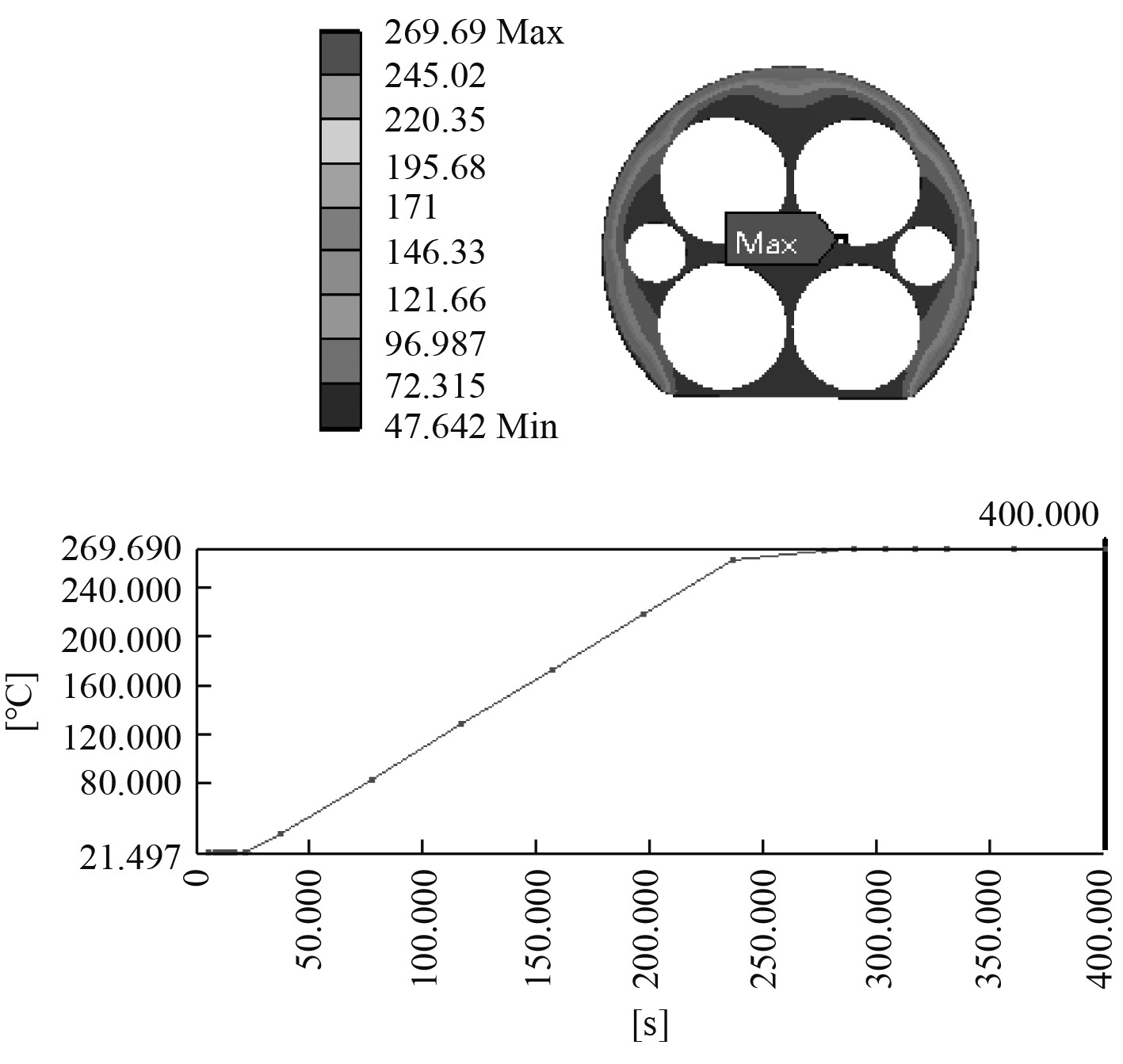
图13为后安装板400 s时的温度场分布云图及温升曲线。可以看出，后安装板在400 s时的最高温度为269 ℃，最低温度为47 ℃。由于后安装板与发热体存在热传导作用，故其最高温度在400 s时趋于定值270 ℃。

对比前后安装板的温升曲线可以看出，两者的温升曲线不同，其原因为前安装板的温度升高主要靠3个螺栓以及辐射作用，故导热较慢，在400 s时间内温度是逐渐上升的过程。后安装板由于与发热体直接接触，故最高温度很快上升到270 ℃，随后保持不变。

3.2 变形及应力分析结果

结构变形及应力结果如图14所示。可以看出，由于温度引起的结构变形量最大为4.3 mm，位于后安装板侧，这与舱段各部分的安装方式有很大关系，壳体内部部分包括发热体及安装板是一端固定在壳体上，另一端采用弹簧垫片与壳体进行连接，这种形式可以释放由于热胀冷缩而引起的变形，进而会很大程度上减少拘束造成的热应力。壳体的最大变形为0.49 mm，最大变形在后安装板端侧。

前安装板的最大变形0.1 mm，最大变形位置在板的边缘（见图15）。后安装板的最大变形为4.1 mm，整个后安装板由于发生整体轴向变形，因此最小变形也在4.0 mm左右，这是由于变形结果是相对于全局坐标系而言的。

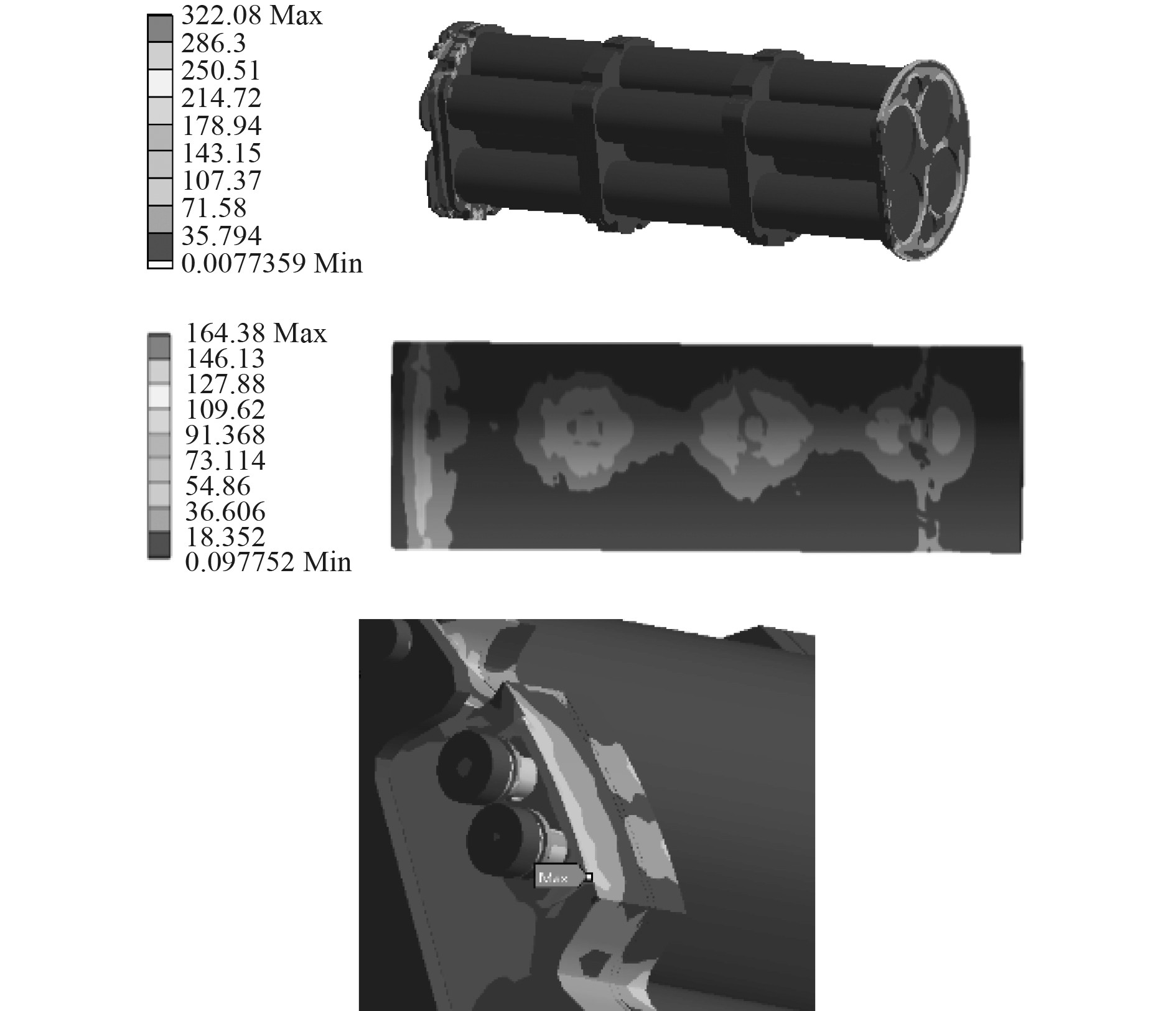
舱段整体的最大等效应力为322 MPa，最大等效应力的位置出现在安装孔小凸台的边缘顶角处，结构在这个尖角位置存在应力集中，且应力幅值超过了材料的屈服强度，但由于此处属于结构不关注且不重要部位，且其余部分的应力幅值均低于相应材料的屈服强度，故可认为结构整体上是安全的，强度满足要求。从图中可以看出壳体最大等效应力在164 MPa左右，低于壳体材料的屈服强度343 MPa，如图16所示。

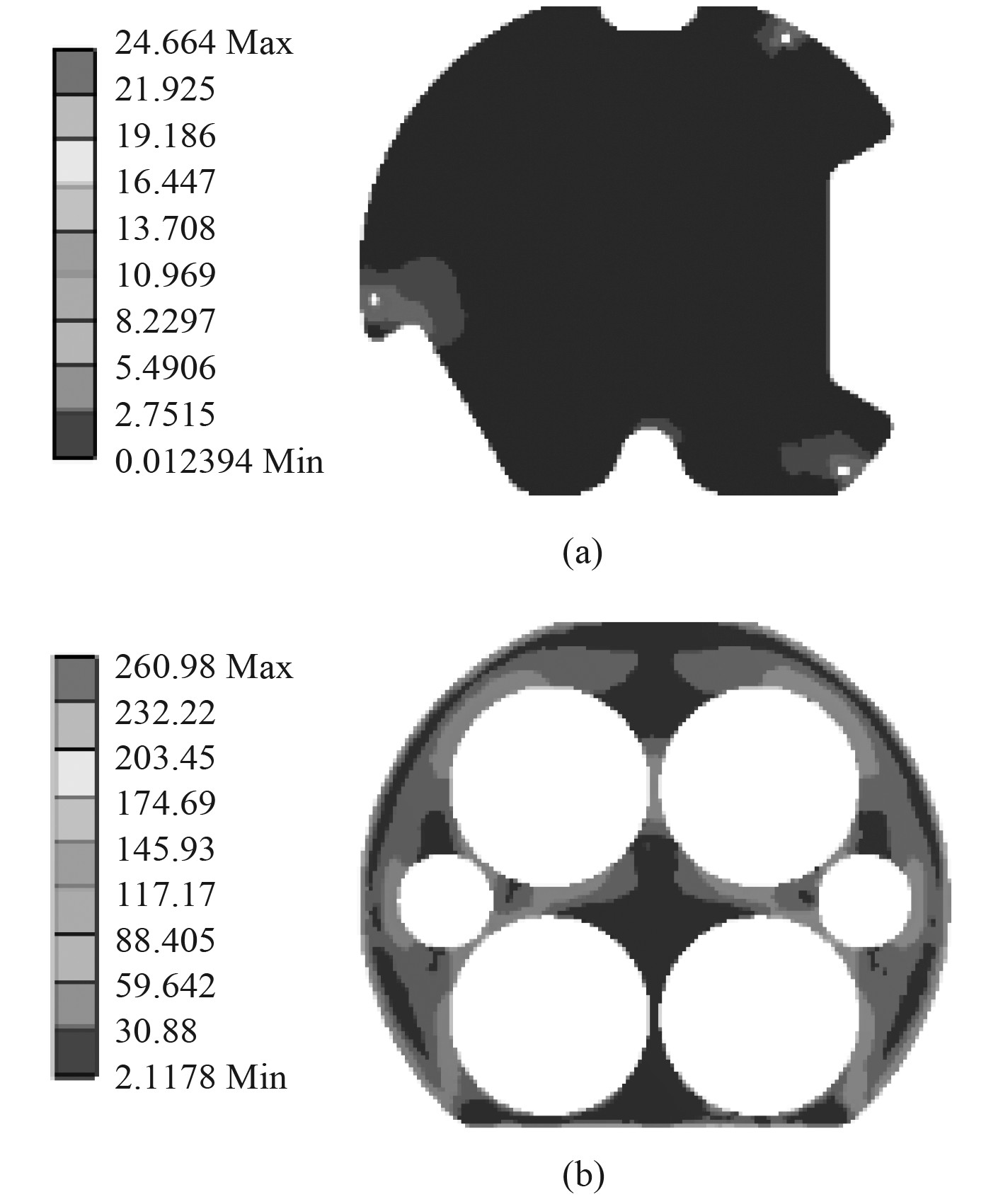
前安装板的等效应力如图17(a)所示。可以看出，前安装板最大等效应力为24 MPa，远小于前安装板材料（变形铝合金）的屈服强度155 MPa。后安装板的等效应力如图17(b)所示。可以看出后安装板的最大等效应力为260 MPa，后安装板的屈服强度为825 MPa，其应力远小于屈服强度，故结构安全。

4 结　语

本计算采用Ansys Workbench对舱段进行了温度场和静强度分析，得到了该结构在实际工况载荷下的温度场分布以及结构应力变形结果，对实际结构设计和试验起到一定的指导作用。

1）舱段瞬态温度场分析结果表明, 壳体在400 s时温度最高是172 ℃，前安装板的最高温度为54 ℃，后安装板的最高温度为269 ℃。

2）舱段应力场计算结果表明，舱段整体最大变形量为4.3 mm，在结构设计时，要充分考虑这个热变形量，否则会因热拘束而导致结构某些部位出现大的热应力。

3）本次计算的热应力最大为322 MPa，出现在安装螺栓的小凸台的顶角位置，属于典型的应力集中现象，但此处不属于结构关心区域，且其余各部分应力幅值均小于各部分材料的屈服强度，因此舱段整体结构的强度满足要求，结构安全。