2. 上海中建东孚投资发展有限公司,上海 200125
2. Shanghai Zhongjian Dongfu Investment Development Co. Ltd., Shanghai 20015, China
随着海洋技术迅速发展以及水下作业需求的增加,人类水下作业装备多种多样,包括无人无缆的,载人潜器等。其中水下滑翔机属于无人无缆深潜器,该概念最早在1989年由Stommel[1]提出,其在水中作业处于滑翔状态,通过调节重心位置,重力、浮力来调节姿态,从而完成滑翔运动,滑翔覆盖广泛的海域面积,在滑翔的同时可以完成对区域水文信息采集、海底地貌探测、矿物勘探、军事侦察等工作,同时水下滑翔机滑翔所消耗的能量极少,续航力在上千千米,且水下滑翔机制造成本低,可重复使用,因此可以大量投放,对大面积海域进行作业。因此水下滑翔机在海洋探索、军事等领域具有广泛的应用场景。Rudnick[2]给出了典型的水下滑翔机型号及其应用场景。
针对水下滑翔机水动力性能,国内外学者进行了广泛研究。Henry Stommel[1]率先提出了水下滑翔机的概念,其通过调整压载水舱水位,实现重量,重心位置的调节,利用重力、浮力实现不断的滑翔运动,完成水下作业。在此构想的基础上美国设计生产了最初的水下滑翔机。中国对水下滑翔机概念的研究较晚,最早是中国科学院沈阳自动化所研究开始水下滑翔机的设计研究工作[3]。关于水下滑翔机的水动力性能,国内外学者都做了多个方面的研究,包括滑翔机体的外形(主要有水滴形,低阻层流形)[4],水翼剖面类型(多为NACA翼型),水翼位置布置等。Chen[5]使用CFD方法对3种外形的水下滑翔机在滑翔状态的阻力特性进行了数值模拟,并给出了不同滑翔角度状态下的滑翔能量转换效率,为水下滑翔机工作状态的选择提供了理论支持;Liu[6]用模型试验和数值模拟2种方法对水下滑翔机水动力性能进行了研究,其同样对滑翔机不同攻角和不同滑行角度状态的阻力,纵倾、横倾、转首、力矩的变化进行了分析,同时数值计算结果也与风洞试验结果进行了对比验证;Li[7]对装配仿生形水翼的水下滑翔机水动力性能进行了分析,其使用CFD方法模拟了4种异型的推进效率,讨论了不同机翼形式对水下滑翔机巡航效率的影响;Fan[8]使用参数化表达水下滑翔机几何外形,并通过理论分析了滑翔机外形和其水动力性能、稳定性的关系,并给出了机翼外形位置和对应的最大升力阻力比;Jagadeesh[9]同样使用模型试验和数值计算2种方法对某型水下滑翔的水动力性能进行了研究,对不同航速不同滑翔姿态角度做了一系列的研究,用以指导水下滑翔机的工作导航和控制系统。
本文针对某型水下滑翔机,研究其机翼不同位置,不同攻角情况下的升力、阻力变化情况,本文使用OpenFOAM开源CFD库对不同的机翼布置状态下的水动力性能进行数值模拟,给出升力、阻力特性的同时还能给出详细的速度、压力、涡量场信息,这样有助于深入理解水下滑翔机水动力性能,更好设计、优化水下滑翔机的几何外形,机翼位置、攻角,附体设置等参数。
1 数值方法数值计算基于开源CFD库OpenFOAM,OpenFOAM在船舶海洋水动力学领域有着广泛的应用,其计算结果可靠。OpenFOAM基于有限体积法(FVM)开发,本文计算水下滑翔机水动力学特性,故求解单相非定常不可压缩粘性流体,求解器使用pimpleFoam,求解不可压缩RANS方程为:
| $\nabla \cdot {{U}} = 0{\text{,}}$ |
| $\begin{split} \frac{{\partial \rho U}}{{\partial t}} + \nabla \cdot (\rho ({{U}} - {{{U}}_g}){{U}}) =& - \nabla {p_d} - {{g}} \cdot {{x}}\nabla \rho + \nabla \cdot ({\mu _{eff}}\nabla {{U}}) +\\ &(\nabla {{U}}) \cdot \nabla {\mu _{eff}} + {f_s}{\text{。}}\\[-10pt]\end{split}\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!$ |
式中:
速度压力解耦采用PIMPLE算法。该算法是SIMPLE算法和PISO算法的组合,即每个PISO迭代之外又进行了若干次SIMPLE迭代,兼具了2种算法的优点,且通过参数设置可以退化为SIMPLE算法或者PISO算法。PISO算法可以更好捕捉瞬态问题的瞬时特性,SIMPLE算法收敛更快。本文计算工况为定常来流工况,类似稳态问题,但是考虑到湍流特性,还是使用PIMPLE算法。本文计算时间项离散使用2阶退步格式,对流项离散使用2阶迎风格式,扩散项离散使用中心差分格式。计算中使用变时间步长保证Courant数小于1。
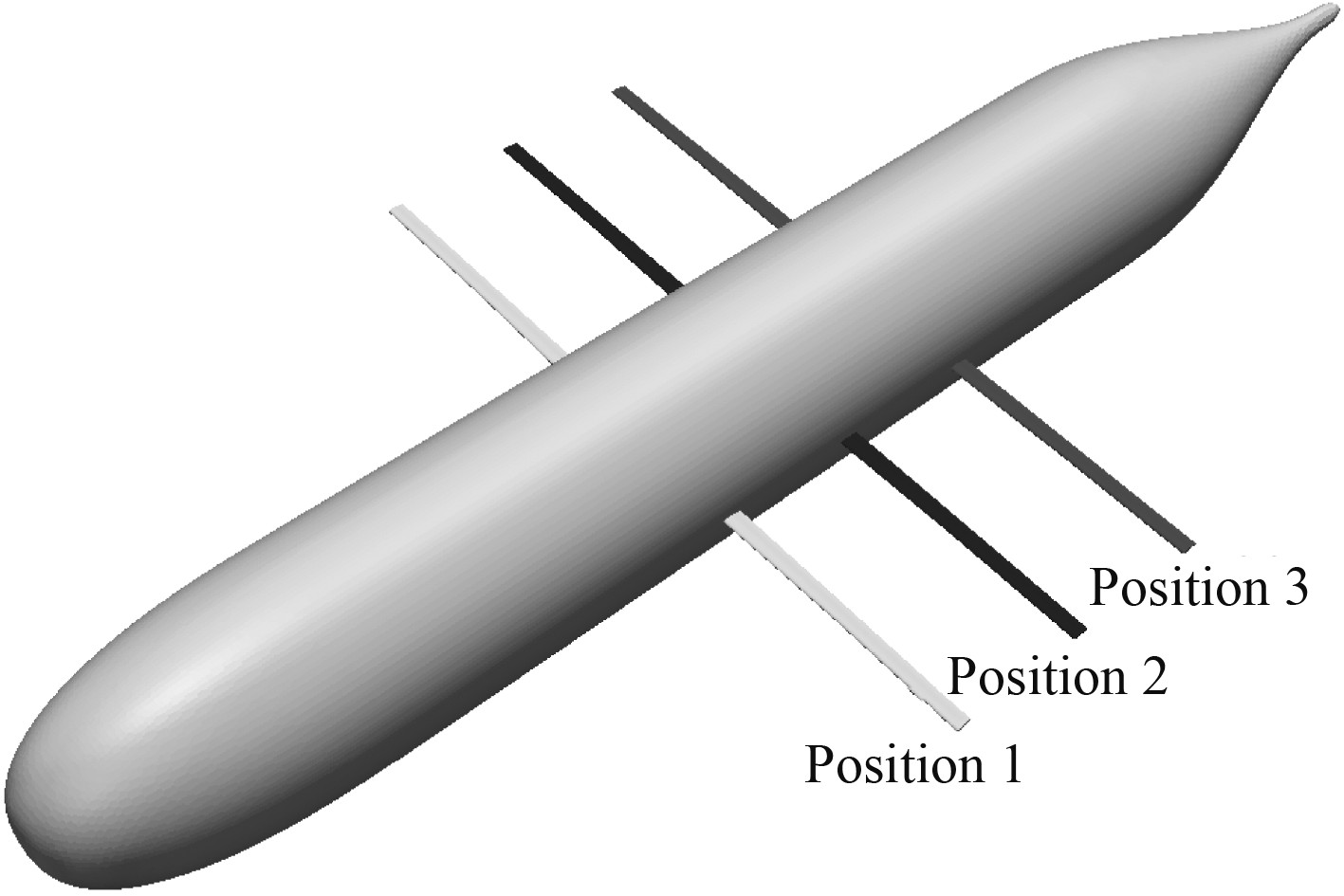
2 算例设置本文计算水下滑翔机主尺度艇长L为5.75 m,机翼弦长15 cm,计算航速为6 kn,模型参考如图1所示。机翼3种布置位置见图1,其中每个位置考虑4种机翼的初始安装攻角0°,3°,6°,9°。计算机翼在不同位置,不同角度状态下,水下滑翔机的水动力性能。
|
图 1 水下滑翔机模型及机翼位置图 Fig. 1 Schematic of the underwater glider model and wing location |
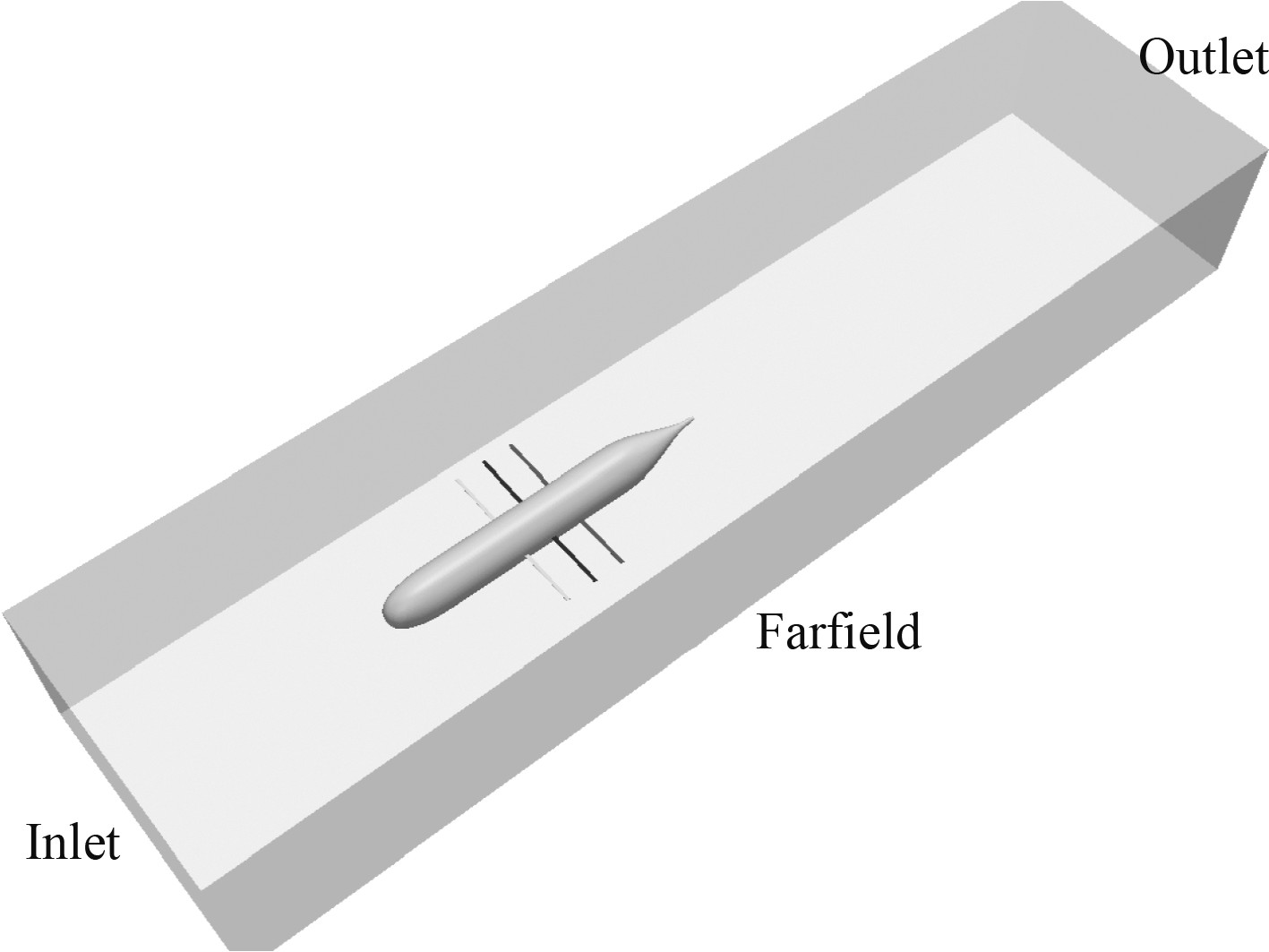
算例计算域大小如图2所示。其中入口边界距离滑翔机部1L,出口边界距离滑翔机尾部2L,滑翔机距离上下左右远场边界0.5L。其中入口边界条件为定常来流,出口边界为压力定值,速度零梯度,远场边界速度压力均取零梯度边界条件。艇体和机翼物面为不可滑移物面边界条件。
|
图 2 计算域与边界示意图 Fig. 2 Schematic of the computational domain and boundary |
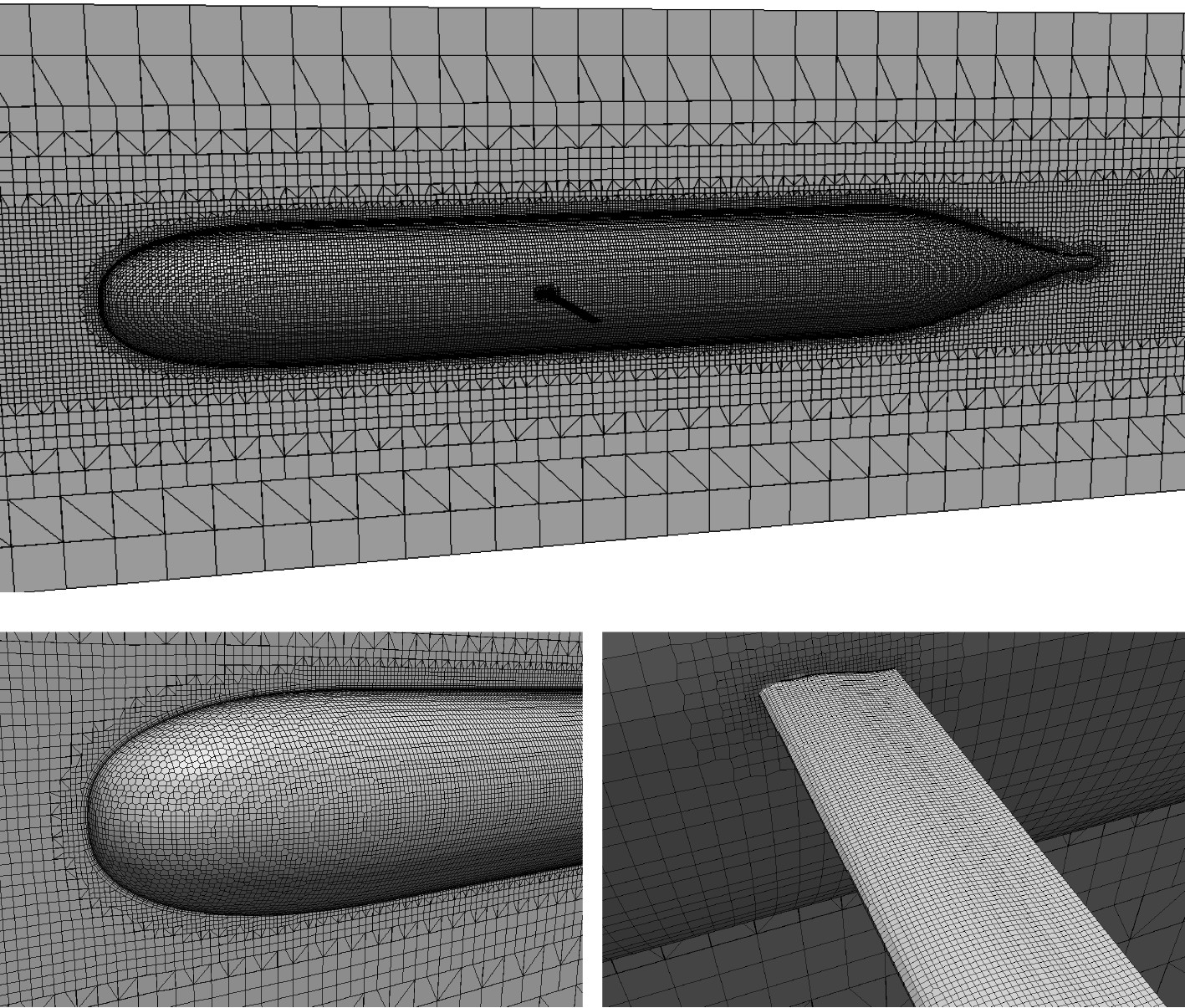
计算网格是使用blockMesh和snappyHexMesh工具生成的任意多面体网格,该类型网格适用于OpenFOAM使用的有限体积数值方法,首先使用blockMesh工具生成正六面体背景网格,覆盖整个计算域。随后使用snappyHexMesh工具从背景网格中挖去滑翔机艇体所在区域网格,并进行滑翔机艇体周围流场区域的局部加密,并在艇体边界生成边界层网格。本文使用计算网格数量185万,边界层网格尺寸保证计算工况y+值在30~60之间。计算网格示意图,首部网格加密,边界层如图3所示。
|
图 3 计算网格 Fig. 3 Computational mesh |
首先从水动力的角度分析,表1列出了机翼在3种不同位置、不同攻角工况下,滑翔机整体受到的阻力和升力变化情况。可以看出,无论机翼的位置如何,随着机翼攻角的增大,滑翔机所受到的升力、阻力均增大,这也符合对机翼的认识。
|
|
表 1 滑翔机不同工况所受阻力升力 Tab.1 Resistance and lift of glider under different working conditions |
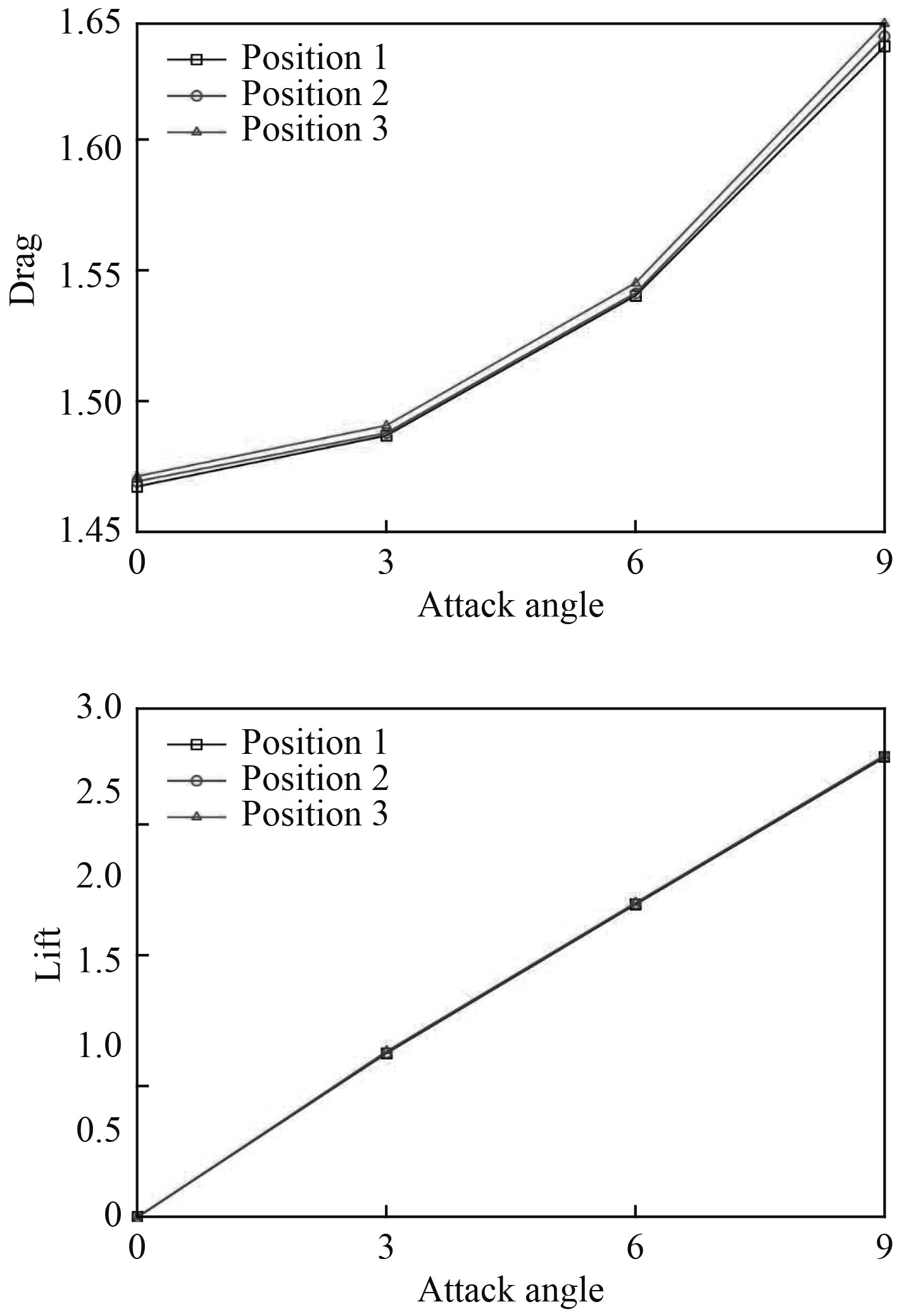
图4为机翼不同位置滑翔机阻力和升力随攻角变化而变化的曲线。可以看出,随着攻角增大,阻力非线性增长,增速快,升力基本线性变化。
|
图 4 滑翔机机翼不同位置攻角状态下阻力、升力变化 Fig. 4 Resistance and lift performance at the different underwater glider wing positions |
对比机翼所处不同位置时滑翔机受到阻力、升力的变化,可以发现随着机翼位置从首部向尾部移动,滑翔机受到的阻力和升力均增大,但是增加的幅值不显著,可以将滑翔机机体和机翼2个系统分开考虑。由于机翼位置变化,其所处滑翔机绕流场的位置不同,受到的水动力也会相应变化,即在不同的背景流场中,机翼的阻力、升力特性会发生变化。这也可以看作是滑翔机艇体对机翼的影响。另一方面,由于机翼位置发生变化,也会使流场发生变化进而影响滑翔机艇体受到的水动力,这可以看作是机翼对滑翔机艇体的影响。本文研究的滑翔机及其机翼,机翼相对常规水下滑翔机其弦长较小,因此对流场扰动及对滑翔机艇体的影响可以忽略不计。这也是机翼不同布置位置,水下滑翔机整体受到阻力、升力变化不大的原因。而机翼位置改变,由于处在滑翔机艇体绕流场的不同位置,因此其阻力、升力会发生一定变化。这也是随着机翼从滑翔机艏部移动向滑翔机尾部阻力、升力略有增大的原因。
由于本文所计算所有工况流场相似,所以只给出了机翼9°攻角,尾部布置情况时的滑翔机表面压力和边界层流场信息,如图5所示。可以看出,滑翔机艇体部为钝体,因此在部形成驻点,压力峰值。图中,横切面为流场中纵向速度小于99%来流速度的部分,即边界层部分。可以看出流场一直到滑翔机尾部均未发生边界层分离,在滑翔机尾部形成较大区域的死水区,在后续推进器及控制模块的设计中也要考虑到死水区存在对其效率产生的影响,适当的尾部型线优化可以改进这一问题。
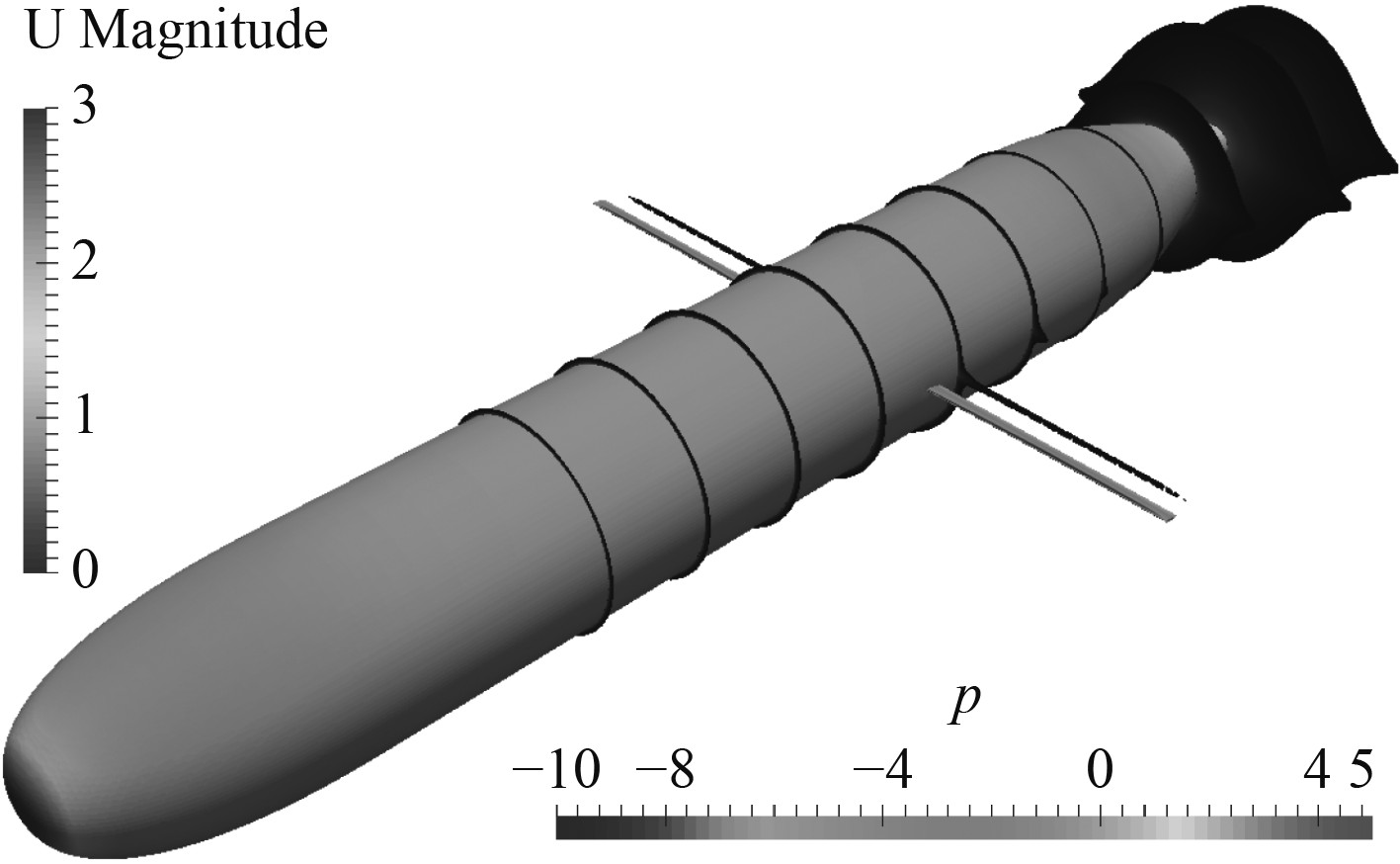
|
图 5 速度-压力分布图 Fig. 5 The1 map of the velocity-pressure distribution |
通过对某型水下滑翔机机翼在不同位置、不同攻角状态下的水动力性能计算,发现由于该型水下滑翔机机翼弦长相对较小,因此其位置改变对整个水下滑翔机系统水动力性能影响不大。随着其位置从首部到尾部移动,滑翔机阻力、升力略有增加,增幅不大。因此在后期设计过程中,机翼位置的选取主要考虑设备布置、安全等因素,可以忽略其对滑翔机水动力性能的影响。另外通过对滑翔机流场信息的分析,发现在滑翔机尾部会存在较大范围的死水区,在后续附体设置的过程中要考虑此因素,或者通过型线优化手段,避免该死水区的出现。
| [1] |
STOMMEL H. The Slocum Mission[J]. Oceanography, 1989, 2(1): 22-25. DOI:10.5670/oceanog.1989.26 |
| [2] |
RUDNICK D L, DAVIS R E, ERIKSEN C C, et al. Underwater gliders for ocean research[J]. Marine Technology Society Journal, 2004, 38(2): 73-84. DOI:10.4031/002533204787522703 |
| [3] |
俞建成, 张奇峰, 吴利红等. 水下滑翔机器人系统研究[J]. 海洋技术, 2006, 25(1): 6-10. DOI:10.3969/j.issn.1003-2029.2006.01.002 |
| [4] |
李志伟, 崔维成. 水下滑翔机水动力外形研究综述[J]. 船舶力学, 2012, 16(7): 829-837. DOI:10.3969/j.issn.1007-7294.2012.07.014 |
| [5] |
CHEN Y, CHEN H, ZHENG M A, et al. Hydrodynamic analyses of typical underwater gliders[J]. Journal of Hydrodynamics, 2015, 27(4): 556-561. DOI:10.1016/S1001-6058(15)60516-9 |
| [6] |
LIU Y, MA J, MA N, et al. Experimental and numerical study on hydrodynamic performance of an underwater glider[J]. Mathematical Problems in Engineering, 2018, 1-13. |
| [7] |
LI Y, PAN D, ZHAO Q, et al. Hydrodynamic performance of an autonomous underwater glider with a pair of bioinspired hydro wings–A numerical investigation[J]. Ocean Engineering, 2018, 51-57. |
| [8] |
FAN S, WOOLSEY C A. Elements of underwater glider performance and stability[J]. Marine Technology Society Journal, 2013, 47(3): 81-98. DOI:10.4031/MTSJ.47.3.4 |
| [9] |
JAGADEESH P, MURALI K, IDICHANDY V G, et al. Experimental investigation of hydrodynamic force coefficients over AUV hull form[J]. Ocean Engineering, 2009, 36(1): 113-118. DOI:10.1016/j.oceaneng.2008.11.008 |
| [10] |
MENTER, F. R. (1994), Two-equation eddy-viscosity turbulence models for engineering applications[J] AIAA Journal, 32, (8): 1598-1605.
|
 2020, Vol. 42
2020, Vol. 42
