0 引　言

水下拖曳组件是进行水下探测或水声系统自身的重要组成部分，广泛应用于海洋研究、军事等领域。在水下航行体上拖带水下拖曳组件，可以更好地拓展其水声功能，但由于航行体自身需要布放，在完成该动作前，为了避免拖缆打结、挂断等危害情况发生，通常需要将拖缆盘绕起来，布置在水下航线体内部或外挂在航线体尾部。当拖缆外挂时，在航行过程中，由于水流作用在拖缆及其盘绕器上，会产生迎流阻力，为了提高拖缆安装可靠性，减小盘绕器阻力对航线体姿态影响，须对拖缆盘绕器进行减阻特性分析，以获得流阻较小的盘绕器外形。

正三角形截面、矩形截面和正六边形截面柱体绕流的阻力系数C_d时均值均大于圆形截面柱体绕流的阻力系数C_d时均值，也就是说在上述4种形状截面柱体中，圆形截面的绕流阻力最小^[1]。因此，选择圆形截面作为盘绕器的基本截面，采用CFX软件，对圆形截面的盘绕器进行了数学建模和仿真计算。在圆形截面基础上，采用卡克斯线型和前后对称水滴线型对其截面进行优化。通过比较3种不同截面的盘绕器阻力值，确定前后对称水滴型截面阻力最小方案，试制盘绕器样机，并通过试验验证了仿真模型。

1 圆形截面盘绕器有限元仿真 1.1 控制方程

不可压缩粘性流体的运动可用Navier-Stokes方程描述，其连续性方程与动量方程如下式：

$\left\{\begin{aligned} & \frac{\partial {u}_{i}}{\partial {x}_{i}}=0 {\text{，}}\\ & \frac{\partial {u}_{i}}{\partial t}+\frac{\partial }{\partial {x}_{j}}\left({u}_{i}{u}_{j}\right)=-\frac{1}{\rho }\frac{\partial p}{\partial {x}_{i}}+\frac{\partial }{\partial {x}_{j}}\left(v\frac{\partial {u}_{i}}{\partial {x}_{j}}\right)\;{\text{。}}\end{aligned}\right. $

(1)

式中： ${u}_{i}$ 为速度分量； $p$ 为压力；ρ为流体的密度； $v$ 为流体的运动粘性系数^[2]。

通过计算雷诺数，确定流体为湍流运动。对于湍流运动的情况，本文采用基于Shear Stress Transport（SST）模型的 $k-{\rm{\omega }}$ 模型进行分析。SST模型考虑了湍流剪应力的传输，可以精确地预测流动的开始和负压梯度下流体的分离量。SST模型的最大优点在于考虑了湍流剪应力，从而不会对涡流黏度造成过度预测^[3]。SST模型的湍动能及比耗散率输运方程为：

$\left\{\begin{aligned} & \rho \frac{{\rm{d}}k}{{\rm{d}}t}+\rho \frac{\partial \left(k{u}_{i}\right)}{\partial {x}_{i}}=\frac{\partial }{\partial {x}_{j}}\left({T}_{k}\frac{\partial k}{\partial {x}_{j}}\right)+{G}_{k}-{Y}_{k}{\text{，}}\\ & \rho \frac{{\rm{d}}\omega }{{\rm{d}}t}+\rho \frac{\partial \left(\omega {u}_{i}\right)}{\partial {x}_{i}}=\frac{\partial }{\partial {x}_{j}}\left({T}_{\omega }\frac{\partial \omega }{\partial {x}_{j}}\right)+{G}_{\omega }-{Y}_{\omega }+{D}_{\omega }\;{\text{。}}\end{aligned}\right.$

(2)

式中：ρ为流体的密度； ${G}_{k}$ 为由层流速度梯度产生的湍流动能； ${G}_{\omega }$ 为由ω方程产生的湍流动能； ${T}_{k}$ 为k的扩散率； ${T}_{\omega }$ 为ω的扩散率； ${Y}_{k}$ 和 ${Y}_{\omega }$ 为由扩散而产生的湍流； ${D}_{\omega }$ 为正交发散项。

1.2 几何模型与网格划分

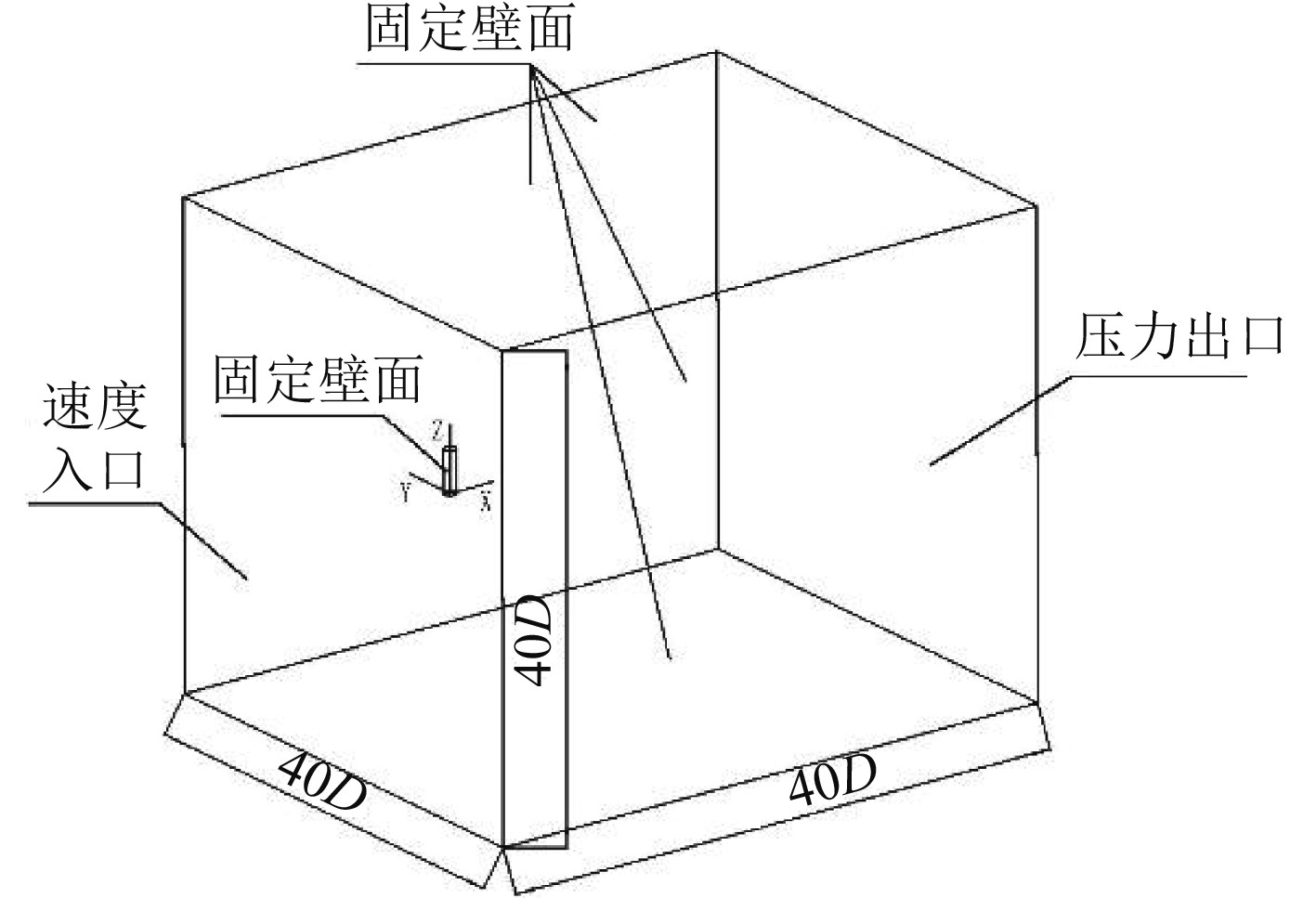
根据航行体尾部可用空间大小及拖缆直径、长度等参数，初步选定盘绕器缠绕拖缆之后的直径为42.8 mm，长度为155 mm，并在此基础上建立计算域模型，如图1所示。在笛卡尔参考坐标系中，坐标原点在圆柱底面中心处，X，Y，Z向分别为顺流向、横流向和圆柱轴向。以圆柱的直径D为特征尺度，计算域的长、宽、高分别为50D，40D，40D，圆柱中心距离上下游断面的距离分别为10D和40D，距离两侧的距离为20D。

为了提高模型计算准确性，整个计算域被划分成376213个六面体单元。在盘绕器边界，由于物理参数在边界层处的梯度变化很大，为了精确地描述这些参数，采用Inflation法对边界层处的网格进行了处理：第1层网格高度为0.05 mm，最大层数为20层，网格增长率为1.2。模型网格如图2所示。

1.3 边界条件

边界条件设置为速度入口、压力出口、壁面，分别对应几何模型的入口面、出口面和4个侧面。计算域入口设置为定常流速，速度为 ${U}_{0}$ =0.091 m/s，出口设置为压力出口，相对压力值设为0，计算域壁面及盘绕器边界处均设置为固定壁面。

1.4 模型验证

流场中的流体为水介质，其密度为1000 kg/m³，在温度20 ℃时，流体的运动粘性系数为1×10^-6，当来流速度为0.091 m/s时，按式（3）计算得雷诺数 ${R}_{e}$ 为3.9×10³。

${R}_{e}=\frac{uD}{v}{\text{。}}$

(3)

式中： $u$ 为来流速度； $D$ 为圆柱直径（本文为0.042 8 m）； $v$ 为流体运动粘性系数。

在CFX软件中，计算求解得来流速度方向上的总阻力 $F$ 为0.02 N，按式（4）求解得阻力系数 ${C}_{d}$ 为0.728。

${R}_{e}=\frac{2F}{\rho {u}^{2}DL}{\text{。}}$

(4)

式中： $F$ 为阻力；ρ为流体的密度； $u$ 为来流速度； $D$ 为圆柱直径； $L$ 为圆柱长度。

将计算结果与前人所做的实验和数值模拟结果进行对比，如表1所示。本文计算的阻力系数为0.728，参考文献[4]中实验获得的阻力系数为0.990，参考文献[5]计算的阻力系数为0.746。

相比无限长圆柱体实验结果，本文计算的阻力系数偏小，其主要原因在于计算模型为有限长圆柱体，存在自由端面。自由端的存在明显改变了圆柱受力，导致有限长圆柱阻力系数偏小，本文计算结果与参考文献[5]中有限长圆柱计算结果吻合较好，从而验证了仿真模型。

1.5 按实际工况计算盘绕器阻力

水下航行体在实际航行状态下，航速范围为3～8 m/s，并且在特定高速条件下，速度达到22 m/s。由于盘绕器跟随航行体航行，因此其来流速度与航行体速度一致。按照来流速度3 m/s，4 m/s，5 m/s，6 m/s，7 m/s，8 m/s，22 m/s分别计算圆柱模型所受到的阻力，其结果如表2所示。

2 盘绕器优化设计 2.1 优化方法选择

对盘绕器进行优化，长度方向受到拖缆缠绕长度的约束，不进行调整，保持155 mm，仅对圆形截面进行优化，以减小流体阻力。对于截面线型优化，工程设计时通常采用现有的线型进行参数调整，或者以阻力作为优化的目标函数^[6]，以获得阻力最小的外形曲线。本文使用第1种方法，分别采用卡克斯线型和前后对称水滴线型对盘绕器截面进行优化。

2.2 卡克斯线型截面计算结果

盘绕器截面选择对称的2组卡克斯线型绘制^[7]，其线型方程如下式：

$Y=\frac{\left(X-f\right)\sqrt{LX-{X}^{2}}}{2k} \cdot D{\text{。}}$

(5)

式中： $f$ = 3.45×10²； $k$ = −1.1023×10⁴； $L$ = 70.65 mm； $D$ = 42.8 mm；变量 $X$ 的取值范围为0～62.8 mm。

按式（5）绘制的卡克斯线型截面图如图3所示。

按圆柱体模型方法建模、划分网格、加载边界条件，计算卡克斯线型截面的盘绕器在不同来流速度下的阻力值，其结果如表3所示。

2.3 前后对称水滴线型截面计算结果

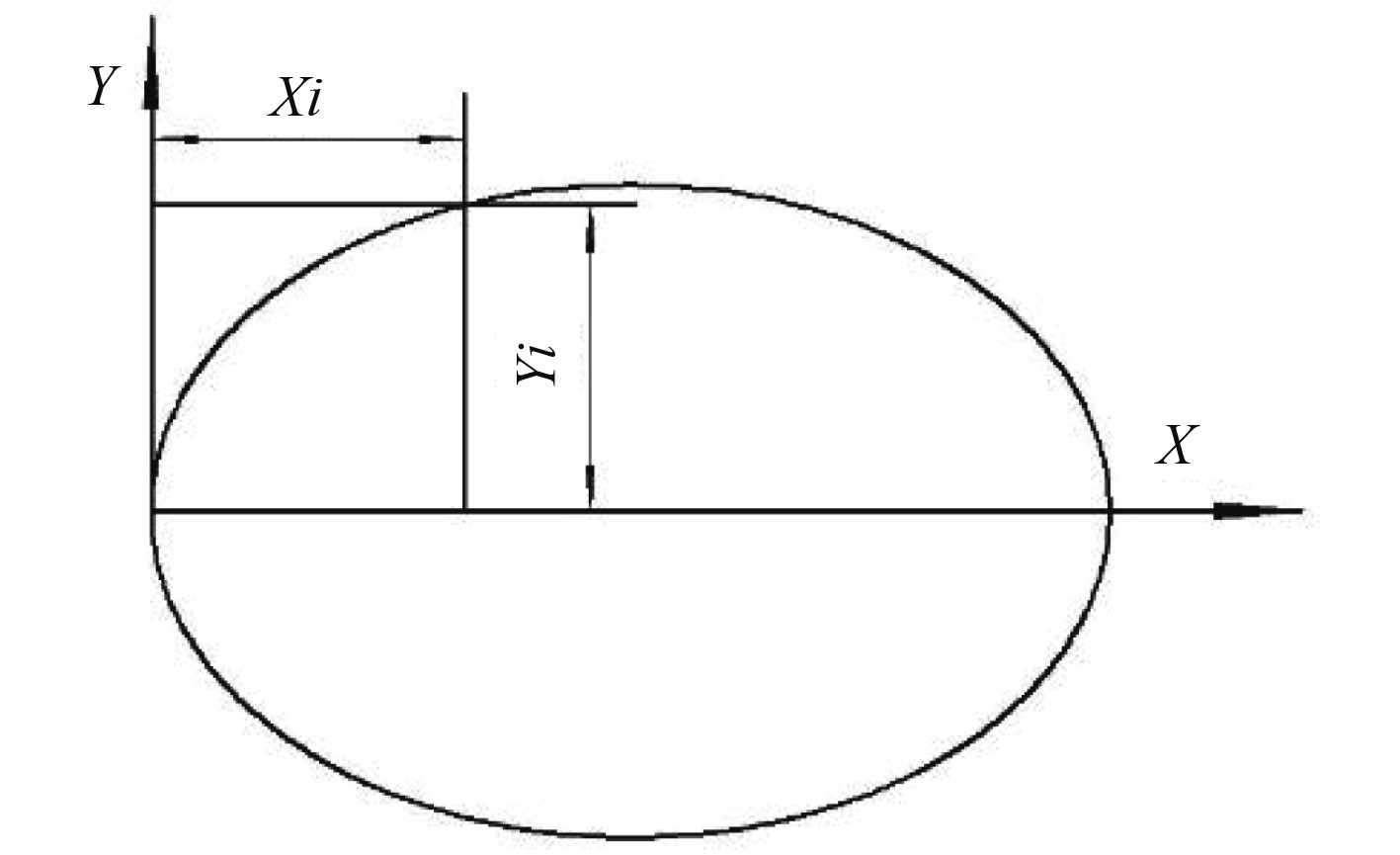
水滴型外形由头部和尾部两部分组成^[8]，由于水滴型尾部线型收敛较快，其丰满度不利于拖缆盘绕，因此，盘绕器截面选择头部水滴型线型，尾部线型则与头部对称，如图4所示。水滴型头部线型方程如下式：

$y=0.5D{\left[1-{\left(\frac{x}{{L}_{f}}\right)}^{{n}_{f}}\right]}^{\frac{1}{{n}_{f}}}\;{\text{。}}$

(6)

式中： $D$ 为水滴型的直径，取值为42.8 mm； ${L}_{f}$ 为水滴型头部长度，取值为31.4 mm； ${n}_{f}$ 为头部指数参数，取值为2。

按圆柱体模型方法建模、划分网格、加载边界条件，计算前后对称水滴型截面的盘绕器在不同来流速度下的阻力值，其结果如表4所示。

2.4 不同线型截面阻力计算结果对比

将圆形截面、卡克斯线型截面以及前后对称水滴型截面的盘绕器迎流阻力值进行比较，如表5所示。

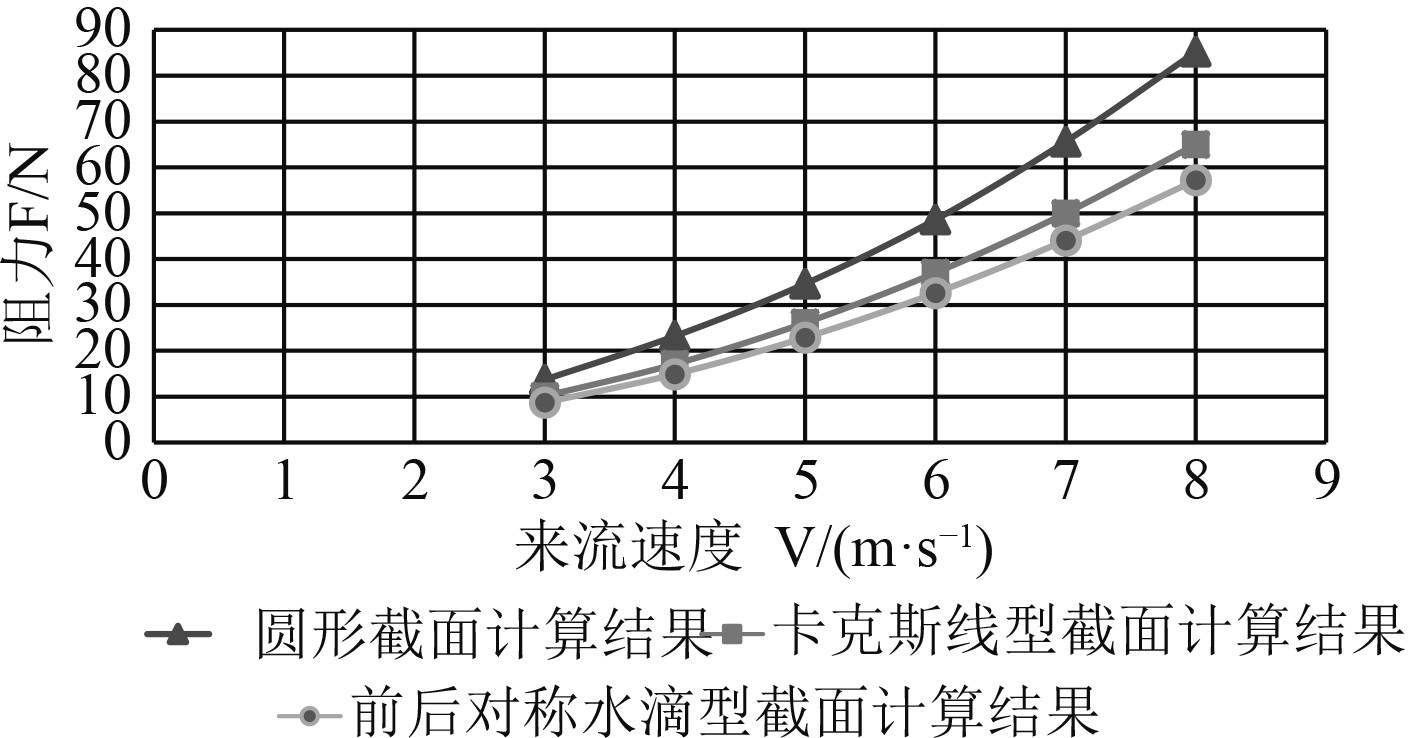
不同截面的盘绕器在低速度条件下的阻力值如图5所示。

可以看出，相对圆形截面来说，前后对称水滴型截面的盘绕器减阻效果最好，在低速条件下（航速3 m/s），最大减阻百分比可达36.5%，在特定高速条件下（航速22 m/s），可减少阻力213.9 N，减阻百分比达33.9%。因此，选择前后对称水滴型截面作为盘绕器最终的设计方案。

3 试验验证

按照前后对称水滴型线型设计盘绕器，并试制样机。

将盘绕器安装在航行体上，通过弹簧推动楔块，约束盘绕器迎流方向的位移，当盘绕器在水中的阻力大于500 N时，盘绕器将会被动解脱，否则需要主动解脱。盘绕器主动解脱前，在高速（速度达到22 m/s）航行过程中，一直未脱离航行体，说明优化后的盘绕器迎流阻力不大于500 N，从而验证了仿真模型。当体通过控制系统主动解脱盘绕器时，盘绕器能够顺利解锁，释放展开拖曳电缆，达到了预期的效果。

4 结　语

在雷诺数 ${R}_{e}$ =3.9×10³工况下对圆形截面的盘绕器进行数值模拟，通过与文献研究结果对比，证明了本文所采用方法的正确性，为后续实际工况下的阻力计算和优化奠定了基础。通过采用CFX软件对水下航行体拖缆盘绕器进行模拟计算研究，得出如下主要结论：

1）从模拟计算结果可以看出，前后对称水滴型截面盘绕器迎流阻力小于卡克斯线型截面及圆形截面的盘绕器。相对圆形截面盘绕器，前后对称水滴型截面盘绕器最大可减阻36.5%，并且在试验过程中，前后对称水滴型截面盘绕器取得了较好的工程效果。

2）通过借用已有的线型，对水中航行物进行外形优化，可以降低航行物的迎流阻力，从而为快速进行工程设计提供了一种可行的设计方法。