2. 中国人民解放军92196部队,山东 青岛 266011
2. No. 92196 Unit of PLA, Qingdao 266011, China
管道在工业尤其是造船业上应用非常广泛,如潜艇上的液压系统、输水系统、高压气系统以及应急吹除系统等,由于其工作节点遍及各个舱室,管道作为其主要组成部分,起着连接系统总站与各目标节点的重要作用。然而,由于潜艇内部空间狭窄,设备数量众多,为满足设备安装及总体布局需求,在各系统管路中必然要采用大量不同偏转角度与弯曲半径的弯管。
弯管较好地解决了系统连接与空间布局的问题,但同时也带来了诸多弊端。例如由于受到弯头弯曲程度、流体流动马赫数和流体运动方向等诸多因素的影响,弯头内流场呈现出十分复杂的流动特性。在管壁附近会形成分离区,特别是弯头横截面上产生的二次流动,会造成流体总压和能量的损失[1],进而在一定程度上影响系统的工作效率。潜艇高压气应急吹除主压载水舱时,高压气体从气瓶经管路迅速供入水舱,相比于油、水等液体介质,高速流动的气体经过弯管时所引起的局部压降则更为显著。因此,在研究潜艇高压气应急吹除系统的工作效率并建立相应数学模型时,必须考虑弯管效应对沿程压力损失的影响。
目前,国内学者在研究高压气应急吹除主压载水舱过程时,采用的方法主要有理论分析法[2]、小比例模型实验法[4]和CFD数值仿真法[5],张建华等[6-7]采用VOF两相流模型对该过程进行了数值仿真,研究了主压载水舱内气液界面的生成发展及吹除速率的变化规律。然而,上述研究针对的仅是应急吹除的最后一个阶段,即高气压进入水舱后的膨胀排水过程,未对该阶段之前的高压气体输送过程进行分析以揭示高压气体在管道内的流动状态及作用机理,特别是弯管对沿程压力损失的影响,因而缺失了建立系统完整的高压气吹除数学模型的关键环节。文献[2]在建立系统模型时虽考虑了管路问题,但只提到使用当量长度法进行等效,而未给出量化的等效方法。
本文以现有研究结论[8]为基础,采用基于重整化群方法提出的RNG k-ε湍流模型封闭弯管内部流场的RANS方程,通过直接数值求解该方程,对90°弯管的内部流场形态进行仿真,给出在高压状态下90°弯管的等效长度计算方法,重点分析弯管内的压力分布、速度分布、二次流现象以及对总沿程压力损失的影响。
1 湍流模型由于在弯曲流线情况下,湍流是各向异性的,此时的湍动粘度为各向异性的张量,而标准k-ε模型中,雷诺应力各个分量的湍动粘度却是各向同性的标量,因此,采用Yakhot及Orzag于1986年提出的RNG k-ε湍流模型[9]来封闭雷诺平均N-S方程。该模型中的产生项不仅与流动情况有关,而且还是空间坐标的函数,因而可以更好地处理高应变率及流线弯曲程度较大的流动,其输运方程为[10]:
| $\frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + {G_b} - \rho \varepsilon - {Y_M}{\text{,}} $ | (1) |
| $\begin{split}\frac{{\partial (\rho \varepsilon )}}{{\partial t}} +& \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {{\alpha _\varepsilon }{\mu _{eff}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\ &{C_{1\varepsilon }}\frac{\varepsilon }{k}({G_k} +{C_{3\varepsilon }}{G_b}) - C_{2\varepsilon }^*\rho \frac{{{\varepsilon ^2}}}{k}{\text{。}}\end{split}$ | (2) |
式中:
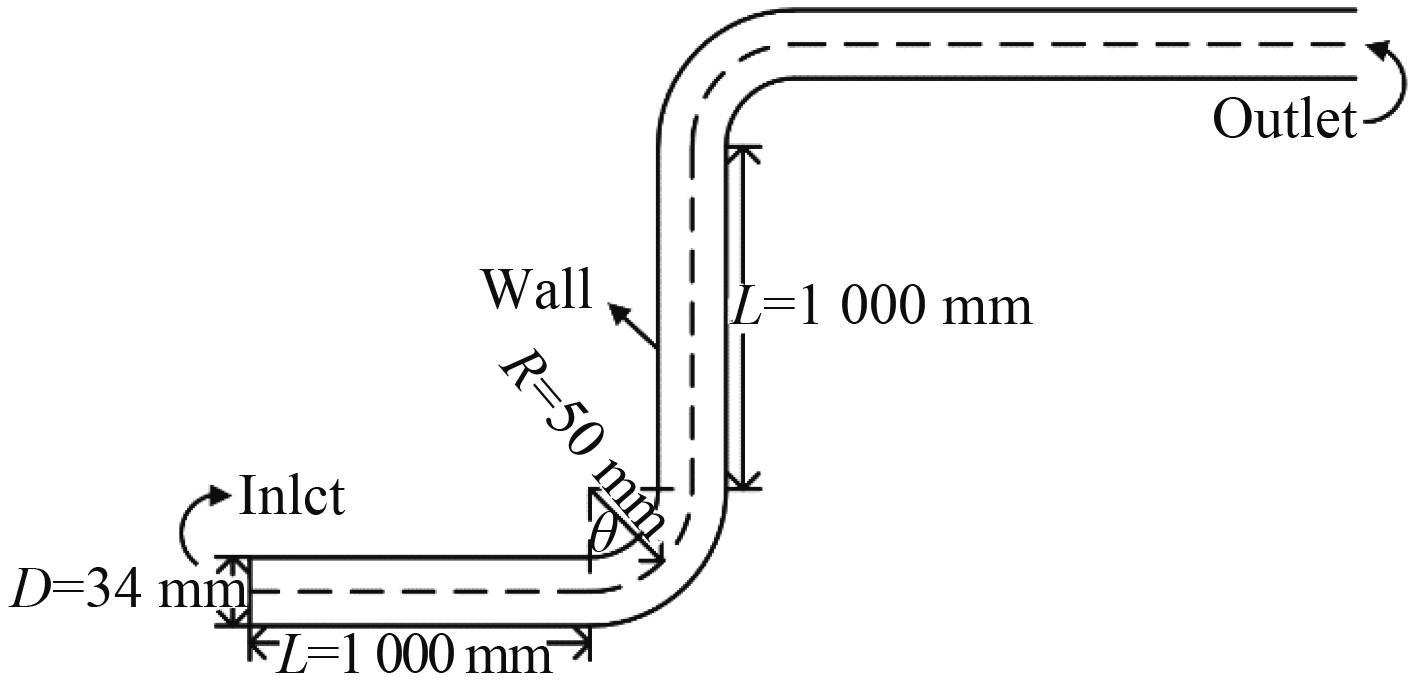
设管路总长度为10 m,弯管数量分别为0,2,4,6,8个,弯曲半径均为50 mm,弯管上游直管长度为1000 mm,原点O位于弯管曲率的回转中心,θ为极角,并定义弯曲段的主流入口截面处θ为0°,弯曲段出口截面处θ为90°,如图1所示。
|
图 1 管路及弯头尺寸参数 Fig. 1 Dimensions of the pipe and elbow |
入口边界:定义为压力入口20 MPa;
出口边界:定义为压力出口1 MPa;
固壁边界:管壁定义为无滑移固壁边界条件,无滑移条件u=v=w=0。
采用有限体积法对控制方程进行离散,采用SIMPLE算法处理离散控制方程中的压力—速度耦合问题。
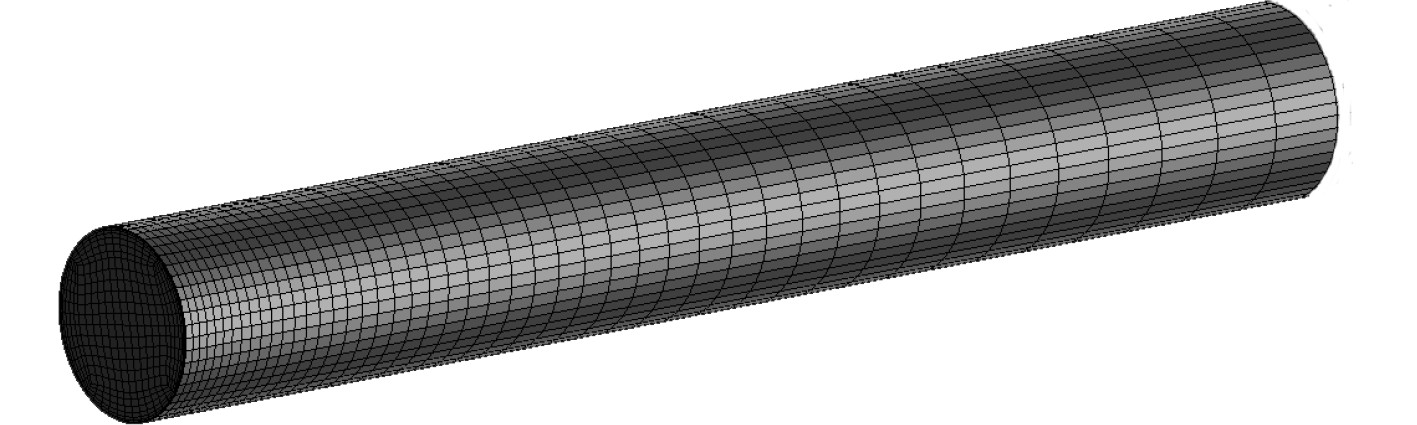
3.2 离散网格采用六面体网格单元对管路进行结构化网格划分,为提高计算效率,并保证在流动较剧烈的区域能够捕捉到较精确的流动细节,对直管段较长的部分沿主流方向采用抛物线型节点分布规律,同时对弯管及其附近区域进行网格加密,如图2所示。采用近壁模型法来求解近壁区粘性底层及过渡层内的流动,第1层网格节点与端点之间的距离设为1.5 mm,网格增长比率为1.05,如图3所示。5个算例的网格总数均为32万左右,仿真研究发现,当管路长度方向上的网格节点数达到以上设置密度时,网格的数值解已经达到了网格独立解。

|
图 2 弯管部分网格划分 Fig. 2 Mesh of the elbow |
|
图 3 直管部分网格划分 Fig. 3 Mesh of the straight pipe |
在实验方案中设计了不同弯头数的多条管路,其目的是为了便于研究其等效管路长度,而弯头对于各管路内具体流场形态的影响则具有相似性,因此,以下数值仿真结果分析中,仅以具有2个弯管的管路为例,重点对弯管内部流程形态进行分析。
4.1 弯管及其附近压力分布规律图4 为弯管对称面上的等压线分布。可以看出,弯头对管内的压力分布会产生显著影响。从管路入口处到弯头1的直管段,其对称面上压力分布均匀。而从弯头1出口至弯头2入口的直管段,因受到弯头1的影响,其对称面上的压力呈非均匀分布,靠近管壁的区域压力较高,靠近管路中心的区域压力较低,这一现象在弯头2下游的直管段中逐渐消失,压力又重新达到均匀分布状态。同时也可发现,由于分子黏性导致流体沿管道壁面产生了沿程损失和二次流损失,使得弯管下游直管段处的压力值小于上游直管段处的压力值。

|
图 4 对称面上等压线分布 Fig. 4 Isobaric distribution of the symmetry plane |
在弯头内,沿径向的压力梯度非常大,呈现出靠近内壁面区域的压力值小,而靠近外壁面区域压力值较大的分布形态,产生这一现象的主要原因是气体在流动过程中受到弯管曲率的影响,离心力作用使其向曲率半径较大的外壁面附近移动,导致众多流体推挤外侧壁面所致[11]。
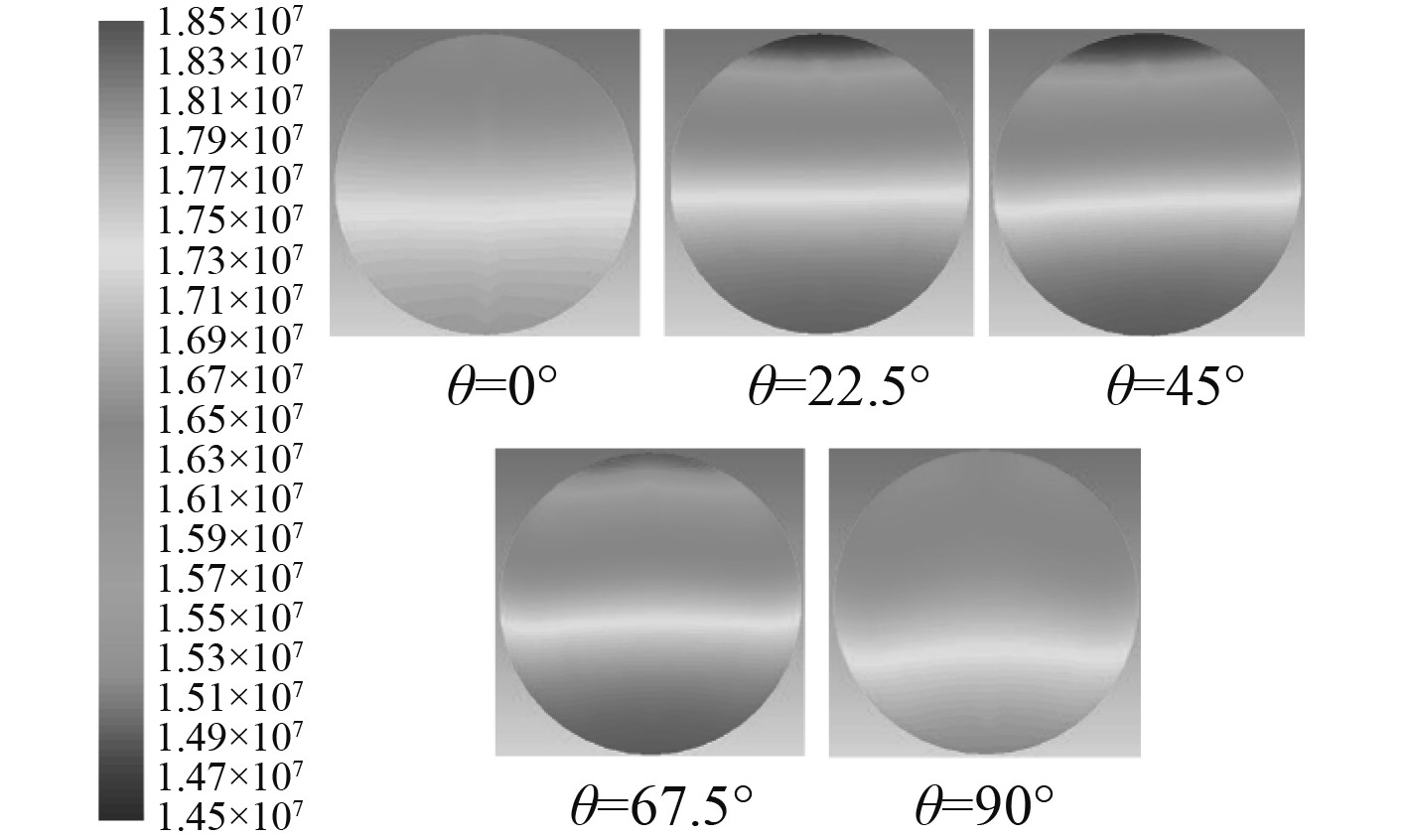
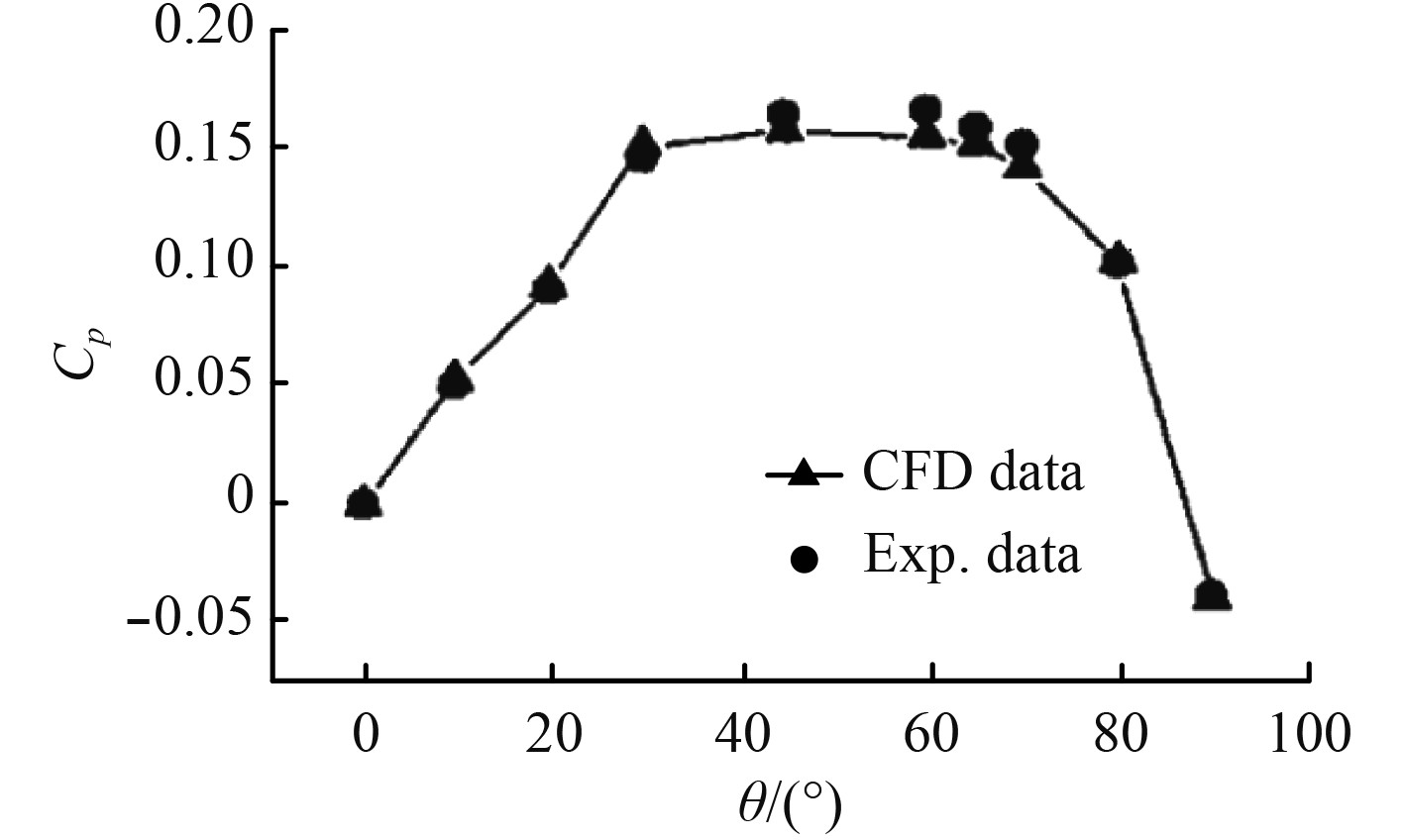
为进一步研究压力分布在弯头不同极角截面处的发展变化规律,提取弯头1上θ=0°,θ=22.5°,θ=45°,θ=67.5°和θ=90°五个不同截面上的压力分布云图,如图5所示。图中上部为弯头内侧,下部为弯头外侧。由图显见,压力在弯头横截面上呈现出内低外高的分布态势,且在θ=45°截面之前,内侧压力逐渐降低,外侧压力逐渐升高。而在θ=45°截面之后,内侧压力又逐渐升高,外侧压力则开始逐渐降低。这是因为,在θ=45°截面之前,气体所受离心力逐渐增大,而在θ=45°截面之后,离心力开始逐渐减小所导致的,这与文献[12]所进行的理论研究结论和数值研究结论相一致,如图6所示。
|
图 5 弯管不同极角截面上的压力分布云图 Fig. 5 Pressure distribution contours of different polar-angle sections of the elbow |
|
图 6 弯头外侧壁面上压力系数随极角的变化关系[12] Fig. 6 Pressure factor versus polar-angle on the outer wall |
表1为管路中存在不同数量的弯头时,管路入口截面和出口截面的平均静压以及气体在管路中总的沿程压力损失。
|
|
表 1 不同数量弯头对管路沿程压力损失的影响 Tab.1 Influence of different number of elbows to the pressure loss along the pipe |
通过该表计算可知,此实验方案中每2个弯头所产生的局部压降大约相当于0.5 m相同直径的直管所产生的摩擦压力降,且与无弯管时的沿程压力损失比较而言,8个90°弯管可额外造成0.8 MPa的压降,这对潜艇高压气的应急吹除效率来说无疑将造成较大的影响。因此,在潜艇设计建造阶段,应对高压气管路进行合理布局,尽可能少地采用弯管尤其是偏转角度较大的弯管进行连接,以提高潜艇在紧急情况下的高压气吹除速率,保证潜艇应急上浮能力。
4.2 弯管及其附近速度分布规律弯管的存在会改变管路内的压力分布,也必然会对管路内的速度分布产生影响,图7为管路弯曲段的速度分布云图及速度矢量图。由图可知,在弯头1入口截面之前,管路内的主流速度基本呈均匀分布,而进入弯头1后,其主流速度明显发生畸变,弯头内侧速度增大,外侧速度减小,这一趋势大约持续到θ=45°截面处。随后,内侧速度开始减小,外侧速度开始增大。由于流速较高,在惯性作用下,气体在穿过θ=90°截面后,其主流方向不再与直管段平行,而是与其形成一定角度,并随着流动的发展,管内速度场逐渐趋向于均匀分布,同时气体也得到进一步加速。从图中可清晰看出,弯头2内侧速度明显高于弯头1内侧速度。

|
图 7 弯管对称面速度分布及速度矢量图 Fig. 7 Velocity distribution and vectorgraph of the elbow symmetry plane |
气体在弯管不同极角截面上的速度分布及其变化规律如图8所示。由图可知,速度分布在θ=22.5°和θ=45°截面之间大致相同,而在θ=67.5°截面上,弯头内侧靠近壁面的区域开始出现低速区,当到达θ=90°截面时,由于弯管内侧逆压梯度很大,导致主流速度急剧减小而产生分离,使得该低速区已发展相当明显。从整体看,随着流动的发展,弯管内主流速度的最大值逐渐向外侧偏移,但始终在弯管内侧与中轴线之间区域,这与文献[13]开展的实验研究所得结论相一致。

|
图 8 弯管不同极角截面上的速度分布云图 Fig. 8 Velocity distribution contours of different polar-angle sections of the elbow |
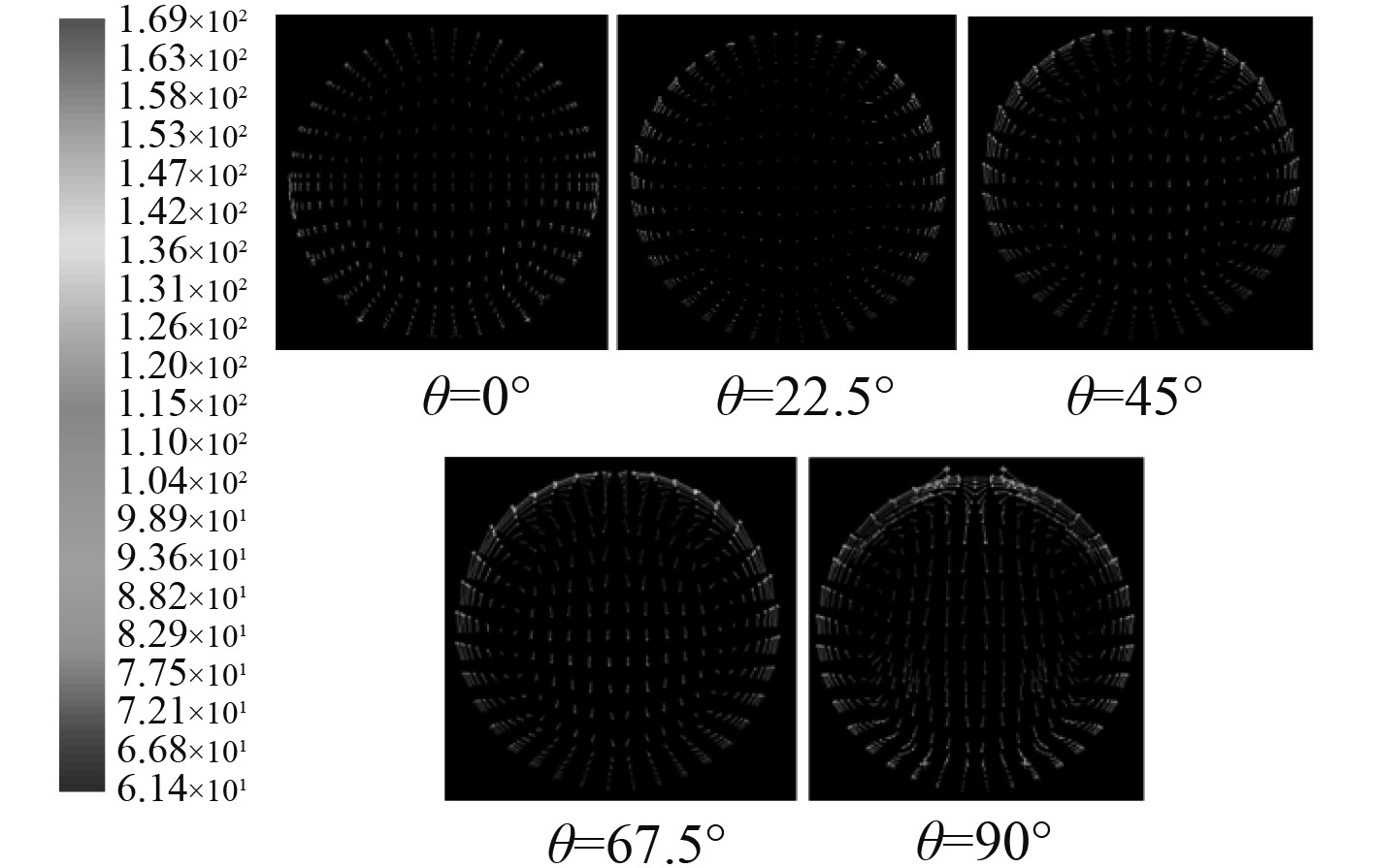
图9为速度矢量在弯管不同极角截面上的投影图,可以清楚地看到二次流的形成和发展过程。在θ=0°截面上,弯管的预效应还不明显,速度矢量在该截面上的投影几乎为零。当进入弯管后,在流场逆压梯度和分子黏性的共同作用下,二次流开始逐渐形成;在θ=67.5°截面上,已能较清晰看到一对二次流漩涡;在弯管终端即θ=90°截面上,二次流涡对发展最为充分,并由于惯性会继续向下游发展一段距离。二次流导致了弯管内横截面方向上的动能和能量交换,既改变了主流方向的平均速度,又减少了流场的总压。由此也说明,选用RNG k-ε湍流模型模拟弯管内带旋转和分离的流动以及捕捉二次流漩涡有效且可靠。
|
图 9 弯管横截面上二次流图像 Fig. 9 Secondary flow pictures on the sections of elbow |
本文通过直接数值求解可压缩气体的RANS方程,采用RNG k-ε湍流模型对潜艇上90°弯管内的极高压气体流动过程进行模拟,分析弯管内的流场形态及其对压力降的影响,通过比对其他学者的实验数据,验证了所采取的数值方法的有效性,并得到以下结论:
1)在管路总长度不变情况下,弯管引起的局部压力降会较大程度增加管路总的沿程压力损失,在文中所述压力条件下,一个弯管所产生的局部压降约为0.2 MPa,其当量长度约为0.25 m。
2)弯头内沿流动方向上的压力分布规律为内侧压力先减小后增大,外侧压力先增大后减小,但外侧压力始终大于内侧压力;速度分布规律为内侧速度先增大后减小,外侧速度先减小后增大,且在弯头终端截面,其内侧会形成低速区。
3)流体进入弯头后,由于流场逆压梯度和分子黏性的共同作用,会有二次流产生,从而导致弯管内横截面上发生动能和能量的交换。
| [1] |
江山, 张京伟, 吴崇健, 等. 基于FLUENT的90°圆形弯管内部流场分析[J]. 中国舰船研究, 2008, 3(1): 37-41. JIANG Shan, ZHANG Jingwei, WU Chongjian, et al. Numerical simulation of inner flow in 90° bending duct of circular-section based on FLUENT[J]. Chinese Journal of Ship Research, 2008, 3(1): 37-41. DOI:10.3969/j.issn.1673-3185.2008.01.009 |
| [2] |
金涛, 刘辉, 王京齐, 等. 舱室进水情况下潜艇的挽回操纵[J]. 船舶力学, 2010, 14(1-2): 34-43. JIN Tao, LIU Hui, WANG Jingqi, et al. Emergency recovery of submarine with flooded compartment[J]. Journal of Ship Mechanics, 2010, 14(1-2): 34-43. |
| [3] |
叶剑平, 戴余良, 李亚楠. 潜艇主压载水舱高压气吹除系统数学模型[J]. 舰船科学技术, 2007, 29(2): 112-115. YE Jianping, DAI Yuliang, LI Yanan. The mathematical model of the pneumatic blowing system of the submarine's ballast tanks[J]. Ship Science and Technology, 2007, 29(2): 112-115. |
| [4] |
刘辉, 浦金云, 李其修, 等. 潜艇高压气吹除主压载水舱系统实验研究[J]. 哈尔滨: 哈尔滨工程大学学报, 2013, 34(1): 34-39. LIU Hui, PU Jinyun, LI Qixiu, et al. The experiment research of submarine high-pressure air blowing off main ballast tanks[J]. Journal of Harbin Engineering University, 2013, 34(1): 34-39. |
| [5] |
杨晟, 余建祖, 程栋, 等. 潜艇应急燃气吹除过程的数值仿真及实验验证[J]. 北京: 北京航空航天大学学报, 2010, 36(2): 227-230. YANG Sheng, YU Jianzu, CHENG Dong, et al. Numerical simulation and experimental validation on gas jet blowing-off process of submarine emergency[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(2): 227-230. |
| [6] |
张建华, 胡坤, 刘常波. 潜艇高压气吹除主压载水舱过程的数值模拟[J]. 船舶力学, 2015, 19(4): 363-368. ZHANG Jianhua, HU Kun, LIU Changbo. Numerical simulation on compressed gas blowing ballast tank of submarine[J]. Journal of Ship Mechanics, 2015, 19(4): 363-368. DOI:10.3969/j.issn.1007-7294.2015.04.003 |
| [7] |
张建华, 杨伟, 徐亦凡. 基于Fluent的潜艇高压气排水速率深度影响研究[J]. 舰船科学技术, 2013, 35(11): 34-37. ZHANG Jianhua, YANG Wei, XU Yifan. Research on depth influence upon draining rate of submarine compressed gas based on Fluent[J]. Ship Science and Technology, 2013, 35(11): 34-37. DOI:10.3404/j.issn.1672-7649.2013.11.008 |
| [8] |
丁珏, 翁培奋. 三种湍流模式数值模拟直角弯管内三维分离流动的比较[J]. 计算物理, 2003, 20(5): 386-390. DING Yu, WENG Peifen. Numerical study on three dimensional turbulent separated Flow in right-angled curved duct by three turbulent models[J]. Chinese Journal of Computational Physics, 2003, 20(5): 386-390. DOI:10.3969/j.issn.1001-246X.2003.05.003 |
| [9] |
V. YAKHOT, S. A. ORZAG. Renormalization group analysis of turbulence: basic theory[J]. Journal of Scientific Computing, 1986, 1(1): 39-51. |
| [10] |
王福军. 计算流体动力学分析—CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
|
| [11] |
孙业志, 胡寿根, 赵军等. 不同雷诺数下90°弯管内流动特性的数值研究[J]. 上海: 上海理工大学学报, 2010, 32(6): 525-529. SUN Yezhi, HU Shougen, ZHAO Jun, et al. Numerical study on flow characteristics of 90°bend pipe under different reynolds number[J]. Journal of University of Shanghai For Science And Technology, 2010, 32(6): 525-529. DOI:10.3969/j.issn.1007-6735.2010.06.004 |
| [12] |
丁珏, 翁培奋. 90°弯管内流动的理论模型及流动特性的数值研究[J]. 计算力学学报, 2004, 21(3): 314-321, 329. DING Yu, WENG Peifen. Numerical simulation of theoretical models & flow characteristics in 90° bending duct[J]. Chinese Journal of Computational Mechanics, 2004, 21(3): 314-321, 329. DOI:10.3969/j.issn.1007-4708.2004.03.010 |
| [13] |
尚虹, 王尚锦, 席光, 等. 90°圆截面弯管内三维紊流场实验研究[J]. 航空动力学报, 1994, 9(3): 263-266. SHANG Hong, WANG Shangjin, XI Guang, et al. Experimental study of 3-D turbulent flow field in a 90° bend pipe[J]. Journal of Aerospace Power, 1994, 9(3): 263-266. |
 2020, Vol. 42
2020, Vol. 42
