2. 中国船舶科学研究中心,江苏 无锡 214082
2. China Shipping Research Center, Wuxi 214082, China
对商船而言,减摇主要是为了避免货物损坏、减小船员晕船以及防止船舶在高海况下倾覆等;对战舰而言,减摇对直升机起降、编队控制、海上补给和保障船员战斗力等方面有重要意义。主被动减摇执行器(装置)有舭龙骨、减摇水舱、减摇鳍和减摇舵系统(RRD,Rudder Roll Damping)和陀螺横摇稳定器等。目前,船舶减横摇运动主要靠减摇鳍和舵鳍联合控制系统,但舵减摇系统,相对减摇鳍造价较低,不增加整船建造的额外费用,也具有较好的减摇效果,不增加船舶阻力和水下噪声,因此,舵减摇具有广泛的应用前景。
喷流舵是一种升力型高效舵,其工作机理源于航空领域的环量控制翼[1-2],环量控制翼的概念是20世纪60年代航空界为获取机翼高升力提出的,是一种采用翼面吸力和离心力的平衡效应来推迟边界层分离的高升力机翼[3]。喷流舵的优点是:1)通过喷出少量流体使舵获得较高的升力;2)改变喷流动量系数的大小,可实时迅速地控制舵面环量;3)在相同升力性能的条件下,舵面线型要求比普通舵的低,在机械结构上也无可动部件,与普通襟翼舵相比,结构更加简单有效[3]。喷流舵在船舶上的应用研究工作始于20世纪80年代初,虽然已有一些学者用实验方法确定了喷流舵的特性,但对喷流舵的应用研究并不多。
舵减摇自20世纪70年代被提出以来,国内外学者对舵减摇进行了广泛研究。Van Gunsteren,Cowley和Lambert,Carley,Lloyd,Baitis,Van Amerongen和Van der Klugt,Lauvdal和Fossen,Blanke和Christensen,Hearns和Blank等[7-12]提出相关舵减摇研究成果。21世纪,Blanke[14]为舵减摇设计多模态控制器,根据不同波浪周期转换不同控制器,以更有效地处理海浪波谱范围和波浪低频干扰;Perez等[13]提出限制性模型预测控制(model predictive control,MPC),可有效处理舵机的非线性问题;Tzeng等[7]提出内模控制,并通过减少控制器输出避免了舵机饱和。
本文针对舵的航向横摇控制模型设计一种单入双出的FDLQR控制器,以实现高海况下的横向减摇控制。所设计的控制器有如下优点:1)在控制器前段引入高通滤波器和低通滤波器,利用舵减摇的物理分频特性,即舵对航向角和舵对横摇角响应的频率带宽的分离,实现控制输入的解耦;2)引入全状态反馈和参考前馈,化为一种LQ轨迹最优控制问题。本文采用的控制方法主要参考文献[6],对RRD系统执行器喷流舵的研究主要参照文献[4]的试验结果提出控制方案,首次将喷流舵引入RRD系统,并结合FDLQR控制方法验证喷流舵系统(Jet Rudder Roll Damping,JRRD)的有效性和高效性。
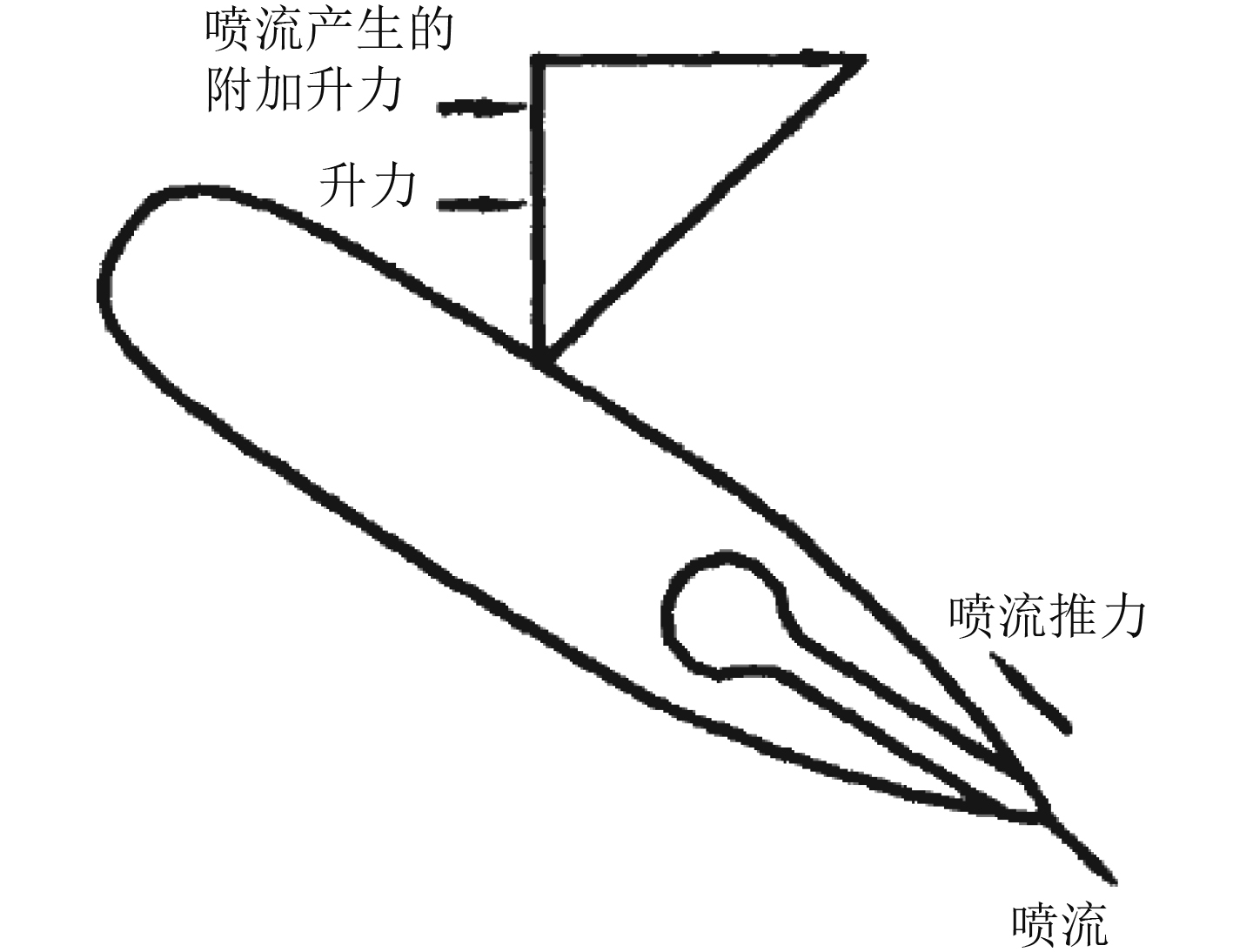
1 喷流舵流体动力特性分析喷流舵流体动力原理源于航空界的可控环量翼,喷流舵是在翼面尾部附近进行切向喷流,将尾部分流点沿尾缘下表面推移,从而控制和增加舵面流动环量。而常规舵仅仅通过攻角获得升力,因此,从原理上来说,喷流舵必然比常规舵高效。喷流舵流体动力特性原理如图1所示。
|
图 1 喷流舵流体动力原理 Fig. 1 Hydrodynamic principle of jet rudder |
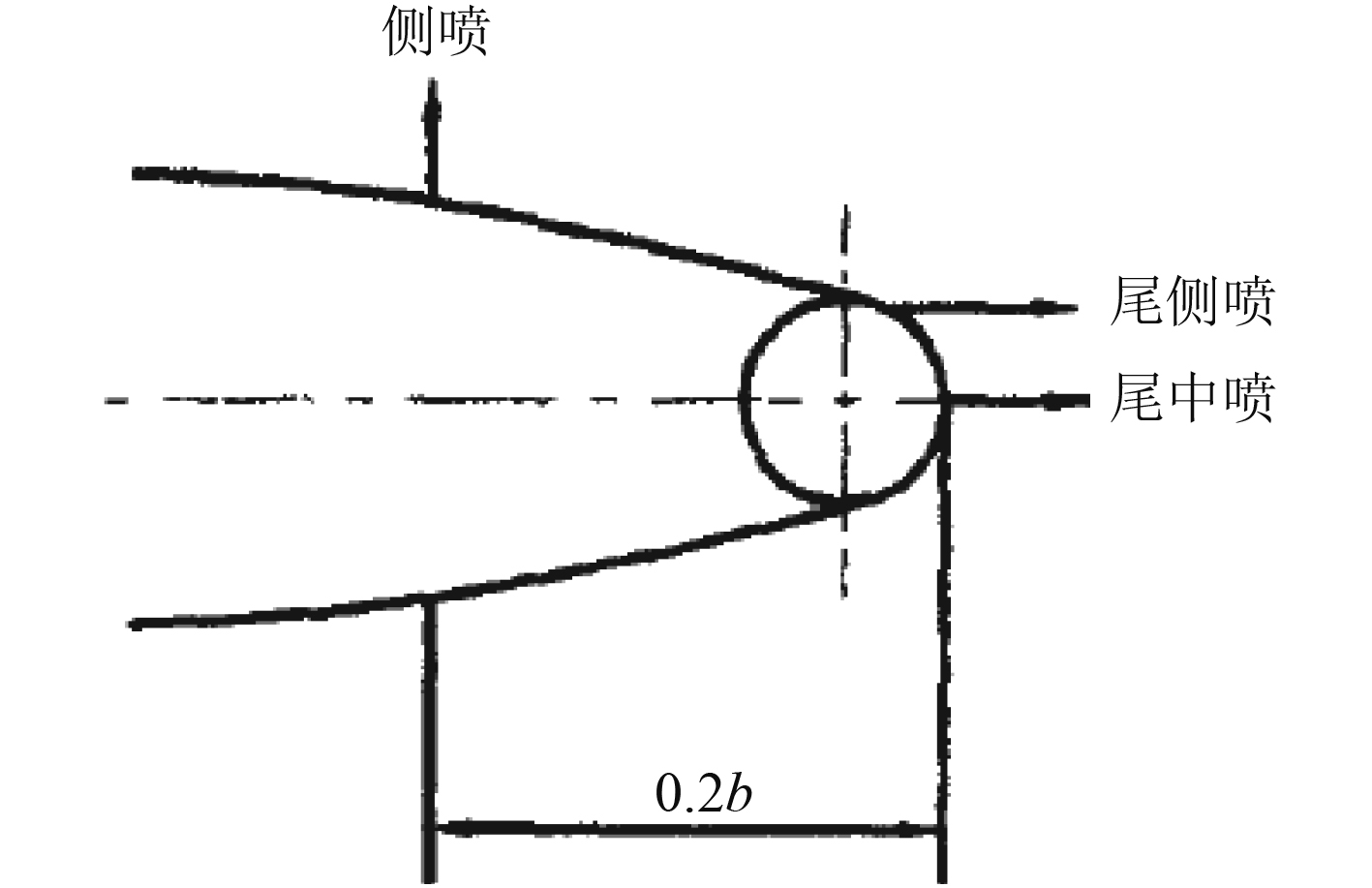
根据文献[4]的结论,侧喷、尾侧喷和尾中喷3种喷流形式中,3种喷流如图2所示。尾侧喷具有最大升力系数,其值随着
| ${C_{\mu} }=\frac{{{\rho _J}Q{V_j}}}{{\frac{1}{2}{\rho _{\infty} }V_0^2A}}=\frac{{2{Q^2}}}{{V_0^2bS\Delta hS'}}{\text{。}}$ | (1) |
式中:
|
图 2 喷流舵喷流形式 Fig. 2 Patterns of jet rudder |
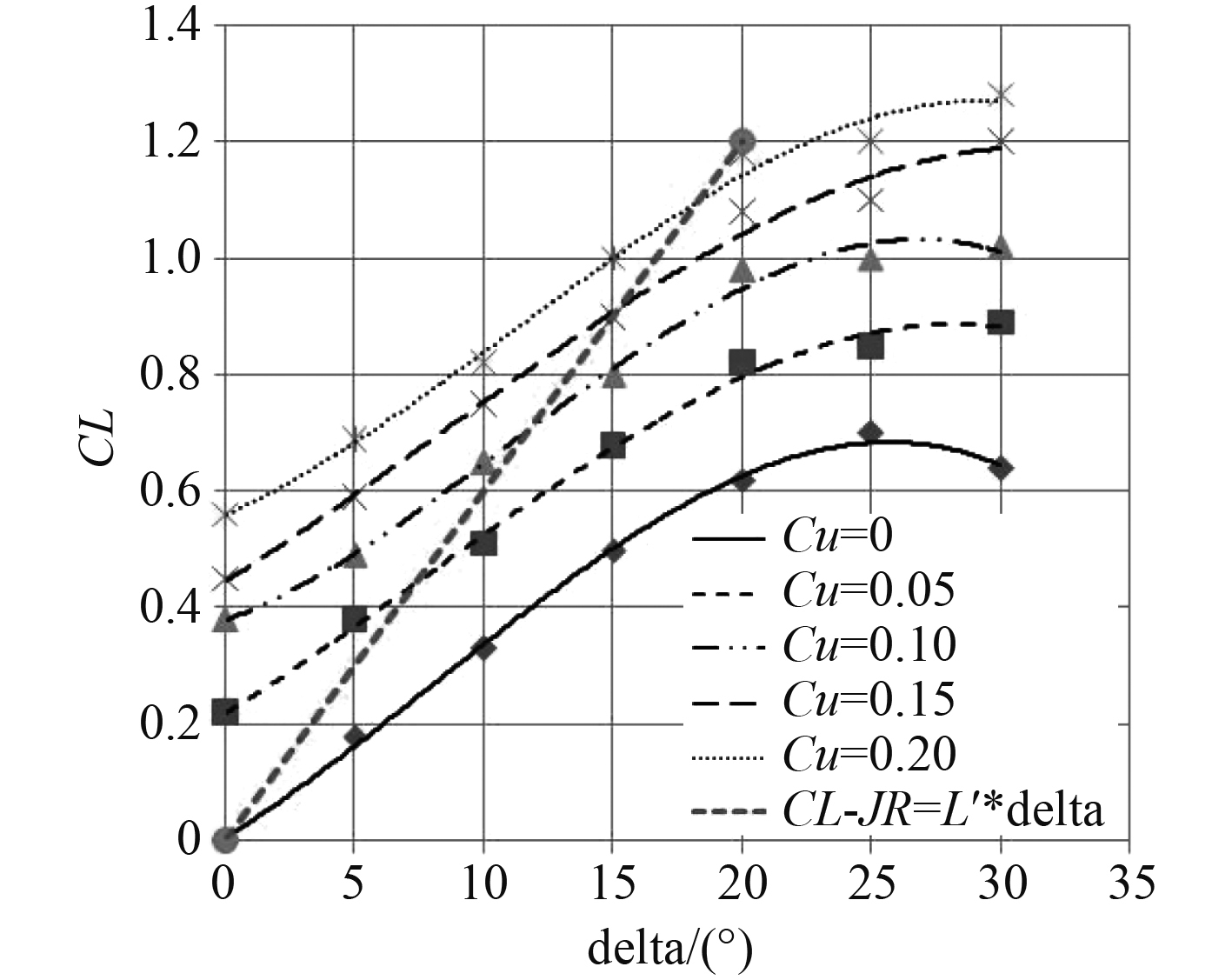
假设喷流动量系数在
|
图 3 喷流舵升力系数特性图 Fig. 3 Characteristic chart of lift coefficient of jet rudder |
| ${C_{L - {\rm{JR}}}}=f({C_{\mu} }(\delta ),\delta )={L'_{{\rm{J}}\delta }}\delta \;{\text{。}}$ | (2) |
式中,
实际船舶运动是六自由度的,相互耦合,六自由度模型可根据实际研究重点进行简化或解耦。船舶横向运动如横荡与艏摇运动,纵向运动如垂荡与纵摇运动等耦合作用较强。通常,纵向运动,只考虑纵摇和垂荡2个自由度;横向运动,仅考虑横摇、横荡和首摇3个自由度或横摇、横荡、首摇和纵荡4个自由度。
只考虑纵荡、横摇、摇和横摇5个运动状态时,忽略升沉和纵摇对该4自由度运动的影响,即
1)运动坐标系原点
2)
根据动力学一般方程形式:
| $\left\{ \begin{array}{l} m(\dot u - vr)={X_{\sum} } \;{\text{,}} \\ m(\dot v + ur)={Y_{\sum} } \;{\text{,}}\\ {I_x}\ddot \phi ={K_{\sum} } \;{\text{,}}\\ {I_z}\dot r={N_{\sum} } \;{\text{。}}\\ \end{array} \right.$ | (3) |
方程左侧为船舶自身运动产生的惯性力(力矩),
| $\left\{ \begin{array}{l} (m + {m_x})\dot u - (m + {m_y})vr=X {\text{,}}\\ (m + {m_y})\dot v + (m + {m_x})ur + {m_y}{\alpha _y}\dot r - {m_y}{l_y}\ddot \phi =Y {\text{,}}\\ ({I_x} + {J_x})\ddot \phi - {m_y}{l_y}\dot v - {m_x}{l_x}ur + W \cdot \overline {GM} \cdot \phi =K {\text{,}}\\ ({I_z} + {J_z})\dot r + {m_y}{\alpha _y}\dot v=N {\text{。}}\\ \end{array} \right.$ | (4) |
式中:
写成非线性系统一公式如下:
| ${\dot{ x}}={{f}}({{x}},{{u}},{{d}}){\text{。}}$ | (5) |
式中:状态变量
| $\left[ {\begin{array}{*{20}{c}} {\dot u} \\ {\dot v} \\ {\dot r} \\ {\dot \psi } \\ {\dot p} \\ {\dot \phi } \end{array}} \right]{\rm{=}}\left[ {\begin{array}{*{20}{c}} {\frac{{{\tau _X}}}{{m + {m_x}}}} \\ {\frac{{({I_x} + {J_x})({I_z} + {J_z}){\tau _Y} + ({I_z} + {J_z}){l_y}{m_y}{\tau _K} - ({I_x} + {J_x}){\alpha _y}{m_y}{\tau _N}}}{{({I_x} + {J_x})({I_z} + {J_z})(m + {m_y}) - ({I_x} + {J_x})\alpha _y^2m_y^2 - ({I_z} + {J_z})l_y^2m_y^2}}} \\ {\frac{{ - ({I_x} + {J_x}){\alpha _y}{m_y}{\tau _Y} - {\alpha _y}{l_y}m_y^2{\tau _K} + (({I_x} + {J_x})(m + {m_y}) - l_y^2m_y^2){\tau _N}}}{{({I_x} + {J_x})({I_z} + {J_z})(m + {m_y}) - ({I_x} + {J_x})\alpha _y^2m_y^2 - ({I_z} + {J_z})l_y^2m_y^2}}} \\ {r\cos \phi } \\ {\frac{{({I_z} + {J_z}){l_y}{m_y}{\tau _Y} + (({I_z} + {J_z})(m + {m_y}) - \alpha _y^2m_y^2){\tau _K} - {\alpha _y}{l_y}m_y^2{\tau _N}}}{{({I_x} + {J_x})({I_z} + {J_z})(m + {m_y}) - ({I_x} + {J_x})\alpha _y^2m_y^2 - ({I_z} + {J_z})l_y^2m_y^2}}} \\ p \end{array}} \right]\;{\text{。}}$ | (6) |
式中:
| $\begin{split} {\tau _X}=\;&(m + {m_y})vr + {X_{uu}}{u^2} + {X_{vr}}vr + {X_{vv}}{v^2} + {X_{rr}}{r^2} +\\ &{X_{\phi \phi }}{\phi ^2} + (1 - {t_{\rm{p}}})\rho {n^2}D_{\rm{P}}^4{k_T} - \frac{1}{2}(1 - {t_R})\rho {A_{\rm{R}}}{f_a}U_{\rm{R}}^2\\ &\sin {\alpha _{\rm{R}}}\cos \delta + {X_{{\rm{env}}}} \;{\text{,}}\\ {\tau _Y}= \;&- (m + {m_x})ur + {Y_v}v + {Y_r}r + {Y_p}p + {Y_{\phi} }\phi + {Y_{vvv}}{v^3} + \\ &{Y_{rrr}}{r^3} + {Y_{vvr}}{v^2}r + {Y_{vrr}}v{r^2} + {Y_{vv\phi }}{v^2}\phi + {Y_{v\phi \phi }}v{\phi ^2} +\\ & {Y_{rr\phi }}{r^2}\phi +{Y_{r\phi \phi }}r{\phi ^2} - \frac{1}{2}(1 + {a_{\rm{H}}})\rho {A_{\rm{R}}}{f_a}U_{\rm{R}}^2\\ &\sin {\alpha _{\rm{R}}}\cos \delta {\rm{ + }}{Y_{{\rm{env}}}} \;{\text{,}}\\ {\tau _K}=\;&{m_x}{l_x}ur - WGM\phi + {K_v}v + {K_r}r + {K_p}p + {K_{\phi} }\phi +\\ & {K_{vvv}}{v^3} + {K_{rrr}}{r^3} + {K_{vvr}}{v^2}r + {K_{vrr}}v{r^2} + {K_{vv\phi }}{v^2}\phi + \\ &{K_{v\phi \phi }}v{\phi ^2} + {K_{rr\phi }}{r^2}\phi + {K_{r\phi \phi }}r{\phi ^2} + \frac{1}{2}(1 + {a_{\rm{H}}})\\ &{z_{\rm{R}}}\rho {A_{\rm{R}}}{f_a}U_{\rm{R}}^2\sin {\alpha _{\rm{R}}}\cos {\delta _{\rm{R}}} + {K_{{\rm{env}}}} \;{\text{,}}\\ {\tau _N}=\;&{N_v}v + {N_r}r + {N_p}p + {N_\varphi }\varphi + {N_{vvv}}{v^3} + {N_{rrr}}{r^3} + \\ &{N_{vvr}}{v^2}r + {N_{vrr}}v{r^2} + {N_{vv\phi }}{v^2}\phi + {N_{v\phi \phi }}v{\phi ^2} +\\ &{N_{rr\phi }}{r^2}\phi + {N_{r\phi \phi }}r{\phi ^2} - \frac{1}{2}({x_{\rm{R}}} + {a_{\rm{H}}}{x_{\rm{H}}})\\ &\rho {A_{\rm{R}}}{f_a}U_{\rm{R}}^2\sin {\alpha _{\rm{R}}}\cos \delta + {N_{{\rm{env}}}} \;{\text{。}} \end{split} $ |
方程变量的含义详见文献[5]。
2.2 船舶直航运动模型假设船舶为直航运动控制,并保持固定航速,在此情况下,可以省略纵荡运动方向的方程,同时忽略非线性项。因此,可以将四自由度非线性耦合运动模型简化为只考虑横荡、横摇和偏航的三自由度直航运动方程,满足RRD控制器设计需要。假设舵的入流角
| ${{M}}{\dot{ \nu}} + {{N}}({u_0}){{\nu}} + {{G}}{{\eta}} ={{b}}\delta\;{\text{。}} $ | (7) |
式中:舵角为
惯性系数矩阵为:
科氏力、向心力和阻尼系数矩阵为:
广义重(浮)力和恢复力(矩)系数为:
广义速度向量为
将式(7)中的各系数矩阵用无因次表示,得
| $\begin{split}{{TM}}'{{{T}}^{ - 1}}{\dot{ \nu}} + \frac{U}{L}{{TN}}'({u_0}){{{T}}^{ - 1}}{{\nu}} +& {\left(\frac{U}{L}\right)^2}{{TG}}'{{{T}}^{ - 1}}{{\eta}} =\\ & \frac{{{U^2}}}{L}{{Tb}}'\delta {\text{。}} \end{split}$ | (8) |
式中,
将式(8)写成状态空间标准形式,令
| $\begin{array}{l} {{x}}={{Ax}} + {{Bu}} \;{\text{,}}\\ {{y}}={{Cx}} \;{\text{。}}\\ \end{array} $ | (9) |
式中:
| ${{A}}=\left[ {\begin{array}{*{20}{c}} {{{({{{A}}_{11}})}_{3 \times 3}}}&{{{({{{A}}_{12}})}_{3 \times 2}}} \\ {{{({{{A}}_{21}})}_{2 \times 3}}}&{{{({{{A}}_{22}})}_{2 \times 2}}} \end{array}} \right]{\text{,}} $ |
| ${({{{A}}_{11}})_{3 \times 3}}=- {{{M}}^{ - 1}} \frac{{{U_0}}}{L}{{TN}}{{{T}}^{ - 1}}{\text{,}} $ |
| ${({{{A}}_{12}})_{3 \times 2}}=- {{{M}}^{ - 1}}\frac{{{U_0}}}{L}{{TG}}{{{T}}^{ - 1}} (:,[2,3]){\text{,}} $ |
| ${({{{A}}_{21}})_{2 \times 3}}=\left[ \begin{array}{*{20}{c}} 0&1&0 \\ 0&0&1 \end{array} \right] {\text{,}}{({{{A}}_{22}})_{2 \times 2}} =\left[ {\begin{array}{*{20}{c}} 0&0 \\ 0&0 \end{array}} \right] {\text{,}}$ |
| ${{B}}={\left[ {\begin{array}{*{20}{c}} {{{({B_1})}_{3 \times 1}}}&0&0 \end{array}} \right]^{\rm{T}}}{\text{,}}{B_1}={{{M}}^{ - 1}}\frac{{U_0^2}}{L}{{Tb}}'{\text{,}} $ |
| ${{C}}=\left[ \begin{array}{*{20}{c}} 0&1&0&0&0 \\ 0&0&1&0&0 \\ 0&0&0&1&0 \\ 0&0&0&0&1 \end{array} \right]{\text{。}}$ |
式中:
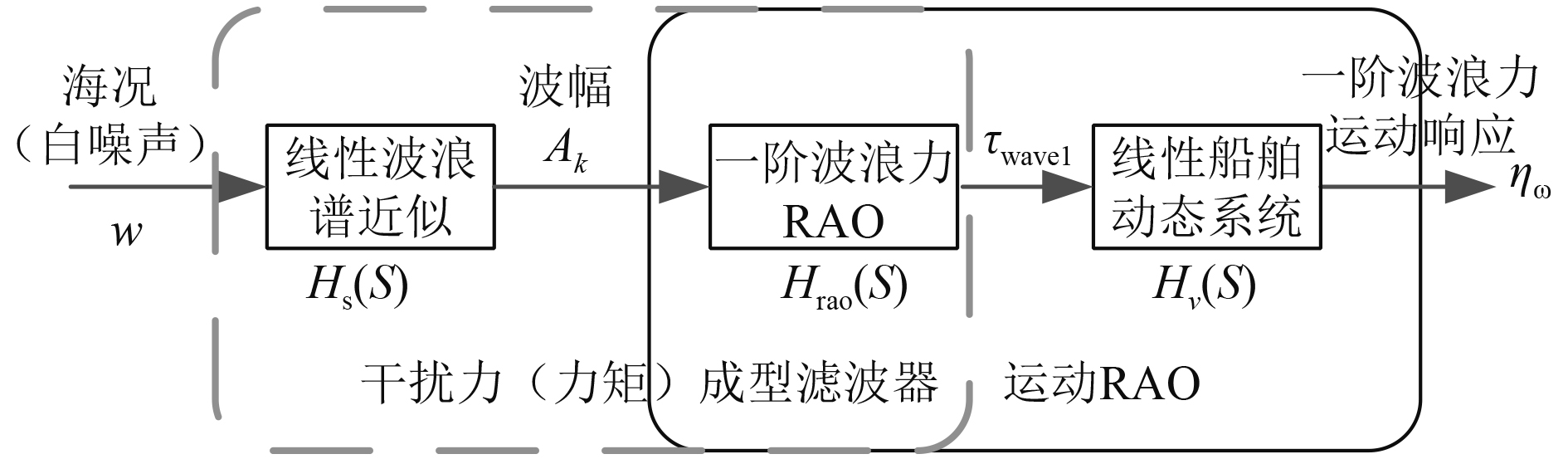
船舶运动控制领域波浪干扰力模拟与运动响应关系如图4所示。具体方法有:1)通过切片理论计算,获得波幅至波浪力的频率响应,然后根据能量叠加法将频域值叠加扩展成时域波浪时间历程;2)根据切片理论计算得到的波幅至波浪力的频率响应,采用非线性最小二乘法进行传递函数拟合,以获得波幅至波浪干扰力的传递函数;3)利用白噪声谱特性,以白噪声为输入,生成波浪干扰力成型滤波器,最后通过成型滤波器(功率谱)拟合的方法获得白噪声至波浪干扰力的传递函数;4)基于切片计算理论,将船型看作长方体,根据简化公式估算波浪力;5)以白噪声输入,进行线性波谱近似和波浪力幅值调整相结合的方法获得波浪干扰力传递函数或状态空间方程(常用2阶)[6],其中,后2种仿真方法最为简便,常用于检验控制方法,考虑到方便,本文工况1中波浪干扰力仿真采用第5种方法,工况2中波浪干扰力仿真采用第4种方法。
|
图 4 波浪干扰力模拟与运动响应关系 Fig. 4 The relationship between wave disturbance force simulation and motion response |
一个自由度的波浪干扰力(矩)表达式用状态空间表达式为:
| $\begin{array}{l} {{{\dot{ x}}}_{\rm{w}}}={{{A}}_{\rm{w}}}{{{x}}_{\rm{w}}} + {{{B}}_{\rm{w}}}u \;{\text{,}}\\ {{{y}}_{\rm{w}}}{\rm{=}}{{{C}}_{\rm{w}}}{{{x}}_{\rm{w}}} \;{\text{。}}\\ \end{array} $ | (10) |
式中:
RRD系统的控制目标是同时控制航向和横摇,即使得目标航向角
| ${{J}}=\min \left\{ {\frac{1}{2}\int_0^{\rm{T}} {({{{\tilde{ y}}}^{\rm{T}}}{{Q}}{\tilde{ y}} + {{{u}}^{\rm{T}}}{{Ru}}){{{\rm{d}}}}\tau } } \right\}\;{\text{。}}$ | (11) |
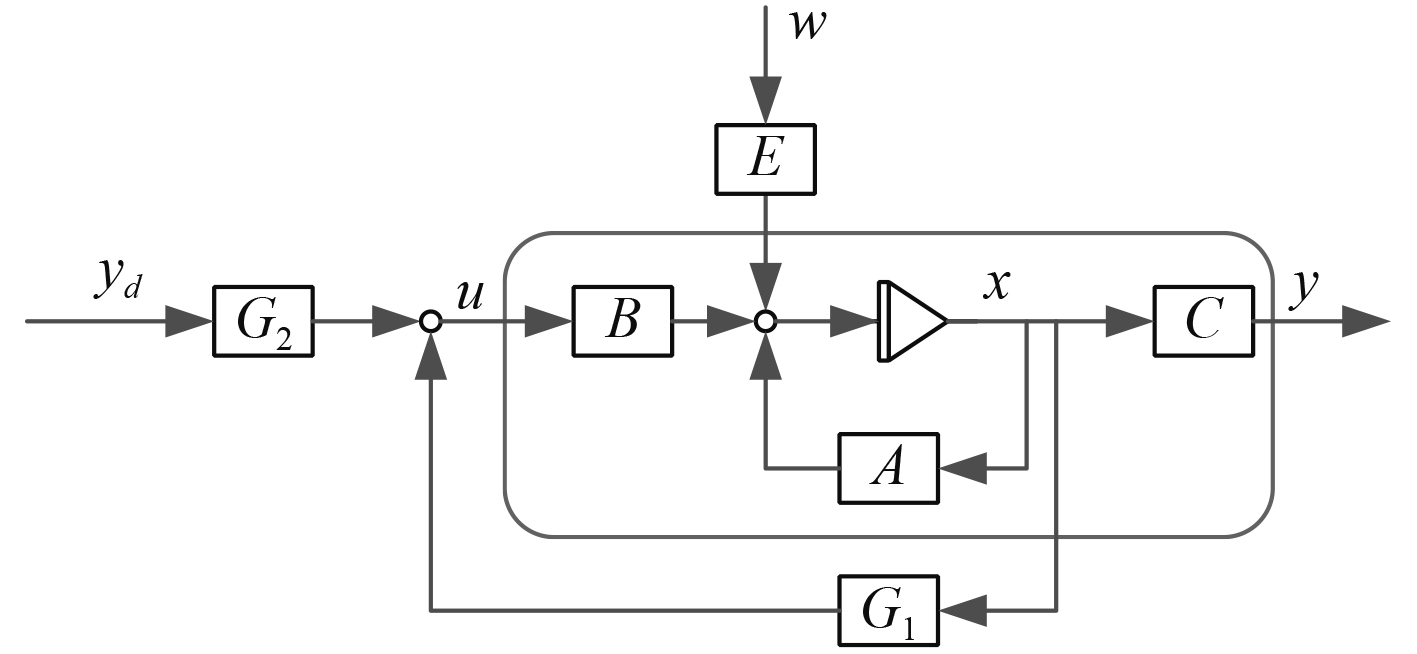
式中,
|
图 5 全状态反馈LQ跟踪控制原理图 Fig. 5 Principle diagram of full state feedback LQ tracking control |
检验能控性和能观性:根据rank[B AB]=5,rank[C;CA]=5满足全维状态可控,可观。
控制规律:
| $ {{u}}={{{G}}_1}{{x}} + {{{G}}_{\bf{2}}}{{{y}}_{\rm{d}}} \;{\text{。}}$ | (12) |
式中,
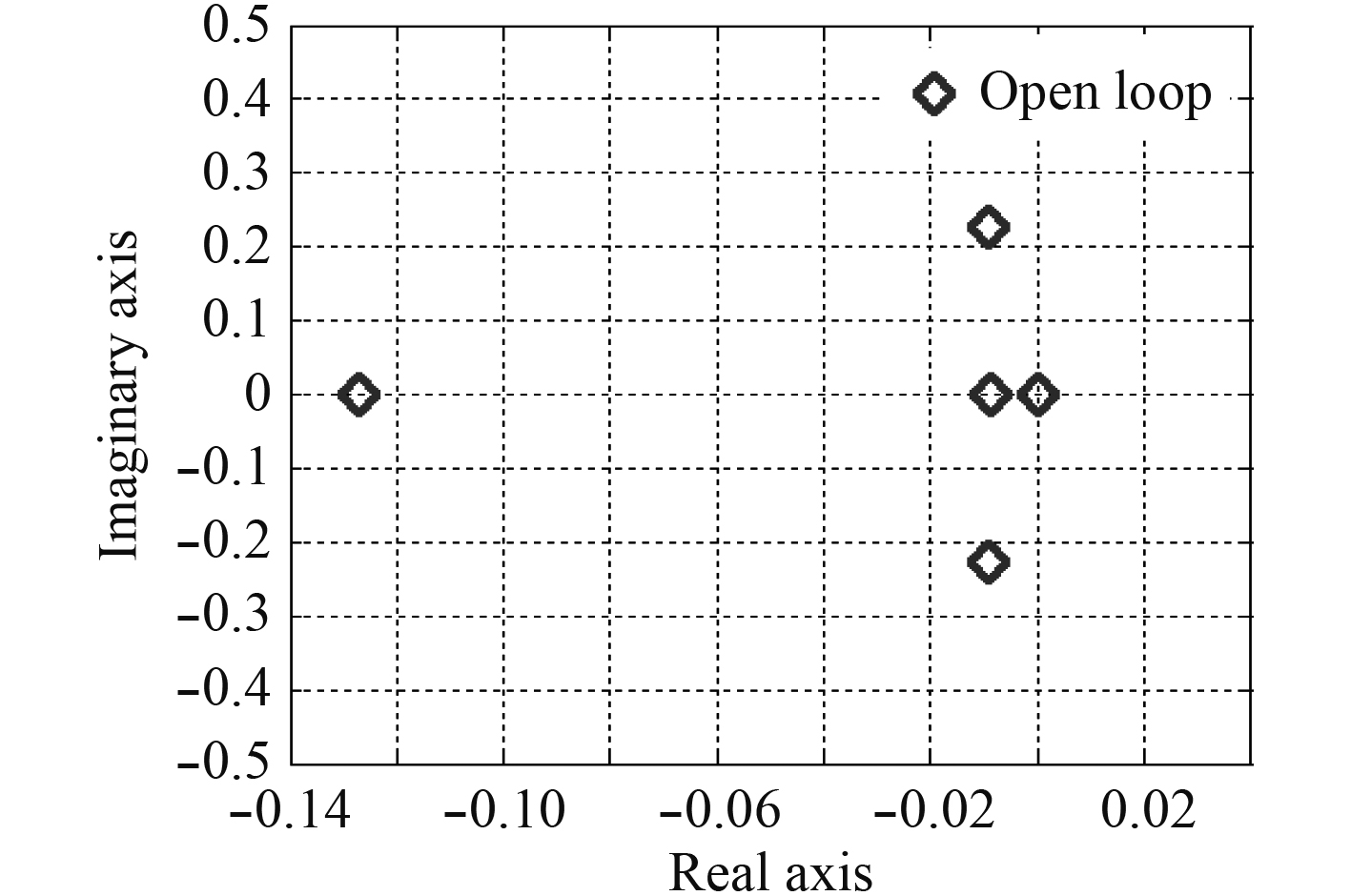
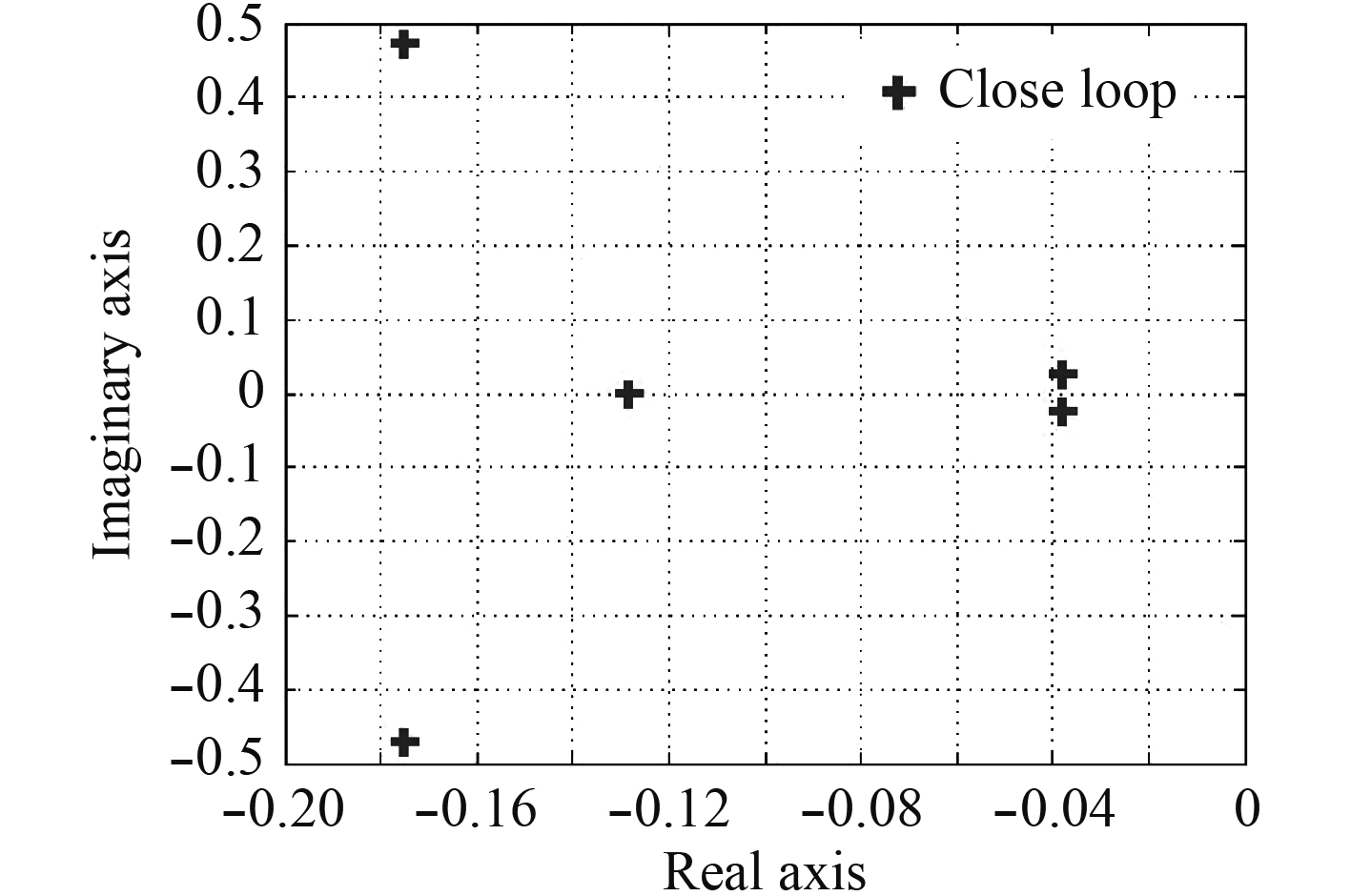
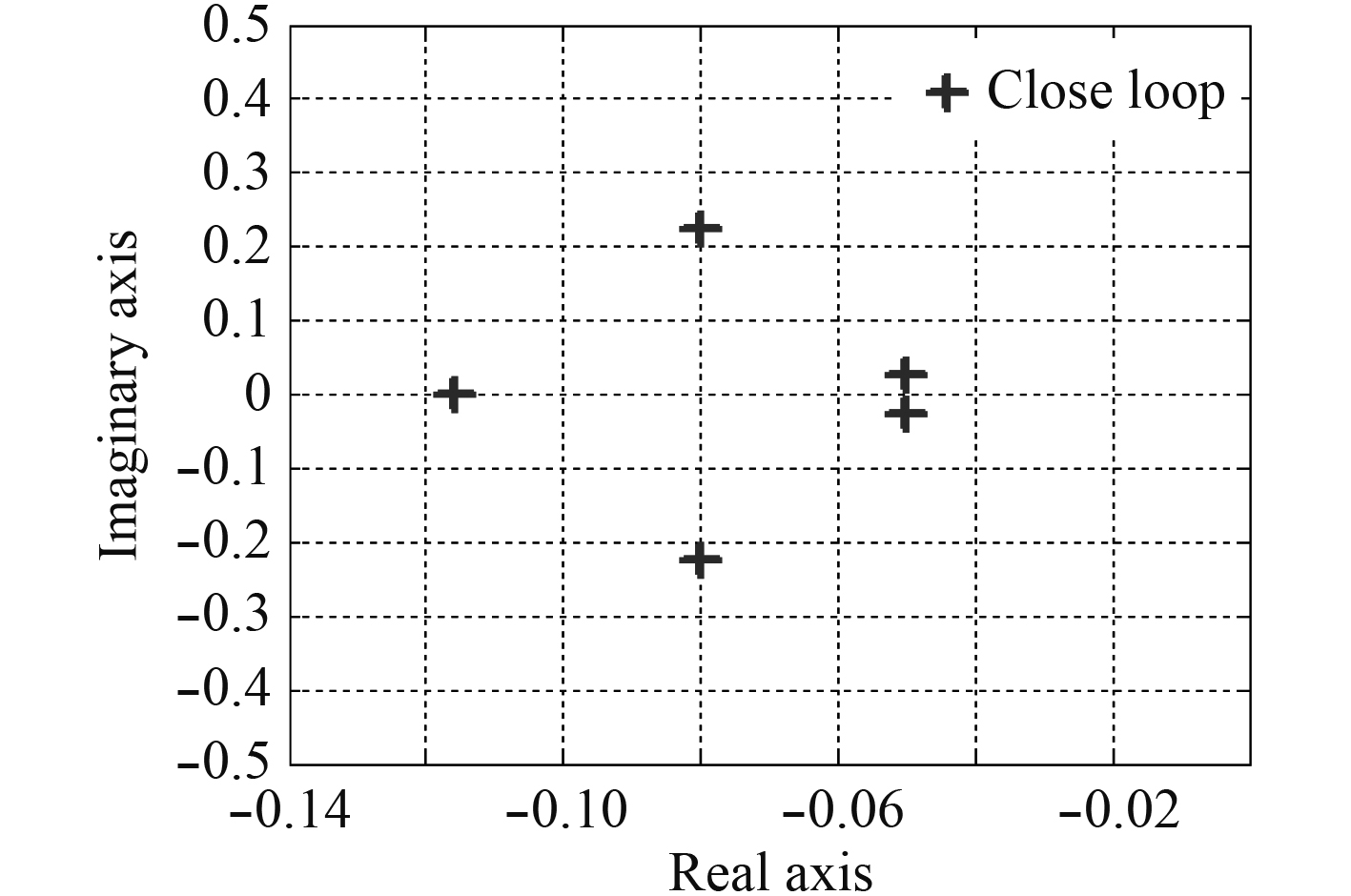
由线性系统稳定性特征根判据,U=7.4 m/s时的系统特征根图如图6~图9所示,满足闭环系统特征方程的所有特征根均具有负实部,故闭环跟踪系统渐进稳定。
|
图 6 常规舵开环系统特征根 Fig. 6 Open-loop system eigenvalues of conventional rudder |
|
图 9 喷流舵闭环系统特征根 Fig. 9 Close-loop system eigenvalues of jet rudder |
|
图 7 常规舵闭环系统特征根 Fig. 7 Close-loop system eigenvalues of conventional rudder |
|
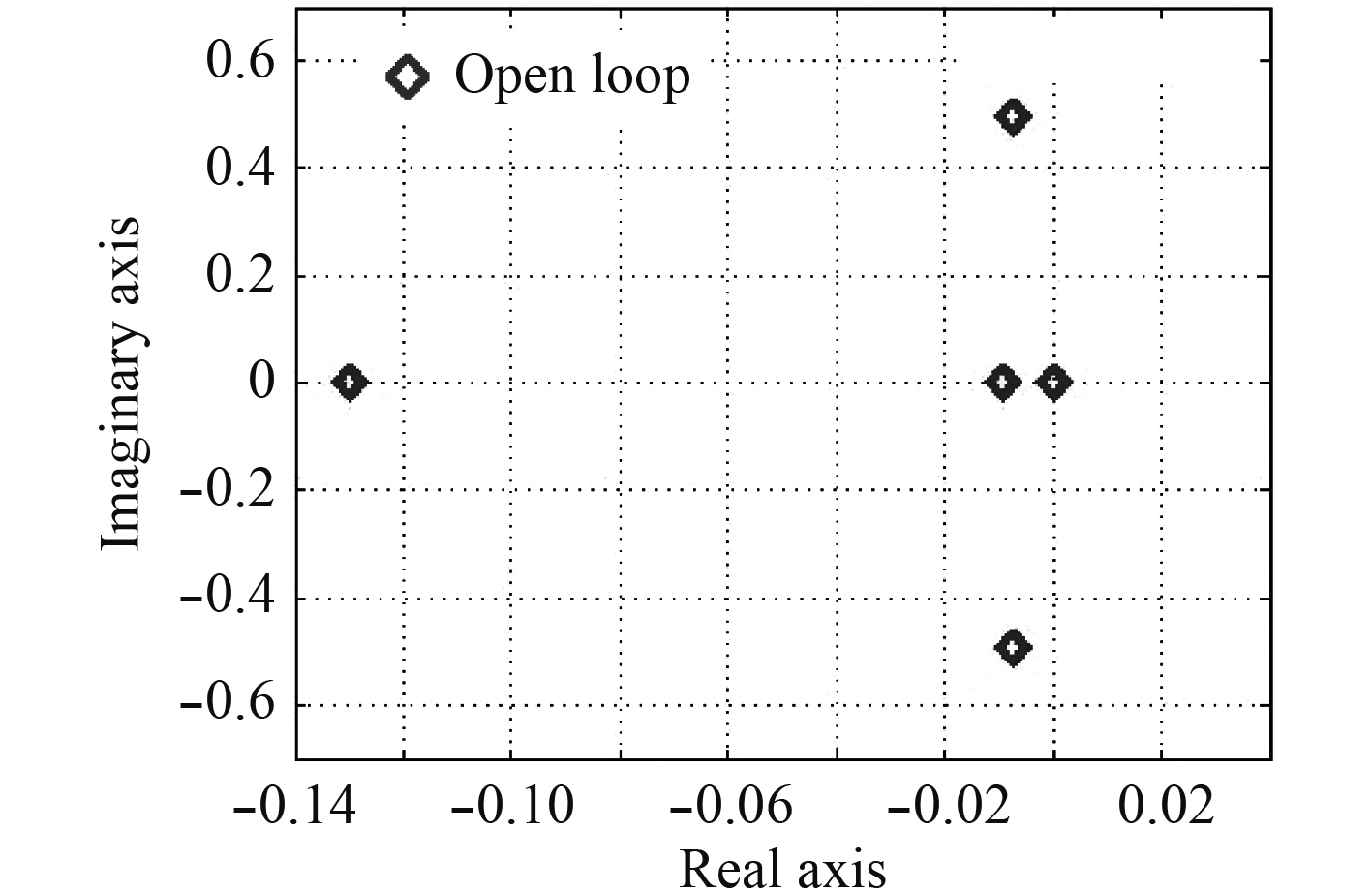
图 8 喷流舵开环系统特征根 Fig. 8 Open-loop system eigenvalues of jet rudder |
舵减摇在实现航向控制的同时实现减横摇,就是因为首摇角对舵的频率响应带宽和横摇角对舵的频率响应带宽相差较大,航向响应频率远低于横摇自振频率,即
低通滤波器
| ${h_l}(s)=\frac{{{\psi _{{\rm{filter}}}}}}{\psi }=\frac{1}{{{T_l}s + 1}}\;,$ | (13) |
式中,
高通滤波器
| ${h_h}(s)=\frac{{{\phi _{{\rm{filter}}}}}}{\phi }=\frac{{{T_h}s}}{{{T_h}s + 1}}\;{\text{。}}$ | (14) |
式中,
| $ \begin{split} & {{{x}}_{\psi f}}(k + 1)={e^{ - h/{T_l}}}{{{x}}_{\psi f}}(k) + (1 - {e^{ - h/{T_l}}}){{{u}}_{\psi} }(k) \;{\text{,}}\\ & {{{y}}_{\psi f}}(k)={{{x}}_{\psi f}}(k) \;{\text{,}}\\ & {{{u}}_{\psi} }(k){\rm{=}}{{{x}}_{\psi} }(k) \;{\text{。}} \end{split} $ | (15) |
式中:
| $\begin{split} & {{{x}}_{\phi f}}(k + 1)={e^{ - h/{T_h}}}{{{x}}_{\phi f}}(k) + ({e^{ - h/{T_h}}} - 1){{{u}}_{\phi} }(k) \;{\text{,}}\\ & {{{y}}_{\phi f}}(k)={{{x}}_{\phi f}}(k) + {{{x}}_{\phi} }(k) \;{\text{,}}\\ & {{{u}}_{\phi} }(k){\rm{=}}{{{x}}_{\phi} }(k) \;{\text{。}} \end{split} $ | (16) |
状态变量x分成
| $ {{u}}={G_1}{{{x}}_f} + {G_{\bf{2}}}{{{y}}_{\rm{d}}\;{\text{。}}} $ | (17) |
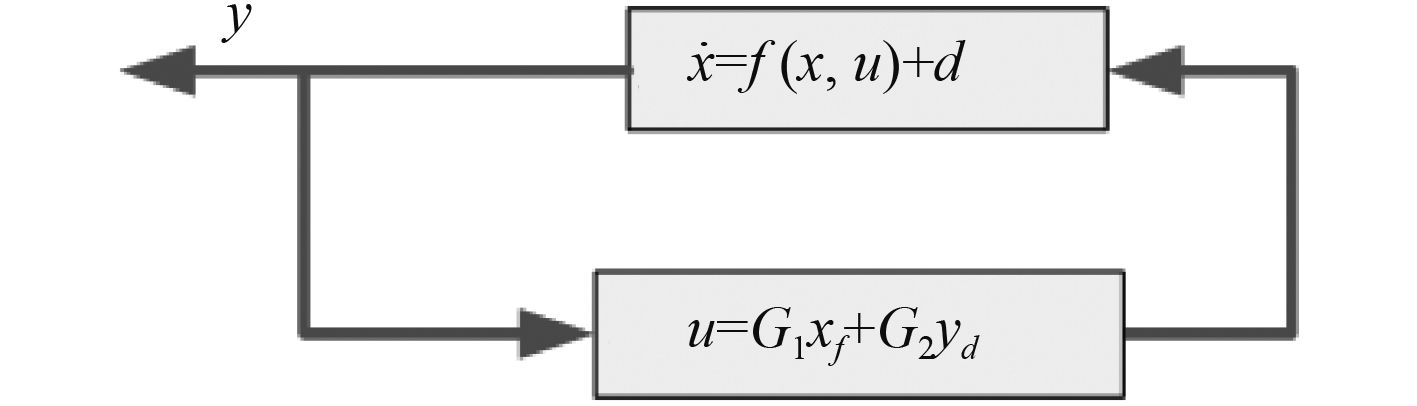
因此,结合式(6)、式(15)和式(16),可得基于FDLQR的航向横摇控制仿真模型,通过循环迭代,可实时控制并更新状态变量,如图10所示。
|
图 10 基于FDLQR的航向横摇控制仿真模型示意图 Fig. 10 Schematic diagram of simulation model for course rolling control based on FDLQR |
进行仿真时,采用非线性耦合运动模型,以螺旋桨转速恒定的方式工作,并经对应波浪工况下转速和航速匹配性调试,设置相应螺旋桨转速,以适配该浪况下船舶航速。仿真时设置输入限幅舵角为±35º。
目标船控制仿真参数如表1所示。
|
|
表 1 仿真参数 Tab.1 Simulation parameters |
工况1:在设计控制器时,假设纵向速度恒定,并设置标称航速U=7.4 m/s(对应14.4 kn)。设起始航向角为0°,任意设定航向角为10°。图11~图14表示航向横摇控制过程中输入输出量的时间历程,300~750 s时间段是开启舵减摇的控制时域,0~300 s和750~1000 s时域中,舵仅用于控制航向。仿真统计中,将300~750 s时间段数据作为开启舵减摇的样本,将200~275 s这一稳定时间段数据作为仅开启舵控制航向的样本。
|
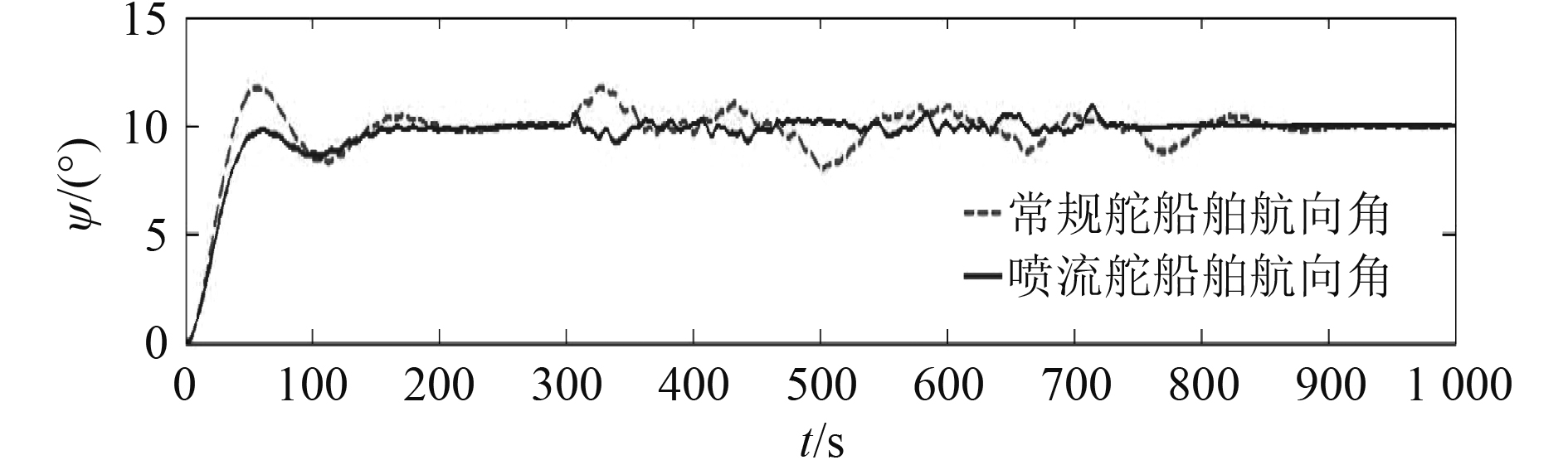
图 11 常规舵和喷流舵船舶航向角时间历程(U=7.4 m/s) Fig. 11 The ship course angle time history of ships using conventional rudder and jet rudder (U=7.4 m/s) |
|
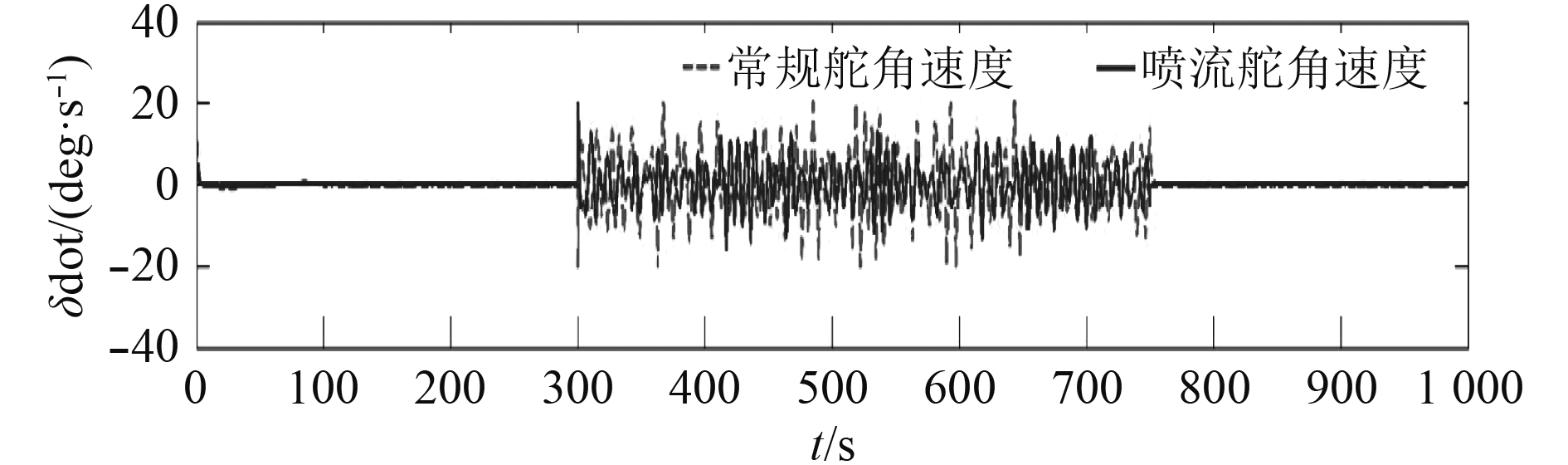
图 14 常规舵和喷流舵角速度时间历程(U=7.4 m/s) Fig. 14 The angle rate time history of conventional rudder and jet rudder (U=7.4 m/s) |
尽管喷流舵船舶航向横摇控制和常规舵船舶航向横摇控制均采用分频LQR方法,但由于输入系数矩阵不同,改变了系统参数,因此,相应控制参数一般不一致,需要重新调整,但喷流舵和常规舵的FDLQR控制方法中的控制信号权重R保持一致,以保证LQR控制能量的比较仅与输入舵角相关。喷流舵和常规舵的LQR误差跟踪权重QR=diag([10000 150 10 10 ]),QJR=diag([4000 90 12 2.1])。
由图11和表2可知,不管是常规舵还是喷流舵船舶航向角由0°~10°稳定后,航向角很稳定,常规舵和喷流舵的差异对航向控制精度的影响差别不大,在整个控制过程中,均可实现一定精度的航向控制。开启舵减摇模式后,航向角仍然可以保持一定精度,但出现略微变差,经观察,与设定航向角相比最大偏差约1°,这是由于舵角在控制航向的同时,分担了一部分能力进行舵减摇,从而导致略微影响航向精度。
|
|
表 2 常规舵和喷流舵输入输出量统计值(U=7.4 m/s) Tab.2 Statistics of input and output of conventional rudder and jet rudder (U=7.4 m/s) |
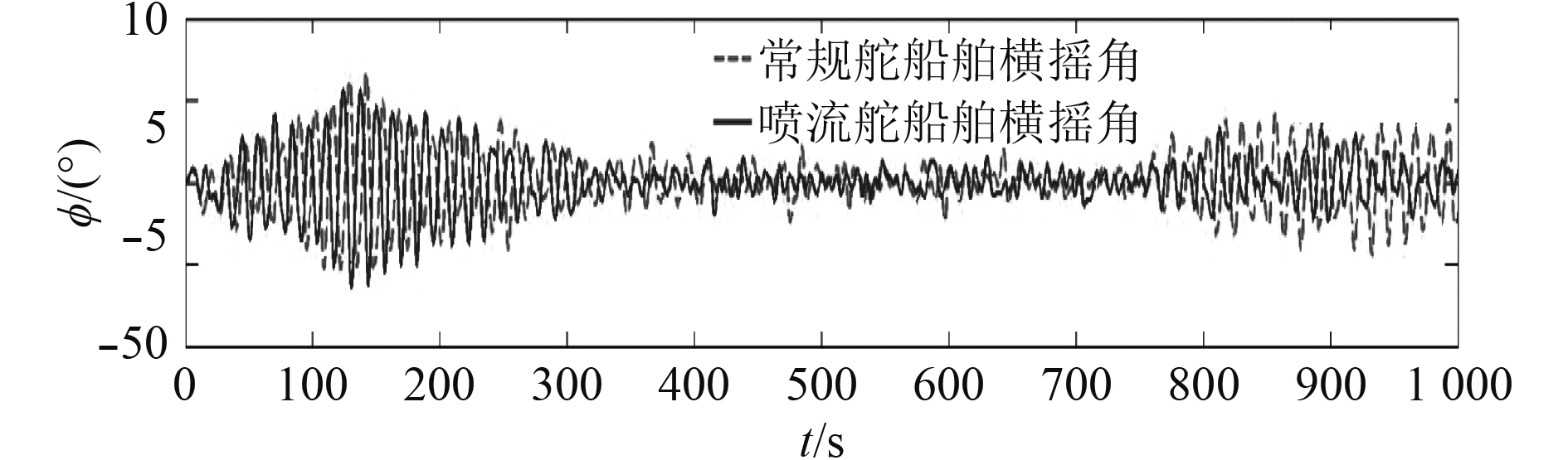
由图12和表2可知,常规舵和喷流舵均实现了较好地减摇效果,常规舵横摇减摇率达61%,横摇角能够减摇至有义值1.33°,喷流舵横摇减摇率达72%,横摇角能够减摇至有义值0.91°。
|
图 12 常规舵和喷流舵船舶横摇角时间历程(U=7.4 m/s) Fig. 12 The ship rolling angle time history of ships using conventional rudder and jet rudder (U=7.4 m/s) |
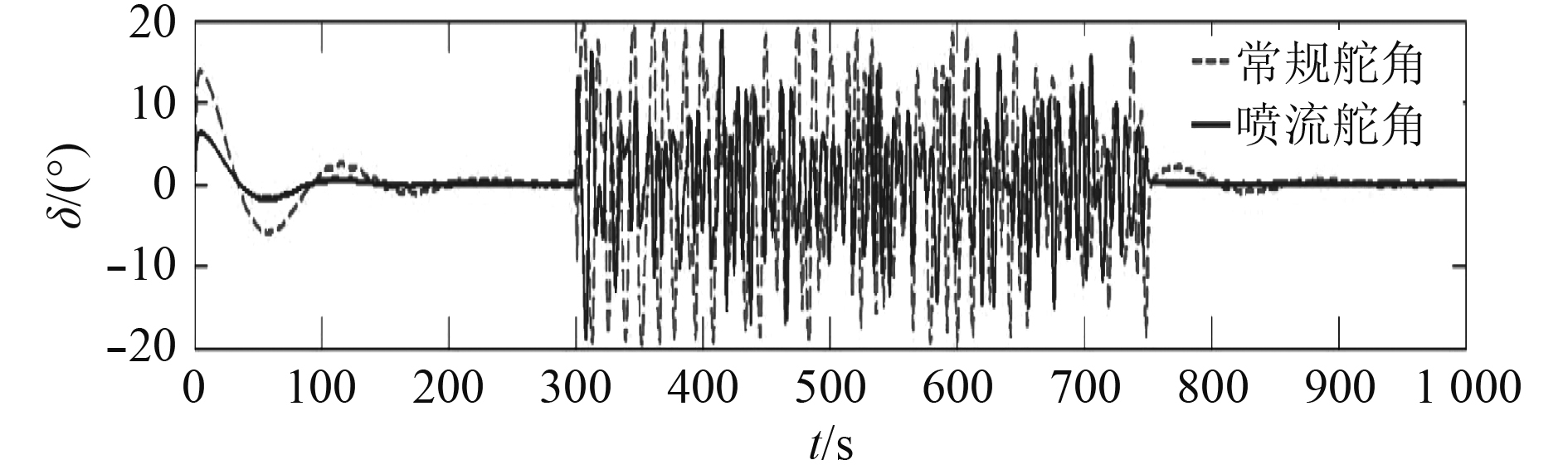
由图13和表2可知,常规舵仅用于航向控制时,舵角标准差为0.22°,用于减横摇时,舵角标准差为10.45°;喷流舵仅用于航向控制时,舵角标准差为0.054°,同时用于减横摇时,舵角标准差为6.85°,可见喷流舵作为控制执行机构,舵角降幅为34.4%,舵机能量降幅达57%。
|
图 13 常规舵和喷流舵角时间历程(U=7.4 m/s) Fig. 13 The angle time history of conventional rudder and jet rudder (U=7.4 m/s) |
由图14和表2可知,常规舵仅用于航向控制时,舵角速度标准差为0.047°/s,用于减横摇时,舵角速度标准差为7.33°/s;喷流舵仅用于航向控制时,舵角标准差为0.029°/s,同时用于减横摇时,舵角标准差为5.33°/s。一般常规舵机为液压驱动,角速度不易太高,一般不超过2~7°/s,否则容易出故障。喷流舵作为控制执行机构,舵角速度显著下降,降幅为27.3%,可有效减少舵机工作故障率。
工况2:假设在某海况下船舶纵向速度恒定,并设置标称航速U=4 m/s(对应7.8 kn),调整螺旋桨转速。图15~图18表示在该航速下航向横摇控制过程中输入输出量的时间历程,300~750 s时间段是开启舵减摇的控制时域,0~300 s和750~1000 s时域中,舵仅用于控制航向。仿真统计中,将300~750 s时间段数据作为开启舵减摇的样本,因起始航向控制过渡时间较长,将750~1000 s这一稳定时间段数据作为仅开启舵控制航向的样本。在仿真中,常规舵和喷流舵控制参数设置一致,均为Q =diag([10000 900 60 70])。
|
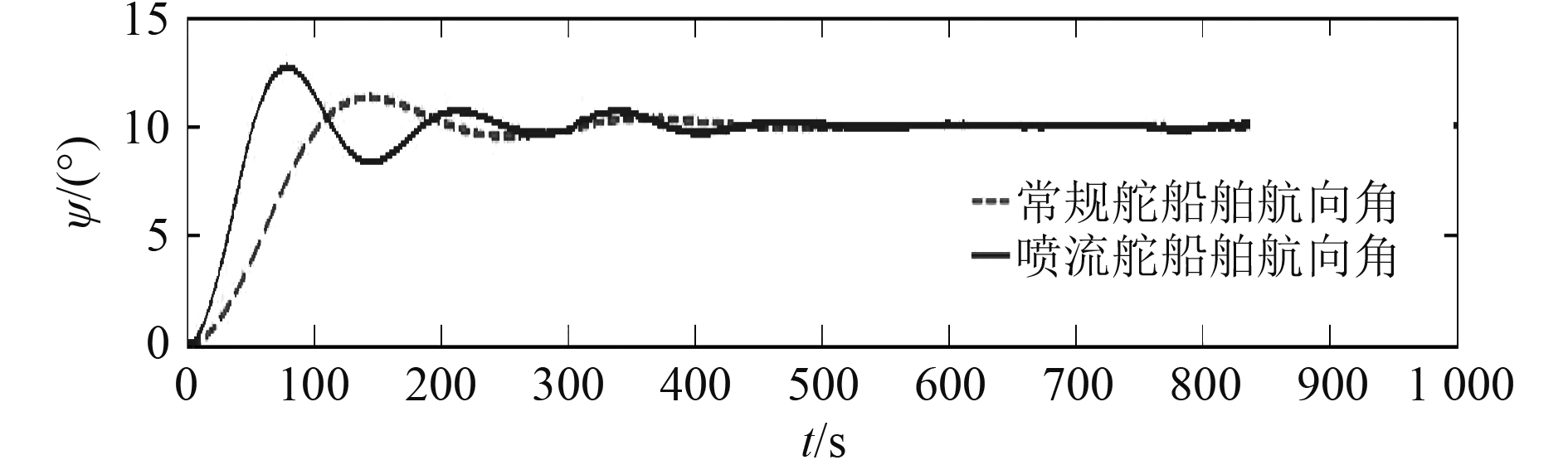
图 15 常规舵和喷流舵船舶航向角时间历程(U=4 m/s) Fig. 15 The ship course angle time history of ships using conventional rudder and jet rudder (U=4 m/s) |
|
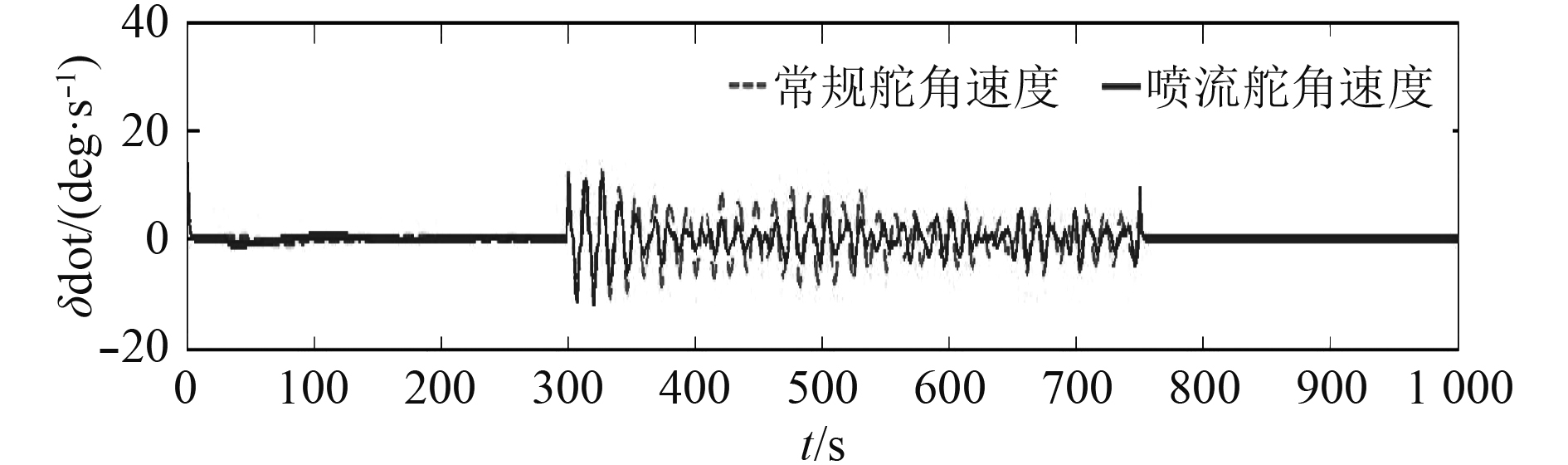
图 18 常规舵和喷流舵角速度时间历程(U=4 m/s) Fig. 18 The angle rate time history of conventional rudder and jet rudder (U=4 m/s) |
由图15和表3可知,在低速U=4 m/s时,不管是常规舵还是喷流舵船舶航向角由0°至10°稳定后,航向角很稳定,常规舵和喷流舵的差异对航向控制精度的影响差别不大,在整个控制过程中,均可实现一定精度的航向控制。开启舵减摇模式后,航向角精度影响不大,仍然可以保持较高水平。
|
|
表 3 常规舵和喷流舵输入输出量统计值(U=4 m/s) Tab.3 Statistics of input and output of conventional rudder and jet rudder (U=4 m/s) |
由图16和表3可知,在低航速下,常规舵减摇效果不佳,而喷流舵的减摇效果比较明显,喷流舵横摇减摇率达64%,横摇角能够减摇至有义值0.85°。
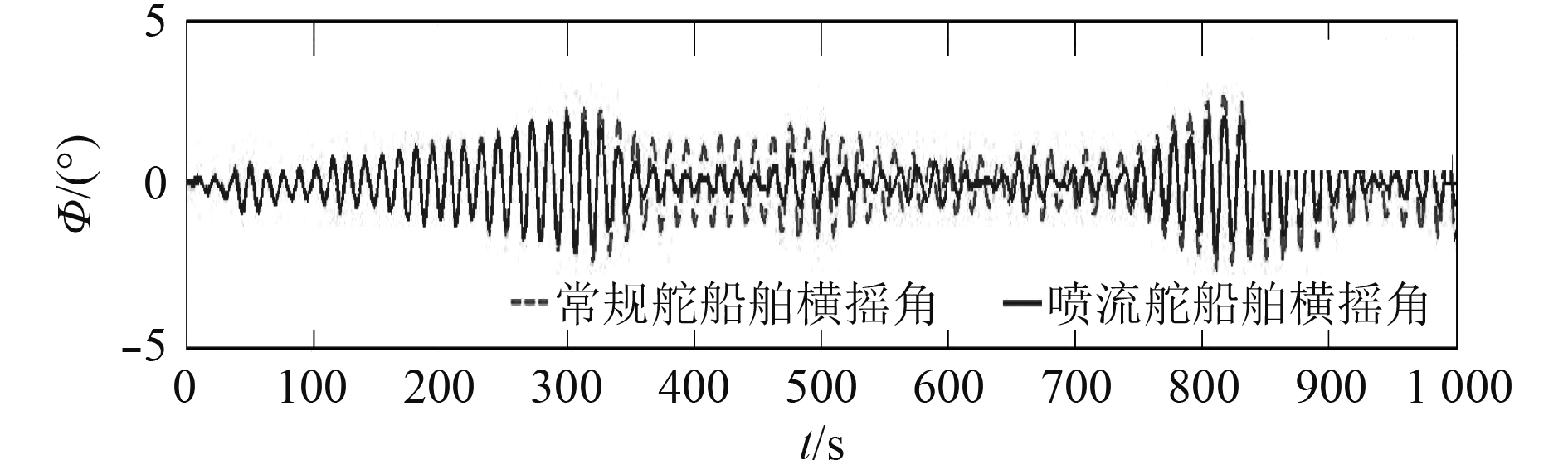
|
图 16 常规舵和喷流舵船舶横摇角时间历程(U=4 m/s) Fig. 16 The ship rolling angle time history of ships using conventional rudder and jet rudder (U=4 m/s) |
由图17和表3可知,常规舵仅用于航向控制时,舵角标准差为0.39°,用于减横摇时,舵角标准差为9.68°;喷流舵仅用于航向控制时,舵角标准差为0.54°,同时用于减横摇时,舵角标准差为6.01°,可见喷流舵作为控制执行机构,舵角降幅为37.9%,舵机能量降幅达61.6%。
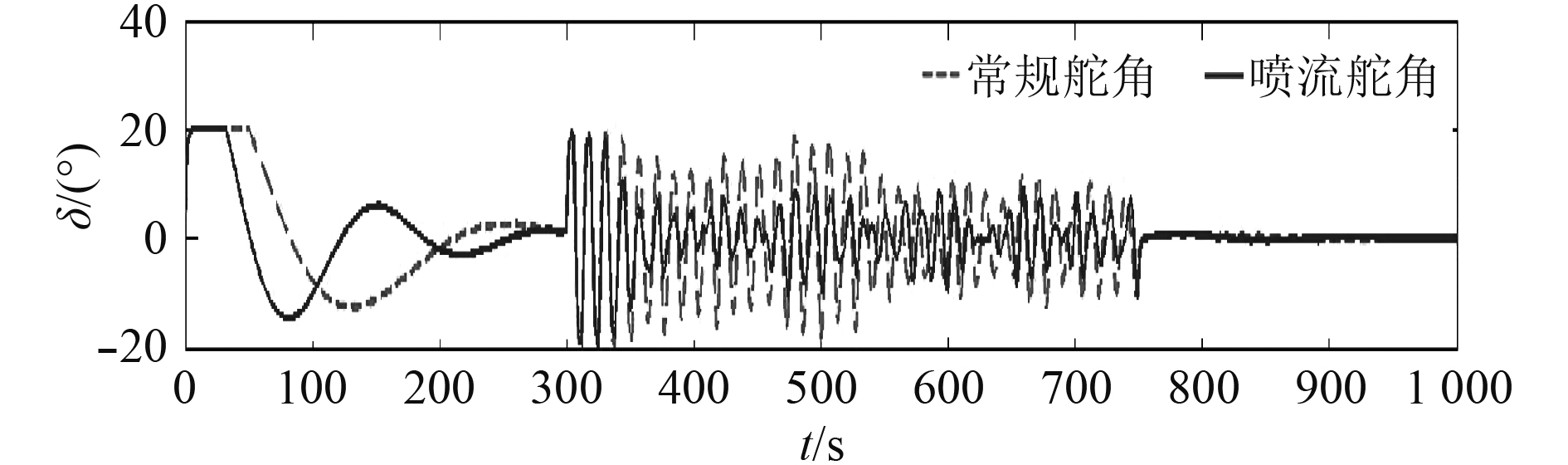
|
图 17 常规舵和喷流舵角时间历程(U=4 m/s) Fig. 17 The angle time history of conventional rudder and jet rudder (U=4 m/s) |
由图18和表3可知,常规舵仅用于航向控制时,舵角速度标准差为0.23°/s,用于减横摇时,舵角速度标准差为4.54°/s;喷流舵仅用于航向控制时,舵角标准差为0.44°/s,同时用于减横摇时,舵角标准差为2.91°/s。喷流舵作为控制执行机构,舵角速度显著下降,降幅为35.9%,可有效减少舵机工作故障率。
5 结 语本文介绍了基于FDLQR控制的舵减摇一般控制方法,并初步应用喷流舵对船舶航向横摇进行了控制仿真研究。仿真结果表明,FDLQR方法在RRD系统控制具有普适性以及喷流舵在船舶航向横摇控制具有有效性、优越性,尤其是在低速时,常规舵减摇能力不足,喷流舵依然能产生较好的减摇效果。
本文是在结合控制方法的基础上选择不同类别的执行机构(常规舵和喷流舵)综合研究船舶航向和横摇控制性能,研究获取的结果不仅与输入执行机构有关,也与控制器参数设置有关,是两者共同影响的结果。本文在有限工况、特定目标下设计了控制器,实际上,在仿真中发现,FDLQR控制对控制器参数和随机海浪工况有一定敏感性,有待进一步研究具有较强鲁棒性的控制方法。另外,本文强行线性化喷流舵的输出特性,将输入简化为仅与输入舵角有关,实际上喷流舵舵效与舵角、喷流动量系数等均有关,即使在喷流动量系数一定的情况下,也是一类非线性输入控制问题,这方面的研究将在后续工作中开展。
| [1] |
KIND R. J AND MAULL D. J. An experimental investigation of a low-speed circulation-controlled aerofoil[J]. The Aeronautical Quarterly, 1968(5): 170-182. |
| [2] |
CHEESEMAN I. C, FRAES and SEED A R.. The application of circulation control by blowing to helicoter roor[J]. journal of the royal aeronautical society, 1966(71): 679. |
| [3] |
ENGLAR R. J, HUSON G. G. Development of advanced circulation control wing high-lift airfoils[J]. Journal of Airfoils. Journal of Aircraft, 1984, 21: 476-483. DOI:10.2514/3.44996 |
| [4] |
沈定安, 夏贤, 田于逵, 等. 喷流舵水动力试验研究[J]. 船舶力学, 2005, 9(1): 51-56. DOI:10.3969/j.issn.1007-7294.2005.01.008 |
| [5] |
SON, K. H. and NOMOTO, K. On the coupled motion of steering and rolling of a high speed container ship[J]. Naval Architects of Japan, 1981, 150: 232-244. |
| [6] |
FOSSEN. Handbook of marine craft hydrodynamics and motion control[M]. 2011.
|
| [7] |
TRISTAN P. Ship motion control course keeping and roll stabilization using rudder and fins[M]. Springer, 2005.
|
| [8] |
COWLEY W E, LAMBERT T H. The Use of Rudder as a Toll Stabilizer[C]. Proceeding of SCSS’72, 2, Bath, UK, 1972(Ⅶ): C-1.
|
| [9] |
VAN der KLUGT P F M. Rudder roll stabilization PhD thesis[D]. Netherlands Delft University of Technology, the1987.
|
| [10] |
VAN A J, VAN der KLUGT P G M, VAN nauta. Lempke H R. rudder roll stabilization for ships[J]. Automatic AUT, 1990(4): 679-690. |
| [11] |
LAUVDAL T, FOSSEN T I. Rudder roll stabilization of ship subject to input rate saturation using a gain scheduled control law[C]. Proceeding of CAMS’98, Fukuoka. Japan. 1998: 121-126.
|
| [12] |
BLANKE M, HAALS P, ANDREASEN K K. Rudder roll damping experience in demark[C]. Proceeding of CAMS’89 Lyngby, Denmark, 1989: 149-160.
|
| [13] |
PEREZ T, TZENG C Y, GOODWIN G C. Model predictive rudder roll stabilization control for ships[C]. Proceeding of MCMC 2000, Aalborg Denmark, 2000: 39-44.
|
| [14] |
BLANKEM, et al. Rudder roll damping in coastal region sea conditions[C]. Proceeding of MCMC’2000, Aalborg Denmark, 2000: 45-50.
|
 2020, Vol. 42
2020, Vol. 42
