当船舶航行时,物面湍流边界层内的速度扰动产生随机的脉动压力。这种随机脉动压力一方面直接产生辐射噪声,另一方面激励物面弹性结构振动并产生辐射噪声。在低马赫数情况下,船舶的水动力噪声主要由脉动压力激励船体产生的辐射噪声构成。目前国内外对流激噪声的研究都进行了一定程度的简化。Davies[1]针对矩形平板,采用频率—波数谱概念,求解弹性结构受湍流脉动压力激励的振动和声辐射。彭临慧等[2]通过分析湍流脉动压力频率谱特性,总结了回转体受湍流脉动压力激励频谱分布经验公式。吕世金等[3]运用功率谱的概念和模态平均法计算子单元受湍流脉动压力激励产生的声辐射,建立了航行体水动力噪声的计算方法。近年来,随着计算机技术的迅速发展,使得运用计算流体力学(CFD)以及声学有限元(FEM)方法对实船进行湍流脉动压力的数值模拟以及水下辐射噪声的预报逐渐成为可能。张楠等[4]使用大涡模拟的方法对SUBOFF潜艇模型进行了表面脉动压力的分析,结果表明大涡模拟的计算精度是可靠的。张晓龙等[5]针对平板壁面湍流脉动压力及其波数-频率谱进行了数值计算,并探讨了湍流脉动压力的变化规律。江文成[6]利用大涡模拟求解了潜艇的绕流场,将流场计算得到的脉动压力作为外载荷施加于潜艇结构,研究了流固耦合作用下潜艇的流激噪声。
本文基于某小水线面双体船,首先针对缩比模型进行CFD数值模拟,利用大涡模拟技术得到其结构表面的湍流脉动压力分布,并与试验数据进行对比,验证该方法的可靠性。在此基础上,对实船湍流脉动压力分布进行模拟,并将脉动压力频谱作为输入,采用声学有限元方法预报了双体船的水下辐射噪声。
1 数值计算方法 1.1 大涡模拟控制方程在大涡模拟方法中,对于一个瞬时流体变量
| $\phi = \overline \phi + \phi '{\text{,}}$ | (1) |
其中,
滤波后的连续性方程和NS方程可以表示为:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}(\rho {\bar u_i}) = 0{\text{,}}$ | (2) |
| $\frac{\partial }{{\partial t}}(\rho {\bar u_i}) + \frac{\partial }{{\partial {x_j}}}(\rho {\bar u_i}{\bar u_j}) = \frac{\partial }{{\partial {x_j}}}(\mu \frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}}) - \frac{{\partial \bar p}}{{\partial {x_i}}} - \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}}{\text{,}}$ | (3) |
其中,
通过对无量纲的连续性方程与NS方程进行网格滤波可以得到滤波后的运动方程:
| $ \frac{{\partial {{\bar u}_i}}}{{\partial {x_i}}} = 0{\text{,}} $ | (4) |
| $\frac{{\partial {{{\tilde {\bar u}}}_i}}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}({{\tilde {\bar u}}_i}{{\tilde {\bar u}}_j}) = - \frac{{\partial {\tilde {\bar p}}}}{{\partial {x_i}}} - \frac{{\partial {T_{ij}}}}{{\partial {x_j}}} + \frac{1}{{\rm{Re} }}\frac{{{\partial ^2}{\tilde {\bar u}}{}_i}}{{\partial {x_j}\partial {x_j}}}{\text{,}}$ | (5) |
其中亚格子尺度应力为:
| ${T_{ij}} = \widetilde {\overline {{u_i}{u_j}} } - {{\tilde {\bar u}}_i}{{\tilde {\bar u}}_j}{\text{。}}$ | (6) |
采用有限元方法首先将辐射声场进行离散,假设观测区域内有n个节点,任意一点的声场声压可近似表示为:
| $p\left( {\vec r} \right) \approx \sum\limits_{i = 1}^n {{N_i}\left( {\vec r} \right){p_i}} = \left[ {{N_i}} \right]\left\{ {{p_i}} \right\}{\text{。}}$ | (7) |
其中:
对于一个有限区域内的流体声场,任意节点
| $\left\{ {\left[ {{K_a}} \right] + j\omega \left[ {{C_a}} \right] - {\omega ^2}\left[ {{M_a}} \right]} \right\}\left\{ {{p_i}} \right\} = \left\{ {{P_a}} \right\}{\text{,}}$ | (8) |
其中:
结构受激振动声辐射动力学方程可以写作:
| $\left\{ {\left[ {{K_s}} \right] + j\omega \left[ {{C_s}} \right] - {\omega ^2}\left[ {{M_s}} \right]} \right\}\left\{ {{\delta _i}} \right\} = \left\{ {{F_s}} \right\}{\text{,}}$ | (9) |
其中:
将结构有限元方程和流体声学有限元方程结合,得到流固耦合有限元方程:
| $\begin{split} & \left\{ {\left[ {\begin{array}{*{20}{c}} {{K_s}}&{{K_c}} \\ 0&{{K_a}} \end{array}} \right] + j\omega \left[ {\begin{array}{*{20}{c}} {{C_s}}&0 \\ 0&{{C_a}} \end{array}} \right] - {\omega ^2}\left[ {\begin{array}{*{20}{c}} {{M_s}}&0 \\ { - {\rho _0}K_c^{\rm{T}}}&{{M_a}} \end{array}} \right]} \right\}\\ &\left\{ {\begin{array}{*{20}{c}} {{\delta _i}} \\ {{p_i}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{F_s}} \\ {{P_a}} \end{array}} \right\}{\text{。}}\end{split}$ | (10) |
其中
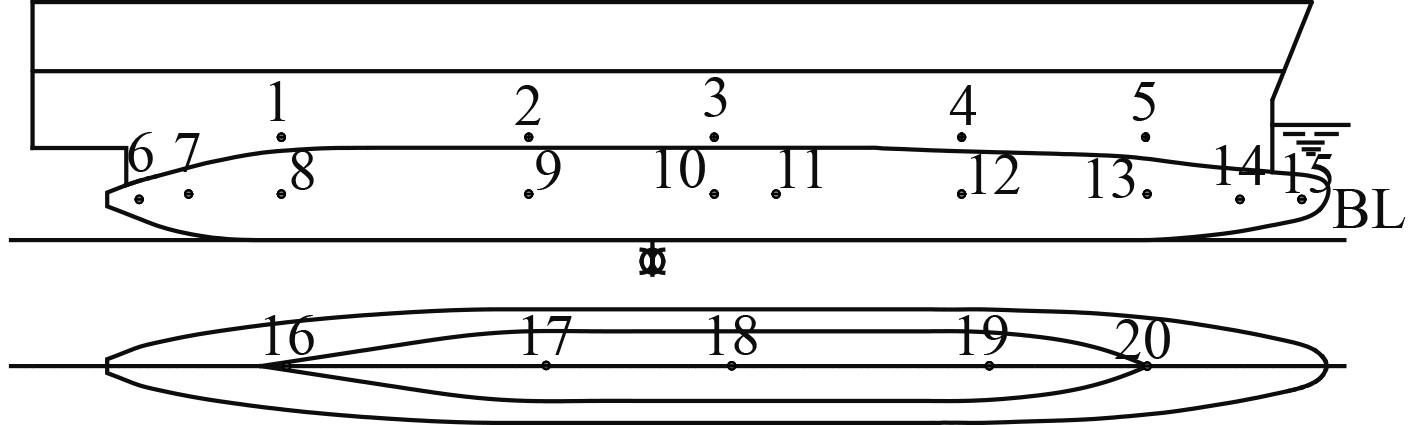
双体船湍流脉动压力试验在低速风洞中进行,模型长4.5 m,宽0.36 m,高0.45 m,缩尺比为1:20。试验中总共沿船长及型深范围设置了20个测点,其位置如图1所示。
|
图 1 测点布置 Fig. 1 Measuring-point arrangement |
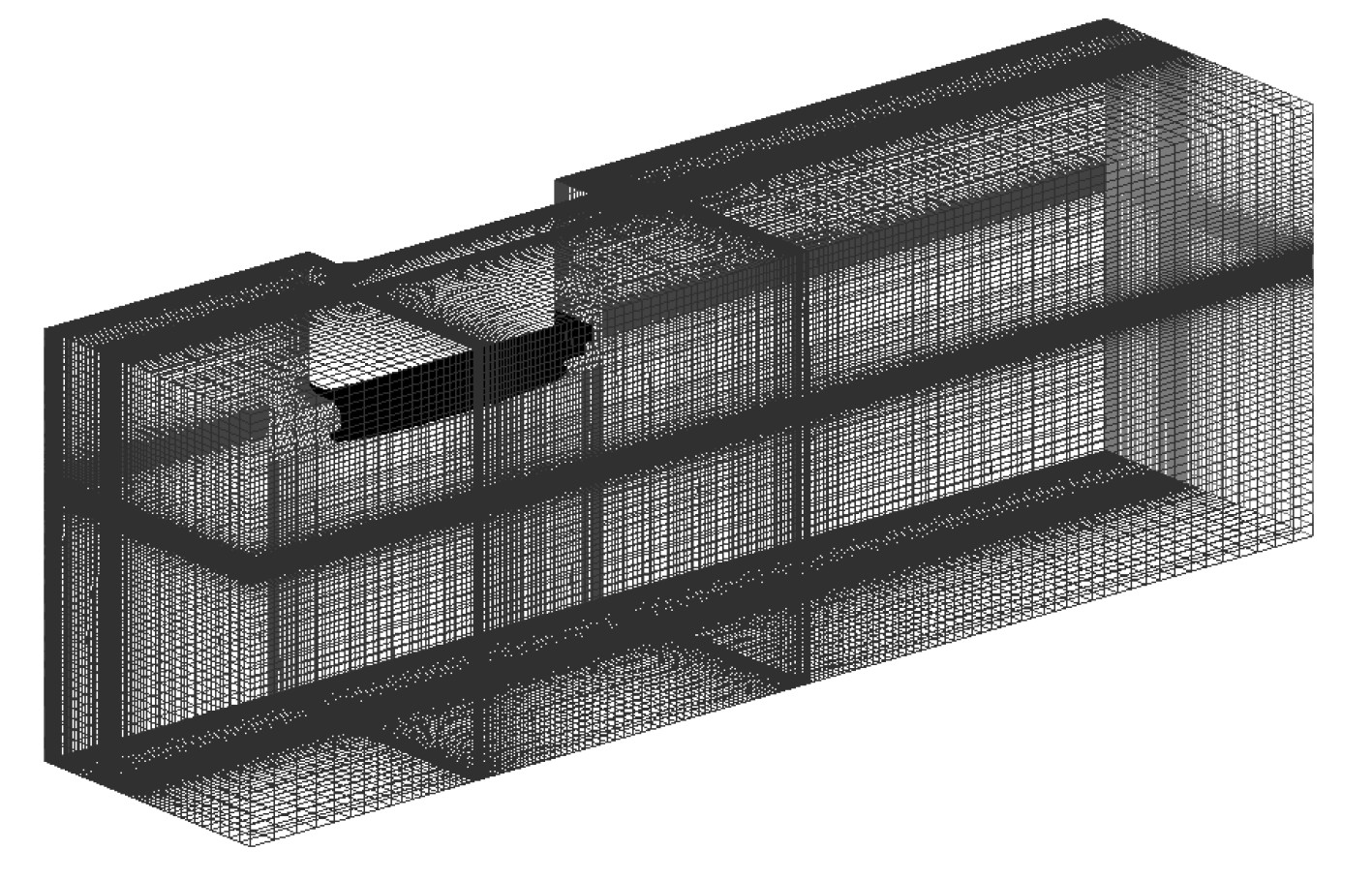
数值模拟计算区域取为从船首向前1倍船长至船尾向后2倍船长的范围,网格划分示意图如图2所示。模型网格总数为415万,实船网格总数为1127万。
|
图 2 双体船计算与网格划分 Fig. 2 Computational domain and meshing of the catamaran |
计算域前方边界条件设定为速度入口,后方为压力出口;中纵剖面处为对称边界条件;船体为壁面边界条件。为消除流体在边界上产生的虚假声波对于近场流体真实脉动的影响[7],在入口边界与侧面边界施加Bogey辐射条件,并在计算域下游设置了消声区。时间步长
本文针对风速40 m/s的工况进行了计算,参考声压为

|
图 3 P1点脉动压力计算与试验对比 Fig. 3 Comparison between simulation and experiment of turbulent pressure fluctuations at point P1 |
|
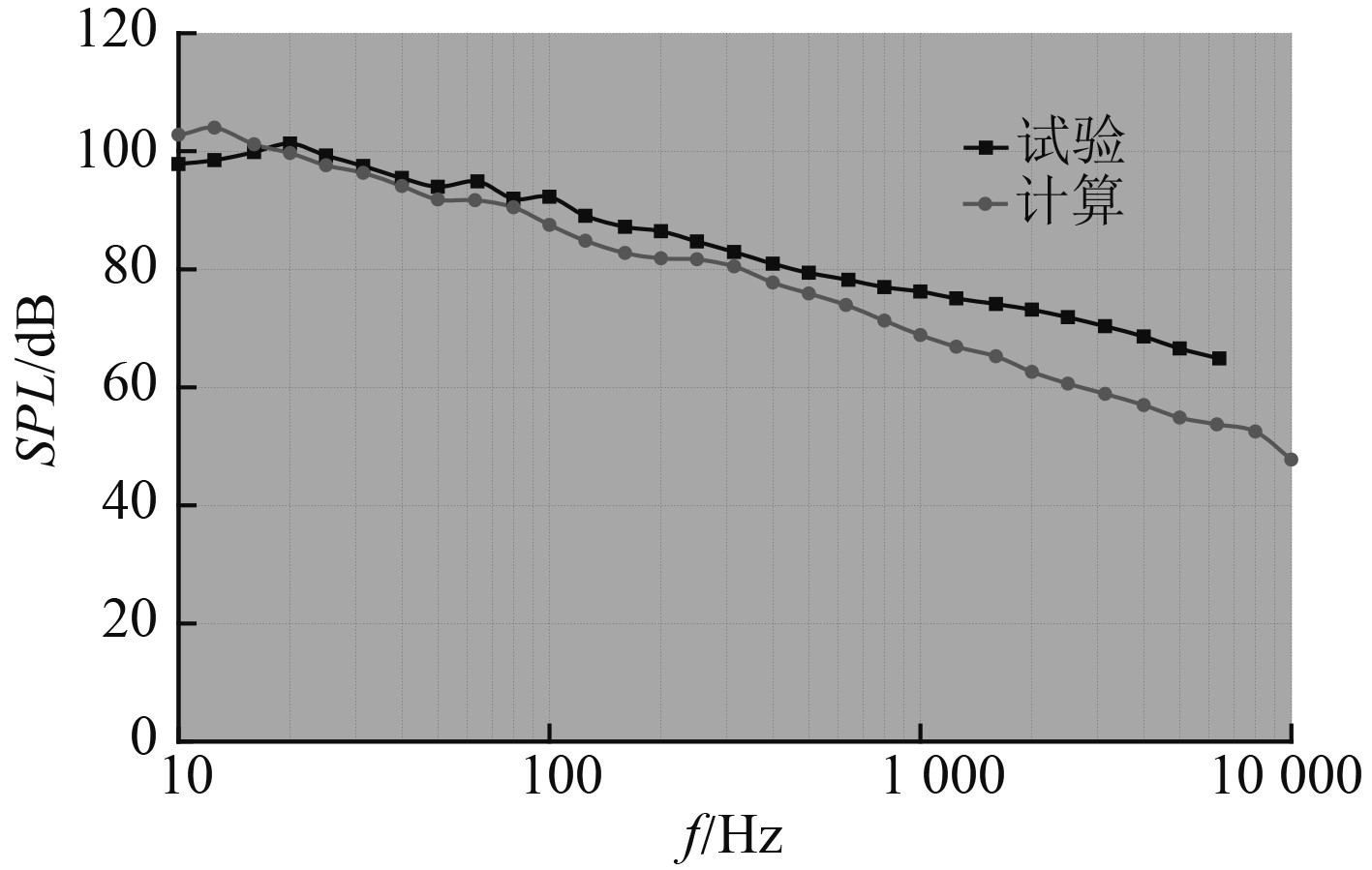
图 4 P5点脉动压力计算与试验对比 Fig. 4 Comparison between simulation and experiment of turbulent pressure fluctuations at point P5 |

|
图 5 P10点脉动压力计算与试验对比 Fig. 5 Comparison between simulation and experiment of turbulent pressure fluctuations at point P10 |

|
图 6 P19点脉动压力计算与试验对比 Fig. 6 Comparison between simulation and experiment of turbulent pressure fluctuations at point P19 |

|
图 7 实船表面流线分布 Fig. 7 Streamline distribution of full scale ship |
从模型脉动压力频谱计算与试验对比图可知:计算得到的脉动压力功率谱谱型与试验吻合良好;在2 500 Hz以下频段,计算误差为1~5 dB;在2500 Hz以上频段,计算误差为3~7 dB。由此可知上述计算方法是可靠的。
2.2.2 实船脉动压力计算以6 km航速为例,实船流场计算结果如图7和图8所示。从实船流线和压力分布的计算结果可以看出,双体船2个片体周围的流场并没有出现相互干扰的情况。对于片体而言,在自由面附近的流动出现些微波动,远离自由面位置上的流动则相对光顺。

|
图 8 实船水下部分压力分布 Fig. 8 Pressure distribution of underwater part of full scale ship |
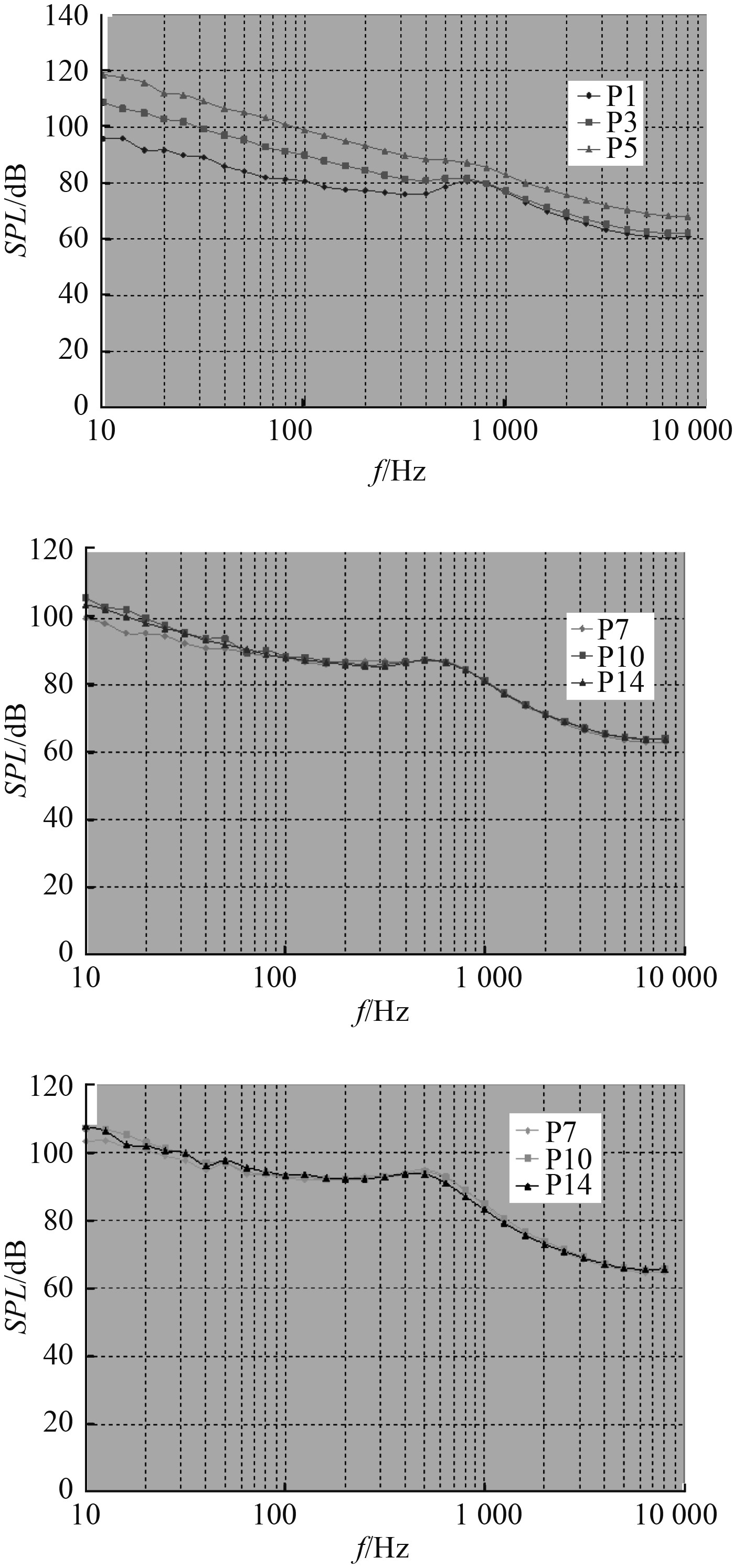
实船脉动压力频谱计算结果如图9所示,脉动压力计算结果用1/3倍频程(1/3 oct)形式表达。从计算结果看,不同位置的脉动压力自谱频响曲线变化趋势接近,整体趋势都是低频幅值较高,到了中高频幅值开始衰减,与以往回转体的脉动压力自谱变化趋势一致。
|
图 9 实船各测点脉动压力(1/3 oct) Fig. 9 Turbulent pressure fluctuations of full scale ship at different points(1/3 oct) |
通过2.2节中CFD仿真得到了双体船水线以下表面脉动压力频谱,将其作为激励加载到结构表面,利用声学有限元法计算船体的水下辐射噪声。由于实船船体结构尺寸较大,网格数量较多,采用常规的有限元流固耦合建模方法将会带来巨大的计算量,因此在计算过程中采用 自动匹配层(AML)技术,该方法可以大大降低声学网格量,而且对声学边界的形状没有要求,从而可以大大提升计算速度。
为了验证声学有限元法的可靠性,以几何形状简单的平板为算例进行计算。Heatwole C.M等[8-9]曾对简支板的流激噪声进行过仿真计算和试验研究,图10为文献[8-9]中的试验值及本文仿真计算结果。从图中可见仿真计算结果与试验结果吻合良好,从而验证了本文数值计算方法对板壳流激噪声的适用性和准确性。

|
图 10 试验及仿真计算结果 Fig. 10 Comparison between simulation and experiment result |
双体船声学有限元模型及振动测点的位置如图11~图13所示。结构部分包含139214个单元,其中梁单元39028个,三角形壳单元4773个,四边形壳单元95413个,流体部分包含9508256个体单元,计算频率取为20 ~150 Hz。

|
图 11 双体船水下结构有限元模型 Fig. 11 FEM model of the catamaran’s underwater structure |

|
图 12 外场流体区域有限元模型 Fig. 12 FEM model of fluid region |

|
图 13 振动测点位置 Fig. 13 Positions of vibration measuring-points |
图14和图15为6 kn 航速下船体表面不同位置的法向振速谱级。从图中可以看出,不同测点处的振速随频率变化规律较为接近,在20~60 Hz的范围内振速谱级幅值随着频率增加而降低,在高于60 Hz以后,振速谱级幅值趋于平稳。
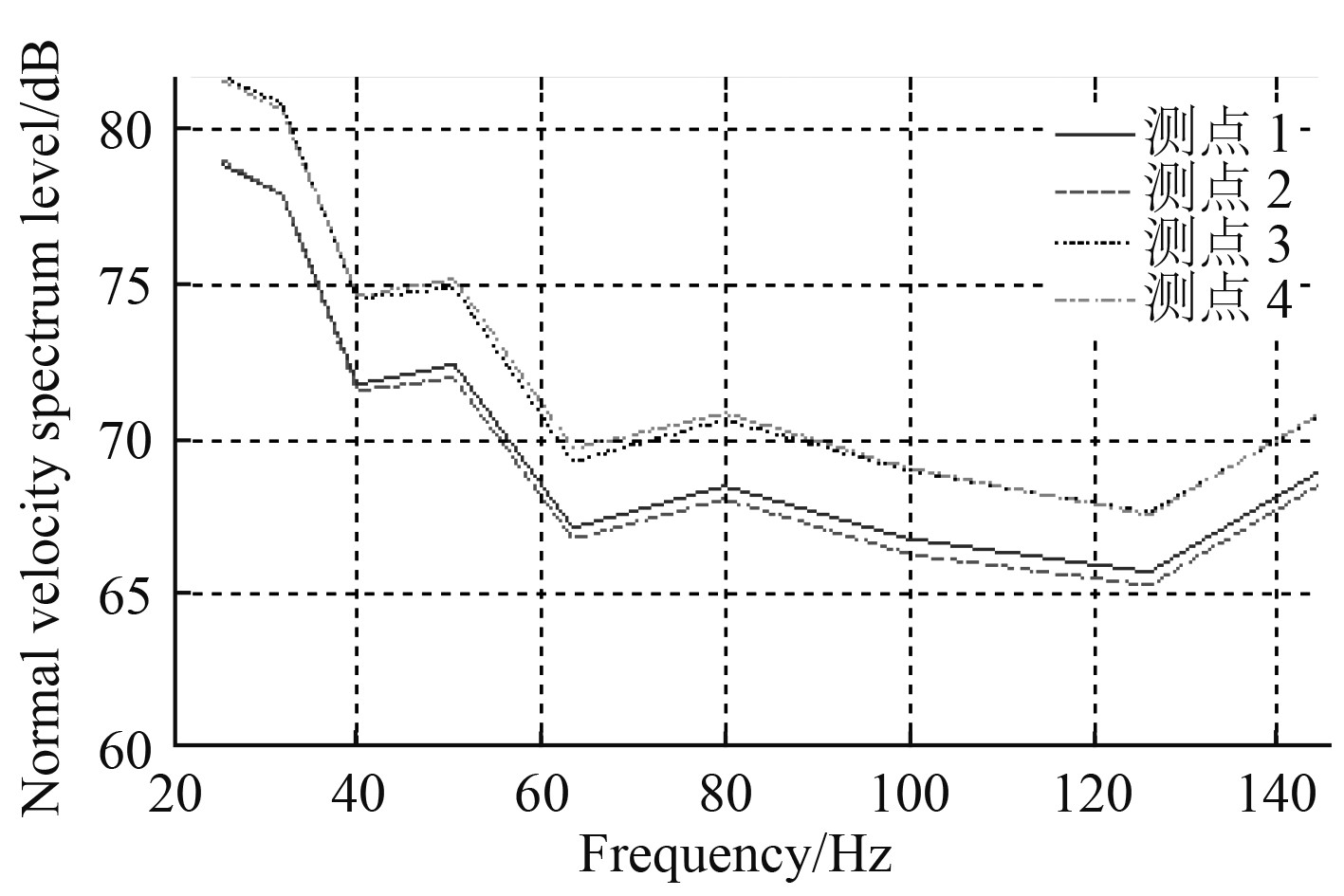
|
图 14 支柱测点法向振速谱级(1/3 oct) Fig. 14 Normal vibration velocity spectrum level of measuring-points on pillar area |
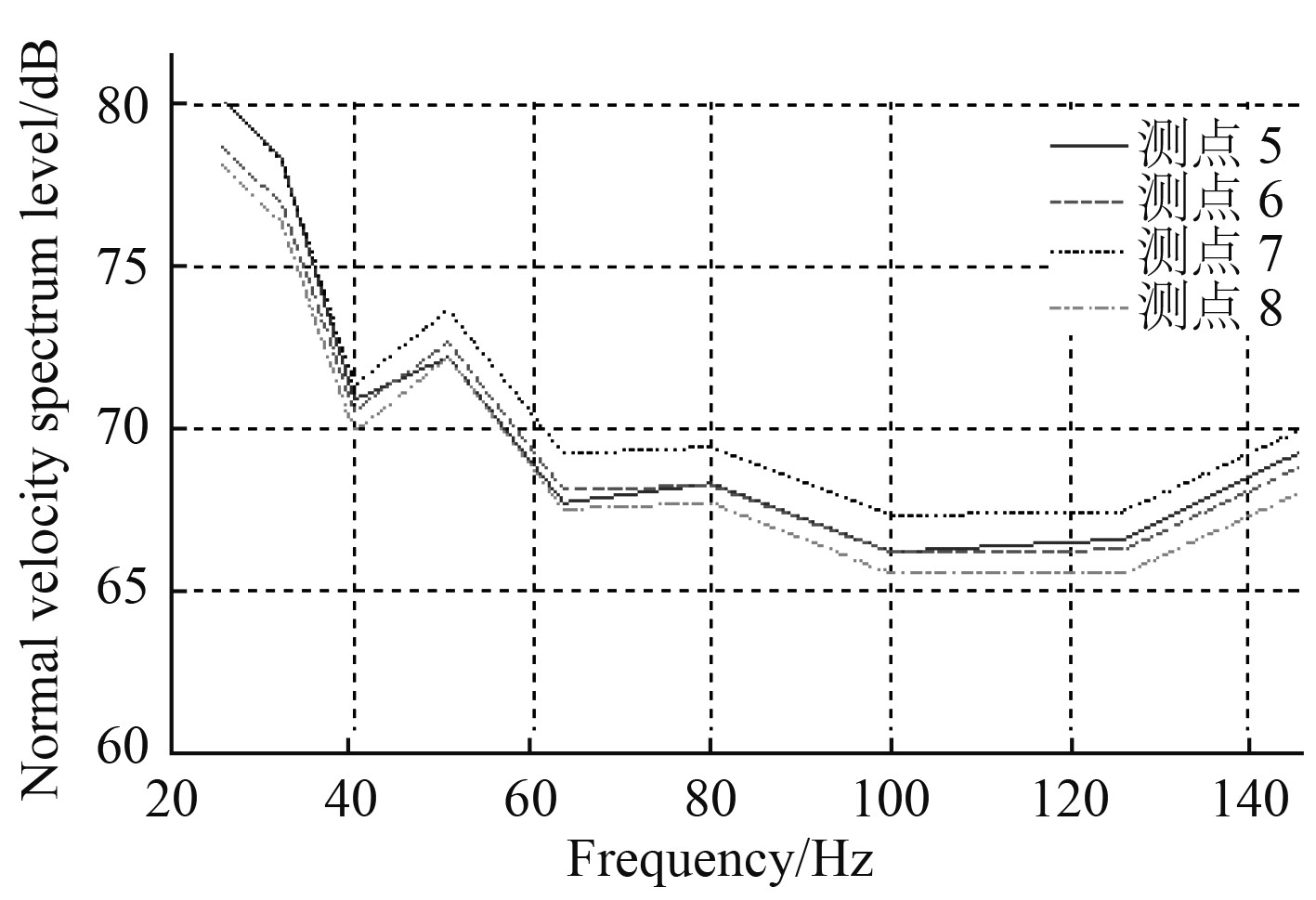
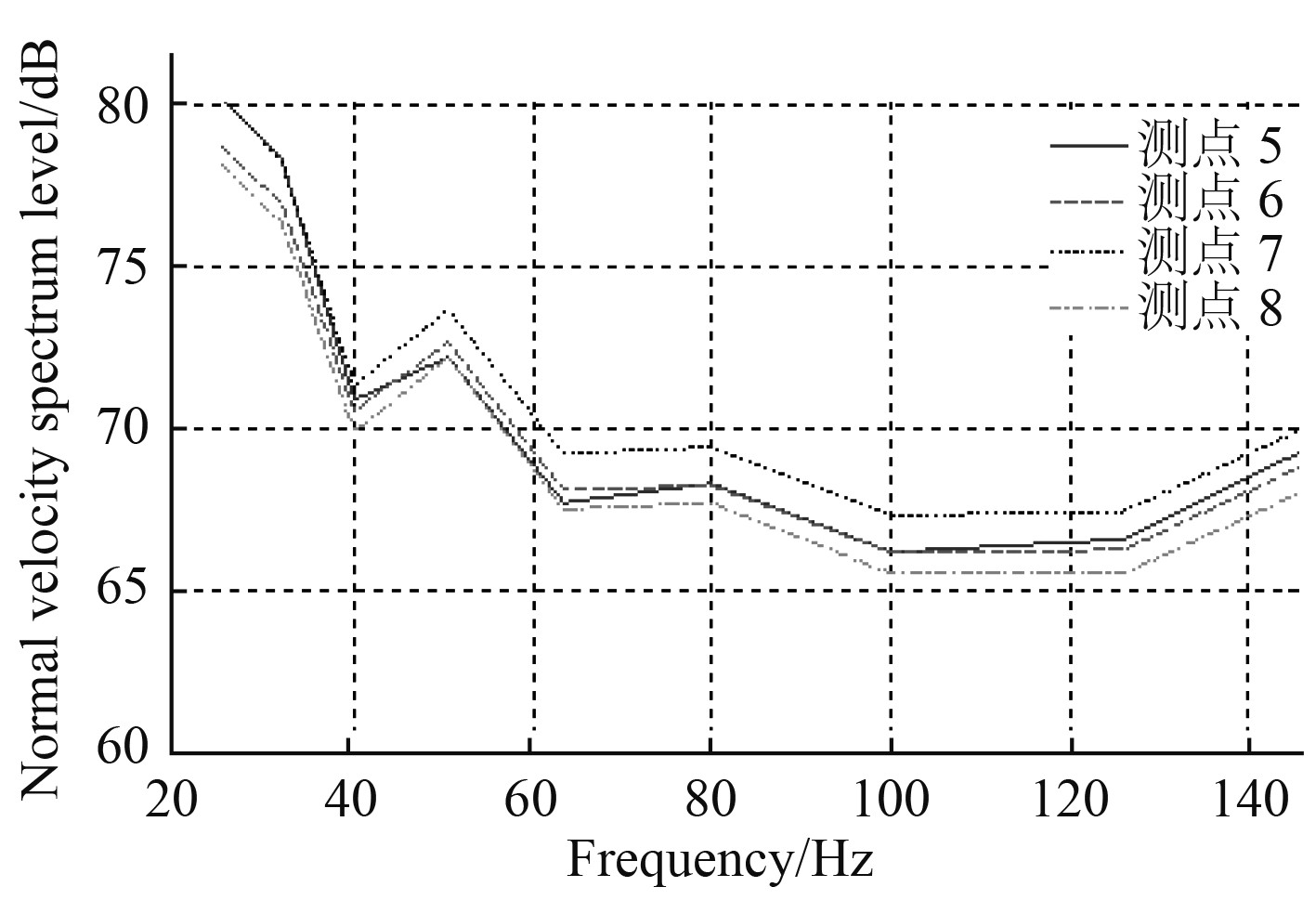
|
图 15 潜体测点法向振速谱级(1/3 oct) Fig. 15 Normal vibration velocity spectrum level of measuring-points on submersible area |
图16为采用声学有限元方法(FEM)与文献[3]所采用的统计能量法(SEA)计算得到的双体船在6 kn 航速下距离船体1 m处的辐射噪声结果。从图中可以看出,在低频范围内有限元计算结果要高于统计能量法的计算结果,而在高频段范围内两种方法的计算结果趋势逐渐一致。这可以归因于统计能量法在低频段模态密度不够,统计能量法计算声辐射本身存在一定的误差,而采用声学有限元法则不存在该问题,因此采用有限元(FEA)法计算双体船声辐射是较为合理的。
|
图 16 有限元法与统计能量法计算结果对比 Fig. 16 Comparison between results from FEM and SEA method |
本文采用大涡模拟技术,通过数值模拟计算得到了小水线面双体船水下部分结构表面的湍流脉动压力分布情况,并以此为激励源,利用声学有限元方法计算得到了双体船航行状态下的流激辐射噪声。经计算发现采用大涡模拟技术能够有效地模拟航行时船体周围的湍流脉动压力分布,较为准确地得到船体湍流脉动压力。同时,声学有限元法可以克服统计能量法在低频段模态密度不足的缺点。计算结果表明,其在低频段水下辐射噪声的计算结果高于统计能量法,随着频率的提高二者的计算结果逐渐趋于一致,因此能够较好地预报双体船的流激辐射噪声。
| [1] |
DAVIES H. G. Sound from turbulent boundary layer excited [J] panels , Journal. Acoust. Soc. Am., 1971;49(3): 878~889.
|
| [2] |
彭临慧, 陆建辉, 邱晓芳, 等. 水下回转体湍流边界层压力起伏谱经验公式[J]. 声学学报, 2001, 26(1): 51-54. PENG Lin-hui, LU Jian-hui, QIU Xiao-fang, et al. Empirical formula of turbulent boundary layer pressure fluctuation spectrum on underwater body of revolution[J]. ACTA ACUSTICA, Chinese version, 2001, 26(1): 51-54. DOI:10.3321/j.issn:0371-0025.2001.01.009 |
| [3] |
吕世金, 俞孟萨, 李东升. 水下航行体水动力辐射噪声预报方法研究[J]. 水动力学研究与进展, 2007, 22(4): 475-482. LV Shi-jin, YU Meng-sa, LI Dong-sheng. Prediction of hydrodynamic radiation noise of underwater vehicle[J]. Journal of hydrodynamics, 2007, 22(4): 475-482. DOI:10.3969/j.issn.1000-4874.2007.04.012 |
| [4] |
张楠, 沈泓萃, 姚惠之, 等. 水下航行体壁面脉动压力的大涡模拟研究[J]. 水动力学研究与进展, 2010, 25(1): 106-112. ZHANG Nan, SHEN Hong-cui, YAO Hui-zhi, et al. Large eddy simulation of wall pressure fluctuations of underwater vehicle[J]. Journal of Hydrodynamics, 2010, 25(1): 106-112. DOI:10.3969/j.issn.1000-4874.2010-01.015 |
| [5] |
张晓龙, 张楠, 吴宝山. 平板壁面湍流脉动压力及其波数—频率谱的大涡模拟计算分析研究[J]. 船舶力学, 2014, 18(10): 1151-1164. ZHANG Xiao-long, ZHANG Nan, WU Bao-shan. Computation of turbulent wall pressure fluctuation and its wavenumber -frequency spectrum using large eddy simulation[J]. Journal of Ship Mechanics, 2014, 18(10): 1151-1164. DOI:10.3969/j.issn.1007-7294.2014.10.001 |
| [6] |
江文成. 潜艇流噪声与流固耦合作用下流激噪声的数值模拟[D]. 上海: 上海交通大学, 2013. JIANG Wen-cheng. Numerical simulation on flow noise and flow-excited noise of submarine under fluid structure interaction[D]. Shanghai: Shanghai Jiao Tong University, 2013. |
| [7] |
BRUN C, et al. (Eds.) Numerical Simulation of turbulent flows & noise generation [U]. Springer-Verlag Berlin Heidelberg. 2009.
|
| [8] |
HEATWOLE CM, FRANCHEK MA, BERNHARD RJ. Robust feedback control of flow induced structural radiation of sound [V]. Herrick Laboratory Internal Report, #0278-1, 7-97.
|
| [9] |
HEATWOLE CM, FRANCHEK MA, BERNHARD RJ. A robust feedback controller implementation for flow induced structural radiation of sound [J]. In: Noise-Con 96, Seattle, Wash, 1996, 62-357.
|
 2020, Vol. 42
2020, Vol. 42
