2. 船舶振动噪声重点实验室,湖北 武汉 430064
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430064, China
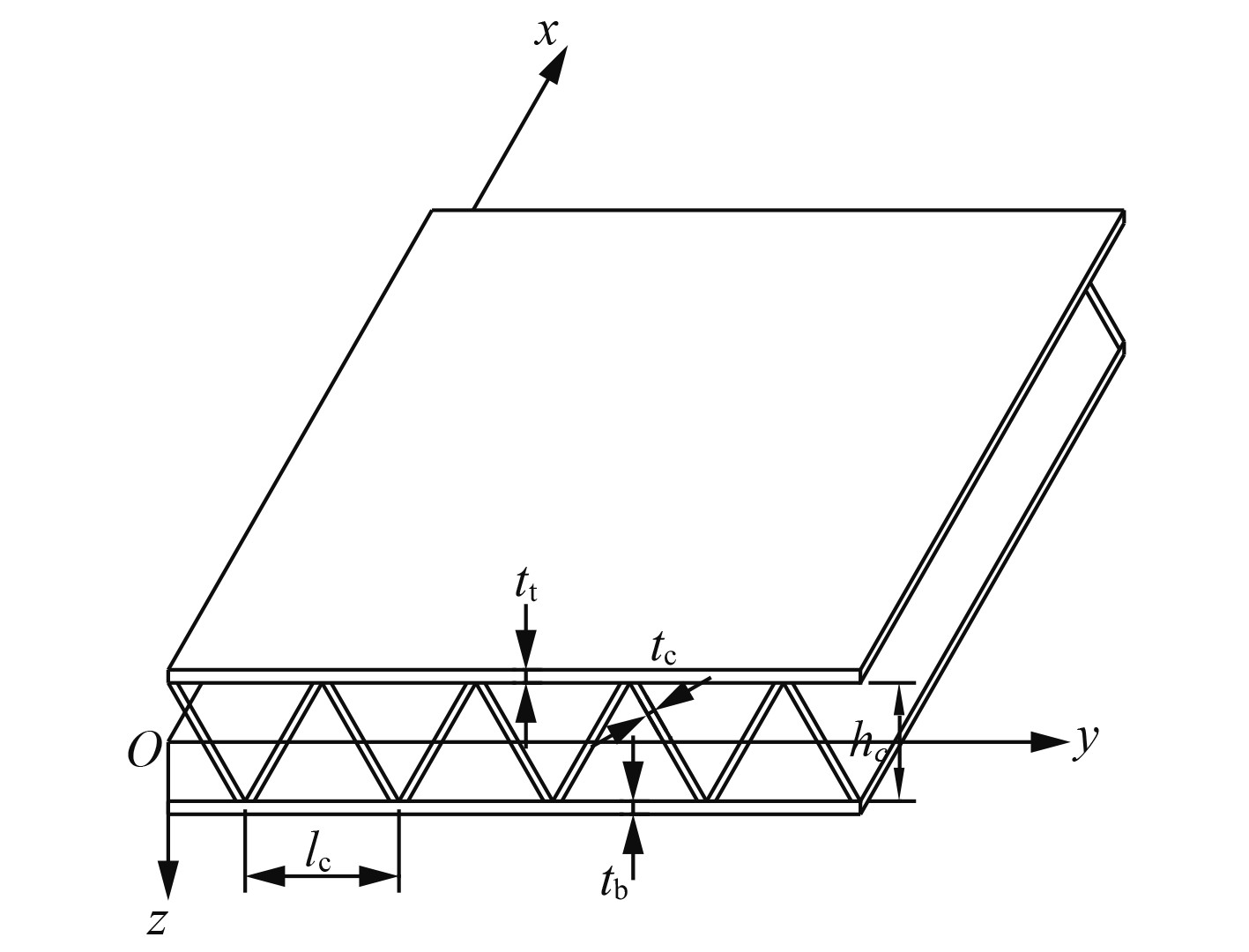
夹层板是由强度大的上下面板和密度较小的心层组成,通常上下面板可以是钢板,碳纤维或者玻璃钢等,心层可以是木材,铝蜂窝或者泡沫塑料。心层的设计还有一种思路来降低等效密度,可以把心层设计成空心的波纹状结构,通过粘结[1-2]或者激光焊接[3-4]与上下面板相连,这就是波纹夹层板(见图1)。这样组成的新结构具有比强度高、比刚度高的优点,经常被应用到航空航天工程,船舶海洋工程,建筑桥梁工程和车辆工程等。
|
图 1 波纹夹层板结构示意图 Fig. 1 Corrugated sandwich structure |
对于夹层板固有频率的研究,最经典的著作是文献[5],其中以Hoff理论研究了夹层板的振动频率,分别研究了不同边界条件下,固有频率的计算方法。吴晖把夹层板看作正交异性体,借鉴文献[5]中的结论,认为垂直波纹方向的剪切刚度无限大,推导出固有频率的解析表达式[6];Hossein Zamanifar等运用精细切片法研究了夹层板的自由振动和强迫振动,通过等效参数,将三维的夹层板通过等效参数转化成二维正交异性板,求解了无量纲的自由振动频率,与前人的研究成果吻合一致[7]。Zig-Zag理论在复合材料或层合板领域应用很广泛[8-10]。白瑞祥等以3层均质复合材料(或等效成3层均质复合材料)夹层板为研究对象,引入一阶Zig-Zag理论,建立了夹层板自由振动的有限元模型,采用子空间迭代法求解自由振动固有频率[11]。对于上下面板之间是非连续介质的心层夹层板,目前采用一阶Zig-Zag理论来建立运动方程的文献很少。本文提出一种考虑波纹夹层板心层不连续形状的情况下,上下3层都应用一阶Zig-Zag理论建立夹层板的运动方程的方法。
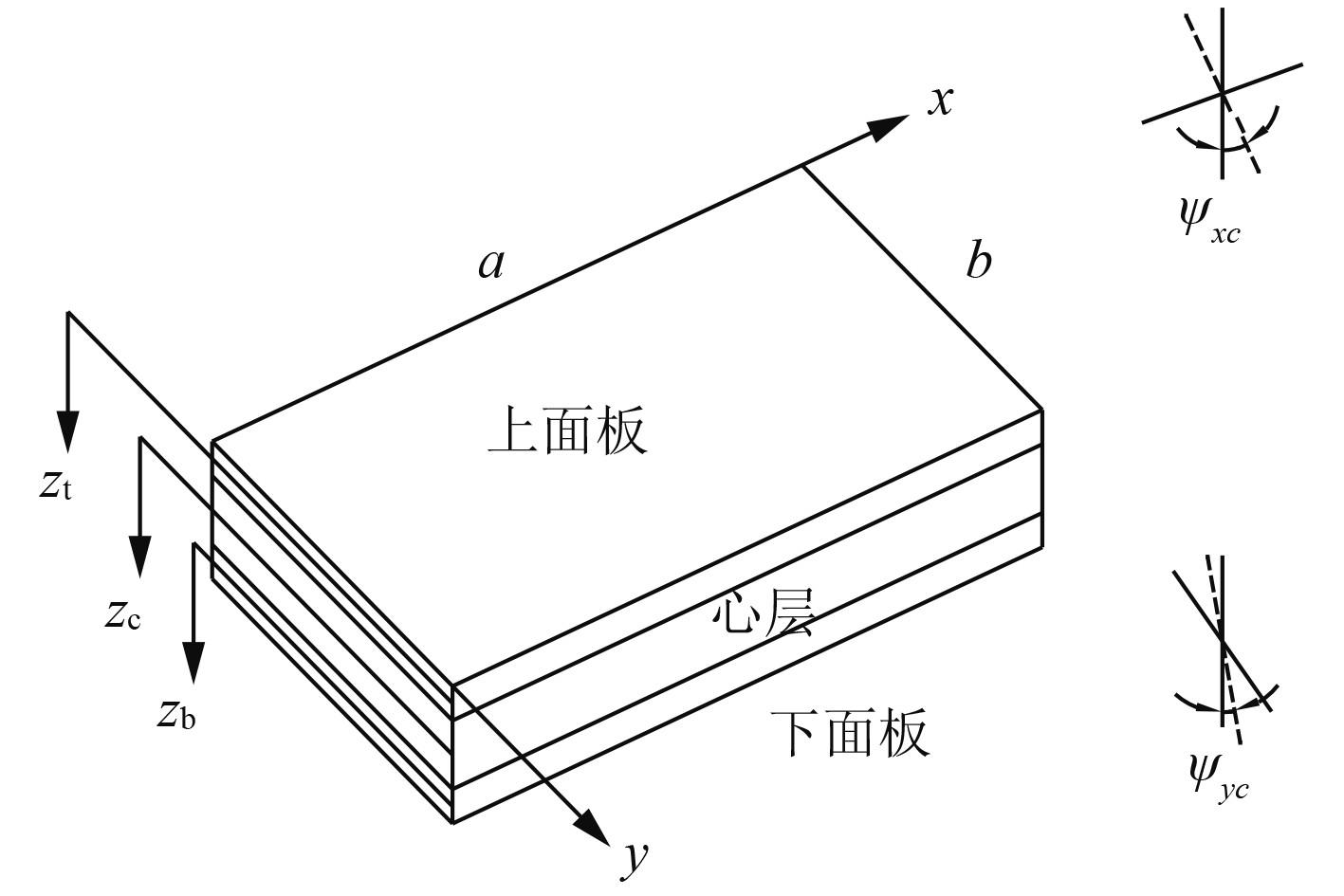
1 振动微分方程如图2所示,波纹夹层板由上下面板和中间心层组成。在波纹夹层板中建立坐标系统。
|
图 2 夹层板坐标系统 Fig. 2 Coordinate system of corrugated sandwich |
图中:tt为上面板厚度,tb为下面板厚度,tc为中间心层的厚度;心层的静高度为hc,心层的周期间距为lc。在线弹性理论分析,做以下基本假设:
1)夹层板的上下面板为普通薄板,考虑其抗剪作用,应用一阶剪切变形理论;
2)心层横向不可压缩,即假定
3)考虑心层的剪切作用,则心层中面法线在变形后保持为直线,但不再垂直于变形后的中面;
4)心层仅考虑其沿波纹方向的弯曲作用,忽略其垂直波纹方向的弯曲作用;
5)上下3层结构的面内位移沿板厚方向分段连续。
1.1 坐标系统与位移表达根据假设1~假设4和图2中夹层板的坐标系统,上下面板的位移函数可以表示为:
| ${u_k}\left( {x,y,{z_k},t} \right) = {u_{ok}}\left( {x,y,t} \right) + {z_k}{\phi _{xk}}\left( {x,y,t} \right) {\text{,}}$ | (1) |
| $ {v_k}\left( {x,y,{z_k},t} \right) = {v_{ok}}\left( {x,y,t} \right) + {z_k}{\phi _{yk}}\left( {x,y,t} \right) {\text{,}} $ | (2) |
| ${w_k}\left( {x,y,{z_k},t} \right) = w\left( {x,y,t} \right) {\text{。}}$ | (3) |
式中:k取t,表示上面板;k取b,表示下面板。
心层的位移函数可以表示为:
| ${u_c}\left( {x,y,{z_c},t} \right) = {u_{oc}}\left( {x,y,t} \right) + {z_c}{\phi _{xc}}\left( {x,y,t} \right) {\text{,}}$ | (4) |
| ${v_c}\left( {x,y,{z_c},t} \right) = {v_{oc}}\left( {x,y,t} \right) + {z_c}{\phi _{yc}}\left( {x,y,t} \right) {\text{,}}$ | (5) |
| ${w_c}\left( {x,y,{z_c},t} \right) = w\left( {x,y,t} \right) {\text{。}}$ | (6) |
其中:
根据假设5,可以列出位移连续条件如下:
| ${u_t}\left( {x,y,{z_t} = \frac{{{t_t}}}{2}} \right) = {u_c}\left( {x,y,{z_c} = - \frac{{{h_c}}}{2}} \right) {\text{,}}$ | (7) |
| ${v_t}\left( {x,y,{z_t} = \frac{{{t_t}}}{2}} \right) = {v_c}\left( {x,y,{z_c} = - \frac{{{h_c}}}{2}} \right) {\text{,}}$ | (8) |
| ${u_b}\left( {x,y,{z_b} = - \frac{{{t_b}}}{2}} \right) = {u_c}\left( {x,y,{z_c} = \frac{{{h_c}}}{2}} \right) {\text{,}}$ | (9) |
| ${v_b}\left( {x,y,{z_b} = - \frac{{{t_b}}}{2}} \right) = {v_c}\left( {x,y,{z_c} = \frac{{{h_c}}}{2}} \right) {\text{。}}$ | (10) |
将式(1)~式(5)代入式(7)~式(10),求出:
| ${u_{ot}}\left( {x,y} \right) = {u_{oc}}\left( {x,y} \right) - \frac{{{h_c}}}{2}{\phi _{xc}}\left( {x,y} \right) - \frac{{{t_t}}}{2}{\phi _{xt}}\left( {x,y} \right) {\text{,}}$ | (11) |
| ${v_{ot}}\left( {x,y} \right) = {v_{oc}}\left( {x,y} \right) - \frac{{{h_c}}}{2}{\phi _{yc}}\left( {x,y} \right) - \frac{{{t_t}}}{2}{\phi _{yt}}\left( {x,y} \right) {\text{,}}$ | (12) |
| ${u_{ob}}\left( {x,y} \right) = {u_{oc}}\left( {x,y} \right) + \frac{{{h_c}}}{2}{\phi _{xc}}\left( {x,y} \right) + \frac{{{t_b}}}{2}{\phi _{xb}}\left( {x,y} \right) {\text{,}}$ | (13) |
| ${v_{ob}}\left( {x,y} \right) = {v_{oc}}\left( {x,y} \right) + \frac{{{h_c}}}{2}{\phi _{yc}}\left( {x,y} \right) + \frac{{{t_b}}}{2}{\phi _{yb}}\left( {x,y} \right) {\text{。}}$ | (14) |
将式(11)~式(14)代入式(1)和式(2),联合式(3)~式(6),则所有的位移函数都用心层的中面位移函数表达。
应用弹性理论的应变位移关系,对于上面板:
| $\varepsilon _x^t = \frac{{\partial {u_t}}}{{\partial x}} = \frac{{\partial {u_{oc}}\left( {x,y} \right)}}{{\partial x}} - \frac{{{h_c}}}{2}\frac{{\partial {\phi _{xc}}\left( {x,y} \right)}}{{\partial x}} + \left( {{z_t} - \frac{{{t_t}}}{2}} \right)\frac{{\partial {\phi _{xt}}\left( {x,y} \right)}}{{\partial x}} {\text{,}}$ | (15) |
| $\begin{split}\varepsilon _y^t = \frac{{\partial {v_t}}}{{\partial y}} =& \frac{{\partial {v_{oc}}\left( {x,y} \right)}}{{\partial y}} - \frac{{{h_c}}}{2}\frac{{\partial {\phi _{yc}}\left( {x,y} \right)}}{{\partial y}} + \left( {{z_t} - \frac{{{t_t}}}{2}} \right)\\& \frac{{{\partial ^2}w(x,y)}}{{\partial {y^2}}}\frac{{\partial {\phi _{yt}}\left( {x,y} \right)}}{{\partial y}}{\text{,}}\end{split} $ | (16) |
| $\begin{split} \gamma _{xy}^t = & \frac{{\partial {u_t}}}{{\partial y}} + \frac{{\partial {v_t}}}{{\partial x}} = \frac{{\partial {u_{oc}}\left( {x,y} \right)}}{{\partial y}} - \frac{{{h_c}}}{2}\left( {\frac{{{\phi _{yc}}\left( {x,y} \right)}}{{\partial x}} + \frac{{\partial {\phi _{xc}}\left( {x,y} \right)}}{{\partial y}}} \right) + \\ & \left( {{z_t} - \frac{{{t_t}}}{2}} \right)\left( {\frac{{{\phi _{yt}}\left( {x,y} \right)}}{{\partial x}} + \frac{{\partial {\phi _{xt}}\left( {x,y} \right)}}{{\partial y}}} \right) {\text{,}}\\[-18pt] \end{split} $ | (17) |
| $\gamma _{xz}^t = \frac{{\partial {u_t}}}{{\partial {z_t}}} + \frac{{\partial w}}{{\partial x}} = {\phi _{xt}}\left( {x,y} \right) + \frac{{\partial w}}{{\partial x}}{\text{,}}$ | (18) |
| $\gamma _{yz}^t = \frac{{\partial {u_t}}}{{\partial {z_t}}} + \frac{{\partial w}}{{\partial x}} = {\phi _{yt}}\left( {x,y} \right) + \frac{{\partial w}}{{\partial y}}{\text{。}}$ | (19) |
对于下面板也可以类似推导。
对于心层,正应变和剪应变分别为:
| $\varepsilon _x^c = \frac{{\partial {u_c}\left( {x,y,{z_c}} \right)}}{{\partial x}} = \frac{{\partial {u_{oc}}\left( {x,y} \right)}}{{\partial x}} + {z_c}\frac{{\partial {\phi _{xc}}\left( {x,y} \right)}}{{\partial x}}{\text{,}}$ | (20) |
| $\begin{split}\gamma _s^c =& \left[ {\frac{{\partial {u_c}\left( {x,y,{z_c}} \right)}}{{\partial {z_c}}} + \frac{{\partial {w_c}\left( {x,y} \right)}}{{\partial x}}} \right]\sin \theta =\\&\left[ {{\phi _{xc}}\left( {x,y} \right) + \frac{{\partial w\left( {x,y} \right)}}{{\partial x}}} \right]\sin \theta{\text{,}} \end{split}$ | (21) |
| $\gamma _{yz}^c = \frac{{\partial {v_c}\left( {x,y,z} \right)}}{{\partial {z_c}}} + \frac{{\partial {w_c}\left( {x,y} \right)}}{{\partial y}} = {\phi _{yc}}\left( {x,y} \right) + \frac{{\partial w\left( {x,y} \right)}}{{\partial y}}{\text{。}}$ | (22) |
其中,
上下面板和心层的每一个构件材料,认为它是各向同性的,则由弹性理论可以求出应力。
| $\sigma _x^k = \frac{E}{{1 - {\mu ^2}}}\left( {\varepsilon _x^k + \mu \varepsilon _y^k} \right){\text{,}}$ | (23) |
| $\sigma _y^k = \frac{E}{{1 - {\mu ^2}}}\left( {\varepsilon _y^k + \mu \varepsilon _x^k} \right){\text{,}}$ | (24) |
| $\tau _{xy}^k = \frac{E}{{2\left( {1 + \mu } \right)}}\gamma _{xy}^k{\text{,}}$ | (25) |
| $\tau _{xz}^k = \frac{E}{{2\left( {1 + \mu } \right)}}\gamma _{xz}^k{\text{,}}$ | (26) |
| $\tau _{yz}^k = \frac{E}{{2\left( {1 + \mu } \right)}}\gamma _{yz}^k{\text{。}}$ | (27) |
其中,
| $\sigma _x^c = {E_c}\varepsilon _x^c{\text{,}}$ | (28) |
| $\tau _s^c = \frac{{{E_c}}}{{2\left( {1 + {\mu _c}} \right)}}\gamma _s^c{\text{,}}$ | (29) |
| $\tau _{yz}^c = G_{yz}^c\gamma _{yz}^c{\text{。}}$ | (30) |
根据文献[12]和文献[13]的结论,心层yz平面的剪切弹性模量
| $G_{yz}^c = \frac{{{E_c}{t_c}{{\sin }^2}\theta \cos \theta }}{{{h_c}}}{\text{。}}$ | (31) |
哈密尔顿(Hamilton)原理提出稳定系统的动能和势能之差(动势)必然是最小值。对于振动分析的波纹夹层板而言,系统存在动能T和势能U,但是没有外力做功,势能仅包括系统的应变能。根据变分法,则应该使得
| $\delta \left( {T - U} \right) = 0{\text{。}}$ | (32) |
系统的动能包括3部分,分别是上下面板动能和心层动能。
| $T = {T_t} + {T_b} + {T_c}{\text{,}}$ | (33) |
| $\small{T_k} = \frac{\rho }{2}\left\{ {{{\int_{ - {t_k}/2}^{{t_k}/2} {\left( {\frac{{\partial {u_k}}}{{\partial t}}} \right)} }^2}{\rm{d}}{z_k} + {{\int_{ - {t_k}/2}^{{t_k}/2} {\left( {\frac{{\partial {v_k}}}{{\partial t}}} \right)} }^2}{\rm{d}}{z_k} + {{\int_{ - {t_k}/2}^{{t_k}/2} {\left( {\frac{{\partial w}}{{\partial t}}} \right)} }^2}{\rm{d}}{z_k}} \right\}{\text{,}}$ | (34) |
| $\begin{split}{T_c} = &\frac{{{\rho _c}}}{2}\left\{ {{{\int_{{z_c} - {t_c}/(2\cos \theta )}^{{z_c} + {t_c}/(2\cos \theta )} {\left( {\frac{{\partial {u_c}}}{{\partial t}}} \right)} }^2}{\rm{d}}{z_c} + {{\int_{ - {t_c}/2}^{{t_c}/2} {\left( {\frac{{\partial {v_c}}}{{\partial t}}} \right)} }^2}{\rm{d}}{z_c}}+\right.\\& \left.{{\int_{ - {t_c}/2}^{{t_c}/2} {\left( {\frac{{\partial w}}{{\partial t}}} \right)} }^2}{\rm{d}}{z_c} \right\}{\text{,}}\\[-18pt]\end{split}$ | (35) |
系统的势能主要是指构件的应变能,应变能也包括3部分,分别是上下面板应变能和心层应变能。
| $U = {U_t} + {U_b} + {U_c}{\text{,}}$ | (36) |
其中:
| $\begin{split} {U_k} = & \frac{1}{2}\smallint _{ - {t_k}/2}^{{t_k}/2}{\text{d}}{z_k}\int {\int_A {} } \hfill \\ & \left( {\sigma _x^k\varepsilon _x^k + \sigma _y^k\varepsilon _y^k + \tau _{xy}^k\gamma _{xy}^k + \tau _{xz}^k\gamma _{xz}^k + + \tau _{yz}^k\gamma _{yz}^k} \right){\text{d}}x{\text{d}}y \end{split} $ | (37) |
| $\begin{split}{U_c} = &\frac{1}{2}\int\nolimits_{{z_c} - {t_c}/(2\cos \theta )}^{{z_c} + {t_c}/(2\cos \theta )} {{\rm{d}}{z_c}\iint\nolimits_A {\left( {\sigma _x^c\varepsilon _x^c + \tau _s^c\gamma _s^c} \right)dxdy}} + \\& \frac{1}{2}\int_{ - {h_c}/2}^{{h_c}/2} {{\rm{d}}{z_c}} \iint\limits_A {\tau _{yz}^c\gamma _{yz}^c{\rm{d}}x{\rm{d}}y}{\text{。}}\end{split}$ | (38) |
将式(33)~(38)代入式(32),应用变分法中的拉格朗日–欧拉方程,经过复杂的推导、运算,得出以下振动微分方程:
| $\begin{split}& - \frac{1}{2}\rho t_b^2\frac{{{\partial ^2}{\varphi _{xb}}}}{{\partial {t^2}}} + \frac{1}{2}\rho {h_c}\left( {{t_t} - {t_b}} \right)\frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial {t^2}}} + \frac{1}{2}\rho t_t^2\frac{{{\partial ^2}{\varphi _{xt}}}}{{\partial {t^2}}} - \rho \left( {{t_t} + {t_b}} \right)\frac{{{\partial ^2}{u_{0c}}}}{{\partial {t^2}}} +\\& \frac{{Et_b^2}}{{4\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xb}}}}{{\partial {y^2}}} + \frac{{E{h_c}\left( {{t_b} - {t_t}} \right)}}{{4\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial {y^2}}} - \frac{{Et_t^2}}{{4\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xt}}}}{{\partial {y^2}}} +\\& \frac{{E\left( {{t_b} + {t_t}} \right)}}{{4\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{u_{0c}}}}{{\partial {y^2}}} + \frac{{Et_b^2}}{{4\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yb}}}}{{\partial x\partial y}} + \frac{{E{h_c}\left( {{t_b} - {t_t}} \right)}}{{4\left( {1 - \mu } \right)}} \frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial x\partial y}} -\\& \frac{{Et_t^2}}{{4\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial x\partial y}} + \frac{{E\left( {{t_b} + {t_t}} \right)}}{{2\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{v_{0c}}}}{{\partial x\partial y}} + \frac{{Et_b^2}}{{2\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{xb}}}}{{\partial {x^2}}} + \\&\left[ {\frac{{E{h_c}\left( {{t_b} - {t_t}} \right)}}{{2\left( {1 - {\mu ^2}} \right)}} + \frac{{{E_c}{t_c}{z_c}}}{{\cos \theta }}} \right] \frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial {x^2}}} - \frac{{Et_t^2}}{{2\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{xt}}}}{{\partial {x^2}}} + \\&\left[ {\frac{{E\left( {{t_b} + {t_t}} \right)}}{{1 - {\mu ^2}}} + \frac{{{E_c}{t_c}}}{{\cos \theta }}} \right]\frac{{{\partial ^2}{u_{0c}}}}{{\partial {x^2}}} = 0 {\text{,}}\\[-24pt] \end{split} $ | (39) |
| $\begin{split}& - \frac{1}{2}\rho t_b^2\frac{{{\partial ^2}{\varphi _{yb}}}}{{\partial {t^2}}} + \frac{1}{2}\rho {h_c}\left( {{t_t} - {t_b}} \right)\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial {t^2}}} + \frac{1}{2}\rho t_t^2\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial {t^2}}} -\\& \rho \left( {{t_t} + {t_b}} \right)\frac{{{\partial ^2}{v_{0c}}}}{{\partial {t^2}}} + \frac{{Et_b^2}}{{2\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{yb}}}}{{\partial {y^2}}} + \frac{{E{h_c}\left( {{t_b} - {t_t}} \right)}}{{2\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial {y^2}}} -\\& \frac{{Et_t^2}}{{2\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial {y^2}}}+ \frac{{E\left( {{t_b} + {t_t}} \right)}}{{1 - {\mu ^2}}}\frac{{{\partial ^2}{v_{0c}}}}{{\partial {y^2}}} + \frac{{Et_b^2}}{{4\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xb}}}}{{\partial x\partial y}} + \\&\frac{{E{h_c}\left( {{t_b} - {t_t}} \right)}}{{4\left( {1 - \mu } \right)}} \frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial x\partial y}} - \frac{{Et_t^2}}{{4\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xt}}}}{{\partial x\partial y}} + \frac{{E\left( {{t_b} + {t_t}} \right)}}{{2\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{u_{0c}}}}{{\partial x\partial y}} + \frac{{Et_b^2}}{{4\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yb}}}}{{\partial {x^2}}} + \\&\frac{{E{h_c}\left( {{t_b} - {t_t}} \right)}}{{4\left( {1 + \mu } \right)}} \frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial {x^2}}} - \frac{{Et_t^2}}{{4\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial {x^2}}} + \frac{{E\left( {{t_b} + {t_t}} \right)}}{{2\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{v_{0c}}}}{{\partial {x^2}}} = 0 {\text{,}}\\[-14pt] \end{split} $ | (40) |
| $\begin{split}& - \frac{{{E_c}t{}_c{{\sin }^2}\theta }}{{2\left( {1 + {\mu _c}} \right)\cos \theta }}{\varphi _{xc}} - \frac{1}{4}\rho {h_c}t_b^2\frac{{{\partial ^2}{\varphi _{xb}}}}{{\partial {t^2}}} - \frac{1}{4}\rho h_c^2\left( {{t_t} + {t_b}} \right)\frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial {t^2}}} -\\& \frac{1}{4}\rho {h_c}t_t^2\frac{{{\partial ^2}{\varphi _{xt}}}}{{\partial {t^2}}} + \frac{1}{2}\rho {h_c}\left( {{t_t} - {t_b}} \right)\frac{{{\partial ^2}{u_{0c}}}}{{\partial {t^2}}} +\frac{{E{h_c}t_b^2}}{{8\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xb}}}}{{\partial {y^2}}} +\\& \frac{{Eh_c^2\left( {{t_b} + {t_t}} \right)}}{{8\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial {y^2}}} +\frac{{E{h_c}t_t^2}}{{8\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xt}}}}{{\partial {y^2}}} + \frac{{E{h_c}\left( {{t_b} - {t_t}} \right)}}{{4\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{u_{0c}}}}{{\partial {y^2}}} -\\& \frac{{{E_c}{t_c}{{\sin }^2}\theta }}{{2\left( {1 + {\mu _c}} \right)\cos \theta }}\frac{{\partial w}}{{\partial x}} +\frac{{E{h_c}t_b^2}}{{8\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yb}}}}{{\partial x\partial y}} + \frac{{Eh_c^2\left( {{t_b} + {t_t}} \right)}}{{8\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial x\partial y}} +\\& \frac{{E{h_c}t_t^2}}{{8\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial x\partial y}} + \frac{{E{h_c}\left( {{t_b} - {t_t}} \right)}}{{4\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{v_{0c}}}}{{\partial x\partial y}} + \frac{{E{h_c}t_b^2}}{{4\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{xb}}}}{{\partial {x^2}}} +\\& \left[ {\frac{{Eh_c^2\left( {{t_b} + {t_t}} \right)}}{{4\left( {1 - {\mu ^2}} \right)}} + \frac{{{E_c}{t_c}z_c^2}}{{\cos \theta }} + \frac{{{E_c}t_c^3}}{{12{{\cos }^3}\theta }}} \right] \times\\& \frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial {x^2}}} + \frac{{E{h_c}t_t^2}}{{2\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{xt}}}}{{\partial {x^2}}} +\left[ {\frac{{E{h_c}\left( {{t_b} - {t_t}} \right)}}{{2\left( {1 - {\mu ^2}} \right)}} + \frac{{{E_c}{t_c}{z_c}}}{{\cos \theta }}} \right]\frac{{{\partial ^2}{u_{0c}}}}{{\partial {x^2}}} = 0{\text{,}} \end{split} $ | (41) |
| $\begin{split}& - 2G_{yz}^c{h_c}{\varphi _{yc}} - \frac{1}{4}\rho {h_c}t_b^2\frac{{{\partial ^2}{\varphi _{yb}}}}{{\partial {t^2}}} - \frac{1}{4}\rho h_c^2\left( {{t_t} + {t_b}} \right)\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial {t^2}}} -\\& \frac{1}{4}\rho {h_c}t_t^2\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial {t^2}}} +\frac{1}{2}\rho {h_c}\left( {{t_t} - {t_b}} \right)\frac{{{\partial ^2}{v_{0c}}}}{{\partial {t^2}}} - 2G_{yz}^c{h_c}\frac{{\partial w}}{{\partial y}} +\\& \frac{{E{h_c}t_b^2}}{{4\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{yb}}}}{{\partial {y^2}}} + \frac{{Eh_c^2\left( {{t_b} + {t_t}} \right)}}{{4\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial {y^2}}} + \frac{{E{h_c}t_t^2}}{{4\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial {y^2}}} +\\& \frac{{E{h_c}\left( {{t_b} - {t_t}} \right)}}{{2\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{v_{0c}}}}{{\partial {y^2}}} + \frac{{E{h_c}t_b^2}}{{8\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xb}}}}{{\partial x\partial y}} + \frac{{Eh_c^2\left( {{t_b} + {t_t}} \right)}}{{8\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial x\partial y}} +\\& \frac{{E{h_c}t_t^2}}{{8\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial x\partial y}} + \frac{{E{h_c}\left( {{t_b} - {t_t}} \right)}}{{4\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{u_{0c}}}}{{\partial x\partial y}} + \frac{{E{h_c}t_b^2}}{{8\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yb}}}}{{\partial {x^2}}} + \\&\frac{{Eh_c^2\left( {{t_b} + {t_t}} \right)}}{{8\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial {x^2}}} + \frac{{E{h_c}t_t^2}}{{8\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial {x^2}}} + \frac{{E{h_c}\left( {{t_b} - {t_t}} \right)}}{{4\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{v_{0c}}}}{{\partial {x^2}}} = 0{\text{,}} \end{split} $ | (42) |
| $\begin{split}& q\left( {x,y} \right) - \left[ {\rho \left( {{t_t} + {t_b}} \right) + \frac{{{\rho _c}{t_c}}}{{\cos \theta }}} \right]\frac{{{\partial ^2}w}}{{\partial {t^2}}} +\\& \frac{{E{t_b}}}{{2\left( {1 + \mu } \right)}}\left( {\frac{{\partial {\varphi _{xb}}}}{{\partial x}} + \frac{{\partial {\varphi _{yb}}}}{{\partial y}}} \right) + 2G_{yz}^c{h_c}\frac{{\partial {\varphi _{yc}}}}{{\partial y}} + \\&\frac{{E{t_t}}}{{2\left( {1 + \mu } \right)}}\left( {\frac{{\partial {\varphi _{xt}}}}{{\partial x}} + \frac{{\partial {\varphi _{yt}}}}{{\partial y}}} \right) + \left[ {2G_{yz}^c{h_c} + \frac{{E\left( {{t_b} - {t_t}} \right)}}{{2\left( {1 + \mu } \right)}}} \right]\frac{{{\partial ^2}w}}{{\partial {y^2}}} +\\& \frac{{{E_c}{t_c}{{\sin }^2}\theta }}{{2\left( {1 + {\mu _c}} \right)\cos \theta }} \times \frac{{\partial {\varphi _{xc}}}}{{\partial x}} +\\& \left[ {\frac{{E\left( {{t_b} + {t_t}} \right)}}{{2\left( {1 + \mu } \right)}}+ \frac{{{E_c}{t_c}{{\sin }^2}\theta }}{{2\left( {1 + {\mu _c}} \right)\cos \theta }}} \right]\frac{{{\partial ^2}w}}{{\partial {x^2}}} = 0 {\text{,}} \\[-18pt] \end{split} $ | (43) |
| $\begin{split}& - \frac{{E{t_t}}}{{2\left( {1 + \mu } \right)}}{\varphi _{xt}} - \frac{1}{4}\rho {h_c}t_t^2\frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial {t^2}}} - \frac{1}{3}\rho t_t^3\frac{{{\partial ^2}{\varphi _{xt}}}}{{\partial {t^2}}} + \frac{1}{2}\rho t_t^2\frac{{{\partial ^2}{u_{0c}}}}{{\partial {t^2}}} + \\&\frac{{E{h_c}t_t^2}}{{8\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial {y^2}}} + \frac{{Et_t^3}}{{6\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xt}}}}{{\partial {y^2}}} - \frac{{Et_t^2}}{{4\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{u_{0c}}}}{{\partial {y^2}}} -\\& \frac{{E{t_t}}}{{2\left( {1 + \mu } \right)}}\frac{{\partial w}}{{\partial x}} + \frac{{E{h_c}t_t^2}}{{8\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial x\partial y}} + \frac{{Et_t^3}}{{4\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial x\partial y}} - \\&\frac{{Et_t^2}}{{4\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{v_{0c}}}}{{\partial x\partial y}} + \frac{{E{h_c}t_t^2}}{{4\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial {x^2}}} + \frac{{Et_t^3}}{{3\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{xt}}}}{{\partial {x^2}}} -\\& \frac{{Et_t^2}}{{2\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{u_{0c}}}}{{\partial {x^2}}} = 0 {\text{,}}\\[-18pt] \end{split} $ | (44) |
| $\begin{split}& - \frac{{E{t_t}}}{{2\left( {1 + \mu } \right)}}{\varphi _{yt}} - \frac{1}{4}\rho {h_c}t_t^2\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial {t^2}}} - \frac{1}{3}\rho t_t^3\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial {t^2}}} + \frac{1}{2}\rho t_t^2\frac{{{\partial ^2}{v_{0c}}}}{{\partial {t^2}}} - \\&\frac{{E{t_t}}}{{2\left( {1 + \mu } \right)}}\frac{{\partial w}}{{\partial y}} + \frac{{E{h_c}t_t^2}}{{4\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial {y^2}}} + \frac{{Et_t^3}}{{3\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial {y^2}}} - \frac{{Et_t^2}}{{2\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{v_{0c}}}}{{\partial {y^2}}} + \\&\frac{{E{h_c}t_t^2}}{{8\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial x\partial y}} + \frac{{Et_t^3}}{{6\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xt}}}}{{\partial x\partial y}} - \frac{{Et_t^2}}{{4\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{u_{0c}}}}{{\partial x\partial y}} + \frac{{E{h_c}t_t^2}}{{8\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial {x^2}}} +\\& \frac{{Et_t^3}}{{6\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yt}}}}{{\partial {x^2}}} - \frac{{Et_t^2}}{{4\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{v_{0c}}}}{{\partial {x^2}}} = 0 {\text{,}}\\[-18pt] \end{split} $ | (45) |
| $\begin{split}& - \frac{{E{t_b}}}{{2\left( {1 + \mu } \right)}}{\varphi _{xb}} - \frac{1}{3}\rho t_b^3\frac{{{\partial ^2}{\varphi _{xb}}}}{{\partial {t^2}}} - \frac{1}{4}\rho {h_c}t_b^2\frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial {t^2}}} - \frac{1}{2}\rho t_b^2\frac{{{\partial ^2}{u_{0c}}}}{{\partial {t^2}}} + \\&\frac{{Et_b^3}}{{6\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xb}}}}{{\partial {y^2}}} + \frac{{E{h_c}t_b^2}}{{8\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial {y^2}}} + \frac{{Et_b^2}}{{4\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{u_{0c}}}}{{\partial {y^2}}} - \frac{{E{t_b}}}{{2\left( {1 + \mu } \right)}}\frac{{\partial w}}{{\partial x}} +\\& \frac{{Et_b^3}}{{6\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yb}}}}{{\partial x\partial y}} + \frac{{E{h_c}t_b^2}}{{8\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial x\partial y}} + \frac{{Et_b^2}}{{4\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{v_{0c}}}}{{\partial x\partial y}} + \frac{{Et_b^3}}{{3\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{xb}}}}{{\partial {x^2}}} + \\&\frac{{E{h_c}t_b^2}}{{4\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial {x^2}}} + \frac{{Et_b^2}}{{2\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{u_{0c}}}}{{\partial {x^2}}} = 0 {\text{,}}\\[-18pt] \end{split} $ | (46) |
| $\begin{split}& - \frac{{E{t_b}}}{{2\left( {1 + \mu } \right)}}{\varphi _{yb}} - \frac{1}{3}\rho t_b^3\frac{{{\partial ^2}{\varphi _{yb}}}}{{\partial {t^2}}} - \frac{1}{4}\rho {h_c}t_b^2\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial {t^2}}} - \frac{1}{2}\rho t_b^2\frac{{{\partial ^2}{v_{0c}}}}{{\partial {t^2}}} - \\&\frac{{E{t_b}}}{{2\left( {1 + \mu } \right)}}\frac{{\partial w}}{{\partial y}} + \frac{{Et_b^3}}{{3\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{yb}}}}{{\partial {y^2}}} + \frac{{E{h_c}t_b^2}}{{4\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial {y^2}}} + \frac{{Et_b^2}}{{2\left( {1 - {\mu ^2}} \right)}}\frac{{{\partial ^2}{v_{0c}}}}{{\partial {y^2}}} +\\& \frac{{Et_b^3}}{{6\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xb}}}}{{\partial x\partial y}} + \frac{{E{h_c}t_b^2}}{{8\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{\varphi _{xc}}}}{{\partial x\partial y}} + \frac{{Et_b^2}}{{4\left( {1 - \mu } \right)}}\frac{{{\partial ^2}{u_{0c}}}}{{\partial x\partial y}} + \frac{{Et_b^3}}{{6\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yb}}}}{{\partial {x^2}}} +\\& \frac{{E{h_c}t_b^2}}{{8\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{\varphi _{yc}}}}{{\partial {x^2}}} + \frac{{Et_b^2}}{{4\left( {1 + \mu } \right)}}\frac{{{\partial ^2}{v_{0c}}}}{{\partial {x^2}}} = 0 {\text{。}}\\[-18pt] \end{split} $ | (47) |
对于简支的夹层板,其边界条件为:
在x=0或a
| ${v_{0c}} = 0,\frac{{\partial {\phi _{xc}}}}{{\partial x}} = \frac{{\partial {\phi _{xk}}}}{{\partial x}} = 0,{\phi _{yc}} = {\phi _{yk}} = 0,w = 0,\frac{{{\partial ^2}w}}{{\partial {x^2}}} = 0{\text{,}}$ | (48) |
在y=0或b
| ${u_{0c}} = 0,{\phi _{xc}} = {\phi _{xk}} = 0,\frac{{\partial {\phi _{yc}}}}{{\partial x}} = \frac{{\partial {\phi _{yk}}}}{{\partial x}} = 0,w = 0,\frac{{{\partial ^2}w}}{{\partial {y^2}}} = 0{\text{。}}$ | (49) |
根据边界条件式(48)和式(49),可以取双傅里叶级数为式(39) ~ 式(47)的解,则
| ${u_{0c}} = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{u_{mn}}\cos \frac{{m\text{π} x}}{a}} } \sin \frac{{n\text{π} y}}{b}{e^{i\varpi t}}{\text{,}}$ | (50) |
| ${v_{0c}} = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{v_{mn}}\sin \frac{{m\text{π} x}}{a}} } \cos \frac{{n\text{π} y}}{b}{e^{i\varpi t}}{\text{,}}$ | (51) |
| ${\phi _{xc}} = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{\phi _{xmn}}\cos \frac{{m\text{π} x}}{a}} } \sin \frac{{n\text{π} y}}{b}{e^{i\varpi t}}{\text{,}}$ | (52) |
| ${\phi _{yc}} = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{\phi _{ymn}}\sin \frac{{m\text{π} x}}{a}} } \cos \frac{{n\text{π} y}}{b}{e^{i\varpi t}}{\text{,}}$ | (53) |
| $w = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{w_{mn}}\sin \frac{{m\text{π} x}}{a}} } \sin \frac{{n\text{π} y}}{b}{e^{i\varpi t}}{\text{,}}$ | (54) |
| ${\phi _{xk}} = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{\phi _{xkmn}}\cos \frac{{m\text{π} x}}{a}} } \sin \frac{{n\text{π} y}}{b}{e^{i\varpi t}}{\text{,}}$ | (55) |
| ${\phi _{yk}} = \sum\limits_{m = 1}^\infty {\sum\limits_{n = 1}^\infty {{\phi _{ykmn}}\sin \frac{{m\text{π} x}}{a}} } \cos \frac{{n\text{π} y}}{b}{e^{i\varpi t}}{\text{。}}$ | (56) |
将式(50)~式(56)代入式(39)~式(47),然后比较两边的系数,则可以列出关于
夹层板四边简支,长边a=2 000 mm,短边b=1 500 mm,上下面板厚度tt=tb=3 mm,心层厚度tc=2 mm,心层静高度hc=40 mm,心层周期间距lc=50 mm,上下面板和夹心都是同样材料,弹性模量E=Ec=2.1×105 MPa,泊松比
为了形成对比,验证方法的准确性,分别用4种方法分别计算这个算例。
1)方法1
按照文献[5]所列公式计算固有频率(即Hoff理论),不过其中的剪切刚度不能采用连续介质心层的公式,而是采用等效剪切刚度,即采用式(56);
2)方法2
按照文献[6]中所列公式求解(即简化的Reisser理论),其中的剪切刚度也是采用方法1中的等效剪切刚度;
3)方法3
采用Ansys软件,用shell181单元模拟面板和心层,三维有限元计算固有频率;
4)方法4
本文方法。
表1列出了这4种方法计算的前9阶固有频率。从表1看出关于前8阶固有频率,上述4种方法的计算结果都非常接近,误差小于10%。因此本文的计算方法是有效可信的。
| $C = G_{yz}^c{\left( {{h_c} + {t_t}} \right)^2}/{h_c} = {E_c}{t_c}{\sin ^2}\theta \cos \theta {\left( {{h_c} + {t_t}} \right)^2}/h_c^2{\text{。}}$ | (57) |
|
|
表 1 各种方法关于前9阶频率的计算结果 Tab.1 Calculation results of freconcy from above methods |
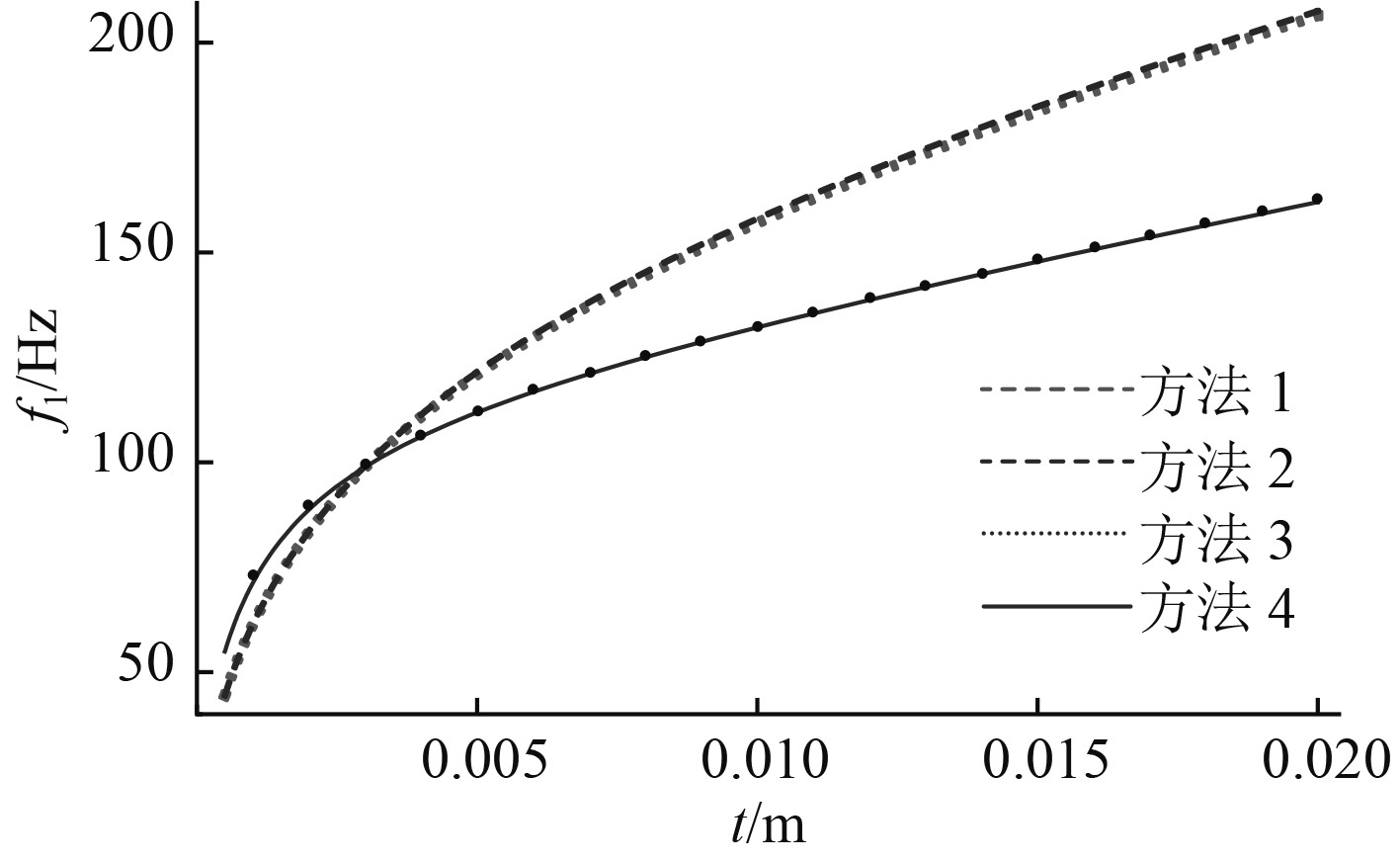
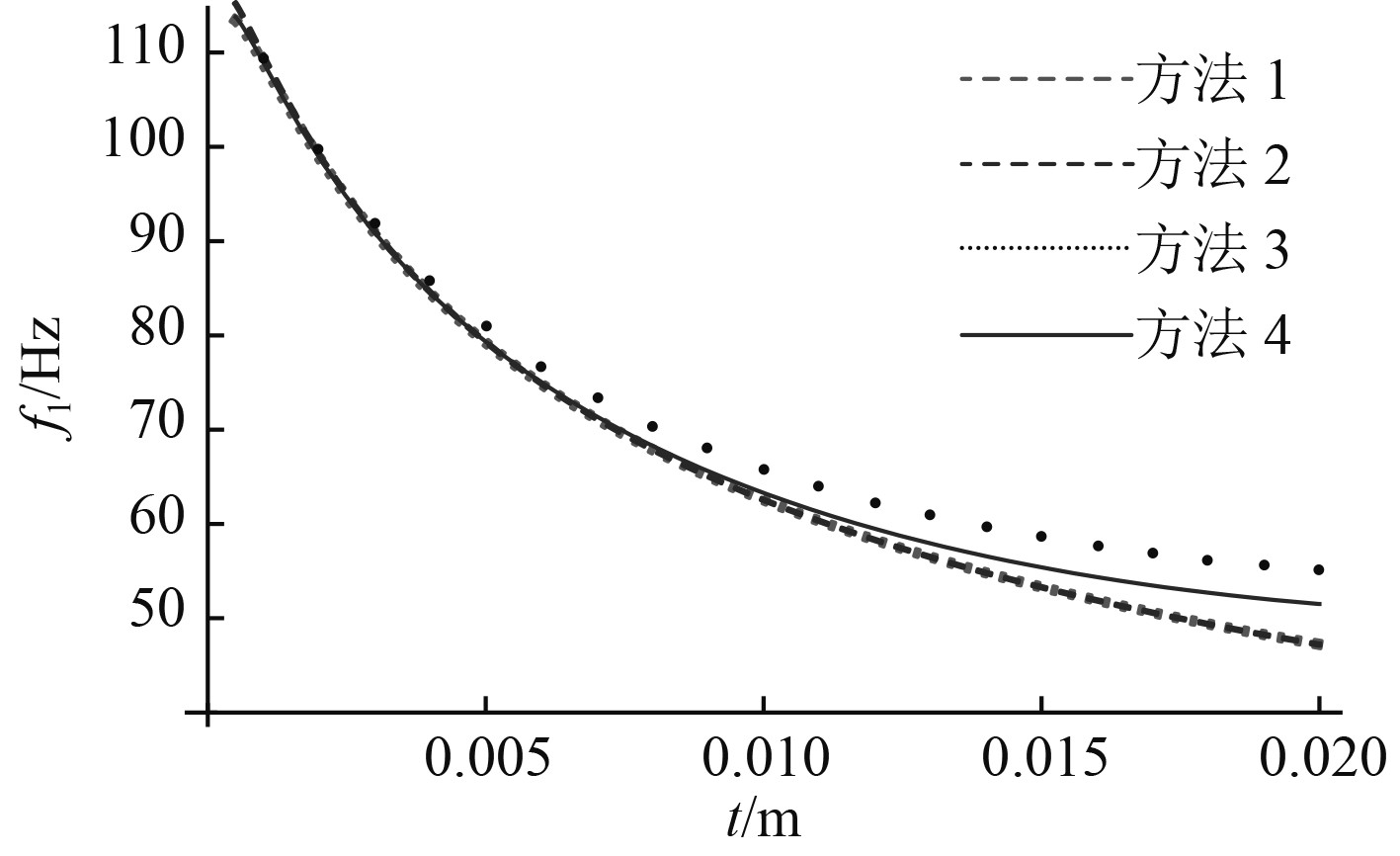
当面板厚度较小的时候,忽略面板的剪切作用造成的误差是很小的。但是当面板厚度增加,剪切作用就表现比较明显。以第4节中算例的参数为基础,固定其他变量,分别以面板厚度和心层厚度为自变量,一阶频率为因变量,图3为不同方法计算的夹层板一阶频率随面板厚度变化曲线(上下面板相等,且同步变化),图4为不同方法计算的夹层板一阶频率随心层厚度变化曲线。
|
图 3 面板厚度与一阶频率关系曲线 Fig. 3 Face sheet thinkness and first order frequency relationship curves |
|
图 4 心层厚度与一阶频率关系曲线 Fig. 4 Core sheet thinkness and first order frequency relationship curves |
从图3和图4看出,面板厚度较小,不同方法计算的结果差别很小,面板厚度大于5 mm后,差别则很明显。同时,因为各类方法都考虑了心层的剪切作用,不管心层厚度如何变化,不同计算方法计算的固有频率都很接近。
5 结 语通过应用一阶Zig-zag理论,同时考虑心层的实际形状,建立波纹夹层板的振动微分方程。用算例验证了本方法计算的前8阶固有频率的计算误差都在10%以内。
波纹夹层板面板板厚较小,忽略面板剪切作用的影响,导致的计算误差可以忽略;当面板厚度大于心层厚度1/8时,则误差是明显的,并且厚度越大,误差也越大。
因为Hoff理论中考虑了心层的剪切作用,因此波纹心层厚度的增加,不管是用Hoff理论计算还是简化的Hoff理论计算,都与本文方法计算结果极为接近。
| [1] |
KNOX.E.COWLING.M, M.J. Adhesively bonded steel corrugated core sandwich construction for marine application[J]. Marine Structure, 1998(11): 185-204. |
| [2] |
Ye YU, Wen-bin Hou. Elastic constants for adhesively bonded corrugated core sandwich panels[J]. Composite Structures, 2017(176): 449-459. |
| [3] |
KUJALA.P ,ROMANOFF. J . All steel sandwich panels – design challenges for practical applications on ships[C]. 9th Symposium on Practical Design of Ships and Other Floating Structures.
|
| [4] |
RAJAPAKSE Y D S, HUI D. Marine composite and sandwich structures[J]. Composites: Part B, 2008, 39: 1-4. |
| [5] |
中科院北京力学研究所. 夹层板的弯曲稳定和振动[M]. 北京: 科学出版社, 1977.
|
| [6] |
吴晖, 俞焕然. 四边简支正交各向异性波纹型夹心矩形夹层板的固有频率[J]. 应用数学和力学, 2001, 22(9): 919-926. WU Hui, Yu Huan-ran. Natural frequency for rectangular orthotropic corrugated_core sandwich plates with all edges simply_supported[J]. Applied Mathematics and Mechanics, 2001, 22(9): 919-926. DOI:10.3321/j.issn:1000-0887.2001.09.005 |
| [7] |
ZAMANIFAR H, SARRAMI-FOROUSHANI S, et al. Static and dynamic analysis of corrugated-core sandwich plates using finite strip method[J]. Engineering structures, 2019(183): 30-51. |
| [8] |
ICARD U, SOLA F. Assessment of recent Zig-Zag theories for laminated and sandwich structure[J]. Composites Part B, 2019(97): 26-52. |
| [9] |
FANG Taoxie, Yegao QU, et al. Nolinear areothermoelastic analysis of composite laminated panels using a general higher-order shear deformation zig-zag theory[J]. International Journal of Mechanical Sciences, 2019(150): 226-237. |
| [10] |
AZHARI F, BOROOMAND B, et al.. Exponential basis function in the solution of laminated plates using a higer-order Zig-Zag theory[J]. Composite Structures, 2013(105): 398-407. |
| [11] |
白瑞祥, 张志锋, 陈浩然. 基于Zig-Zag变形假定的复合材料夹层板的自由振动[J]. 力学季刊, 2004, 25(4): 528-534. BAI Rui-xiang, ZHANG Zhi-feng, CHEN Hao-ran. Free vibration of composite sandwich plates based on Zig-Zag deformation assumption[J]. Chinese Quarterly of Mechanics, 2004, 25(4): 528-534. DOI:10.3969/j.issn.0254-0053.2004.04.015 |
| [12] |
何力. 船舶板架结构动力优化设计方法研究[D]. 武汉: 华中科技大学. 2011. HE Li. Dynamic Optimization of Ship Grillages[D]. Wuhan: Huazhong University of Science and Technology. 2011. |
| [13] |
Hong-xia WANG, SAMUEL W.Chung.. Equivalent elastic constants of truss core sandwich plates[J]. Journal of Pressure Vessel Technology, 2011(133): 041203-1-041203-6. |
 2020, Vol. 42
2020, Vol. 42
