0 引　言

爆炸容器是指专门用于限制爆炸能量和爆炸作用范围的一种特殊密封压力容器^[1]。与无限空间爆炸和外部爆炸冲击作用相比，爆炸容器在内爆过程中冲击波与结构层相互作用，产生反射与透射现象，具有能量利用率高、冲击波波系复杂等特点。目前，爆炸容器的器壁主要有单层结构和复合多层结构两类，当爆炸容器器壁为复合多层结构时，不同结构层的分界面会分别对冲击波进行反射，冲击波在复合多层结构的不同结构层间的传播形式与连续单层结构的传播形式不同。本文研究复合壁面对爆炸容器内爆冲击波透反射规律的影响，对爆炸容器测量设备、辅助试验仪器的选择；对爆炸容器内部流体状态与壁面响应状态的进一步认识；对爆炸容器外形和结构设计；对爆炸容器壁面材料选取；对爆炸容器的安全使用等具有重要的现实意义。

对于爆炸容器内部爆炸冲击响应问题，目前已有不少的研究成果。饶国宁等^[2-3]对平板封头圆柱形爆炸容器（长径比为1∶1）在内部爆炸载荷作用下的动力响应进行了数值模拟，得到内部流场的规律；曹玉忠等^[4]采用计算流体动力学中的二阶精度TVD差分格式和特殊算子分法，为爆炸容器结构设计提供了一个从爆炸流场计算到结构动力响应分析的完整的辅助设计软件；李蕾等^[5]研究得到了一种能较好地解决由内爆引起的壳体流固耦合问题的GEL耦合程序；柏劲松等^[6]提出了一种基于MVPPM的流固耦合方法，并成功将这种流固耦合数值方法应用于椭球封头和类球形爆炸容器的数值计算；胡八一等^[7-8]运用DYtran程序中的欧拉计算方法，模拟了作用于球形爆炸容器内壁的反射超压波形。运用解析法和三维有限元程序Ls-dyna，对容器壳体在反射超压作用下的动力响应进行了强度分析，给出了容器的几个特征点的等效应力历史和重要区域的等效应力云图。从查阅的文献来看，有关复合多层壁面爆炸容器内爆作用下动力响应特征的研究文献较少，查找到的与之相关的研究主要有以下几个方面：钟方平等^[9-10]研究了多层钢筒在内部装药爆炸所产生的载荷作用下的动力响应，结果表明在采用了多层容器结构和薄壁钢管能量吸收装置等措施后, 容器安全地承受了爆炸装置形成的弹片和冲击波的破坏作用；崔霄云等^[11]采用爆心单位环面塑性变形吸能的设计方法，考察了多层钢筒结构动态响应和变形吸能特征，结果表明爆心单位环面塑性变形吸能的设计方法可以较好地预估给定药量下爆心截面所需防护钢筒的厚度；李兴珠等^[12]将爆炸容器内外壁中间夹层填充发泡塑料以构成多层复合抗爆结构，研究了钢板-发泡塑料-钢板复合结构下的爆炸容器的吸能降噪效果；邓贵德、陈勇军等^[13-15]研究了离散多层厚壁爆炸容器抗爆炸性能及其工程设计方法。

鉴于目前对爆炸容器复合多层壁面动力响应问题的研究不足，本文将爆炸容器复合多层结构作为数值模拟的目标，使用Ls-dyna有限元数值模拟软件，并结合ALE方法建立不同形状单一多层壁面爆炸冲击波透反射模型，随后将计算模型导入有限元分析软件Ls-dyna中，数值模拟在内爆作用下复合多层结构爆炸容器的冲击响应，以获得在不同复合壁面形状、超弹性层与移动壁面条件下爆炸容器的冲击波透反射规律，为爆炸容器的强度设计和安全使用提供参考。

1 有限元模型 1.1 模型及工况

由于声固耦合算法的局限性，采用Ls-dyna软件进行有限元研究，建立不同形状单一多层壁面爆炸冲击波透反射模型，模型与测点位置如图1所示，工况参数如表1所示。反射面分为3层，每层厚度10 mm，材料均为Q345钢，爆点距反射面最近的点0.3 m，边界条件为四周固定，其中工况1反射面为平面。

1.2 钢材料模型

在数值仿真时，对Q345钢采用随动塑性材料模型，该模型是一种考虑应变效应的双线性硬化塑性模型^[16]。 $\beta $ ( $0 \leqslant \beta \leqslant 1$ )用来调整材料中各向同性硬化与随动硬化的影响，通过定义失效应变删除失效单元。屈服应力通过引入考虑了应变率的Cowper-Symonds模型来表示。状态方程如下：

${\sigma _y} = \left[ {1 + {{\left( {\frac{{\dot \varepsilon }}{C}} \right)}^{\frac{1}{P}}}} \right]\left( {{\sigma _0} + \beta {E_P}\varepsilon _p^{eff}} \right) {\text{。}}$

(1)

式中： ${\sigma _0}$ 为初始屈服应力； $\varepsilon _p^{eff}$ 为有效塑性应变； $\dot \varepsilon $ 为应变率；C和P为Cowper-Symonds应变率参数； ${E_P}$ 为硬化模量， ${E_P} = {{{E_{\tan }}E}}/{{E - {E_{\tan }}}}$ ； ${E_{\tan }}$ 为切向模量； $E$ 为弹性模量。

1.3 空气材料模型

空气采用MAT_NULL材料模型进行模拟，采用EOS_LINE_POLYNOMIAL线性多项式状态方程描述。状态方程如下^[16]：

$\begin{split} {P_a} = &{C_0} + {C_1}{\mu _a} + {C_2}{\mu _a}^2 + {C_3}{\mu _a}^3 +\\& ({C_4} + {C_5}{\mu _a} + {C_6}{\mu _a}^2){E_a} {\text{。}}\\ \end{split} $

(2)

式中：P_a为空气压力； ${\mu _a}$ 为气体介质压缩比， ${\mu _a} = {{{\rho _a}}}/{{{\rho _{a0}}}} - 1$ ； ${\rho _{a0}}$ 为常温状态下空气初始密度； ${\rho _a}$ 为计算过程中空气的实时密度；如果 ${\mu _a} < 0$ ，则设置 ${C_2}{\mu _a}^2 = 0,\;{C_6}{\mu _a}^2 = 0$ ；E_a为气体单位体积内能；C₀～C₆为线性多项式状态方程系数，对于空气而言，取C₀=C₁=C₂=C₅=C₆=0，C₃=C₄=0.4。

1.4 水材料模型

水采用MAT_NULL材料模型进行模拟，采用Gruneisen状态方程定义压缩材料的压力。状态方程如下^[16]：

$\begin{split} {P_w} = &\frac{{{\rho _{w0}}{C^2}{\mu _w}\left[ {1 + \left( {1 - \dfrac{{{\gamma _0}}}{2}} \right){\mu _w} - \dfrac{a}{2}{\mu _w}^2} \right]}}{{{{\left[ {1 - \left( {{S_1} - 1} \right){\mu _w} - {S_2}\dfrac{{{\mu _w}^2}}{{{\mu _w} + 1}} - {S_3}\dfrac{{{\mu _w}^3}}{{{{\left( {{\mu _w} + 1} \right)}^2}}}} \right]}^2}}} + \\ & \left( {{\gamma _0} + a{\mu _w}} \right){E_w} {\text{。}}\\ \end{split} $

(3)

式中：P_w为水压力； ${\rho _{w0}}$ 为常温状态下水初始密度；C为介质中声速，取C=1480 m/s；S₁，S₂，S₃为冲击波输入参数，为无量纲参数，取S₁=2.56，S₂= -1.986，S₃=0.2268； ${\gamma _0}$ 是Gruneisen常数，取 ${\gamma _0} = 0.4934$ ； ${\mu _w} = {{{\rho _w}}}/{{{\rho _{w0}}}}{\rm{ - }}1$ ， ${\rho _w}$ 为计算过程中水的实时密度；a是 ${\gamma _0}$ 和 ${\mu _w}$ 的一阶体积修正量，a=1.3937；E_w为液体单位体积内能。

1.5 爆炸材料模型

炸药采用MAT_HIGH_EXPLOSIVE_BURN材料模型进行模拟，采用EOS_JWL状态方程描述。状态方程如下^[16]：

${P_e} = A\left( {1 - \frac{\omega }{{{R_1}V}}} \right){{\rm{e}}^{ - {R_1}V}} + B\left( {1 - \frac{\omega }{{{R_2}V}}} \right){{\rm{e}}^{ - {R_2}V}} + \frac{{\omega {E_e}}}{V}{\text{。}}$

(4)

式中：P_e为爆炸产物的压力；V为爆轰产物的相对比容， $V = {v/{{v_0}}}$ ，为无量纲量， $v = {1/\rho }$ 是爆炸产物的比容， ${v_0}$ 是爆炸前炸药的初始比容； ${E_e}$ 为爆轰产物的内能；A，B，R₁，R₂， $\omega $ 为实验确定的材料参数。本文中的炸药采用TNT，参数如表2所示。表中： $\rho $ 为炸药密度； ${v_D}$ 为爆炸速度； ${p_{CJ}}$ 为爆轰波正面压力； ${E_0}$ 为单位体积炸药内能； ${v_0}$ 为爆炸前炸药的初始体积。

2 数值研究方法与验证 2.1 模拟流固耦合界面的ALE算法

ALE算法兼具Euler算法和Lagrange算法的优势，ALE描述引入了一个可以独立运动的构型^[17]，可以通过计算网格的合理运动满足在适应流固耦合边界变形的同时保持良好的网格质量，从而提高计算效率。在ALE算法中，引入连续体在初始时刻的构形 ${\Omega _X}$ ；任意时刻的构形记作 ${\Omega _X}$ ，并引入Lagrange物质坐标系 $O{X_1}{X_2}{X_3}$ 与Euler空间坐标系 $O{x_1}{x_2}{x_3}$ ，其中物质坐标系与物体固结，以初始构形为参考；空间坐标系与空间固定，以现时构形为参考。

同时，ALE算法中引入独立于2种构形的参考构形 ${\Omega _\delta }$ ，相对于观察者固定，并以参考坐标系 $O{\delta _1}{\delta _2}{\delta _3}$ 描述参考构形中的矢量位置。

物质点在参考坐标系中：

$x = x\left( {X,t} \right);X = x\left( {x,t} \right);\delta = \delta \left( {\delta ,t} \right){\text{，}}$

(5)

参考点在空间坐标系中，对x物质求导得：

${v_i} = {\hat v_i} + \frac{{\partial {x_i}(\delta ,t)}}{{\partial {\delta _i}}}{w_j}{\text{。}}$

(6)

物质点相对于网格点的速度：

${c_i} = {\hat v_i} + \frac{{\partial {x_i}(\delta (x,t),t)}}{{\partial t}}\left| {_X} \right.{\text{，}}$

(7)

任意物理量 $F(\delta ,t)$ 的物质导数可表示为：

$\frac{{\partial F}}{{\partial t}}\left| X \right. = \frac{{\partial F(\delta ,t)}}{{\partial t}}\left| {_\delta } \right. + {c_i}\dfrac{{\partial F}}{{\partial {x_i}}}{\text{。}}$

(8)

ALE描述的控制方程可描述为，动量守恒方程：

${\left. {\frac{\partial }{{\partial t}}} \right|_x}\int_{{\Omega _\delta }} {\rho {v_i}{\rm{d}}{V_\delta }} = \int_{\partial {\Omega _\delta }} {{{\hat t}_i}{\rm{d}}{S_\delta }} + \int_{{\Omega _\delta }} {\rho {f_i}{\rm{d}}{V_\delta }} {\text{，}}$

(9)

整理得：

$\rho {\left. {\frac{{\partial {v_i}}}{{\partial t}}} \right|_\delta } + \rho {c_j}\frac{{\partial {v_i}}}{{\partial {x_j}}} = \frac{{\partial {\sigma _{ij}}}}{{\partial {x_j}}} + \rho {f_i}{\text{。}}$

(10)

质量守恒方程：

$M = \int_{{\Omega _\delta }} {\rho {\rm{d}}{V_\delta }} = \int_{{\Omega _x}} {\rho {\rm{d}}{V_x}} = \int_{{\Omega _x}} {{\rho _0}{\rm{d}}{V_x}}{\text{，}} $

(11)

能量守恒方程：

$\rho {\left. {\frac{{\partial e}}{{\partial t}}} \right|_\delta } + \rho {c_i}\frac{{\partial e}}{{\partial {x_i}}} = \sigma {i_j}\frac{{\partial {v_i}}}{{\partial {x_j}}} - \frac{{\partial {q_i}}}{{\partial {x_i}}}{\text{。}}$

(12)

2.2 数值结果验证

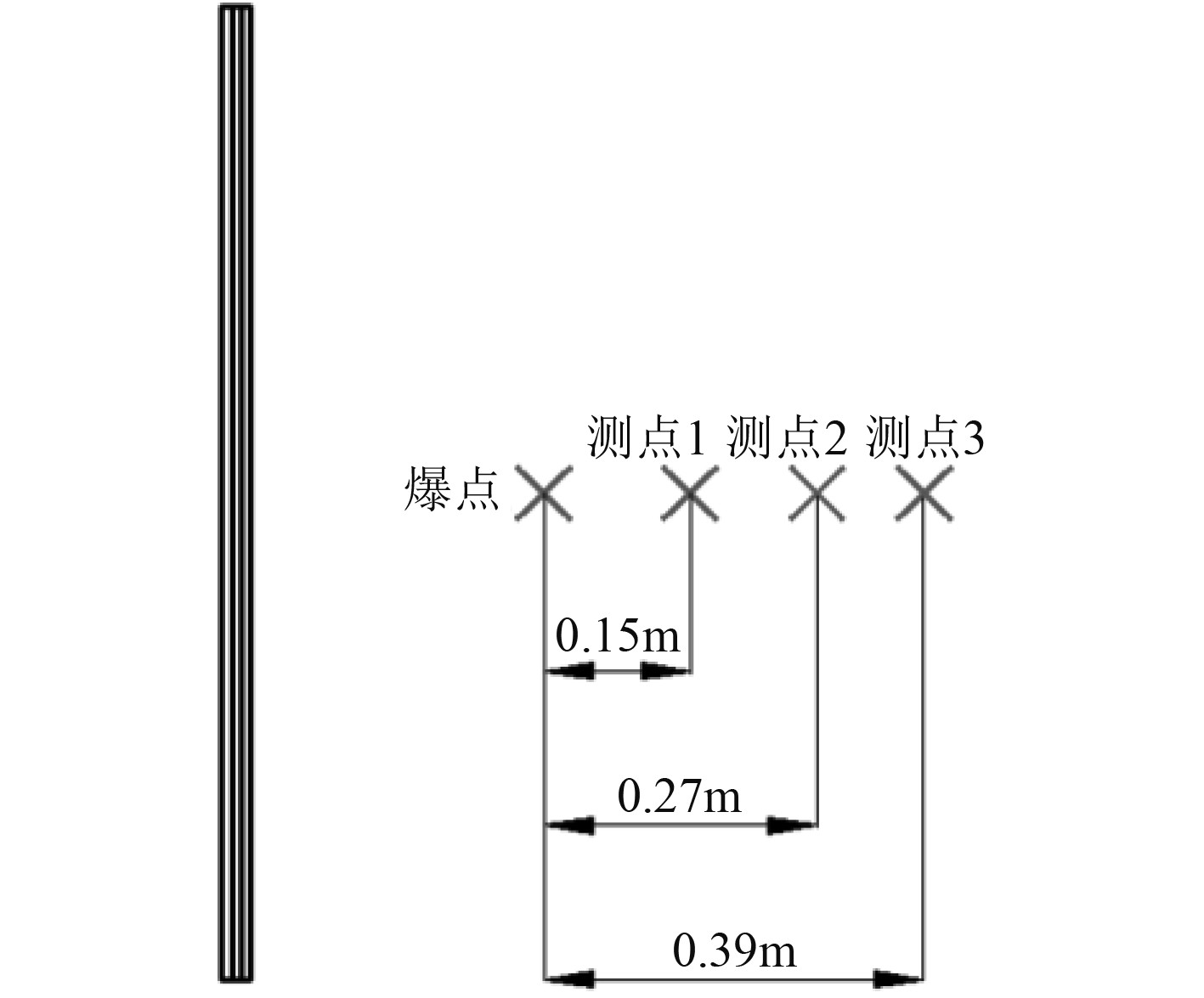
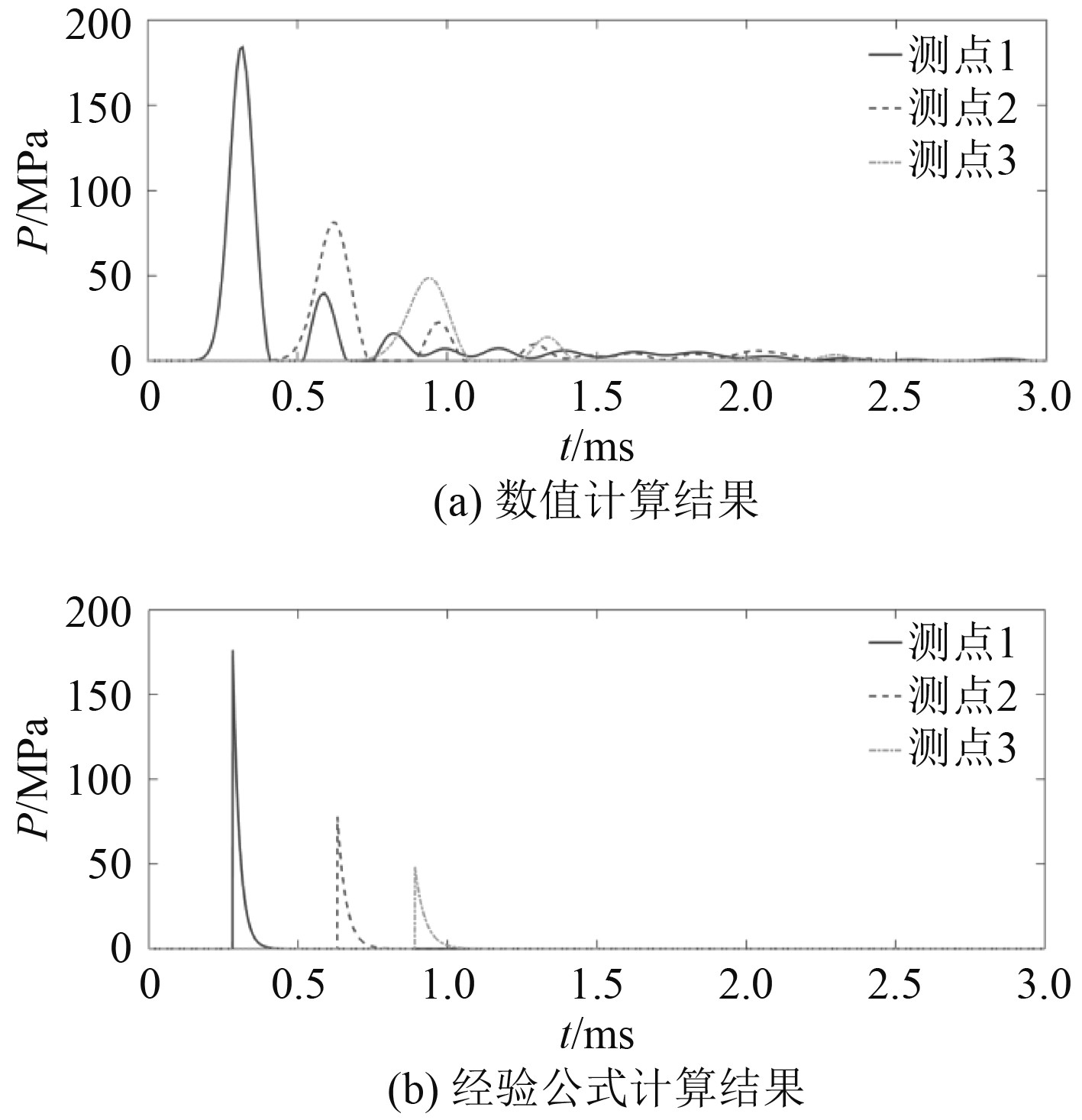
选取流场中无反射面一侧的测点，如图2所示。其自由场压力的数值模拟得到的历时曲线与经验公式计算所得的历时曲线，如图3所示。

由图3数据对比可得，数值模拟得到的结果与经验公式计算相比，自由场压力的峰值，脉宽与出现时间误差均不超过1%，故验证了本文分析模型中利用ALE流固耦合算法在爆炸仿真计算中的有效性。

3 计算结果分析 3.1 复合壁面形状对冲击波透反射规律的影响

不同形状壁面反射爆炸冲击波典型时刻介质中压力云图如图4所示。其中：水介质中左侧图中时间为1.26 ms，右侧图中时间为1.5 ms；空气介质中左侧图中时间为0.54 ms，右侧图中时间为0.8 ms。

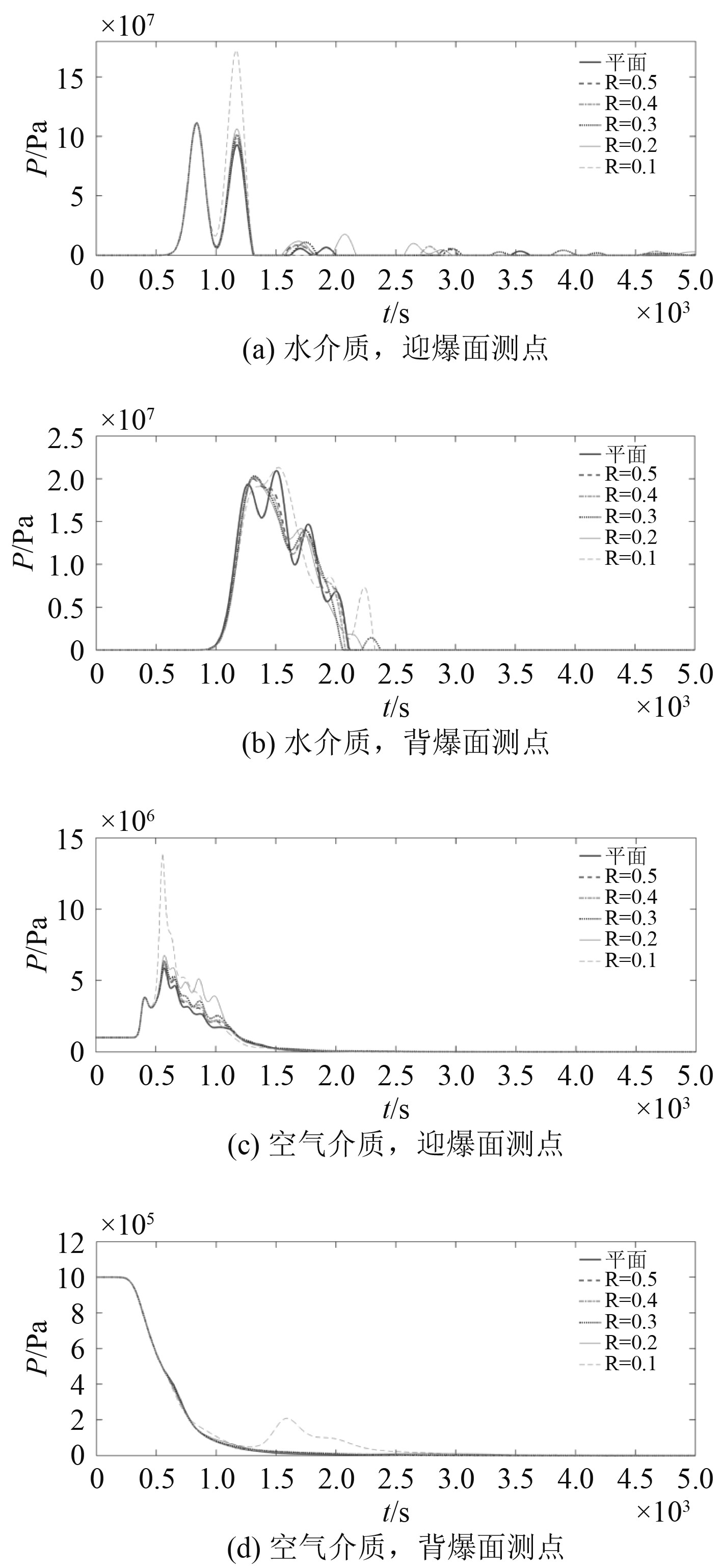
由仿真结果提取得到迎爆面与背爆面的测点自由场压力曲线如图5所示。其中，测点距反射面0.05 m，测点位置如图1（a）。

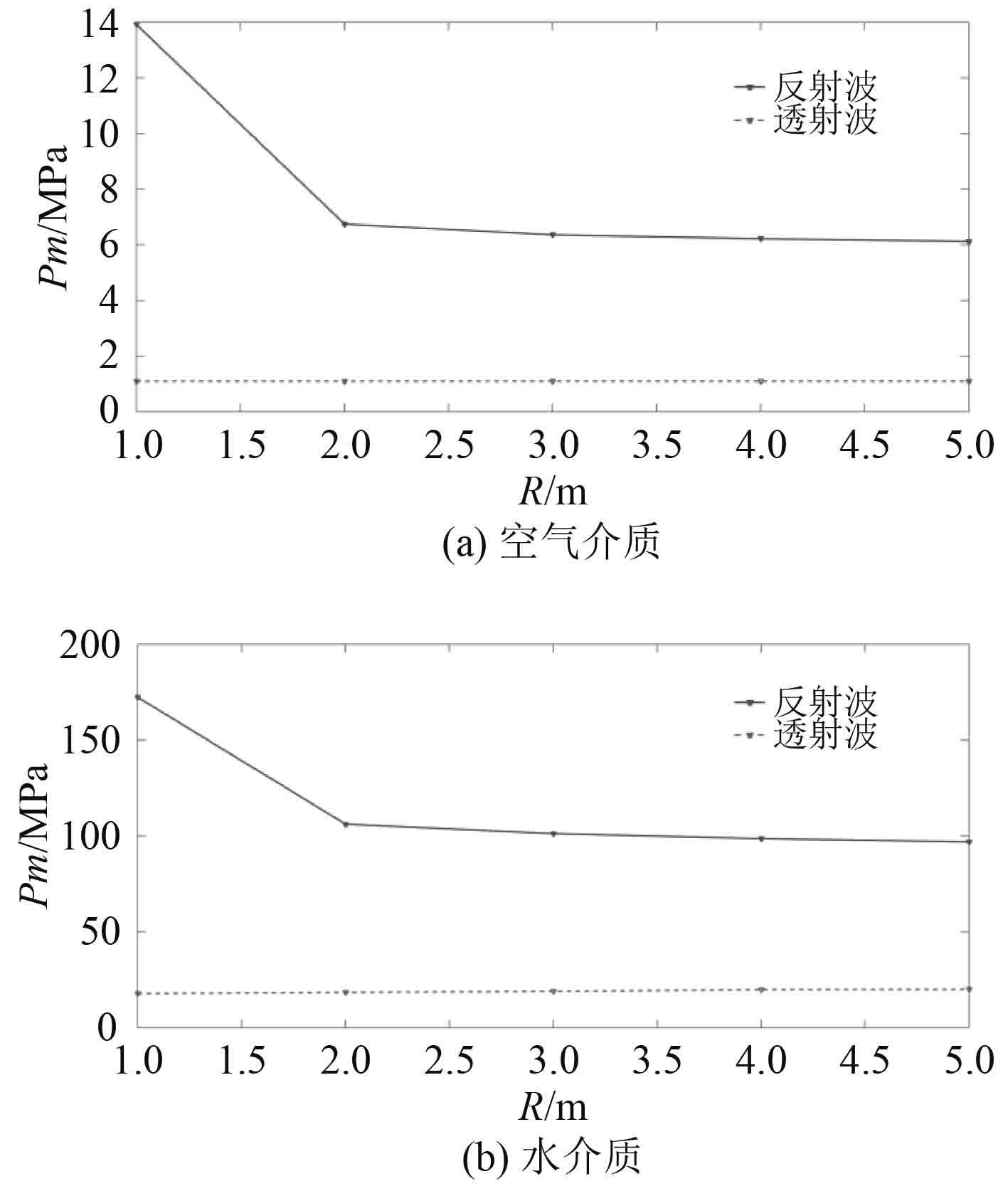
由图中的数据可得，爆炸介质为水时，曲面对反射冲击波的聚焦作用与对透射冲击波的发散作用随曲率增大而增大；爆炸介质为空气时，曲面对反射冲击波的聚焦与发散作用随曲率增大而增大，对透射冲击波基本无影响。拟合可得，药量300 g，爆点距反射面0.3 m时，透反射冲击波自由场压力峰值与曲率半径的关系如图6所示。其中：反射压力峰值为迎爆面自由场压力曲线中的第2个波峰；透射压力峰值为背爆面自由场压力曲线中的第1个波峰；R=0.1时，背爆面突出的压力峰值为绕射波。

3.2 超弹性层与移动壁面对冲击波透反射规律的影响

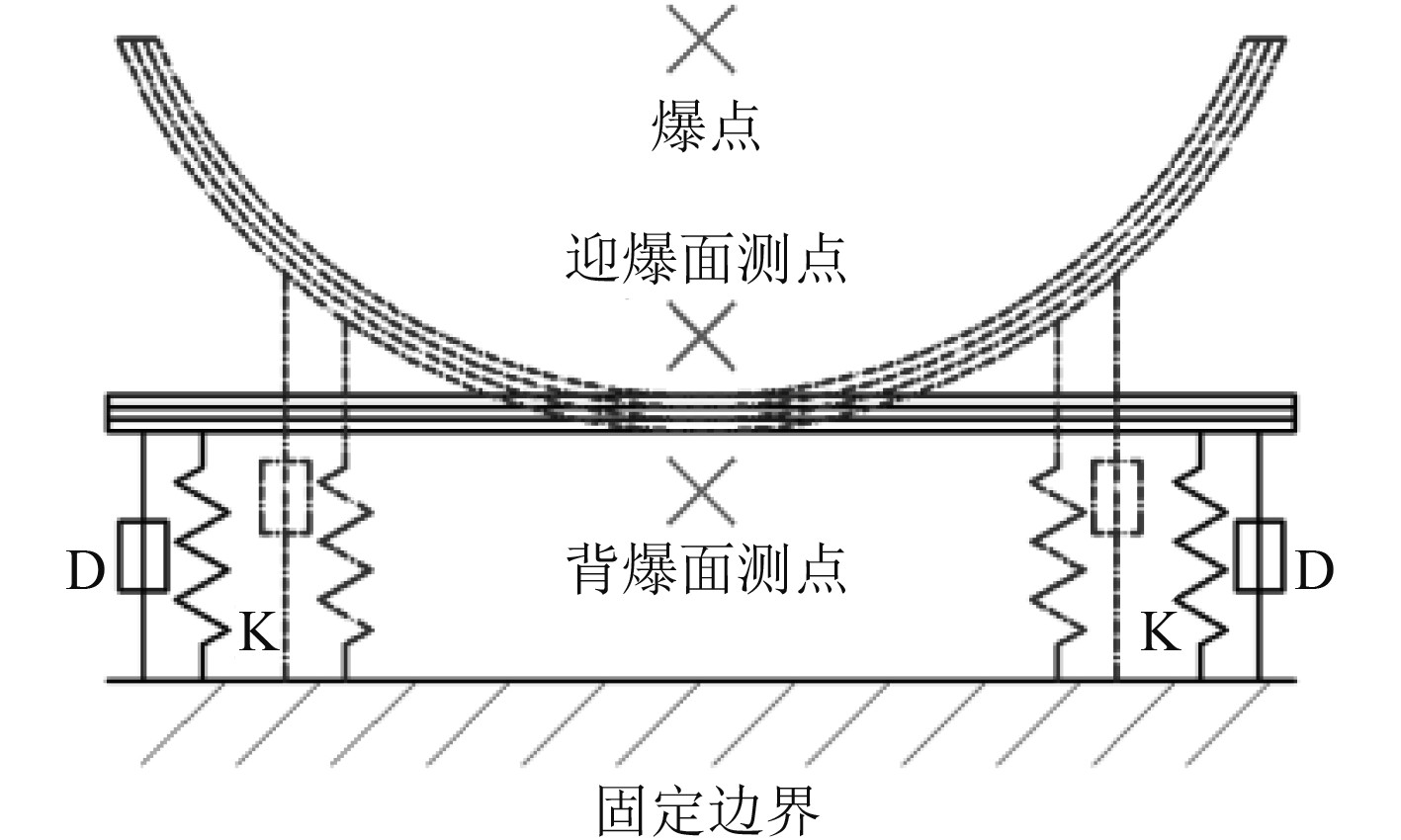
将复合多层结构中的中间夹层换为超弹性材料，并将四边的固定约束取消，更换为用弹簧阻尼固定在固定点上，如图7所示。根据容器模型质量与弹性底座的刚度比值，确定并列弹簧总刚度为8 000 N/m；整体阻尼系数20 Ns/m，弹簧与阻尼器各4个，均匀分布，尺寸如表3所示。其中超弹性层的材料为丁基橡胶，采用Mooney-Rivlin模型，材料参数如表4所示。

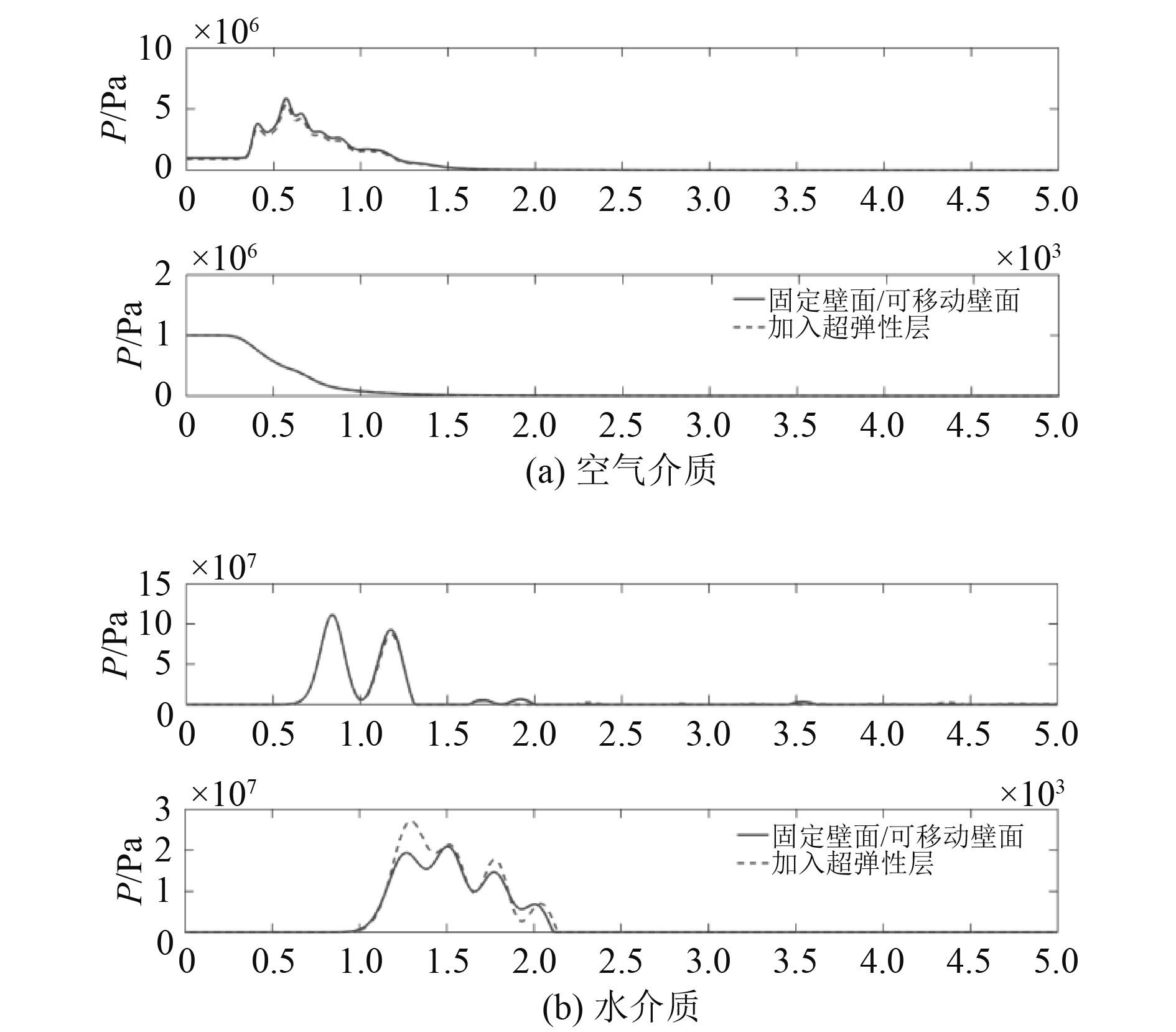
加入超弹性层与弹性壁面后的透反射冲击波自由场压力曲线对比图如图8所示。

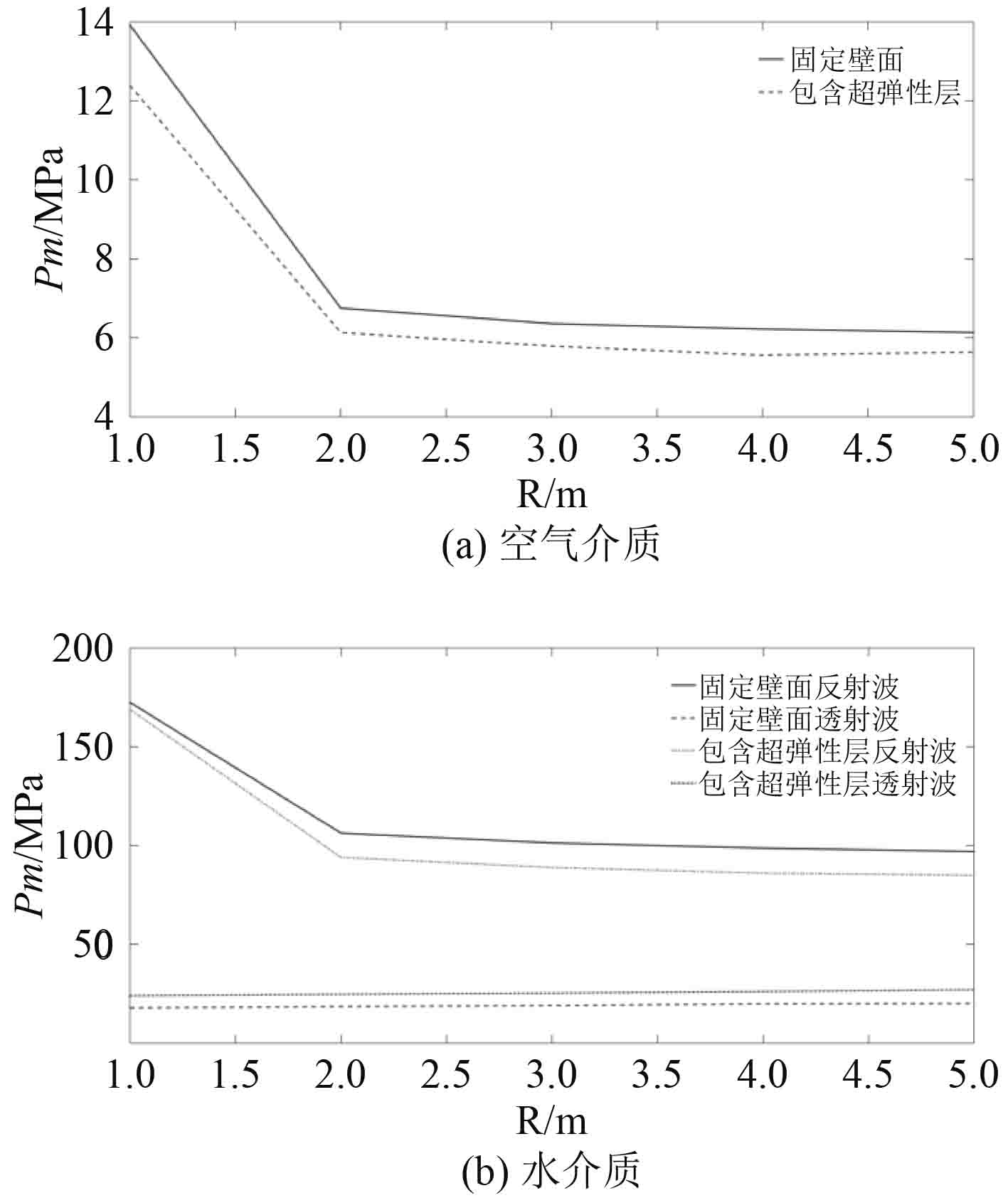
图中，迎爆面第1个自由场压力峰值为冲击波波阵面第1次到达时的自由场压力，相同介质中不同工况下数值完全相同；第2个自由场压力峰值为反射压力峰值，背爆面第1个自由场压力峰值为透射压力峰值。由计算结果可得，由于冲击波脉宽较短，等效频率远高于弹性壁面的固有频率，加入弹性底座后对透反射冲击波压力无影响；加入超弹性层与弹性壁面后透反射冲击波压力峰值与曲率半径的关系如图9所示。由于介质为空气时透射波峰值不变，未在图中出现。

由图中数据可得，超弹性材料会增加反射面的透射率，爆炸介质为水时，加入超弹性层后反射冲击波压力峰值减小9%，透射冲击波压力峰值增大17%；爆炸介质为空气时，加入超弹性层后反射冲击波压力峰值减小14%，透射冲击波压力不变。

4 结　语

1）利用ALE算法进行内爆作用下复合多层壁面对冲击波透反射特征的仿真模拟，仿真模拟得到的结果与经验公式计算相比，自由场压力的峰值，脉宽与出现时间误差均不超过1%，说明本研究所进行的仿真模拟是可信的。

2）壁面曲率对反射冲击波的聚焦作用和对透射冲击波的发散作用都有明显影响。当爆炸介质为水时，曲面对反射冲击波的聚焦作用与对透射冲击波的发散作用随曲率增大而增大，当爆炸介质为空气时，曲面对反射冲击波的聚焦与发散作用随曲率增大而增大，对透射冲击波基本无影响。

3）当结构层中存在刚度较小且带有粘弹性的夹层时，内层结构会产生刚体运动，吸收一定的能量与噪声，使透反射冲击波发生改变；加入弹性底座后对透反射冲击波压力无影响。

4）本试验的研究方法和研究结果可供类似爆炸容器的强度设计和安全使用参考。