潜器是现代海军最重要的威慑力量之一,操纵性的优劣是衡量潜器技战术指标的重要标准。潜器运动就操纵意图来说,可分为两大类:保持潜器既有的航行状态和改变潜器的航行状态,相对应运动稳定性和机动性2种重要的操纵性能。优良的操纵性使潜器既具有足够的运动稳定性,又具有良好的机动性。随着海洋开发及国防事业的不断发展,潜器的近水面作业越来越频繁。
潜器在水下的空间运动具有横摇、纵摇、首摇、纵荡、横荡、垂荡6个自由度,潜器近水面航行时,受到海浪和水面等因素的作用,产生波浪力干扰力矩,从而出现横摇、纵摇及垂荡运动等主要的不良现象,严重地影响潜器的正常作业,甚至还会影响其安全性。通过对潜器近水面航行时波浪力的研究,可以设计航行控制器,预报潜器在波浪中的运动,从而对潜器的实际操纵进行指导。美国“弗吉尼亚”级核潜艇的操纵系统具有根据实际海况条件判断预估波浪干扰力的功能,用于指导潜艇近水面作业和操纵。
根据流体力学的知识,艇体和操纵面的水动力特性与速度有较强的依赖关系[1]。潜器在零航速或极低航速下,舵效会明显下降,很难通过舵力和力矩实现对潜器的控制[2]。因此,需要采用合适的控制方法和工作模式进行有效的控制。潜器在水下运动时,受到复杂压力场和流场的作用,不能精确地进行数值模拟并计算流体动力,而依靠潜艇的约束模型试验,也存在大量财力物力的消耗问题。目前普遍的做法是在约束模型试验的基础上建立数学模型,再通过自航试验补充和完善特定运动状态下的耦合项和非线性力[3]。
随着控制理论的发展,潜艇的数值模拟融入了新的元素,合适的控制方法可以极大提高数值分析的多样性和准确性,建立在不同控制理论上的潜艇操纵性分析成为主流。本文从数学建模、近水面波浪力计算、控制算法等3个方面概述国内外相关学者的研究。
1 潜艇操纵运动建模技术研究目前,通常采用水动力模型和响应模型对潜器的运动进行建模分析。
水动力模型可根据操纵运动方程中水动力表达方式的不同分为整船式模型和分离式模型。Martin A.Abkowitz教授于20世纪60年代提出了整船式模型,后面一般称其为Abkowitz模型。该模型中将水动力视为一个整体力作用在船-桨-舵系统上,将其表达成运动参数和控制参数的函数,并用泰勒级数在匀速直航运动状态附近展开,展开式中各项的系数成为水动力导数;根据准定常假设(quasi-steady supposition),这些导数被认为是和时间无关的常数。假设潜器操纵运动的幅度很小,则可以将非线性Abkowitz模型中的非线性项省略,得到线性的Abkowitz模型[4]。基于Abkowitz模型,日本操纵运动数学模型建模小组(Mathematical Modeling Group,MMG)于20世纪70年代提出了分离式模型,后面一般称为MMG模型[5]。该模型将操纵运动方程中的水动力表达成作用船、桨、舵3部分的水动力之和,其中采取了类似Abkowitz模型中的船体水动力的表达,包含线性和非线性项,而桨、舵水动力的表达式基于单独桨、舵的水动力表达并包含了反映船-桨-舵水动力相互影响的干扰系数。Abkowitz模型和MMG模型有三自由度(纵向运动、横向运动和转首运动)的和四自由度(纵向运动、横向运动和转首运动、横摇运动)2种。对于舰船而言,常常有必要采用四自由度的数学模型。
响应模型表达的是舰船转首运动对舵角的响应关系,包括1阶、2阶和线性、非线性响应模型。其中2阶线性响应模型可通过二自由度(横向运动和转首运动)线性Abkowitz模型导出,其中的系数K,T1、T2和T3是几种线性水动力导数的组合,和舰船的操纵性密切相关,因而通常被称为操纵性指数。令2阶线性响应模型中的控制参数(舵角)为0,可得到判别舰船是否具有直线稳定性(固有稳定性)的稳定性衡准数C。C也是几种线性水动力导数的组合,其值的正负和大小可用以判断舰船是否具有直线稳定性以及稳定性的优劣程度。1阶线性响应模型可基于低频运动假设通过2阶线性响应模型导出,由于该模型是野本谦作(KensakuNomoto)教授于20世纪50年代首次导出的,一般称为Nomoto模型。该模型中的操纵性指数K,T(T=T1+T2-T3)和操纵性有直接的关系,其中K和回转性相关,T和应舵性(初始回转能力)及直线稳定性(固有稳定性)相关,可用来定性地评估舰船操纵性。非线性响应模型可由线性响应模型加上一个非线性项(通常是回转角速度的三次方项,其系数为非线性系数,是一个经验系数)得到。
确定数学模型中的水动力导数和船-桨-舵水动力干扰系数是建立数学模型(操纵运动方程)的关键[6]。在设计阶段求取舰船操纵运动水动力导数和船-桨-舵水动力干扰系数可采用的方法有:1)经验公式估算方法;2)自由自航船模试验方法;3)约束船模试验(斜拖试验、舵角试验、旋臂试验、平面运动机构试验、圆周运动试验等)方法;4)理论与数值计算方法。
1.1 经验公式估算和数据库方法经验公式估算方法是在进行大量约束船模试验的基础上,分析确定船-桨-舵水动力干扰系数、水动力导数和主尺度、船型系数等之间的关系,从而建立计算水动力导数及船-桨-舵水动力干扰系数的回归公式和数据库,由此实现对水动力导数及船-桨-舵水动力干扰系数的快速计算。这类方法的水动力导数及船-桨-舵水动力干扰系数的计算精度取决于所设计舰船是否与导出经验公式(回归公式)和建立数据库时所用的船型属于同类的船型,因而其适用的船型有限制。
1.2 船模试验方法约束船模试验方法是在专门的水池(拖曳水池、悬臂水池、操纵性水池)中对设计制作的舰船几何相似模型进行一系列的约束船模试验,并通过分析试验测得的水动力得到水动力导数及船-桨-舵水动力干扰系数。约束船模试验方法的缺点在于存在“尺度效应”的影响,而且和耗费大量人力物力,不便分析船型和操纵装置(如舵)的变化对水动力导数及船-桨-舵水动力干扰系数的影响[7]。
自由自航船模试验方法是采用系统辨识方法对自由自航船模试验的控制量和运动量测量数据进行分析,得到数学模型中的水动力导数及船-桨-舵水动力干扰系数。该方法基于自由自航船模试验数据,因而得到的水动力导数及船-桨-舵水动力干扰系数存在“尺度效应”的影响[8]。系统辨识方法也可以用于对实船标准操纵性试验测量数据进行分析,从而可以避免“尺度效应”的影响。而将该方法同时用于对自由自航船模试验和实船操纵性试验测量数据进行分析,可以分析“尺度效应”的影响,但这些工作不是在设计阶段,而是在实船建造出来以后才有可能进行,因而已经不属于操纵性“预报”的问题了。早在几十年前,系统辨识方法就已应用于船舶操纵运动建模,近十余年来,试验测量技术不断进步并且出现了很多新的系统辨识方法(如神经网络方法、支持向量机方法),基于实船操纵性试验或自由自航船模试验的系统辨识方法逐渐获得了优势,有了更好的应用前景。
1.3 理论与数值计算方法理论与数值计算方法经历了近半个世纪的发展,从早期基于势流理论的横流理论、短翼理论、细长体理论等简单方法,到近20余年来的基于势流理论的三维面元法(边界元法),再到近10余年来的基于粘性流求解的现代CFD方法,计算能力和预报精度不断提高,得到的数值解越来越准确。目前国际上已能应用基于粘性流求解的CFD方法数值模拟带桨、舵等附体的舰船操纵运动粘性流场,计算操纵运动水动力。已能数值模拟各种约束船模试验的非定常粘性流场,计算得到线性和非线性的水动力导数和船-桨-舵水动力干扰系数。相比之下,我国在应用基于粘性流求解的CFD方法计算舰船操纵运动水动力方面还远远落后于国际先进水平。目前我国只能应用CFD商业软件对作定常运动或简单的非定常运动的裸船体或简单的船-舵组合体的粘性流场进行数值模拟,求解出线性水动力导数,而对于非线性水动力导数及船-桨-舵水动力干扰系数的计算还处于起步阶段。
2 近水面波浪力计算方法研究潜艇在近水面运动时,受到波浪力的作用,会产生摇摆、推进器出水等现象。潜艇受到水面波吸力的影响,破坏了水下原有的静力平衡的状态,导致其深度难以控制,航行稳定性降低,还可能会因为低频吸力的作用而出现“露背”现象[9]。
预报波浪力的基本方法有理论法和试验法[10]2种,理论法是求解基于波浪力理论建立的数学模型;试验法是利用实艇或进行模型试验直接测定其在波浪作用下的运动响应。由于试验法对物力财力人力的消耗较大,经济快速的理论研究得以迅速发展,本文仅介绍理论方法。
通常将波浪力对潜艇的作用分为1阶波浪力(线性分量)和2阶波浪力(非线性分量),能够清晰地反映出波浪不同成分对潜艇的影响[11]。国内外很多学者对此类问题进行了研究,并逐渐得到几种较为合适及成熟的理论方法,例如切片法、STF理论、面元法和Frank源分布紧密结合法[12]等。
2.1 切片理论切片理论是指在计算船体水动力时,假定船体由许多横向薄片组成,每片都当成无限长柱体的一个横剖面,然后用流体力学中二维绕流来确定该剖面的附加质量、阻尼力、扰动力等系数,最后再沿船长积分以求出对船体的作用力。由于常规切片法是用相对概念导出船舶迎浪纵向运动方程的系数,只适用于计算船舶在迎浪中的垂荡和纵摇运动[13]。为了可以计算船舶在任意浪向下各个自由度的摇荡作用,产生了应用二因次流体理论计算附加质量和阻尼的修正切片法。
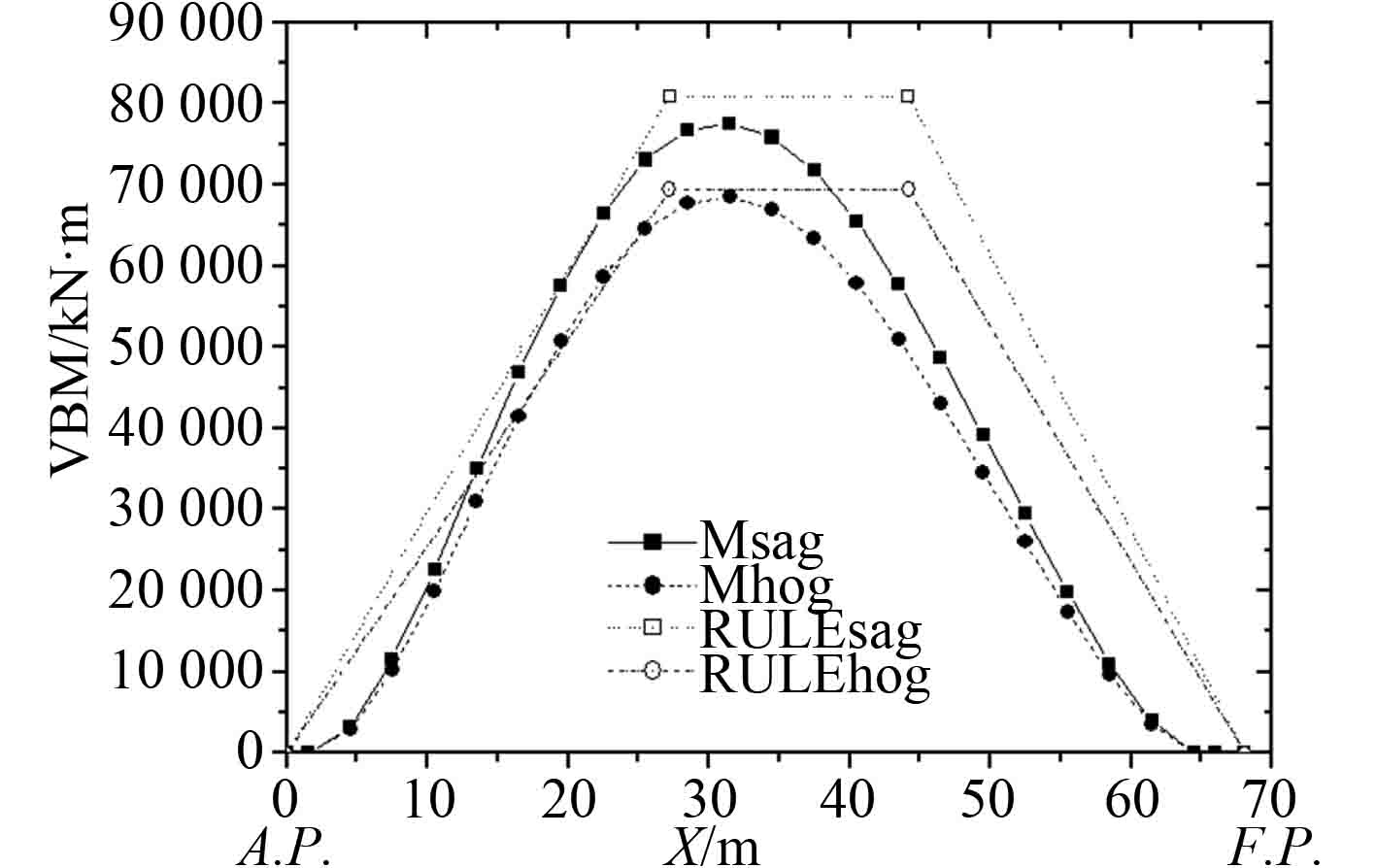
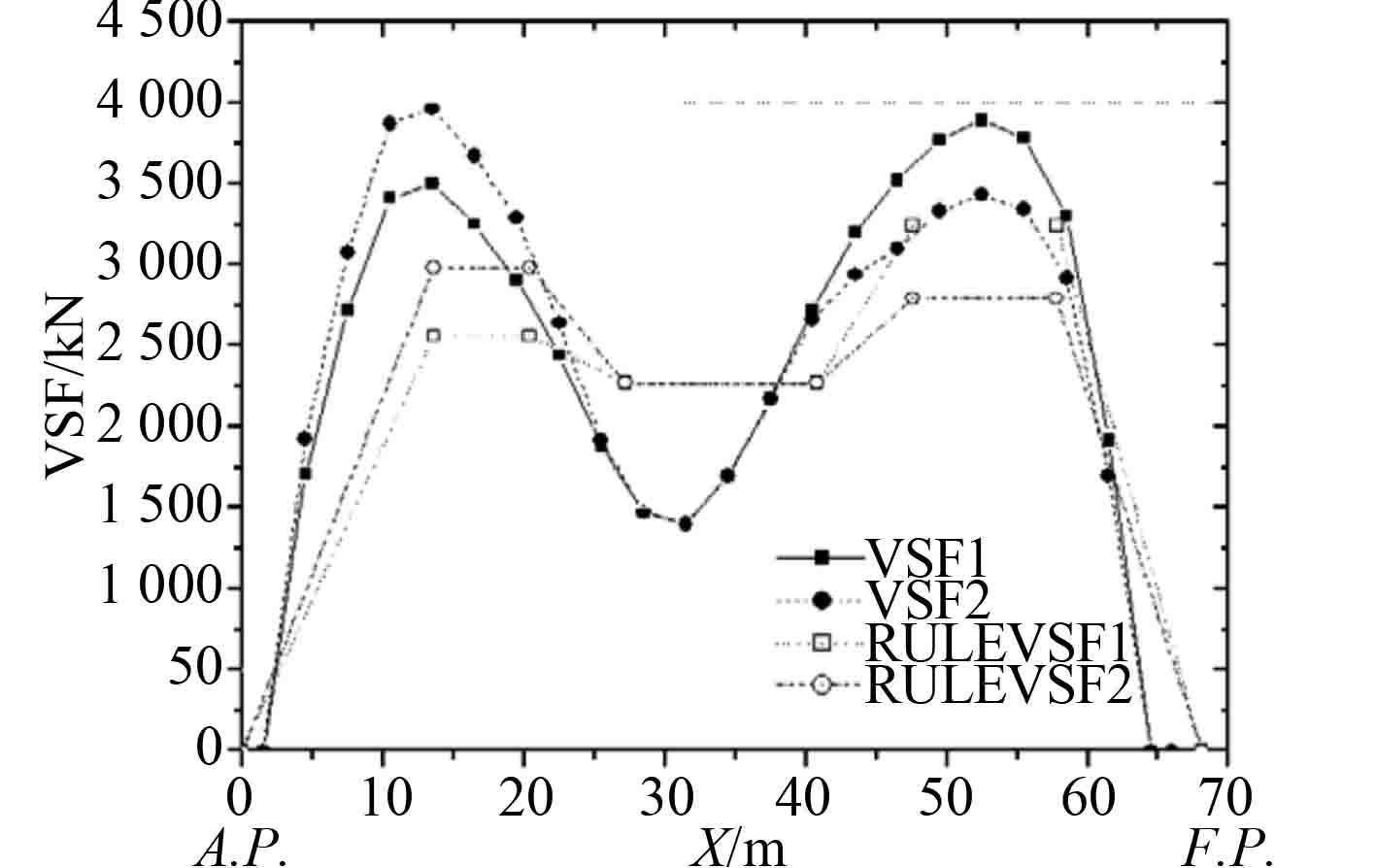
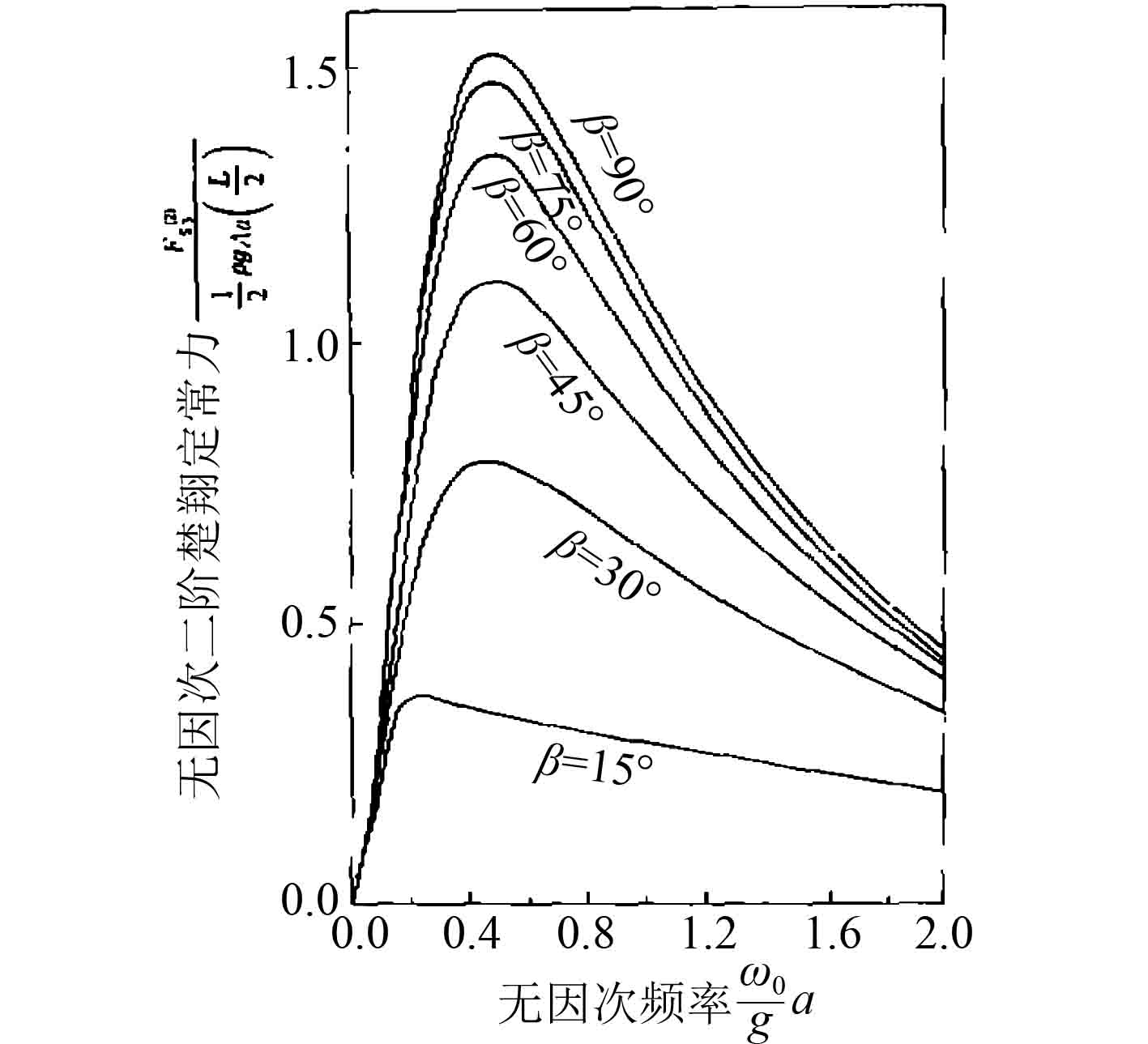
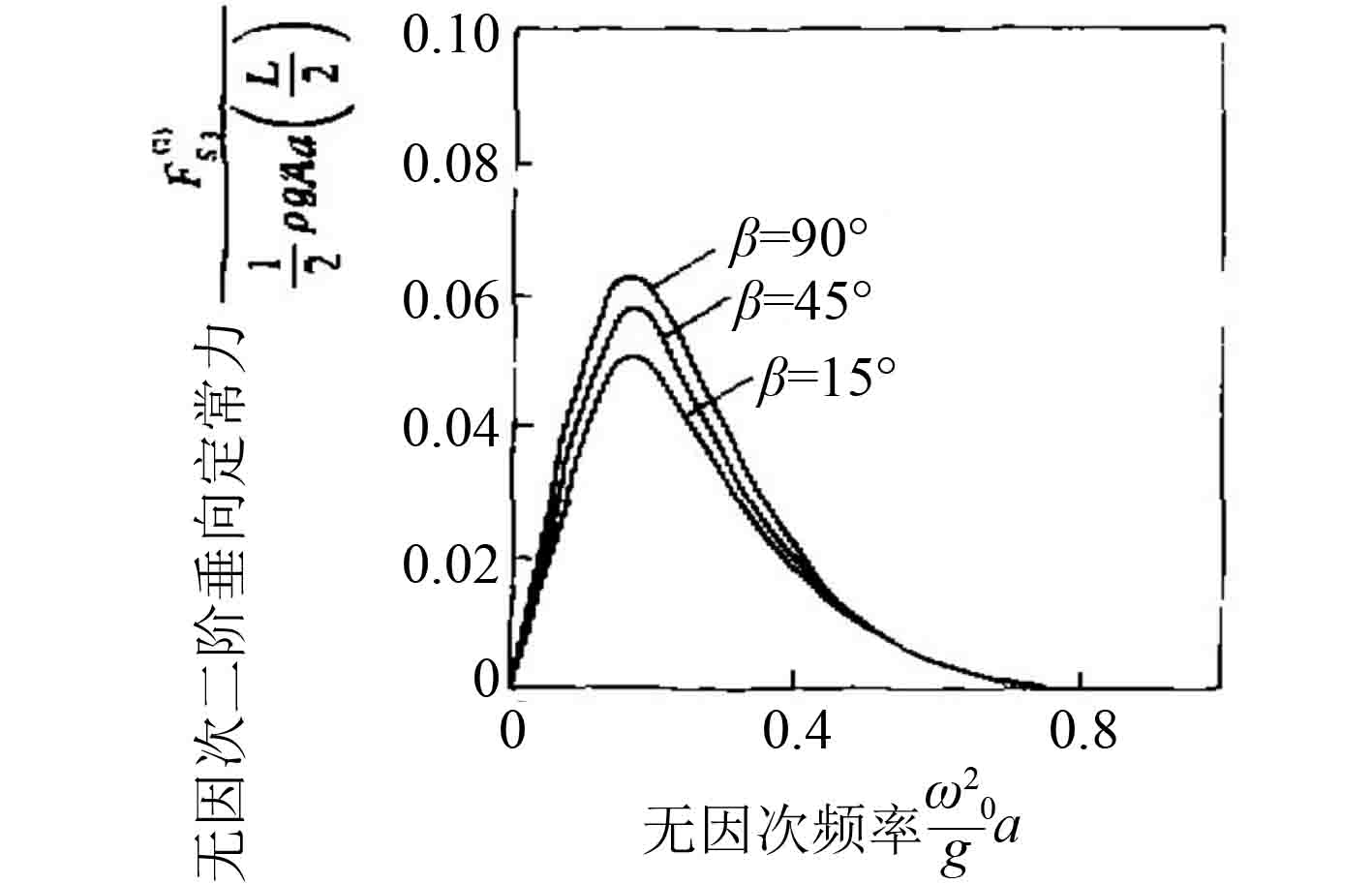
吴小平[14]基于切片理论,对波浪中载荷的非线性效应在频域范围内进行了数值模拟,得到的结果与实船的范围值相近(见图1和图2)。缪国平等[15]讨论了一种斜浪中细长体2阶势的计算方法,并对潜器在不同浪向和潜深时倍频力及2阶定常力的变化规律进行了讨论(见图3和图4)。此外,缪国平等[16]还在切片理论的基础上,对潜器在不同浪向和深度时的垂向定常力及变化规律进行了研究。韩晓光等[17]在舰船耐波性问题上,基于切片法,对船模迎浪航行时不同航速下的纵摇、垂荡的幅值响应进行了计算,结果显示修正切片法在高航速下的预报结果较常规切片法有明显的改善。倪绍毓[18]对切片法进行了多级展开,计算和分析了横浪规则波的波浪漂移力。在求解无穷远处反射波复数波幅及运动响应时,利用多级展开法可以通过较小的计算量获得合理的结果。
|
图 1 垂向波浪弯矩直接计算值与规范值比较 Fig. 1 Comparison between direct calculation value of vertical wave bending moment and standard value |
|
图 2 垂向波浪剪力直接计算值与规范值比较 Fig. 2 Comparison between direct calculation value of vertical wave shear force and standard value |
|
图 3 不同浪向角时二阶垂向定常力与波浪频率的关系(d/a=1.5) Fig. 3 Celationship between second order vertical steady force and wave frequency at different wave directions (d/a=1.5) |
|
图 4 不同浪向角时二阶垂向定常力与波浪频率的关系(d/a=6.0) Fig. 4 Celationship between second order vertical steady force and wave frequency at different wave directions (d/a=6.0) |
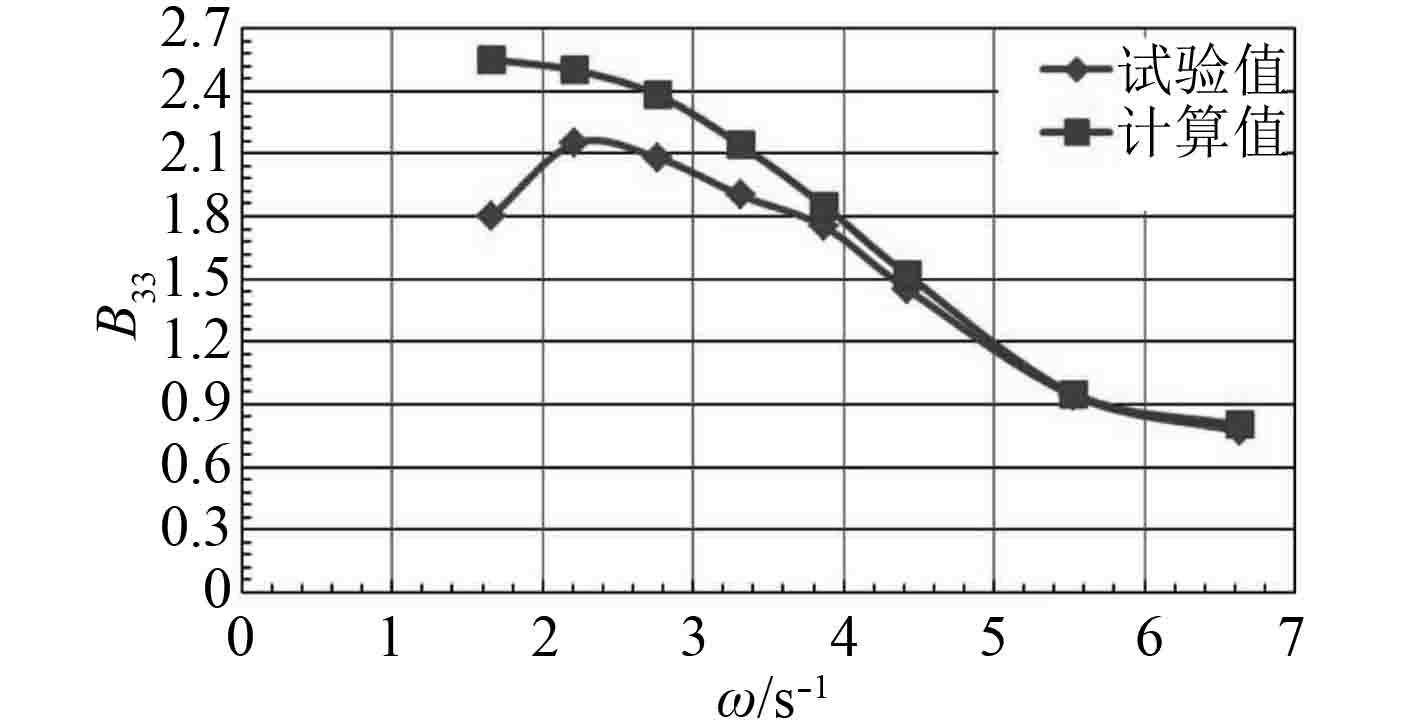
STF切片方法是基于细长体理论的。该方法是从三维物体在波浪中的一般情况出发,对物体在流场中的流体动力和波浪扰动力进行推导,在运动方程流体动力系数的表达上反映了航速影响和艇体对波浪流场的绕射影响[19]。其避开了对绕射进行直接的复杂计算,通过Haskind关系,利用辐射速度势进行直接的复杂计算,替换对扰流场绕射势的直接计算。潘昊然等[20]对浅水船舶的纵向运动特性进行了数值预报,通过对垂荡和纵摇模态下不同水深时的阻尼系数进行计算,在可行性上对STF理论进行了验证(见图5和图6)。
|
图 5 垂荡模态的阻尼系数 Fig. 5 Damping coefficient of heave mode |
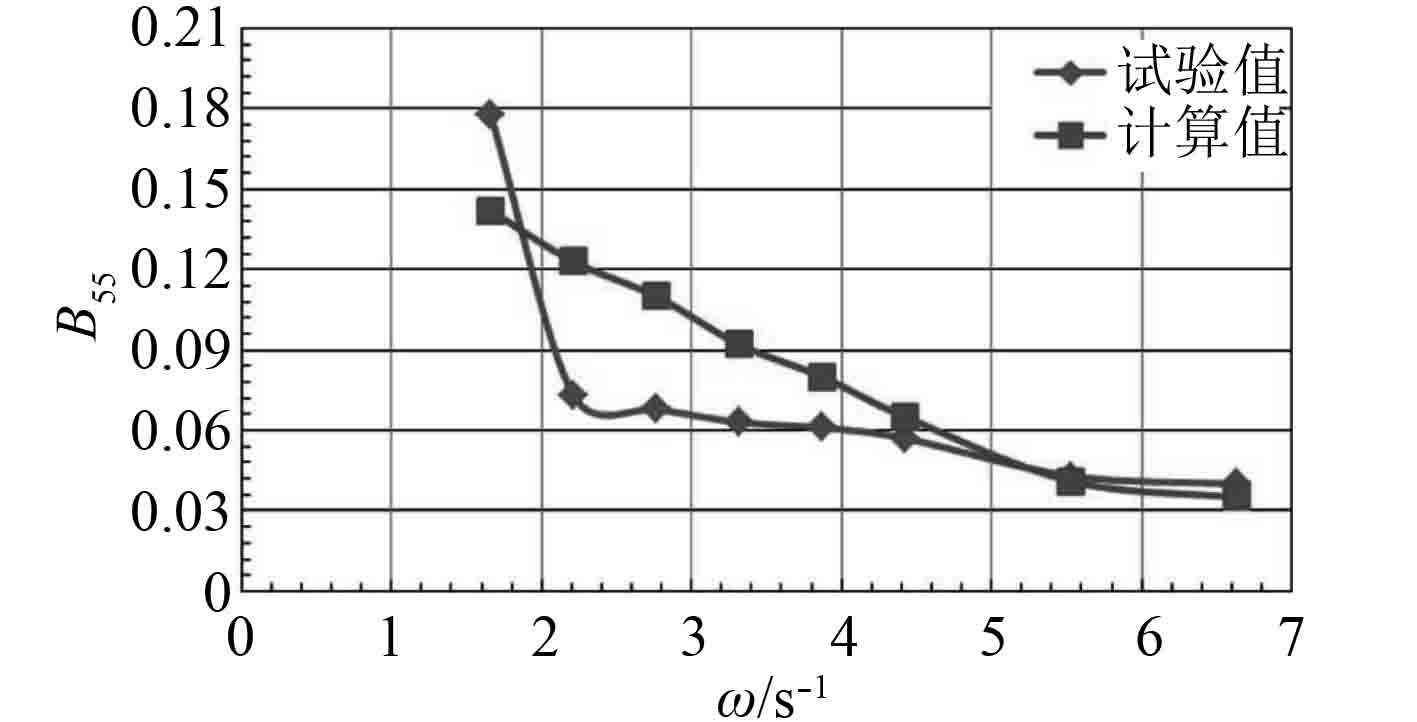
|
图 6 纵摇模态的阻尼系数 Fig. 6 Damping coefficient of pitch mode |
由于某些实际船舶带有附体,其剖面轮廓外形不规则,导致在布置计算节点时非常不方便,而通过结合Frank源分布紧密拟合法,使得潜器剖面流体动力系数和速度势的计算大大简化[21-22]。冯学知等[23]成功地对水下细长体近水面的波频运动进行了预报。匡晓峰等[24]计算了水下航行体近水面下的波浪力响应。李伟坡[25]在自航模试验中,对其在规则波中的幅频响应进行了预报分析。
2.3 面元法面元法(panel method)是将物体表面或机翼中弧面等特征面进行离散,生成网格后对每个网格,用一个平面或曲面代替原来的物面成为面元,在该面元上布置流动的奇点如源、涡、偶极子及其组合,进行求解启动问题的方法。
夏奇[26]根据Pinkster近场法理论计算得到了潜艇二阶波浪力较为准确完整的结果。朱冬健等[27]建立了某一船型的四自由度模型,利用三位面元法,通过二维插值计算了波浪力,对船舶在波浪中的摇摆运动进行了仿真。Haas[28]通过结合面元法和区域分解技术,对二维非线性波浪和三维非线性波浪进行了时域内的数值求解。在Haas提出的方法中,边界积分方程代替了原有的拉普拉斯方程,将流域分解成许多相对独立的子域,采用并行系统进行计算,提高了计算效率。Lee等[29]对水下细长回转体波浪中的一阶力和二阶力进行了研究,结果表明,三维面元法在二阶力矩上的计算精度比细长体近似法更高,而在一阶力矩上的效果低于细长体近似法。Musker[30]在忽略水表面对扰动势影响的基础上,计算了潜艇近水面运动时的水动力及力矩向量。王庆云等[31]模拟研究了系列舵翼SUBOFF潜艇的阻力性能,在计算附加质量时采用了基于三角网格的面元法计算程序,并由此得到了潜艇的3个惯性类水动力导数。
3 潜艇操纵控制算法研究潜艇的运动具有6个自由度,与水面船舶相比,其各自由度之间的关系更为复杂,非线性化也更为突出。近年来,由于海洋事业的不断发展,国内外对潜艇的研究越来越注重其在空间的六自由度运动,伴随着控制理论的不断发展,潜艇自动控制方法从以前的单平面控制到集中控制、智能控制,逐步完善和走向成熟。
3.1 PID控制方法PID控制是目前应用最为广泛的控制器,因为其是基于数学模型而进行求解的,很多工程实际中由于建模方便准确,因此可以得到较为满意的控制效果。
胡坤等[32]在潜艇垂直面的仿真计算中,通过优化控制器参数,得到了稳定的控制效果。郝英泽等[33]利用HSIC-PID对潜艇深度进行控制,在实现潜艇深度保持的同时降低了打舵频率。温秉权[34]通过设计PID控制器,对潜器的运动姿态进行了控制,在稳定性和鲁棒性的控制上较为理想。ElhamJavanfar等[35]通过基于低通滤波器自整定PID控制器对处于干扰状态下潜望镜的轨迹跟踪进行了控制,提出了一种整定PID参数的简单方法,对于工况点有变动的非线性系统,效果更明显。
考虑到潜器的六自由度标准方程与其实际的运动还有一定的差异,因此以往基于潜器运动模型设计的PID自动舵存在一定弊端。为了改进由于潜器运动的复杂性而导致的建模不精确,基于模糊控制的PID理论应运而生。Minh等[36]提出了基于模糊控制和线性控制相结合的船舶自动舵构造新方法,由该方法设计出的船舶自动舵可以很好地适应参数变化大的环境,Matlab仿真的结果表明与普通PID船舶自动舵相比新的船舶自动舵效率较高。杨永鹏[37]针对潜艇水下悬停状态,通过系统解耦,设计了模糊自适应PID控制器,在控制精度及系统时效性方面都有良好的特性。
3.2 滑模变结构控制方法滑模变结构控制系统(VSS)是一类特殊的非线性系统,其非线性表现为控制的不连续性。
袁昌斌[38]设计了一种AUV分布式滑模控制系统,在存在海浪干扰的情况下有效控制了AUV的航向。施小成[39]针对滑模变结构控制的控制增益Kf进行了调整,消除了稳态误差并且有效地抑制了抖振现象。张丰[40]改进了滑模面的设计,在抑制抖振的基础上,使其滑动模态阶段的收敛速度得到了提高。
从滑模变结构控制的工作原理可以看出,在切换开关的过程中,控制会出现不连续性,从而使系统发生抖振。李军红[41]对传统方法进行改进,提出了自适应模糊积分变结构控制方案,对不确定性线性系统进行抖振抑制。ErtugrulM等[42]基于连续的RBF函数,设计了由切换函数作为输入的控制器,舍去了切换项,从而对抖振进行了消除。在指数趋近率减轻抖振的基础上,盛严[43]提出了下述方程代替传统方程:
| $ \dot S = - \varepsilon {S^2}{\bf{sgn}}\left( S \right) - kS \text{。} $ |
Morioka H等[44]考虑到非线性控制和等价控制会加大抖振现象,采用不同的神经网络对其进行控制实现,试验结果证明了其有效性。
3.3 神经网络控制方法神经网络控制是指将神经网络技术应用到控制系统中,对难以精确建模的复杂非线性对象进行神经网络辨识,具有优化计算、推理和故障诊断等多种功能。由于其非线性拟合能力强,学习规则简单,已开始用于部分水面船舶和水下航行体。
赵阳[45]基于模糊神经网络,设计了潜艇垂直面运动状态下的自动舵控制器,仿真结果显示对潜艇的深度和纵倾控制有较好的效果。D.A. Derradji[46]提出了一种基于神经网络结构的控制方案,将BP算法作为自适应算法,适用于多输入输出系统,对潜艇的横摇、偏航角速度以及俯仰姿态进行了仿真研究,与最优线性二次型算法相比,有效性得到了验证。但杨文等[47]设计了一种新的控制算法,该控制算法不以模型为基础,而是将扩展卡尔曼滤波与神经网络相结合设计出了新型模糊控制器。KhoshnamShojaei[48]设计了基于神经网络的控制器,对在环境干扰下输入力矩受限的水下机器人进行了仿真研究,试验结果证明该控制器产生信号的幅度有限,从而减小了执行器饱和的风险。
4 结 语潜器在近水面的航行是一个复杂的运动状态,涉及多种环境变量,其中波浪力的确定和计算是研究的重点。此外,随着近年来多种控制算法的不断出现,相比传统的PID控制,在稳定性和鲁棒性等方面有了提高。基于此,本文最后提出两点仍需改善的问题:
1)对于2阶波浪力和对潜艇作用的数值解算问题还有待于进一步解决,并通过突破2阶力的试验验证技术,以提高波浪力干扰模型的精度。
2)各类控制算法对不同船型、作业工况的适应性,还需持续研究和深入探讨,以达到提高工程实用性的目标。
| [1] |
韦斯林, 计算流体力学原理[M]. 北京: 科学出版社, 2006.
|
| [2] |
施生达, 潜艇操纵性[M]. 北京: 国防工业出版社, 1995.
|
| [3] |
苏玉民, 庞永杰. 潜艇原理 [M]. 哈尔滨: 哈尔滨工程大学出版社, 2013.
|
| [4] |
罗伟林. 基于支持向量机方法的船舶操纵运动建模研究 [D]. 上海: 上海交通大学, 2009.
|
| [5] |
梅斌, 孙立成, 史国友. 基于模型参考和随机森林算法的船舶操纵运动辨识建模[J]. 大连: 大连海事大学学报, 2018, 44(2): 15-21. |
| [6] |
WANG X, WU M, YING R R. Numerical calculation of hydrodynamic interference coefficients between hull, rudder and propeller[J]. Advanced Materials Research, 2012, 591-593: 1949-1953. DOI:10.4028/www.scientific.net/AMR.591-593.1949 |
| [7] |
邢磊. 三体船水动力导数及操纵性能预报研究 [D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [8] |
刘祥珺, 孙存楼. 数值水池船模自航试验方法研究[J]. 舰船科学技术, 2011, 33(2): 28-31. DOI:10.3404/j.issn.1672-7649.2011.02.006 |
| [9] |
周广礼, 欧勇鹏, 高霄鹏, 等. 潜艇操纵性预报研究现状与前景展望[J]. 中国造船, 2018, 59(03): 203-214. DOI:10.3969/j.issn.1000-4882.2018.03.021 |
| [10] |
冯学知, 缪泉明, 蒋强强. 潜体近水面波浪力试验研究[J]. 船舶力学, 1977, 1(2): 24-28. |
| [11] |
CHEN J M, GUO P Z, JIANG X, et al. Experimental research on calculating wave force through wave pressure measurement[J]. Advanced Materials Research, 2011, 317-319: 2293-2296. DOI:10.4028/www.scientific.net/AMR.317-319.2293 |
| [12] |
戴余良, 刘祖源, 俞科云. 近水面潜艇波浪力计算研究评述[J]. 舰船科学技术, 2007, 29(2): 41-46. |
| [13] |
MITTAL N, GARG V K. Computation Slicing: Techniques and Theory[J]. 2001.
|
| [14] |
吴小平. 基于切片理论的波浪载荷直接计算[J]. 上海: 上海造船, 2010(4): 21-25. |
| [15] |
缪国平, 刘应中, 王海平. 细长体上二阶波浪力的切片理论[J]. 自然科学进展, 1996(3): 42-48. |
| [16] |
缪国平, 刘应中, 糜振星. 二阶波浪力的切片理论与潜体上的垂向定常力[J]. A辑, 1993(4): 435-447. |
| [17] |
韩晓光, 杨艳明, 郭航. 基于切片法的高速船摇荡运动预报研究[J]. 广州: 广州航海学院学报, 2009, 17(4): 7-10. DOI:10.3969/j.issn.1009-8526.2009.04.003 |
| [18] |
倪绍毓. 用切片法计算波浪漂移力[J]. 哈尔滨: 哈尔滨工程大学学报, 2008. DOI:10.3969/j.issn.1006-7043.2008.01.018 |
| [19] |
戴遗山. 舰船在波浪中运动的频域与时域势流理论 [M]. 北京: 国防工业出版社, 1998.
|
| [20] |
潘昊然, 胡晓峰. 基于STF切片理论的狭窄航道中船舶纵向运动研究 [J]. 船舶. 2016, 27(3): 21-26.
|
| [21] |
FRANK W. Oscillation of cylinders in or below the free surface of deep fluids[R]. AD-668338, 1966.
|
| [22] |
BEDEL J W, LEE C M. Numerical calculation of cylinders oscillating in or below a free surface[R]. AD-722690, 1966.
|
| [23] |
冯学知, 蒋强强, 缪泉明, 等. 潜体波浪中近水面不同潜深和航向运动和波浪力计算[J]. 船舶力学, 2002(2): 1-14. DOI:10.3969/j.issn.1007-7294.2002.02.001 |
| [24] |
匡晓峰, 汪玉, 缪泉明, 等. 水下航行体波浪力理论预报 [J]. 船舶力学. 2006(1): 28-35.
|
| [25] |
李伟坡. 潜艇自航模适航性STF理论预报和试验研究 [D]. 哈尔滨: 哈尔滨工程大学. 2014.
|
| [26] |
夏奇. 潜艇二阶波浪力数值预报方法研究 [D]. 哈尔滨: 哈尔滨工程大学. 2014.
|
| [27] |
朱东健, 马宁, 顾解忡. 波浪中船舶操纵性横摇预报及舵效影响分析[J]. 中国造船, 2015(z1): 146-154. DOI:10.3969/j.issn.1000-4882.2015.z1.020 |
| [28] |
HAAS D P C A. Numerical simulation of nonlinear water waves using a panel method; domain decomposition and applications[J]. UniversiteitTwente. 1997.
|
| [29] |
LEE C H, NEWMAN J N. First and second order wave effects on a submerged spheroid[J]. Pitch, 1991. |
| [30] |
MUSKER. A J. Prediction of wave forces and moments on a near-surface submarine[J]. International Shipbuilding Progress. 1984.
|
| [31] |
王庆云, 庞永杰, 李伟坡. 系列舵翼潜艇水动力系数数值计算及试验研究[J]. 舰船科学技术, 2015, 37(11): 21-26. DOI:10.3404/j.issn.1672-7649.2015.11.004 |
| [32] |
胡坤, 王树宗, 郝英泽. 基于PSO优化的潜艇深度非线性PID控制[J]. 控制工程, 2009, 16(6): 752-755. DOI:10.3969/j.issn.1671-7848.2009.06.027 |
| [33] |
郝英泽, 胡建军. 潜艇定深运动仿人智能综合自动控制[J]. 船海工程, 2007, 36(2): 97-99. DOI:10.3963/j.issn.1671-7953.2007.02.029 |
| [34] |
温秉权, 小型浅水域水下自航行器系统设计与试验研究 [D]. 天津: 天津大学, 2005.
|
| [35] |
JAVANFAR E, TEHRANI N M, VALI A. Adaptive self-tuning PID control of submarine periscope[C]// IEEE, International Conference on Electronics Information and Emergency Communication. IEEE, 2014: 189-192.
|
| [36] |
LE M D, NGUYEN T H, NGUYEN T T, et al. A new and effective fuzzy PID autopilot for ships[C]// IEEE International Symposium on Computational Intelligence in Tobotices and Automation, 2003. Proceedings. IEEE, 2003: 1411-1415 vol. 3.
|
| [37] |
杨永鹏. 潜艇水下悬停运动建模与操纵控制技术研究 [D]. 哈尔滨: 哈尔滨工程大学, 2011.
|
| [38] |
袁昌斌, 董升亮, 李超. 滑模变结构在AUV航向控制中的应用[J]. 现代电子技术, 2012, 35(20): 117-120. DOI:10.3969/j.issn.1004-373X.2012.20.035 |
| [39] |
施小成, 周佳加, 边信黔. 模糊滑膜变结构控制在AUV纵倾控制中的应用[J]. 计算机仿真, 2008, 25(10): 168-171. DOI:10.3969/j.issn.1006-9348.2008.10.043 |
| [40] |
张丰. 滑模变结构控制理论在非线性系统中的应用 [D]. 沈阳: 沈阳理工大学, 2013.
|
| [41] |
李军红. 变结构控制抖振问题的研究及仿真 [D]. 沈阳: 沈阳理工大学, 2013.
|
| [42] |
ERTUGRUL M, KAYNAK O. Neuro sliding mode control of robotic manipulators[J]. Mechatronics, 2000, 10(1-2): 239-263. DOI:10.1016/S0957-4158(99)00057-4 |
| [43] |
盛严, 王超, 陈建斌. 结构变结构控制的指数趋近率改进方法[J]. 西安: 西安交通大学学报, 2013, 37(1): 108-110. DOI:10.7652/xjtuxb201301019 |
| [44] |
MORIOKA H, WADA K, SABANOVIC A, et al. Neural network based chattering free sliding mode control[C]// Sice '95. Proceedings of the, Sice Conference. International Session Papers. IEEE, 1995: 1303-1308.
|
| [45] |
赵阳, 邢继峰. 潜艇垂直面运动自适应神经网络模糊控制仿真[J]. 计算机仿真, 2009, 26(6): 26-29. DOI:10.3969/j.issn.1006-9348.2009.06.007 |
| [46] |
DERRADJI D A, MORT N. Neural network controller for a multivariable model of submarine dynamics[J]. Neural Computing & Applications, 1998, 7(4): 295-308. |
| [47] |
但杨文, 林莉, 李明. 基于EKF神经网络的潜艇运动模糊控制[J]. 舰船科学技术, 2010, 32(1): 63-66. DOI:10.3404/j.issn.1672-7649.2010.01.010 |
| [48] |
SHOJAEI K. Neural network formation control of underactuated autonomous underwater vehicles with saturating actuators[J]. Neurocomputing, 2016, 194(5): 372-384. |
 2020, Vol. 42
2020, Vol. 42
