舰载机着舰是一项难度极大、危险性极高的任务[1-2],为了提升舰载机的着舰性能,确保着舰安全,众多学者对舰载机的着舰控制开展了研究。文献[3]采用H∞控制方法为F-14战斗机设计了自动着陆的控制律;文献[4]根据H∞控制理论,设计出基于H∞理论的输出反馈控制器,并通过对某型飞机的纵向着陆仿真,证明了该控制器具备较好的着陆下滑轨迹跟踪能力;为了进一步改善H∞控制系统的性能,文献[5]采用了H2/H∞综合控制技术,设计出了鲁棒性更好的飞机自动着陆控制系统;文献[6]构建了某型无人机的纵向小扰动线性化模型,通过对比PID控制器和H∞控制器的控制效果,发现H∞控制器具有比传统PID控制器更优良的鲁棒性。文献[7]基于动态逆方法设计了无人机的控制律,实现了无人机对高度的跟踪和速度的保持,通过仿真证明了基于动态逆方法设计的控制律使飞机具备良好的动态性能;文献[8]为了增强动态逆控制器的鲁棒性,将改进的神经网络与动态逆控制器相结合,从而实现对模型动态误差的补偿,通过仿真证明了改进的控制器能够在一定程度上抑制舰尾流的扰动。此外,文献[9-17]分别将鲁棒自适应技术、自抗扰技术、滑模控制技术、μ综合方法、人工神经网络、模糊控制理论同动态逆方法结合,设计出具备鲁棒性和抗扰动能力的控制系统。
本文针对舰载无人机着舰的纵向控制,将动态逆方法同H∞最优控制理论结合,同时考虑舰载无人机在着舰过程中遇到的的风扰动和传感器测量误差,提出一种基于鲁棒动态逆的舰载无人机着舰纵向轨迹跟踪控制律设计方法,能够有效抑制舰载无人机在着舰过程中的舰尾流扰动和传感器测量噪声,使舰载无人机实现对着舰轨迹的精确跟踪。
1 舰载无人机纵向数学模型某型舰载无人机纵向数学模型可被描述为:
| ${\dot {{x}}} = {Ax} + {Bu + G}{{{u}}_{{w}}}\text{。}$ | (1) |
其中:
| $ \begin{gathered} {A} = \left[ {\begin{array}{*{20}{c}} {{a_{11}}} & {{a_{12}}} & 0 & {{a_{14}}} & 0 & {{b_{11}}} & {{b_{12}}} \\ {{a_{21}}} & {{a_{22}}} & {{a_{23}}} & {{a_{24}}} & 0 & {{b_{21}}} & {{b_{22}}} \\ 0 & {{a_{32}}} & {{a_{33}}} & 0 & 0 & {{b_{31}}} & {{b_{32}}} \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ {{a_{51}}} & {{a_{52}}} & 0 & {{a_{54}}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {{{ - 1} \mathord{\left/ {\vphantom {{ - 1} {{T_e}}}} \right. } {{T_e}}}}&0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {{{ - 1} \mathord{\left/ {\vphantom {{ - 1} {{T_T}}}} \right. } {{T_T}}}} \end{array}} \right], \hfill \\ {B = }\left[ {\begin{array}{*{20}{c}} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ {{1 \mathord{\left/ {\vphantom {1 {{T_e}}}} \right. } {{T_e}}}} & 0 \\ 0 & {{1 \mathord{\left/ {\vphantom {1 {{T_T}}}} \right. } {{T_T}}}} \end{array}} \right],\\ {G = }{\left[ {\begin{array}{*{20}{c}} {{g_{11}}} & {{g_{21}}} & 0 & 0 & {{g_{51}}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {{g_{52}}} & 0 & 0 \end{array}} \right]^{\text{T}}} \end{gathered} $ |
舰尾流扰动的存在会对舰载无人机动力学模型中的
| ${g_{11}} = - {a_{11}},\;\;{g_{21}} = - {a_{12}},\;\;{g_{51}} = - {a_{51}},\;\;{g_{52}} = 1\text{。}$ | (2) |
由于舰载无人机纵向着舰控制的目标是纵向高度的跟踪和速度的保持,因此选取可控输出向量
在设计控制系统时,以动态逆控制器作为主控制回路用于保证系统对参考速度和参考轨迹精确跟踪的能力,以H∞输出反馈控制器作为补偿回路以增强系统的鲁棒性。同时,为了产生动态逆控制器所需的高阶微分信号并避免计算膨胀问题的发生,在动态逆控制前设计了指令滤波器以对参考信号进行处理。由于舰载无人机的反馈信号是由传感器测量得到的,控制系统中的输出反馈信号中可能存在传感器噪声。为了减小这种噪声对控制系统的影响,本文设计H∞最优滤波器以对输出反馈信号进行滤波。
控制器基本形式为:
| ${{u}} = \bar {{u}} + {{{u}}_\infty }\text{。}$ | (3) |
其中:
根据动态逆控制理论,需要将输出变量连续微分直至方程中出现控制变量,最终得到动态逆的动态逆控制器形式为:
| ${{u}} = {({{C}}{{{U}}_n})^{ - 1}}({{{r}}^{\left( n \right)}} - {{C}}{{{A}}^n}{{x}} + {{v}})\text{,}$ | (4) |
其中,
为了推导动态逆控制器的表达式,分别对
| $ \left\{ \begin{aligned} \ddot V = & {{a'}_{11}}V + {{a'}_{12}}\alpha + {{a'}_{13}}q + {{a'}_{14}}\theta + {{a'}_{16}}{\delta _e} + {{a'}_{17}}{\delta _T} + \\ & {B_{u11}}{\delta _{ec}} + {B_{u12}}{\delta _{Tc}} + {{g'}_{11}}{V_V} + {{g'}_{12}}{V_w} + {{g''}_{11}}{{\dot V}_V} + \\ & {{g''}_{12}}{{\dot V}_w} + {{g'''}_{11}}{{\ddot V}_V} + {{g'''}_{12}}{{\ddot V}_w}, \\ \dddot H = &{{a'}_{51}}V + {{a'}_{52}}\alpha + {{a'}_{53}}q + {{a'}_{54}}\theta + {{a'}_{56}}{\delta _e} + {{a'}_{57}}{\delta _T} + \\ & {B_{u51}}{\delta _{ec}} + {B_{u52}}{\delta _{Tc}} + {{g'}_{51}}{V_V} + {{g'}_{52}}{V_w} + {{g''}_{51}}{{\dot V}_V} + n \\ & {{g''}_{52}}{{\dot V}_w} + {{g'''}_{51}}{{\ddot V}_V} + {{g'''}_{52}}{{\ddot V}_w} \text{。} \end{aligned} \right. $ | (5) |
其中,各变量的系数可通过矩阵运算得到。
因此,对变量
| $ \begin{aligned} & \overline u = {B_u}^{ - 1}\left( {{{\overline z }^{\left( r \right)}} - {A_x}x - {G^\prime }{u_w} - } \right. \hfill \\ & \quad\quad\left. {{G^{\prime \prime }}{{\mathop u\limits^. }_w} - {G^{\prime \prime \prime }}{{\mathop u\limits^{..} }_w} + {K_2}\mathop e\limits^{..} + {K_1}\mathop e\limits^. + {K_0}e} \right) \text{,} \end{aligned} $ |
其中,
根据动态逆控制器的表达式,控制器的实现需要指令信号的高阶导数。直接对输入指令进行微分可能导致计算膨胀问题[18],设计如下形式的指令滤波器:
| $ \left\{ {\begin{aligned} & {\frac{{\bar H\left( s \right)}}{{{{\bar H}_c}\left( s \right)}} = \frac{{p\omega _1^2}}{{\left( {s + p} \right)\left( {{s^2} + 2{\xi _1}{\omega _1}s + \omega _1^2} \right)}}}\text{,} \\ & {\frac{{\bar V\left( s \right)}}{{{{\bar V}_c}\left( s \right)}} = \frac{{\omega _2^2}}{{{s^2} + 2{\xi _2}{\omega _2}s + \omega _2^2}}}\text{。} \end{aligned}} \right. $ | (6) |
由于H∞输出反馈控制器需要将控制系统输出变量作为控制器的输入变量,进入控制器的系统输出变量值是由传感器测量得到的,这些测量值中可能存在噪声信号,这将影响控制器的性能[19]。为了抑制测量信号中传感器噪声对控制系统的影响,在H∞输出反馈控制器前设计了一个H∞滤波器,输出测量信号在经过滤波器滤波后进入输出反馈控制器。
假设系统的状态方程可表示为:
| $ \left\{ {\begin{aligned} & {\mathop { x}\limits^. = { Ax} + { B_1}{ u_w} + { B_2}u} \text{,}\\ & { y = { C_2}x + { D_{21}}{ u_w}}\text{,} \\ & { z = { C_1}x + { D_{12}} u} \text{。} \end{aligned}} \right. $ | (7) |
其中:
H∞滤波器能够使系统传感器测量噪声到滤波器估计值同实际值之间误差的传递函数小于某一特定值,即确保估计误差在噪声信号的干扰下小于某特定值。对于式(7)描述的系统,H∞最优滤波器的求解等价于求解算子
| $\left\| {{w}} \right\|_{2,\left[ {0,{t_f}} \right]}^2 = \int_0^{{t_f}} {{{{u}}_w}^{\rm{T}}{{{u}}_w}{\rm{d}}t} \text{。}$ |
若选取
| $ \left\{ {\begin{aligned} & {\mathop {\widehat { x}}\limits^. = A\widehat { x} + { L}\left( { y - { C_2}\widehat { x}} \right) + { B_2} u} \text{,}\\ & {\widehat { x}\left( 0 \right) = {{\widehat { x}}_0}}\text{。} \end{aligned}} \right. $ | (8) |
其中,
| $\left\{ {\begin{aligned} & \bar {{B}}{{\bar {{B}}}^T} + \bar {{A}}{{P}} + {{P}}{{\bar {{A}}}^{\rm{T}}} - {{P}}\left( {{{C}}_2^{\rm{T}}{{{C}}_2} - {\gamma ^{ - 2}}{{C}}_1^{\rm{T}}{{{C}}_1}} \right){{P}} = 0\text{,} \\ & \bar {{B}}{{\bar {{B}}}^{\rm{T}}} = {{{B}}_1}\left( {{{I}} - {{D}}_{21}^{\rm{T}}{{{D}}_{21}}} \right){{B}}_1^{\rm{T}}\text{,} \\ & \bar {{A}} = {{A}} - {{{B}}_1}{{D}}_{21}^{\rm{T}}{{{C}}_2} \text{。} \end{aligned}} \right. $ | (9) |
对于式(7)描述的系统,H∞输出反馈控制器的求解即为求解
| $\left\| {{{{G}}_{zw}}} \right\|_{\infty ,\left[ {0,{t_f}} \right]}^2 = \mathop {\sup }\limits_{\left\| {w\left( t \right)} \right\|_{2,\left[ {0,{t_f}} \right]}^2 \ne 0} \frac{{\left\| {{{z}}\left( t \right)} \right\|_{2,\left[ {0,{t_f}} \right]}^2}}{{\left\| {{{{u}}_w}\left( t \right)} \right\|_{2,\left[ {0,{t_f}} \right]}^2}} < {\gamma ^2}\text{。}$ |
其中:
当
| $\left\{ {\begin{aligned} & {{\tilde {{A}}}^{\rm{T}}}{{S}} + {{S}}\tilde {{A}} - {{S}}\left( {{{{B}}_2}{{B}}_2^{\rm{T}} - {\gamma ^{ - 2}}{{{B}}_1}{{B}}_1^{\rm{T}}} \right){{S}} + {{\tilde {{C}}}^{\rm{T}}}\tilde {{C}} = 0\text{,} \\ & {{\tilde {{C}}}^T}\tilde {{C}} = {{C}}_1^{\rm{T}}\left( {{{I}} - {{{D}}_{12}}{{D}}_{12}^{\rm{T}}} \right){{{C}}_1} \text{,}\\ & \tilde {{A}} = {{A}} - {{{B}}_2}{{D}}_{12}^{\rm{T}}{{{C}}_1} \text{。} \end{aligned}} \right. $ | (10) |
由于复合控制器为
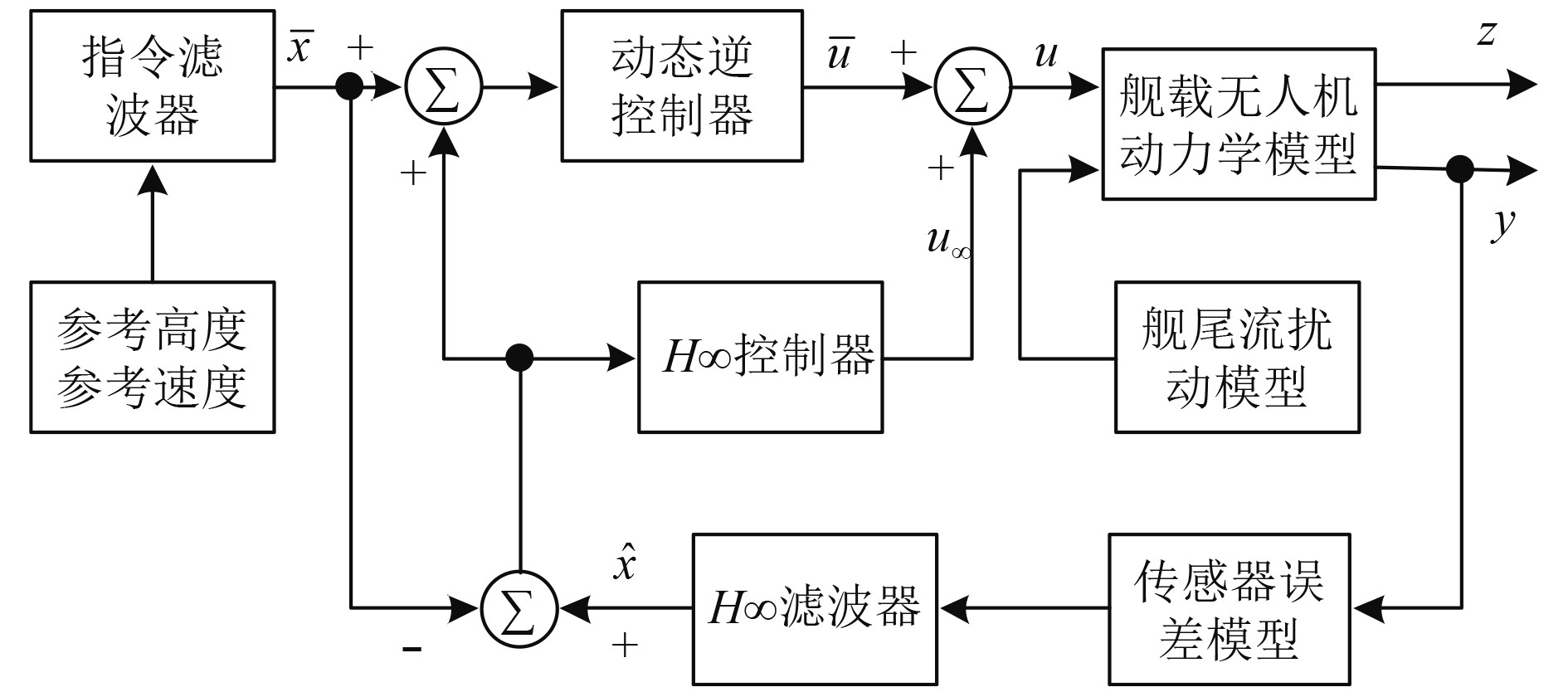
|
图 1 纵向着舰控制系统结构图 Fig. 1 Structure diagram of longitudinal landing control system |
根据MIL-F-8785C军用规范,舰尾流扰动可以视为4种气流扰动分量的合成。由于本文仅研究纵向着舰控制,因此仅考虑纵向的舰尾流扰动分量,最终合成了水平纵向扰动分量
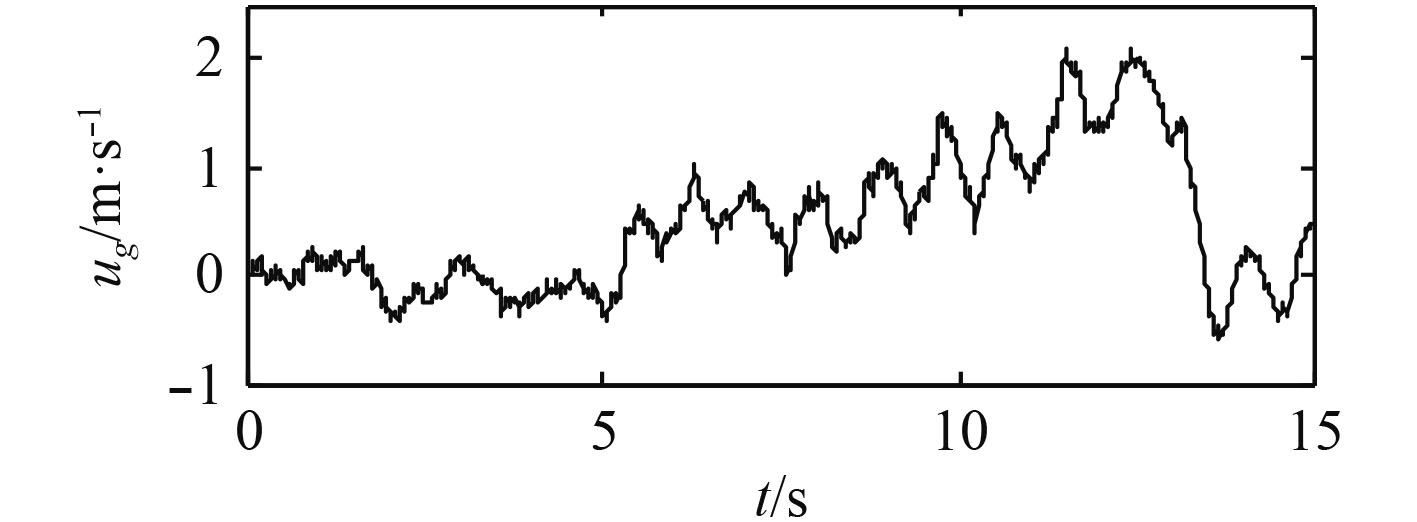
|
图 2
|
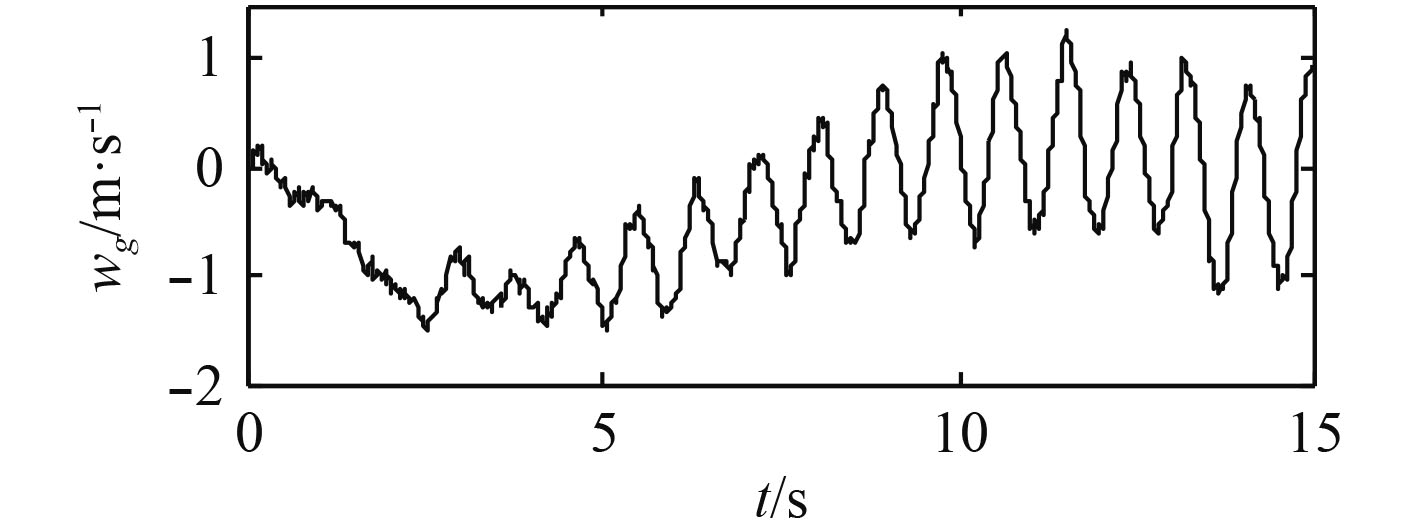
|
图 3
|
传感器误差模型[20]可用下式描述:
| $\Theta = \left( {{\Theta _i} + S \cdot {a_r} + B + v} \right)\left( {1 + \frac{{\Delta K}}{K}} \right)\text{。}$ | (11) |
其中:
某型舰载无人机在着舰时基准速度为
为了衡量控制系统对基准下滑速度和基准轨迹的跟踪精度,定义函数ATE(Average Tracking Error),该函数可用于计算实际输出值同参考输入值之间误差的方差。ATE的函数表达式为:
| ${\rm{ATE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{z_i} - {z_{ci}}} \right)}^2}} } \text{。}$ | (12) |
其中,
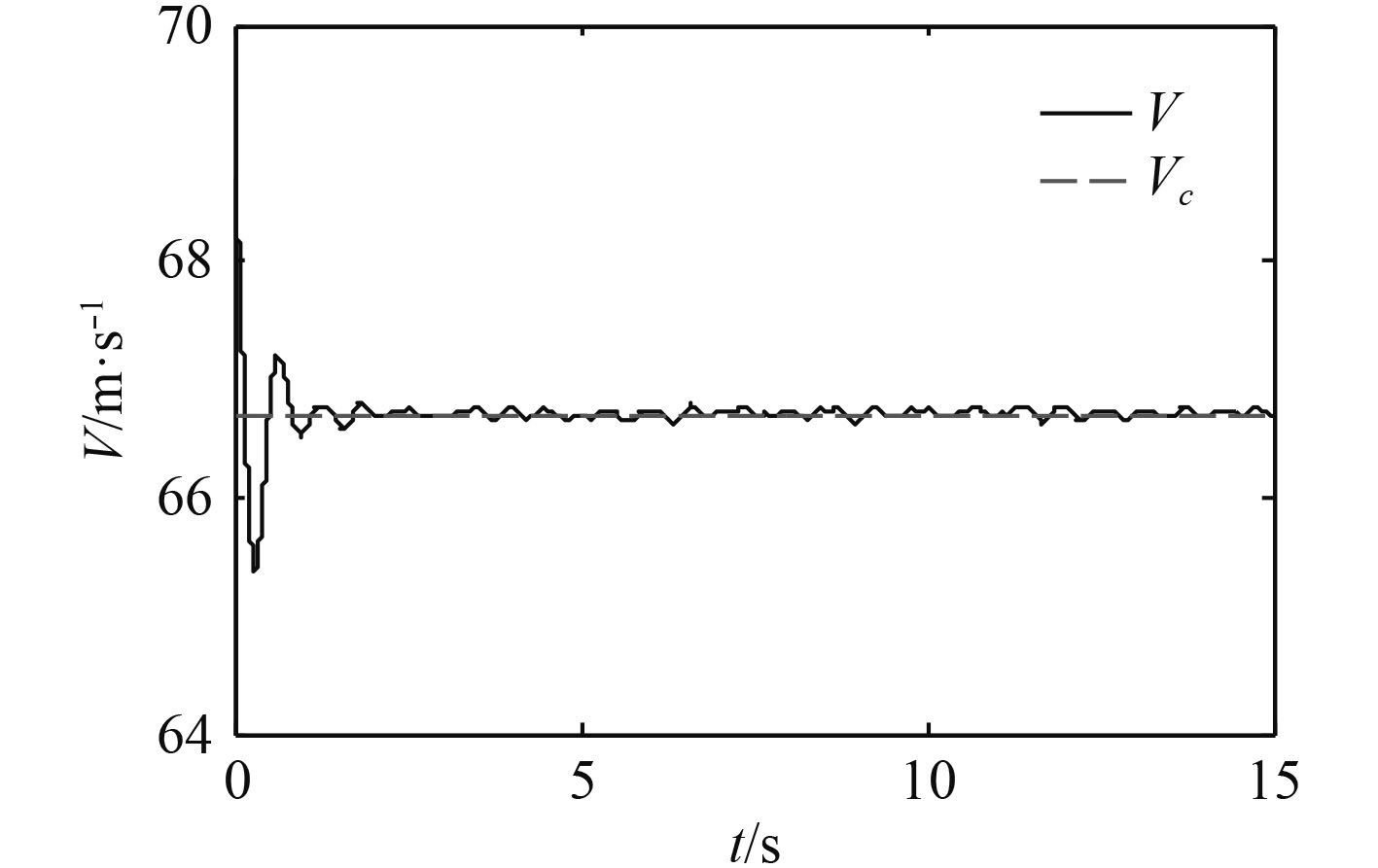
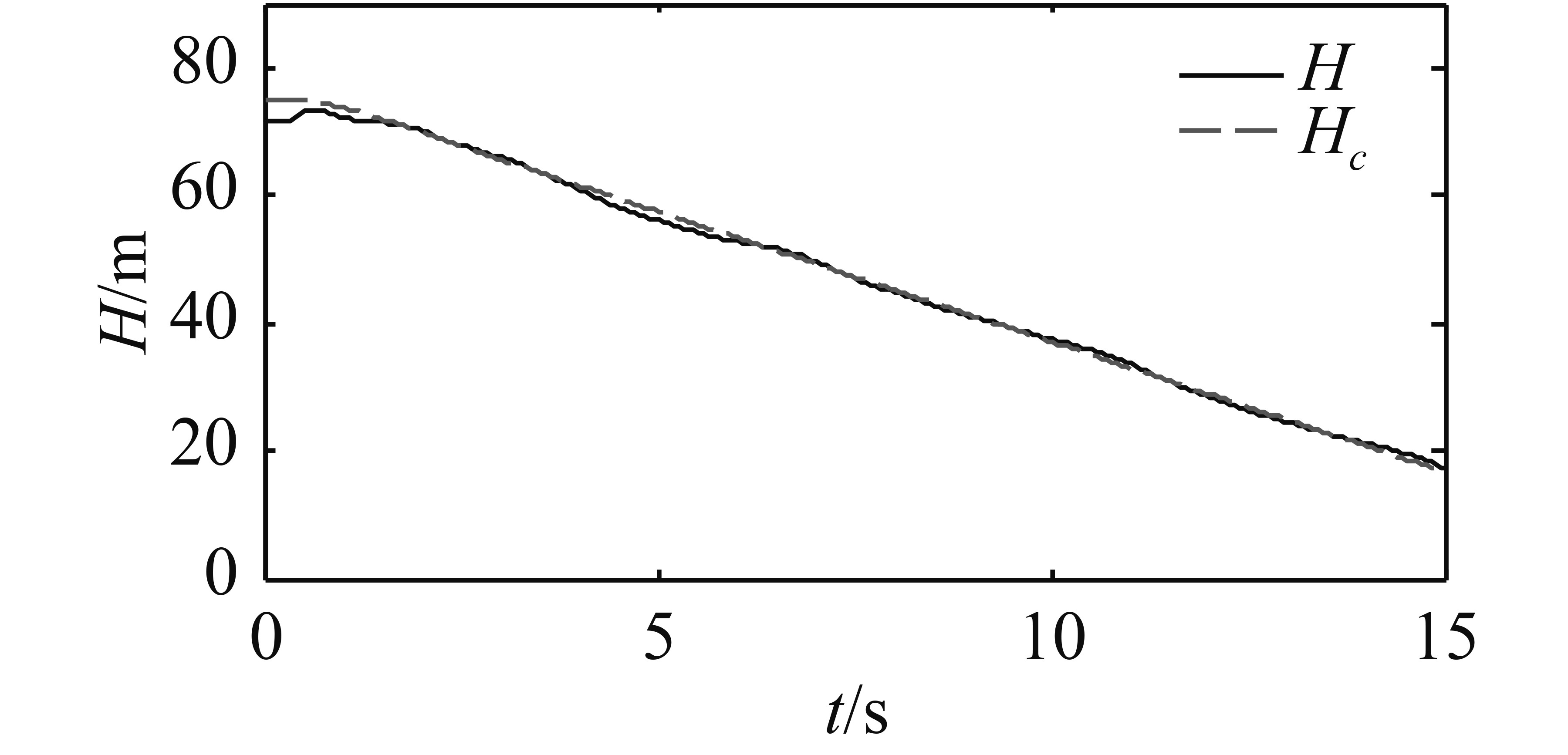
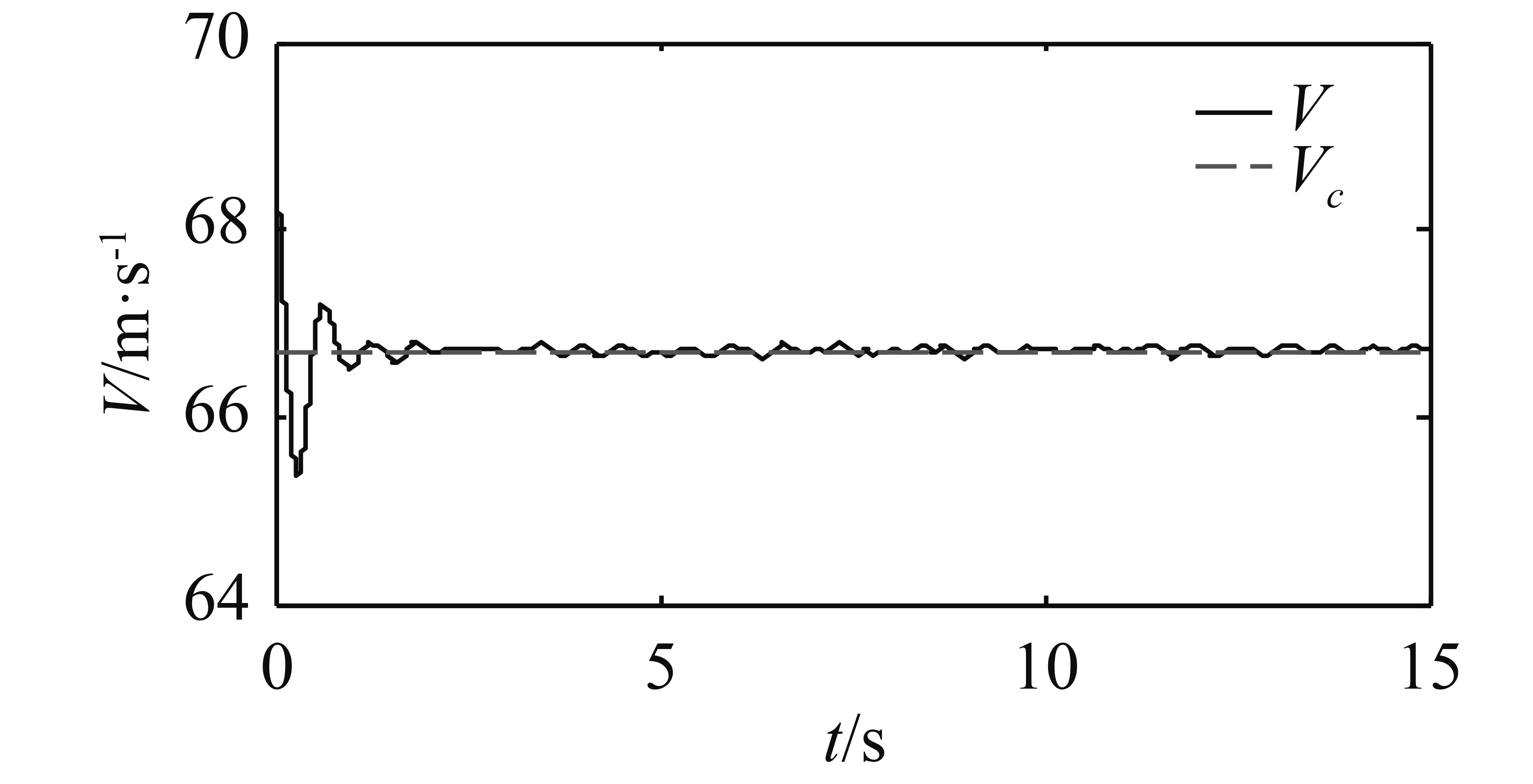
图4~图9为未加入舰尾流扰动信号和传感器噪声信号的仿真结果。
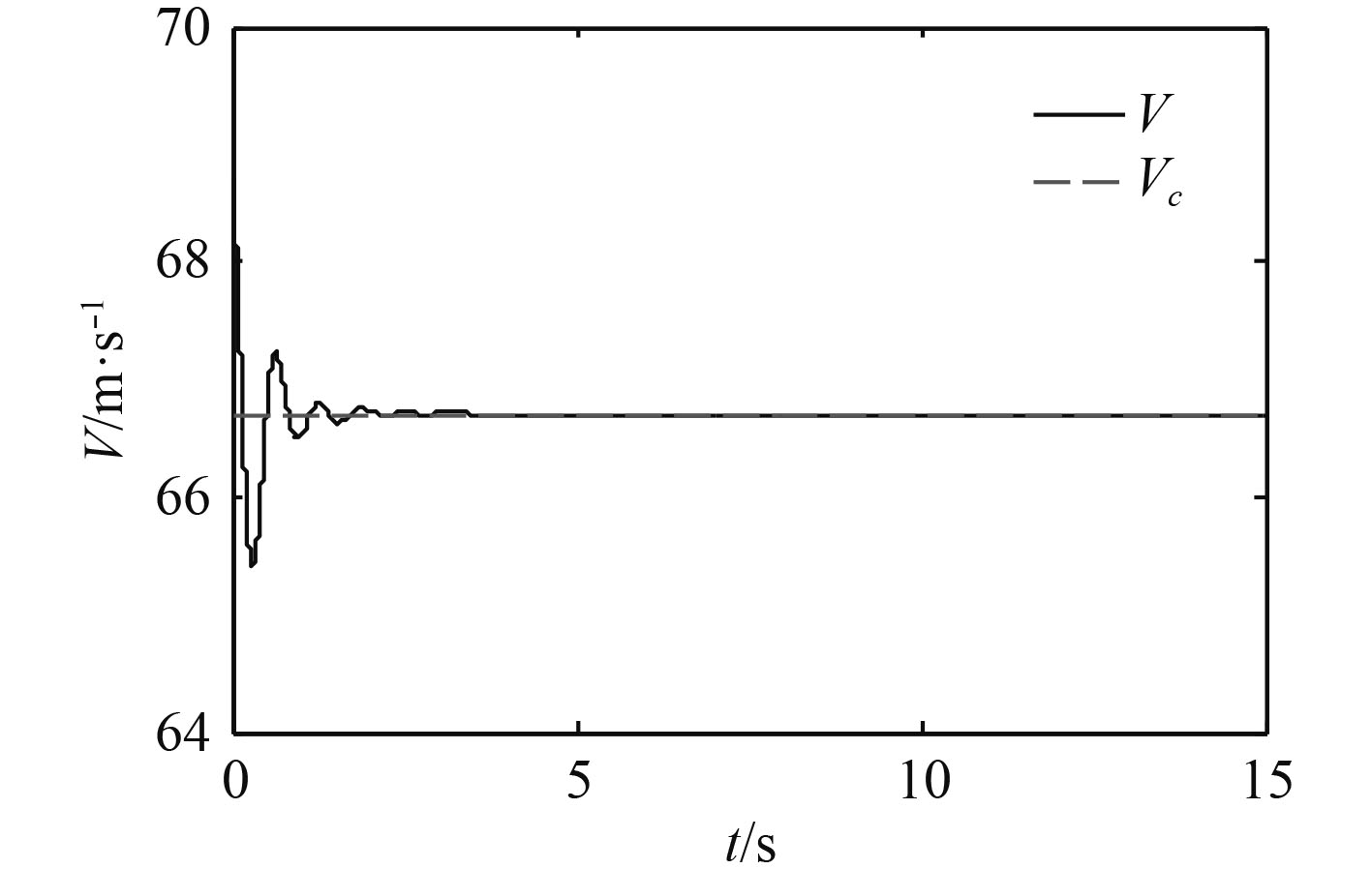
|
图 4 随时间的变化 Fig. 4 Graph of the relationship between V and t |
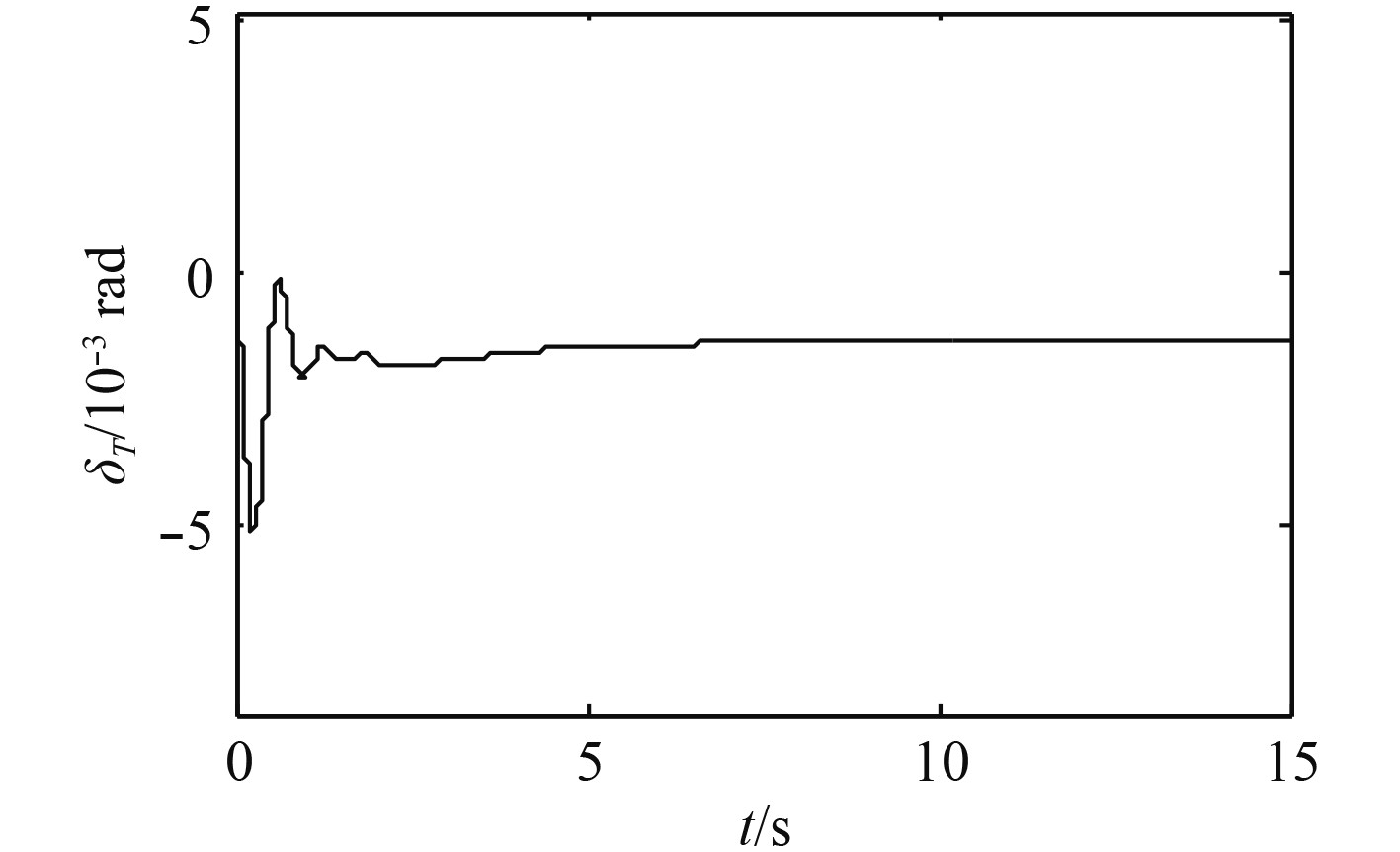
|
图 9
|
根据图4和图5可以分析出,本文设计的控制系统对于速度和高度的跟踪效果良好,舰载无人机的速度能够快速收敛到参考值
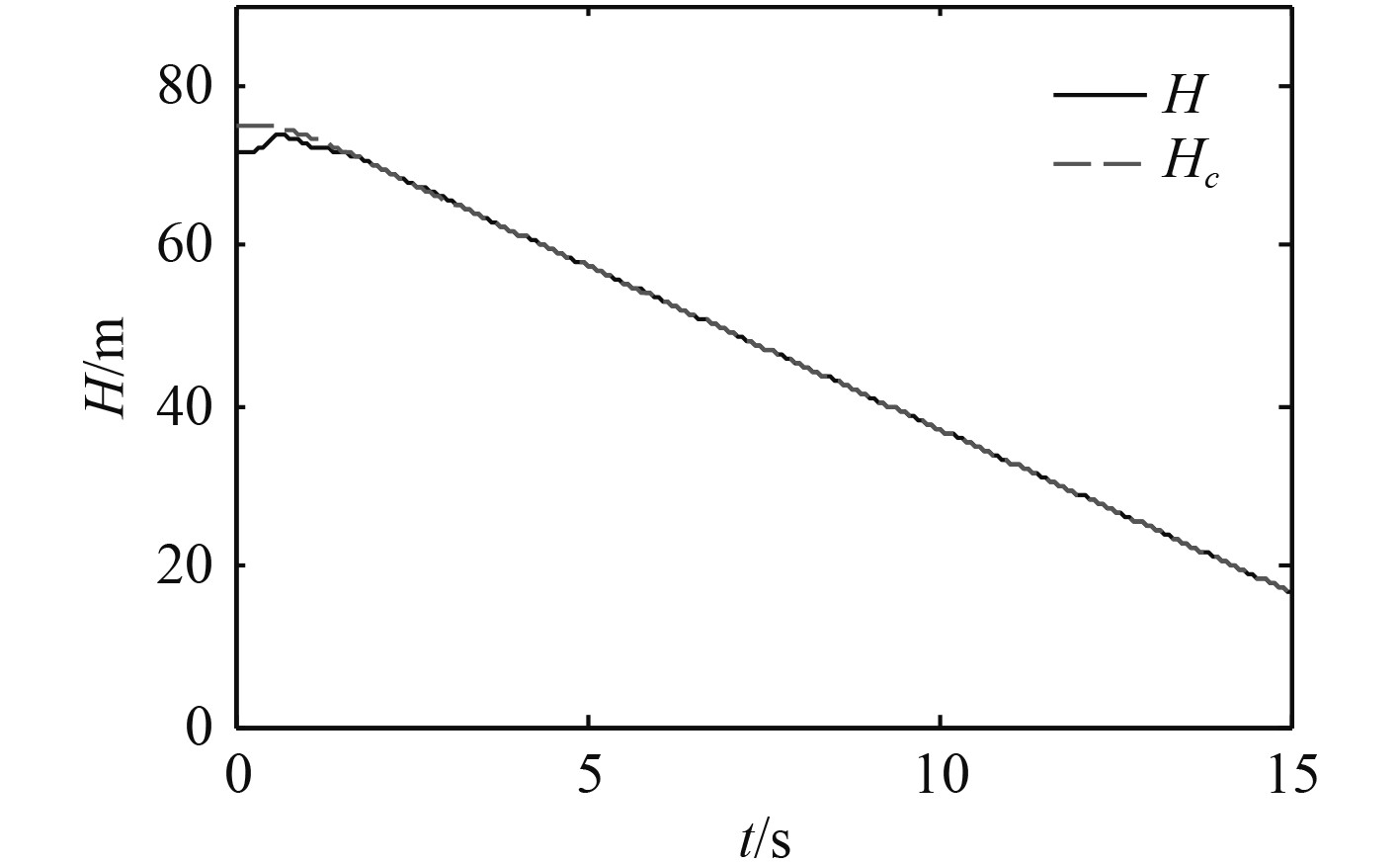
|
图 5 随时间的变化 Fig. 5 Longitudinal landing trajectory of carrier aircraft |
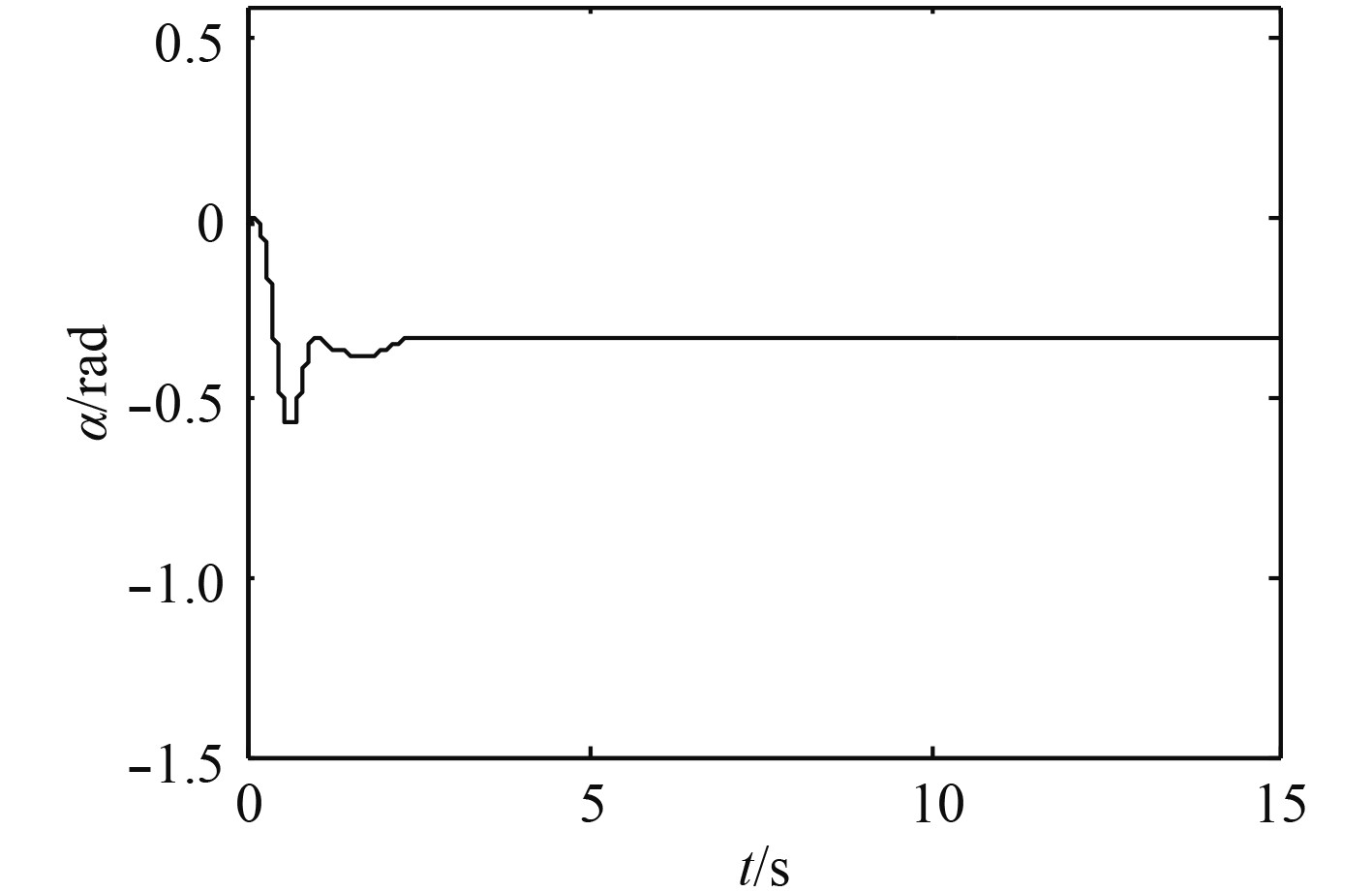
|
图 6
|
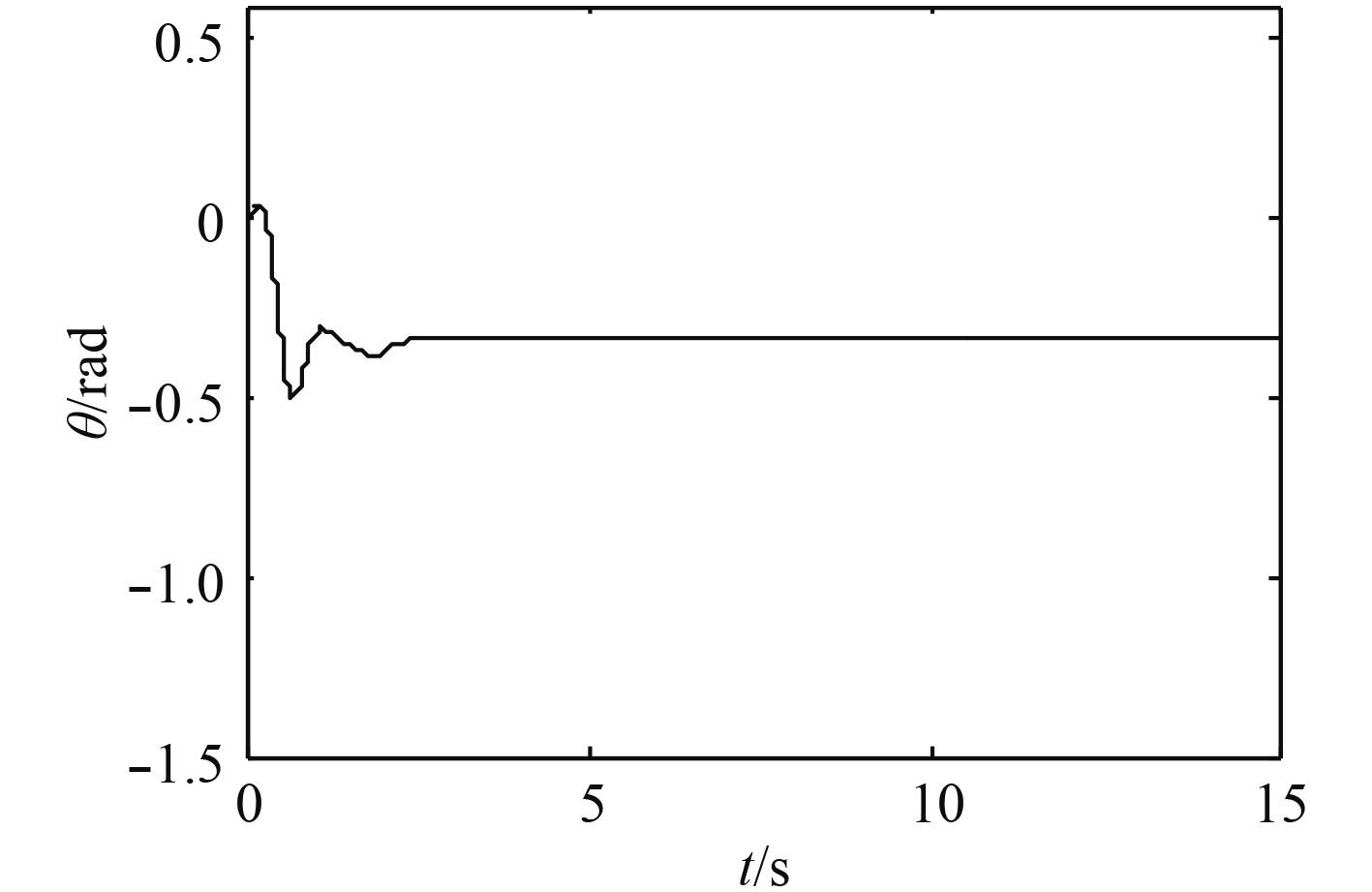
|
图 7
|
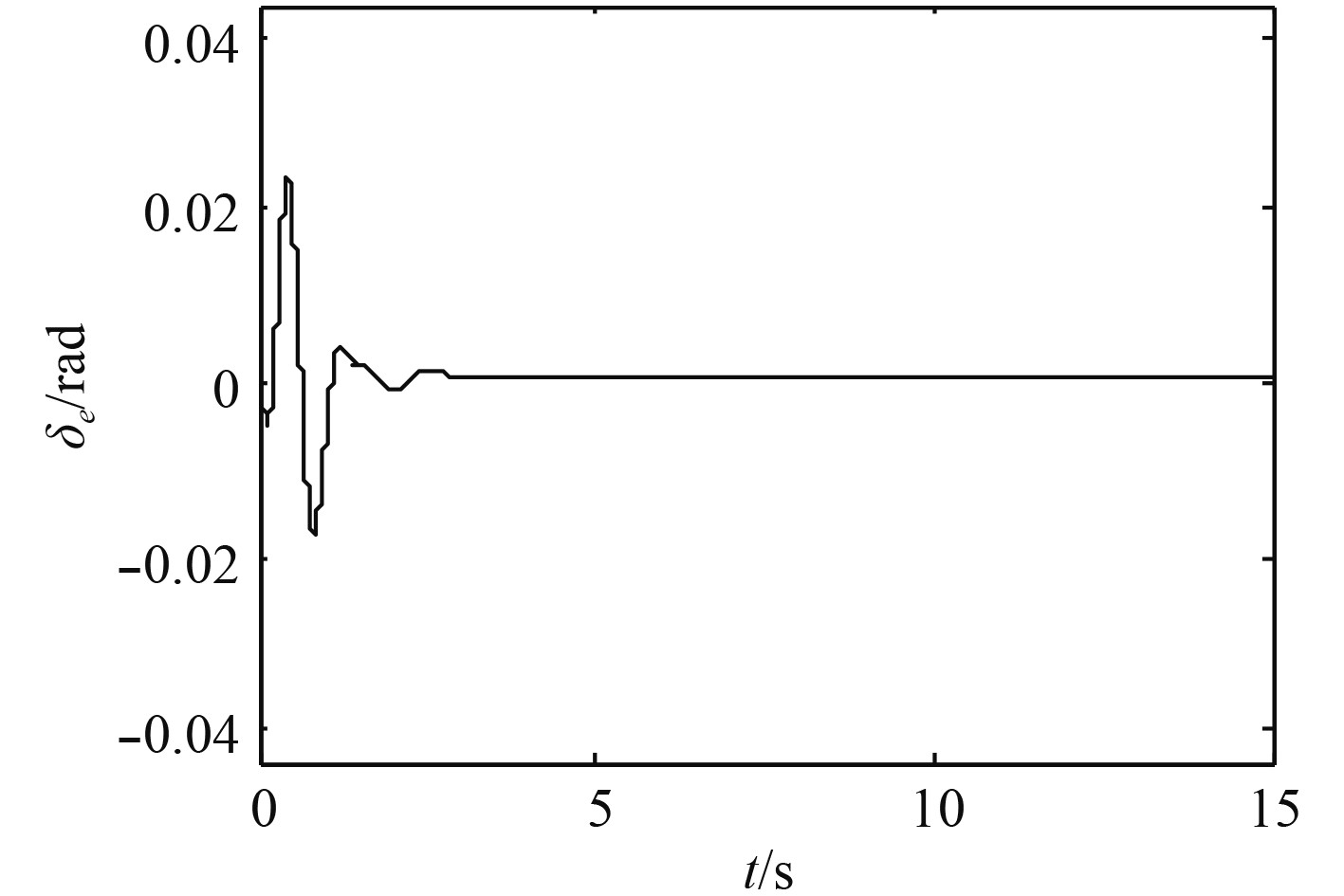
|
图 8
|
图10~图15分别表示单独加入舰尾流扰动信号、单独加入传感器噪声信号和同时加入这2种信号的仿真结果。分别表示不同干扰情况下舰载无人机对速度和着舰下滑轨迹的跟踪情况。
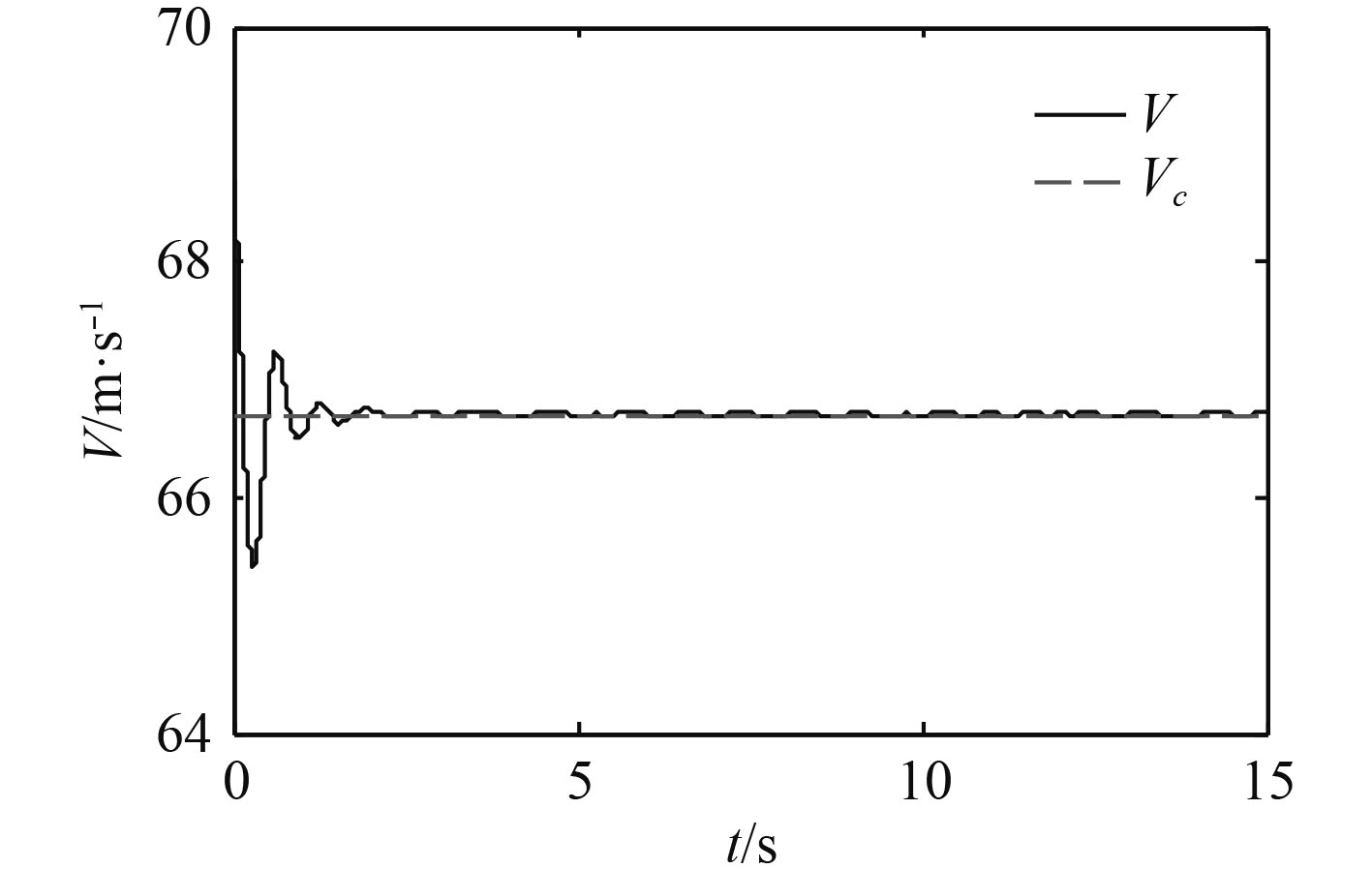
|
图 10
仅加入传感器噪声时
|
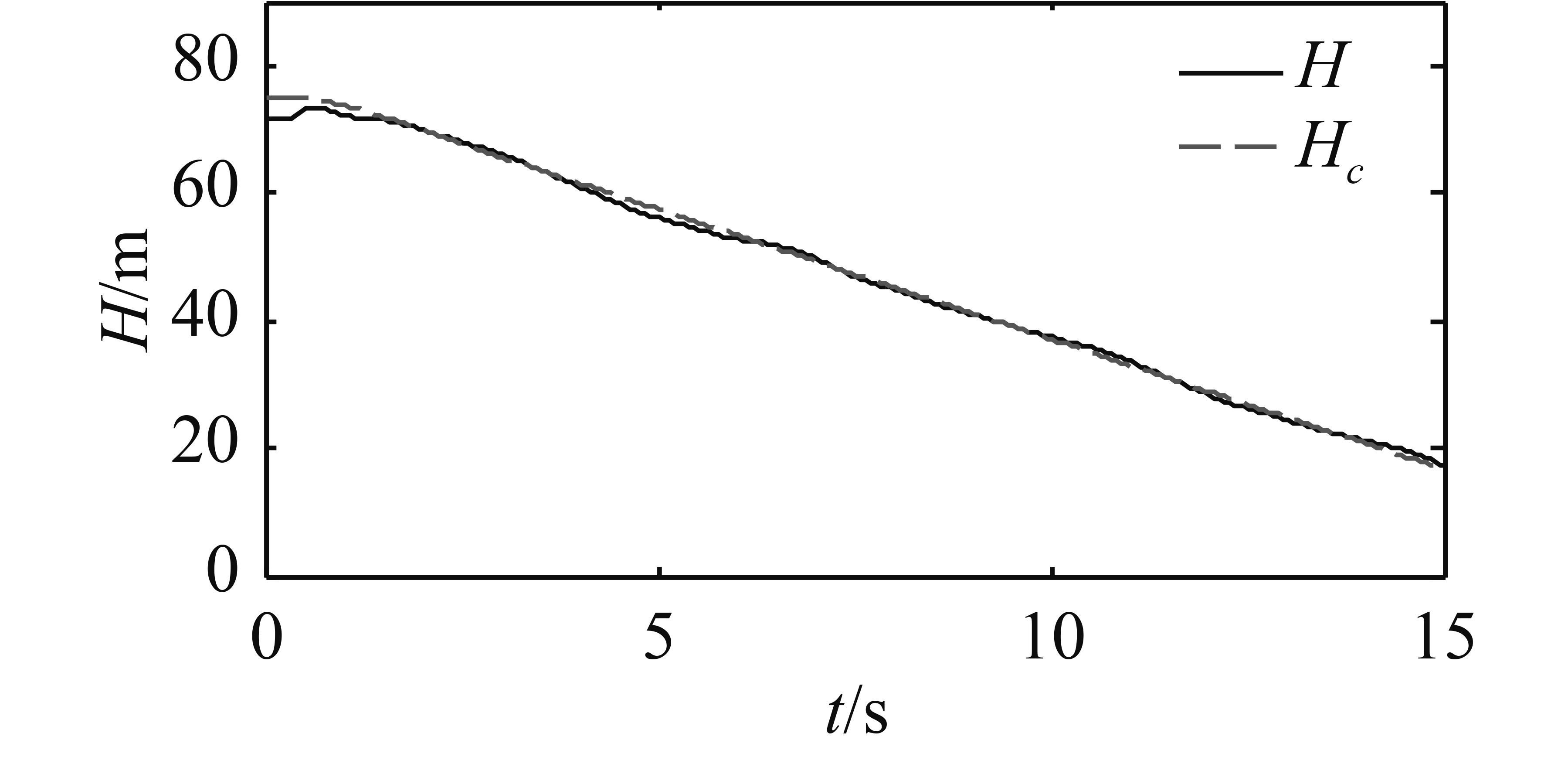
|
图 15
同时加入舰尾流扰动和传感器噪声时
|
对比图4和图10的结果,可以发现图4和图10的结果相同,这说明传感器噪声几乎不影响舰载无人机对速度的跟踪。同理,通过对比图5和图11的结果,可以发现传感器噪声也几乎不影响舰载无人机对着舰下滑轨迹的跟踪。这表明本文设计的控制系统对于传感器噪声具有良好的抑制能力。而根据图12和图13可以分析出,舰尾流扰动的存在会影响舰载无人机对速度和高度的跟踪,但这种影响很小,处于可接受的范围之内。
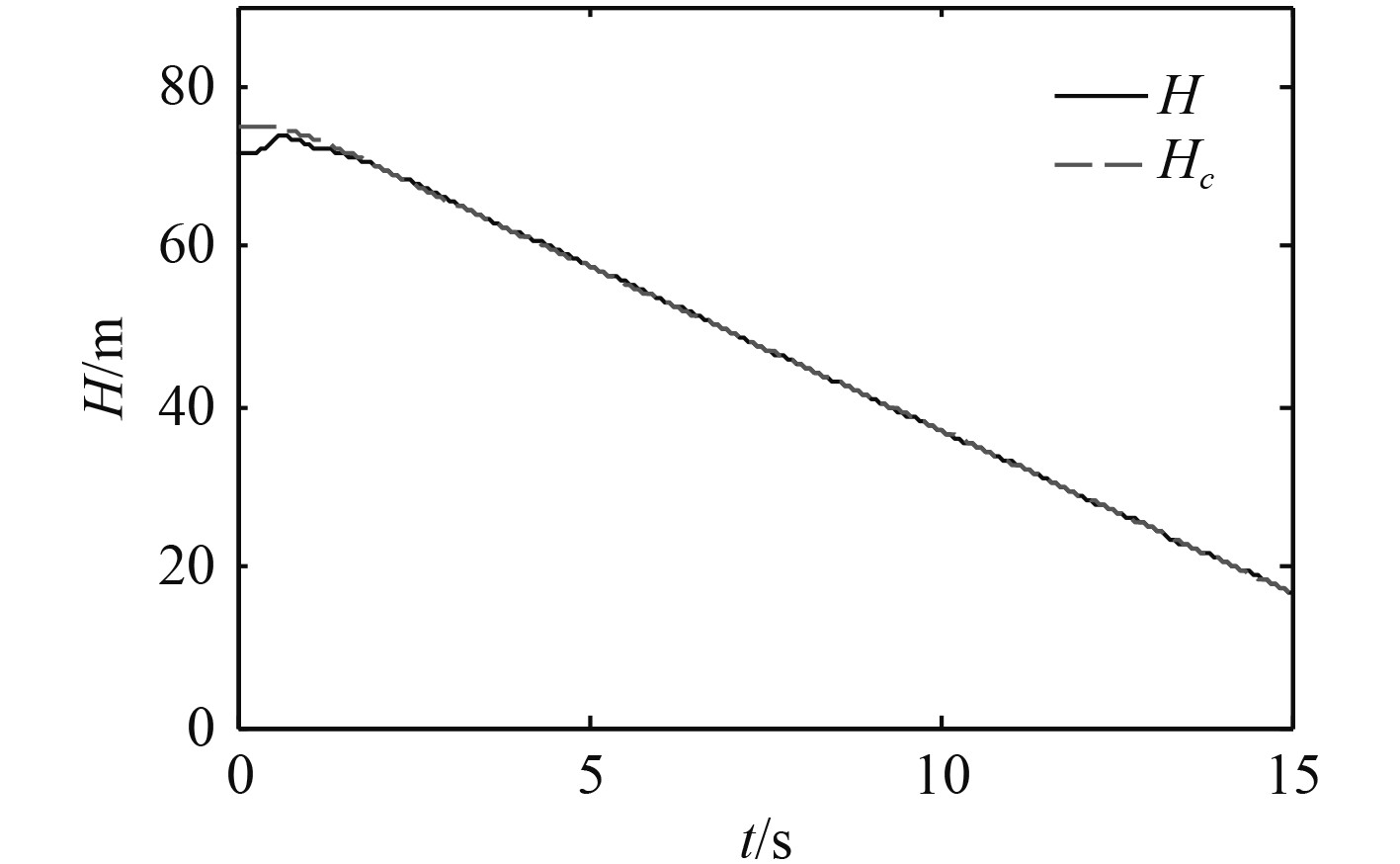
|
图 11
仅加入传感器噪声时
|
|
图 12
仅加入舰尾流扰动时
|
|
图 13
仅加入舰尾流扰动时
|
图12~图15的结果可得出,图12同图14的结果几乎相同,图13同图15的结果也几乎相同。这是因为前文提到的,控制系统对传感器噪声具有良好的抑制能力,因此同时加入传感器噪声和舰尾流扰动时,舰尾流扰动对控制系统跟踪效果的影响起主导作用。同时,也可以得出类似于图12和图13的结论。
|
图 14
同时加入舰尾流扰动和传感器噪声时
|
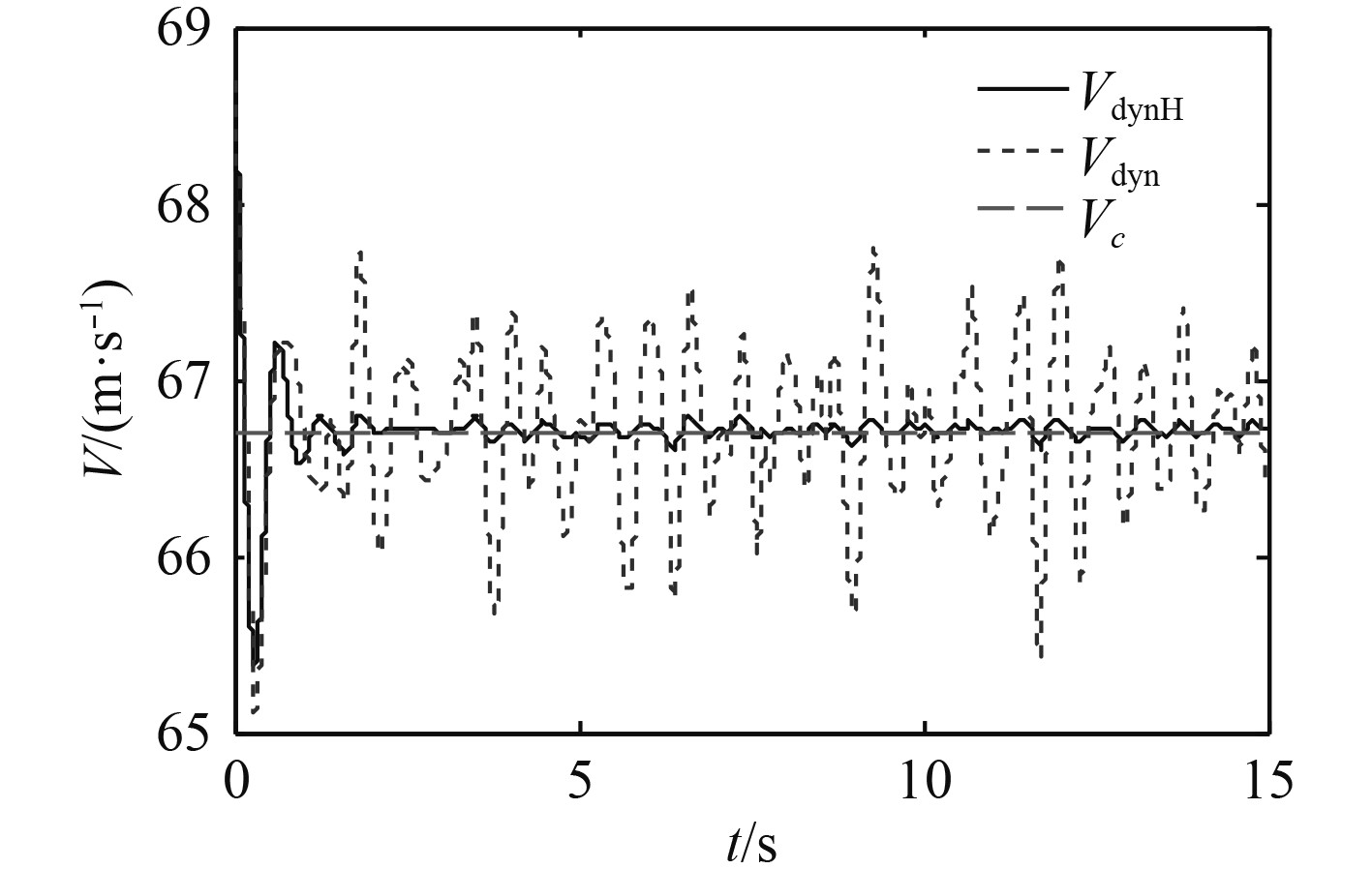
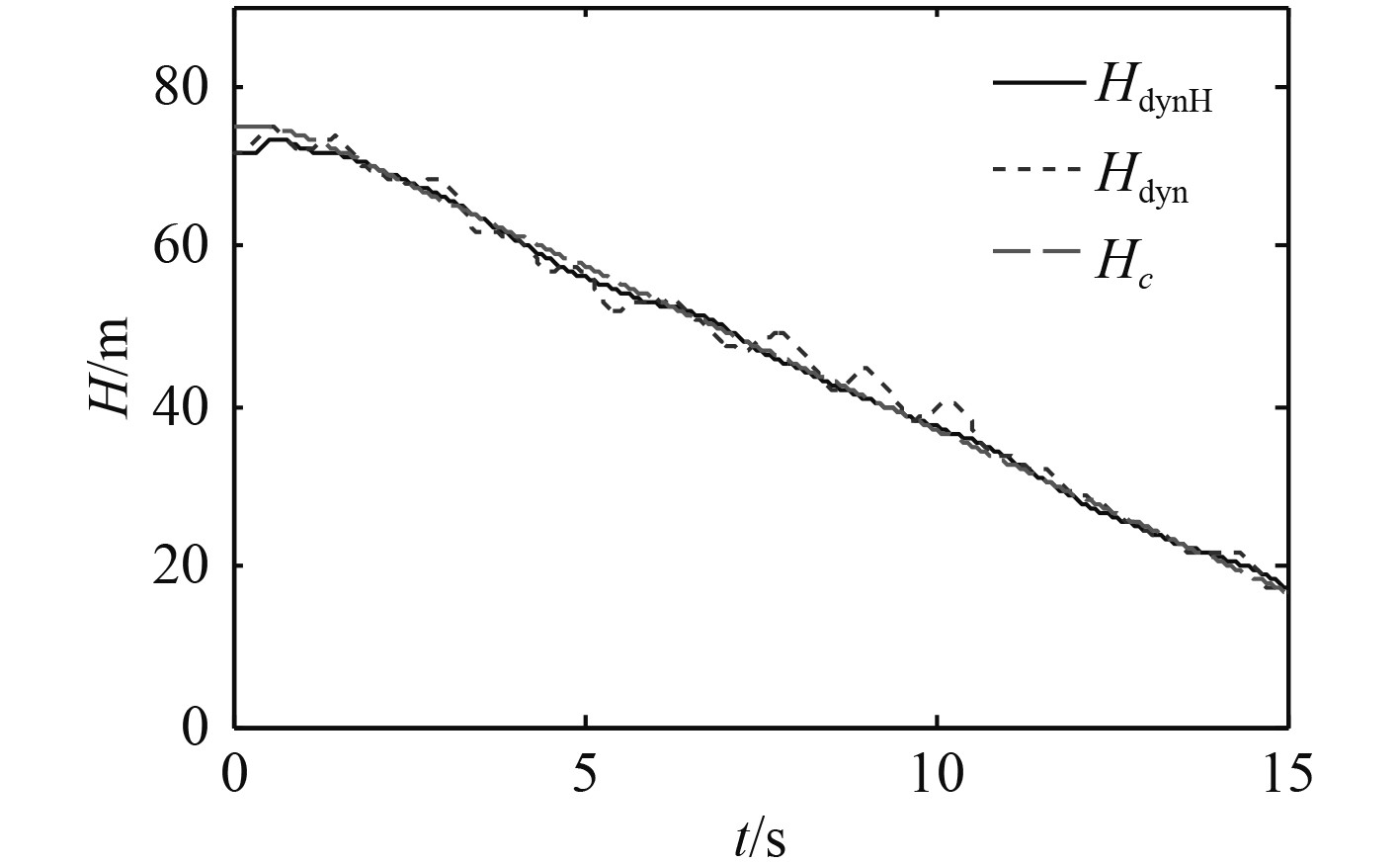
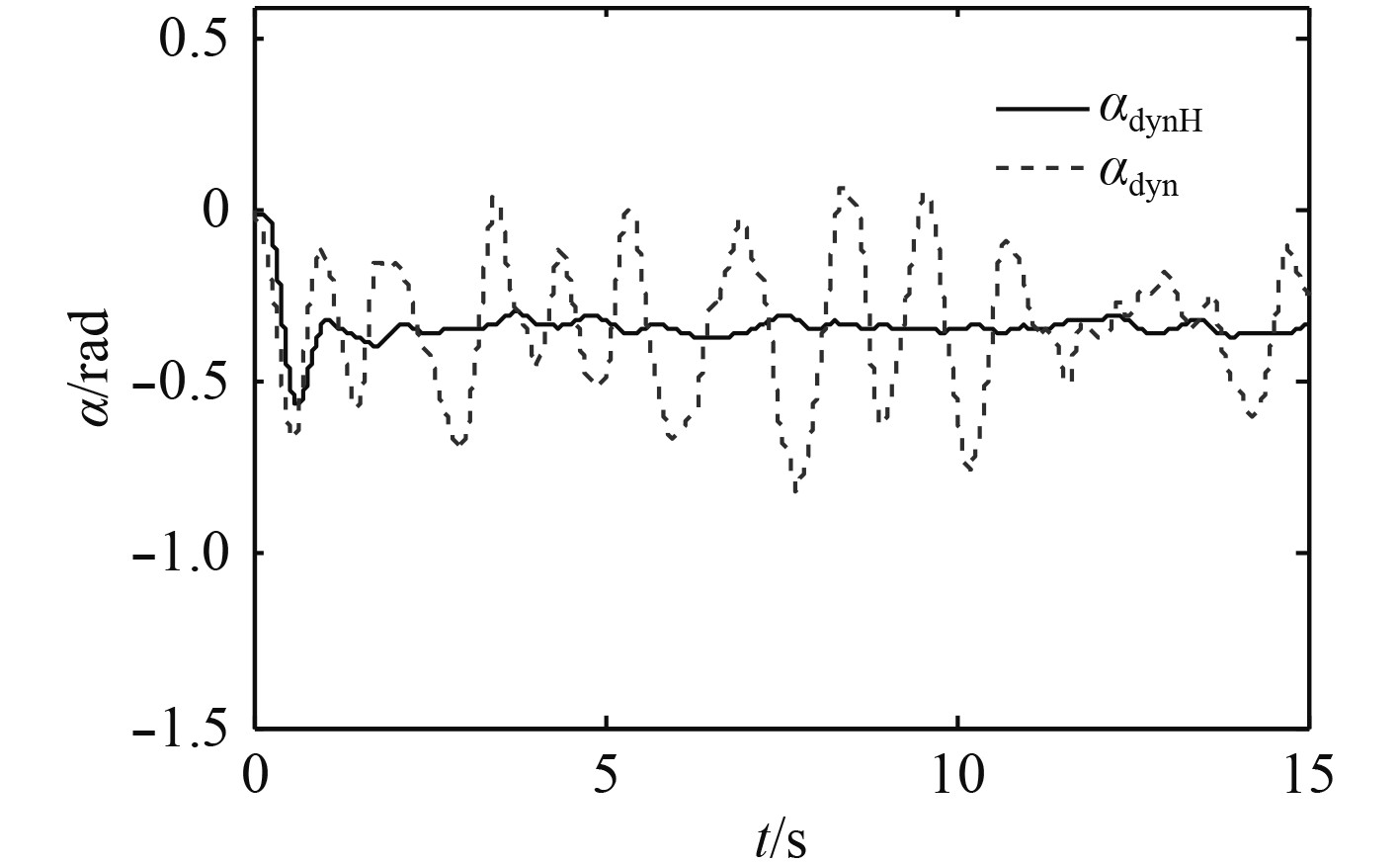
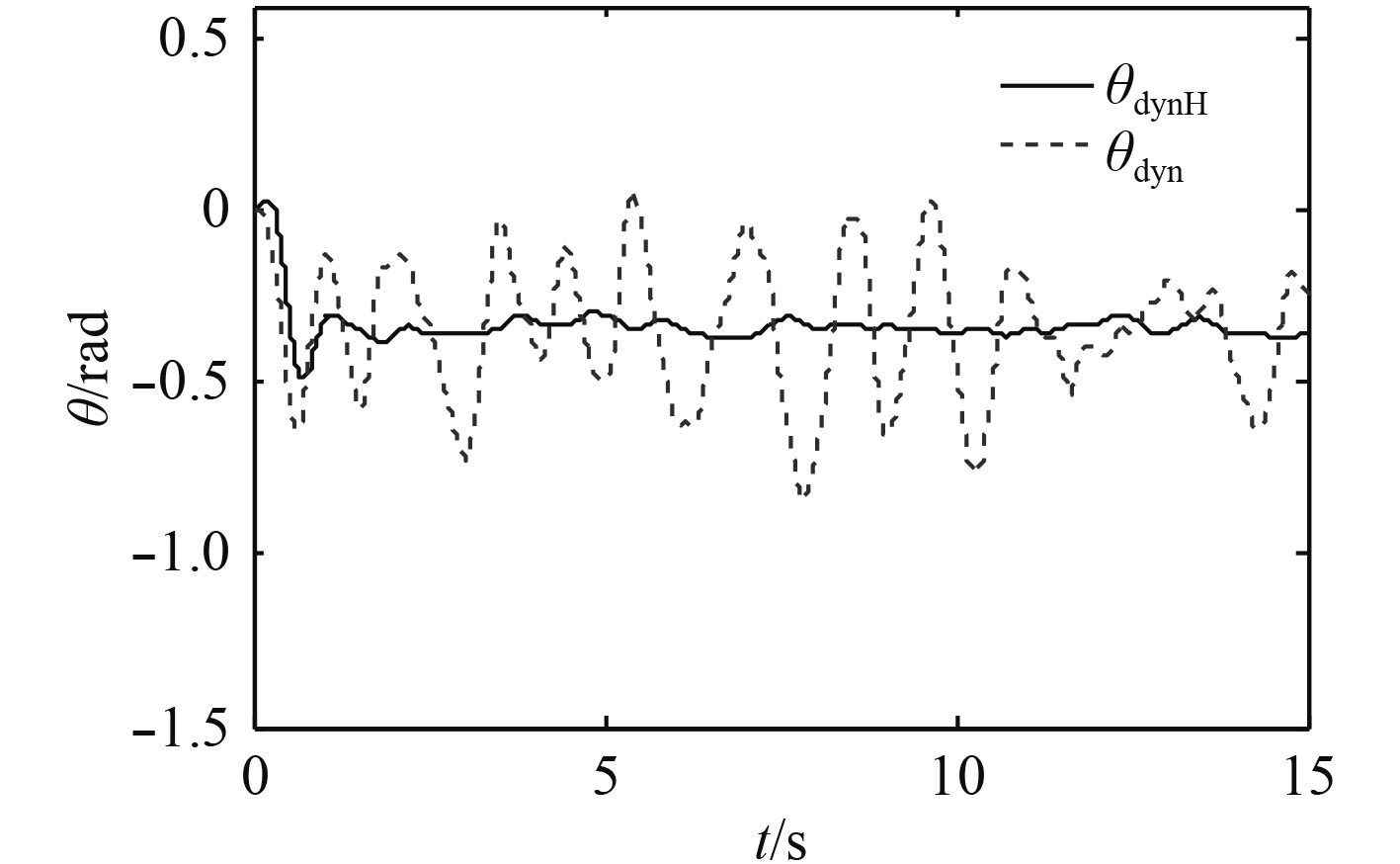
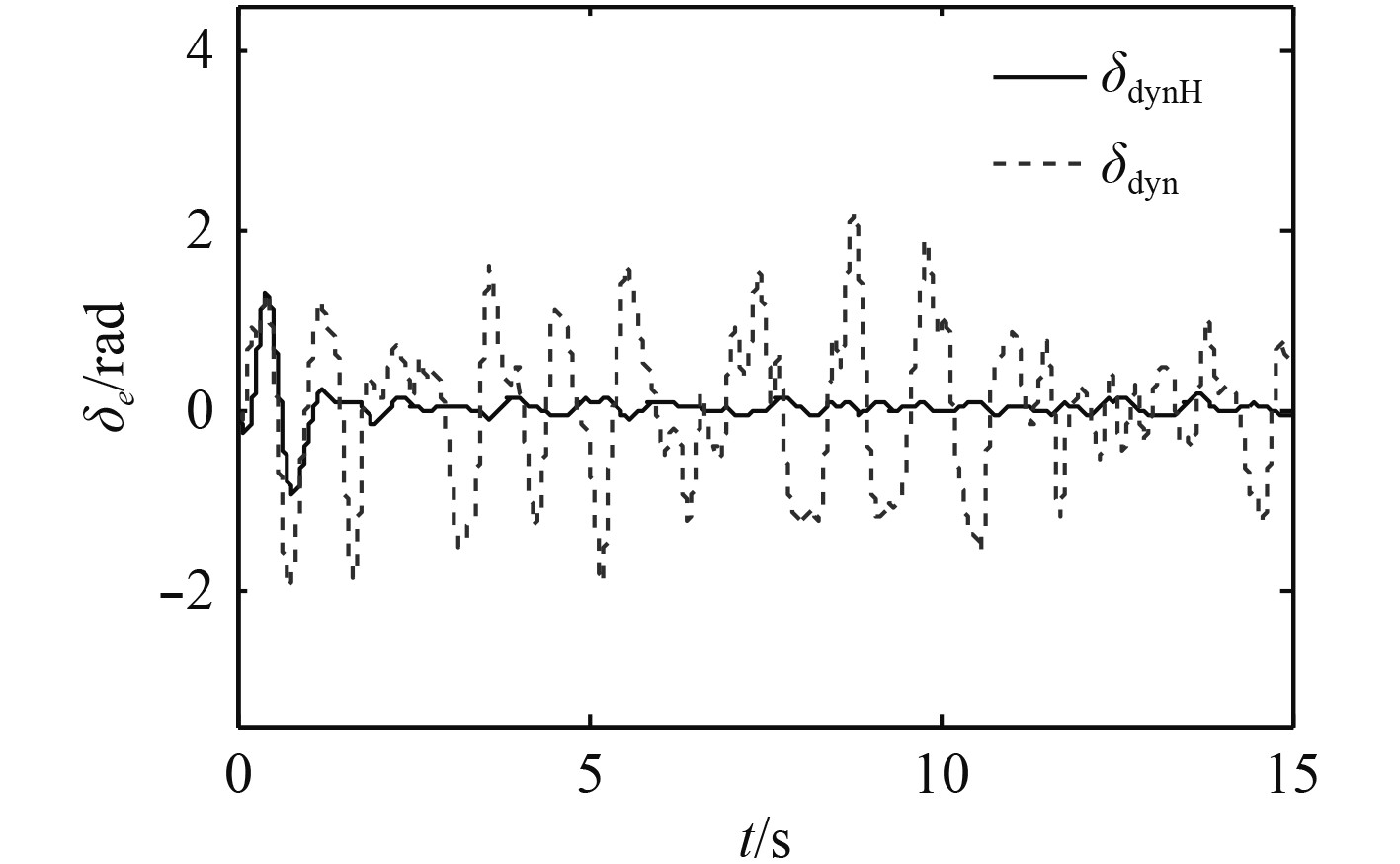
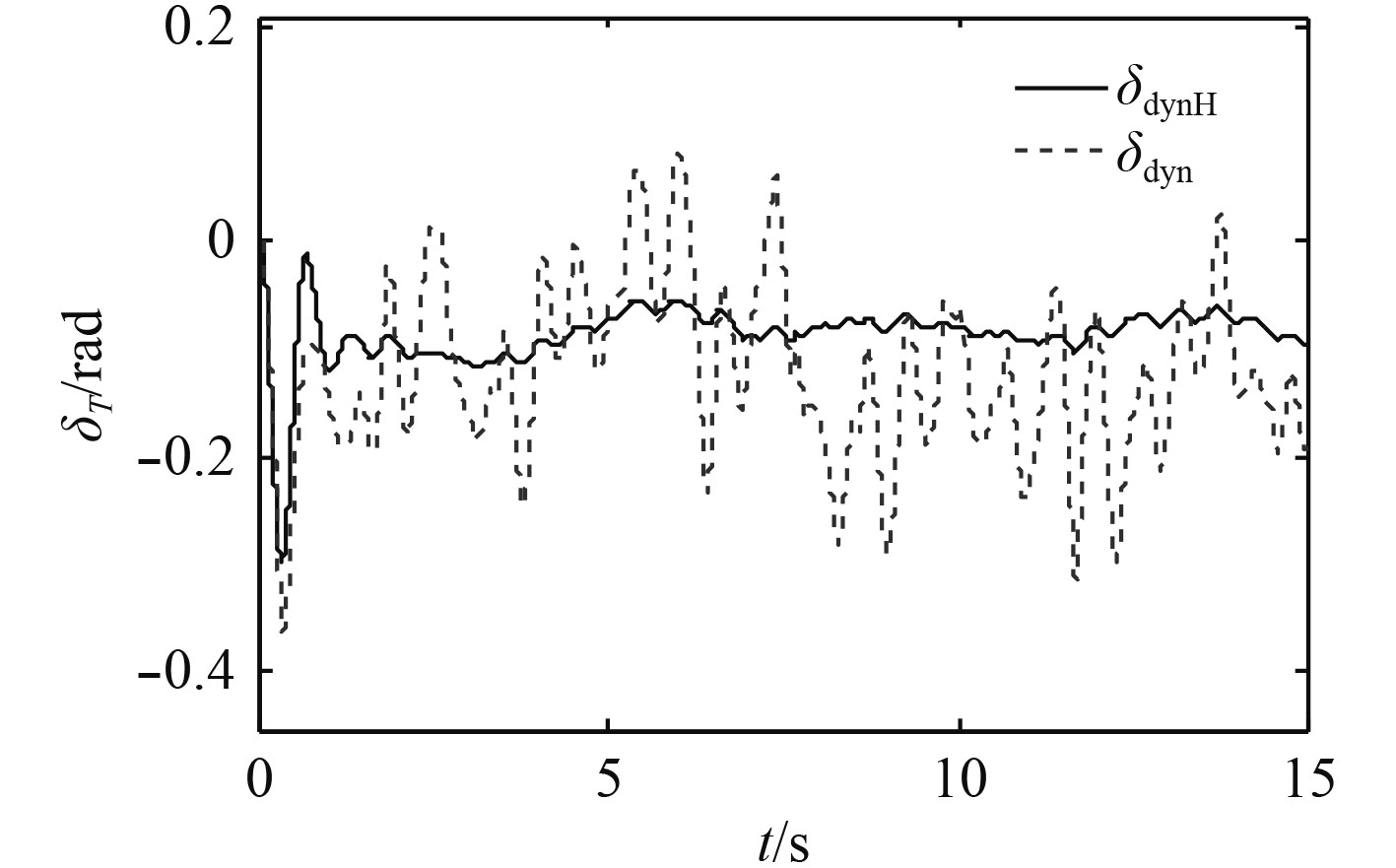
图16~图21为同时加入舰尾流扰动和传感器噪声信号时,本文设计的控制方法同动态逆方法的仿真对比结果。下标
|
图 16
不同方法下
|
|
图 17
不同方法下
|
|
图 18
不同方法下
|
|
图 19
不同方法下
|
|
图 20
不同方法下
|
|
图 21
不同方法下
|
为了定量比较不同情况下舰载无人机对基准速度和基准轨迹的跟踪精度,根据前文提到的方法,分别计算了不同仿真条件下舰载无人机速度和高度的ATE值,其结果见表1。
|
|
表 1 不同仿真条件下的ATE数值 Tab.1 ATE values under different simulation conditions |
由表1可以分析出,在上述5种条件下,无舰尾流扰动和传感器噪声时速度和高度的ATE值均为最小,仅加入传感器噪声条件下的ATE值同无扰动无噪声条件下的ATE值很接近,同时加入噪声和扰动条件下的ATE值同仅加入扰动下的ATE值很接近,而动态逆方法下的ATE值远大于前4种条件,这与前文的结论相一致。
4 结 语本文针对舰载无人机自动着舰问题,提出一种基于鲁棒动态逆的舰载机着舰纵向轨迹跟踪控制律设计方法,实现了将动态逆方法同H∞最优控制理论的结合。为了抑制传感器测量误差对系统的影响,本文基于H∞理论设计了H∞滤波器。同时,为生成动态逆控制器所需的高阶导数并避免计算膨胀问题,设计了指令滤波器。
仿真结果表明,按照本文方法设计的舰载无人机着舰控制系统具有良好的速度保持能力和轨迹跟踪能力,同时对传感器测量噪声和舰尾流扰动具有良好的抑制能力。将动态逆方法与基于本文所提出的控制方法设计的着舰控制系统进行仿真对比试验,验证了本文设计的控制系统具有更好的性能。通过在控制系统中加入不同扰动和噪声来进行仿真试验,发现舰尾流扰动对舰载无人机着舰的影响大于传感器噪声对其的影响。此外,本文还根据所建立的指标函数定量分析了不同条件下控制系统对基准速度和基准轨迹的跟踪精度。
| [1] |
朱齐丹, 张智, 张雯. 航母舰载机安全起飞、着舰技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2016: 1-5.
|
| [2] |
杨一栋. 舰载飞机着舰引导与控制[M]. 北京: 国防工业出版社, 2006: 13-16.
|
| [3] |
NIEWOEHNER R J, KAMINER I I. Design of an autoland controller for an F-14 aircraft using H-infinity synthesis[J]. Journal of Guidance Control & Dynamics, 2012, 19(3): 656-663. |
| [4] |
SERENA C V, FLORENTIN A B. H-Infinity design for automatic landing system[J]. International Journal of Modeling and Optimization, 2017, 7(3): 173-178. DOI:10.7763/IJMO.2017.V7.579 |
| [5] |
SHUE S P, AGARWAL R K. Design of automatic landing systems using mixed H2/H∞ control[J]. Journal of Guidance Control & Dynamics, 1999, 22(1): 103-114. |
| [6] |
金波. 无人机自主着舰纵向控制系统的研究[D]. 南昌: 南昌航空大学, 2015.
|
| [7] |
胡盛华. 基于动态逆的无人机控制律设计技术研究[D]. 南京: 南京航空航天大学, 2012.
|
| [8] |
刘畅, 芦利斌, 苗育红, 等. 基于滑模扩张干扰观测器的固定翼无人机动态逆控制[J]. 电光与控制, 2018, 25(08): 32-38. DOI:10.3969/j.issn.1671-637X.2018.08.007 |
| [9] |
杨秀霞, 高晓冬, 张毅. 基于非线性动态逆的UAV航迹鲁棒跟踪控制研究[J]. 战术导弹技术, 2018(5): 73-77. |
| [10] |
韩维, 陈志刚, 张勇, 等. 基于LESO的无人机飞行姿态动态逆控制[J]. 飞行力学, 2018, 36(1): 43-45+51. |
| [11] |
赵东宏, 李春涛, 张孝伟. 舰载无人机着舰纵向控制律设计[J]. 电光与控制, 2018, 25(8): 43-48. DOI:10.3969/j.issn.1671-637X.2018.08.009 |
| [12] |
朱齐丹, 孟雪, 张智. 基于非线性动态逆滑模的纵向着舰系统设计[J]. 系统工程与电子技术, 2014, 36(10): 2037-2042. DOI:10.3969/j.issn.1001-506X.2014.10.23 |
| [13] |
AIAA. Robust nonlinear dynamic inversion control for a hypersonic cruise vehicle[C]//Aiaa Guidance, Navigation & Control Conference & Exhibit. 2007.
|
| [14] |
Rahideh, A., Shaheed, M. H., Bajodah, A. H.. Neural network based adaptive nonlinear model inversion control of a twin rotor system in real time[P]. Cybernetic Intelligent Systems, 2008. CIS 2008.7th IEEE International Conference on, 2008.
|
| [15] |
杜金刚. 基于动态逆方法的飞行控制系统设计与仿真[D]. 西安: 西北工业大学, 2006.
|
| [16] |
杜金刚, 章卫国, 李广文, 等. 一种改善动态逆控制系统鲁棒性的方法[J]. 弹箭与制导学报. 2005, (S8): 468-469.
|
| [17] |
李林侃, 樊战旗, 杨军. 鲁棒动态逆控制在无人机姿态控制中的应用研究[J]. 弹箭与制导学报. 2008, (1): 83-85.
|
| [18] |
黄得刚, 章卫国, 邵山, 等. 舰载机自动着舰纵向控制系统设计[J]. 控制理论与应用, 2014, 31(12): 1731-1739. DOI:10.7641/CTA.2014.40682 |
| [19] |
王写. 基于H_∞滤波理论和多模型算法的机动目标跟踪研究[D]. 杭州: 浙江大学, 2016.
|
| [20] |
MIHAI L, NIKOS M E, LUCIAN G T. Automat control of the flight altitude using the dynamic inversion and the influence of wind shears and sensors' errors on the aircrafts' landing process[C]. Proceedings of the 13th WSEAS international conference on mathematical methods, computational techniques and intelligent systems.
|
 2020, Vol. 42
2020, Vol. 42
