2. 郑州航空工业管理学院 电子通信工程学院,河南 郑州 450046;
3. 北京航空航天大学 航空科学与工程学院,北京 100191
2. School of Electronics and Communication Engineering, Zhengzhou University of Aeronautics, Zhengzhou 450046, China;
3. School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China
随着探测器的快速发展和技术更新,在距离、精度、视域等性能上均获得了较大提升,对飞行器、舰船、装甲车辆等的低可探测性即隐身性能提出了更高要求,以提高武器系统的战场生存能力[1 – 4]。隐身技术针对雷达、红外、可见光、声等信号,采用技术手段,以降低目标如飞行器、舰船等的信号大小[3]。
从可探测角度来说,水面舰船面临的威胁来自于水面、空中甚至水下,即舰船、飞行器、潜艇等,探测信号包含雷达(电磁波)、声、红外、磁等信号。依据实际任务需求,不同的雷达工作频率有所不同,以舰载雷达为例,用于探测、跟踪、识别等作用的雷达频率主要为L、S、C、X波段,这一波段也同时包含了较多的机载雷达。
为降低舰船的雷达散射截面,采用多种措施的舰船隐身化是其重要途径[1, 5],就当前现状来看,与飞行器电磁隐身技术类似,舰船隐身也可以通过外形隐身改进或设计、吸波材料等技术来实现。舰船舰载雷达、天线本身是较大电磁散射源[6 – 8],在雷达技术提高基础上,经过频率选择表面技术(Frequency Selective Surface,FSS)[9-10]的模块化处理,可有效降低其电磁散射信号,同时也为采用外形隐身技术改进提供了可能。当前主要对舰船上层建筑结构、桅杆等局部部件的隐身特性及技术进行详细研究,但从舰船总体出发来对比研究舰船外形隐身技术文献较少,也缺乏相关散射特性影响和规律结果。
本文从舰船面临的主要威胁频段(L,S,C,X)出发,以2种不同外形布局的舰船为研究对象,采用物理光学法,数值计算了2种舰船电磁模型的不同入射角、不同角域的RCS(Radar Cross Section)[11 – 12]曲线,以分析外形隐身改进措施对舰船电磁散射特性的影响特性,重点研究了外形隐身的多频散射特性、不同角域电磁散射变化特点,对提高舰船电磁隐身性能及生存力有重要影响意义。
1 舰船电磁模型为研究外形隐身改进措施对舰船电磁散射特性的影响,分别以英国45型驱逐舰[5]、美国DDG1000驱逐舰为基础,建立2种舰船的电磁数值计算模型。45型、DDG1000均采用模块式雷达、天线整合方式,与常规水面战舰相比,其上层建筑、舰桥、桅杆等进行了大量集成化处理与改进,有效降低了舰船表面的散射结构,提高了隐身性能。但相对来讲,美国隐身驱逐舰DDG1000全面采用隐身技术,船体设计新颖,表现出优秀的隐身特性,本文分别以这2种实际舰船为基础模型,研究外形隐身对舰船电磁散射特性影响规律。
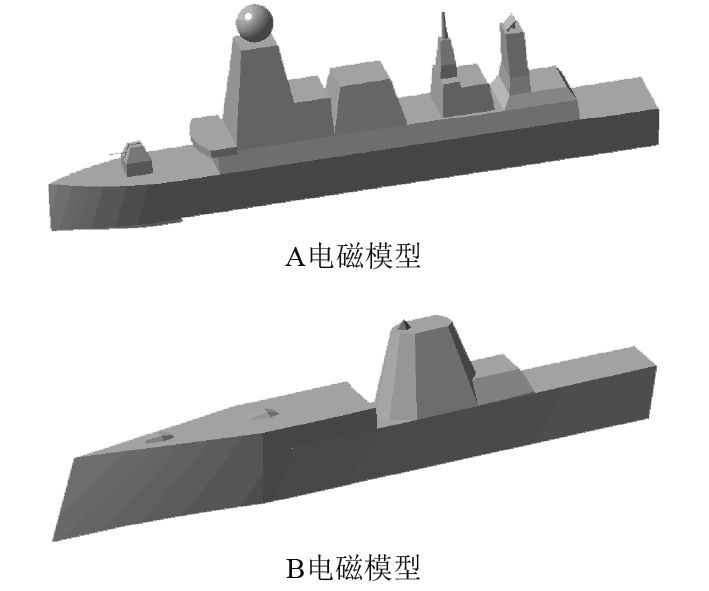
通过调整舰船船体、上层建筑结构的面元方向,模块化设计散射结构,可将电磁散射幅值、方向等进行有针对性的控制,提高隐身性能。基于以上考虑,分别将以上2种舰船电磁模型分别定义为电磁模型A(Type45)和B(DDG1000),为消除几何尺寸带来的影响,A、B模型舰船典型几何尺寸尽量一致,A电磁模型基本参数为船长151.9 m、船宽21.1 m、高42.0 m,B电磁模型基本参数为船长143.8 m、船宽24.3 m、高34.0 m。2种电磁模型如图1所示。
|
图 1 2种舰船电磁计算模型 Fig. 1 Electromagnetic computation models of ships |
以图1舰船电磁模型为研究对象,结合水面舰艇实际威胁探测手段,为对比研究外形隐身改进措施的电磁散射特性影响,入射电磁波频率分别为(0.5,1、3,6,10)GHz,涵盖L,S,C,X探测波段,电磁波入射角(对舰船来说可以理解为方位角)范围为0°~360°,计算仰角分别为:–15°,–10°,–5°,0°,5°,10°,15°。
研究过程中,定义舰船头向30°角域(记为H-30)为舰船正头向左右各15°电磁波入射角范围,相应的可定义头向60°角度(记为H-60)、侧向60°角域(记为S-60)、后向30°角域(记为T-30)、周向360°角域(记为W-360),以对应角域内RCS算术均值为分析依据,研究其波峰幅值变化关系及该角域内的隐身特性。
2 RCS计算方法及精度验证从电尺寸角度来讲,在研究频率内,大于240(0.5 GHz),处于典型的高频散射区域,文中的电磁模型可视为金属目标,可采用金属目标RCS计算方法[13-14]。一般的,RCS数值方法从频率角度来看分为低频和高频计算方法,低频方法如基于矩量法(Method of Moments,MoM)[12]的多层快速多极子算法(Multilevel Fast Multipole Algorithm,MLFMA)[13]、时域有限差分法等,对本文电大尺寸目标来说,占用内存较大,计算速度慢,严重影响分析效率;而高频算法如物理光学法(Physical Optics,PO)、等效电流方法、物理绕射方法等,具有较高的计算效率,同时在高频区可得到满意的计算精度,可用于分析本文的电大尺寸舰船电磁模型。
严格来讲,PO方法基于Stratton-Chu积分方程,与MLFMA[13, 14]基本方程一致,区别于MLFMA,PO方法仅考虑面元自身耦合作用,而将目标各部分之间的耦合作用忽略,以提高电大尺寸目标RCS求解效率,而本文研究目标表面光滑,局部结构之间的影响可略去,适合采用PO方法计算。采用切平面近似,得到面元上的RCS平方根为:
| $\sqrt \sigma = - {j}\frac{k}{{\sqrt {\text{π}} }}\int_{{S_1}} {\widehat n \cdot } \left({\widehat e_r} \times {\widehat h_i}\right)\exp \left[jkr\left(\widehat i - \widehat s\right)\right]{\rm d}S{\text{。}}$ | (1) |
基于目标网格划分,对所有散射面元求和,按相位叠加得到:
| $\sigma = \left| {\sum\limits_i^{} {\sqrt {{\sigma _i}} } } \right|{\text{。}}$ | (2) |
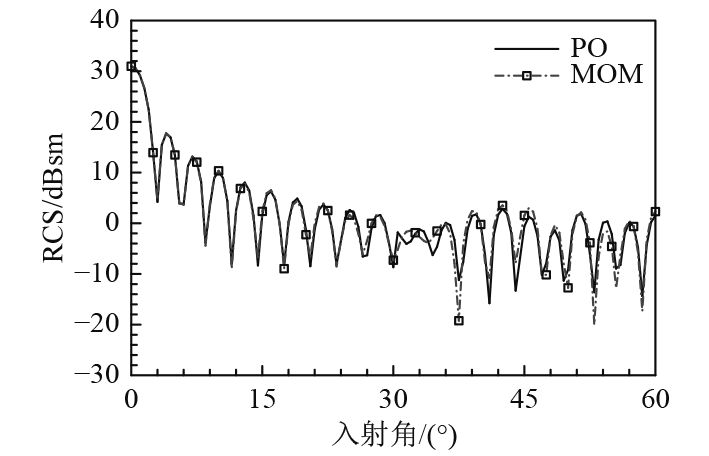
为验证本文采用的PO方法数值结果正确性,以边长为1 m的等边三角形金属柱为计算分析对象,入射电磁波波长0.1 m,俯仰角0°。分别采用PO和高精度MOM方法计算,RCS曲线对比结果见图2,由于为等边三角形,仅计算了0°~60°角域范围。
|
图 2 金属柱RCS计算对比曲线 Fig. 2 RCS comparison curves of metal pillar |
由图2可以看出,2种方法RCS计算曲线基本一致,0°~60°角域算术均值分别为0.819 0,0.894 4 dBsm,误差为0.075 4 dB,说明本文PO方法有足够好的计算精度,可满足本文研究对象和计算频率。
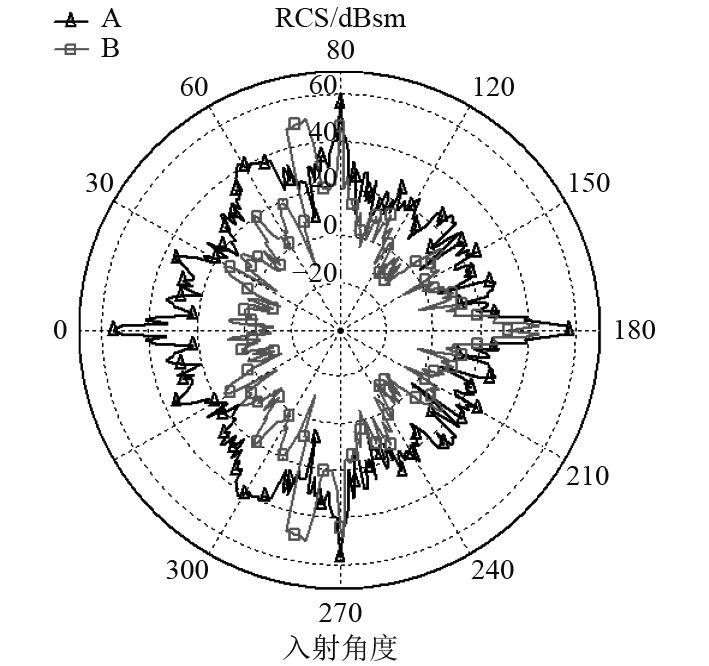
3 舰船模型电磁散射特性 3.1 RCS曲线分布特性对A,B两种电磁模型,分别研究0°俯仰角下的RCS散射曲线分布特点,入射频率0.5 GHz时的RCS曲线如图3所示。
|
图 3 两舰船模型RCS计算对比(0.5 GHz) Fig. 3 RCS Comparison of 2 ship models (0.5 GHz) |
入射频率为0.5 GHz时,对2种电磁模型,依然处于高频区(A,B模型电尺寸分别为253,240)。由图3可以看出,RCS分布形式与舰船外形有较大关系,对舰船A电磁模型,前向30°角域有一较大波峰,为船体前端、上层建筑在前向接近镜面散射叠加,同时该波峰较宽,除0°左右尖锐散射波峰外,在前向60°角域也表现为较强较宽的散射波峰。前向左右60°和90°附近的波峰是船体上层建筑侧向及相应模块综合散射效果。同时,其后向也存在一波峰,为船体后端面、上层建筑在此方向的各部件耦合效果。
对B舰船模型,由于在船体、上层建筑采用了外形隐身处理技术,并综合考虑平台模块化,其对应前向30°、60°角域的前向峰值获得极大降低,证明了外形隐身的有效性。在前向左右60°方位角附近的峰值向侧向移动,进一步提高了前向大范围的隐身性能,侧向、后向2个波峰为船体和上层建筑对应截面的镜面散射,而外形隐身在后部其他角域也有一定贡献。此外,从周向RCS曲线分布来看,除侧向和后向波峰变化较小外,采外形隐身改进措施的B舰船模型在其他角域内的RCS向内收缩,提高了隐身性能。
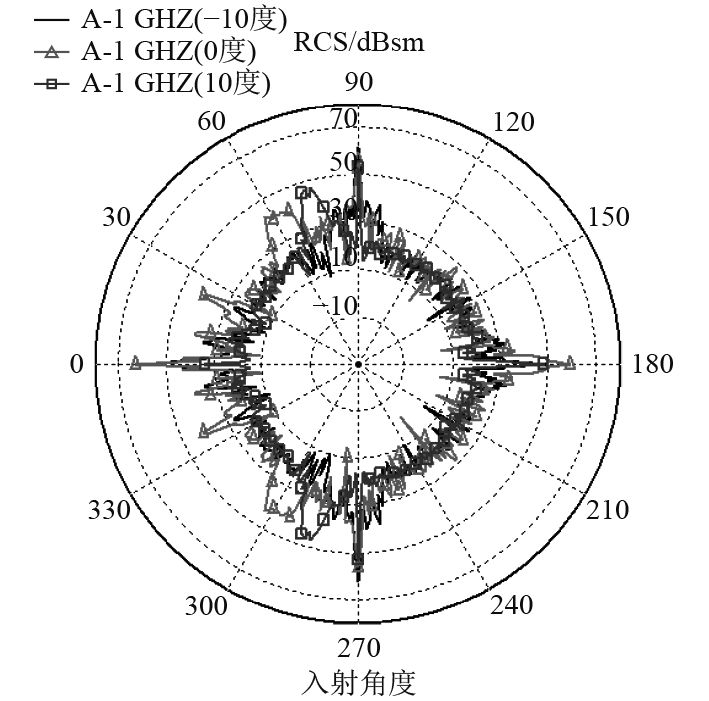
3.2 RCS曲线俯仰角特性由于A,B模型电磁散射特性类似,因此在讨论RCS曲线俯仰角和频率特性时,分别以A和B模型为对象研究,同时,选择了典型状态曲线进行分析,俯仰角选择–10°,0°,10°,频率为0.5,3,10 GHz。图4为A模型1 GHz下不同俯仰角的RCS曲线对比。
|
图 4 A模型不同俯仰角RCS计算曲线 Fig. 4 RCS curves in different pitch angles of model A |
舰船在执行任务过程中,将面临来自水面、水下和空中探测器、武器系统的威胁,可以俯仰角和方位角来分析期影响。由图4可以看出,俯仰角的变化会对RCS曲线分布形式产生影响,–10°和10°时,前向30°,60°角域的RCS峰值有较大降低,分析原因是在0°入射时,舰船和上层建筑的电磁散射为镜面散射叠加,而有迎角时船体表面、结构等为非镜面散射,将明显降低电磁散射强度;后向波峰变化趋势及原因与前向类似,但正侧向变化不大,这是因为迎角的变化不会引起侧向镜面散射机理的变化。同时,迎角为正时,即电磁波由水面上方入射至舰船,在前向60°方位角左右有一散射波峰,该波峰随着迎角增大而后移,这一特性可提高其隐身性能。
3.3 RCS曲线频率特性B模型0°俯仰角时多频RCS曲线如图5所示。
|
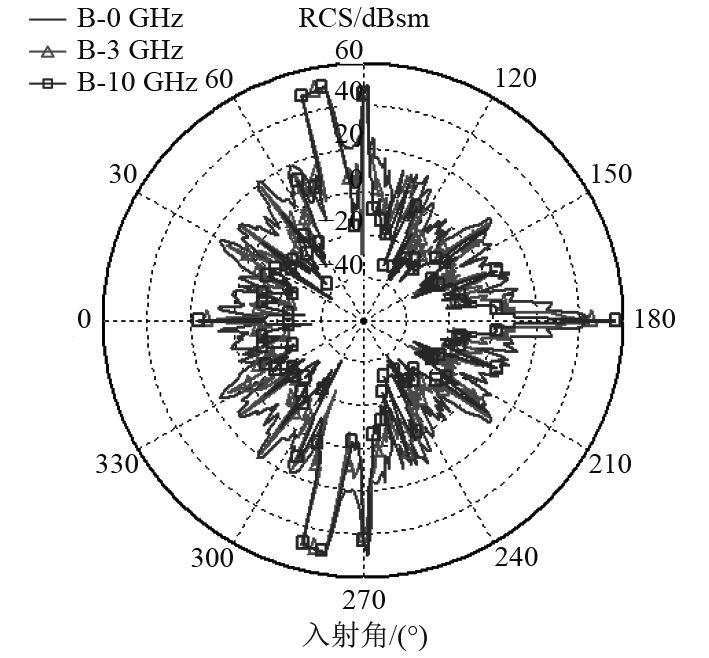
图 5 B模型多频RCS计算曲线 Fig. 5 RCS curves with different frequencies of model B |
可以看出,电磁波入射频率变化时,不会引起RCS曲线分布形式的较大变化,但会对RCS幅值和震荡趋势有一定影响。频率由0.5增至10 GHz时,表现在2个方面,一是曲线震荡更加明显,波峰变窄;二是散射曲线内陷,即RCS曲线幅值降低。就曲线震荡趋势来看,主要集中在舰船前向和后向一定角域,说明频率高时,舰船各部件或各部分的散射叠加较为明显,震荡加剧但振幅变小,而侧向角域的2个波峰变化较小;同时,前向和后向波峰变得更为尖锐。与上类似,除侧向角域外,前向和后向角域的RCS幅值随频率增加而减小。
4 外形隐身改进散射影响分析 4.1 外形隐身电磁散射影响分析方法从当前舰船技术发展来看,外形隐身及改进是降低其重点威胁角域RCS的重要技术方法,首先,结合RCS计算曲线分布特点,通过2个模型RCS曲线对比,从波峰大小、位置等与舰船外形结构的关系及变化特点,来研究外形隐身改进的影响性能。
其次,基于2种舰船电磁计算模型,在重点威胁角域内,以外形隐身前后2种电磁模型为目标,以二者多个角域内RCS算术均值及算术均值差异来研究外形隐身措施带来的电磁散射特性影响。
定义2种舰船电磁模型RCS相对增值为:
| $ G = {\sigma _{{A}}} - {\sigma _{{B}}}{\text{。}} $ | (3) |
其中:σA,σB分别为A,B电磁模型在相应威胁研究角域内的RCS算术均值;G为RCS相对增值,dB。如该值大于0,则说明外形隐身有效,值越大,隐身效果越明显。
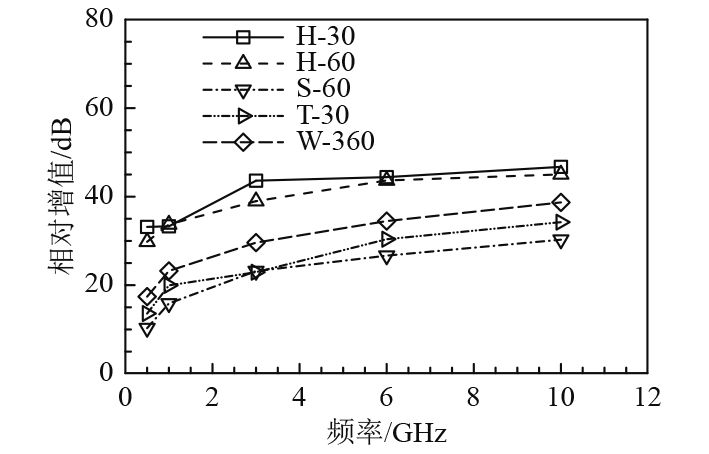
4.2 电磁散射特性影响分析水面舰船在执行巡航、侦察、作战任务时,面临各种武器平台的威胁,表现为不同角域、不同频率下电磁波探测、识别、跟踪等,基于上述RCS相对增值,从不同频率、不同角域的变化情况进行分析。重点关注舰船头向、尾向及周向各角域内的RCS幅值大小,可采用算术均值表示。不同角域内RCS相对增值随频率变化的响应曲线(俯仰角0°)见图6,随俯仰角变化的响应曲线(入射频率1 GHz)见图7。值得一提的是,如前所述,相对增值越大,说明对应角域内的外形隐身改进的效果越好,如该值接近或小于0,则无隐身改进效果。
|
图 6 不同角域RCS相对增值频率响应曲线(俯仰角0°) Fig. 6 Curves of RCS relative values with different frequencies in different angular domains (with pitch angle of 0°) |
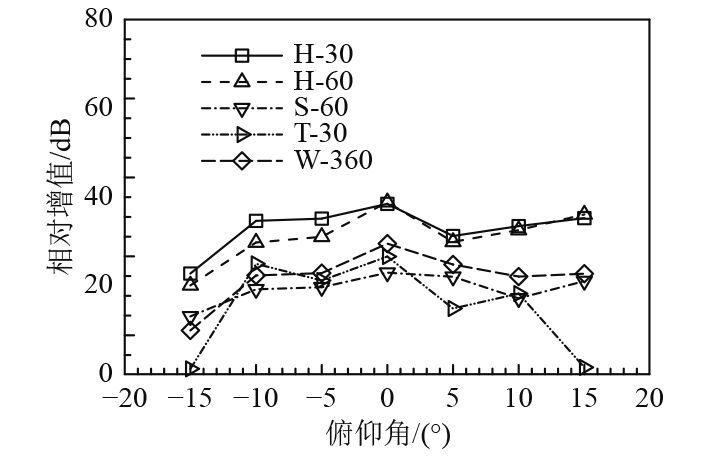
|
图 7 不同角域RCS相对增值俯仰角响应曲线(1 GHz) Fig. 7 Curves of RCS relative values with different pitch angles in different angular domains (with frequency of 1 GHz) |
由图6可以看出,频率由0.5 GHz提高至10 GHz时,各角域内的相对增值均有所增加,说明通过对船体和上层建筑的外形隐身改进,可有效提高舰船隐身性能。图6也表明,外形隐身在舰船各角域上的影响各异,前向30°和60°角域RCS相对增值最高,之后依次为周向、后向30°角域、侧向60°角域;前向相对增值较大(10 GHz时前向30°角域达46.734 0 dB),是由于通过舰船结构修形,前向的镜面散射或接近镜面散射的船体结构倾斜或融合过渡后,有效降低了前向峰值;而侧向,主要受限于船体、舰桥、隐身桅杆等上层建筑侧向镜面散射的影响,导致外形隐身效果较差;后向角域相对增值变化规律及产生机理与前向类似。
图7相对增值曲线表明,俯仰角变化时,相对增值在俯仰角较低时较大,此时也是外形隐身设计的主要研究和改进状态,通过外形设计,将镜面散射波峰外移,减低前向波峰大小,甚至使其消失,而当俯仰角增大(正向或负向)时,采用外形隐身技术的一些结构模块表面的散射将会逐渐增加,从而降低外形隐身效果,表现为相对增值俯仰角0°附近时较大(前向30°为33.301 3 dB),两端减小。此外,与频率效应相似,各不同角域的俯仰角效应有一定区别,依然表现为前向30°和60°角域,RCS相对增值较大,其他角域较小,后向30°角域在±15°迎角时隐身改进效果消失。
5 结 语针对2种舰船模型,采用物理光学法计算分析了不同频率、不同俯仰角下的电磁散射特性,并进行对比性研究,得出以下结论:
1)舰船RCS曲线分布特性:曲线波峰及其分布特性与舰船外形结构特点有直接关系,A电磁模型沿周向对称分布有强弱散射波峰6个,B模型5个波峰,不存在前向波峰,有较好隐身性,2个模型各波峰分别对应舰船船体和上层建筑重要部件散射,头向波峰是镜面散射的综合影响。
2)RCS曲线分布的俯仰角和频率特性:俯仰角变化会引起散射波峰的幅值和位置变化;频率增加时,曲线震荡性增加,RCS减小,但不影响分布特性。
3)外形隐身改进影响特性:采用基于RCS算术均值的相对增值来分析,频率增加时,各角域相对增值均有所增加,10 GHz前向30°角域可达46.734 0 dB;–15°~15°俯仰角变化时,相对增值震荡变化,0°时最大,为33.301 3 dB。外形隐身改进主要表现在前向角域,频率和俯仰角变化时,该部分角域相对增值最大。
| [1] |
向迎春, 曲长文, 李炳荣, 等. 基于舰船雷达散射特性的对消隐身仿真研究[J]. 系统仿真学报, 2013, 25(1): 104-110. |
| [2] |
刘战合, 姬金祖, 王菁, 等. 飞行器表面规律分布的电磁缺陷散射机理[J]. 系统工程与电子技术, 2017, 39(11): 2428-2433. DOI:10.3969/j.issn.1001-506X.2017.11.06 |
| [3] |
余定峰, 耿攀, 徐正喜, 等. 基于电磁建模的舰船雷达波隐身技. 术[J]. 舰船科学技术, 2014, 36(11): 80-85. DOI:10.3404/j.issn.1672-7649.2014.11.016 |
| [4] |
刘战合, 王菁, 王晓璐, 等. 铌掺杂ITO镀膜玻璃电磁散射特性试验[J]. 航空工程进展, 2018, 9(1): 62-68. |
| [5] |
杜晓佳, 杨飏, 洪明. 英国45型驱逐舰桅杆的隐身性能分析[J]. 舰船科学技术, 2012, 34(11): 165-170. DOI:10.3404/j.issn.1672-7649.2012.11.038 |
| [6] |
杜晓佳, 崔俊伟, 杨飏, 等. 桅杆雷达承载平台隐身性能分析[J]. 舰船科学技术, 2015, 37(1): 102-106. DOI:10.3404/j.issn.1672-7649.2015.01.021 |
| [7] |
杨飏, 杜晓佳, 洪明. 舰船封闭式桅杆雷达隐身优化分析[J]. 大连理工大学学报, 2013, 53(3): 390-396. |
| [8] |
程子君, 吴启华. 隐身桅杆与主船体耦合RCS特性研究[J]. 中国舰船研究, 2011, 6(3): 45-48. DOI:10.3969/j.issn.1673-3185.2011.03.010 |
| [9] |
NAGENDRA Kushwaha, RAJ Kumar. Design of a wideband high gain antenna using FSS for circularly polarized applications[J]. International Journal of Electronics and Communications, 2016, 70(9): 1156-1163. DOI:10.1016/j.aeue.2016.05.013 |
| [10] |
SHIV Narayan, BALASUBRAMANIYAM Sangeetha, THATTANVALAPPIL Vasu Sruthi, et al. Design of low observable antenna using active hybrid-element FSS structure for stealth applications[J]. International Journal of Electronics and Communications., 2017, 80(10): 137-143. |
| [11] |
王仲根, 孙玉发, 王国华, 等. 应用通用特征基函数求解目标宽带雷达散射截面[J]. 电波科学学报, 2015, 30(1): 91-96. |
| [12] |
JI J Z, HUANG P L. Series expansion feasibility of singular integral in method of moments[J]. Journal of Systems Engineering and Electronics, 2014, 25(3): 386-392. DOI:10.1109/JSEE.2014.00044 |
| [13] |
LIU Z H, HUANG P L, GAO X, et al. Multi-frequency RCS reduction characteristics of shape stealth with MLFMA with improved MMN[J]. Chinese Journal of Aeronautics, 2010, 23(3): 327-333. DOI:10.1016/S1000-9361(09)60223-5 |
| [14] |
ERGUL O. Fast and accurate solutions of electromagnetics problems involving lossy dielectric objects with the multilevel fast multipole algorithm[J]. Engineering Analysis with Boundary Elements, 2012, 36(4): 423-432. |
 2020, Vol. 42
2020, Vol. 42
