船舶作为重要的水上交通运输工具,无论是在民用领域还是军事领域都具有不可代替的地位和作用。而船舶螺旋桨作为船舶前进的动力源,其工作条件恶劣,受力复杂。在航行中往往因碰到水上漂浮物、发生搁浅或缠到缆绳导致螺旋桨意外事故发生,从而导致螺旋桨发生变形、折断等故障。
近年来,随着船舶大型化和船舶主机功率的提高,螺旋桨折断事故日益增多。Puris-taylor船舶螺旋桨研究所对螺旋桨断桨故障做了大量的研究工作,除工作中碰上水上漂浮物和搁浅等意外事故造成桨叶折断外,桨叶的断裂主要与材料性能、设计结构、铸件质量等因素有关,常见的有腐蚀疲劳引起螺旋桨桨叶断裂、材料特性引起桨叶断裂、螺旋桨的结构参数不合理引起的桨叶断裂等。螺旋桨的断裂将影响整个推进轴系的正常工作,因此对螺旋桨的状态监测和故障诊断尤为重要。但受螺旋桨水下工作条件的限制,监测难度较大。传统做法通常对螺旋桨进行定期检查来保证船舶的安全航行,但不能在船舶航行过程中及时发现问题。孟昭玉[1]通过对螺旋桨轴油液的性能检测、油液光谱分析等油液检测技术,实现了对螺旋桨轴的故障诊断与分析。黄辉等[2]提出了一种通过分析推进电机定子电流的异常,对电力推进系统的螺旋桨进行故障诊断。本文提出利用数值模拟法来获取螺旋桨压力监测点在不同故障工况下的时域波形和频域波形,从而实现对螺旋桨桨叶折断故障的监测和诊断。不但可以缩短实船试验时间,而且对螺旋桨故障诊断试验具有指导作用。
1 数值模型和计算方法 1.1 控制方程和湍流模型[3]假定螺旋桨所在流场中流体是不可压缩的,流体的连续方程和动量方程分别为:
| $\frac{{\partial {\mu _i}}}{{\partial {x_i}}} = 0 \text{,}$ | (1) |
| $\rho \frac{{\partial \left( {{\mu _i}{\mu _j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_j}}} + \rho {g_i} + \rho \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {\mu _i}}}{{\partial {x_j}}} + \frac{{\partial {\mu _j}}}{{\partial {\mu _i}}}} \right) - \overline {\mu _i'\mu _j'} } \right]\text{。}$ | (2) |
式中:
| $\frac{{\partial \left( {\rho {\rm{k}}} \right)}}{{\partial {\rm{t}}}} + \frac{{\partial \left( {\rho k{\mu _i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial x}}\left[ {\left( {\mu + \frac{{{\mu _i}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon \text{,}$ | (3) |
| $\frac{{\partial \left( {\rho {\rm{\varepsilon }}} \right)}}{{\partial {\rm{t}}}} \!\!+\!\! \frac{{\partial \left( {\rho \varepsilon {\mu _i}} \right)}}{{\partial {x_i}}} \!=\! \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu \!+\! \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \epsilon }}{{\partial {x_j}}}} \right] \!+\! \rho {C_1}E\epsilon \!-\! \rho {C_2}\frac{{{\epsilon ^2}}}{{k \!+\! \sqrt {\nu \epsilon } }}\text{。}$ | (4) |
Realizable k-
本文以上海海事大学教学实习船“育明轮”的定距螺旋桨为研究对象,进行均匀流体中螺旋桨非定常水动力性能的模拟。螺旋桨模型参数如表1所示。
|
|
表 1 螺旋桨模型参数 Tab.1 Parameters of propeller model |
图1(a)是桨叶正常工作时螺旋桨几何模型。为了模拟螺旋桨桨叶折断的流体特性,采用UG软件中的修剪体对其中的一片桨叶进行折断处理,折断位置分别在0.9R,0.8R,0.7R,0.6R处,图1(b)是螺旋桨桨叶折断位置模型。通过STAR-CCM+中的替换零件功能将折断的叶片替换正常工作的叶片,快速建立折断工况下的CFD计算模型进行计算,并作对比分析。
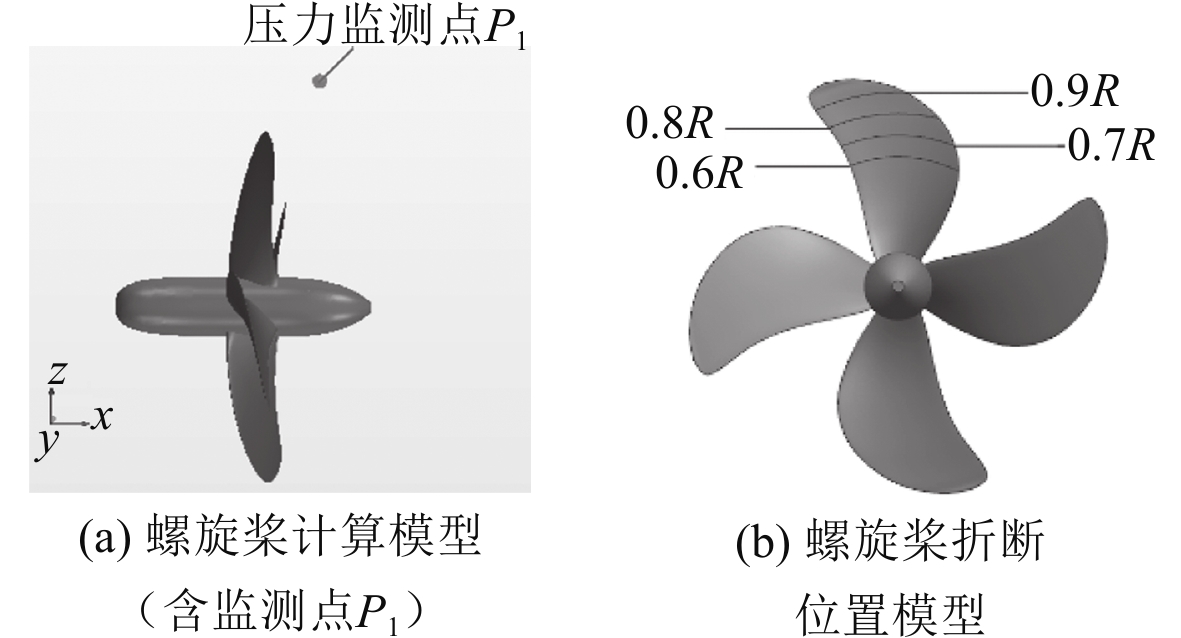
|
图 1 螺旋桨模型 Fig. 1 Propeller model |
在CFD计算时选取船体表面一个监测点P1(0.035, 0, 0.12)对螺旋桨的脉动压力进行监测,如图1所示,达到模拟传感器压力信号采集的目的。采用局部区域压力最大法来提取该监测点处压力变化值,时间步长设为0.000 5 s。通过实时记录该监测点的压力变化,以此来替代实际监测的压力传感器,从而获取螺旋桨在发生折断故障的工况下的脉动压力参数变化,同时对螺旋桨侧向力FY进行监控计算,获取侧向力FY与时间的变化关系曲线。为了便于分析,对螺旋桨侧向力进行无因次化处理,得到螺旋桨侧向力系数KFY,同时将时间转化为对应的螺旋桨旋转的周向角α。
1.3 螺旋桨故障分析方法本文用数值模拟的方法对螺旋桨进行桨叶折断故障监测与分析,重点在于流体压力信号的提取和处理,对比分析正常工况和折断情况下的时域波形图和频谱图,得到桨叶不同折断位置和磨损量等故障信息,进而提出一种基于流体特性分析的船舶螺旋桨桨叶折断故障诊断方法,对螺旋桨的改进和设计具有重要的指导意义。故障诊断流程如图2所示[4-5]。
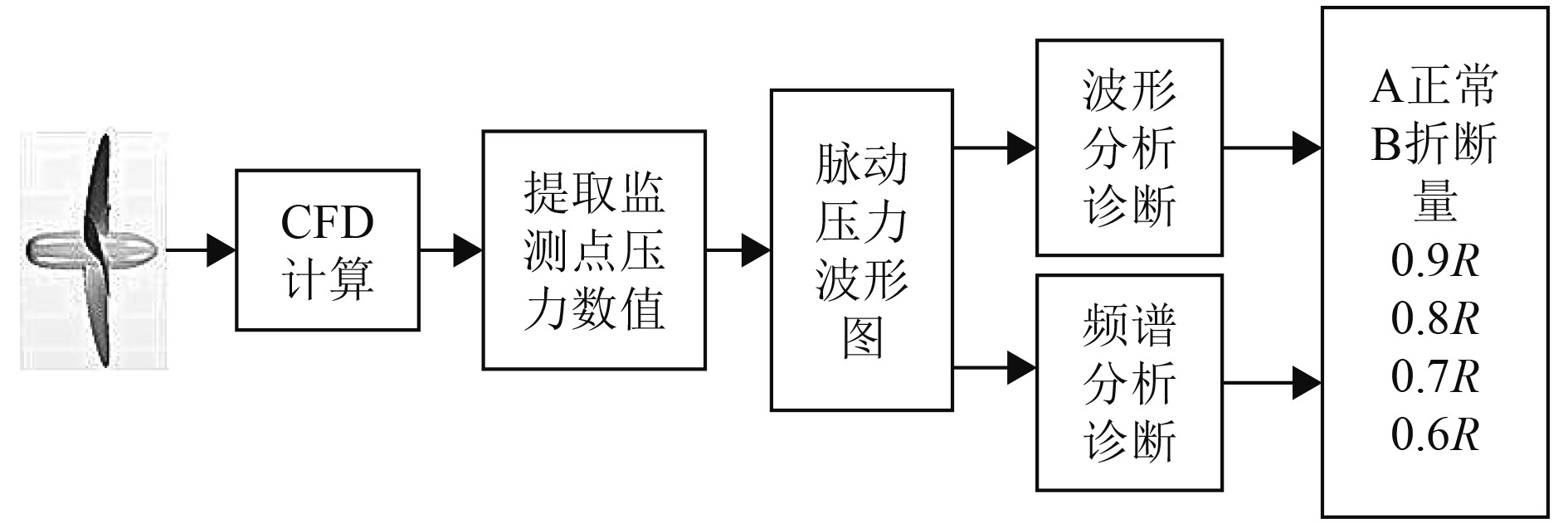
|
图 2 基于CFD的螺旋桨桨叶折断故障诊断流程图 Fig. 2 Flow chart of propeller blade breaking fault diagnosis based on CFD |
为实现均匀流体来流下螺旋桨的非定常瞬态模拟计算,采用滑移网格技术[6],从而得到螺旋桨瞬态流场压力分布,建立的模拟计算域如图3所示。整个计算域网格划分为2部分:一部分随螺旋桨同步旋转来模拟螺旋桨的旋转,即旋转域,采用四面体网格,如图4(a)所示;另一部分模拟螺旋桨旋转所处的流场,即静止域,采用切割体网格,如图4(b)所示。两部分区域均采用与螺旋桨同轴的圆柱流域,且都有各自的独立网格形式,两部分区域边界面的组合定义为交界面,静止域和旋转域以交界面实现相互滑动,从而完成两区域网格间的数据交换来保证其守恒。整个计算域边界条件由速度入口、压力出口、旋转域、静止域及旋转域和静止域的交界面组成。由于不考虑空泡现象,在CFD的计算中,螺旋桨表面设置为无滑移壁面条件,螺旋桨的转速n设定为1 500 r/min,速度入口给定来流速度,来流的参考压力设定为0,压力出口的静压力值设定为0,时间步长0.000 5s 。
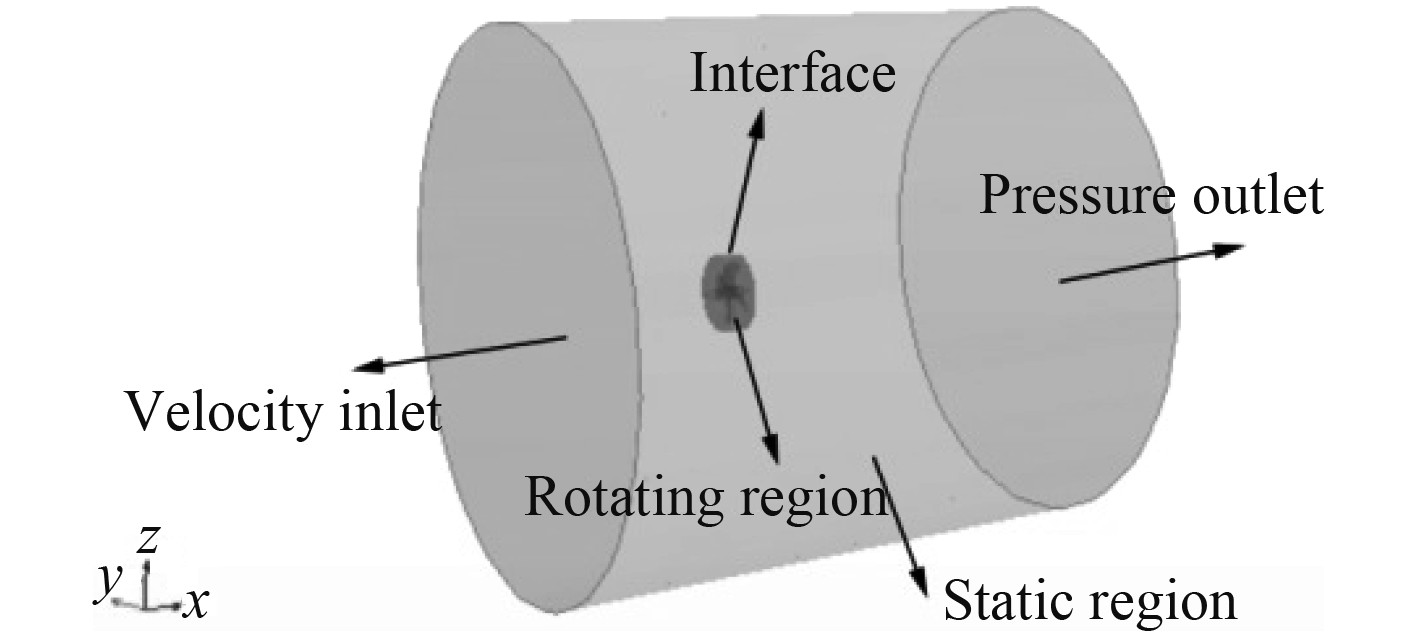
|
图 3 计算域边界条件设置 Fig. 3 Calculate domain boundary condition settings |

|
图 4 螺旋桨计算域 Fig. 4 Propeller calculation domain |
由于要保证雷诺数相同,根据雷诺数的定义
|
|
表 2 不同进速系数下螺旋桨特征参数 Tab.2 Characteristic parameters of propeller under different propulsion coefficients |
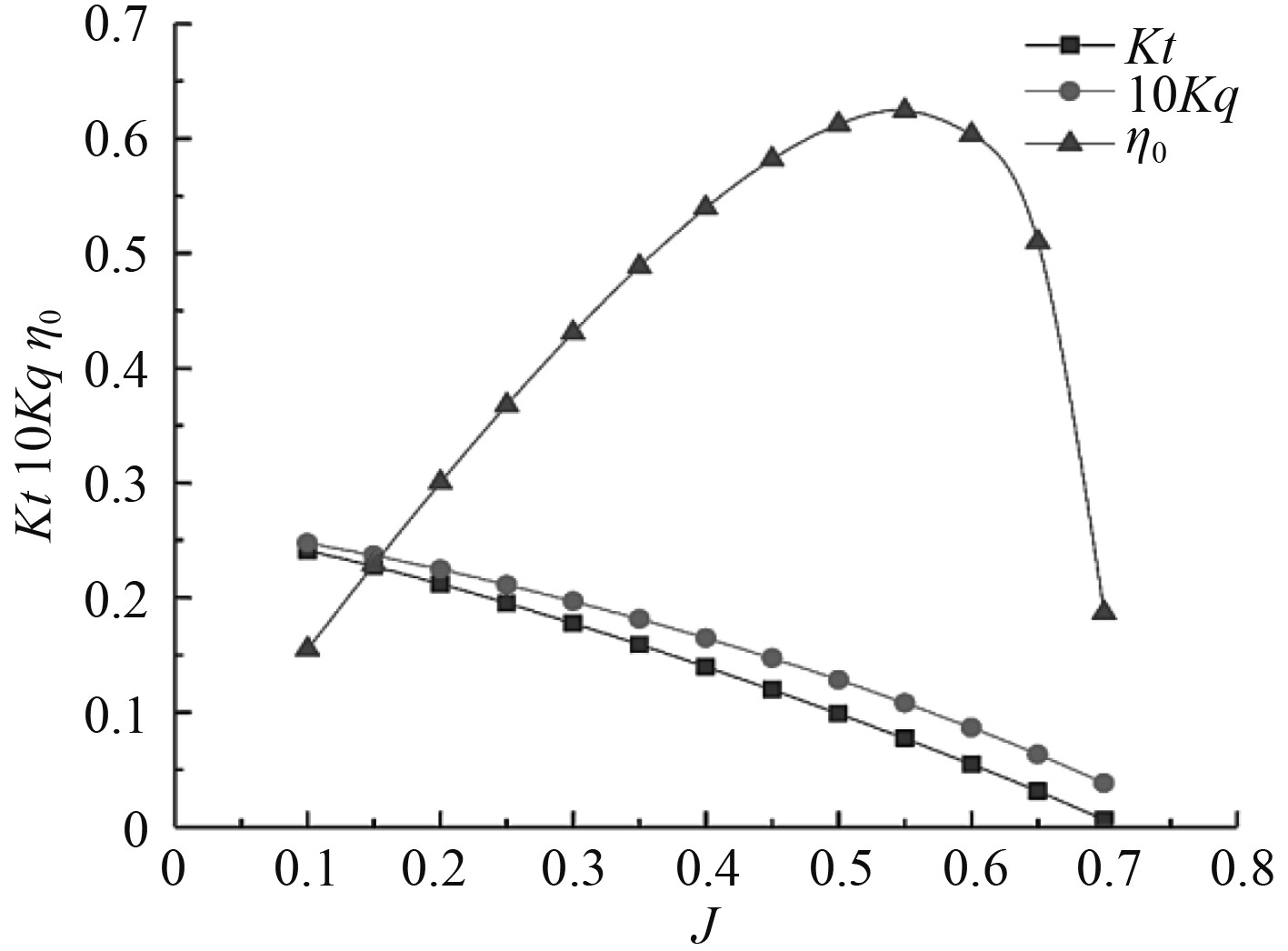
|
图 5 螺旋桨模型敞水性征曲线 Fig. 5 Propeller model open water performance curves |
通过对螺旋桨表面的压力分布分析,可以更加细致地研究流场中螺旋桨的受力情况。在进速系数J=0.45时,螺旋桨不同折断工况下的叶面叶背压力分布云图如图6所示。通过分析得出:1)由于叶片流动阻力的存在,叶面和叶背导边和随边处压力较大。而叶梢部分应力较小,说明导边和随边压力主要受来流流体阻力影响,叶片根部应力主要受叶片轴向推力影响。2)螺旋桨某1桨桨叶折断后,对桨叶压力表面压力的分布影响不大。
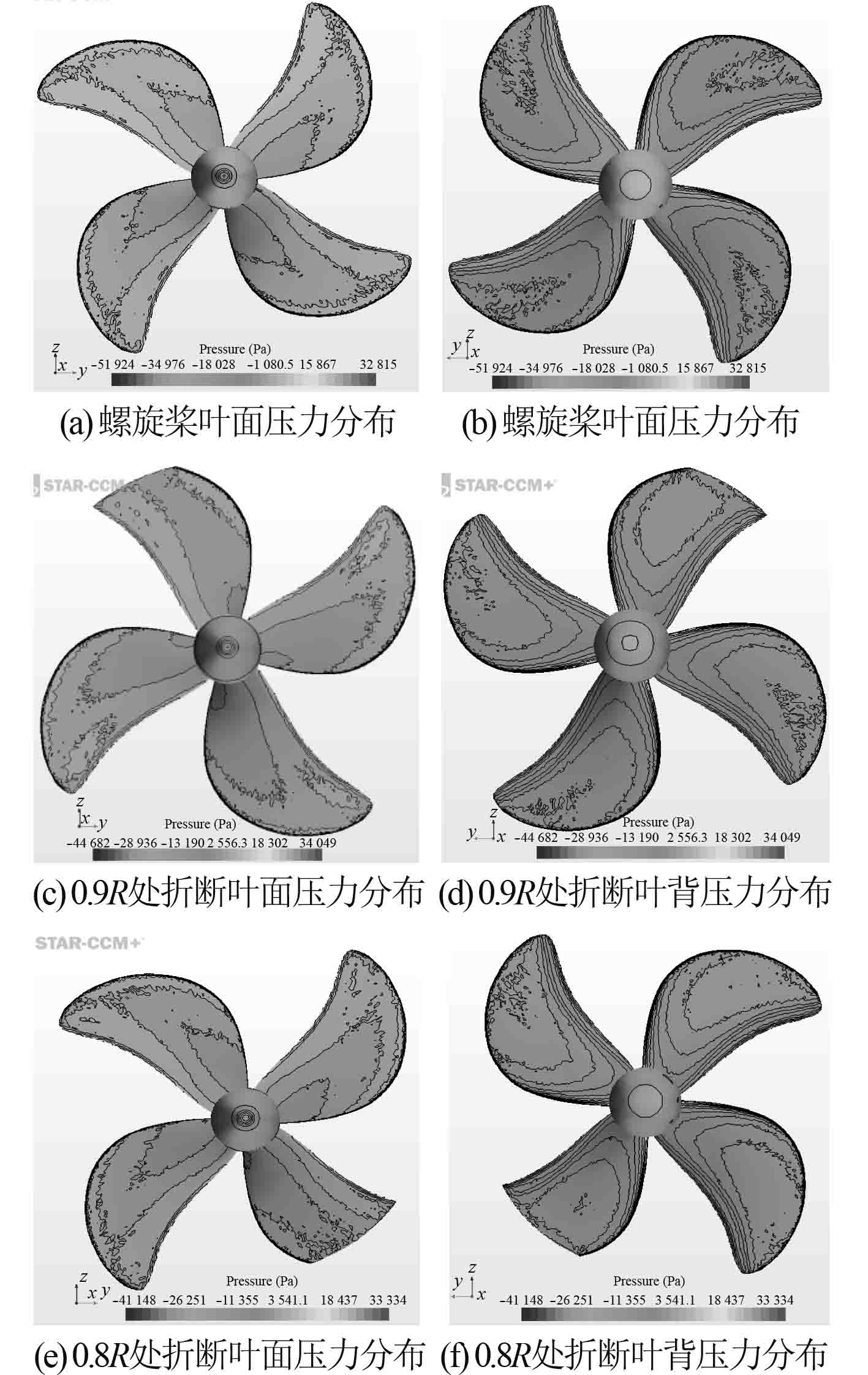
|
图 6 桨叶压力分布云图 Fig. 6 Nephogram of blade pressure distribution |
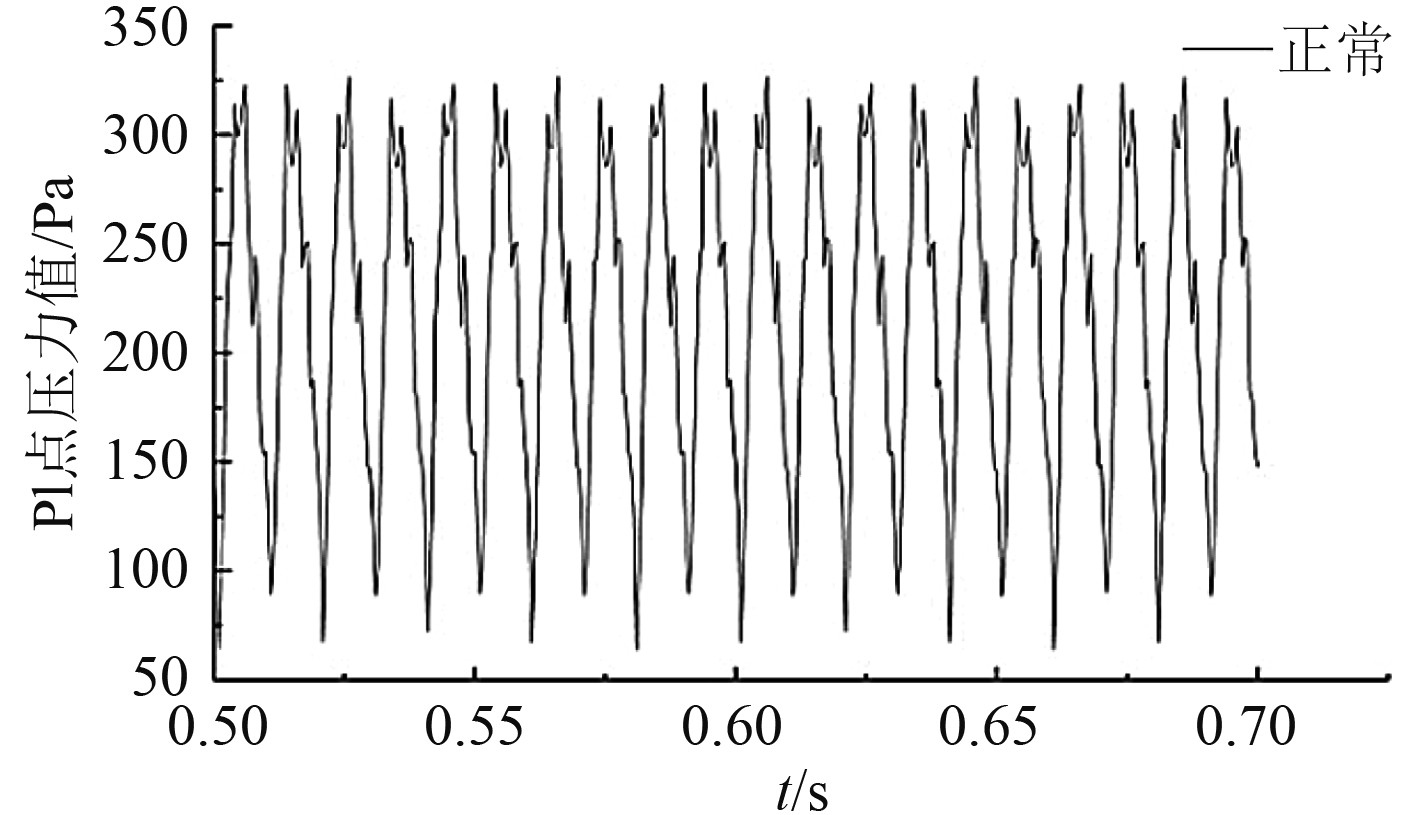
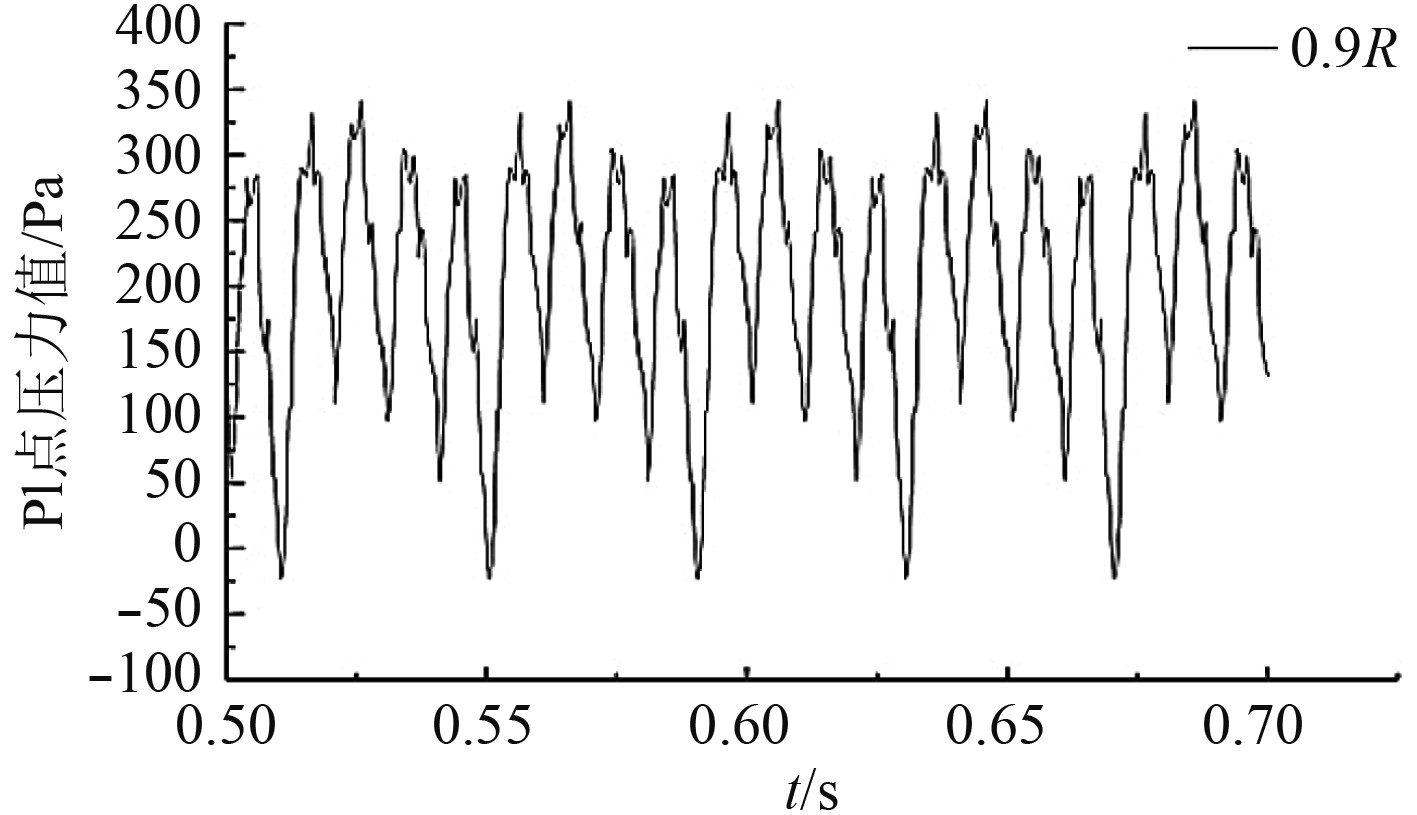
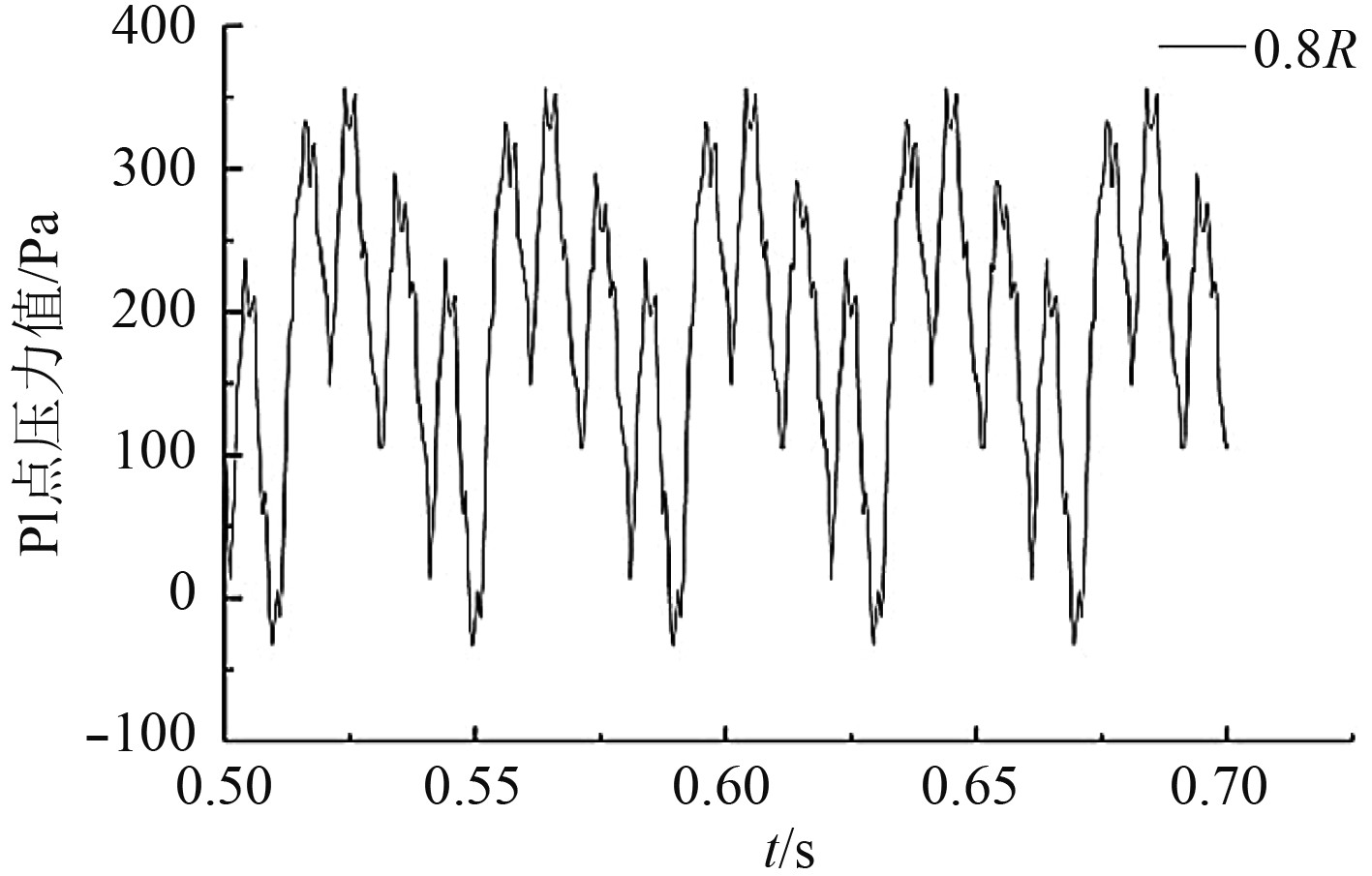
在对螺旋桨模型进行三维非定常水动力计算中,分别提取正常工作状态和桨叶折断下的螺旋桨监测点P1处脉动压力信号和水动力侧向力信号,对脉动压力图进行FFT变换,对水动力侧向力Fy进行无因次处理得到水动力侧向力系数KFy。螺旋桨监测点P1处脉动压力数值模拟结果如图7 ~ 图11所示,对应的频谱图如图12 ~ 图16所示。分析发现,监测点P1处压力及侧向力都出现了规律性变化。
|
图 7 螺旋桨正常工作时的脉动压力图 Fig. 7 Pressure fluctuation of normal working propeller |
|
图 8 螺旋桨桨叶在0.9R处折断时的脉动压力图 Fig. 8 Pressure fluctuation of normal working propeller with blade fractured at 0.9R |
|
图 9 螺旋桨桨叶在0.8R处折断时的脉动压力图 Fig. 9 Pressure fluctuation of normal working propeller with blade fractured at 0.8R |
|
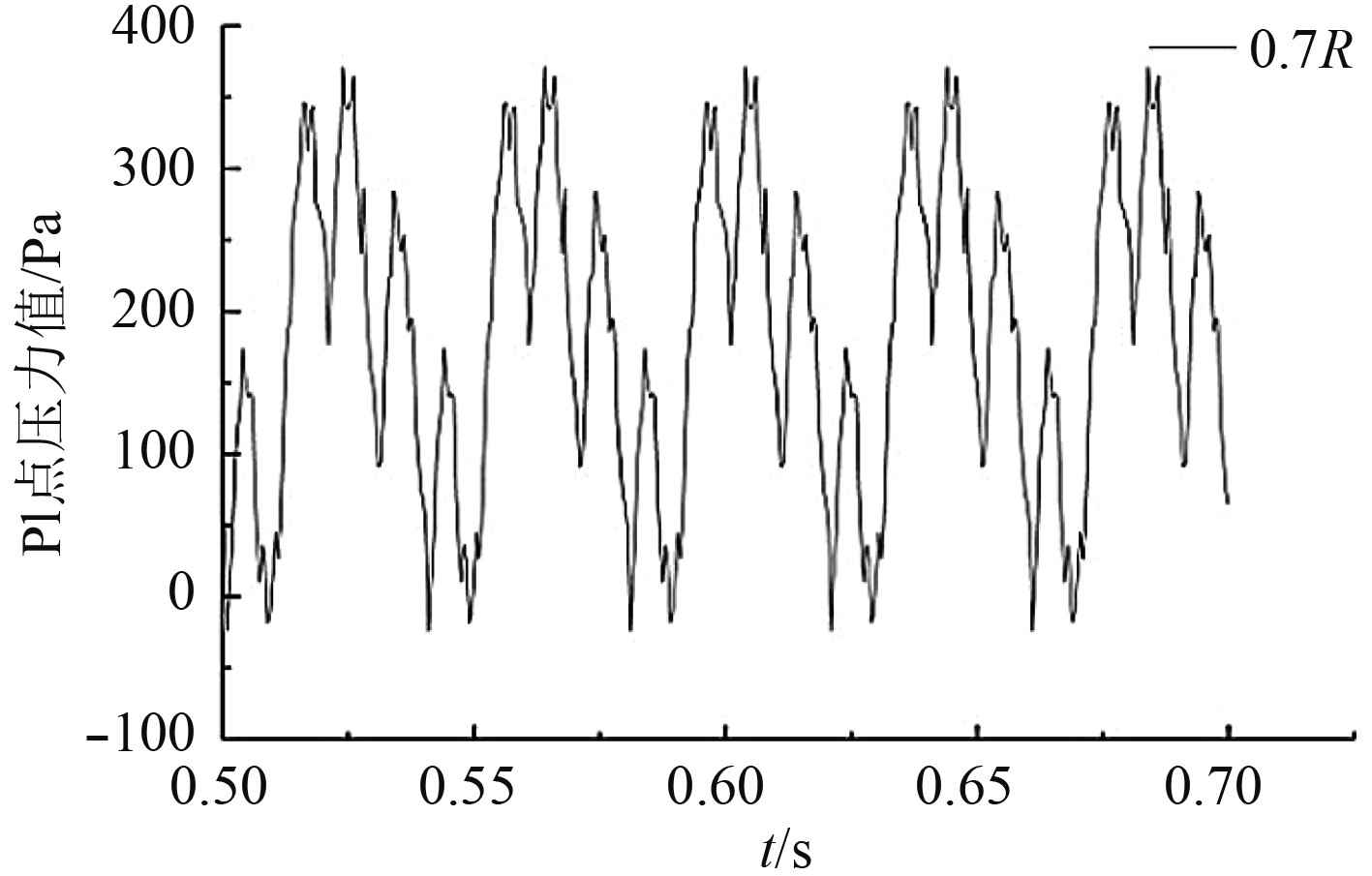
图 10 螺旋桨桨叶在0.7R处折断时的脉动压力图 Fig. 10 Pressure fluctuation of normal working propeller with blade fractured at 0.7R |
|
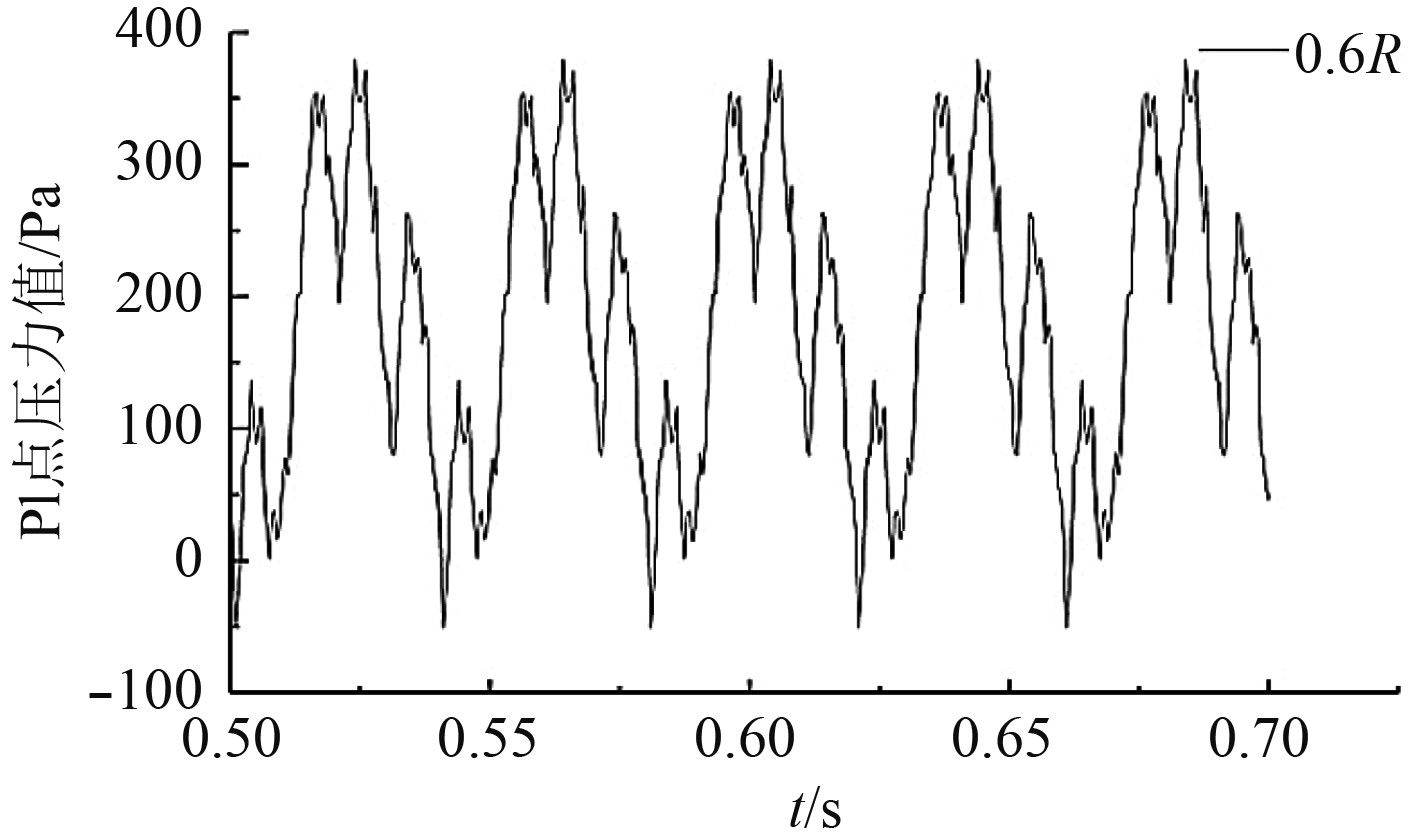
图 11 螺旋桨桨叶在0.6R处折断时的脉动压力图 Fig. 11 Pressure fluctuation of normal working propeller with blade fractured at 0.6R |
|
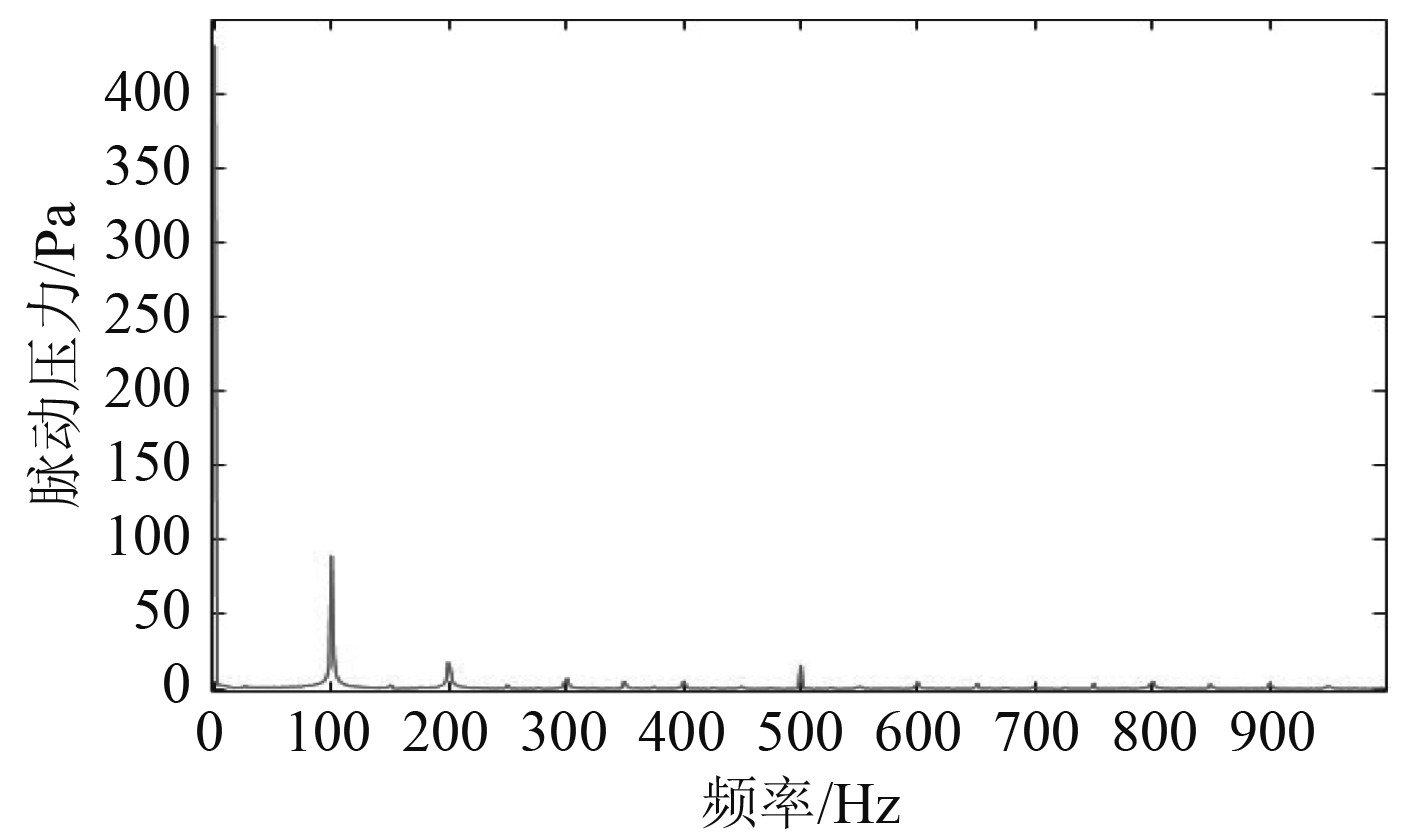
图 12 螺旋桨正常工作时的脉动压力频谱图 Fig. 12 Pressure frequency spectrum graph of normal working propeller |
|
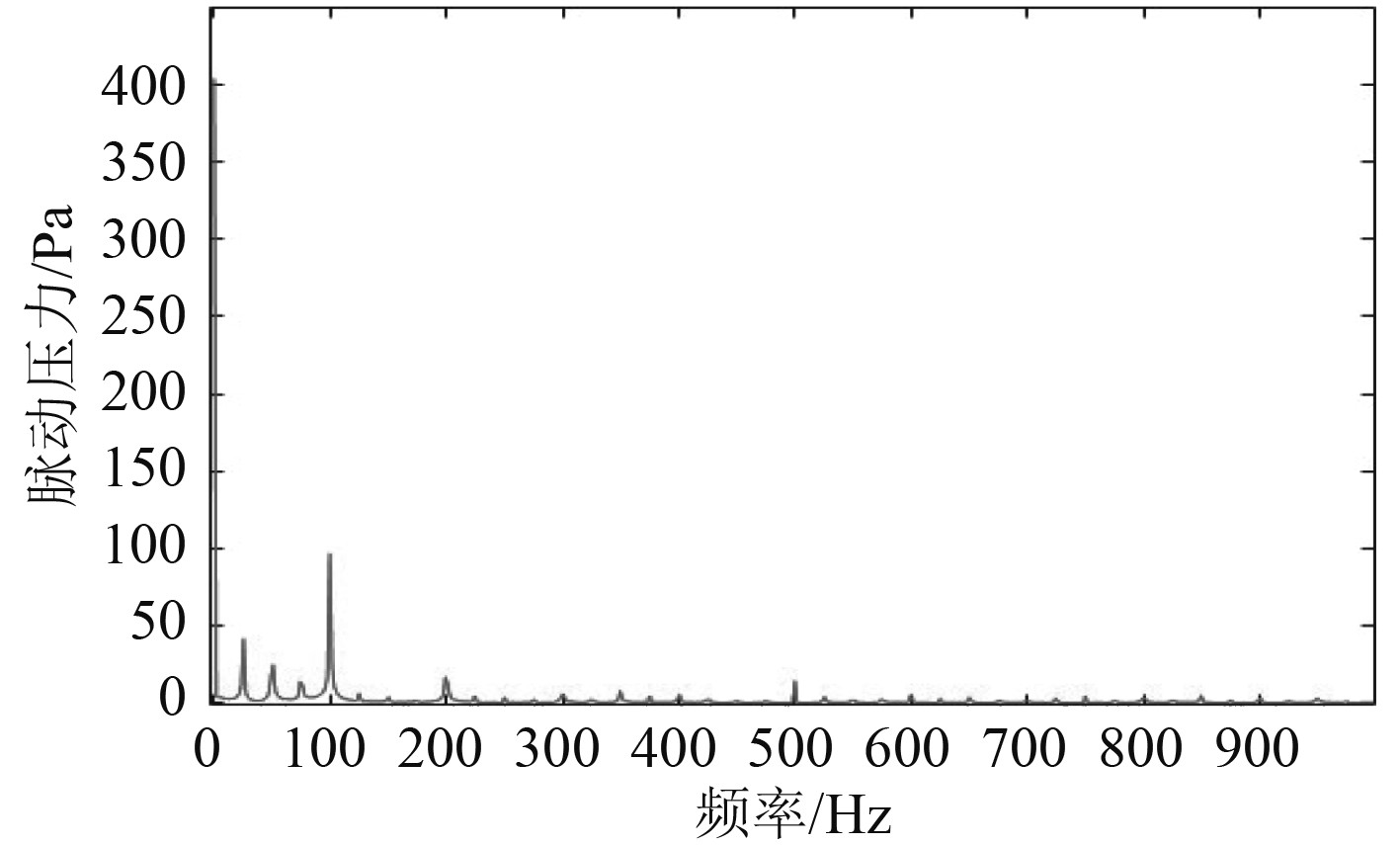
图 13 螺旋桨桨叶在0.9R处折断时的脉动压力频谱图 Fig. 13 Pressure frequency spectrum graph of propeller with blade fractured at 0.9R |
|
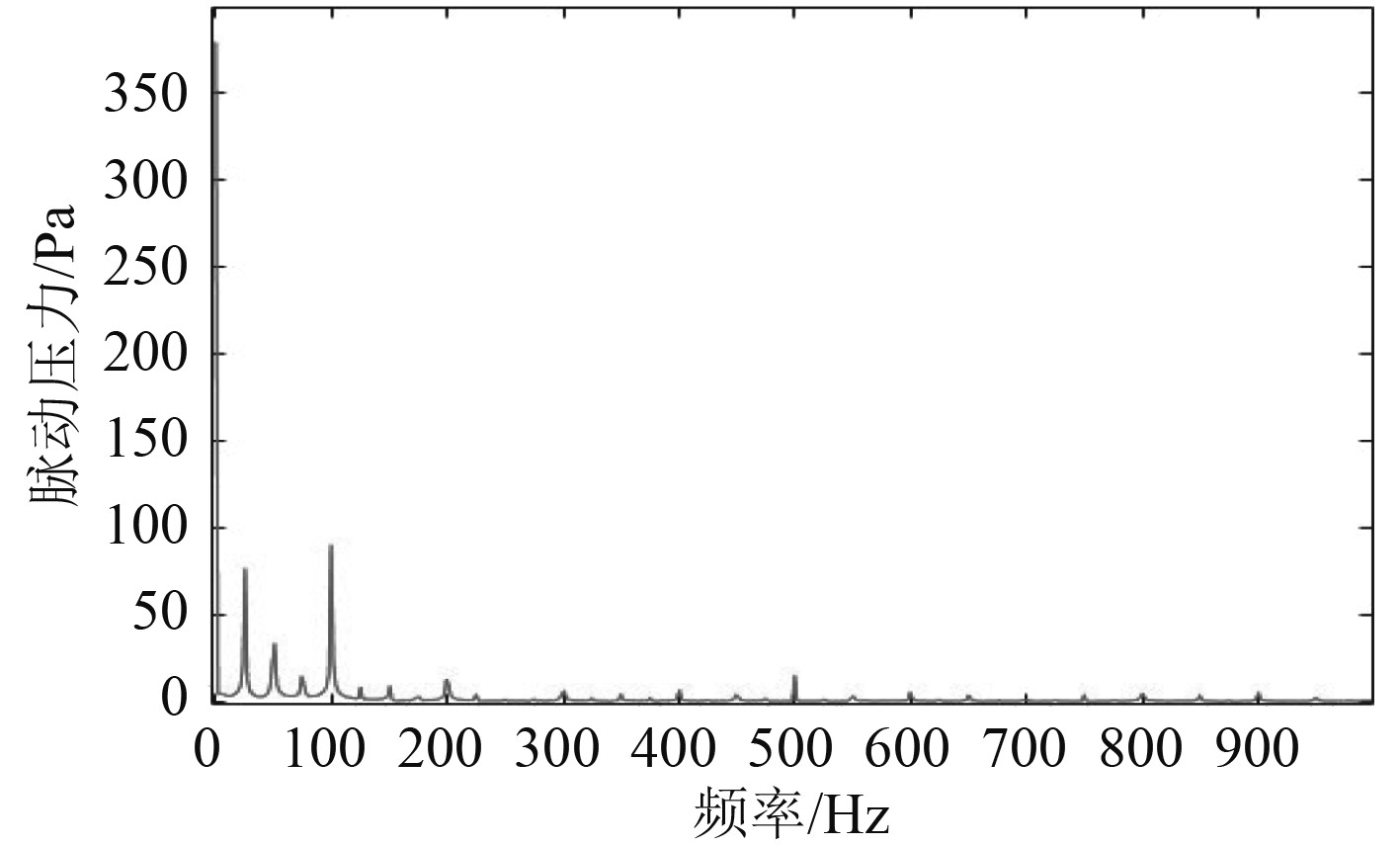
图 14 螺旋桨桨叶在0.8R处折断时的脉动压力频谱图 Fig. 14 Pressure fluctuation of normal working propeller with blade fractured at 0.8R |
|
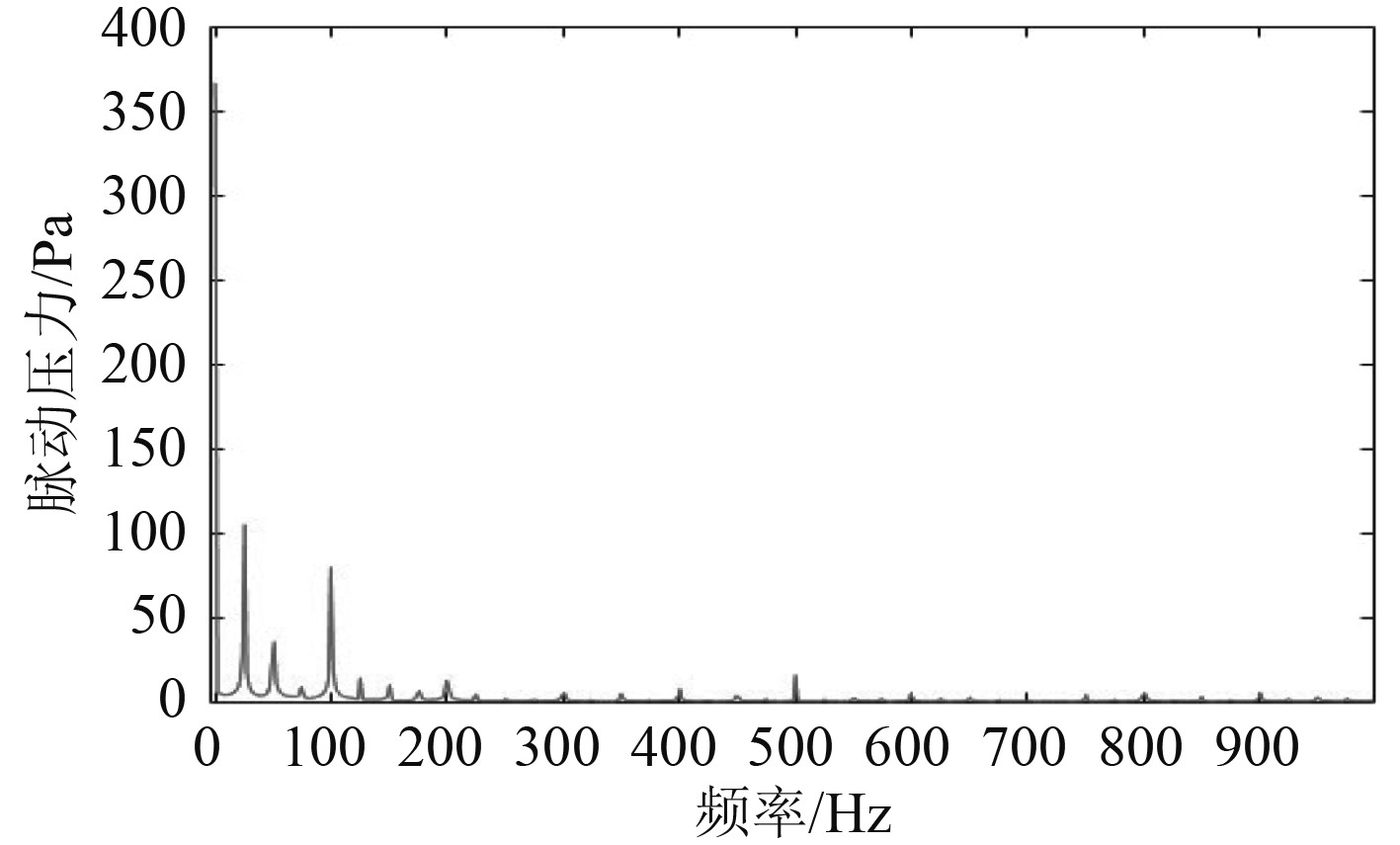
图 15 螺旋桨桨叶在0.7R处折断时的脉动压力频谱图 Fig. 15 Pressure frequency spectrum graph of propeller with blade fractured at 0.7R |
|
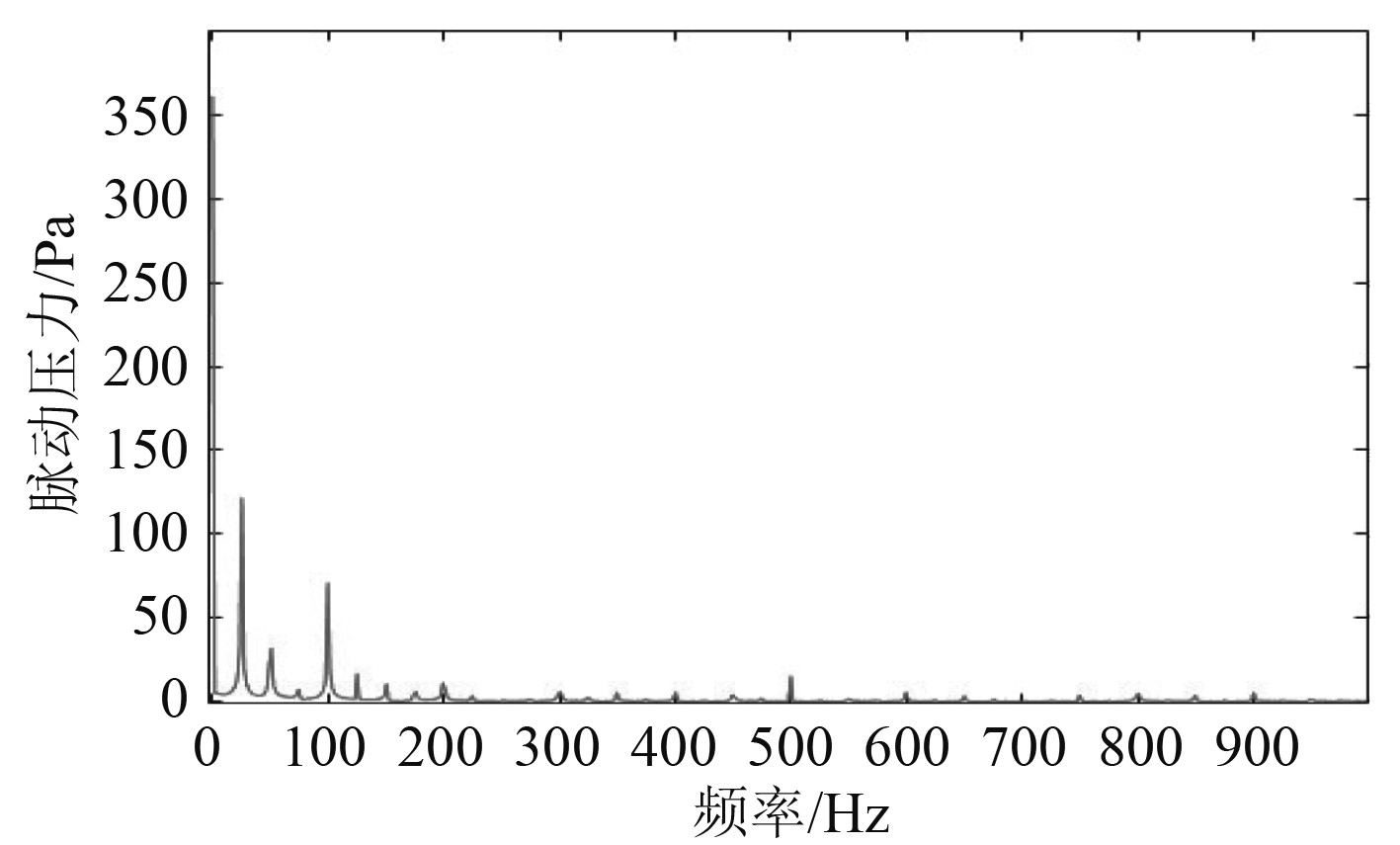
图 16 螺旋桨桨叶在0.6R处折断时的脉动压力频谱 Fig. 16 Pressure fluctuation of normal working propeller with blade fractured at 0.6R |
对比监测点脉动压力波形图可以发现,正常工作状态下的螺旋桨脉动压力近似正弦变化。当某一桨叶出现折断时,近似正弦波的脉动压力波形发生畸变,畸变周期0.04s。主要原因是螺旋桨桨叶折断后,对整个流场产生了扰动,当折断桨叶经过监测点区域时,对监测点区域的流场压力干扰小,使水流速度降低,压力升高;正常桨叶经过监测点区域时,对监测点区域的流场压力干扰大,使水流速度变大,压力降低。通过对比分析螺旋桨桨叶在0.9R,0.8R,0.7R,0.6R折断处脉动压力波形图发现,螺旋桨桨叶折断量越大,波形畸变越严重。因此,通过对脉动压力波形图的分析对比,可以初步判断螺旋桨的折断量。
对监测点脉动压力波形图进行快速傅里叶变换得到压力频谱图。通过对比正常工作状态和折断状态下的频谱图,得到如下几个特征:1)螺旋桨正常工作状态下,信号频谱图中频信号主要以叶频和倍频为主,其他频信号非常微弱,几乎没有;2)螺旋桨桨叶折断后,轴频和倍轴频的信号增强,叶频和倍叶频的频信号有所减弱;3)螺旋桨桨叶折断量越大,轴频和倍轴频的信号越强,甚至强于叶频信号,叶频和倍叶频的频信号越弱。因此,可以通过对轴频和倍轴频的监控判定螺旋桨桨叶折断事故的发生。
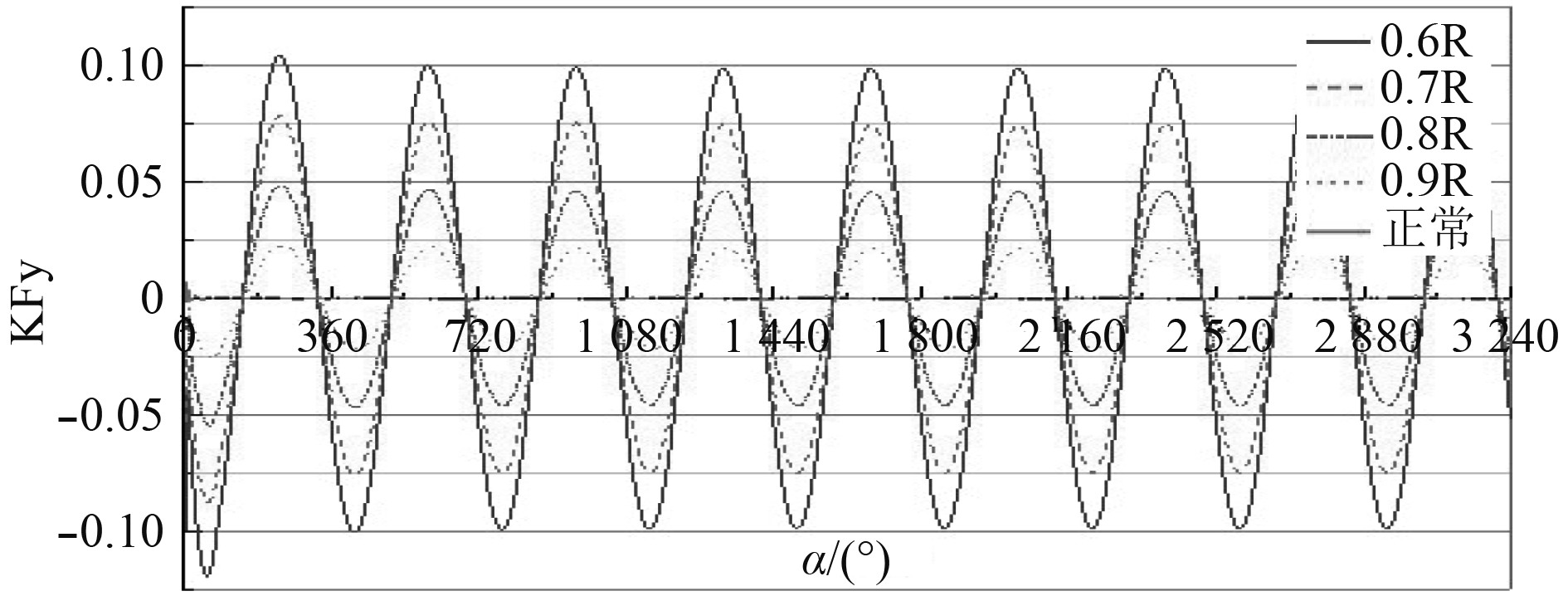
为了便于研究螺旋桨水动力侧向力系数与折断量之间的关系,将正常工况和折断工况放在同一张图进行对比分析。如图17所示,主要特征如下:1)螺旋桨在正常工作状态下,水动力侧向力系数基本无变化;2)螺旋桨在某一桨叶折断后工作,随着折断量的增加,螺旋桨侧向力系数周期性变化幅值随之增加,侧向力系数变化频率不变,仍为基轴频。
|
图 17 某一桨叶在0.6R,0.7R,0.8R,0.9R折断以及正常工况1.0R时KFy随α的变化 Fig. 17 Changes of KFy with α, blade fractured at 0.6R, 0.7R, 0.8R, 0.9R and normal working propeller |
通过对螺旋桨非定常流动模拟计算,获取了螺旋桨桨叶在不同折断位置时的脉动压力和水动力侧向力变化规律。提取时域波形、特征频率、伴随频率和水动力侧向力系数4个特征参量,其中,特征频率、伴随频率对应的特征参数分别为叶频、倍叶频;轴频、倍轴频。可以认为,当基轴频和2倍轴频的信号强度分别大于1倍叶频的20%和10%,即可判断螺旋桨断叶故障发生。随着计算流体力学的进一步发展,可以较为精确地对螺旋桨桨叶折断故障的位置进行诊断。
| [1] |
孟昭玉. 船舶螺旋桨轴状态监测技术[D]. 上海: 上海海事大学, 2005.
|
| [2] |
黄辉, 褚建新, 沈爱弟. 基于定子电流的电力推进船舶螺旋桨故障诊断[J]. 中国航海, 2014, 37(03): 28-31. DOI:10.3969/j.issn.1000-4653.2014.03.007 |
| [3] |
王福军. 计算流体动力学分析[M]. 北京: 清华大学出版社, 2004.
|
| [4] |
欧礼坚. 船舶螺旋桨及推进装置故障诊断关键技术研究与应用[D]. 广州: 华南理工大学, 2010.
|
| [5] |
马骋, 钱正芳, 陈科, 等. 双桨式吊舱推进器水动力性能CFD预报方法研究[J]. 船舶力学, 2014, 18(05): 516-523. DOI:10.3969/j.issn.1007-7294.2014.05.005 |
| [6] |
王雅涛, 庄静. 螺旋桨水动力分析及其故障诊断方法研究[J]. 舰船科学技术, 2017, 39(06): 4-6. |
| [7] |
盛振邦, 刘应中. 船舶原理(下)[M]. 上海: 上海交通大学出版社, 2004.
|
| [8] |
Shin Hyung Rhee, Takafumi Kawamura, Li H Y. Propeller cavitation study using an unstructured grid Based navier-stoker solver. Transactions of the ASME, September, 2005, 127: 986-994.
|
| [9] |
Sing-Kwan LEE. CFD Simulation for propeller four-quadrant flows[R]. ABS Technical Papers 2006: 175-189.
|
 2020, Vol. 42
2020, Vol. 42
