2. 高新船舶与深海开发装备协同创新中心 上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
目前主流的高速艇大多为圆舭、尖舭艇或深V艇,圆舭艇以排水型为主,而尖舭及深V型多见于高速排水型、过渡型及滑行态,随着对舰船要求如可工作海况、航速等的提高,圆舭艇由于高航速时阻力性能变差,将无法满足要求。另一方面虽然尖舭艇高航速下阻力性能相对圆舭艇有较大提升,但高速时艇底受到抨击作用加剧,导致耐波性受到影响[1]。尽管通过改型后的深V艇耐波性有所改善,但是其横向剖面较为尖瘦,舱室容积相对较小,对舰船来说不太有利。因此寻求一种能满足更多苛刻要求的艇型显得至关重要。
目前国外三体滑行艇多用于竞速艇,国内仍处于研究阶段,暂无实艇应用实例。而且由于艇型复杂,无经验公式或图谱进行阻力估算,因此考虑CFD软件分别对深V艇及三体滑行艇的静水性能进行数值模拟,对结果进行比较分析,从而从静水性能方面研究三体滑行艇的优劣势及应用前景。
1 模型参数所设计的三体艇主尺度见表1,三维模型如图1所示,深V艇艇型选取主尺度相近的常见深V艇艇型。
|
|
表 1 船型参数 Tab.1 parameter of tri-planning |
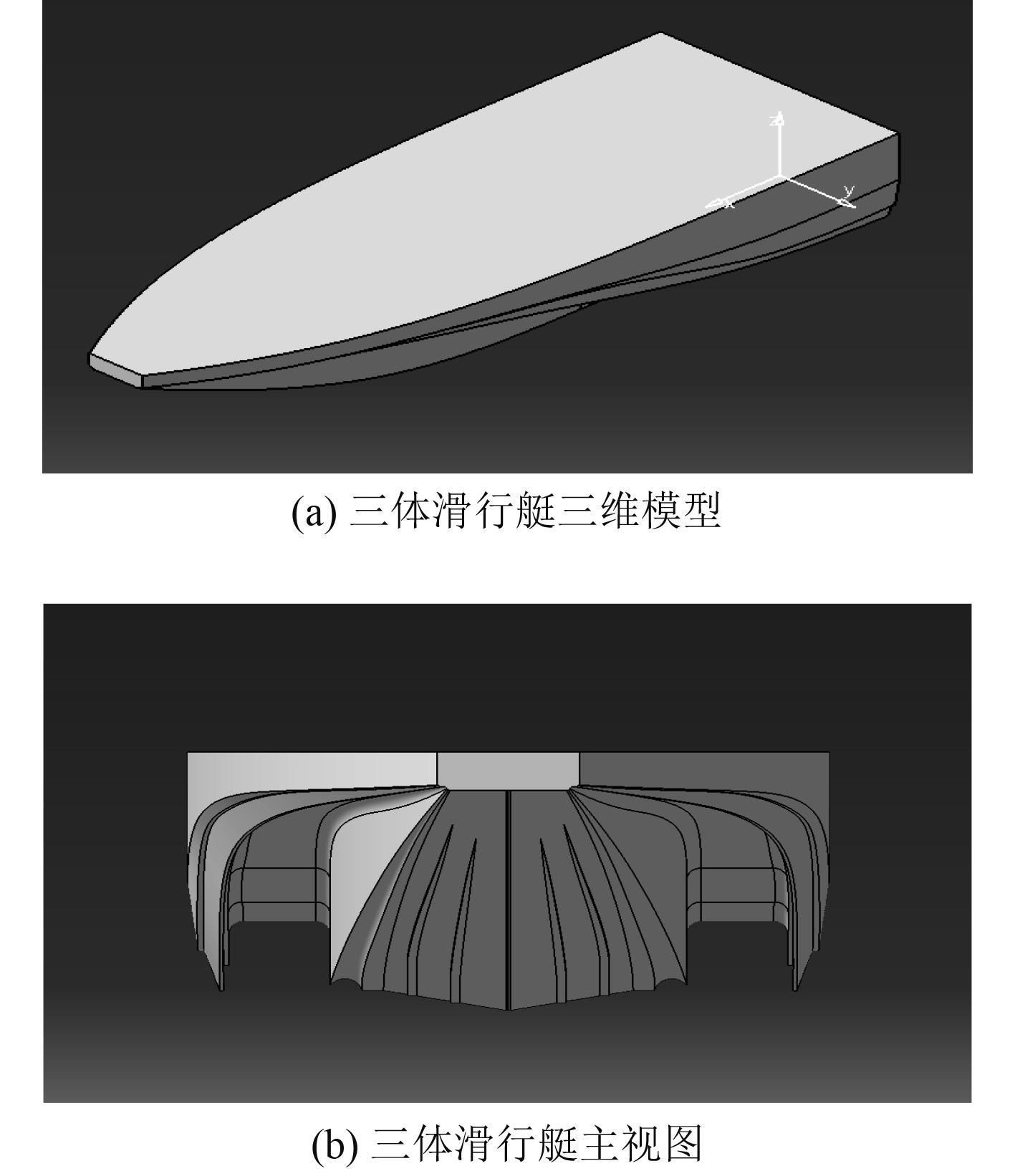
|
图 1 三体艇三维模型 Fig. 1 3D model of tri-planning |
通过商业CFD软件STAR-CCM+进行数值模拟仿真,并通过自由模法,即开放纵倾与升沉2个自由度运动,以达到准确模拟模型在静水中的直航状态。
2.1 控制方程为了应对工程中出现的复杂湍流问题的求解,通常采用时均的N-S方程,也就是RANS方程,其连续性方程和动量方程为:
| $ \begin{split} & \frac{{\partial p}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}} \right)}}{{{x_i}}} = 0{\text{,}}\\ & \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{{x_i}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{{x_j}}}\left( {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {{u_i}^{'}{u_j}^{'}} } \right) + {S_i} {\text{。}} \end{split} $ |
式中:
为使方程组封闭,引入SST方程来将湍流脉动值与时均值相关联。
2.2 SST湍流模型在结合了
其中
| $\frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_i}}}\left( {{\Gamma _k}\frac{{\partial k}}{{\partial {x_i}}}} \right) + {G_k} - {Y_k}{\text{,}}$ |
| $ \frac{\partial }{{\partial t}}\left( {\rho \omega } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \omega {u_i}} \right) = \frac{\partial }{{\partial {x_i}}}\left( {{\Gamma _{\omega} }\frac{{\partial \omega }}{{\partial {x_i}}}} \right) + {G_{\omega} } - {Y_{\omega} }{\rm{ + }}D\omega{\text{。}}$ |
式中:
船模在拖车带动下前进时,会通过扰动其周围的流场,从而达到改变船体周围的压力场和剪切应力场的作用,其所受的力与力矩为:
| $\begin{split} & F=\int_s {\left( {\left[ \tau \right] - p\left[ I \right]} \right) \cdot \overrightarrow n {\rm{d}}S - \overrightarrow {mg} } {\text{,}} \\ & \overrightarrow {{m_c}} = \int_s {\left( {\overrightarrow r - \overrightarrow {{r_c}} } \right)} \left( {\left[ \tau \right] - p\left[ I \right]} \right) \cdot \overrightarrow n {\rm{d}}s{\text{。}} \end{split} $ |
式中:
船模六自由度控制方程为:
| $\begin{split} &\frac{\rm d}{{{\rm d}t}}\left( {m\overrightarrow {{v_c}} } \right) = \overrightarrow F {\text{,}}\\ &\frac{{\rm d}}{{{\rm d}t}}\left( {\left[ {{M_c}} \right] \cdot \overrightarrow {{\omega _c}} } \right) = \overrightarrow {{m_c}}{\text{。}} \end{split} $ |
其中:
根据文献[2-4]计算的结果与试验值对比,其结果与实际情况基本一致,说明采用CFD方法进行阻力预报是可行的。本文数值计算模型缩尺比为1∶5,CFD软件采用STAR-CCM+,计算域为一个长方体,其在艇前1 L、艇后3 L、甲板以上1 L、甲板以下2 L、舷侧1.5 L,船体周围以及水线附近设置2个加密区域,根据文献[5-7]的方法对船体近壁面采用壁面函数法进行网格加密,所得网格如图2所示。由于船左右对称,为了加快计算速度,只计算左舷一侧,计算的阻力值也为一半,在最后数据处理时换算成整船的阻力。
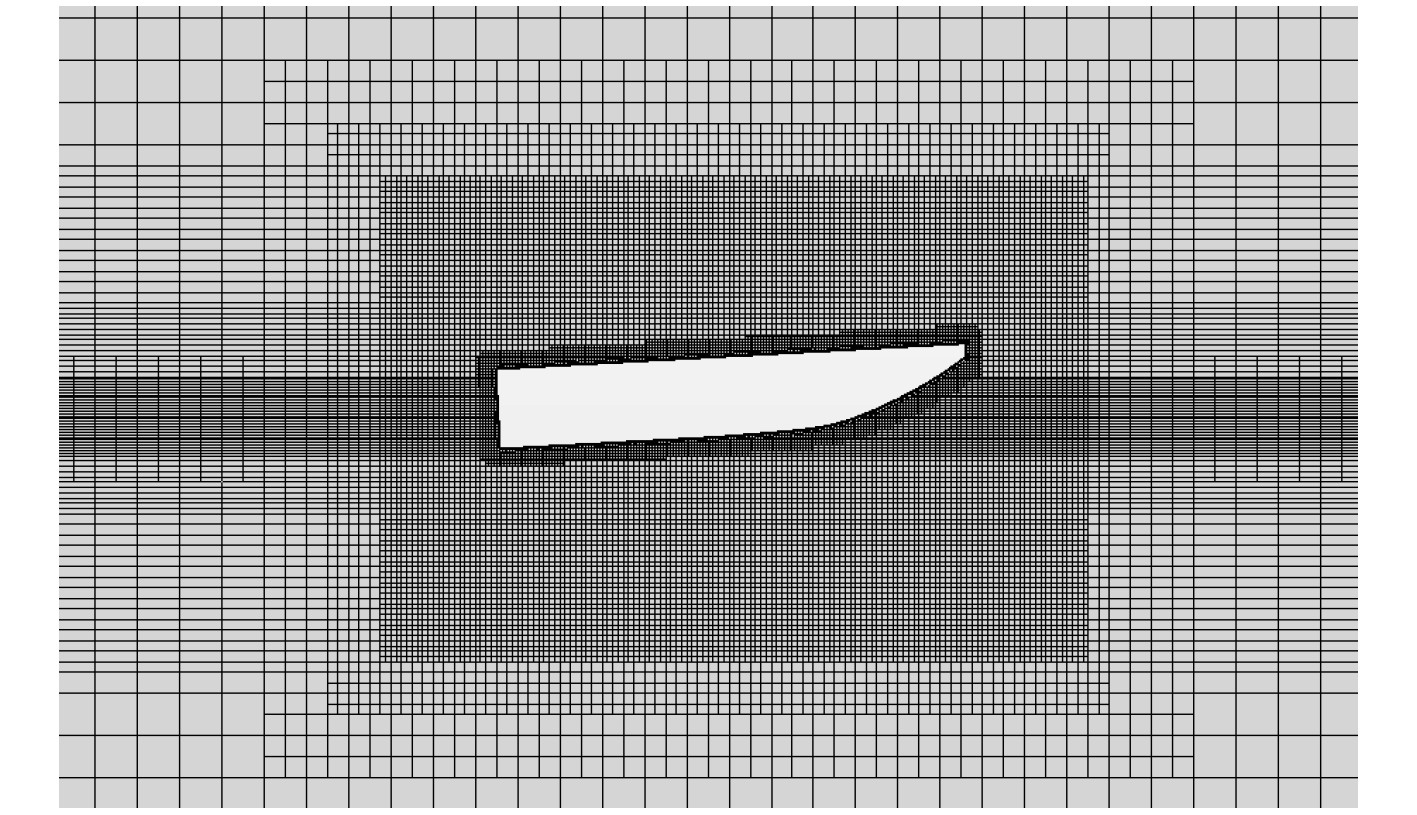
|
图 2 船体周围加密区网格 Fig. 2 Mesh aroud the hull |
根据船型航态划分公式
| $F{r_{\nabla} } = \frac{U}{{\sqrt {g \cdot {\nabla ^{1/3}}} }}{\text{,}}$ |
计算
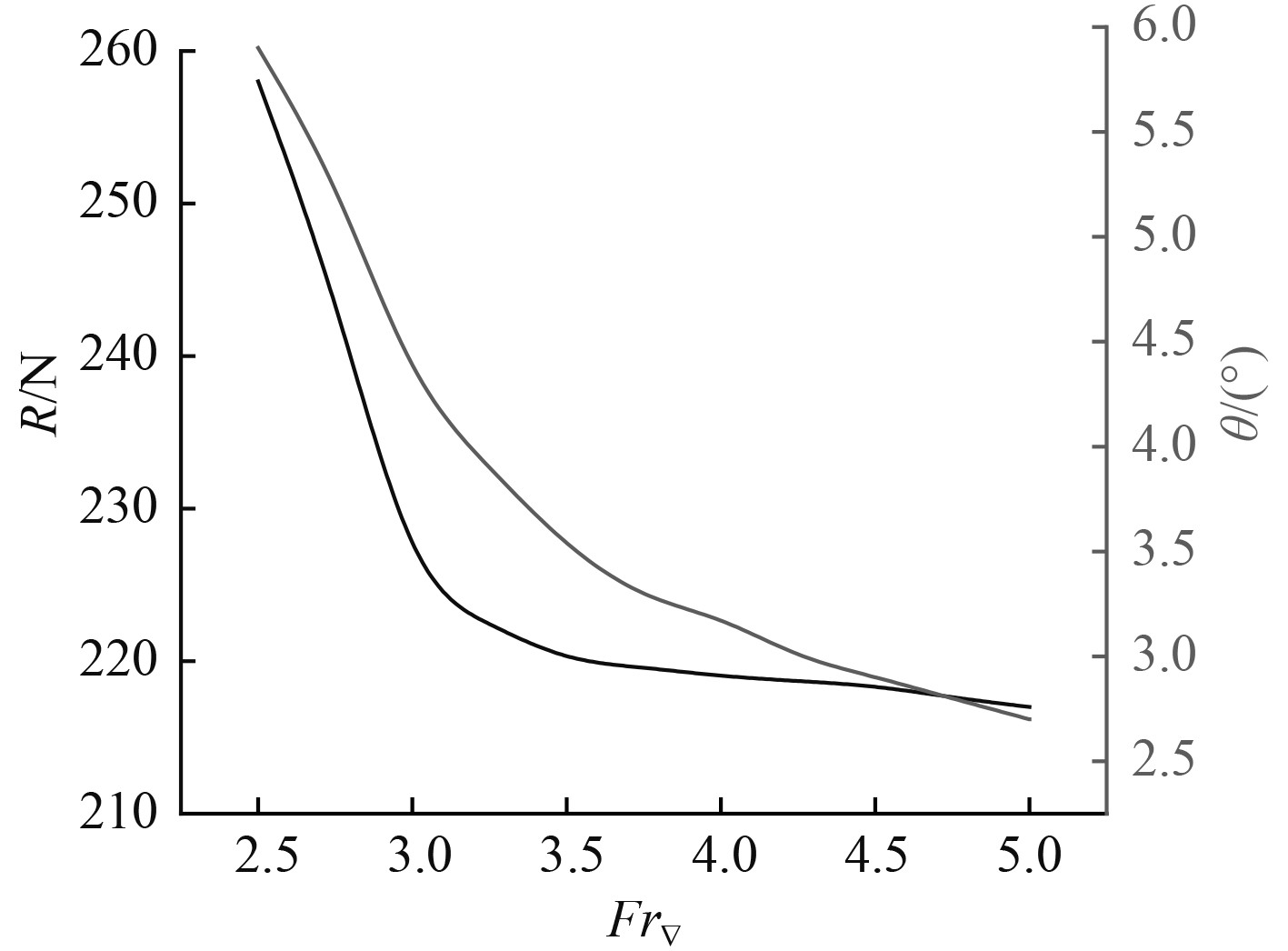
|
图 3 三体艇阻力及纵倾角随航速变化曲线 Fig. 3 Resistance and trim of tri-planning |

|
图 4 深V艇阻力及纵倾角随航速变化曲线 Fig. 4 Resistance and trim of deep V |

|
图 5 各航速下的兴波对比(上为三体艇,下为深V艇) Fig. 5 Free-surface wave comparation (up tri-planning, down deep V) |

|
图 6 艇底压力分布(上为三体艇,下为深V艇) Fig. 6 Pressure of hull bottom (up tri-planning,down deep V) |
由图可见,对于所选航速段,三体艇在过渡态阻力及纵倾角有较大的峰值,主要是由于航速较低时,槽道内仍处于被水浸没的状态,水流作用于主体及槽道前端,加剧了船体的尾倾程度,另外主体与槽道加大了与水的接触面积,从而使得摩擦阻力大幅上升,随着航速的增加,进入滑行态,槽道的存在使得水气混合物在槽道内不断堆积,槽道处于通气状态,水动力和空气动力成为支撑船体的主要部分,船体整体抬升,从而导致之后阻力及纵倾角随着航速的增加而减少,直至
从水面兴波情况上来看,随着航速的增加,艇周围流畅变化比较明显,特别是尾流的变化,两者尾流都向中收敛,空穴也随之边长,但相较于深V艇,三体艇由于槽道及片体的存在,吸收了主船体的兴波及喷溅,同时由于船体因为水动升力与气动升力的存在,整体被抬起,从而减小了尾部的兴波。
从艇底压力分布来看,三体艇由艇底滑行面及槽道的水动力及空气动力来共同支撑艇体,从而减小纵倾改善浮态;深V艇在类似球首处有明显的应力集中现象,且主要支撑面处在船中至球首形成的三角区内,流体对这一区域的抨击较为严重,对船体的振动及噪声都有一定程度的不良影响。
分析上述数据结果可知:
1)在所选航速段内,三体艇在过渡态阻力及纵倾角有较大的峰值,且在
2)水面兴波角度来看,三体艇由于片体及槽道的存在,使得对尾流的影响有较大的改善,且高航速时尾流收敛越明显,有很高的隐蔽性。
3)船底动压力分布显示,三体艇由主体滑行面及槽道共同支撑船体,改善船体的浮态,减小流体对船底的抨击作用。
4 结 语在艇型外观方面,三体艇相对于深V艇有更大的内部空间及更多的甲板面积,但在阻力及浮态方面,过渡态及大部分滑行态时均不及深V艇,但是随着航速的提高将逐渐进入三体艇的优势工作区间,而且由于槽道及片体的存在,使得三体艇对尾流的影响更小,同时由于底部支撑面更大,在结构上可有效降低噪声及振动。军用上,可作为高速无人侦察艇,具有很高的隐蔽性及快速性,同时有利于设备的布置及正常工作,民用上,可作为对舒适性及安全性有很大要求的游艇船型。
本文仅从静水阻力、浮态、兴波及艇底压力分布方面论证三体艇的可行性,在耐波性上仍需进一步比较,以验证此船型的实用性。
| [1] |
邵世民, 王云才, 梁永超, 等. 深V型艇与圆舭型艇的阻力和耐波性比较[J]. 上海交通大学学报, 1996, 30(12): 53-57. |
| [2] |
王硕, 苏玉民, 庞永杰, 等. 高速滑行艇CFD精度研究[J]. 船舶力学, 2013, 2013(10): 1107-1114. DOI:10.3969/j.issn.1007-7294.2013.10.002 |
| [3] |
蒋一. 基于CFD的超高速三体滑行艇快速性分析[D]. 哈尔滨: 哈尔滨工程大学, 2013.
|
| [4] |
王庆旭. 三体滑行艇阻力和稳定性研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [5] |
BAUDIC S F, WILLIAMS A N, KAREEM A. A two-dimensional numerical wave flume-partl: nonlinear wave generation, propagation, and absorption[J]. Journal of Offshore Mechanics and Arctic Engineering, 2001, 2001(123): 70-75. |
| [6] |
RYU S, KIM M H, LYNETT P J. Fully nonlinear wave-current interactions and kinematics by a BEM-based numerical wave tank[J]. Computational Mechanics, 2003, 2003(32): 336-346. |
| [7] |
章丽丽, 孙寒冰, 蒋一, 等. 三体滑行艇槽道的水气动力特性研究[J]. 哈尔滨工程大学学报, 2017, 38(1): 31-36. |
| [8] |
RADOJCJC D, ZGRADIC A, KALAJDZIC M, et al. Resistance prediction for hard chine hulls in the pre-planing regime[J]. Polish Maritime Research, 2014, 21(2): 9-26. DOI:10.2478/pomr-2014-0014 |
| [9] |
邹劲, 姬朋辉, 孙寒冰, 等. 网格因素对三体滑行艇阻力计算影响探究[J]. 船舶, 2016, 03: 8-14. DOI:10.3969/j.issn.1001-9855.2016.02.002 |
| [10] |
FAIRLIE-CLARKE A. C., TVEITNES T. M. CFD analysis and experimental work on water impact forces on transverse sections of planning craft[J]. Ocean Engineering, 2008, 35(7): 706-716. DOI:10.1016/j.oceaneng.2006.11.011 |
| [11] |
朱珉虎. 高速艇与游艇设计手册[M]. 珠海: 珠海出版社, 2009.
|
| [12] |
Yu-min SU, Shuo WANG, Hai-long SHEN, et al. Numerical and experimental analyses of hydrodynamic performance of a channel type planing trimaran[J]. Journal of Hydrodynamics, 2014, 26(4): 549-557. DOI:10.1016/S1001-6058(14)60062-7 |
| [13] |
赵发明, 高成君, 夏琼. 重叠网格在船舶CFD 中的应用研究[J]. 船舶力学, 2011(4): 332-341. DOI:10.3969/j.issn.1007-7294.2011.04.002 |
| [14] |
ROYK, BHARATS, RAJKESHAR S A. Comprehensive generalized mesh system for CFD application[J]. Mathe and Computers in Simulation, 2008, 78: 605-617. DOI:10.1016/j.matcom.2008.04.005 |
| [15] |
苏玉民, 王硕, 沈海龙. 三体槽道滑行艇阻力模型试验研究[J]. 哈尔滨工程大学学报, 2013, 34(7): 832-836. |
| [16] |
SUN Huawei, HUANG Debo, ZOU Jin, et al. Experimental investigation on resistances from stepped trimaran planing boats[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2012, 40(1): 86-89. |
 2020, Vol. 42
2020, Vol. 42
