2. 上海船舶设备研究所,上海200031;
3. 武汉第二船舶设计所,湖北 武汉430064
2. Shanghai of Marine Equipment Research Institute, Shanghai 200031, China;
3. Wuhan second Ship Design and Research Institute, Wuhan 430064, China
摩擦、间隙、刚度、表面粗糙度等因素对机械传动装置振动噪声均有影响。由于影响因素众多,参数分布具有随机性和不确定性,且一些因素相互交织,相互耦合影响,使得机械传动装置振动噪声发生机理复杂,采用传统的方法难以开展机械传动装置的低噪声设计。针对上述问题,本文提出一种基于优化设计理论的机械传动装置低噪声稳健性设计方法。
1 优化方法本文基于离散元方法构建机械传动装置的动力学模型,将含有间隙的运动副之间的约束关系模拟成接近轴承真实状态的“广义力”,且由于广义力模型可以根据真实物理实验台架测得的实验结果进行定义。在此基础上进行DOE试验设计,建立各响应变量跟设计变量之间的关系,获得响应曲面,然后再采用优化算法进行机械传动装置的多目标稳健性参数优化,具体步骤如下:
1)建立机械传动装置系统动力学模型;
2)基于所建立的动力学模型,进行DOE试验设计;
3)根据DOE仿真结果,建立设计变量和响应之间的响应面;
4)判断响应面精度是否满足要求;
5)若满足,用响应面代替动力学模型,并在其基础上进行稳健性参数优化;
6)优化结果验证。
2 优化模型1)数学模型
本文以某点附近微小范围内响应值的极差,来衡量该点的稳健性。在每个设计点微小范围内利用Latin hypercube sampling均匀生成一定数量的样本点,以这些样本点响应的最大值
| $ R = \left( {{\rm{max}}\;{\hat{ y}}} \right) - \left( {{\rm{min}}\;{\hat{ y}}} \right){\text{。}} $ | (1) |
本文分别引入一个评价优化性设计的优化满意度函数和评价稳健性设计的稳健满意度函数。优化满意度函数如下式:
| $ d = \left\{ {\begin{array}{*{20}{l}} 1{\text{,}}&{y \leqslant T}{\text{,}}\\ {{{\left( {\displaystyle\frac{{U - y}}{{U - T}}} \right)}^t}}{\text{,}}&{{{T}} < {{y}} < {{U}}}{\text{,}}\\ 0{\text{,}}&{{{y}} \geqslant {{U}}}{\text{。}} \end{array}} \right. $ | (2) |
机械传动装置响应变量符合望小特性,即响应值越小越好。其中,U为响应变量上限,T为响应变量的目标值。当y超出响应上限U时,满意度为0;y变小时满意度增大,当小于目标值时,满意度达到1。
稳健满意度函数如下式:
| $ dr = \left\{ {\begin{array}{*{20}{l}} 0{\text{,}}&{{{R}} \geqslant {{U}} - T}{\text{,}}\\ {{{\left( {1 - \displaystyle\frac{R}{{U - T}}} \right)}^s}}{\text{,}}&{0 < R < U - T}{\text{,}}\\ 1{\text{,}}&{R = O}{\text{。}} \end{array}} \right. $ | (3) |
式(2)和式(3)中的t和s为响应相对于目标的重要程度,根据机械传动装置的特点,本文取
| $ D = {d^{{\omega _1}}}d_r^{{\omega _2}}{\text{。}} $ | (4) |
其中:
设
| $ \begin{array}{l} 0mm \leqslant {x_2} \leqslant {\rm{0}}{\rm{.35mm}}{\text{,}}\\ {\rm{0}}{\rm{.01}} \leqslant {x_3} \leqslant 0.2{\text{,}} \end{array} $ |
优化目标:
| $ {D_{{a_R}}},{D_{{a_a}}},{D_{{F_{RMS}}}},{D_{{F_{amp}}}},{D_{{M_{RMS}}}},{D_{{M_{amp}}}}{\text{,}} $ |
约束条件:
| $ {y_i} \leqslant Ui{\text{。}} $ |
其中,
2)响应面模型
本文选用均匀设计试验法生成100个初始样本点,各个样本点所对应的响应值通过前面所述的机械传动装置动力学模型计算处理得出。将正交试验获得的数据优化设计模块中,构造响应面得到6个目标的响应面,如图1所示。
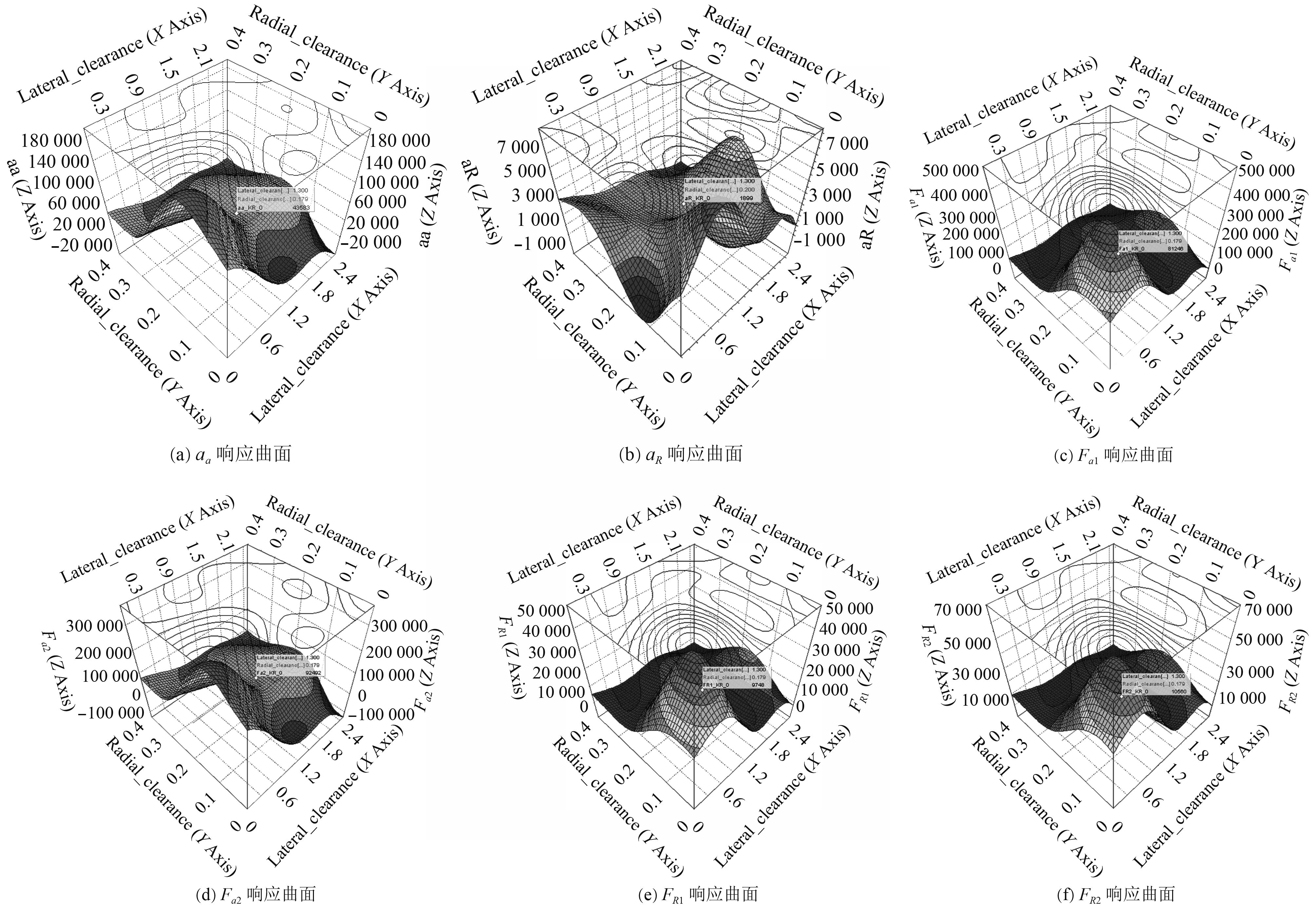
|
图 1 各响应变量对应的响应曲面 Fig. 1 Response surface corresponding to each response variable |
3)优化模型
本文选取NSGA-II(Non-dominated Sorting Genetic Algorithm II)作为优化算法。NSGA-II是对常规遗传算法的改进算法,通过引入快速非支配排序算子设计、个体拥挤距离算子设计和精英策略选择算子设计,较好解决了常规遗产算法参数选取困难和计算效率低等问题,提高了算法的运算速度和鲁棒性。根据本文研究情况,初始种群数量为100,选取20代作为进化代数,杂交率设为0.9。
3 优化结果在20代进化代数后,总共生成2000个设计点,其中包括1403个可行解与55个最优解。图2为各个设计目标的历史迭代图,图中高亮显示的设计点是此次优化结果的最优前沿点。可以看出随着优化迭代的进行,设计点逐渐向最优前沿聚集。
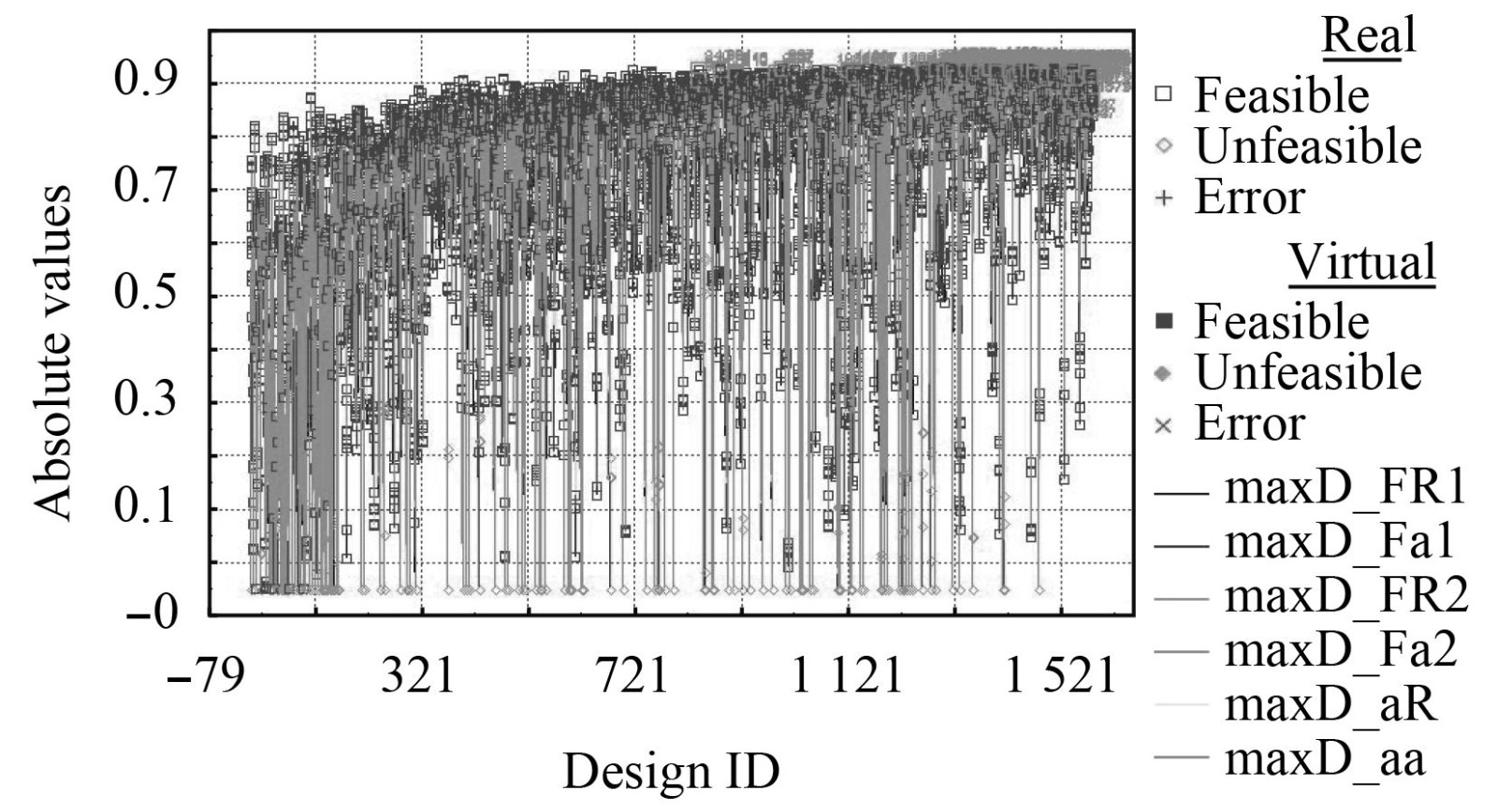
|
图 2 各设计目标的历史迭代图 Fig. 2 Historical iteration diagram of each design objective |
当优化目标是2个以上时,最优前沿不再是一条曲线,变成了一个三维或者更高维度的曲面或超曲面。本文研究总共存在6个优化目标,最优前沿是一个六维的超曲面。为了将这个抽象的六维超曲面表示出来,将6个优化目标拆分出来,用1个
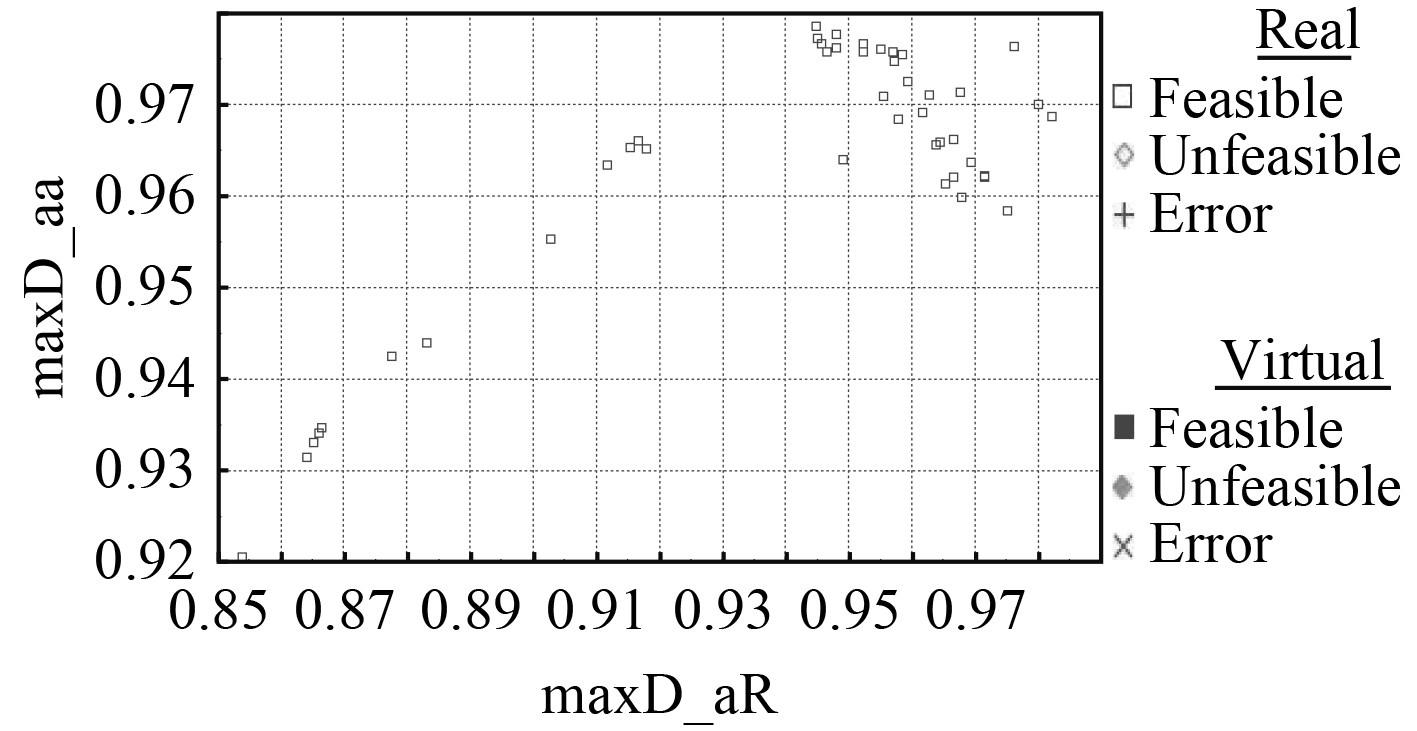
|
图 3
|
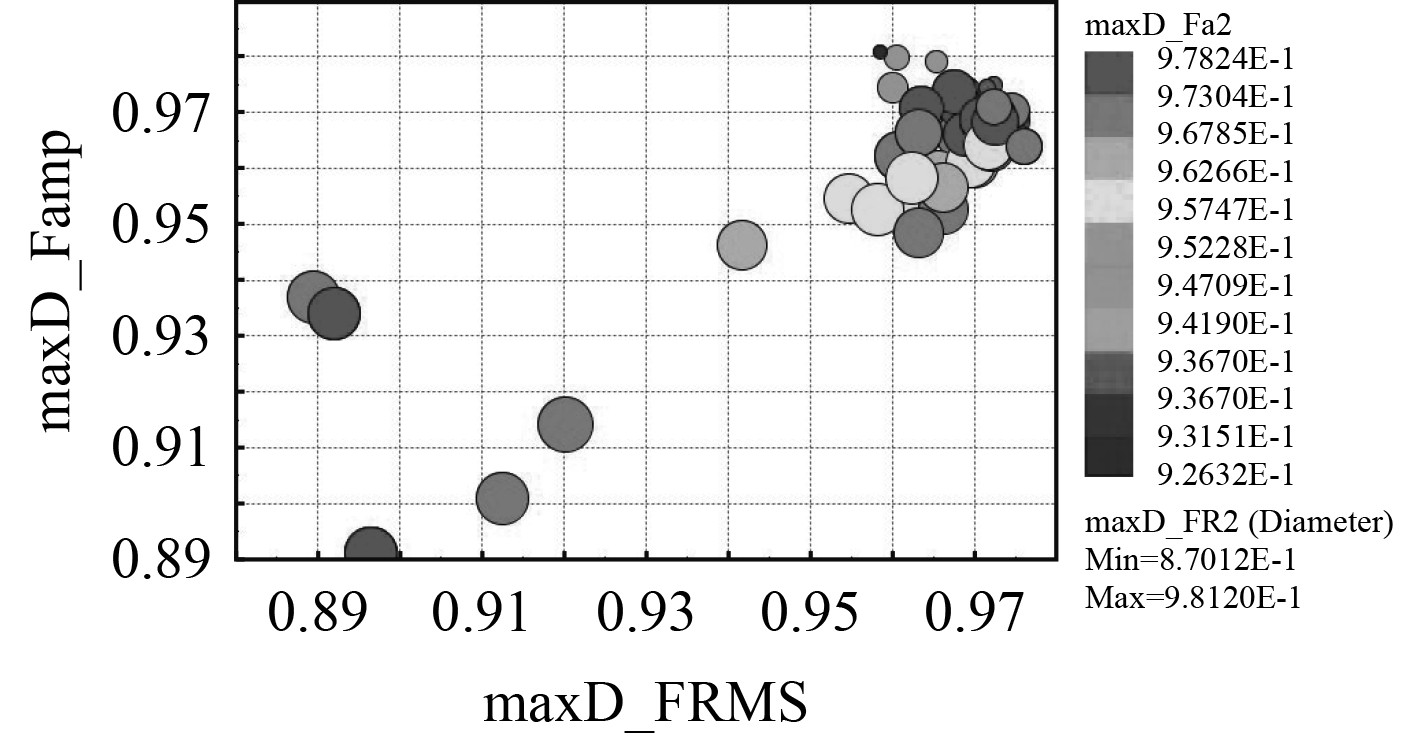
|
图 4
|
图5为所有设计点在设计空间内的3D散点图,高亮显示的是最优前沿点。可以看出,随着优化迭代的进行,大量最优设计点在聚集在区域A中,少量最优设计点分别散布在区域B和区域C内。在机械的设计阶段,根据实际条件,间隙参数应尽量在A,B,C三个设计空间内选择。
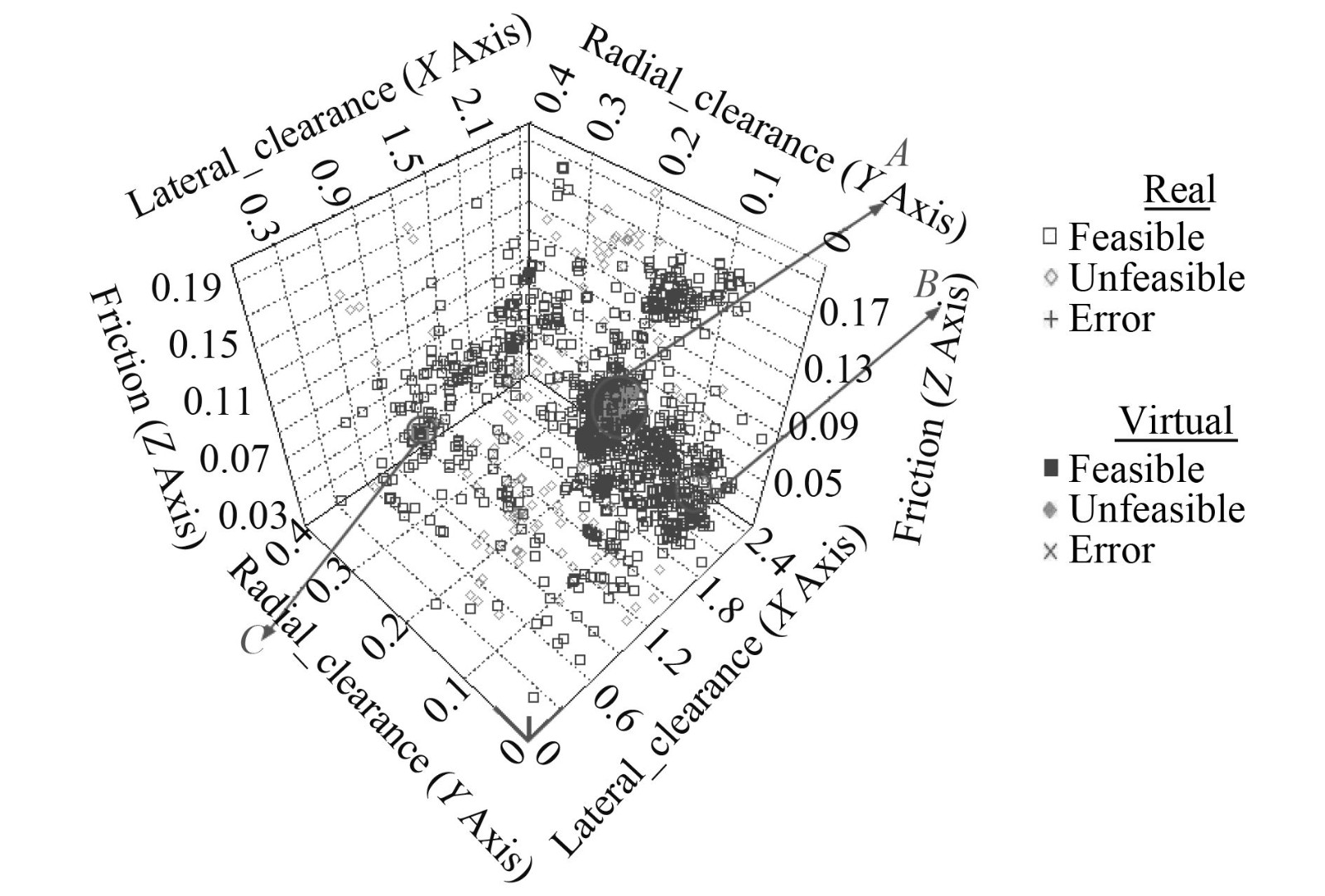
|
图 5 3D散点图 Fig. 5 3D scatter |
为了验证优化结果,在区域A,B,C内任选一个最优设计点,将其响应曲面拟合的响应值与有限元模型的仿真值相比进行误差分析,以验证优化精度。将优化点动力学模型的响应仿真值与原始点的响应仿真值进行对比以验证优化效果。
|
|
表 2 FR1和Fa1拟合模型相对误差 Tab.2 Relative error of fitting models of FR1 and Fa1 |
|
|
表 3 FR2和Fa2拟合模型相对误差 Tab.3 Relative error of fitting models of FR2 and Fa2 |
|
|
表 4 aR和aa拟合模型相对误差 Tab.4 Relative error of fitting models of aR and aa |
由表1~表5可知,优化点响应曲面的拟合值与仿真模型的真实值的相对误差在5%以内,优化结果可靠。与原始设计点相比,优化点的各个响应值均有不同幅度的下降,优化后的机构振动特性明显优于原始机构。
|
|
表 1 优化点与原始点设计变量参数 Tab.1 Design variable parameters of optimization point and original point |
|
|
表 5 原始点与优化点响应变量对比 Tab.5 Comparison of response variables between original point and optimized point |
本文提出一种基于优化设计理论的机械传统装置低噪声稳健性设计方法,建立了包括建模、仿真、分析、优化设计的系统性流程和方法。所采用的基于“离散元”和“基于响应面的稳健性优化”的方法,能够快速地获得实际设计参数与振动响应之间的内在数值联系,使得在工程上开展优化设计成为可能。通过一个机械传动装置的设计实例,获得了工程上可实现的优化设计结果。在轴承的径向间隙取在0.018 mm,摩擦系数为0.085时,可以明显改善机械传动装置的振动,同时保证低噪声设计的稳健性。
| [1] |
胡世武. 含间隙运动副的动力学分析和实验[D]. 大连: 大连理工大学, 2017.
|
| [2] |
KOSHY C. S., FLORES P., LANKARANI H. M.. Study of the effect of contact force model on the dynamic response of mechanical systems with dry clearance joints: computational and experimental approaches[J]. Springer Netherlands, 2013, 73(1-2). |
| [3] |
FLORES P., KOSHY C. S., LANKARANI H. M., et al.. Numerical and experimental investigation on multibody systems with revolute clearance joints[J]. Springer Netherlands, 2011, 65(4). |
| [4] |
邓丰曼. 基于DOE优化设计的机械集成装置运动性能试验分析[J]. 国外电子测量技术, 2019, 38(07): 52-55. |
| [5] |
李建华, 周俊峰. 基于DOE的离散公差稳健设计[J]. 煤矿机械, 2014, 35(06): 121-123. |
| [6] |
王晶. 基于响应曲面法的多响应稳健性参数优化方法研究[D]. 天津: 天津大学, 2009.
|
| [7] |
彭茂林, 杨自春, 曹跃云, 等. 基于响应面法的可靠性稳健设计优化[J]. 航空动力学报, 2013, 28(08): 1784-1790. |
| [8] |
陈志旺, 陈林, 白锌, 等. 求解约束多目标区间优化的交互多属性决策NSGA-II算法[J]. 控制与决策, 2015, 30(05): 865-870. |
| [9] |
左一多. 多目标优化问题的粒子群算法及其性能分析[D]. 中国地质大学(北京), 2013.
|
| [10] |
杨平, 陈正江, 黄巍. 基于多目标遗传算法的舰载液冷板散热优化设计[J]. 舰船科学技术, 2018, 40(11): 134-138. YANG Ping, CHEN Zheng-jiang, HUANG Wei. Optimization design of heat dissipation of shipboard liquid cooling plate based on multi-objective genetic algorithm[J]. Ship Science and Technology, 2018, 40(11): 134-138. DOI:10.3404/j.issn.1672-7649.2018.11.027 |
 2020, Vol. 42
2020, Vol. 42
