2. 沪东中华造船(集团)有限公司,上海 200011
2. Hudong-Zhonghua Shipbuilding (Group) Co., Shanghai 200129, China
由于测量船对船舶的布置有特殊的要求,并且需要在海上长时间的执行任务,使得船体在结构设计上船体瘦长、首部外飘明显,遭遇高海况大波浪的概率更高,但目前国内在大型测量船的波浪载荷方面研究较少,国内外规范对此船型不完全适用。因此,准确预报船体梁波浪载荷,确定载荷设计值对于结构设计而言十分重要。
梁双令[1]对比不同规范在载荷控制参数选取上的区别,并采用设计波法对船体波浪载荷进行预报;单鹏昊[2]对UR S11A和UR S11中关于船体梁波浪载荷长期极值的计算公式进行了比较,对集装箱船设计值的确定提供了参考;王红芳[3]通过理论和试验对比,认为三维势流理论能较好适用大尺度结构船舶;杨朕[4]通过对穿梭油船波浪载荷直接计算分析,认为规范计算不能得到穿梭油船合理的波浪载荷,建议采用直接计算的方法;孙雪荣[5]综合模型试验与理论预报的共同规律对小方型系数目标船的波浪载荷研究,但是并未对目前基于规范的非线性修正提出明确化的建议。
本文以1艘测量船为研究对象,同时采用规范计算法和直接计算法,规范计算采用中国船级社《钢制海船入级规范》[6](简称CCS海规)第二篇2.2.3和劳氏船级社《劳氏军用舰船入级规范与规则》[7](简称LR军规)第5篇第4章第3节计算,其中劳氏军规在载荷计算时考虑了船首外飘砰击载荷,载荷非线性效应与外飘面积系数直接对应。直接计算分别采用三维势流波浪理论方法,结合散布图预报船体的波浪载荷。通过规范计算方法、直接计算方法的对比分析,进行修正分离系数、分布系数、载荷均值,研究确定该综合测量船的波浪载荷设计值。
1 波浪载荷直接计算方法在测量船的直接计算时,假设流体无黏、无旋、不可压缩,基于势流理论计算分析。速度势函数满足拉普拉斯方程,考虑自由水面和不可穿透的物面边界条件,采用满足自由水面条件的频域计算格林函数,采用边界元法计算速度势函数。按照伯努利公式计算物体湿表面上的压力分布。最后再利用达朗贝尔原理,将水动压力转化为船体所关注区域的弯矩和剪力RAO曲线。
选用合适的波浪谱,结合载荷控制参数RAO曲线,可以得到该载荷参数的响应谱及短期预报。基于长期预报理论,认为不同海况组成的短期预报是互相独立的,波浪载荷的长期预报值是各短期预报值和浪向概率分布的加权组合,从而可以得到一定超越概率水平下对应的载荷值。
2 计算模型建立基于相关资料建立其水动力模型,主要包括湿表面模型和质量模型。湿表面模型根据船体型值数据建立,应用SESAM三维建模模块Genie进行建模并划分面元网格,接着利用相关软件接口,生成水动力计算模块SESAM-Hydrod中所需的湿表面模型,湿表面单元总数2 083个。
质量模型根据母型船满载出港状态的全船重量分布,考虑本船的布置特点变化得到,通过编写mass文件以质量点形式按其实际位置布置来模拟,最大限度保证重量分布、重心位置和惯性矩等与实船一致。满足重力与浮力的误差不大于0.000 1Δ;质心与浮心的纵坐标误差不大于0.002 5L;横坐标误差不大于0.001 B的要求。
|
图 1 湿表面网格模型 Fig. 1 Wet surface mesh model |
考虑到船体横向对称性,在进行计算浪向角的选取时,0和180°范围每间隔15°取一个计算浪向,共13个浪向角。在0.2~2.1波频中每隔0.1选取一个计算波浪频率,局部加密,共21个计算频率。
本船波浪载荷的计算剖面沿船长取为21个,峰值区域(船中1/2 L处、尾部1/4 L处)局部加密,其中剖面剪切中心垂向坐标近似选取为船体横剖面垂向中和轴坐标。
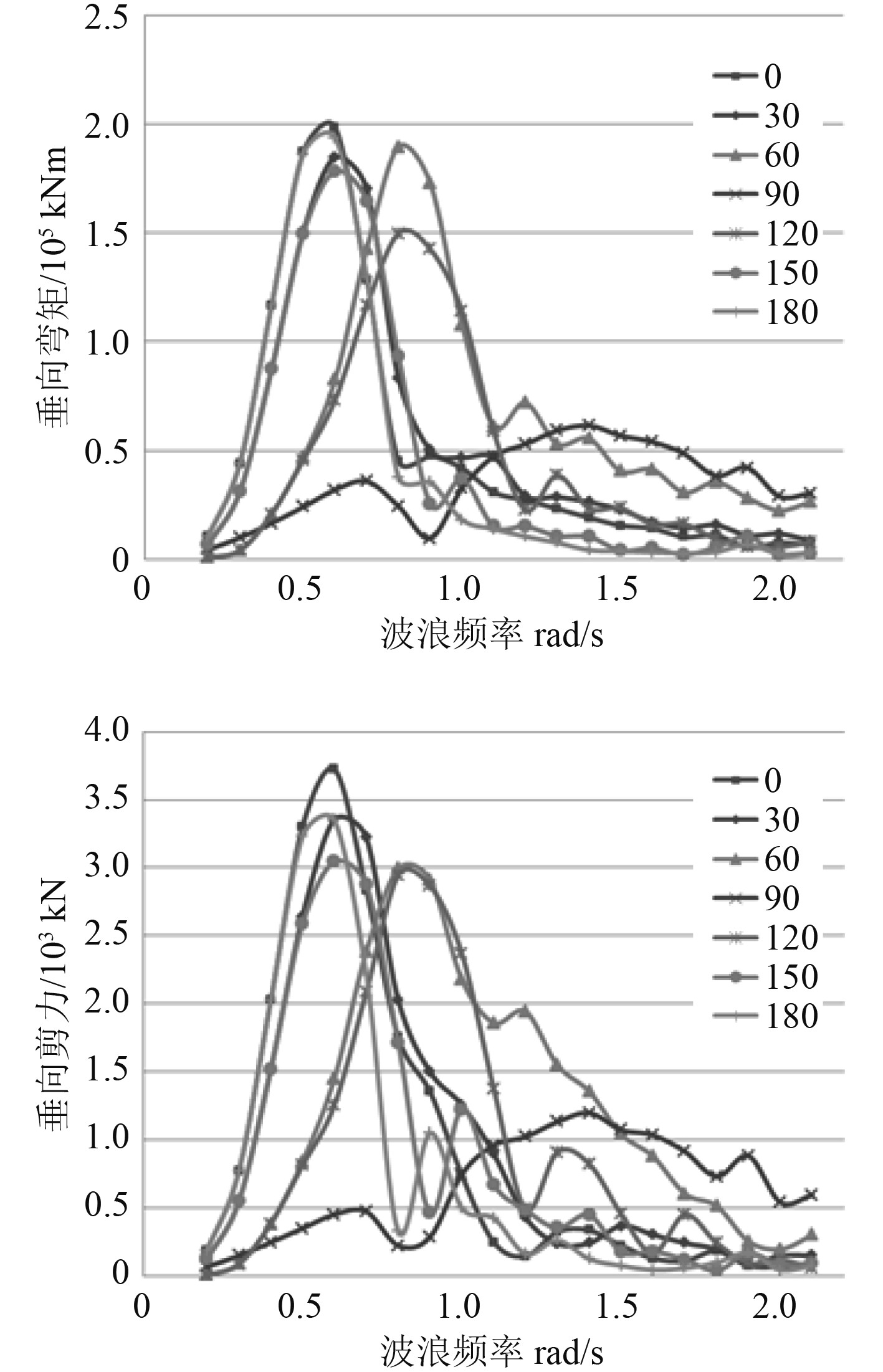
3 波浪载荷计算 3.1 波浪载荷直接计算 3.1.1 剖面载荷RAO响应及设计波确定在总纵强度的校核中,对于单体船而言一般最关心垂向弯矩、垂向剪力,基于三维线性势流理论计算方法,计算得本船在单位波幅下剖面特征载荷的频响函数,结果如图2所示。依据设计波的相关定义,垂向弯矩、剪力RAO出现最大值所对应的波浪频率、浪向、相位角为设计波的相关参数,如表1所示。
|
图 2 船中区域处垂向弯矩RAO曲线图 Fig. 2 RAO curve of vertical bending moment |
|
|
表 1 设计波参数 Tab.1 Design wave parameters |
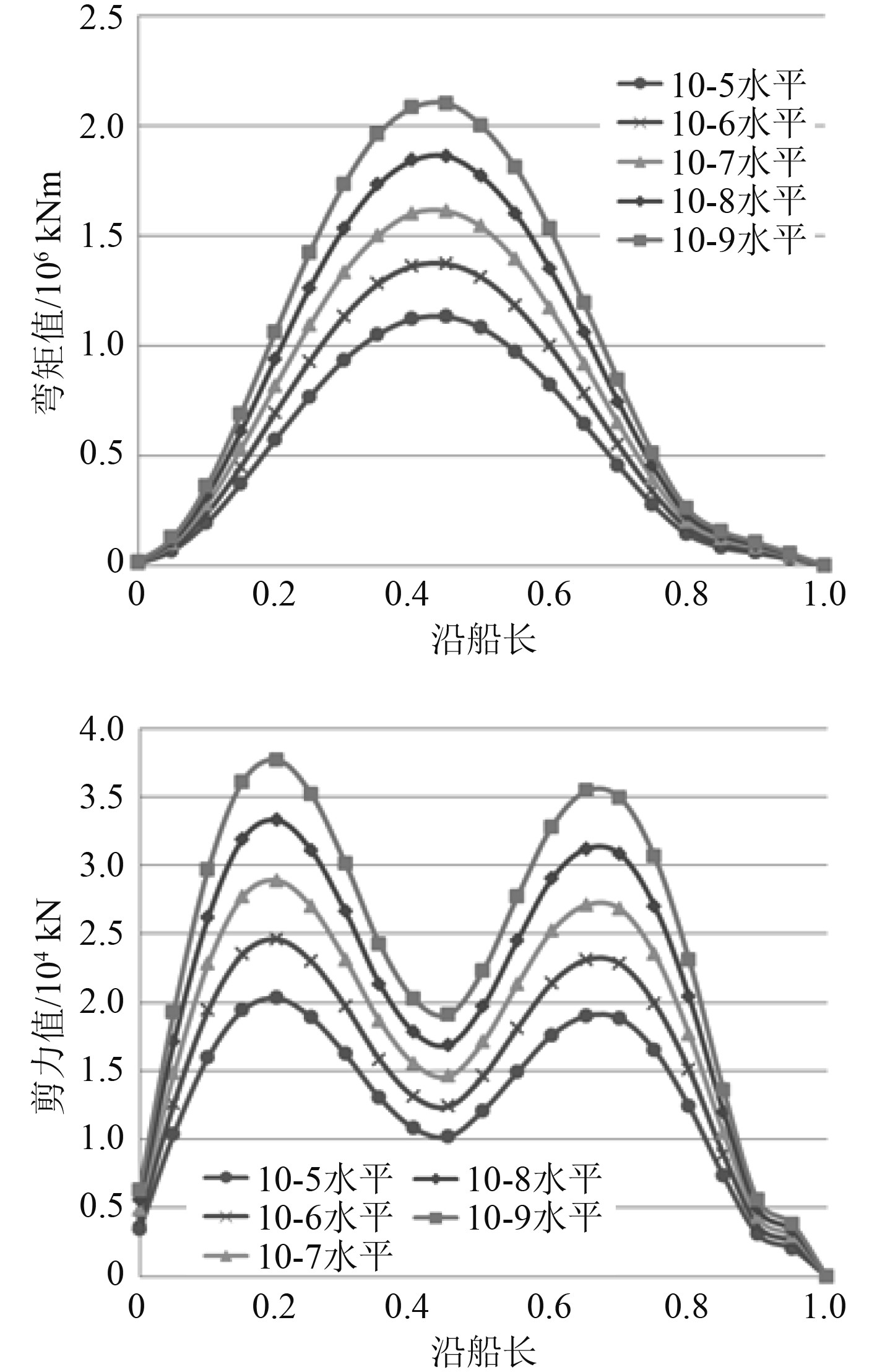
基于北大西洋海洋环境IACS Rec.34波浪统计资料,获取不同超越概率水平下的剖面载荷长期预报结果,如图3所示。可以看出,垂向弯矩在船中区域出现峰值,首尾趋向于0,而垂向剪力在船长1/4 L区域出现最大值,首尾和船中区域较小。
|
图 3 不同概率水平下的波浪弯矩长期预报值 Fig. 3 Long-term prediction value of wave bending moment |
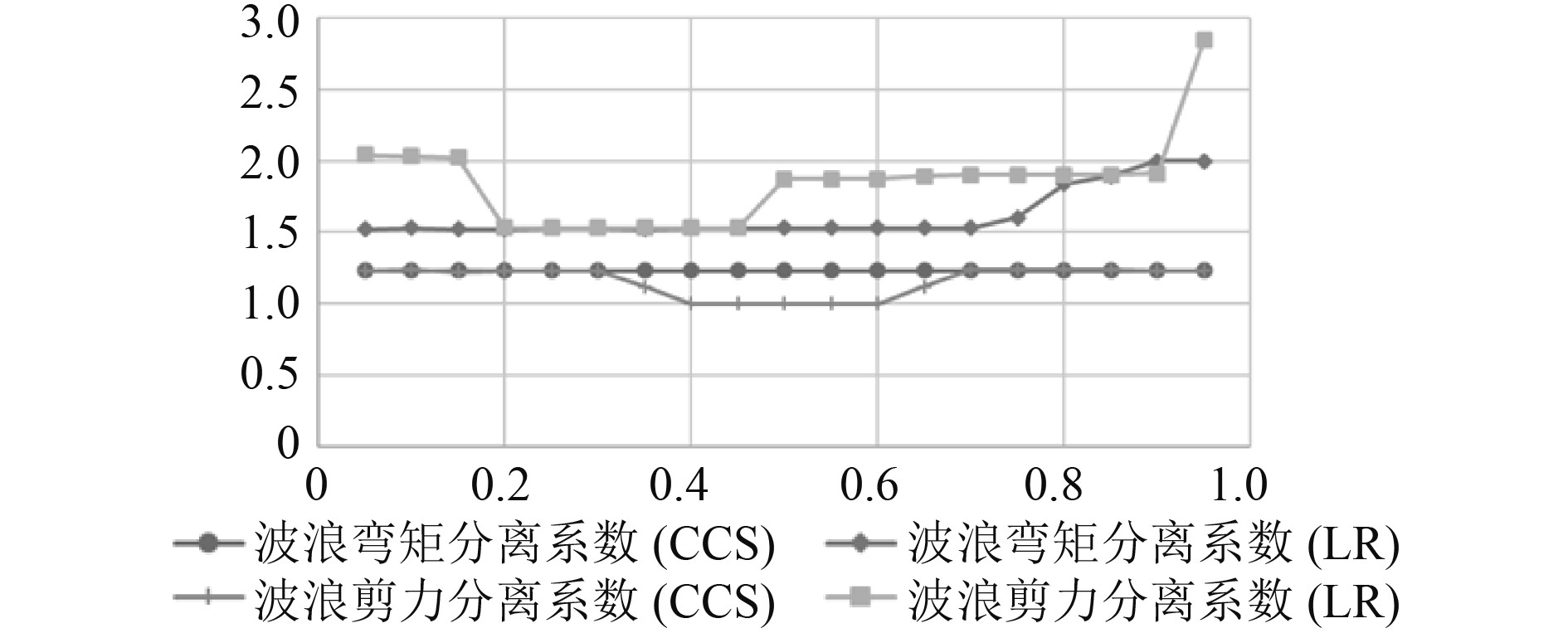
通过线性波浪理论得到的波浪弯矩和波浪剪力值未能考虑中拱中垂非线性分离的影响,由CCS海规和LR军规计算得到的中拱中垂载荷分离系数如图4所示。
|
图 4 不同规范下波浪载荷分离系数对比 Fig. 4 Comparison of wave load separation coefficient under different specifications |
由图中可以看出,CCS海规分离系数小于LR军规分离系数,且CCS海规沿船长分离系数保持不变,而LR军规首部分离系数有一个明显的升高,这主要由于CCS海规分离系数主要用于方形系数来体现,而LR军规的载荷计算中考虑砰击动弯矩和首尾外飘面积的差异,对载荷非线性进行定量计算,考虑更为合理。
考虑本船具有较大首部外飘,砰击载荷的影响显著,中垂中拱载荷非线性分离效应更为显著,这一点从本船的外飘系数即可看出。CCS海规在2.2.3中明确指出,对具有大外飘的船,可要求考虑砰击引起的附加弯矩,但CCS规范并没有给出具体计算方法,而LR军规的载荷计算可以定量考虑砰击动载荷,且CCS海规和LR军规总强度应力计算方法和校核衡准一致,因此为了全面的评估本船的波浪载荷,选取LR军规的中垂中拱分离系数为本船波浪弯矩设计载荷的分离系数。
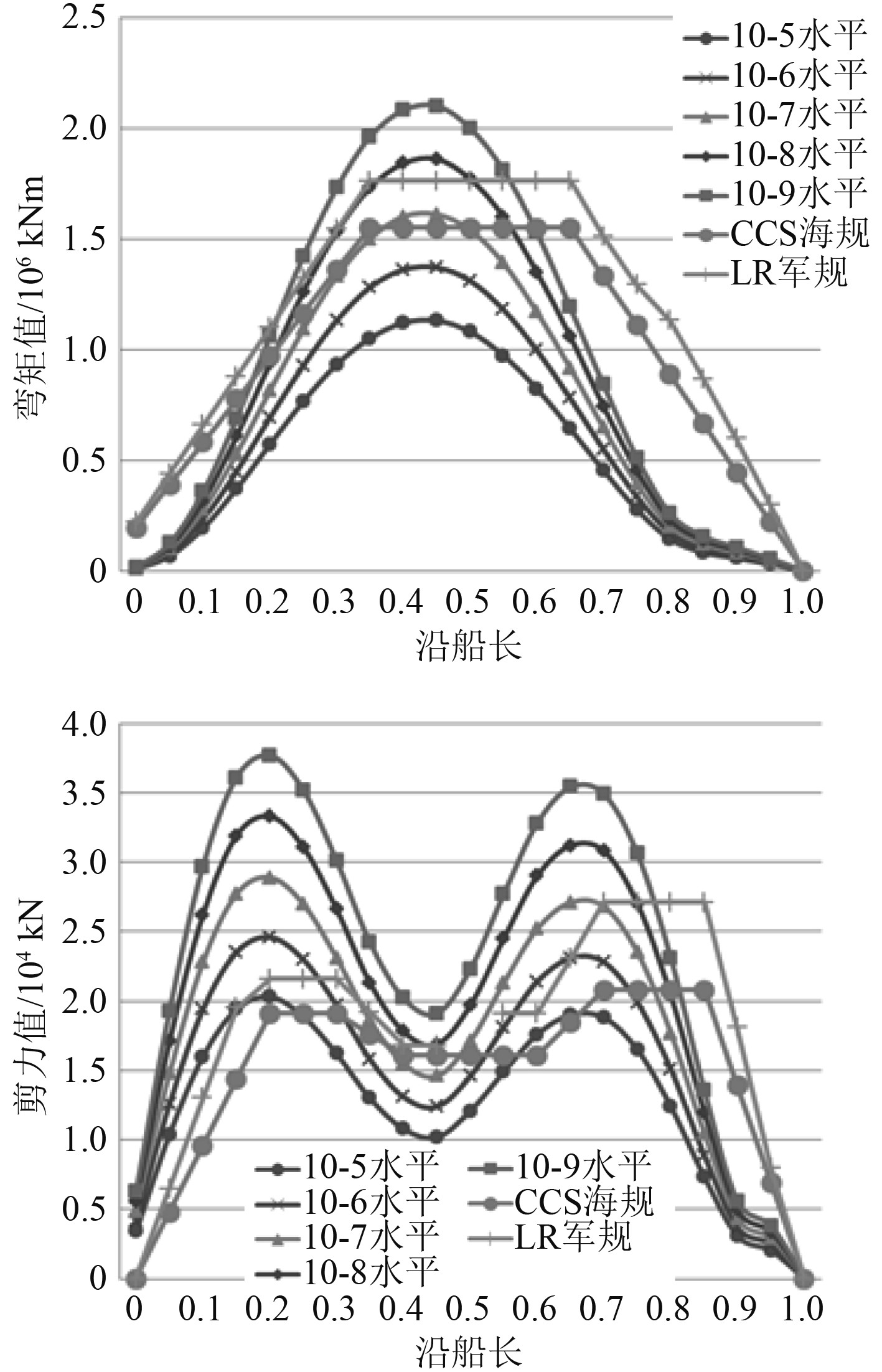
3.2.2 波浪载荷设计均值为了取得波浪载荷设计均值的相当长期预报概率水平,将CCS海规波浪载荷峰值计算值和LR军规波浪载荷峰值计算值进行差值平均,忽略分离系数的影响,与不同概率水平下直接计算长期预报值对比如图5所示。
|
图 5 不同规范下的波浪载荷计算结果与长期预报值对比 Fig. 5 Comparisons of long-term prediction value by different specifications |
可以看出,在忽略波浪载荷分离系数后:
1)CCS海规的波浪弯矩设计值接近10−7概率水平下的直接计算预报值,LR军规的波浪弯矩设计值接近10−8概率水平下的直接计算预报值;CCS海规波浪弯矩峰值范围和LR军规的波浪弯矩峰值范围在0.4 L-0.65 L,直接计算的峰值范围与规范计算值相比往船尾有一个偏移,约在0.425 L左右;
2)CCS海规的波浪剪力计算值接近10−5~10−6概率水平下的直接计算预报值,LR军规的波浪剪力计算值接近10−6~10−7概率水平下的直接计算预报值;直接计算的波浪剪力峰值范围比2个规范的波浪弯矩峰值范围明显往船尾有一个偏移,同时尾部剪力峰值比规范计算值有一个明显的增加。
根据以上分析和CCS海规2.2.9的要求,综合确定选取10-8概率水平下的波浪载荷直接计算长期预报值为波浪载荷设计均值。
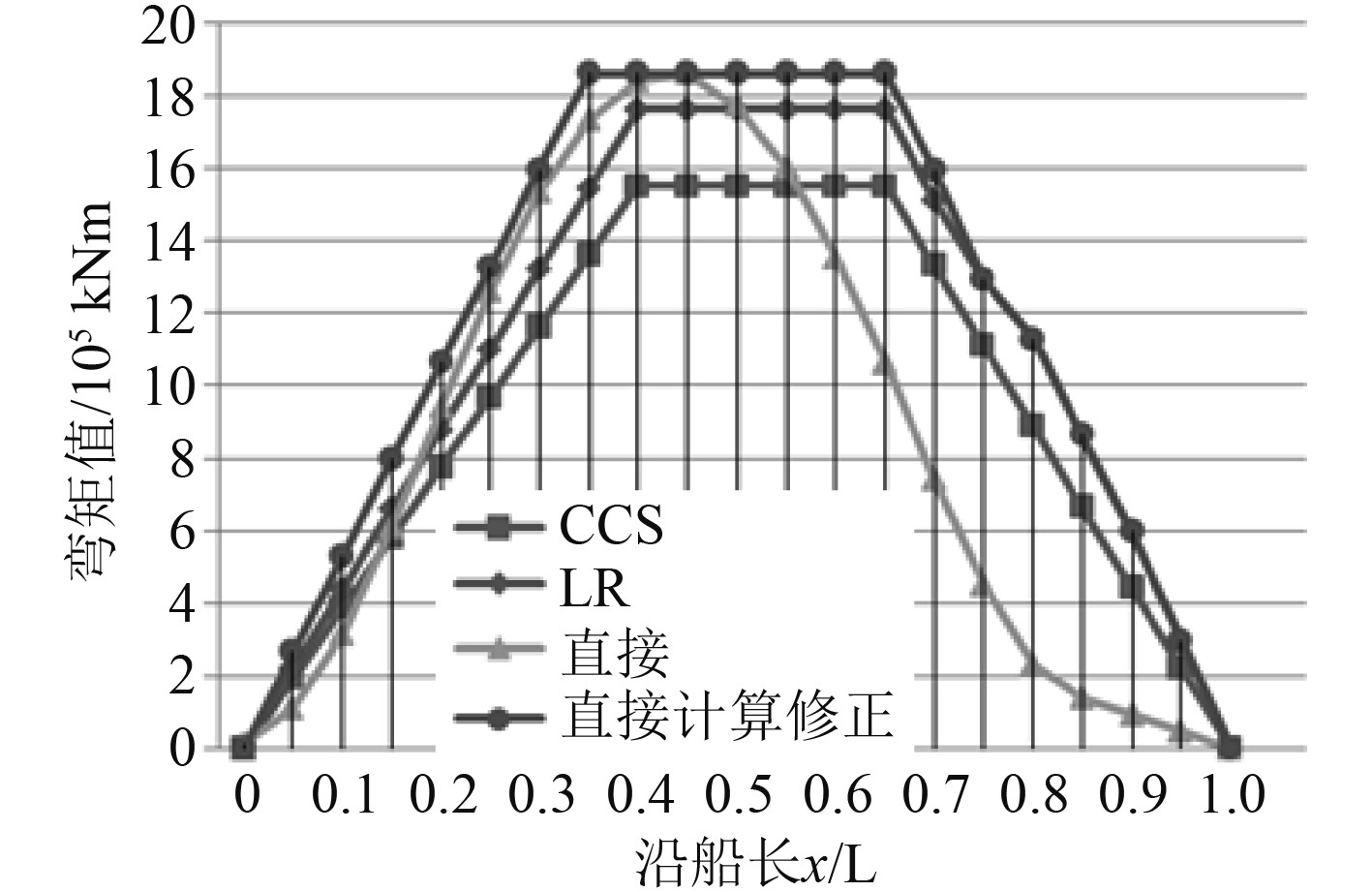
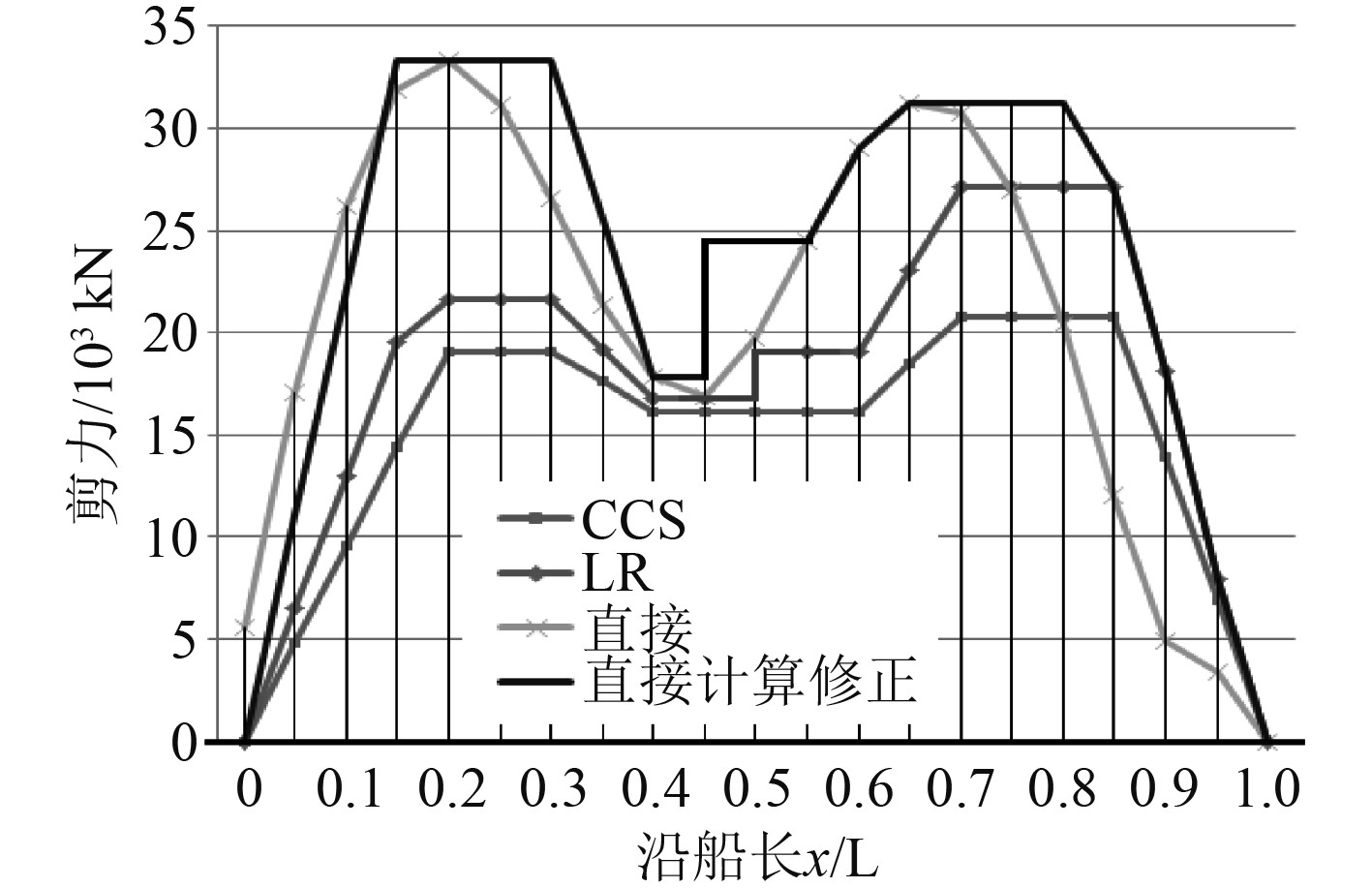
3.2.3 分布系数及波浪载荷设计均值修正综合考虑CCS海规、LR军规、直接计算的波浪载荷沿船长分布情况,规范载荷设计值沿船长分布考虑了波峰和波谷位置的移动的影响,峰值包络值分布纵向有一定范围,比直接计算值范围更大,并且波浪载荷直接计算结果显示了本船载荷峰值分布向船尾偏移的规律,同时LR军规中更合理的考虑了首部砰击载荷的影响。故本船波浪载荷沿船长的分布选择LR军规中的载荷分布系数,并根据直接计算考虑峰值偏移影响,对波浪载荷设计均值的按照该分布系数进行修正。规范计算值、直接计算值(10−8)以及直接计算修正值沿船长对比如图6和图7所示。
|
图 6 规范计算值、直接计算值和修正后的波浪弯矩设计均值对比 Fig. 6 Comparison of design means of wave bending moment |
|
图 7 规范计算值、直接计算值和修正后的波浪剪力设计均值对比 Fig. 7 Comparison of design means of wave vertical shear |
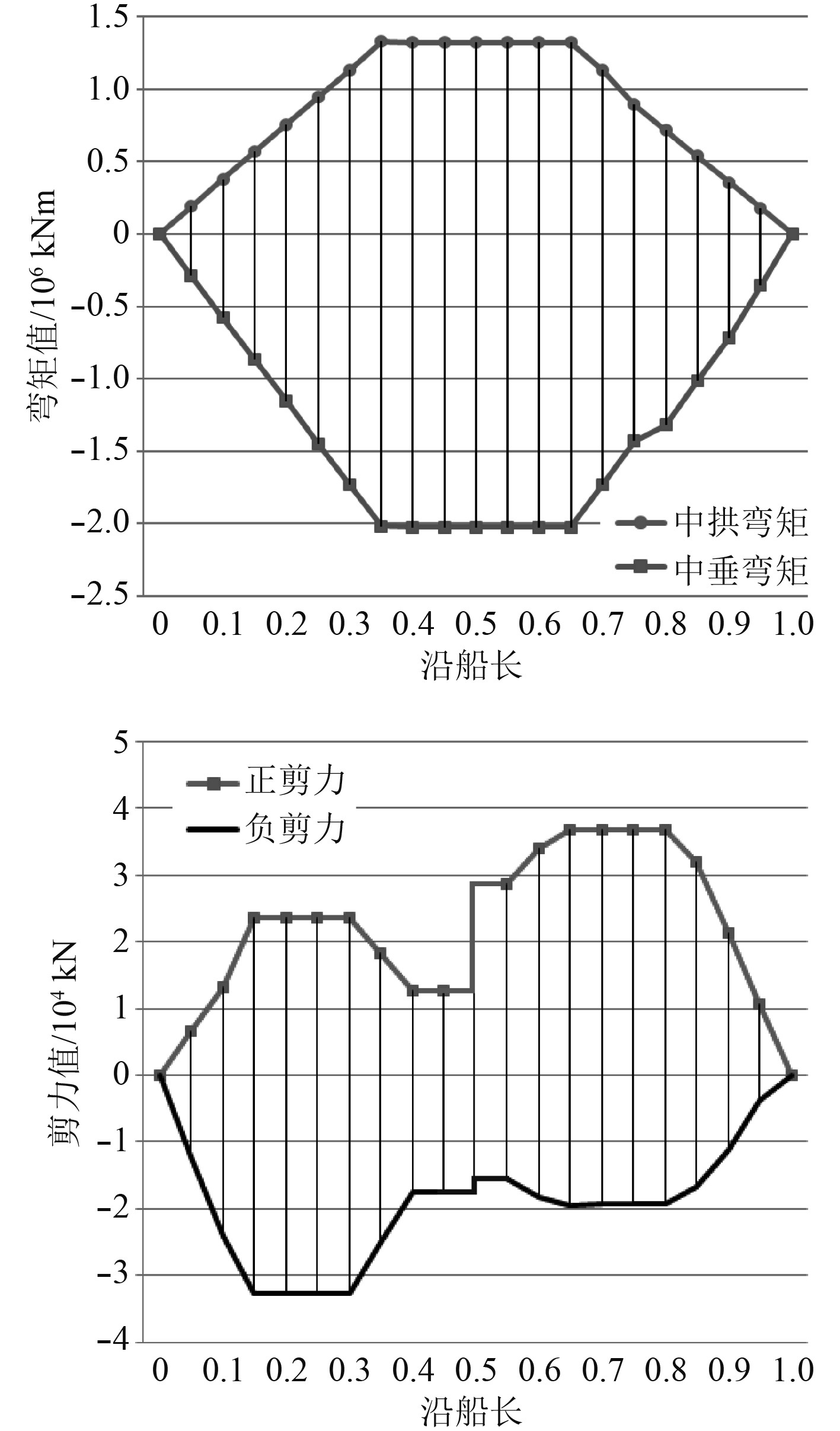
依据得到的中拱中垂非线性分离系数,对根据分布系数修正、波浪载荷设计均值得到的修正值进行中拱中垂分离,得到本船中拱和中垂波浪载荷设计值,分布曲线图如图8所示。
|
图 8 中拱和中垂波浪载荷波浪载荷设计值 Fig. 8 Design value of wave load |
通过不同规范、直接计算针对某测量船的波浪载荷进行了分析,可以得出以下结论:
1)CCS海规与LR军规相比,CCS海规沿船长分离系数保持不变,而LR军规首部分离系数有一个明显的升高,主要是因为LR军规中考虑了砰击动弯矩和首尾外飘面积等非线性因素影响,因此,在针对大外飘、考虑砰击引起的附加弯矩的船型规范计算时选用LR军规更为合理。
2)波浪弯矩、剪力的直接计算值峰值范围往船尾有一个明显偏移,建议前期设计规范计算时可结合直接计算考虑适当扩大峰值区域范围。
3)通过规范与直接计算对比分析,提出分离系数、分布系数、设计均值进行修正的方法,可为相似船型确定波浪载荷设计值提供参考。
| [1] |
梁双令, 章红雨, 齐江辉, 等. 基于设计波法的船体波浪载荷计算[J]. 舰船科学技术, 2018(07). DOI:10.3404/j.issn.1672-7649.2018.07.016 |
| [2] |
单鹏昊, 吴嘉蒙, 王福花. UR S11A对船体梁波浪载荷长期极值的影响研究[J]. 中国造船, 2018(01). DOI:10.3969/j.issn.1000-4882.2018.01.021 |
| [3] |
王红芳. 大尺度结构船舶波浪线性载荷数值计算[J]. 舰船科学技术, 2018(9). DOI:10.3404/j.issn.1672-7649.2018.09.023 |
| [4] |
杨朕, 张利军, 曹 凯, 等. 穿梭油船波浪载荷直接计算分析[J]. 中国航海, 2019(3). |
| [5] |
孙雪荣, 汪战军, 彭亚康. 小方型系数船舶的船体波浪载荷综合研究[J]. 舰船科学技术, 2017(15). |
| [6] |
中国船级社. 钢质海船入级规范[S], 2018.
|
| [7] |
Lloyd′s Register. General information for the rules and regulations for the classification of naval ships[S], 2014.
|
 2020, Vol. 42
2020, Vol. 42
