2. 齐鲁工业大学(山东省科学院),山东省科学院海洋仪器仪表研究所,山东 青岛 266061
2. Institute of Marine Instruments and Instruments, Qilu University of Technology (Shandong Academy of Sciences), Qingdao 266061, China
圆柱壳结构具有特殊的几何构型,对于轴压、径压、扭转以及组合载荷均具有很好的承载作用,在船舶与海洋工程等各类领域中都有十分广泛的应用。圆柱壳的主要失效模式为失稳,针对其失稳稳定性问题,特别是轴压作用下的圆柱壳失稳载荷和模态,一直是学者研究最为活跃的课题之一[1]。
早期针对轴压作用下薄壁圆柱壳的稳定性试验表明结构实际的失稳承载能力和理论上理想的完善壳体相比较小,原因就在于初始缺陷的存在会引起轴压薄壁圆柱壳临界失稳载荷很大程度的折减。祝恩淳等[2]针对轴压作用下薄壁圆柱壳的试验数据,采取统计分析的方法给出了结构失稳应力的经验计算公式。Lauren Kougias[3]采用有限元数值方法研究了壳体不圆度对轴压圆柱壳稳定性的影响,认为圆柱壳不圆度与壳体厚度相当时,临界承载能力降低可达75%。Muggeridge等[4]研究认为局部轴对称缺陷对圆柱壳失稳临界载荷的影响很大。龚友根等[5]研究凹坑形式的轴对称缺陷对轴压圆柱壳失稳承载能力的影响。王小明[6]研究了纵骨对环肋圆柱壳壳板稳定性的影响。
一系列的研究表明,研究分析方法对于问题的适用性以及结果准确度存在突出的影响。针对圆柱薄壳结构的失稳问题,Croll等[7-8]提出的刚度折减方法(Reduced Stiffness Method,RSM)在一定程度上理论值可以与实验值很好的吻合,随即引发了基于RSM开展不同类型以及不同承载的薄壁壳体结构失稳载荷的研究。Rossana C. Jaca等[9]应用RSM法研究了风载荷作用下圆柱壳结构的失稳失稳问题,认为采用RSM方法得到的失稳下界与非线性分析结果较为一致。Hongtao Wang等[10]采用RSM方法对圆柱壳体结构的失稳承载能力进行了优化研究,认为在给定材料和几何参数的范围内,改善了失稳临界载荷。Eduardo M. Sosa等[11]基于RSM方法分析了风载荷作用下含有初始缺陷的圆锥壳结构失稳临界载荷。Xu Bai等[12]分析了刚度折减对环肋圆柱壳承载能力的影响,研究结果表明周向薄膜刚度对圆柱壳的稳定性影响最大,轴向的弯曲刚度对圆柱壳稳定性的影响较小。
在现有基础上,本文采取RSM针对具有轴对称缺陷的轴压圆柱壳的稳定性进行研究。
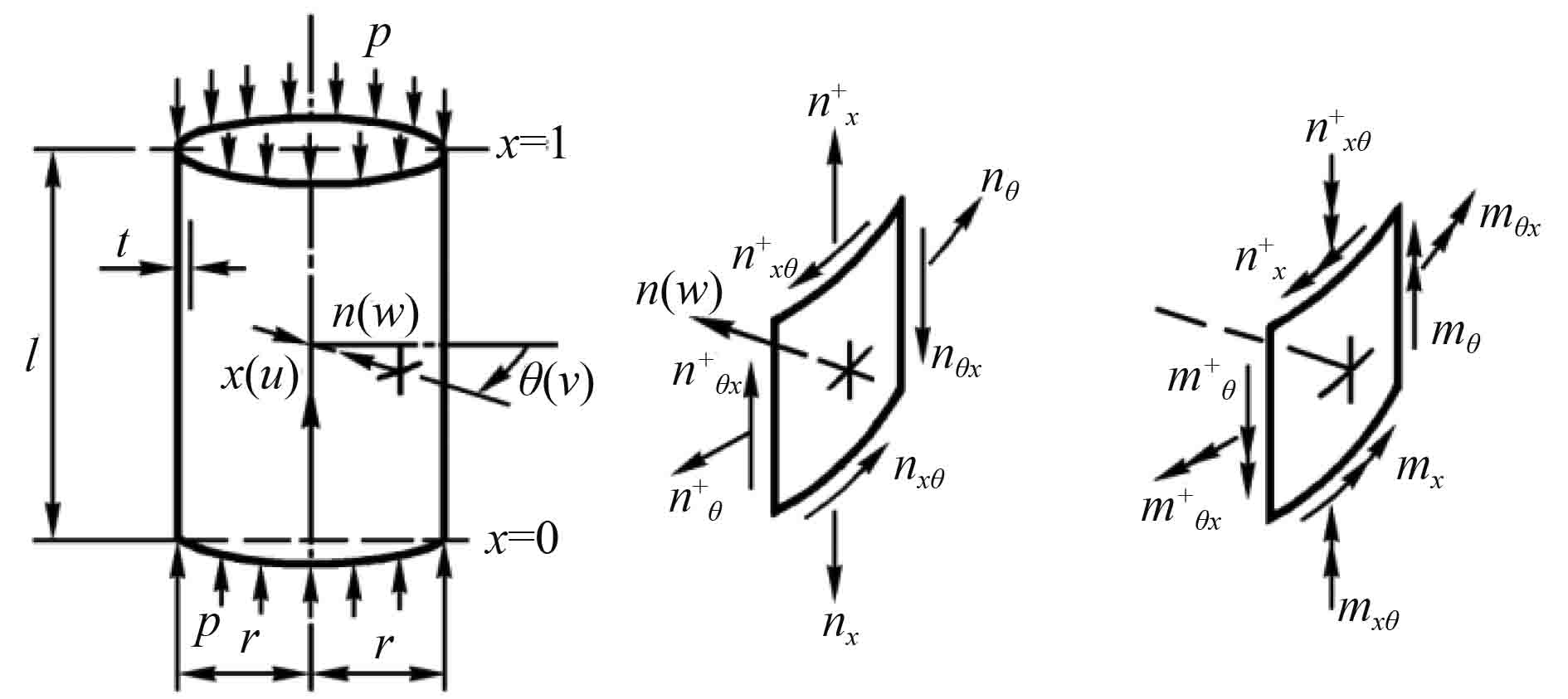
1 轴压下完善圆柱壳的失稳载荷 1.1 失稳载荷轴压作用下完善薄壁圆柱壳模型如图1所示。圆柱壳两端自由支持在刚性周界,设定长度为
|
图 1 轴压完善圆柱壳模型 Fig. 1 Perfect cylindrical shell model under axial compression |
依据薄壳理论,圆柱壳失稳前的应力状态下:
| $ \left( {\sigma _x^F,\sigma _\theta ^F} \right) = \left( { - p,0} \right) \text{,} $ | (1) |
| $ \left( {E_x^F,E_\theta ^F} \right) = \left( { - \frac{p}{E},\frac{{\mu p}}{E}} \right) \text{;} $ | (2) |
失稳后的平衡状态为:
| $ \left\{ \begin{array}{l} U = U_\sigma ^F + u \text{,} \\ V = V_\sigma ^F + v \text{,} \\ W = W_\sigma ^F + w \text{。} \end{array} \right. $ | (3) |
其中:
失稳后,总应力、应变、弯矩、转角可以写为:
| $ \left\{ \begin{array}{l} {\sigma _x} = \sigma _x^F + {n_x}\text{,} \\ {\sigma _\theta } = \sigma _\theta ^F + {n_\theta }\text{,} \\ {\sigma _{x\theta }} = \sigma _{x\theta }^F + {n_{x\theta }} = {n_{x\theta }} \text{;} \end{array} \right. $ | (4) |
| $ \left\{ \begin{array}{l} {E_x} = E_x^F + {\varepsilon _x}\text{,} \\ {E_\theta } = E_\theta ^F + {\varepsilon _\theta } \text{,} \\ {E_{x\theta }} = E_{x\theta }^F + {\varepsilon _{x\theta }} = {\varepsilon _{x\theta }} \text{;} \end{array} \right. $ | (5) |
| $ \left\{ \begin{array}{l} {M_x} = M_x^F + {m_x} = {m_x}\text{,} \\ {M_\theta } = M_\theta ^F + {m_\theta } = {m_\theta }\text{,} \\ {M_{x\theta }} = M_{x\theta }^F + {m_{x\theta }} = {m_{x\theta }}\text{;} \end{array} \right. $ | (6) |
| $ \left\{ \begin{array}{l} {X_x} = X_x^F + {\gamma _x} = {\gamma _x} \text{,} \\ {X_\theta } = X_\theta ^F + {\gamma _\theta } = {\gamma _\theta } \text{,} \\ {X_{x\theta }} = X_{x\theta }^F + {\gamma _{x\theta }} = {\gamma _{x\theta }} \text{。} \end{array} \right. $ | (7) |
其中公式右边第1项为失稳前,第2项为失稳后相对增量。
将应变、应力分成线性项部分
| $ V = {V_0} + {V_1} + {V_2} + ... \text{。} $ | (8) |
其中:
| $ \begin{aligned} & {V_0} = \frac{1}{2}\int\nolimits_0^l {\int\nolimits_0^{2{\text{π}} } {(N_x^FE_x^F} } + N_\theta ^FE_\theta ^F + 2N_{x\theta }^FE_{x\theta }^F)tr{\rm d}\theta {\rm d}x - \\ & \frac{1}{2}\int\nolimits_0^{2{\text{π}} } {ptU_\sigma ^F\left| {_0^lr{\rm d}\theta } \right.} {\text{,}} \end{aligned} $ | (9) |
| $ \begin{aligned} & {V_1} = \frac{1}{2}\int\nolimits_0^l {\int\nolimits_0^{2{\text{π}} } {(N_x^F{{\varepsilon '}_x}} } + {{n'}_x}E_x^F + N_\theta ^F{{\varepsilon '}_\theta } + {{n'}_\theta }E_\theta ^F + \\ & 2N_{x\theta }^F{{\varepsilon '}_{x\theta }} + 2{{n'}_{x\theta }}E_{x\theta }^F)tr{\rm d}\theta {\rm d}x - \int\nolimits_0^{2{\text{π}} } {ptu\left| {_0^lr{\rm d}\theta } \right.} {\text{,}} \end{aligned} $ | (10) |
| $ \left\{ \begin{aligned} & {V_2} = {V_{\rm{m}}} + {V_b} + {V_{2m}} {\text{,}} \\ & {V_{\rm{m}}} = \frac{1}{2}\int\nolimits_0^l {\int\nolimits_0^{2{\text{π}} } {({{n'}_x}{{\varepsilon '}_x}} } + {{n'}_\theta }{{\varepsilon '}_\theta } + 2{{n'}_{x\theta }}{{\varepsilon '}_{x\theta }})r{\rm d}\theta {\rm d}x {\text{,}}\\ & {V_b} = \frac{1}{2}\int\nolimits_0^l {\int\nolimits_0^{2{\text{π}} } {({{m'}_x}{{\gamma '}_x} + {{m'}_\theta }{{\gamma '}_\theta } + 2{{m'}_{x\theta }}{{\gamma '}_{x\theta }})} } r{\rm d}\theta {\rm d}x {\text{,}} \\ & {V_{2m}} = \frac{1}{2}\int\nolimits_o^l {\int\nolimits_0^{2{\text{π}} } {(N_x^F{{\varepsilon ''}_x} + {{n''}_x}E_x^F + N_\theta ^F{{\varepsilon ''}_\theta } + {{n''}_\theta }E_\theta ^F)} } r{\rm d}\theta {\rm d}x {\text{。}} \end{aligned} \right. $ | (11) |
圆柱壳位移选取为:
| $ \left\{ \begin{aligned} & u = {u_{ij}}\cos i\theta \cos j{\text{π}} x/l\text{,} \\ & v = {v_{ij}}\sin i\theta \sin j{\text{π}} x/l \text{,} \\ & w = {w_{ij}}\cos i\theta \sin j{\text{π}} x/l \text{。} \end{aligned} \right. $ | (12) |
其中:
依据文献[13]中圆柱壳几何方程和胡克定律,可以得到:
| $ \begin{split} & {V_m} = \frac{{K{\text{π}} L}}{8}\left( {1 - \mu } \right){\left( {{v_{ij}}\lambda - {u_{ij}}i} \right)^2} - \\ & \frac{{K{\text{π}} L}}{4}\left( {\mu \left( {{v_{ij}}i - {w_{ij}}} \right) - {u_{ij}}\lambda } \right){u_{ij}}\lambda + \\ & \frac{{K{\text{π}} L}}{4}\left( {{v_{ij}}i - {w_{ij}} - \mu {u_{ij}}\lambda } \right)\left( {{v_{ij}}i - {w_{ij}}} \right) {\text{,}} \end{split} $ | (13) |
其中:
| $ \begin{split} & {V_b} = \frac{{K{\text{π}} L}}{2}\frac{{\left( {1 - \mu } \right)w_{ij}^2{i^2}{\lambda ^2}}}{\alpha } + \\ & \frac{{K{\text{π}} L}}{4}\frac{{\left( {{w_{ij}}{\lambda ^2} + \mu {w_{ij}}{i^2}} \right){w_{ij}}{\lambda ^2}}}{\alpha } + \\ & \frac{{K{\text{π}} L}}{4}\frac{{\left( {{w_{ij}}{i^2} + \mu {w_{ij}}{\lambda ^2}} \right){w_{ij}}{i^2}}}{\alpha } {\text{,}} \end{split} $ | (14) |
其中:
| $ {V_{2m}} = - \frac{{pt{\text{π}} L}}{4}w_{ij}^2{\lambda ^2}\text{,} $ | (15) |
由于总势能二次项部分在任意条件下的偏导为0,因而可转化为特征值方程问题:
| $\left[ \begin{array}{l} {A_{11}}\quad {A_{12}}\quad {A_{13}} \\ {A_{21}}\quad {A_{22}}\quad {A_{23}} \\ {A_{31}}\quad {A_{32}}\quad {A_{33}} \\ \end{array} \right]\left\{ \begin{array}{l} {u_{ij}} \\ {v_{ij}} \\ {w_{ij}} \\ \end{array} \right\} = 0\text{,}$ | (16) |
其中:
| $ \left\{ \begin{aligned} & {{A'}_{11}} = {\lambda ^2} + \frac{1}{2}\left( {1 - \mu } \right){i^2} \text{,} \\ & {{A'}_{12}} = - \frac{1}{2}\left( {1 + \mu } \right)i\lambda\text{,} \\ & {{A'}_{13}} = \mu \lambda \text{,} \\ & {{A'}_{22}} = {i^2} + \frac{1}{2}\left( {1 - \mu } \right){\lambda ^2}\text{,} \\ & {{A'}_{23}} = - i \text{,} \\ & {{A'}_{33}} = \frac{1}{\alpha }{\left( {{i^2} + {\lambda ^2}} \right)^2} + 1 \text{,} \\ & {{A''}_{11}} = {{A''}_{22}} = {{A''}_{13}} = {{A''}_{23}} = {{A''}_{12}} = 0\text{,} \\ & {{A''}_{33}} = \left( {1 - {\mu ^2}} \right){\lambda ^2} \text{。} \end{aligned} \right. $ | (17) |
其中:
式(16)存在任意解的条件是系数行列式为0,因而
| $ \Lambda = \frac{{\dfrac{{\left( {1 - {\mu ^2}} \right){\lambda ^4}}}{{{{\left( {{i^2} + {\lambda ^2}} \right)}^2}}} + \dfrac{{{{\left( {{i^2} + {\lambda ^2}} \right)}^2}}}{\alpha }}}{{\left( {1 - {\mu ^2}} \right){\lambda ^2}}}\text{。} $ | (18) |
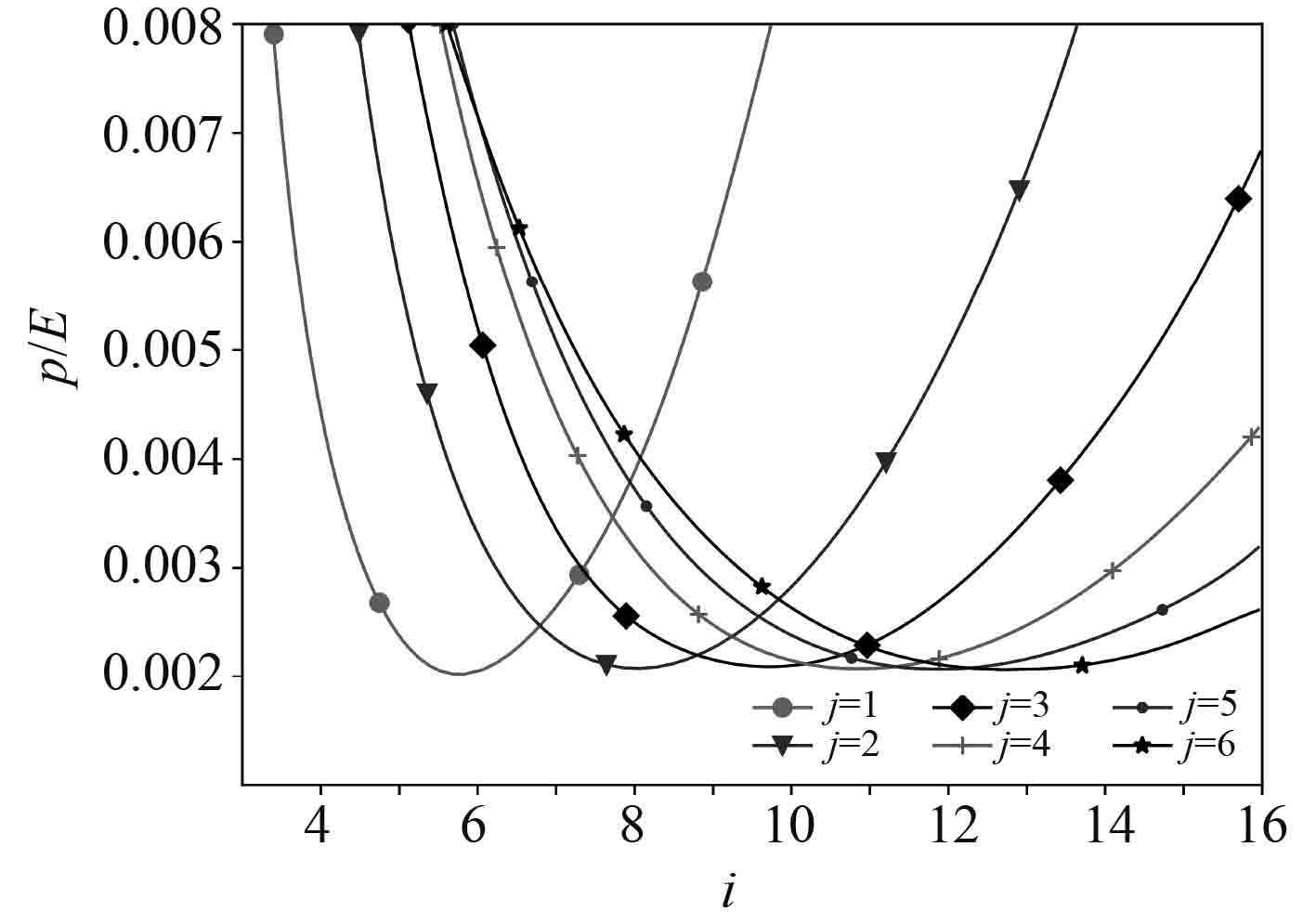
图2给出了应用式(18)得到的轴压作用下完善圆柱壳结构的失稳载荷(
|
图 2 轴压圆柱壳失稳载荷图谱 Fig. 2 Instability load spectrum of axial compression cylindrical shell |
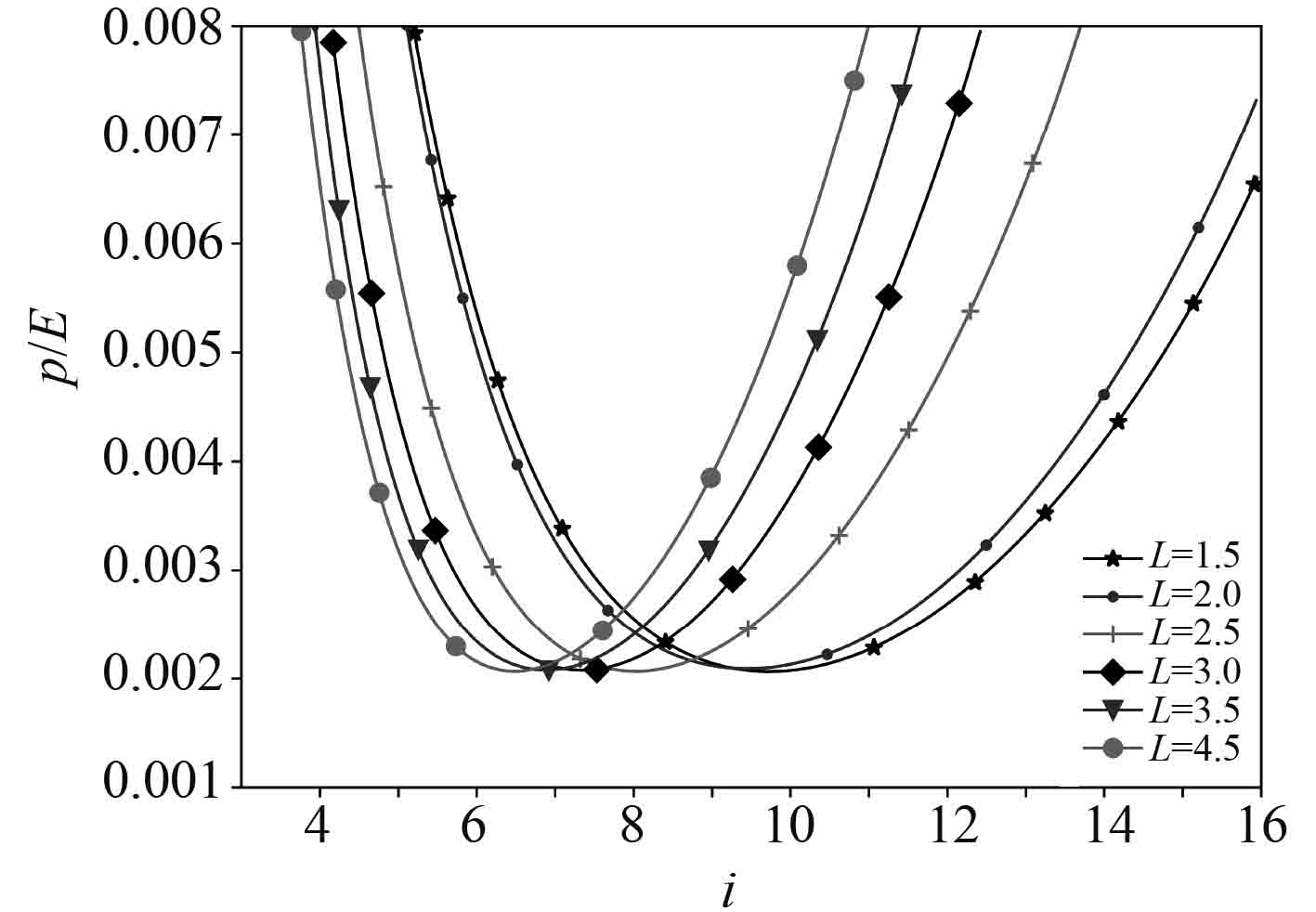
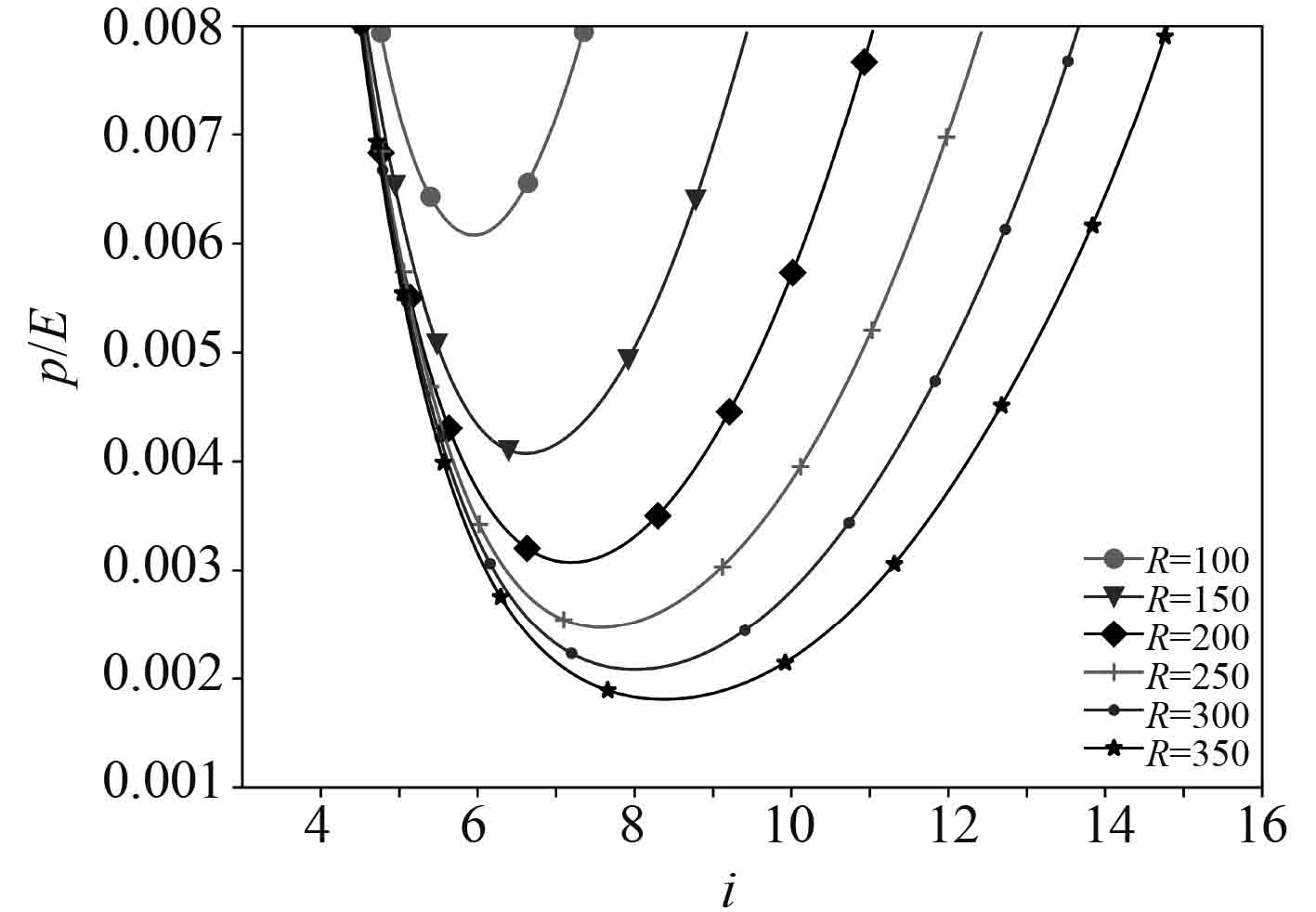
从图3和图4中可以看出,承受轴向压力圆柱壳的失稳载荷仅与圆柱壳半径与厚度的比R有关,与长度和半径的比L无关。因此在式(18)中,求其最小值,得
|
图 3 不同L下的失稳载荷 Fig. 3 Instability load at different L |
|
图 4 不同R下的失稳载荷 Fig. 4 Instability load at different R |
| $ \Lambda = \frac{1}{{\sqrt {3\left( {1 - {\mu ^2}} \right)} }}\frac{1}{R} \text{。} $ | (19) |
与经典弹性临界应力公式相同。
2 轴压圆柱壳的刚度折减分析依据式(11),轴压完善圆柱壳失稳总势能中的
| ${V_2} = \int\nolimits_0^l {\int\nolimits_0^{2{\text{π}}} {\left( {{V_m} + {V_b} - \Lambda \frac{{\partial {V_{2m}}}}{{\partial \sigma }}} \right)} } r{\rm d}\theta {\rm d}x\text{。} $ | (20) |
通过壳体的稳定条件,将轴向压力下圆柱壳稳定性问题转化为求解特征方程的特征值问题:
| $ \left( {{K_m} + {K_b} - {\Lambda ^C}{K_G}} \right)\varPhi = 0\text{。} $ | (21) |
式中:
当圆柱壳各刚度折减时,式(22)应写为:
| $ \left( {\beta {K_m} + \xi {K_b} + \Lambda '{K_G}} \right)\Phi ' = 0 \text{。} $ | (22) |
其中:
因此式(18)中的系数将变为:
| $ \left\{ \begin{aligned} & {{A'}_{11}} = \beta {\lambda ^2} + \frac{\beta }{2}\left( {1 - \mu } \right){i^2} \text{,} \\ & {{A'}_{12}} = - \frac{\beta }{2}\left( {1 + \mu } \right)i\lambda \text{,} \\ & {{A'}_{22}} = \beta {i^2} + \frac{\beta }{2}\left( {1 - \mu } \right){\lambda ^2}\text{,} \\ & {{A'}_{23}} = - \beta i \text{,} \\ & {{A'}_{13}} = \beta \mu \lambda \text{,} \\ & {{A'}_{33}} = \frac{\xi }{\alpha }{\left( {{i^2} + {\lambda ^2}} \right)^2} + \beta \text{,} \\ & {{A''}_{33}} = \left( {1 - {\mu ^2}} \right){\lambda ^2} \text{,} \\ & {{A''}_{11}} = {{A''}_{22}} = {{A''}_{13}} = {{A''}_{23}} = {{A''}_{12}} = 0 \text{。} \end{aligned} \right. $ | (23) |
可得含有折减系数的临界载荷方程:
| $\Lambda ' = \frac{{\dfrac{{\left( {1 - {\mu ^2}} \right)\beta {\lambda ^4}}}{{{{\left( {{i^2} + {\lambda ^2}} \right)}^2}}} + \dfrac{{\xi {{\left( {{i^2} + {\lambda ^2}} \right)}^2}}}{\alpha }}}{{\left( {1 - {\mu ^2}} \right){\lambda ^2}}} \text{。} $ | (24) |
通过分析,临界载荷方程分子的两项分别代表薄膜刚度和弯曲刚度对临界载荷的贡献,在公式(24)中,求其最小值得:
| $ \Lambda ' = \frac{{\sqrt {\beta \xi } }}{{\sqrt {3\left( {1 - {\mu ^2}} \right)} }}\frac{1}{R} \text{。} $ | (25) |
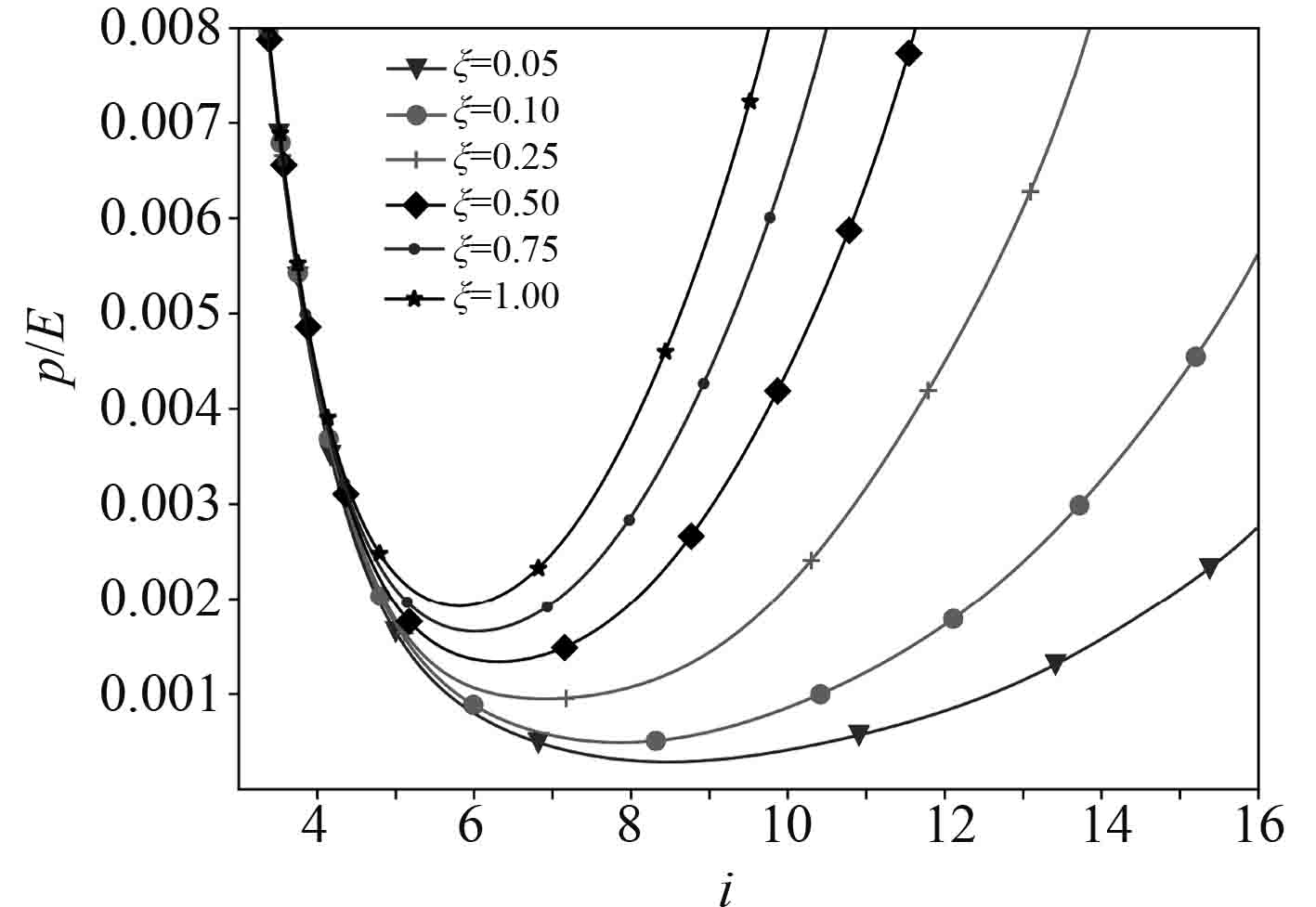
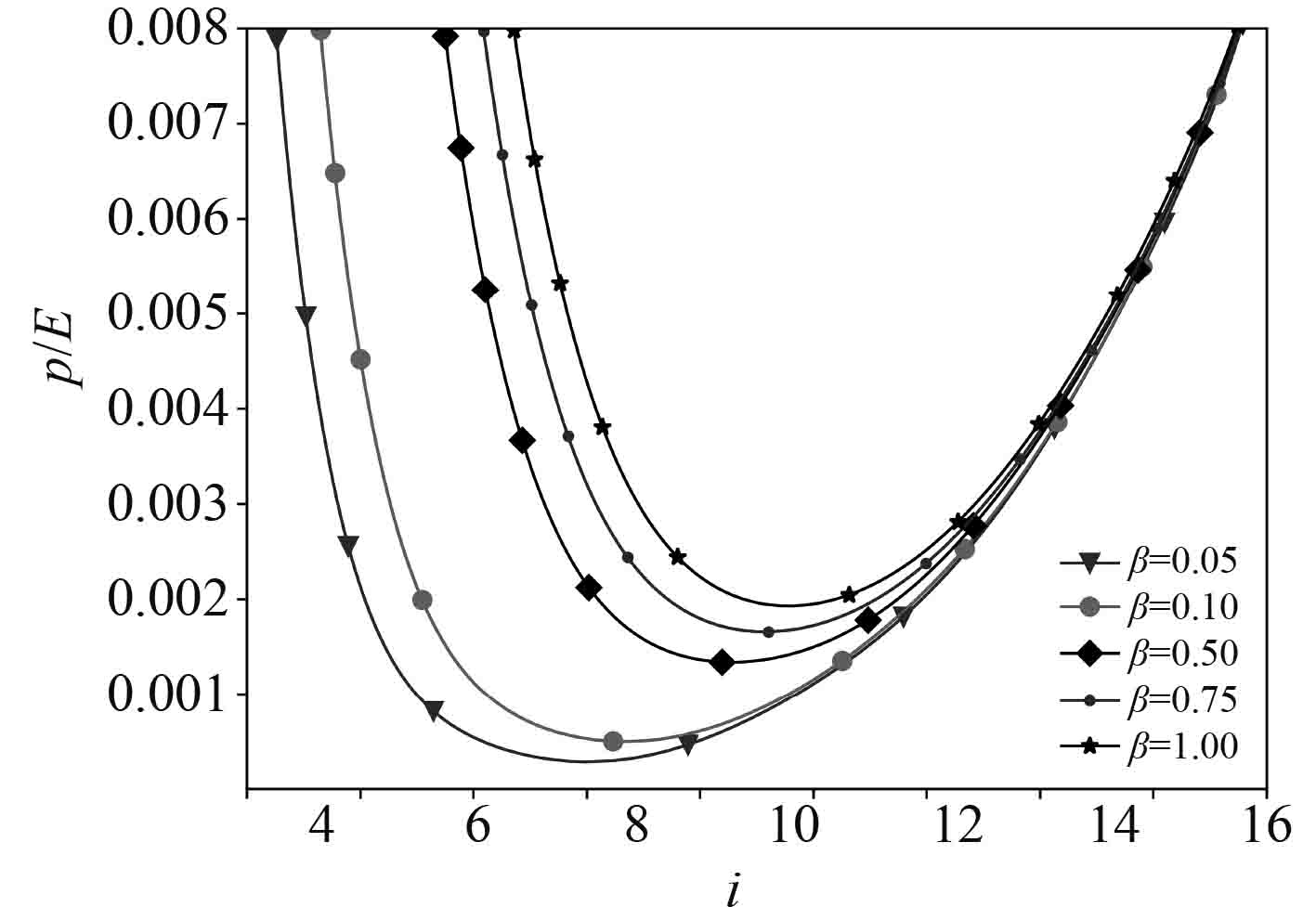
图5和图6给出了不同刚度折减系数对轴向受压薄壁圆柱壳失稳载荷的影响。
|
图 5 弯曲刚度折减失稳载荷图谱 Fig. 5 Instability load spectrum of bending stiffness reduction |
|
图 6 薄膜刚度折减失稳载荷图谱 Fig. 6 Instability load spectrum of film stiffness reduction |
可以看出,无论是薄膜刚度还是弯曲刚度的降低都会影响轴压圆柱壳的失稳模态。轴压圆柱壳失稳时周向波数随着薄膜刚度的减少而减少,随着弯曲刚度的降低而增加。
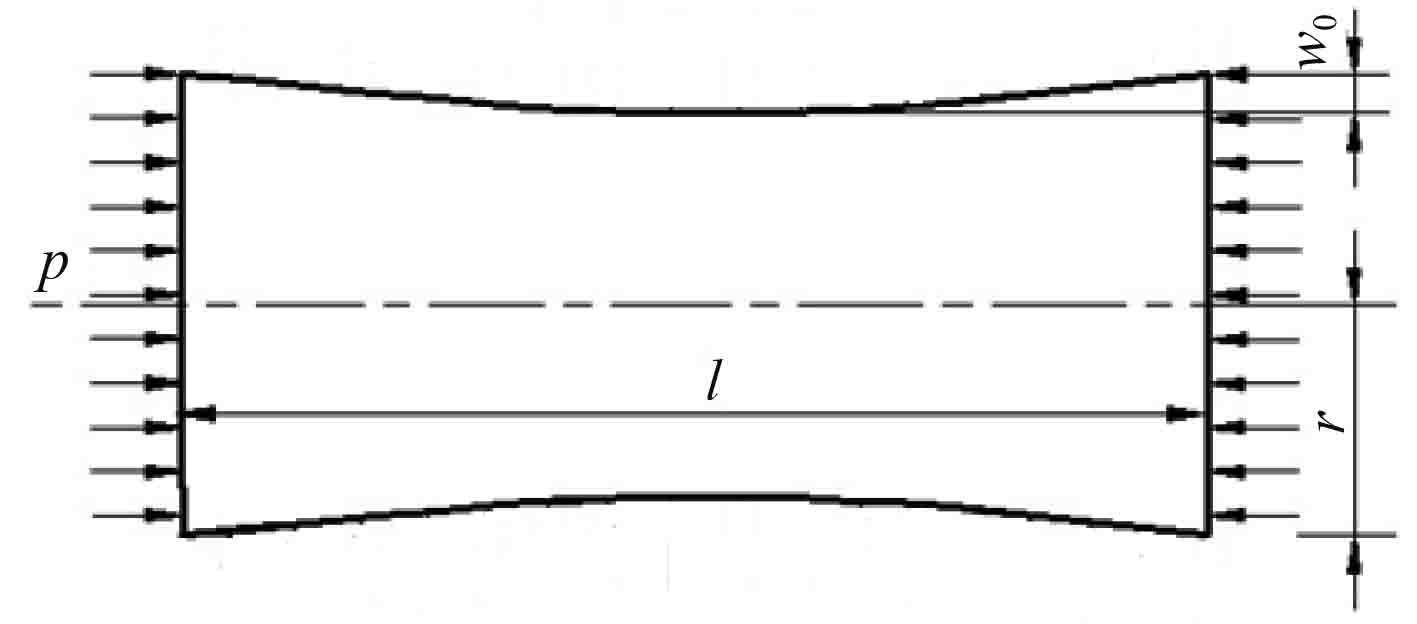
3 含轴对称缺陷圆柱壳失稳分析 3.1 基于RSM的失稳载荷计算含轴对称初始缺陷圆柱壳模型如图7所示。设定长度为
|
图 7 含轴对称缺陷轴压圆柱壳模型 Fig. 7 Axially compressed cylindrical shell model with axisymmetric defects |
缺陷幅值相对于半径为小量,忽略对圆柱壳应力分布的影响,壳体失稳前应力和应变仍然为式(1)和式(2),而几何方程如下:
| $ \left\{ \begin{aligned} & {{\varepsilon '}_x} = \frac{{\partial u}}{{\partial x}} + \frac{w}{\rho },{{\gamma '}_x} = \frac{{{\partial ^2}w}}{{\partial {x^2}}} + \frac{w}{{{\rho ^2}}}\text{,}\\ & {{\varepsilon '}_\theta } = \frac{1}{r}\frac{{\partial v}}{{\partial \theta }} - \frac{w}{r},{{\gamma '}_\theta } = \frac{1}{{{r^2}}}\frac{{{\partial ^2}w}}{{\partial {\theta ^2}}}\text{,}\\ & {{\varepsilon '}_{x\theta }} = \frac{1}{2}\left( {\frac{{\partial v}}{{\partial x}} + \frac{1}{r}\frac{{\partial u}}{{\partial \theta }}} \right),{{\gamma '}_{x\theta }} = \frac{1}{r}\frac{{{\partial ^2}w}}{{\partial x\partial \theta }}\text{,}\\ & {{\varepsilon ''}_x} = {\left( {\frac{{\partial w}}{{\partial x}}} \right)^2},{{\varepsilon ''}_\theta } = \frac{1}{{2{r^2}}}{\left( {\frac{{\partial w}}{{\partial \theta }}} \right)^2}\text{。} \end{aligned} \right.$ | (26) |
因此相对于完善壳体,式(13)~式(15)分别表述为:
| $ \begin{aligned} & {V_m} = \frac{{{\text{π}} KL}}{2}\left( {1 - \mu } \right){\left( {\frac{1}{2}{v_{ij}}\lambda - \frac{1}{2}{u_{ij}}i} \right)^2} +\\ & \frac{{{\text{π}} KL}}{4}\left( {\mu \left( {{v_{ij}}i - {w_{ij}}} \right) - {u_{ij}}\lambda + {w_{ij}}\bar r} \right)\left( {{w_{ij}}\bar r - {u_{ij}}\lambda } \right) + \\ & \frac{{{\text{π}} KL}}{4}\left( {{v_{ij}}i - {w_{ij}} + \mu \left( {{w_{ij}}\bar r - {u_{ij}}\lambda } \right)} \right)\left( {{v_{ij}}i - {w_{ij}}} \right) \text{;} \end{aligned} $ | (27) |
其中:
| $ \begin{aligned} & {V_b} = \frac{{{\text{π}} LK}}{2}\frac{{\left( {1 - \mu } \right)w_{ij}^2{\lambda ^2}{i^2}}}{\alpha }+ \\ & \frac{{K{\text{π}} L}}{4}\frac{{\left( {{w_{ij}}{{\bar r}^2} - {w_{ij}}{\lambda ^2} - \mu {w_{ij}}{i^2}} \right)\left( {{w_{ij}}{{\bar r}^2} - {w_{ij}}{\lambda ^2}} \right)}}{\alpha } - \\ & \frac{{{\text{π}}KL}}{4}\frac{{\left( { - {w_{ij}}{i^2} + \mu \left( {{w_{ij}}{{\bar r}^2} - {w_{ij}}{\lambda ^2}} \right)} \right){w_{ij}}{i^2}}}{\alpha } \text{;} \end{aligned} $ | (28) |
其中:
| $ {V_{2m}} = - \frac{{pt{\text{π}} L}}{4}w_{ij}^2{\lambda ^2}\text{。} $ | (29) |
根据壳体稳定条件得到系数行列式的系数为:
| $ \left\{ \begin{aligned} & {{A'}_{11}} = {\lambda ^2} + \frac{1}{2}\left( {1 - \mu } \right){i^2},{{A'}_{12}} = - \frac{1}{2}\left( {1 + \mu } \right)i\lambda\text{,} \\ & {{A'}_{22}} = {i^2} + \frac{1}{2}\left( {1 - \mu } \right){\lambda ^2},{{A'}_{23}} = - i + \mu i\bar r\text{,}\\ & {{A'}_{13}} = \mu \lambda - \lambda \bar r\text{,}\\ & {{A'}_{33}} = \frac{1}{\alpha }{\left( {{i^2} + {\lambda ^2}} \right)^2} + \frac{1}{\alpha }\left( {{{\bar r}^4} - 2{\lambda ^2}{{\bar r}^2} - 2\mu {i^2}{{\bar r}^2}} \right)\text{,}\\ & + 1 + {{\bar r}^2} - 2\mu \bar r\text{,}\\ & {{A''}_{11}} = {{A''}_{22}} = {{A''}_{13}} = {{A''}_{23}} = {{A''}_{12}} = 0\text{,}\\ & {{A''}_{33}} = \left( {1 - {\mu ^2}} \right){\lambda ^2}\text{。} \end{aligned} \right. $ | (30) |
得含轴对称缺陷的轴压圆柱壳失稳临界载荷:
| $ \Lambda = \frac{{\dfrac{{{{\left( {{i^2}\bar r - {\lambda ^2}} \right)}^2}}}{{{{\left( {{i^2} + {\lambda ^2}} \right)}^2}}} + \dfrac{{{{\left( {{i^2} + {\lambda ^2}} \right)}^2} - \left( {2\mu {i^2}{{\bar r}^2} + 2{{\bar r}^2}{\lambda ^2} - {{\bar r}^4}} \right)}}{{\alpha \left( {1 - {\mu ^2}} \right)}}}}{{{\lambda ^2}}}\text{。} $ | (31) |
为便于分析初始缺陷对薄膜刚度和弯曲刚度的影响,令
| $ \left\{ \begin{aligned} & {a_1} = {i^2}\bar r \text{,} \\ & {a_2} = 2\mu {i^2}{{\bar r}^2} + 2{{\bar r}^2}{\lambda ^2} - {{\bar r}^4} \text{,} \end{aligned} \right.$ | (32) |
式(31)可写为:
| $ \Lambda = \frac{{\dfrac{{{{\left( {{a_1} - {\lambda ^2}} \right)}^2}}}{{{{\left( {{i^2} + {\lambda ^2}} \right)}^2}}} + \dfrac{{{{\left( {{i^2} + {\lambda ^2}} \right)}^2} - {a_2}}}{{\alpha \left( {1 - {\mu ^2}} \right)}}}}{{{\lambda ^2}}} \text{。} $ | (33) |
由图8中可以看出,

|
图 8 缺陷在轴压圆柱壳失稳的影响 Fig. 8 Effect of defects on the instability of cylindrical shells under axial compression |
| $ \Lambda = \frac{{\dfrac{{{{\left( {{i^2}\bar r - {\lambda ^2}} \right)}^2}}}{{{{\left( {{i^2} + {\lambda ^2}} \right)}^2}}} + \dfrac{{{{\left( {{i^2} + {\lambda ^2}} \right)}^2}}}{{\alpha \left( {1 - {\mu ^2}} \right)}}}}{{{\lambda ^2}}}\text{。} $ | (34) |
从式(34)可以看出,轴对称缺陷是经过圆柱壳失稳时轴向波数二次方放大,所以很小的初始缺陷将会对圆柱壳的稳定承载能力产生较大影响。
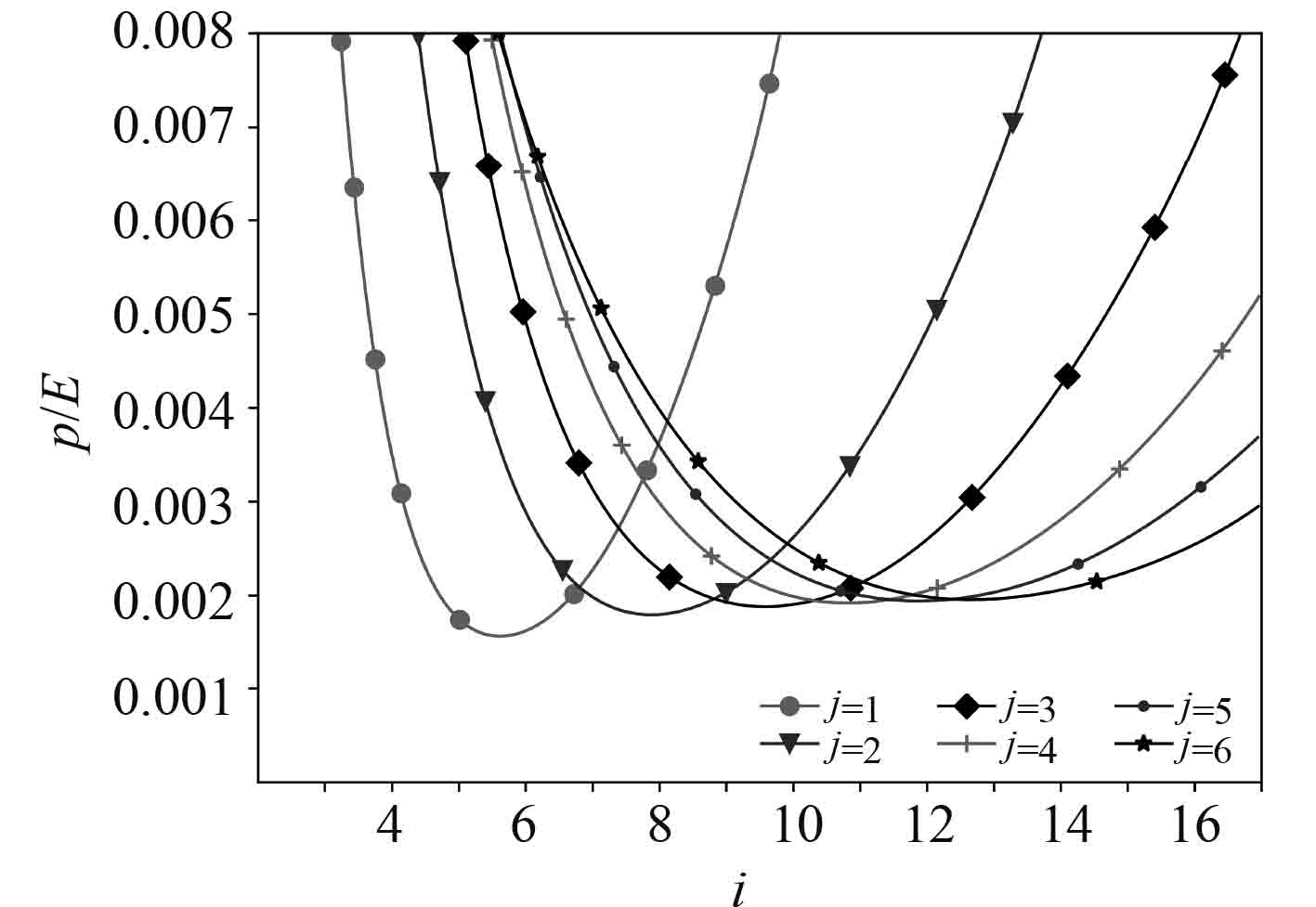
由图9可以看出,与无缺陷时轴向受压圆柱壳的失稳模式不同,当纵向失稳波数是1时,含轴对称初始缺陷的轴压受压圆柱壳的失稳载荷有最小值。比较式(34)和式(25)可得含轴对称缺陷圆柱壳承受轴向均匀压力时,薄膜刚度折减系数与轴对称初始缺陷的关系为:
|
图 9 含轴对称缺陷轴压圆柱壳的失稳临界载荷图谱 Fig. 9 Instability critical load spectrum of axially compressed cylindrical shells with axisymmetric defects |
| $\beta = \frac{{{i^4}{{\bar r}^2} - 2{i^2}{\lambda ^2}\bar r + {\lambda ^4}}}{{{\lambda ^4}}}\text{。}$ | (35) |
采用RSM方法针对轴压载荷作用下完善圆柱壳以及具有轴对称缺陷圆柱壳结构的稳定性进行了分析,主要结论如下:
1)轴压作用下完善圆柱壳结构的失稳载荷与半径、厚度的比有关,与长度、半径比无关。
2)轴压圆柱壳结构的薄膜刚度、弯曲刚度均影响其失稳模态,失稳周向波数随着薄膜刚度的减少而减少,随着弯曲刚度的降低而增加。
3)由于轴对称缺陷通过圆柱壳失稳的轴向波数二次方放大来影响薄膜刚度,故对其临界承载能力影响很大。
| [1] |
乔丕忠, 王艳丽, 陆林军. 圆柱壳稳定性问题的研究进展[J]. 力学季刊, 2018(2): 223-236. QIAO Pizhong, WANG Yanli, LU Linjun. Advances in stability study of cylindrical shells[J]. Chinese Quarterly of Mechanics, 2018(2): 223-236. |
| [2] |
祝恩淳, MANDAL P., CALLADINE C.R.. 轴压圆柱壳的失稳分析[J]. 土木工程学报, 2001, 34(3): 18-22. ZHU Enchun, MANDAL P., CALLADINE C.R.. Analysis of buckling of thin cylindrical shells under axial compression[J]. China Civil Engineering Journal, 2001, 34(3): 18-22. DOI:10.3321/j.issn:1000-131X.2001.03.004 |
| [3] |
LAUREN K. A Study of the effect of imperfections on buckling capability in thin cylindrical shells under axial loading: [R]. Rensselaer Polytechnic Institute, 2009.
|
| [4] |
MUGGERIDGE D B, TENNYSON R C. Buckling of axisymmetric imperfect circular cylindrical shells under axial compression[J]. Aiaa Journal, 2015, 7(11): 2127-2131. |
| [5] |
龚友根, 贺玲凤. 含有初始缺凹陷圆柱壳稳定承载能力的实验研究与数值计算[J]. 实验力学, 2010, 25(1): 73-80. GONG Yougen, HE Lingfeng. Experimental study and numerical calculation of stability and load-carrying capacity of cylindrical shell with initial dent[J]. Journal of Experimental Mechanics, 2010, 25(1): 73-80. |
| [6] |
王小明. 纵骨对环肋圆柱壳肋间壳板稳定性的影响[J]. 舰船科学技术, 2017, 39(4): 35-39. DOI:10.3404/j.issn.1672-7619.2017.04.007 |
| [7] |
白旭, 李金华, 王晓天. 肋骨刚度对环肋圆柱壳失稳载荷的影响分析[J]. 江苏科技大学学报(自然科学版), 2014, 28(4): 3078-312. BAI Xu, LI Jinhua, WANG Xiaotian. Effect of rib stiffness on buckling load of stiffened cylindrical shells[J]. Journal of Jiangsu University of Science and Technology (Natural Science Edition), 2014, 28(4): 3078-312. |
| [8] |
CROLL J G A, GAVRILENKE G D. Reduced-stiffness method in the theory of buckling of stiffened shells[J]. Strength of Material, 2000, 32(2): 168-177. DOI:10.1007/BF02511677 |
| [9] |
ROSSANA C. J., LUIS A. G., FERNANDO G. F., et al. A reduced stiffness approach for the buckling of open cylindrical tanks under wind loads[J]. Thin-Walled Structures, 2007, 45: 727-736. DOI:10.1016/j.tws.2007.07.001 |
| [10] |
Hongtao WANG, JAMES G. A.. Croll optimisation of shell buckling using lower bound capacities[J]. Thin-Walled Structures, 2008, 46: 1011-1020. DOI:10.1016/j.tws.2008.01.035 |
| [11] |
EDUARDO M. Sosa and LUIS A. Godoy. Challenges in the computation of lower-bound buckling loads for tanks under wind pressures[J]. Thin-Walled Structures, 2010, 48: 935-945. DOI:10.1016/j.tws.2010.06.004 |
| [12] |
Xu BAI, Weijun XU, Huilong REN, et al. Analysis of the influence of stiffness reduction on the load carrying capacity of ring-stiffened cylindrical shell[J]. Ocean Engineering, 2017, 135: 52-62. DOI:10.1016/j.oceaneng.2017.02.034 |
| [13] |
白旭, 乐智斌, 李金华, 等. 静水压力下轴对称初始缺陷圆柱壳承载能力研究[J]. 船舶力学, 2015(11): 1334-1343. BAI Xu, YUE Zhibin, LI Jinhua, et al. Load-carrying capacity of cylindrical shells with axisymmetric initial imperfections under hydrostatic pressure[J]. Journal of Ship Mechanics, 2015(11): 1334-1343. DOI:10.3969/j.issn.1007-7294.2015.11.006 |
 2020, Vol. 42
2020, Vol. 42
