0 引　言

潜艇和类似于“深海勇士”这样的载人潜水器具有活动范围大、机动性能好、智能化等众多优点，可以实现海洋资源勘探、管道铺设、海底施工等诸多功能。然而，海底环境复杂，这类深海装备在近海底自航作业时存在着与海山、礁石等海底固定物发生碰撞的可能性^[1]。深海装备的耐压壳体在水下航行时本身处于高应力状态，结构强度接近于屈服强度，这种在高应力状态下的碰撞会对结构产生很大破坏，直接影响耐压壳体的极限承载能力，对作业人员和设备的安全产生威胁。

深水工作环境决定了耐压壳体要具有更高的结构强度和稳定性。为了满足结构强度的要求，同时保证壳体内部足够的空间，耐压壳体多采用钛合金等高性能材料，但这类材料比强度较高，薄壳结构容易发生失稳。因此，常采用失稳临界载荷 $ {P}_{cr} $ 来表征结构的极限承载能力。国内外对耐压球壳和环肋圆柱壳的极限承载能力做了许多研究。Zolly^[2]用小变形假设导出受外压球壳的临界压力；施德培等^[3]用能量法推导出环肋圆柱壳的临界压力；Koiter^[4]研究了初挠度对结构屈曲的影响；Mackay^[5]，王自力等^[6]研究了初始缺陷对于耐压球壳极限承载能力的影响。

本文主要研究水下碰撞对于2种典型耐压壳体结构极限承载能力的影响。通过非线性显式有限元程序Ls-dyna建立2种常见耐压壳体的水下碰撞模型，得到碰撞后结构的强度变化及损伤情况。将带有损伤变形的耐压结构导入隐式有限元软件Ansys中，计算碰撞后的失稳临界载荷，与碰撞前完善壳体的临界载荷进行对比。引入剩余强度因子，重点讨论碰撞速度对结构塑性变形和剩余强度因子的影响。本文建立了研究水下碰撞对深海装备耐压壳体极限承载能力影响问题的思路和方法，所得结果可以为水下碰撞失效模式判断和深海装备自航安全性保证提供借鉴。

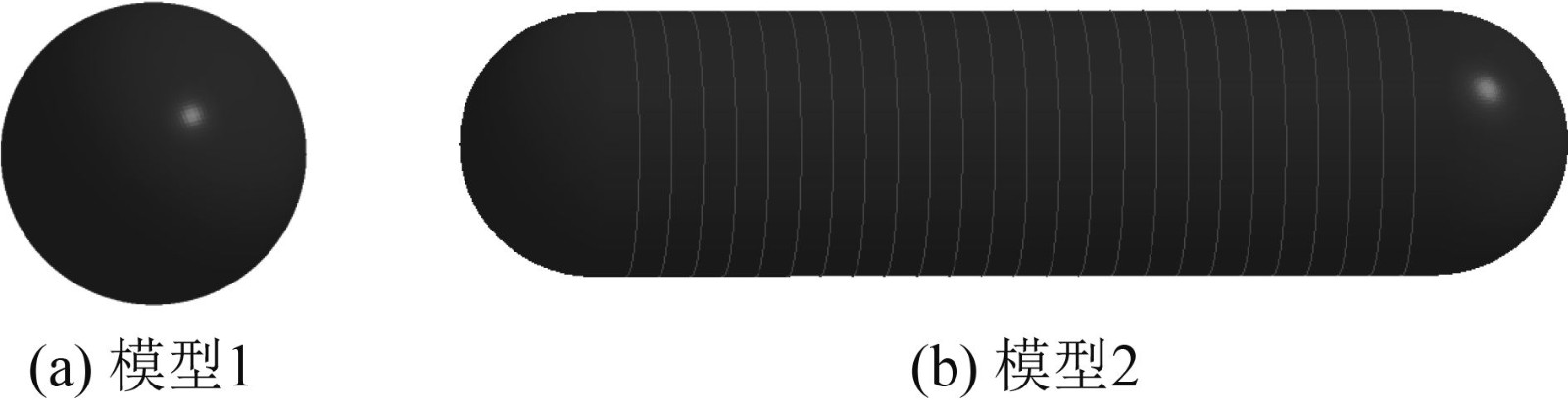
1 稳定性计算与水下碰撞模型

本文选取2个最为典型的深海装备耐压壳体进行碰撞计算，如图1所示。模型1是厚度为42 mm，半径为1.65 m的耐压球壳。模型2为球柱组合结构，圆柱壳内部布置有周向T型环肋，T型环肋截面尺寸为 $ \displaystyle\frac{{28 \, {\rm mm} \times 210 \,{\rm mm}}}{{46 \,{\rm mm} \times 120 \, {\rm mm}}}$ ，其余结构参数如表1所示。

耐压壳体结构为TC4钛合金材料，在进行特征值屈曲计算时，采用理想弹性体模型；进行非线性屈曲计算时，采用理想弹塑性模型；弹性模量为1.1 $ \times {10}^{11} $ Pa，泊松比为0.34。由于该模型的厚度半径比为0.025，属于薄壳结构，在建模时采用shell181单元，单元长度为50 mm，沿厚度方向的积分点个数为5。对完善的球壳和球柱组合结构分别进行特征值屈曲和非线性屈曲分析，计算结果如表2所示。

水下碰撞过程是一个大变形和高应变率的冲击过程，因此在进行碰撞计算时，TC4钛合金材料使用能够综合考虑应变、应变率和温度影响的J-C本构和失效模型，J-C本构模型的具体形式为：

${\sigma _e} = \left[ {A + B{{\left( {{{\bar \varepsilon }^{ - p}}} \right)}^n}} \right]\left[ {1 + Cln{\varepsilon ^*}} \right]\left[ {1 - {{\left( {T*} \right)}^m}} \right]\text{。}$

(1)

式中： $ {\sigma }_{e} $ 为Von-Mises流变应力；A，B，n，C，m为材料参数； $ {\varepsilon }^{*} $ 为无量纲应变率， $ {\varepsilon }^{*} $ = $ {{\dot {\bar \varepsilon}} ^p}/{\varepsilon _0}$ ； $\dot {\bar {\varepsilon}} $ 为有效塑性应变率；ε为参考塑性应变率，一般取 $ {\varepsilon }_{0}=1{s}^{-1} $ ； ${T^*} = \displaystyle\frac{{T - {T_r}}}{{{T_m} - {T_r}}}$ 为无量纲温度； $ {T}_{r} $ 为室温； $ {T}_{m} $ 为熔点温度。J-C本构模型综合考虑应力三轴度、应变率和温度对材料失效的影响，具体形式为：

${\varepsilon _f} = \left[ {{D_1} + {D_2}\exp \left( {{D_3}{\sigma ^*}} \right)} \right]\left( {1 + {D_4}ln{{\dot {\varepsilon} }^*}} \right)\left( {1 + {D_5}{T^*}} \right)\text{。}$

(2)

式中： $ {D}_{1} \sim {D}_{5} $ 为材料参数； ${\sigma ^{*}} = \displaystyle\frac{p}{\rho } = - \frac{{{\sigma _m}}}{{{\sigma _{eq}}}} = - \eta $ ， $ \eta $ 为应力三轴度，p为静水压力，σ为等效应力。

该失效模型应用损伤累计准则来考虑材料的失效过程，单元的累计损伤参量可以表示为：

$ D = \int_0^{{\varepsilon _e}} {\frac{{{\rm d}{\varepsilon _e}}}{{{\varepsilon _f}({\sigma ^*},{{\dot {\varepsilon} }_e},T)}}}\text{。} $

(3)

式中：D值在0～1之间变化，初始时D = 0，材料失效D = 1； $ \Delta {\varepsilon }_{f} $ 为一个时间步内的塑性应变增量； $ {\varepsilon }_{f} $ 为在该时刻应力三轴度、应变率和温度状态下的失效应变，可以通过式（2）确定。本文所用材料的J-C本构和失效模型的参数如表3所示。

碰撞仿真时耐压壳体单元类型为shell163单元，网格大小为50 mm，厚度方向积分点数目为3。对首部碰撞区域的半球型封头处的网格进行细化，大小为20 mm；被撞厚板为刚性体，采用solid164单元建模，网格大小为50 mm，接触算法选用面面接触中的自动接触算法（ASTS）。

通过在K文件中定义加载曲线的方式对耐压壳体进行加载，使其在碰撞过程始终承受10 MPa的静水压力。再使用Ls-dyna程序对带有预应力状态的耐压壳体进行显式计算。壳体的初始运动速度为2 kn，与一块3.3 m×3.3 m×0.2 m的方形刚体厚板发生碰撞，撞击角度为90°，碰撞前初始的间距为0.1 m。计算完成后，在LS-PREPOST后处理器中得到碰撞过程结构动力响应情况。

碰撞结束后的耐压壳体首部凹陷产生大量的塑性变形。为了研究耐压壳体的剩余承载能力，使用从显式到隐式的方法（Explic to Implic），将Ls-dyna计算的碰撞后的塑性变形导入Ansys中进行非线性稳定性计算。将显式壳单元shell163转换为隐式壳单元shell181，重新定义网格属性，厚度方向积分点数目改为5。通过弧长法（Riks Method）计算得失稳临界载荷^[8]。

2 计算结果分析

计算工况结果如表4所示。

以工况3和工况9为例分别说明球壳结构和球柱组合结构耐压壳体发生水下碰撞时的情况。图2为碰撞结束后球壳的应力情况，碰撞区域最大应力433.3 MPa，是正常航行时最大应力的2.2倍。图3为碰撞结束后球壳的塑性变形情况，最大塑性变形为1.378 $ \times {10}^{-3} $ ，最大撞击深度为106.2 mm。将带有撞击变形的耐压壳体导入Ansys，通过弧长法计算得失稳临界载荷为24.4 MPa。引入剩余强度因子^[9] $ {\rm{\gamma }} $ ： ${\rm{\gamma }} = \displaystyle\frac{{P_{cr}^{'}}}{{{P_{cr}}}}$ ， $ {P}_{cr}^{'} $ 为发生碰撞后耐压壳体的失稳临界载荷， ${P_{cr}}$ 为完善耐压壳体的失稳临界载荷，工况3的剩余强度因子为0.61。显然，水下碰撞会显著降低结构的极限承载能力。

图4和图5为碰撞结束后球柱组合结构的应力和塑性变形情况。通过弧长法计算碰撞后的临界载荷为12.1 MPa，剩余强度因子为0.35。后处理结果显示，工况9在碰撞结束后发生大变形破坏，结构无法保持整体完整。分析可知，球柱组合结构碰撞后的临界失稳载荷为12.1 MPa，大于环境载荷10 MPa，失稳不是结构发生整体破坏的首要原因。由图5可知，碰撞后首部区域最大应力为818.5 MPa，而TC4钛合金屈服极限为794 MPa，因此，首部碰撞区域的屈服是结构开始发生破坏的主要原因，首部发生破坏后在屈服和屈曲的耦合作用下，结构发生整体破坏。

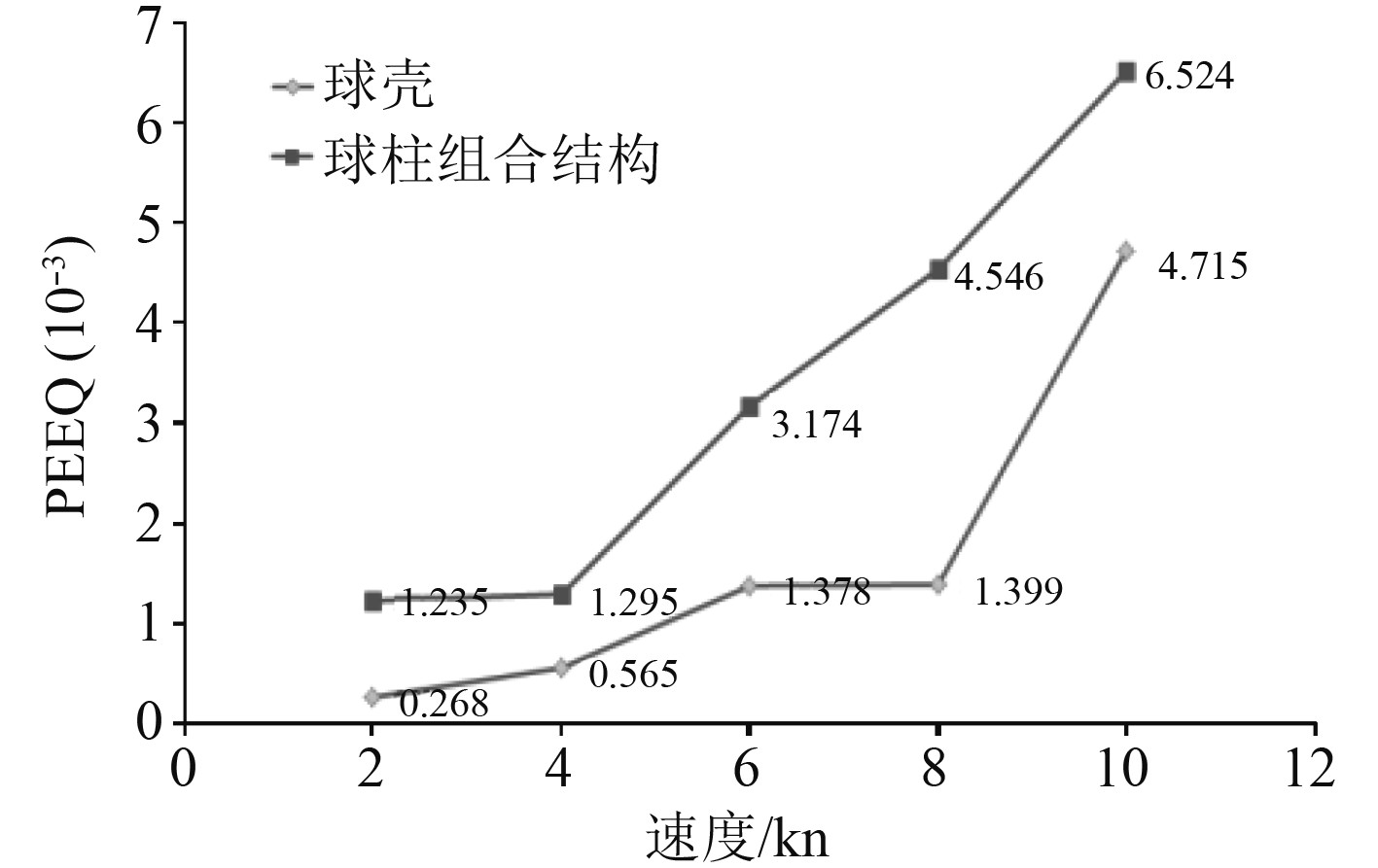
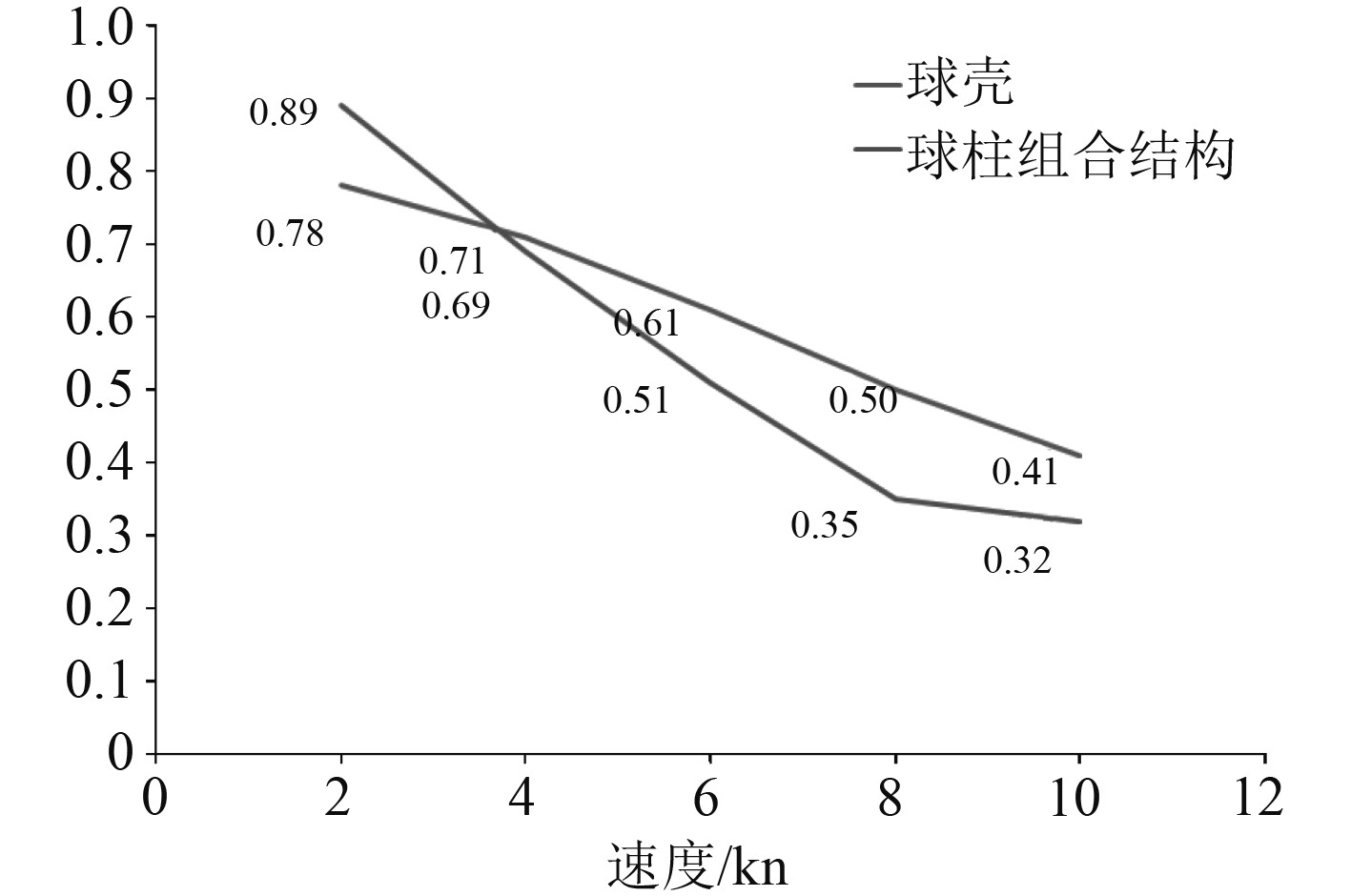
图6为球壳结构和球柱组合结构发生水下碰撞后最大塑性变形随碰撞速度的变化。随着速度增加，耐压壳体动量增加，产生的塑性变形的大小和范围随之增加。由于球柱组合结构整体质量较大，同样速度下产生的塑性变形也始终大于耐压球壳。图7为球壳结构和球柱组合结构发生水下碰撞后剩余强度因子随碰撞速度的变化。剩余强度因子表征了碰撞对耐压壳体极限承载能力的影响，碰撞速度越大，结构塑性变形的大小和范围都会随之增大，剩余强度因子随之减小，相同径厚比的耐压球壳结构的剩余强度因子要大于球柱组合结构。

3 结　语

1）本文建立2种形式耐压壳体的水下碰撞模型，研究了碰撞对结构极限承载能力的影响。有限元计算结果表明，水下碰撞会显著降低耐压壳体的极限承载能力，且碰撞速度越大，剩余强度因子越小。

2）若耐压壳体在碰撞后发生整体破坏，通过比较局部强度和碰撞后的失稳临界载荷判断失效模式。碰撞后耐压壳体局部强度大于材料屈服强度为强度破坏，碰撞后的失稳临界载荷小于环境载荷则为稳定性破坏。

3）同一材料、相同径厚比的球壳结构和球柱组合结构在同一速度下发生水下碰撞后，球柱组合结构产生的塑性变形大小和范围较大，剩余强度因子较低。仅考虑水下碰撞工况，球壳结构更加安全。