2. 船舶振动噪声重点实验室,湖北 武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China
随着对减振性能良好的减振元件器需求的增加,气囊隔振器被大量应用于现代舰艇,尤其是核潜艇[1-3],应用舱段也越来越关键和重要,因此其安全性和可靠性也得到了重点关注。气囊隔振器的爆破压力参数决定了其寿命、安全系数等参数制定,该参数的重要性不言而喻。目前通常是开展气囊爆破试验确定气囊的爆破压力参数,且需要通过提高试验样本数提高参数的精度。因此,通过试验的方法确定气囊隔振器爆破压力参数工作量较大,且存在一定的危险性。
在气囊隔振器爆破试验中,通常是由帘线的断裂造成骨架层承载能力降低,导致囊壁无法承受内压载荷,进而气囊发生爆裂破坏。而囊壁骨架层是气囊隔振器的主要承载部件,可将骨架层承受极限载荷对应的压力视为气囊隔振器的爆破压力。因此,开展囊壁骨架层帘线断裂性能的研究,基于Abaqus软件利用三维实体单元和rebar单元建立气囊隔振器有限元模型,提取囊壁骨架层帘线拉伸强力特性仿真曲线,开展帘线断裂强力试验,建立初始模量和断裂强力Weibull分布曲线,结合95%置信度[4]和帘线拉伸强力特性仿真曲线,预测爆破压力和最小爆破压力,并开展气囊隔振器爆破试验,验证预测方法的精度。
1 爆破压力预测数学模型建立 1.1 断裂强力通常所述的断裂强力,是指纤维、纱线等纺织材料拉伸断裂的平均强力,但是纤维等材料的断裂强力分布并不平均,具有明显的分散性。Weibull分布可较好地拟合芳纶纤维、纱线、棉纶等材料的断裂强力和初始模量等力学性能的分散性,其期望值能够较好地描述材料的平均断裂强力和平均初始模量[5],因此本文用Weibull分布拟合骨架层帘线性能的分散性。
1.2 Weibull分布二参数Weibull分布表达式[6]为:
| $F(f) = 1 - {\rm{exp}}\{ - {(\frac{{{f_i}}}{\eta })^{\beta} }\}\text{。} $ | (1) |
其中:
Weibull分布模型的期望值为:
| $E(f) = \eta \Gamma \left(1 + \frac{1}{\beta }\right) = \eta \int_0^{ + \infty } {{t^{\frac{1}{\beta }}}{e^{ - t}}{\rm d}t}\text{。} $ | (2) |
由于舰艇用气囊隔振器对安全性和可靠性要求较高,结合95%置信度定义帘线的最小拉力,其表达式为:
| $F(f) = 1 - {\rm{exp}}\{ - {\left(\frac{y}{\eta }\right)^{\beta} }\} \geqslant 1 - 95\%\text{,} $ | (3) |
解得:
| $f \geqslant {f_{\min }} = \eta \times \sqrt[\beta ]{{ - \ln (0.95)}}\text{。}$ | (4) |
气囊隔振器的爆破压力参数描述气囊抗冲击的能力,其值越大表明气囊抗冲击的能力越强。气囊隔振器的主要承载部分是囊壁骨架层[7-8],其发生爆裂破坏的原因是帘线无法承受内压载荷而发生断裂,进而引发气囊隔振器的爆裂破坏,故帘线承力能力直接决定了气囊隔振器的爆破压力。
通常帘线的拉力与内压的关系呈线性关系,其函数表达式如下式:
| $f = aP + b\text{。}$ | (5) |
其中:
将式(2)代入式(5),得气囊隔振器爆破压力预测模型表达式为:
| $P = (\eta \int_0^{ + \infty } {{t^{\frac{1}{\beta }}}{e^{ - t}}{\rm d}t} - b)/a\text{。}$ | (6) |
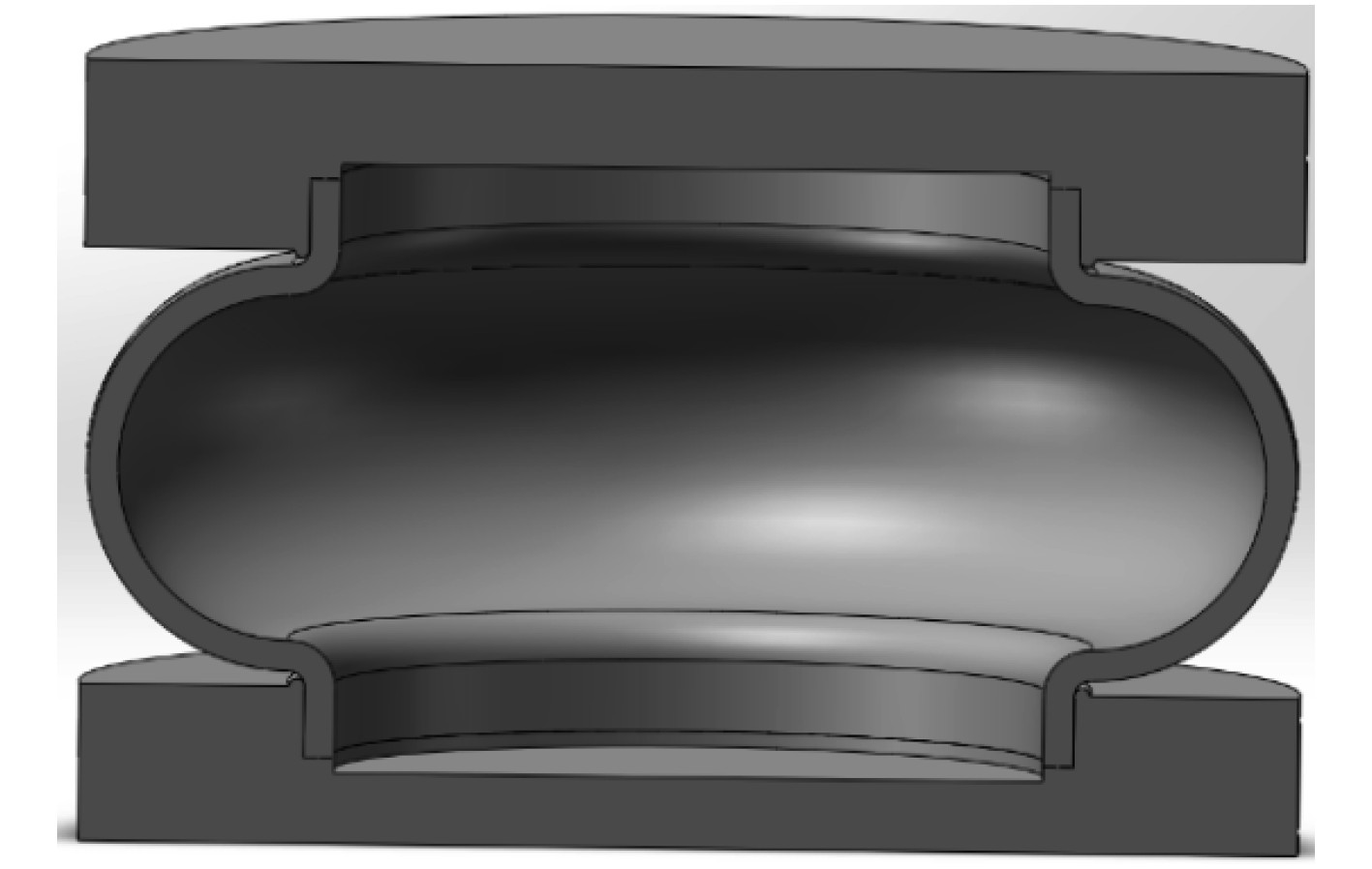
本文以某型气囊隔振器为研究对象,在有限元建模研究中,简化模型能有效缩小建模时间和提高计算速度[7]。因此,建立气囊隔振器简化模型,如图1所示。
|
图 1 气囊隔振器简化模型 Fig. 1 Simplification model of air spring |
本文对研究对象的橡胶部分完成了材料试验,通过本构模型参数拟合发现,Yeoh模型的拟合曲线与试验数据重合度较好,可选用来做橡胶材料的本构模型。Yeoh模型的参数为:
| $ {C_{10}} = 0.673\;36,\;\;{C_{20}} = - 0.277\;22,\;\;{C_{30}} = 0.189\;60\text{。} $ | (7) |
完成断裂强力试验,求得芳纶纤维的初始模量值为48.965 GPa。
在分析模块中,选定帘布层为对象设置场输出,选定rebarforce和rebarangle可分别输出显示载荷周期过程中芳纶帘线上的拉力和角度。
在网格模块,上下盖板不是关注的重点,可划分为缩减积分单元C3D4;气囊囊壁被定义为三维实体单元,为保证橡胶材料的各项同性,将其划分为缩减杂交单元C3D8RH;囊壁骨架层在材料属性模块中被定义为膜单元,为保证一致性,将囊壁骨架层定义为膜单元M3D4R。
2.2 仿真结果1)气压承载特性曲线
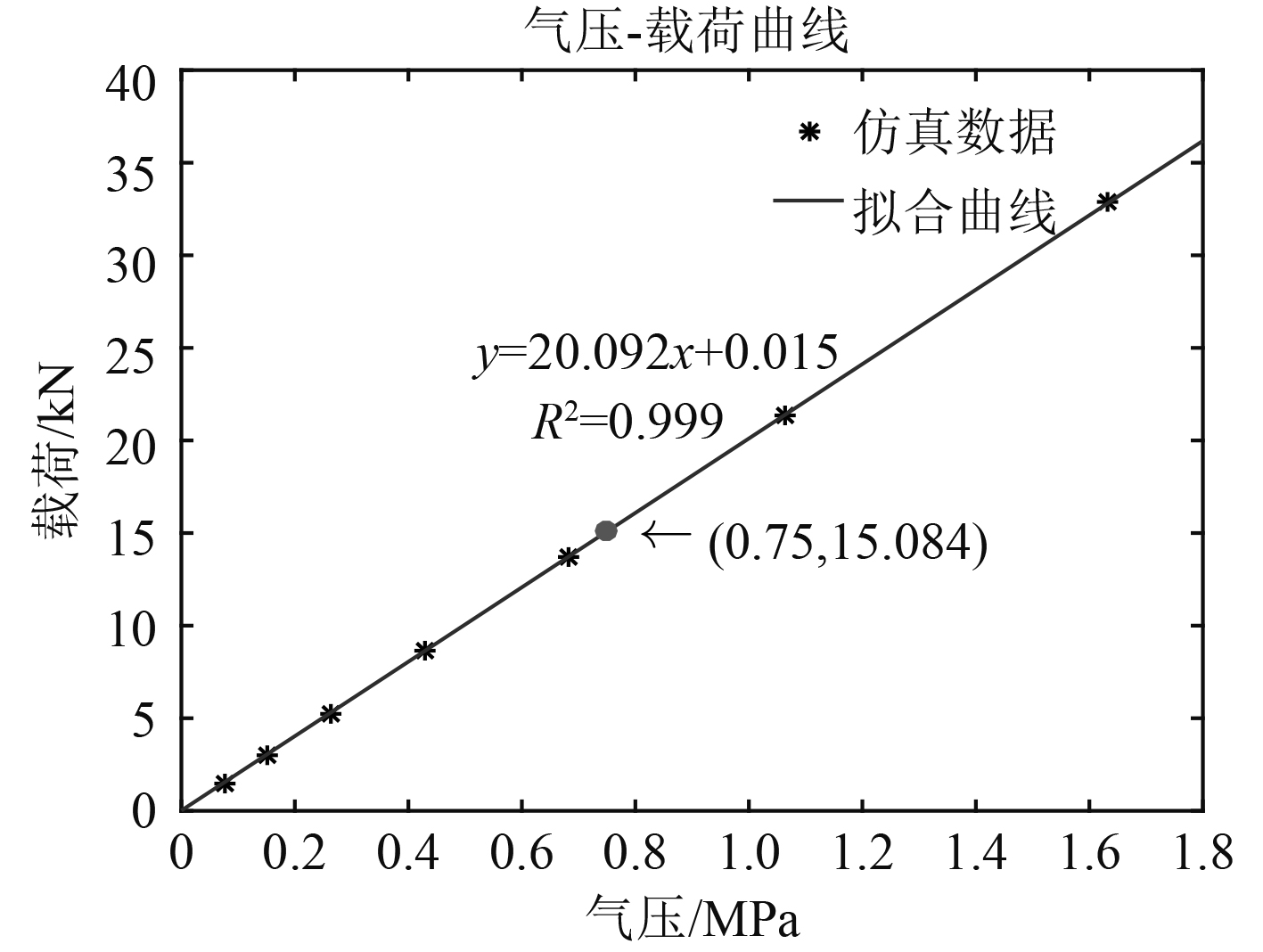
在仿真气压-载荷特性时[9],将隔振器上下盖板固定,使用流体腔单元缓慢给气囊充气至设定值,查看上盖板反作用力值,其结果如图2所示。
|
图 2 气压承载特性曲线 Fig. 2 Curve of pressure and load |
仿真结果线性拟合曲线为:
| $y = 20.092x + 0.015\text{。}$ | (8) |
拟合度
2)帘线拉伸强力特性曲线
利用流体腔单元缓慢给气囊充气至17.5 MPa,提取各压力下芳纶帘线最大拉力值,绘制帘线拉伸强力特性曲线如图3所示,其表达式为:
| $f = 44.84P + 15.47\text{。}$ | (9) |
拟合度

|
图 3 帘线拉伸强力特性曲线 Fig. 3 Curve of cord tension and pressure |
为研究芳纶帘线的断裂性能,基于高强化纤长丝拉伸性能试验方法[10]开展帘线断裂拉伸试验。试验帘线的线密度和直径分别为1670 dtex,0.85 mm,如图4所示。

|
图 4 芳纶帘线Kevlar-119 Fig. 4 Aramid cord Kevlar-119 |
如图5所示,试验前将夹具以标距500 mm固定在试验机上,芳纶帘线缠绕夹持在上下夹具,保持帘线垂直于地面。将引伸仪夹持在帘线中间部分,设置标定距离为200 mm;设置预加力2 N,以250 mm/min加载速度开始试验。直至芳纶帘线拉伸断裂停止试验,记录试验机断裂强力值和引伸仪伸长量,若断裂位置在距离夹具端口5 cm内,则该次试验数据作废。

|
图 5 CMT4303力学试验平台 Fig. 5 CMT4303 mechanical experimental platform |
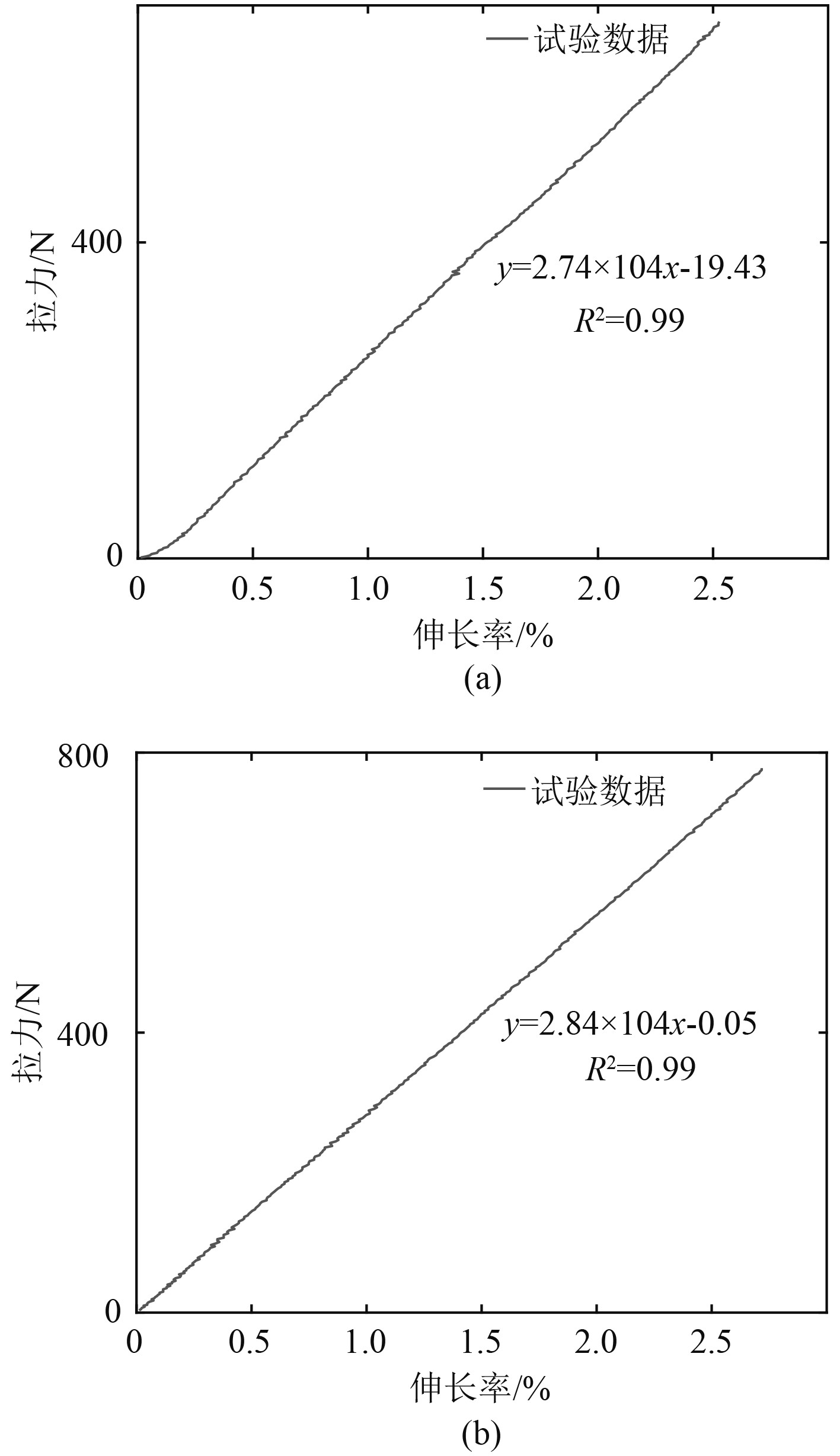
共开展26次试验,其中20次试验数据为有效数据,如表1所示。部分试验所得拉力-伸长率曲线结果如图6所示。
|
|
表 1 帘线拉伸断裂试验数据 Tab.1 Data of cord tensile failure data |
|
图 6 帘线拉力—伸长率曲线 Fig. 6 Curve of cord tension and elongation |
帘线初始模量一般定义为其拉伸伸长为1%时应力的100倍,其值表征帘线对小变形的抵抗能力,在帘线拉伸断裂试验中一般取拉力-伸长率曲线上直线部分的斜率与横截面积的比值作为帘线初始模量,即
| ${M_o} = \frac{{4{k_c}}}{{{\text π} R_c^2}}\text{。}$ | (10) |
式中:
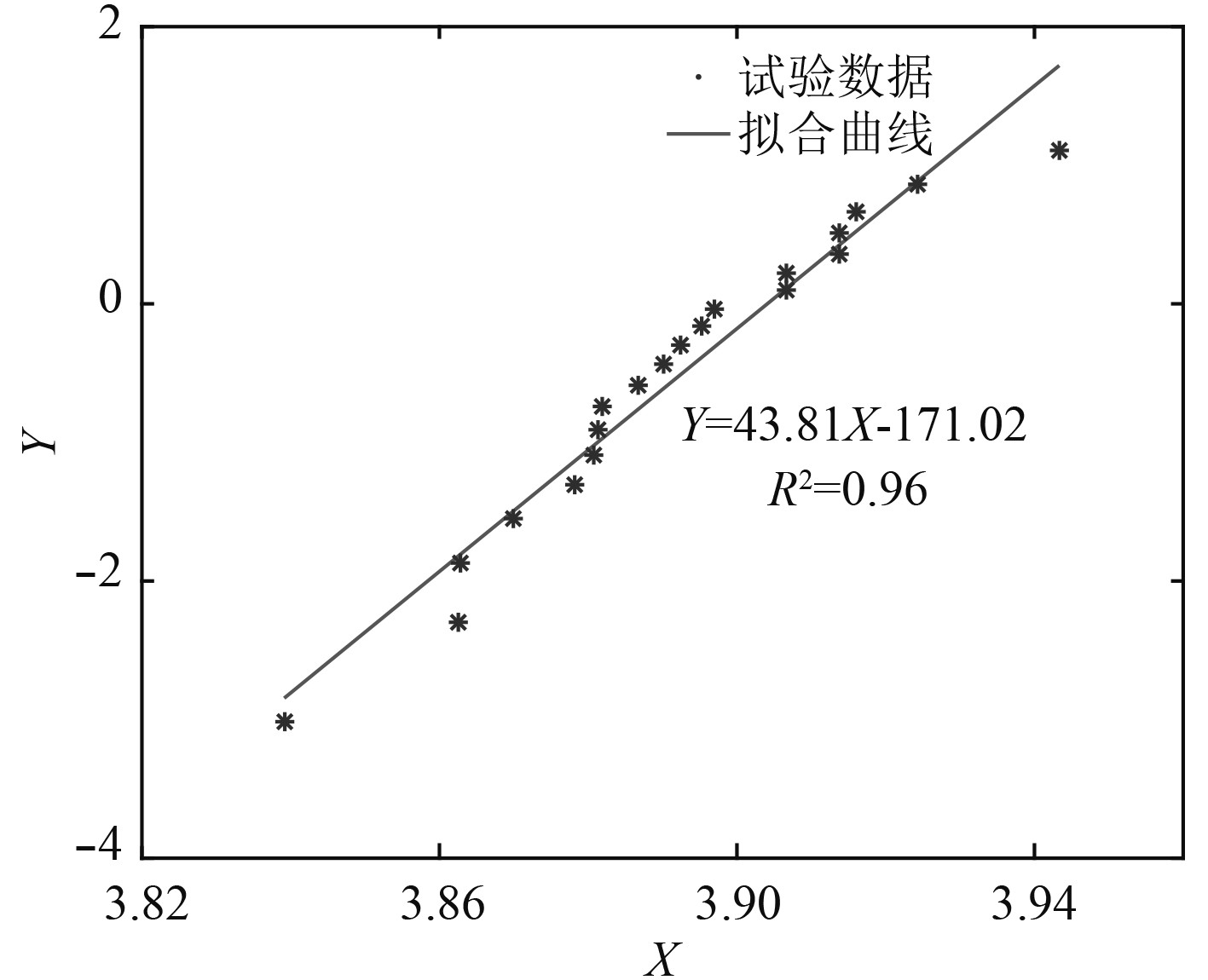
将试验测得各根帘线的初始模量结果按Weibull分布拟合,其结果如图7所示。
|
图 7 初始模量Weibull分布拟合曲线 Fig. 7 Fitting curve of initial modulus′s Weibull distribution |
由图7可知,初始模量Weibull分布拟合度为0.96,拟合精度较高,并解得Weibull分布的尺度参数和形状参数分别为43.81,49.58,将该值代入式(2)得帘线初始模量的期望值为48.965 GPa。
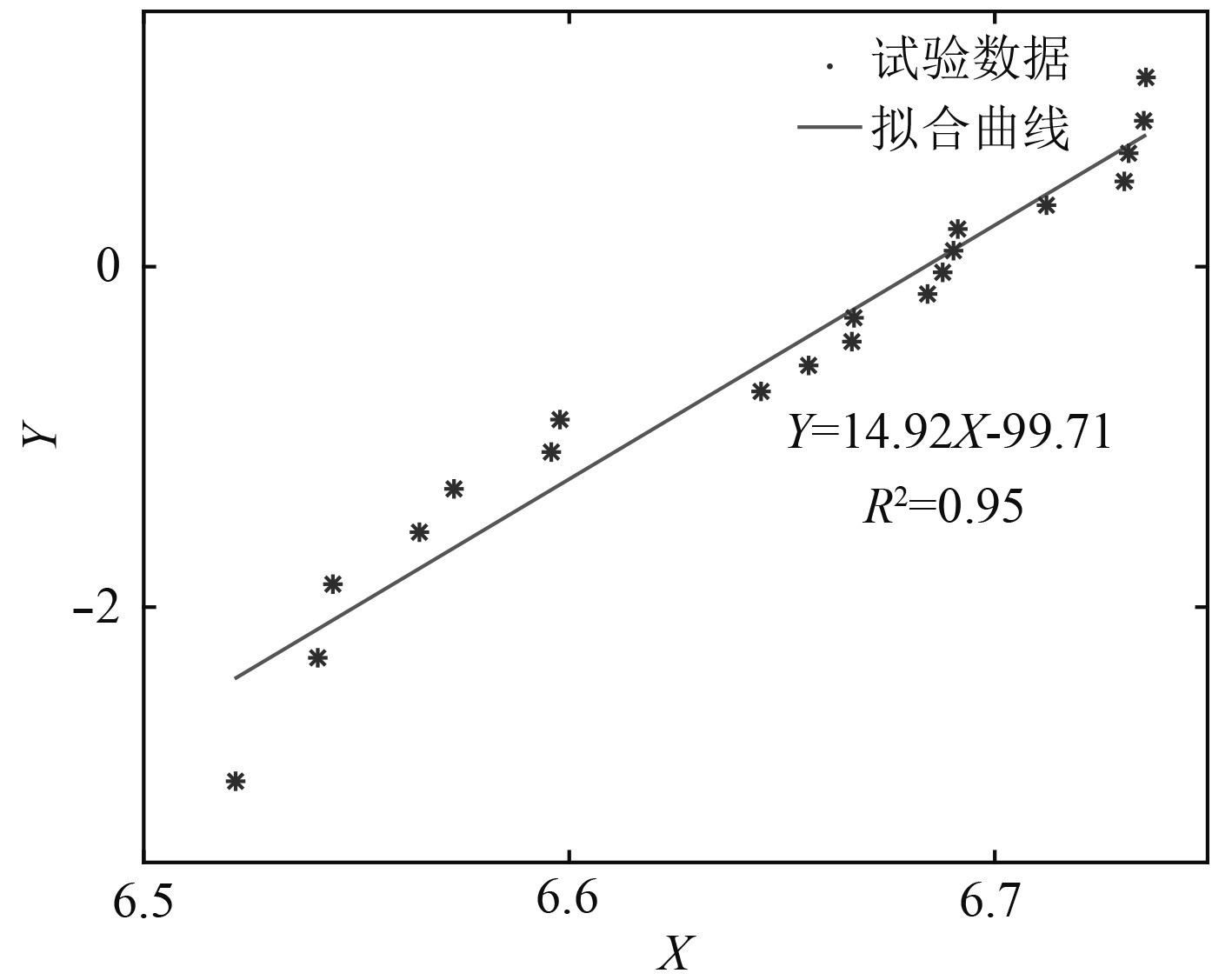
3.2.2 断裂强力将断裂强力试验数据按Weibull分布函数拟合,其结果如图8所示。断裂强力Weibull分布拟合度为0.95,其表达式为:
|
图 8 断裂强力Weibull分布拟合曲线 Fig. 8 Fitting curve of fracture strength’s Weibull distribution |
| $F({\rm{y}}) = 1 - {\rm{exp}}\left\{ - {\left(\frac{y}{{14.92}}\right)^{799.3}}\right\} \text{。}$ | (11) |
解得尺度参数和形状参数分别为14.92,799.248。将尺度参数和形状参数的值代入式(2)和式(4),分别得断裂强力的期望值为771.7 N和最小拉伸强力为655.0 N。
3.3 试验分析帘线初始模量和断裂强力试验数据的最大散度分别为1.12和1.24,可见其具有一定的分散性,但分散性不大;帘线初始模量和断裂强力Weibull分布的拟合度分别为0.96和0.95,可见Weibull分布能较好拟合帘线性能的分散性。
由于骨架层橡胶部分主要是填充作用,帘线承担了载荷,因此帘线的断裂性能即为骨架层的断裂性能。由于囊壁橡胶承载能力很弱,囊壁骨架层是气囊隔振器的主要承载部件,因次囊壁骨架层对应的爆破压力可代表气囊隔振器的爆破压力。
将骨架层断裂强力的期望值和最小拉伸强力代入式(6),分别解得气囊隔振器预测爆破压力为16.86 MPa和最小爆破压力为14.3 MPa。
4 气囊隔振器爆破试验 4.1 试验方案为气囊隔振器预测爆破压力的准确性,设计了气囊隔振器爆破压力试验。
按照以下方法进行气囊隔振器爆破试验:
1)使用爆破试验专用夹具将气囊隔振器的高度固定在额定值154 mm,向气囊内缓慢注水排出气囊内存在的空气;
2)排出空气后,锁紧管路接头,继续向气囊内缓慢注水,直至囊体产生破裂;
3)充压过程中,用摄像机记录囊内压力的变化情况,压力无法继续上升时表明气囊已出现泄漏,检查泄漏位置,若是密封面泄漏,则解决密封问题后继续试验,直到囊体破裂,记录此时的压力即为囊体的爆破压力。
4.2 试验结果及分析经过试验,该型号气囊隔振器的爆破压力为17.5 MPa,气囊破坏后照片如图9所示。

|
图 9 试验结束后爆破的气囊 Fig. 9 Experimental prototype of air spring |
可以看出,气囊隔振器帘线断裂的位置集中囊体与下盖板接触的区域,这与有限元仿真中骨架层拉力最大的位置基本重合,说明仿真与实际相符。
气囊隔振器预测爆破压力与试验值的误差仅为3.7%,表明有帘线断裂强力的期望值与帘线拉力特性仿真曲线预测的气囊爆破压力与实际情况相符,可作为气囊隔振器爆破压力参数指定的方法。气囊最小爆破压力预测值为第一根囊壁骨架层帘线断裂时囊体压力,其余试验值的误差为18.3%,表明在实际情况中第一根帘线的断裂并不会使得气囊直接发生爆裂破坏,但会导致骨架层帘线的拉伸强力载荷重新分配,使得在较短时间内气囊达到爆破压力。气囊最小爆破压力可视为骨架层帘线发生断裂的起始压力,对安全性和可靠性要求较高的舰用气囊隔振器,该参数具有指导和参考意义。
5 结 语结合帘线拉伸特性曲线和帘线断裂强力建立的该型号气囊隔振器爆破压力预测方法,其爆破压力预测结果与试验值得误差仅为3.7%,预测精度满足工程应用要求。在气囊爆破压力预测过程中,最小爆破压力预测值仅能粗略估计爆破压力的大小,该值与试验值存在一定的误差,但对应用于重要舱段和敏感位置的气囊隔振器,为保证较高的安全系数,该值也可作为气囊隔振器的爆破压力。
| [1] |
朱石坚, 何琳. 船舶减振降噪技术与工程设计[M]. 北京: 科学出版社, 2002.
|
| [2] |
何琳, 赵应龙. 舰船用高内亚气囊隔振器理论与设计[J]. 振动工程学报, 2013, 26(6): 886-894. DOI:10.3969/j.issn.1004-4523.2013.06.011 |
| [3] |
赵应龙, 吕志强, 何琳. JYQN舰用气囊隔振器研究[J]. 舰船科学技术, 2006, 28(2): 89-92. |
| [4] |
赵永翔, 杨冰, 彭佳纯. 寿命服从对数正态分布、有置信度概率疲劳S-N曲线的合理重[J]. 应用数学和力学, 2007, 28(4): 413-418. DOI:10.3321/j.issn:1000-0887.2007.04.005 |
| [5] |
陈国华. 机织物拉伸断裂过程模拟及强度预测[D]. 上海: 东华大学, 2006.
|
| [6] |
WEIBULL W A. Statistical distribution function of wide applicability[J]. Journal of Applied Mechanics, 1951, 7(3): 293-297. |
| [7] |
赵应龙, 何琳, 吕志强, 等. 回转型气囊隔振器的冲击刚度研究[J]. 舰船科学技术, 2006, 28(2): 112-116. |
| [8] |
赵应龙, 金著, 何琳. 气囊隔振器囊壁骨架层平衡性研究[J]. 船舶力学, 2017, 21(7): 873-879. |
| [9] |
金著. 膜式气囊隔着你去囊体结构力学特性研究[D]. 武汉: 海军工程大学, 2014.
|
| [10] |
中华人民共和国国家质量监督检验疫检总局. GB/T 19975-2005 高强化纤长丝拉伸性能试验方法[S]. 秦皇岛: 中国标准出版社, 2005.
|
 2020, Vol. 42
2020, Vol. 42
