2. 哈尔滨工程大学 船舶工程学院 黑龙江 哈尔滨 150001
2. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
随着鱼雷在现代战争中地位的日益增强,鱼雷水中弹道的实时预报技术成为世界各国的研究热点。鱼雷在水中的空间运动要受到浪,流等因素的影响,导致其水中弹道很大程度随机。由于海洋环境的复杂性,对于鱼雷水中弹道的研究大多基于一些假设来进行,从而简化计算模型。Peter C Chu和Jillene M Bushnell[1]建立了鱼雷六自由度运动模型,设计了鱼雷在静水中的弹道试验,利用高速相机记录鱼雷水中运动轨迹并进行了相关的数值模拟,讨论了鱼雷初速度,初始攻角等因素对鱼雷运动轨迹的影响,数值模拟结果与试验结果较为吻合,考虑到试验中海流和波浪难以操作,因此忽略了浪流对鱼雷水中弹道的影响;丁宝俊[2]基于Matlab模拟计算了均匀海流作用下的二维水雷弹道,但并未考虑随机海流对水雷弹道的影响;顾闯等[3]分析了水雷无动力运动过程中的受力情况,建立了其水下无动力运动模型和海流影响分析模型,并对随机均匀海流作用下的二维水雷弹道散布进行了数值模拟,给出了仿真结果和分析结论,但并未讨论三维水雷弹道散布情况;房燕飞等[4]利用四元数法模拟了水雷的水中弹道,分析了均匀海流对水雷二维弹道的影响,但并未探讨水雷在随机海流作用下的三维弹道散布;陶润礼等[5]设计了砂袋抛射试验,研究了砂袋在均匀海流作用下的二维运动轨迹,并进行了相关的数值模拟,数值模拟结果与试验结果吻合;文钢和玄兆林[6]基于Matlab编写了空投水雷水下弹道散布程序,模拟了均匀海流作用下的三维水雷弹道,同时模拟了随机均匀海流作用下的三维水雷弹道散布,但随机海流流速是呈线性分布的,散布规律与实际情况不符;Rui Zhang和Zhiyong Yuan等[7]假设了鱼雷在矩形波作用下的加速度函数,基于蒙特卡罗方法模拟了鱼雷在波浪作用下的水中弹道以及命中目标物概率。
基于上述问题,本文编写并求解了鱼雷的六自由度运动方程,模拟了鱼雷三维水中弹道,讨论了海流流速,初始攻角等因素对鱼雷弹道的影响;同时基于海流的随机性,在六自由度运动方程中引入随机海流的影响,模拟了鱼雷在随机海流作用下的三维弹道散布,探讨了鱼雷的弹道散布规律。
1 鱼雷水中运动模型本文研究的鱼雷是一个轴对称物体,雷头为半球,雷体为圆柱,质心与浮心重合,质量以及质量分布在运动过程中恒定。本文仅考虑海流对鱼雷弹道的影响,忽略波浪的作用。建立鱼雷水中运动模型需要选取合适的运动坐标系以及动力学方程。
1.1 运动坐标系研究鱼雷的水下运动轨迹,需要相应的运动坐标系[8],本文选取大地坐标系
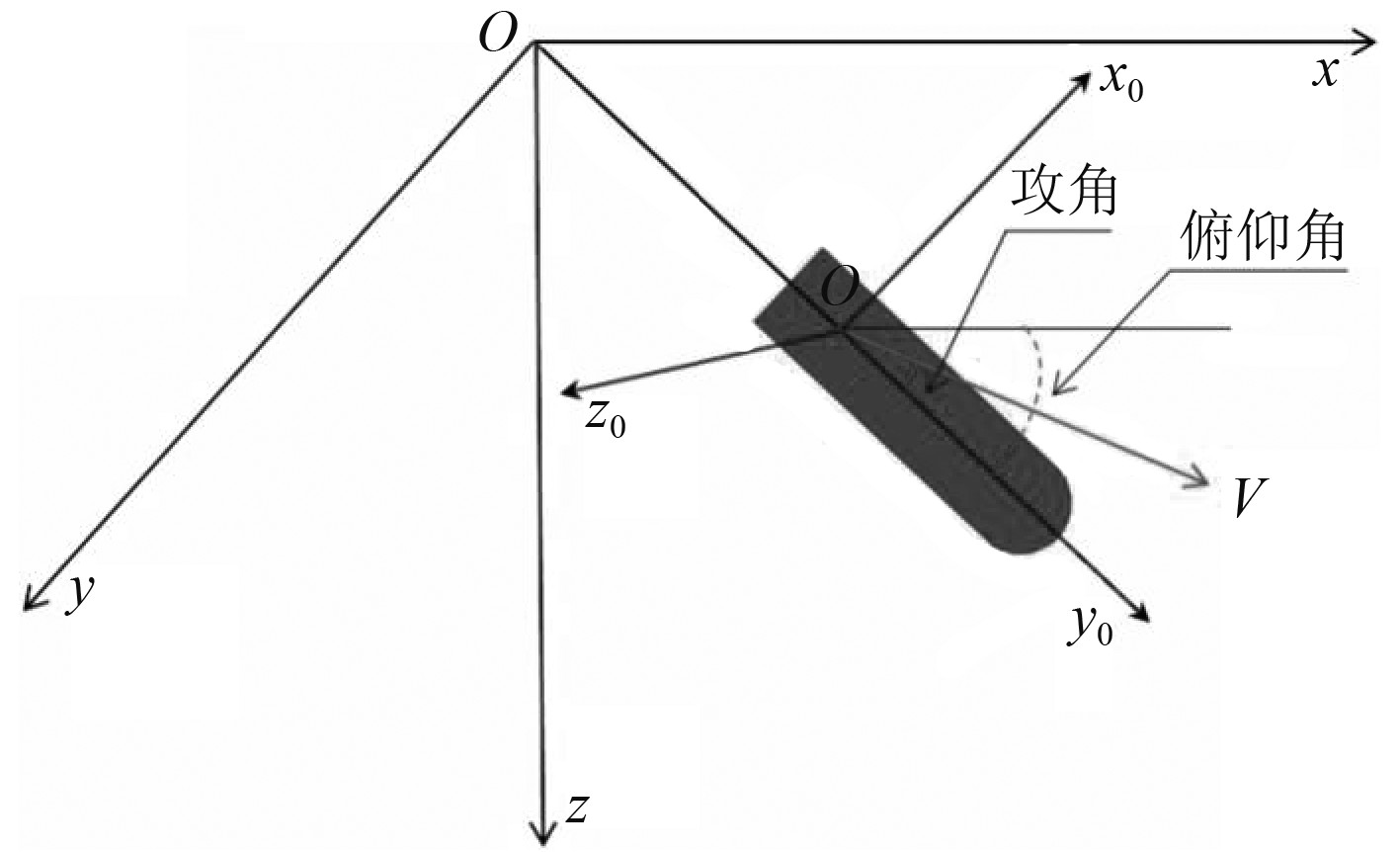
|
图 1 运动坐标系 Fig. 1 Motion coordinate system |
作用在鱼雷上的力和力矩主要有重力,浮力,流体动力,流体阻力,流体动力矩,流体阻力矩等。根据动量定理以及动量矩定理,建立鱼雷水中运动的动力学方程如下[8]:
| ${{ A}_m}\left( \begin{array}{l} {{\dot v}_x} \\ {{\dot v}_y} \\ {{\dot v}_z} \\ {{\dot \omega }_x} \\ {{\dot \omega }_y} \\ {{\dot \omega }_z} \\ \end{array} \right)+{A_{vw}}\left( {{A_m}\left( \begin{array}{l} {v_x} \\ {v_y} \\ {v_z} \\ {\omega _x} \\ {\omega _y} \\ {\omega _z} \\ \end{array} \right)} \right) = {A_F}\text{。}$ | (1) |
其中:
| ${{ A}_{ m}} = \left[\!\!\! {\begin{array}{*{20}{c}} m&0&0&0&{m{z_c}}&{ - m{y_c}} \\ 0&m&0&{ - m{z_c}}&0&{m{x_c}} \\ 0&0&m&{m{y_c}}&{ - m{x_c}}&0 \\ 0&{ - m{z_c}}&{m{y_c}}&{{J_{xx}}}&{ - {J_{xy}}}&{ - {J_{xz}}} \\ {m{z_c}}&0&{ - m{x_c}}&{ - {J_{yx}}}&{{J_{yy}}}&{ - {J_{yz}}} \\ { - m{y_c}}&{m{x_c}}&0&{ - {J_{zx}}}&{ - {J_{zy}}}&{{J_{zz}}} \end{array}} \!\!\!\right]\text{,}$ | (2) |
| ${{ A}_{{vw}}} = \left[ {\begin{array}{*{20}{c}} 0&{ - {\omega _z}}&{{\omega _y}}&0&0&0 \\ {{\omega _z}}&0&{ - {\omega _x}}&0&0&0 \\ { - {\omega _y}}&{{\omega _x}}&0&0&0&0 \\ 0&{ - {v_z}}&{{v_y}}&0&{ - {\omega _z}}&{{\omega _y}} \\ {{v_z}}&0&{ - {v_x}}&{{\omega _z}}&0&{ - {\omega _x}} \\ { - {v_y}}&{{v_x}}&0&{ - {\omega _y}}&{{\omega _x}}&0 \end{array}} \right]\text{,}$ | (3) |
| ${{ A}_{{F}}} = \left[ {\begin{array}{*{20}{c}} {{F_x}} \\ {{F_y}} \\ {{F_z}} \\ {{M_x}} \\ {{M_y}} \\ {{M_z}} \end{array}} \right] = \left[ \begin{array}{l} {F_{x1}} - {F_{x2}} - {F_{x3}} \\ {F_{y1}} - {F_{y2}} - {F_{y3}} \\ {F_g} - {F_f} - {F_{z2}} - {F_{z3}} \\ {M_{x1}} - {M_{x2}} \\ {M_{y1}} - {M_{y2}} \\ {M_{z1}} - {M_{z2}} \\ \end{array} \right]\text{。}$ | (4) |
式中:
| $ \begin{aligned} {F_1} = & 0.5\rho {A_w}{C_d}{u^2},\;{F_2} = 0.5\rho {A_w}{C_d}{V^2},\; \hfill \\ {F_3} =& 0.5\rho {A_w}V{C_d}wL \text{,} \end{aligned} $ | (5) |
| $ {M_1} = 0.5\rho {A_w}{V^2}{C_d}L, \;{M_2} = 0.5\rho {A_w}V{C_d}w{L^2}\text{。} $ | (6) |
式中:
为了分析海流流速,初始攻角对鱼雷水中弹道的影响,模拟鱼雷在均匀海流作用下的运动轨迹,并讨论了海流速度,攻角等因素对鱼雷运动轨迹的影响。同时考虑到真实海流的复杂性,在鱼雷运动方程中引入了随机海流,模拟鱼雷在随机海流作用下的弹道分布,并讨论攻角对鱼雷弹道分布规律的影响。模拟工况参数见表1所示。
|
|
表 1 工况模拟参数 Tab.1 The simulation parameters |
鱼雷初始位置为
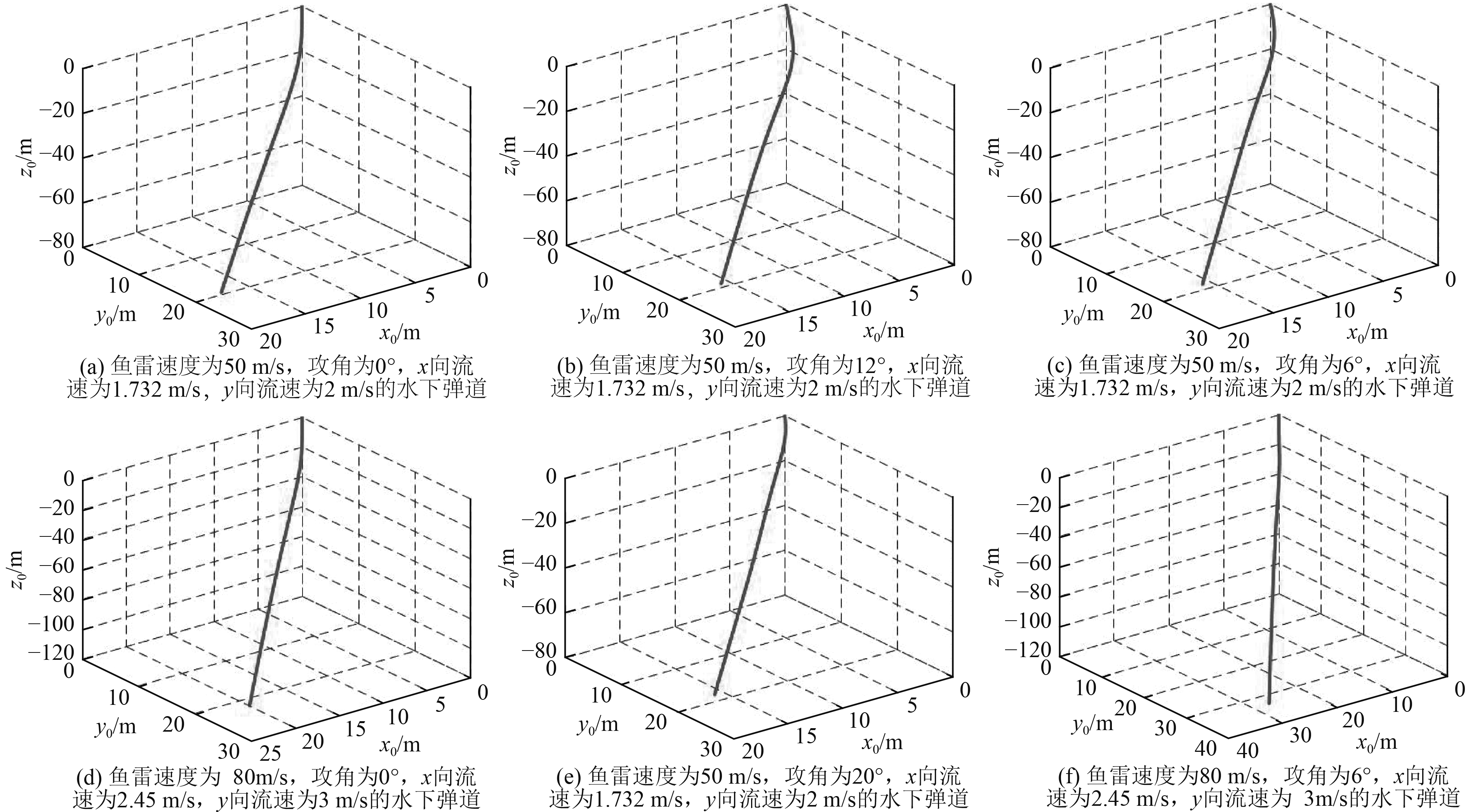
|
图 2 鱼雷水下弹道 Fig. 2 The underwater trajectory of torpedo |
由图可知,鱼雷攻角的变化会导致其水中弹道也发生相应的变化,鱼雷初始阶段的运动是不稳定,随着入水深度的逐渐增加,鱼雷的运动轨迹逐渐稳定。攻角对鱼雷初始阶段的影响较大,对后期运动影响相对较小。海流速度越大,鱼雷的偏移量越大;鱼雷的初始速度对水中弹道的影响相对较小。
图3为鱼雷速度的变化曲线,鱼雷运动速度在砰击瞬间骤减,2 s左右趋于稳定,在随后的运动过程中速度恒定。同时,初始速度越大,稳定阶段的速度也相应越大。当鱼雷速度较大时,海流对鱼雷偏移量影响较小,当鱼雷速度区域稳定后,海流速度与鱼雷速度处于一个量级,海流对鱼雷偏移量影响较大。
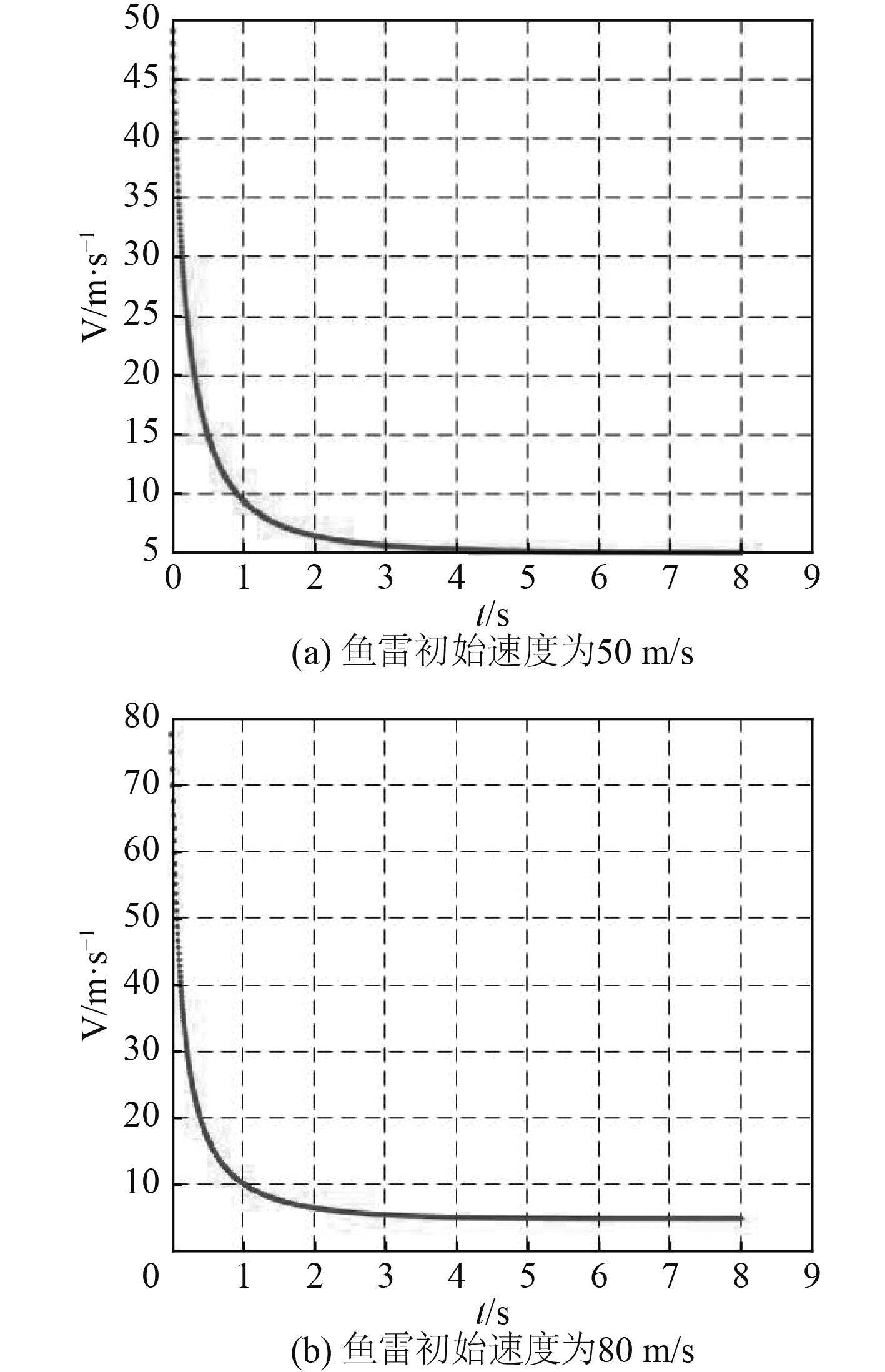
|
图 3 鱼雷速度变化曲线 Fig. 3 The curve of torpedo speed |
由于真实海洋环境的复杂性,鱼雷在水中的运动轨迹要受到海流的影响,因此其运动轨迹也是随机的,很难通过数值方法求得其精确的运动轨迹。在鱼雷六自由度运动方程中引入400个随机海流速度,得到鱼雷的三维弹道散布。鱼雷初始位置为
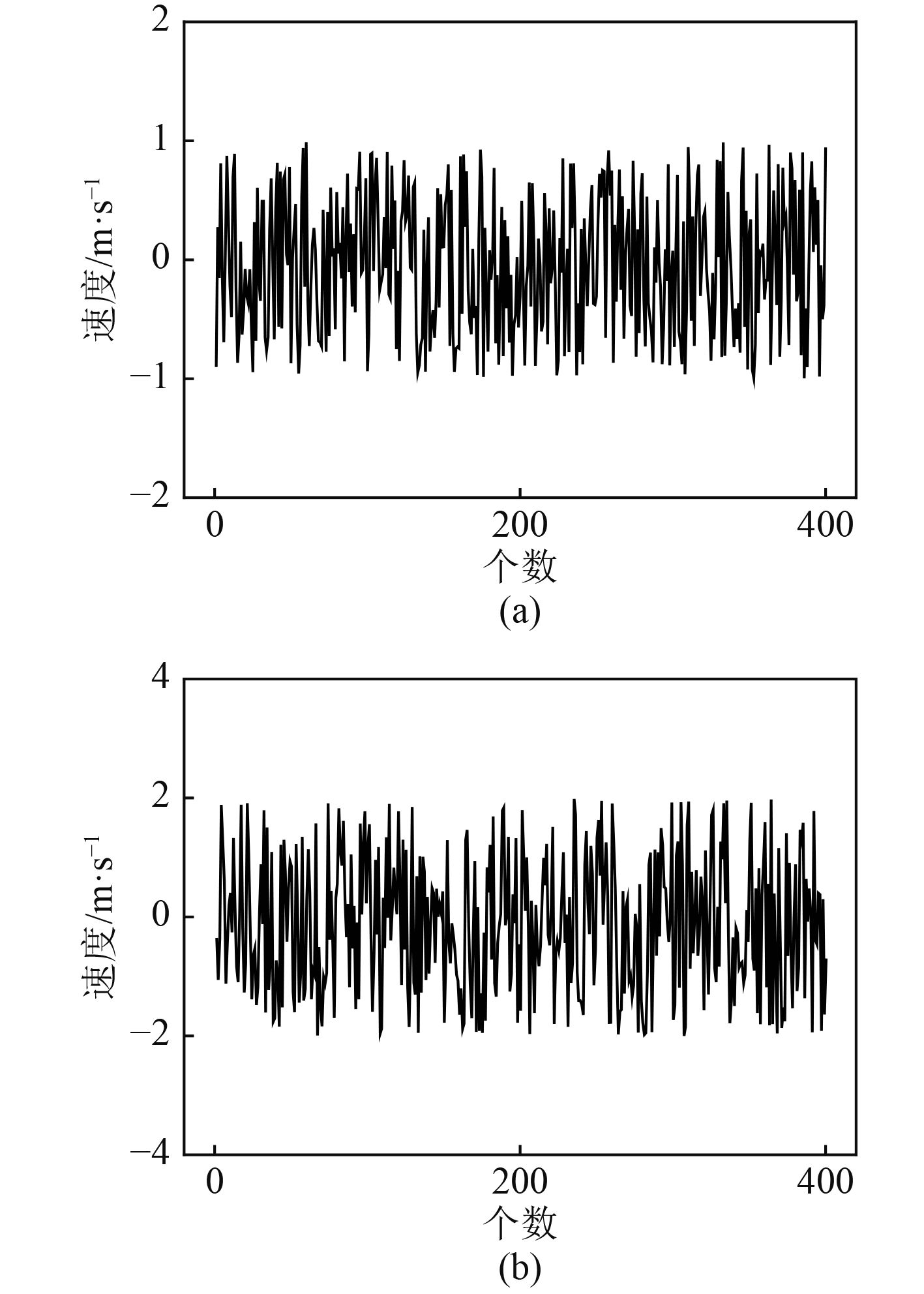
|
图 4 海流速度幅值 Fig. 4 The velocity amplitude of current |
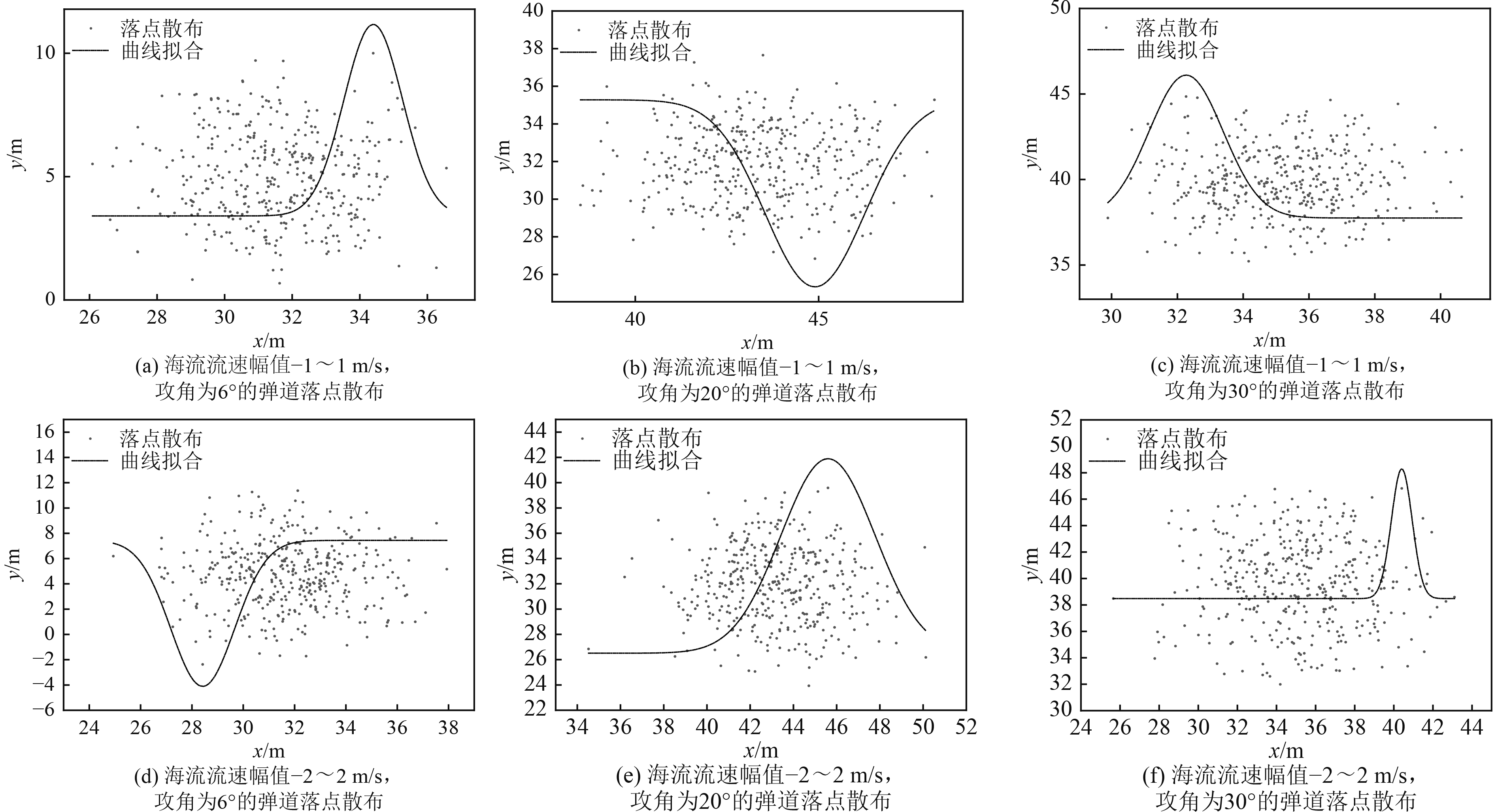
|
图 5 随机海流作用下的鱼雷弹道落点散布图 Fig. 5 Torpedo trajectory sinking position distribution under random current |
随机海流流速分别介于−1~1 m/s,−2~2 m/s,基于Matlab模拟了随机海流作用下的鱼雷三维水中弹道散布,同时讨论了随机海流幅值以及初始攻角对鱼雷弹道落点散布的影响。
由图5可知,随机海流速度幅值和初始攻角差异对鱼雷的最终弹道落点散布有较大影响,随机海流速度幅值越大,弹道落点散布区域越大;初始攻角越大,弹道落点散布整体偏移量越大;弹道落点大多分布在最终落点的中心区域部分,部分弹道落点的偏移量较大,这主要是由于其运动方向与海流方向一致造成的。弹道落点整体呈正态分布趋势。
3 结 语本文编写并求解了鱼雷的六自由度运动方程,模拟了鱼雷三维水中弹道,讨论了海流流速,初始攻角对鱼雷三维弹道的影响。同时考虑到海流的复杂性,在鱼雷六自由度运动方程中引入了随机海流的影响,模拟了随机海流作用下的鱼雷三维水中弹道,分析了随机海流流速幅值以及鱼雷初始攻角等因素对鱼雷三维弹道散布的影响。鱼雷的偏移量随着海流速度的增加而迭代增加,攻角变化只在初始运动阶段影响较大。同时,鱼雷速度在砰击0.5 s内骤减,2 s左右进入稳定阶段,速度恒定。在随机海流作用下,随机海流流速幅值和初始攻角对鱼雷弹道落点散布有较大影响。本文的仿真结果可为空投鱼雷的弹道设计提供参考。
| [1] |
CHU P C, BUSHNELL J M , FAN Chen-wu, et al. Modeling of underwater bomb trajectory for mine clearance[J]. The journal of defense modeling and simulation: Application, Methodology, Technology: JDMS, 2011, 8(1): 25-36. DOI:10.1177/1548512910387807 |
| [2] |
DING Bao-Jun. Simulation analysis of underwater trajectory of air-dropped mine[J]. The journal of Machinery management and development, 2009, 24(5): 51-52. |
| [3] |
GU Chuang. Research on the influence of sea current on underwater trajectory of submarine mine[J]. The journal of Ship electronic engineering, 2010, 30(2): 168-171. |
| [4] |
FANG Yan-Fei. Modeling and simulation on mine’s trajectory of underwater based on ocean current velocity and direction[J]. The journal of ship science and technology, 2013, 35(8): 57-61. |
| [5] |
TAO Li-run, ZHE Chao. Simulation and analysis of the underwater trajectory of small bag sand filling[J]. The journal of China harbour construction, 2017, 37(3): 18-21. |
| [6] |
GANG Wen. Study of dispersion of a certain type hydrobomb under different directions and velocities of seawater[J]. The journal of Wuhan university of technology (Transportation Science& Engineering), 2007(01): 39-42. |
| [7] |
ZHANG Rui, YUAN Zhi-yong, LIU Zhong-le, et al. Anti-torpedo-torpedo intercepting trajectory and analysis of hit probability under sliding mode guidance. In: Proceedings of 10th International Conference on Intelligent Human-Machine Systems and Cybernetics, IHMSC 2018, v 1, p 133-137, November 9, 2018.
|
| [8] |
DUAN Wen-yang, SHI Zhang, CHEN Yun-sai, et al. Research on the probability distribution of the underwater moving of the wrecked targets. In: 38th International Conference on Ocean, Offshore & Arctic Engineer, OMAE2019, June 12, 2019.
|
 2020, Vol. 42
2020, Vol. 42
