0 引　言

在浅海海洋环境下，海水由于季节性变化，海水表层温度较高，其电导率高于中间层和底层海水的电导率。因此海水按电导率不同可以分成不同物性参数的模型。水平电偶极子在浅海海洋环境下空气-海水-海床3层模型可以变为空气-海水多层-海床等n层模型，通过水平电偶极子在海水分层的多层模型中构建数学模型，进行理论推导和仿真计算，以达到更加逼近于真实海洋环境下水平交变电偶极子水下电磁场分布特性的完整呈现。本文将分析时谐水平电偶极子在空气-海水3层-海床等5层模型电场传播规律，并与空气-海水-海床3层模型中电场进行对比分析。

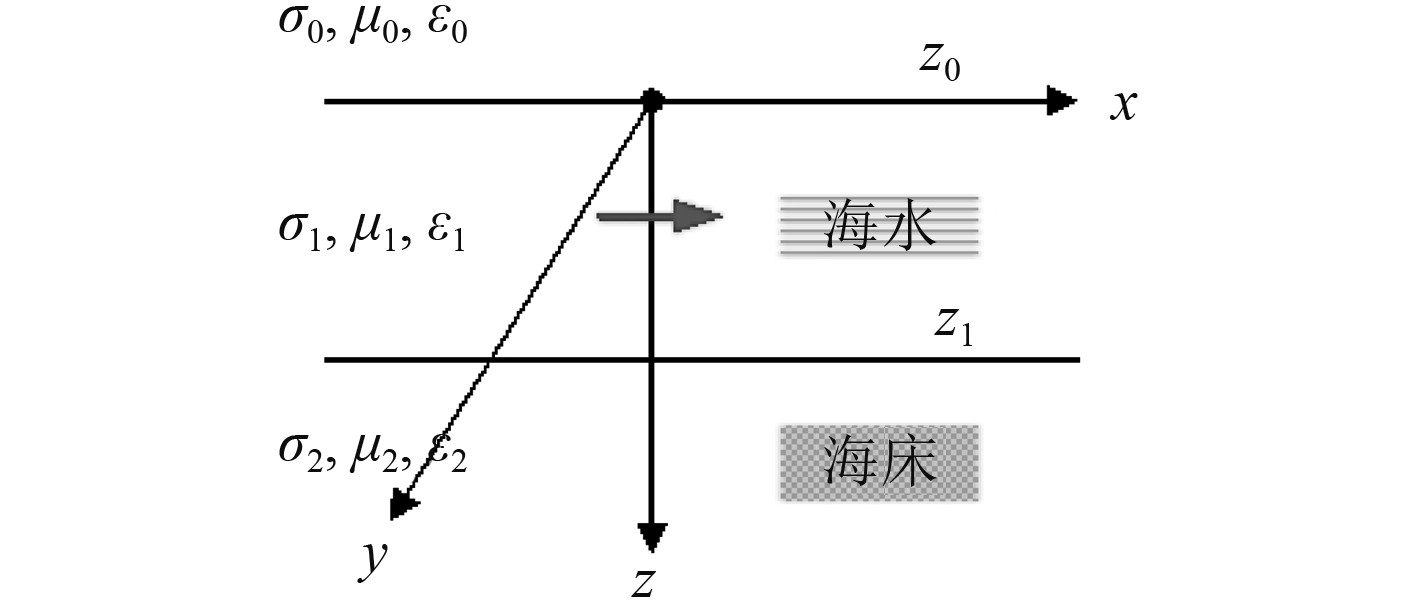
1 三层模型理论^[1-3]

水平电偶极子模型参数：设水平电偶极子位于海水中点 $(0,0,{{h}})$ 处，模型如图1所示。以空气-海水界面作为z=0的平面，z=D为海水-海底界面，空气、海水的电磁参数如图中所示。为了满足边界条件，水平电偶极子的矢量磁位即产生与电偶极子同方向的矢量磁位，还产生与边界面相垂直的矢量磁位，即 ${{{A}}_{{n}}} = {{i}}{{{A}}_{{{nx}}}} + {{k}}{{{A}}_{{{nz}}}}$ 。对于3层模型，空气、海水和海底中矢量磁位分别满足的约束方程：

$\left\{\begin{aligned} & {\nabla ^2}{{{A}}_0} = 0\;{\text{，}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{z}} < 0\;{\text{；}}\\ & {\nabla ^2}{{{A}}_1} + {{k}}_{{1}}^{{2}}{{{A}}_1} = - {\mu _0}{{Ids}}\delta ({{r}})\;{\text{，}}\;\;\;\;\;\;\;\;\;\;\;0 < {{z}} < {{D}}\;{\text{；}}\\ & {\nabla ^2}{{{A}}_2} + {{k}}_{{2}}^{{2}}{{{A}}_2} = 0\;{\text{，}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{z}} > {{D}}\;{\text{。}} \end{aligned}\right. $

(1)

满足的边界条件为：通过边界面的电场的切向分量和磁场是连续的。如果矢量 $k$ 是与边界面垂直的矢量，则有 $k \cdot H$ ， $k \times H$ ， $k \times E$ 是连续的，数学表达式为：

$ \begin{split} & {{k}} \cdot \nabla \times ({{{A}}_{{n}}} - {{{A}}_{{{n}} + 1}}) = 0,\;\;\;{{k}} \times \nabla \times ({{{A}}_{{n}}} - {{{A}}_{{{n}} + 1}}) = \\ & \quad \quad 0,\;{{k}} \times \nabla \nabla \cdot (\frac{{{{{A}}_{{n}}}}}{{{\sigma _{{n}}}}} - \frac{{{{{A}}_{{{n}} + 1}}}}{{{\sigma _{{{n}} + 1}}}}) = 0\;{\text{，}} \end{split} $

(2)

海水中矢量位其通解为：

$ \begin{aligned} & {{{A}}_{{{1x}}}} = \int\nolimits_0^\infty {{\text{d}}\lambda {{{J}}_0}(\rho \lambda )} \left\{ {\frac{{{\mu _0}{{\text{j}}_{\text{x}}}}}{{4\pi }}\frac{\lambda }{{{v_1}}}\exp ( - {v_1}\left| {{{z}} - {{h}}} \right|) + } \right. \hfill \\ & \quad \quad \quad \left. {{{{f}}_{{{1x}}}}\exp ( - {v_1}{{z}}) + {{{g}}_{{{1x}}}}\exp ({v_1}{{z}})} \right\} {\text{，}}\\ & {{{{A}}_{{{1z}}}} = \int\nolimits_0^\infty {{\text{d}}\lambda {{{J}}_0}(\rho \lambda )} \left\{ {{{{f}}_{{{1z}}}}\exp ( - {v_1}{{z}}) + {{{g}}_{{{1z}}}}\left. {\exp ({v_1}{\text{z}})} \right\}} \right.} {\text{。}} \end{aligned} $

(3)

联立边界条件求解矢量位约束方程，求解矢量位A，海水中矢量位系数如下：

$ \begin{gathered} {f_{1x}} = \frac{{ - \lambda {X_{10}}[{e^{ - {u_1}z'}} + {X_{21}}{e^{ - {u_1}(2D - z')}}]}}{{{u_1}(1 + {X_{10}}{X_{21}}{e^{ - 2{u_1}D}})}},\; \\ {g_{1x}} = \frac{{\lambda {X_{21}}[{e^{ - {u_1}(2D - z')}} - {X_{10}}{e^{ - {u_1}(2D + z')}}]}}{{{u_1}(1 + {X_{10}}{X_{21}}{e^{ - 2{u_1}D}})}} \\ {f_{1z}} = \frac{\begin{gathered} \lambda (1 - {X_{10}})[{e^{ - {u_1}z'}} + {X_{21}}{e^{ - {u_1}(2D - z')}}] + \\ \lambda (1 + {X_{21}}){Y_{10}}[{e^{ - {u_1}(2D - z')}} - {X_{10}}{e^{ - {u_1}(2D + z')}}] \;{\text{，}} \\ \end{gathered} }{{{u_1}(1 + {X_{10}}{X_{21}}{e^{ - 2{u_1}D}})(1 - {Y_{21}}{e^{ - 2{u_1}D}})}} -\\ {g_{1z}} = \frac{\begin{gathered} {Y_{10}}\lambda (1 + {X_{21}})[{e^{ - {u_1}(2D - z')}} - {X_{10}}{e^{ - {u_1}(2D + z')}}] - \\ {Y_{21}}\lambda (1 - {X_{10}})[{e^{ - {u_1}(2D + z')}} + {X_{21}}{e^{ - {u_1}(4D - z')}}] \;{\text{，}}\\ \end{gathered} }{{{u_1}(1 + {X_{10}}{X_{21}}{e^{ - 2{u_1}D}})[1 - {Y_{21}}{e^{ - 2{u_1}D}}]}} \;{\text{。}} \\ \end{gathered} $

(4)

其中： ${X_{10}} = \displaystyle\frac{{\lambda - {u_1}}}{{\lambda + {u_1}}}$ ， ${X_{21}} = \displaystyle\frac{{{u_1} - {u_2}}}{{{u_1} + {u_2}}}$ ， ${Y_{10}} = \displaystyle\frac{{{\sigma _1}\lambda - {\sigma _2}\lambda }}{{{\sigma _1}{u_1} + {\sigma _2}{u_1}}}$ ， ${Y_{21}} = \displaystyle\frac{{{\sigma _1}{u_2} - {\sigma _2}{u_1}}}{{{\sigma _1}{u_2} + {\sigma _2}{u_1}}}$ ， $M = \displaystyle\frac{{{\mu _0}P}}{{4\pi }}$ ， $r = \sqrt {{{(x - x')}^2} + {{(y - y')}^2}} $ ， ${u_1} = \sqrt {{\lambda ^2} - k_1^2} $ ， $k_1^2 = - i\omega {\mu _0}{\sigma _1}$ 。

对海水中矢量位进行偏微分可以得到海水中电场三分量：

$ \begin{aligned} & {E_x} = - \hat z{A_x} + \frac{1}{{\hat y}}\frac{\partial }{{\partial x}}(\frac{{\partial {A_x}}}{{\partial x}} + \frac{{\partial {A_z}}}{{\partial z}})\;{\text{，}}\\ & {E_y} = \frac{1}{{\hat y}}\frac{\partial }{{\partial y}}(\frac{{\partial {A_x}}}{{\partial x}} + \frac{{\partial {A_z}}}{{\partial z}})\;{\text{，}}\\ & {E_z} = - \hat z{A_z} + \frac{1}{{\hat y}}\frac{\partial }{{\partial z}}(\frac{{\partial {A_x}}}{{\partial x}} + \frac{{\partial {A_z}}}{{\partial z}})\;{\text{。}} \end{aligned} $

(5)

2 n层模型理论^[4]

将海洋环境等效为5层水平层状均匀各向同性导电媒质，根据边界条件，求解矢量位在各层中满足的微分方程将非常困难。与空气—海水—海床三层模型解法不同，本文将5层海洋环境模型延伸为n层海洋环境模型，水平电偶极子源分解为TE和TM极化模式，利用TE和TM的矢量位求解通解。再求偶极子源的特解，并与通解相加得到边值问题的解，其中通解中的待定系数可利用反射系数确定。对傅氏变换空间中的解进行二维反傅氏变换（或反汉克尔变换）可得到最终解。将矢量位解代入场强公式中可得到海床分层环境中偶极子电磁场的解。

矢量位 $A$ 只有 ${A_x}$ 和 ${A_z}$ 分量，而 ${A_y} = 0$ ，即 $\hat A = i{{\hat{\rm A}}_{\rm{x}}} + k{{\hat{\rm A}}_{\rm{z}}} = i{{\hat{\rm A}}_{\rm{x}}} + k{\partial / {\partial x}}{\hat \Lambda _{\rm{z}}}$ 。矢量位如下式。

$ \begin{aligned} & {{{A}}_{{x}}}(\rho ) = \frac{1}{{2\pi }}\int\nolimits_0^\infty {{{{\hat{ A}}}_{{x}}}(\lambda ,z){{{J}}_0}(\rho \lambda )\lambda {{{\rm{d}}}}\lambda } \;{\text{，}}\\ & {{{A}}_{{z}}}(\rho ) = \frac{1}{{2\pi }}\frac{\partial }{{\partial x}}\int\nolimits_0^\infty {{{\hat \Lambda }_{{z}}}(\lambda ,z){{{J}}_0}(\rho \lambda )\lambda {{{\rm{d}}}}\lambda }\;{\text{。}} \end{aligned} $

(6)

在第i层，在此区域中的场可以写为上行波和下行波的叠加，矢量位解形式如下：

$ \begin{aligned} & {{{\widehat A}_{{\text{x}},{\text{i}}}}(\lambda ,z) = {a_{\text{i}}}{e^{{v_{\text{i}}}(z{\text{ - }}{z_{{\text{i}} + {\text{1}}}})}} + {b_{\text{i}}}{e^{ - {v_{\text{i}}}(z{\text{ - }}{z_{\text{i}}})}} + {\delta _{{\text{ij}}}}\frac{\mu }{{2{v_{\text{j}}}}}{e^{ - {v_{\text{j}}}\left| {z - {z_s}} \right|}}} \text{，}\\ & \quad \quad \quad \quad \quad {{\hat \varLambda }_{{\text{z}},{\text{i}}}}(\lambda ,z) = {c_{\text{i}}}{e^{{v_{\text{i}}}(z{\text{ - }}{z_{{\text{i}} + {\text{1}}}})}} + {d_{\text{i}}}{e^{ - {v_{\text{i}}}(z{\text{ - }}{z_{\text{i}}})}}{\text{– }} \\ & \quad \quad \quad \quad \quad \frac{{{v_i}}}{{{\lambda ^2}}}({a_{\text{i}}}{e^{{v_{\text{i}}}(z{\text{ - }}{z_{{\text{i}} + {\text{1}}}})}} - {b_{\text{i}}}{e^{ - {v_{\text{i}}}(z{\text{ - }}{z_{\text{i}}})}})\text{。} \end{aligned} $

(7)

其中： ${{\rm{z}}_{{i}}}$ 是第i层的深度， $v_i^2 = {\lambda ^2} - i\mu \omega {\sigma _i}$ ， ${\delta _{{{ij}}}} = 1, (i = j),{\delta _{{{ij}}}} = 0,(i \ne j)$ 。偶极子位于第j层，在深度 ${z_s}$ 处。注意向上衰减系数 ${a_i}$ 和 ${c_i}$ 是在这层底界面向上，向下衰减系数 ${b_i}$ 和 ${d_i}$ 确定是在这层的顶部向下。这样矢量势表示成衰减指数。

通过应用切向电场E和磁场B的连续的边界条件推导出衰减系数。在求解系数过程中引入反射系数 $R_i^{}$ ， $S_i^{}$ ，其中对于源点上面的层系数 $R_i^ - = {{{b_i}} / {{a_i}}}$ ， $S_i^ - = {{{d_i}} / {{c_i}}}$ ，其中对于源点下面的层系数 $R_i^ + = {{{a_i}} / {{b_i}}}$ ， $S_i^ + = {{{c_i}} / {{d_i}}}$ 。通过上边界和下边界应用边界条件，在含源层的矢量势系数如下式：

$ \begin{array}{l} {a_j} = ({e^{ - {v_{\rm{j}}}\left| {{z_{j + 1}} - {z_s}} \right|}} + R_j^ - {e^{ - {v_j}\left| {{z_j} - {z_s}} \right|}})\frac{{R_j^ + {e^{{v_{\rm{j}}}{h_j}}}}}{{1 - R_j^ - R_j^ + }}\frac{\mu }{{2{v_{\rm{j}}}}}\;{\text{，}}\\ {b_j} = (R_j^ + {e^{ - {v_j}\left| {{z_{j + 1}} - {z_s}} \right|}} + {e^{ - {v_{\rm{j}}}\left| {{z_j} - {z_s}} \right|}})\frac{{R_j^ - {e^{{v_{\rm{j}}}{h_j}}}}}{{1 - R_j^ - R_j^ + }}\frac{\mu }{{2{v_{\rm{j}}}}}\;{\text{，}}\\ {c_j} = ( - {e^{ - {v_{\rm{j}}}\left| {{z_{j + 1}} - {z_s}} \right|}} + S_j^ - {e^{ - {v_j}\left| {{z_j} - {z_s}} \right|}})\frac{{S_j^ + {e^{{v_{\rm{j}}}{h_j}}}}}{{1 - S_j^ - S_j^ + }}\frac{\mu }{{2{\lambda ^2}}}\;{\text{，}}\\ {d_j} = ( - S_j^ + {e^{ - {v_j}\left| {{z_{j + 1}} - {z_s}} \right|}} + {e^{ - {v_{\rm{j}}}\left| {{z_j} - {z_s}} \right|}})\frac{{S_j^ - {e^{{v_{\rm{j}}}{h_j}}}}}{{1 - S_j^ - S_j^ + }}\frac{\mu }{{2{\lambda ^2}}}\;{\text{。}} \end{array} $

(8)

其中： $R_i^ \pm = \displaystyle\frac{{(r_i^ \pm + R_{i \pm 1}^ \pm {e^{ - {v_{{\rm{i}} \pm {\rm{1}}}}{h_{i \pm 1}}}}){e^{ - {v_{\rm{i}}}{h_i}}}}}{{1 + r_i^ \pm R_{i \pm 1}^ \pm {e^{ - {v_{{\rm{i}} \pm {\rm{1}}}}{h_{i \pm 1}}}}}}$ ； $r_i^ \pm = \displaystyle\frac{{{v_{\rm{i}}} - {v_{{\rm{i}} \pm {\rm{1}}}}}}{{{v_{\rm{i}}} + {v_{{\rm{i}} \pm {\rm{1}}}}}}$ ； $S_i^ \pm = \displaystyle\frac{{(s_i^ \pm \!+\! s_{i \pm 1}^ \pm {e^{ - {v_{{\rm{i}} \pm {\rm{1}}}}{h_{i \pm 1}}}}){e^{ - {v_{\rm{i}}}{h_i}}}}}{{1 + s_i^ \pm S_{i \pm 1}^ \pm {e^{ - {v_{{\rm{i}} \pm {\rm{1}}}}{h_{i \pm 1}}}}}}$ ； $s_i^ \pm \!= \! \displaystyle\frac{{{v_{\rm{i}}}{\sigma _{{\rm{i}} \pm {\rm{1}}}} \!-\! {v_{{\rm{i}} \pm {\rm{1}}}}{\sigma _{\rm{i}}}}}{{{v_{\rm{i}}}{\sigma _{{\rm{i}} \pm {\rm{1}}}} \!+\! {v_{{\rm{i}} \pm {\rm{1}}}}{\sigma _{\rm{i}}}}}$ ； ${h_i} \!=\! {z_{{\rm{i}} \!+\! {\rm{1}}}} \!-\! {z_{\rm{i}}}$ ，为第i层的厚度。符号+表示源点下面的层（i>j），符号-表示源点上面的层（i<j）。

通过递推可以得到任意层的矢量位系数，代入矢量公式，然后通过矢量位偏微分公式（4）获取电场的表达式。

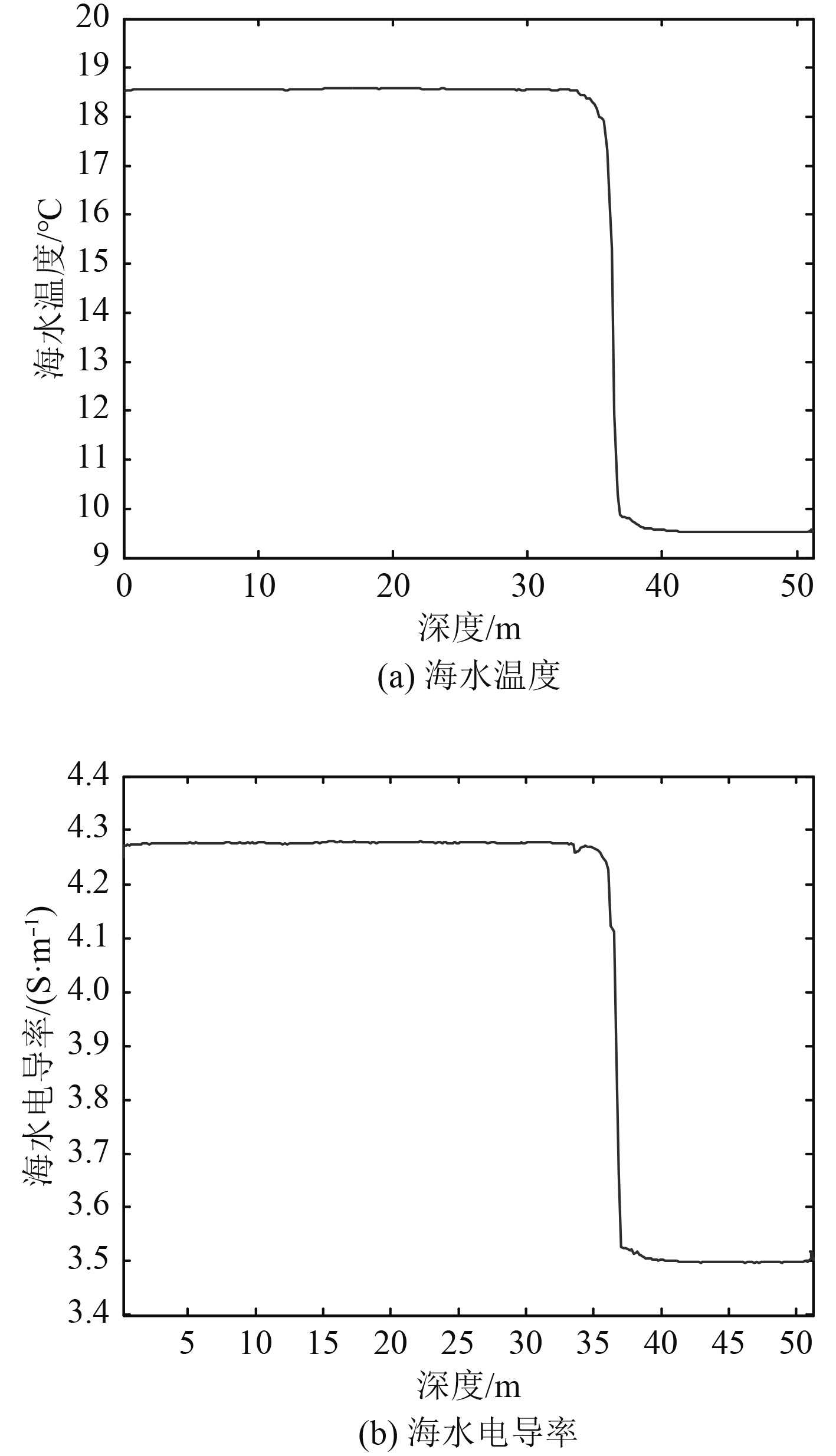
3 海水电性分层海洋环境模型优化

海水电导率受海水温度和盐度的影响而变化。通过海上实际测量海水不同深度下的海水电导率，特别是有不同海水表层温度改变较大时，测量海水不同深度下的海水电导率，获得等效的海水分层模型。海水分层数据为2017年10月份在大连三山岛海域实测温深盐剖面数据。根据海水电导率垂直剖面实测曲线，建立空气—分层海水—海床五层海洋环境模型，其中海水分为3层，各层厚度及电导率数据如表1所示。

4 数值计算

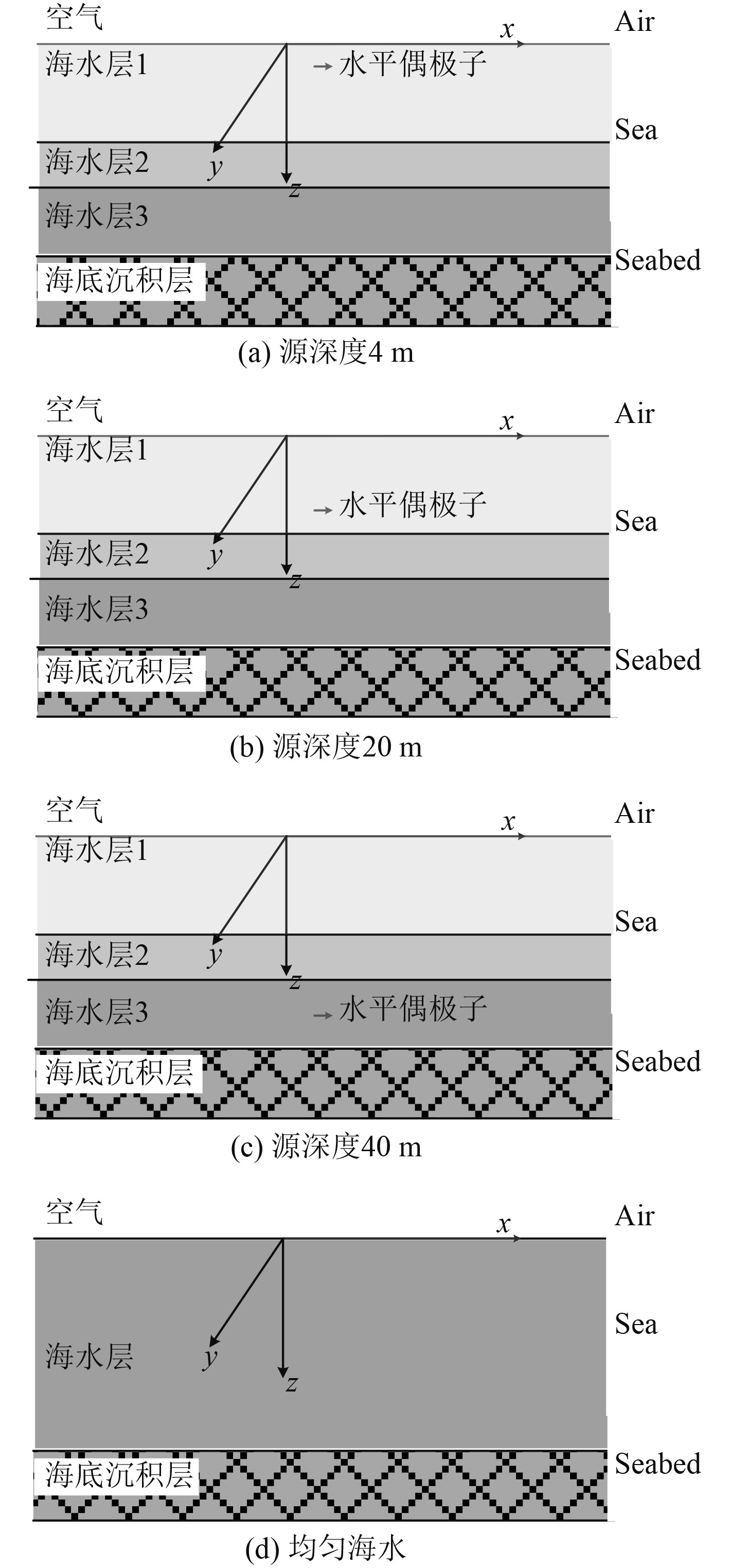
基于上述建立的数学模型，对实测典型海水电导率分层条件下时谐水平电偶极子产生的电场进行了仿真计算，定量分析了海水分层对水下电场量级和分布的影响。取n=5，模型分为5层，分别为空气-分层海水3层-海床。下面对偶极子源位于海水分层3种深度和均匀海水中3种深度情况下电场进行对比分析，偶极子源深度分别为4 m，20 m和40 m，模型示意图如图4所示。图5~图7给出了3种偶极子源深度下，均匀海水和海水分层模型下电场计算对比曲线。

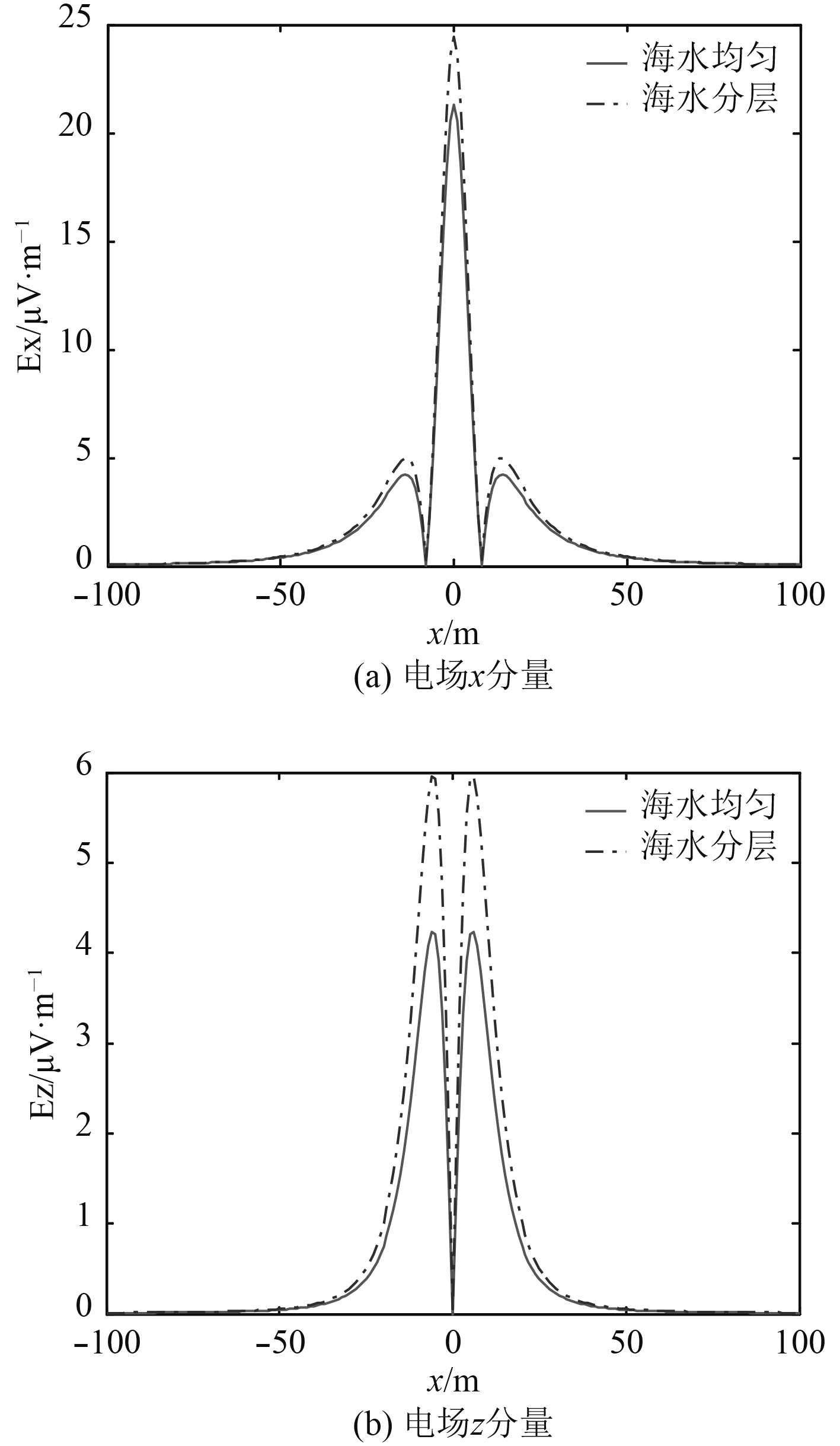
从图5～图7可以看出，电场x分量幅值有3个峰值，最大值位于电偶极子中心正下方，电场z分量有2个峰值，电偶极子中心正下方存在一个波谷。在源深度4 m条件下，海水分层时电场幅值大于海水均匀时电场幅值，曲线形态一致，电场最大值位置未变；海水均匀和分层2种模型下电场x分量计算偏差为4.4%，电场z分量计算偏差为21.9%。在源深度20 m条件下，海水分层时电场幅值大于海水均匀时电场幅值，曲线形态一致，电场x分量最大值位置未变，电场z分量最大值位置稍微外移；海水均匀和分层2种模型下电场x分量计算偏差为4.8%，电场z分量计算偏差为22.1%。在源深度40 m条件下，海水分层时电场幅值大于海水均匀时电场幅值，曲线形态一致，电场x分量最大值位置未变，电场z分量最大值位置稍微外移；海水均匀和分层2种模型下电场x分量计算偏差为13.0%，电场z分量计算偏差为28.9%。因此，随着源深度越深，海水分层对电场幅值影响越大。

5 结　语

根据典型海域实测海水电导率数据，将海洋环境模型等效为空气-海水3层-海床等5层模型。基于上述建立的水平电偶极子电场数学模型，对分层条件下时谐水平电偶极子产生的电场进行了仿真计算，定量分析了海水分层对水下电场量级和分布的影响。电场x分量幅值有3个峰值，最大值位于电偶极子中心正下方，电场z分量有2个峰值，电偶极子中心正下方存在一个波谷；海水分层时电场幅值大于海水均匀时电场幅值，曲线形态一致，电场x分量最大值位置未变，电场z分量最大值位置稍微外移；随着源深度越深，海水分层对电场幅值影响越大，在海水深度51.2 m，源深度40 m情况下，海水均匀和分层2种模型下电场x分量计算偏差达到13.0%。