在信息化时代,信息资源的利用水平直接影响军队信息化建设发展[1]。随着信息化水平的提高,产生的信息数据越来越多也越来越重要。目前,很多数据仍然没有得到充分的应用,大量资源潜在军事效能未得到开发[2],而作为军事通信重要手段的短波通信技术,同样也存在着此类问题。
短波通信又称高频(HF)通信,频率范围为3~30 MHz,主要利用天波经电离层反射后传播信号,无需建立中继站即可实现远距离通信[3, 4]。但因其是天波传播,受电离层变化和多径传播的影响而使通信极不稳定,使得短波通信具有数据传输率低的局限性,而随着信息化战争的发展,对通信传输要求越来越高,尤其对于海上作战的舰艇来说,海上远距离通信达成慢,沟通时间延长,被敌方发现的概率会成倍增加,所以尽可能地提高通信质量,就显得尤为重要。影响短波通信数据传输效果的因素包括通信双方的通信距离,天气情况,发射功率,调制方式,通信时段和信号质量等。其中由于电离层的时变色散特性,短波信道具有明显的窗口效应,使得电离层在不同天气情况和不同时间段具有不同特性,是不可人为控制的通信变量,也是影响短波通信信号质量的重要因素。本文通过对短波通信数据的积累,对影响短波通信效果的天气情况和时间段特征进行分析,挖掘信噪比的潜在变化规律,得出某一通信链路较为合适的通信时间段和天气情况,能有效提升短波通信的接通率和通信过程的信号质量,对通信指挥的决策过程起到重要辅助作用。
1 短波通信数据工程军事数据工程以军事为研究对象,采用军事系统工程为基本研究方法,以数学和计算机为研究工具,为国防军队建设和作战指挥决策提供数据应用服务[5–6]。短波通信数据工程是对通信数据进行采集,整理数据得到可利用的规范化数据,对数据存储、调用和特征分析,最终得出短波通信特征对其影响情况。
本文以公开的短波通信站信号为搜集对象,记录了短波通信过程中的相关参数并进分析。本方案设计主要包括了短波数据的规范化设计,数据清洗与分组过程,短波通信的时间特征和天气特征的影响分析,特征之间与接收信号功率之间的相关性分析,并最终以数据可视化方法得出分析结果。流程图设计如图1所示。
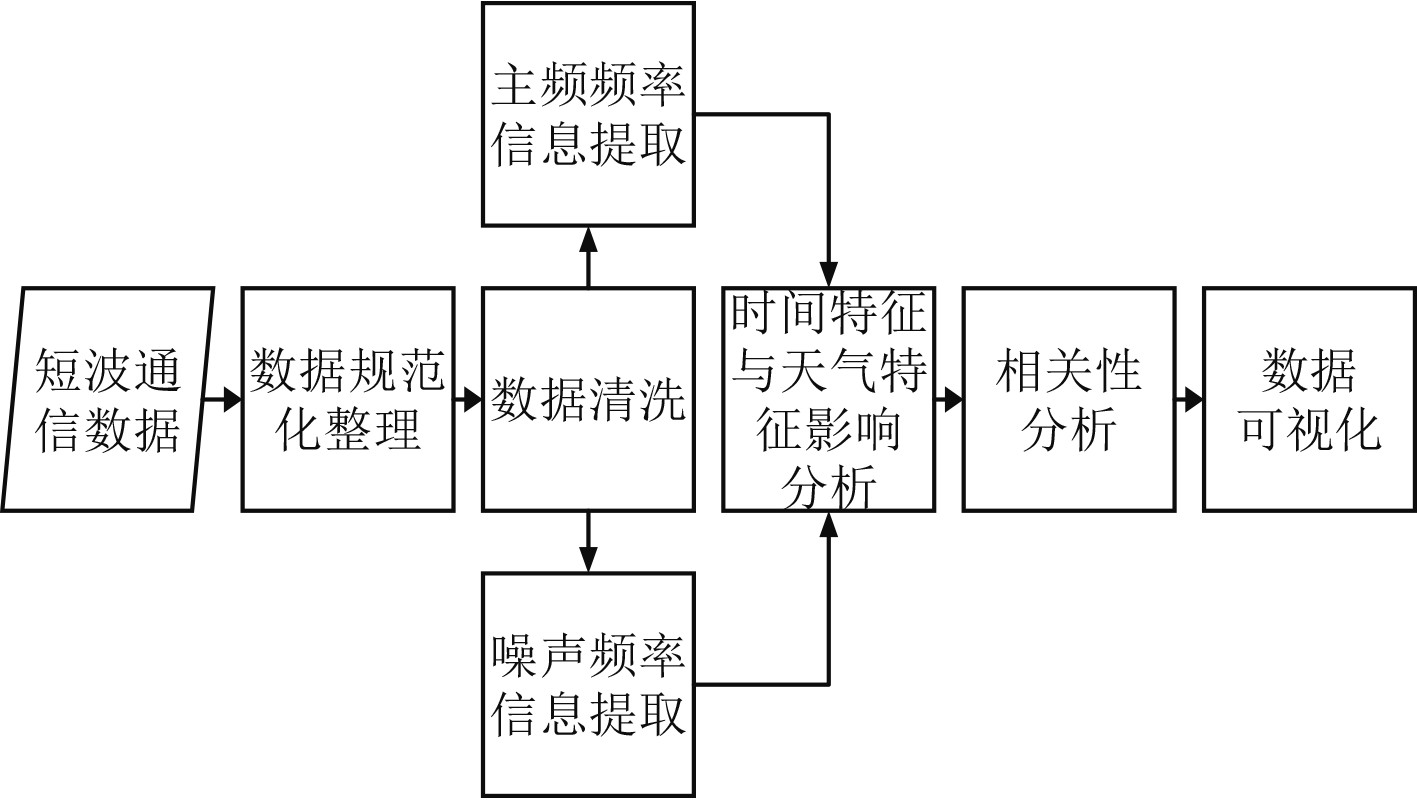
|
图 1 方案流程图 Fig. 1 Flowchat |
数据规范化设计主要是为了便于程序系统处理数据,避免因数据结构的差异而造成与程序不兼容的情况,同时提高程序处理效率。
本实验采集公开短波发信台站的通信时间、频率、调制方式、经纬度和台站编号信息,采集通信频率±5%作为噪声信号来源,计算本站与对方台站之间通信距离,查询双方台站所属地的天气情况,利用短波分析软件确定信号接收增益,带宽和接收功率。为了便于计算机处理采用英文与数字记录,规范后的数据格式如表1所示。收方天气和收方天线类型,均为Excel字符串格式。
|
|
表 1 规范数据表 Tab.1 Standard database |
设置信号采样率为10 s/次。在短波通信中电离层的显著变化在极小的采样周期中可忽略不计,故本文以小时作为时间段,计算接收信号功率均值,目的是降低单一时刻内采样信号的误差概率,同时保留整体时刻内信号强度随时间变化的特性。
在相关性处理中由于天气列表中记录的数值为字符串型,本文采用了字符编码的方法,将不可用于分析的字符变量进行量化处理后得到数字变量,对数据的缺失值使用中位数进行填充,最终得到可用于分析的合格数据。
分组处理是以时间和收发双方天气作为分组依据。假设时间段分布个数为T,发方天气类别数为S,收方天气类别数为R,经过数据表的分组处理,生成的复杂度为
重点对时间段,接收功率与噪声功率,收方天气和发方天气等维度进行组合,假设T,S,R分别为时间段,发方天气和收方天气。
在T,S,R确定的情况下,信号功率值样本为
| $E({P_{T,S,R}}) = \frac{1}{n}\sum\limits_{i = 1}^n {P_{T,S,R}^{(i)}} \text{。}$ |
信号功率
| ${\sigma _{T,S,R}} = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {P_{T,S,R}^{(i)} - E({P_{T,S,R}})} \right)}^2}} } \text{。}$ |
式中:Cov表示协方差,Var表示样本方差,X表示T,R和S的集合。则在确定的T,S,R情况下的功率
| $r = \frac{{\text{Cov}({P_{T,S,R}},X)}}{{\sqrt {\text{Var}({P_{T,S,R}})Var(X)} }}\text{,}$ |
| $\text{s.t.Cov}({P_{T,S,R}},X) = E(({P_{T,S,R}} - E({P_{T,S,R}}))(X - E(X)))\text{,}$ |
| $\text{Var}({P_{T,S,R}}) = \frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{(P_{T,S,R}^{\left( i \right)} - E({P_{T,S,R}}))}^2}} \text{,}$ |
| $\text{Var}(X) = \frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{({X^{(i)}} - E(X))}^2}} \text{,}$ |
| $E(X) = \frac{1}{n}\sum\limits_{i = 1}^n {{X^{(i)}}} \text{,}$ |
| $X = \{ T,S,R\} \text{。}$ |
数据可视化技术[7– 8]利用计算机图形图像和数据挖掘的技术与方法,将数据中隐藏的信息,以交互方式形象生动地展示给使用者。可视化技术可以极大地提升人们分析和理解数据的速度,帮助人们更有效地对海量数据进行探索,从而突破数据分析问题的瓶颈。通过数据可视化方法发掘了信号接收功率的潜在变化规律,通过相关性热图,数据散布图和特征核密度估计图分别展示并发掘了维度之间的相关性与维度自身的分布特性。其中特征核密度估计使用高斯核函数。
假设高斯核函数为K,集合X的标准差为
| $K(X,E(X)) = \exp (\frac{{ - {{\left\| {X - E(X)} \right\|}^2}}}{{{{\left( {2{\sigma _x}} \right)}^2}}})\text{,}$ |
| $X = \{ T,S,R\} \text{,}$ |
| ${\sigma _x} = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{({X^{(i)}} - E(X))}^2}} } \text{。}$ |
使用10 m鞭天线对6.105 MHz,7.275 MHz,9.75 MHz,11.825 MHz与13.79 MHz进行采样分析,采样时间集中于上午8时至11时,下午17时至21时。数据分析实验平台为JupyterNotebook,编程语言为Python3.5。为了便于描述,实验以9.75 MHz数据为例进行相应分析。
2.2 数据整理与量化使用的数据预处理与分析模块为Numpy,Pandas[9]与Scikit-learn[10],利用模块的内嵌函数实现对数据的填充,归类和量化编码。输入为规范化设计的标准数据,输出经过量化和分组的数据结构,并作为数据分析模块的输入参数进行程序分析。
量化后的情况是0代表cloudy天气,1代表sunny天气,2代表shower天气。
2.3 时间特征与天气特征影响图2表示收发双方均为晴天天气。其中虚线1表示通信频率接收场强变化情况,虚线2表示噪声变化情况;虚线3代表接收信号的信噪比;散布点表示采样数据的分布情况。横坐标表示通信时间段,纵坐标表示接收信号强度。从图中分析可知该频率下最佳通信时段即信噪比最高值为下午16时左右。
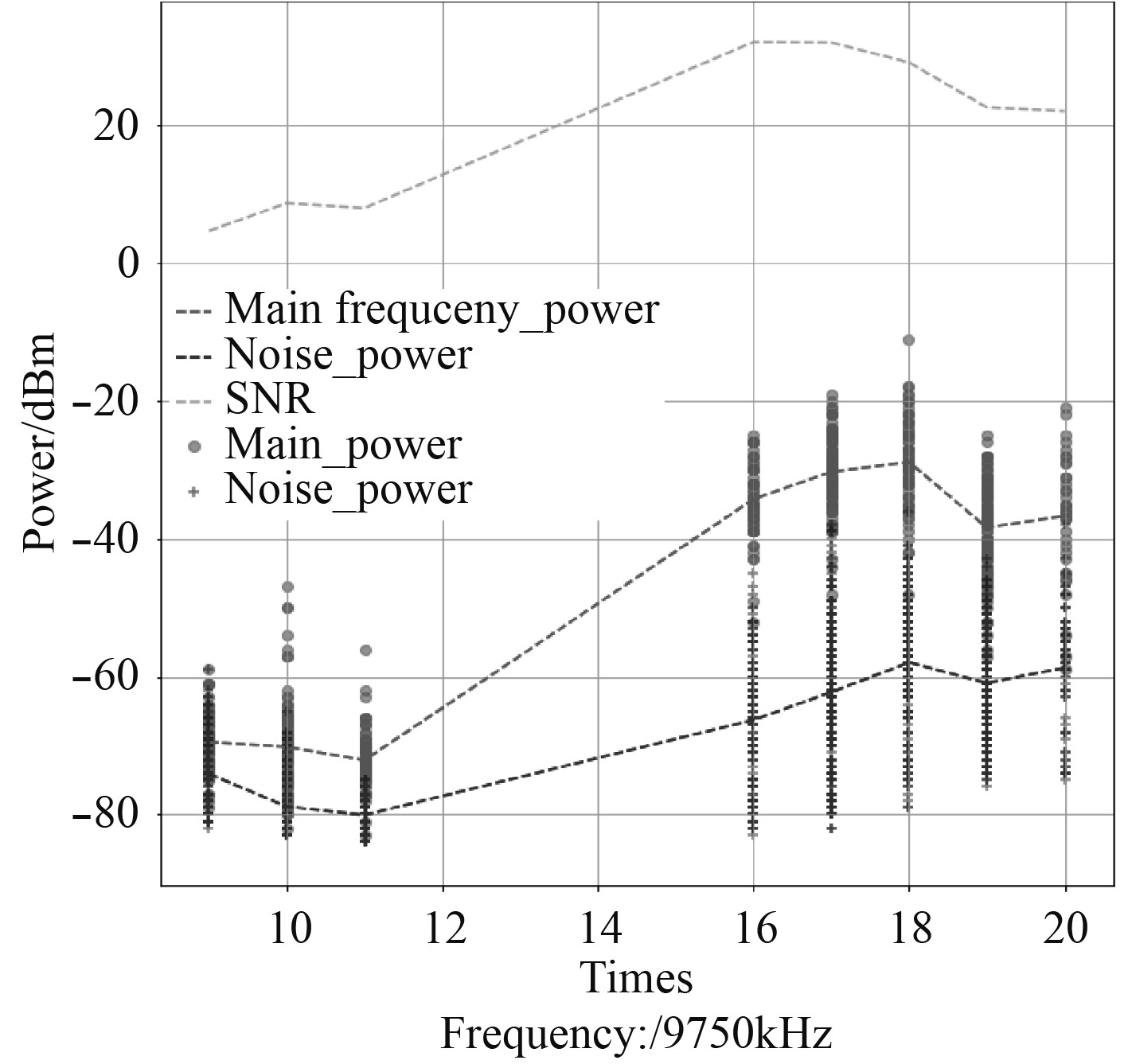
|
图 2 特征影响结果(1) Fig. 2 Influence of characteristics(1) |
图3表示发方为晴天,收方为多云情况下不同时段通信接收频率的变化情况。从图中可以看出,在接收方接收信号强度也伴随一定程度的下降,接收信号强度与噪声信号强度差值有所下降,即信噪比有所降低,且信噪比最高点对应的时刻有所移动,达到傍晚19时左右。
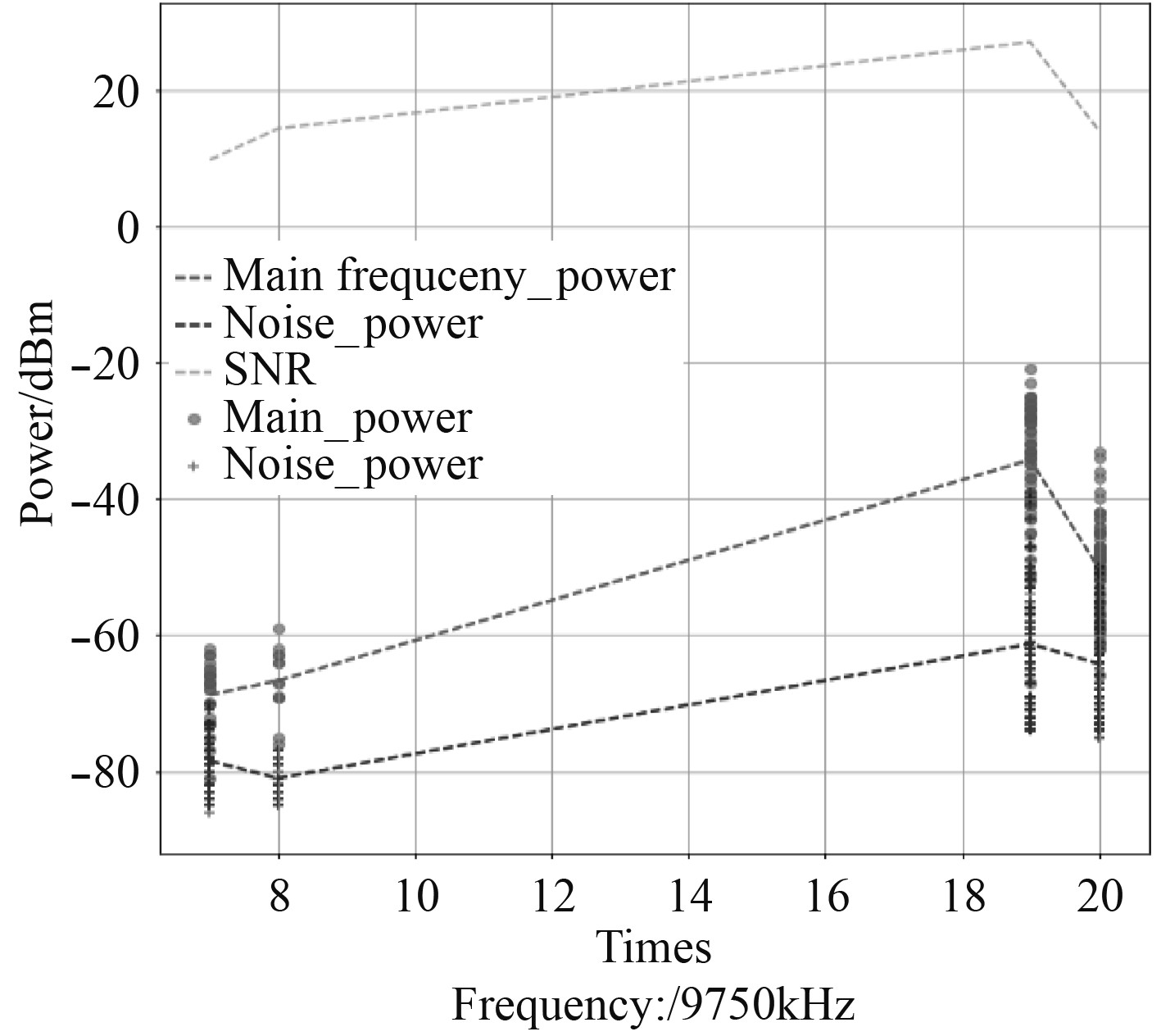
|
图 3 特征影响结果(2) Fig. 3 Influence of characteristics(2) |
数据在维度为n的情况下可以生成
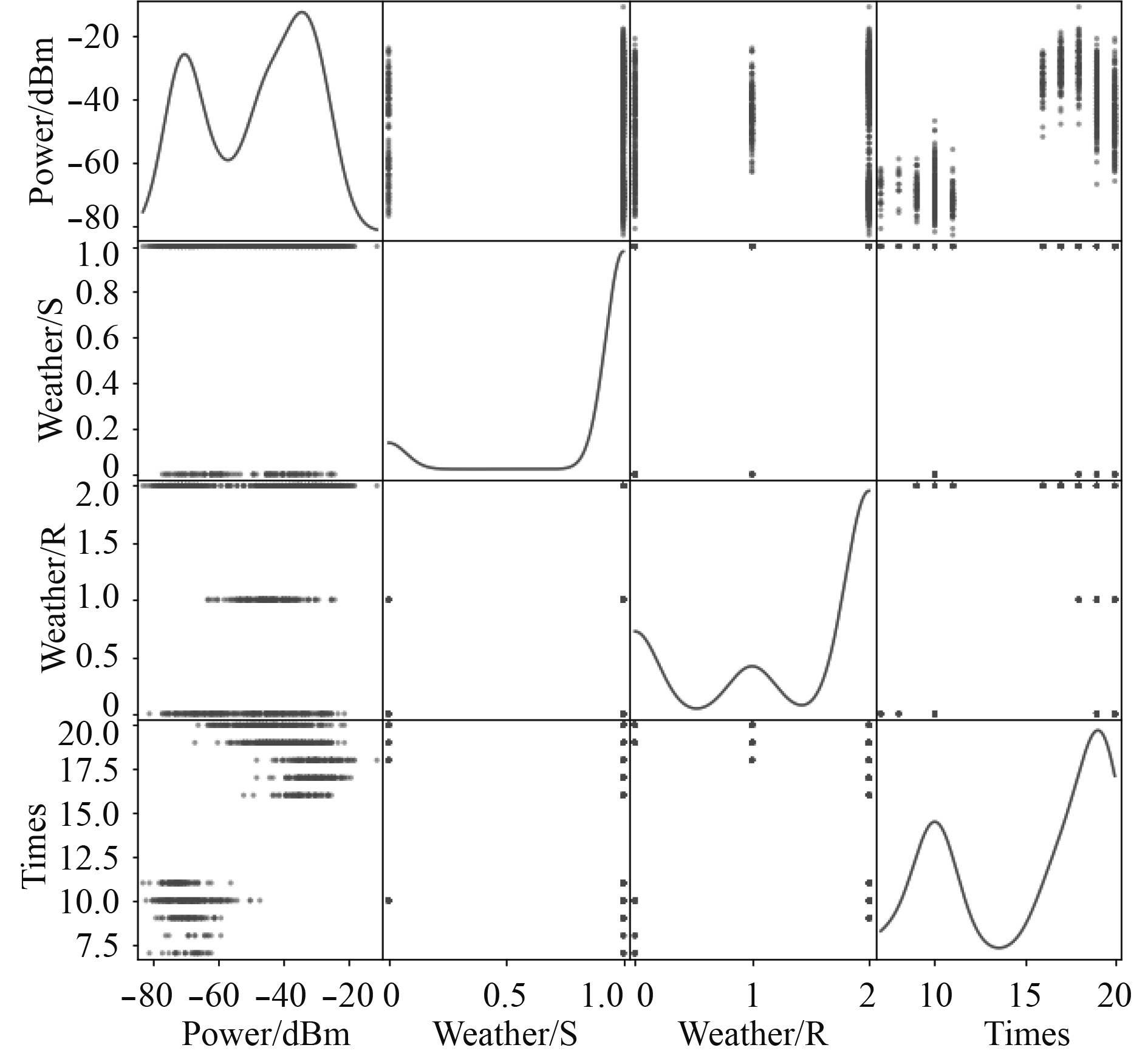
|
图 4 接收信号散布矩阵图 Fig. 4 Scatter matrix of received signal |
由图5可以分析得知,噪声功率集中于–80 dBm~–40 dBm左右。从特征核密度估计图中分析得知噪声功率主要分布于–40 dBm左右。
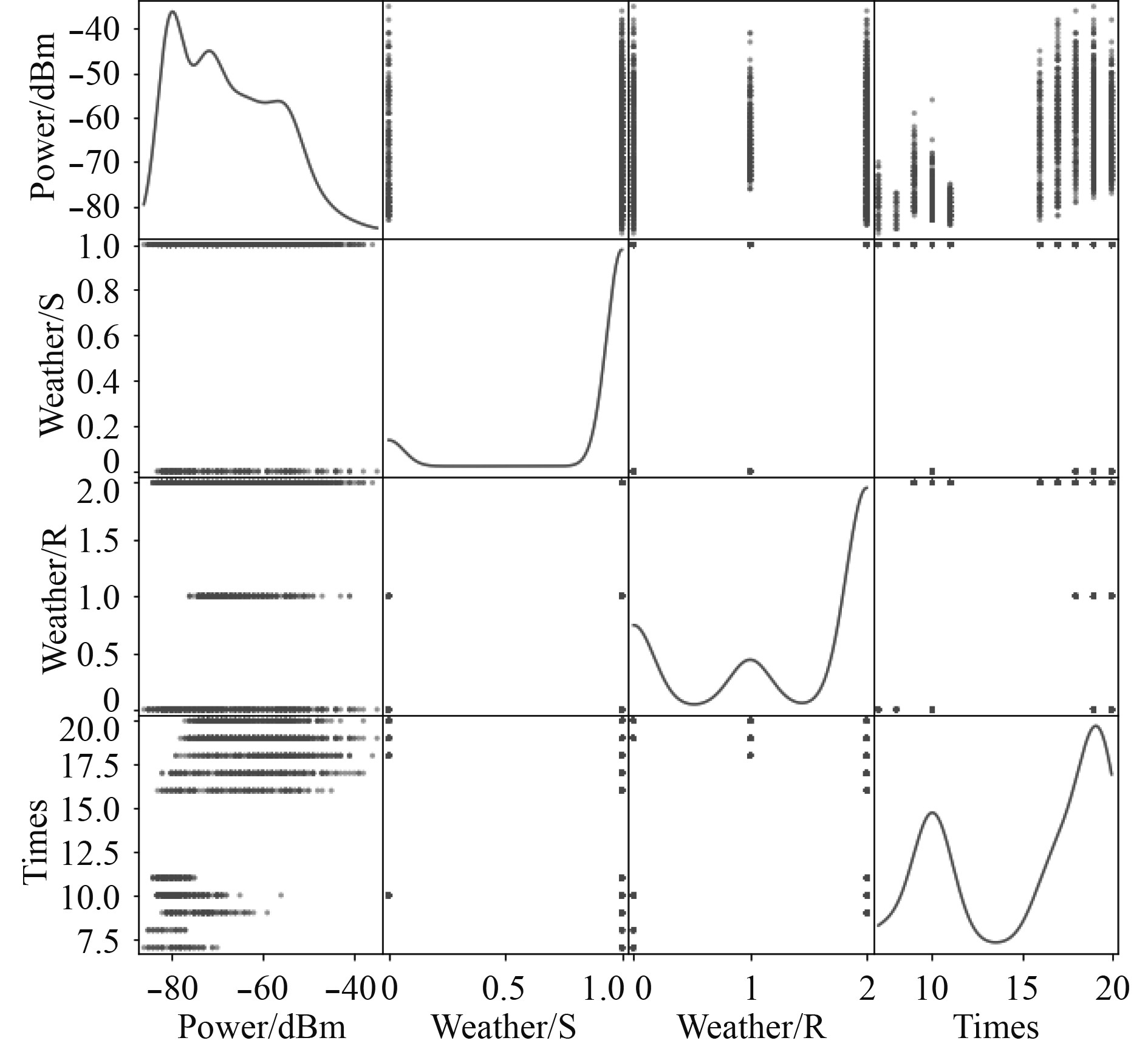
|
图 5 噪声信号散布矩阵图 Fig. 5 Scatter matrix of noise signal |
从图6分析得到接收信号频率与时间分布呈较强的相关性。从图7分析得到噪声与时间分布也呈较强的相关性,相关度低于接收信号。接收信号的功率与发方台站天气的相关性高于噪声信号与发方台站天气的相关性。故为了获得更大的信噪比,接收信号应更加注意发送台站的天气状况。
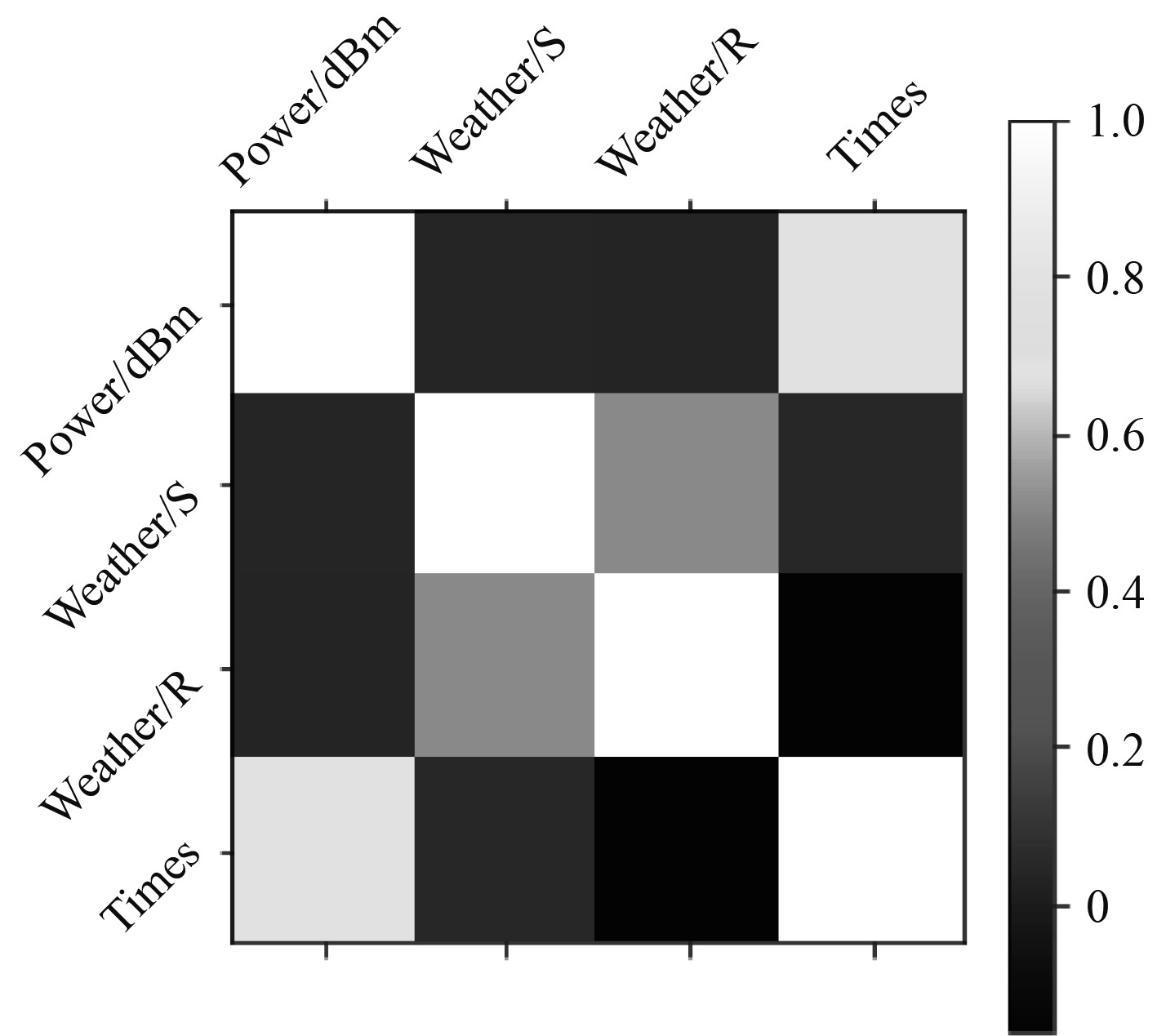
|
图 6 接收信号相关性热图 Fig. 6 Correlation heat-map of received signal |
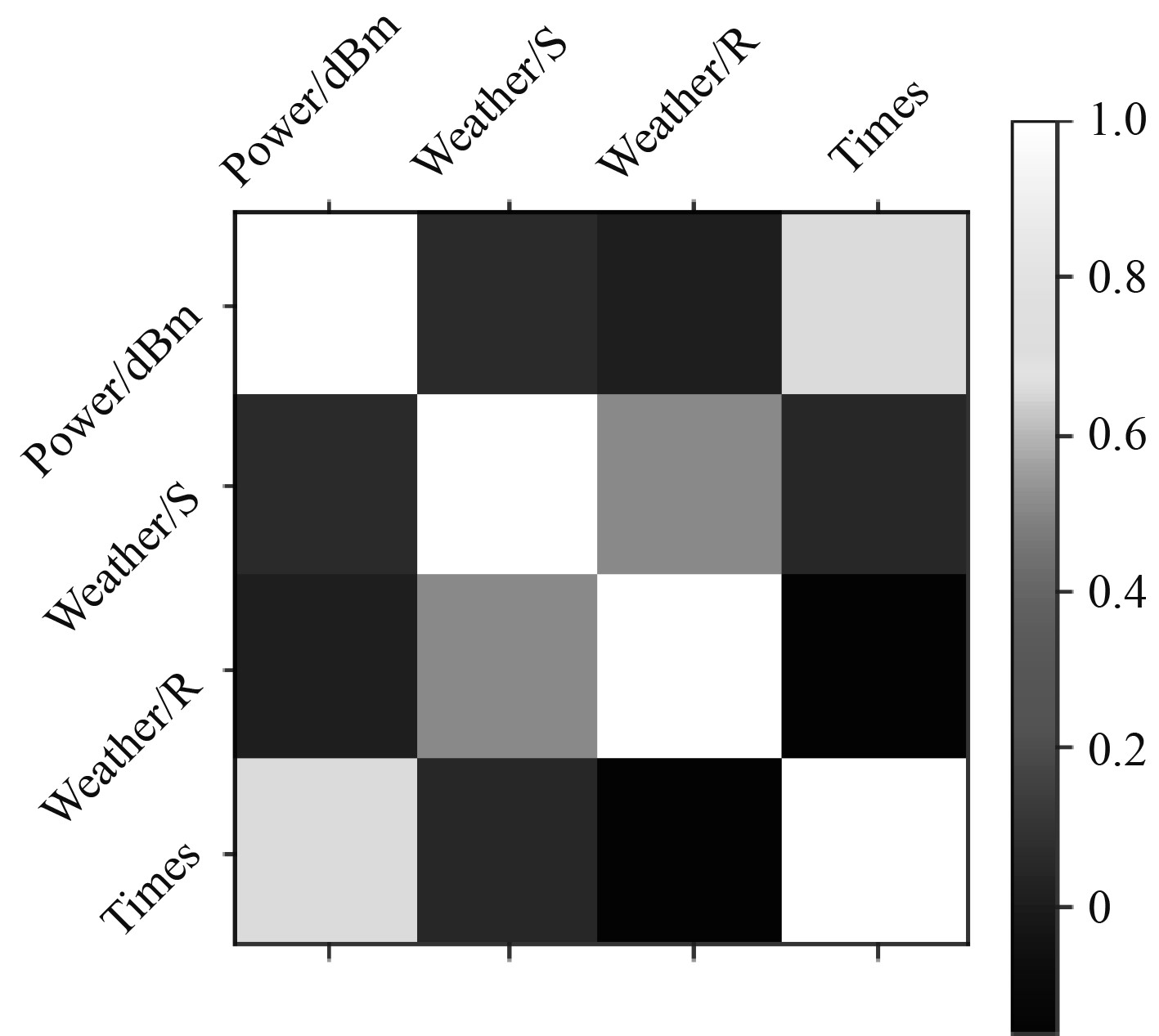
|
图 7 噪声信号相关性热图 Fig. 7 Correlation heat-map of noise signal |
本文利用数据工程方法探究了短波通信数据的挖掘、分析与可视化方法,利用现有的短波通信数据,通过数据清洗,数据挖掘,数据分析和数据可视化等处理方法,提升了数据资源的利用率,得出了短波通信接收信号强度、噪声信号与收发双方天晴情况和接收时间段的分布与相关性,并得到了最高信噪比,分析了同等情况下短波通信效果最好的时段与天气情况。可以为海上行驶的舰船提供最佳通信时间段,压缩了沟通时间,能极大提升舰船生存概率,同时也可为军事短波通信的决策和实施过程起到一定的辅助作用。
| [1] |
吴铭. 大数据时代军事信息资源开发利用探析[J]. 电脑知识与技术, 2015(8): 12-13. Wu Ming. Development and utilization of military information resources in the Age of Big Date[J]. Computer Knowledge and Technology, 2015(8): 12-13. |
| [2] |
王娟, 梅强, 牛晓华. 数据工程在军事通信中的应用设计[J]. 数据通信, 2016(5): 16-21. Wang Juan, Mei Qiang, Niu Xiaohua. The application of data engineering in the Military Field[J]. Data Communication, 2016(5): 16-21. DOI:10.3969/j.issn.1002-5057.2016.05.005 |
| [3] |
董彬虹, 李少谦. 短波通信的现状及发展趋势[J]. 信息与电子工程, 2007, 5(1): 1-5. DONG Bin-hong, LI Shao-qian. Current Status and Developing Tendency for High Frequency Communications[J]. Information and Electronic Engineering, 2007, 5(1): 1-5. DOI:10.3969/j.issn.1672-2892.2007.01.001 |
| [4] |
徐池, 邱楚楚, 李梁, 等. 海上短波通信频率优选技术现状与分析[J]. 通信技术, 2015, 48(10): 1101-1105. XU Chi, QIU Chu-chu, LI Liang, et al. Status and Analysis of Optimum Frequency Selection for Maritime HF Communications[J]. Communications Technology, 2015, 48(10): 1101-1105. DOI:10.3969/j.issn.1002-0802.2015.10.001 |
| [5] |
林平, 刘永辉, 陈大勇. 军事数据工程基本问题分析[J]. 军事运筹与系统工程, 2012(1): 14-17. Lin Ping, Liu Yonghui, Chen Dayong. Analysis of Some Fundamental Issue about military data engineering[J]. Military Operations Research and Systems Engineering, 2012(1): 14-17. DOI:10.3969/j.issn.1672-8211.2012.01.003 |
| [6] |
刘泉生. 船舶通信系统周期性信号分离方法[J]. 舰船科学技术, 2018, 40(12A): 112-114. LIU Quan-sheng. Research on separation method of periodic signals in ship communication system[J]. Ship Science and Technology, 2018, 40(12A): 112-114. |
| [7] |
任磊, 杜一, 马帅, 等. 大数据可视分析综述[J]. 软件学报, 2014, 25(9): 1909-1936. REN Lei, DU Yi, MA Shuai, et al. Visual analytics towards big data[J]. Journal of Software, 2014, 25(9): 1909-1936. |
| [8] |
刘芳. 信息可视化技术及应用研究[D]. 杭州: 浙江大学, 2013. Liu Fang. Research on Information Visualization Technology and Application[D]. Zhejiang University, 2013. |
| [9] |
Wes MCKINNEY. Python for Data Analysis[M]. Sebastopol: O’Reilly Media, 2012.
|
| [10] |
Aurélien GÉRON. Hands on machine learning with scikit-learn&tensorflow[M]. Sebastopol: O’Reilly Media, 2017.
|
 2020, Vol. 42
2020, Vol. 42

