随着武器技术不断发展,为适应多样化的作战需求,次声波武器因其特有的生物杀伤效果在应对地区局部冲突、反恐作战中有着非常广阔的应用前景[1]。由于声波在传播中存在波束发散和能量衰减,相比于高频声波,低频声波在介质中的声吸收效应较弱,对于复杂的地形障碍、隔声材料等有着良好的穿透性。但由于低频声波的波长较长,其波束指向性通常较差,因此实现波束的定向是研制次声武器的关键,否则无法进行攻击反而会危及已方人员[2-3]。
使用声相控阵技术设计扬声器阵列可以实现声波指向性可控,通过调节阵列之间的声程差从而增强主瓣能量,抑制旁瓣达到增强指向性的目的。国内研究学者对高频声波定向方面已有较多研究[4-6],但是声源辐射半径较小,功率有限。对于大辐射半径、高功率的低频声源定向领域上的理论与实验研究相对较少。为此,本文因此本文选取2台低音喇叭,分析和测试了大辐射半径声源在低频声波单向发射上的实现,以此作为后续声波武器研制的基础。
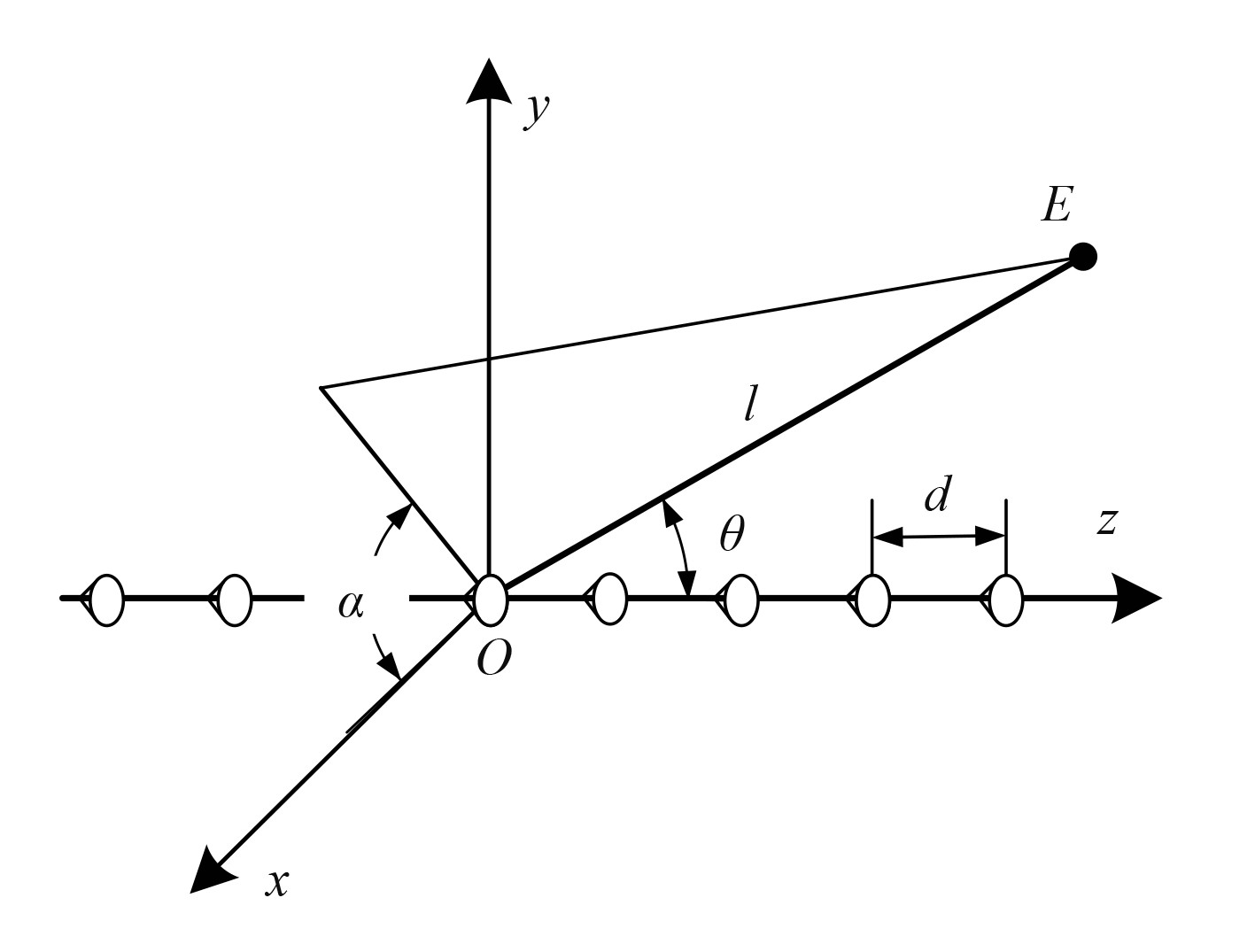
1 原理与设计 1.1 扬声器阵列原理与仿真扬声器阵列的设计基于声波的叠加原理,对于单个扬声器在低频时其锥盆的振动可以近似的看作为圆形活塞式声源[7]。图1为圆形活塞声源组成的线性阵列阵元排列图,α和θ为声线
在远场条件下,忽略声场对辐射面的阻抗效应,假设无限障板的圆形活塞声源半径为a,单个圆形活塞指向性函数为
|
图 1 线阵列阵元排列示意图 Fig. 1 Schematic diagram of line array arrangement |
| ${{D}}{(\alpha ,\theta )_{{{piston}}}}{{ = }}\left| {\frac{{2{{{J}}_1}({{k}}a\cos \theta )}}{{ka\cos \theta }}} \right|,$ | (1) |
式中:
| ${{D}}{(\alpha ,\theta )_{{{linear}}}}{{ = }}\frac{{\sin (N\displaystyle\frac{{kd}}{2}\sin \alpha \cos \theta )}}{{N\sin (\displaystyle\frac{{kd}}{2}\sin \alpha \cos \theta )}},$ | (2) |
根据Bridge乘积定理,圆形活塞声源线性阵列的指向性函数为[8]:
| $\begin{aligned} {{D}}{(\alpha ,\theta )_{{N}}}={{D}}{(\alpha ,\theta )_{{{piston}}}} \times {{D}}{(\alpha ,\theta )_{{{linear}}}}& {{ = }}\\ \left| {\frac{{2{{{J}}_1}({{k}}a\cos \theta )}}{{ka\cos \theta }}} \right| \cdot \frac{{\sin (N\frac{{kd}}{2}\sin \alpha \cos \theta )}}{{N\sin (\frac{{kd}}{2}\sin \alpha \cos \theta )}} \end{aligned}。\text{。}$ | (3) |
由式(3)分析,若圆形活塞半径
如图2中当不设置相位差时指向是垂直于阵列排列方向(Z轴)并且朝向两侧发射;如图2中当设置
基于RC全通桥式电路设计了可改变输入信号相位的移相电路(见图3),通过改变相位达到控制阵列主波束指向偏转的目的。

|
图 2 8元线阵列设置相位差前后声场对比 Fig. 2 Comparison of sound field of 8-element line array under the condition of adjusting phase difference |

|
图 3 移相电路工作示意图 Fig. 3 Schematic diagram of the phase shift circuit |
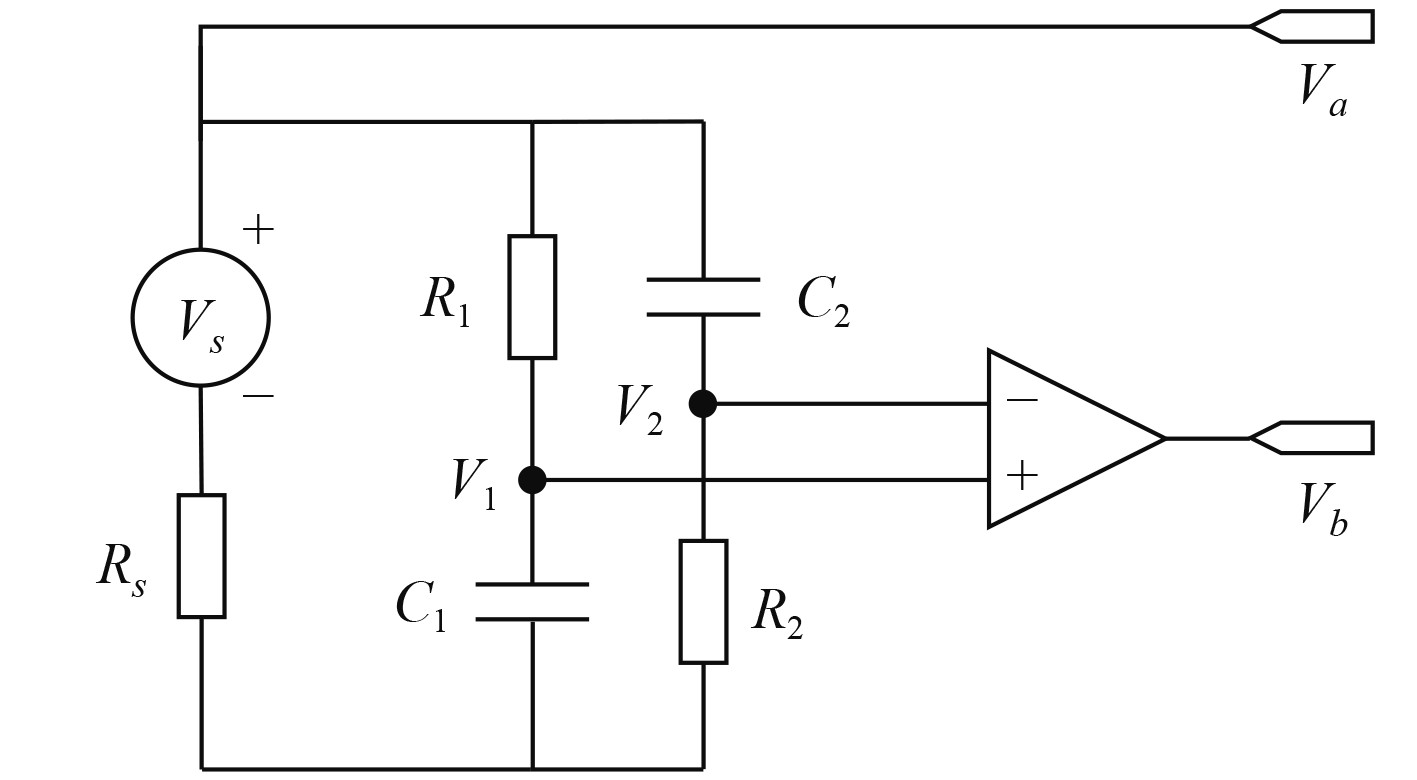
对于双元扬声器阵列,根据图4所示全通桥式电路,
|
图 4 全通桥式电路图 Fig. 4 All-pass bridge circuit |
若
| $\begin{array}{l} {V_{\rm{b}}} = {V_{\rm{1}}} - {V_{\rm{2}}} = {V_{\rm{a}}}(\displaystyle\frac{1}{{1 + {{j}}\omega {C_{\rm{1}}}{R_{\rm{1}}}}} - \displaystyle\frac{{{{j}}\omega {C_{\rm{2}}}{R_{\rm{2}}}}}{{1 + {{j}}\omega {C_{\rm{2}}}{R_{\rm{2}}}}})= \\ \begin{array}{*{20}{c}} {}&{ {V_{\rm{a}}}\angle 2\arctan (\omega {C_{\rm{1}}}{R_{\rm{1}}})}\text{。} \end{array} \end{array} $ | (4) |
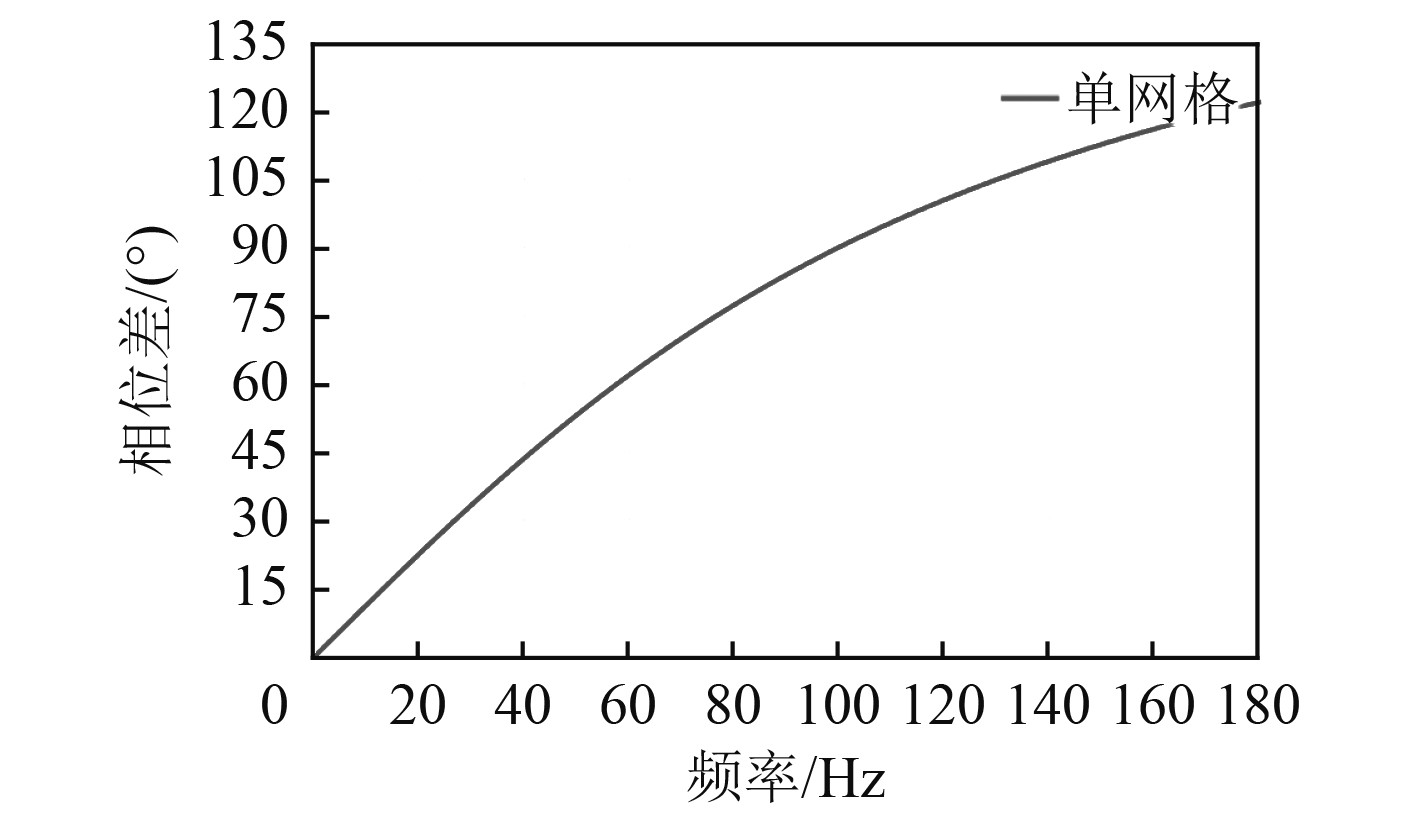
假设
|
图 5 单网络相位差随频率变化 Fig. 5 The variation of single network phase difference with frequency |
可以看出,不同频率
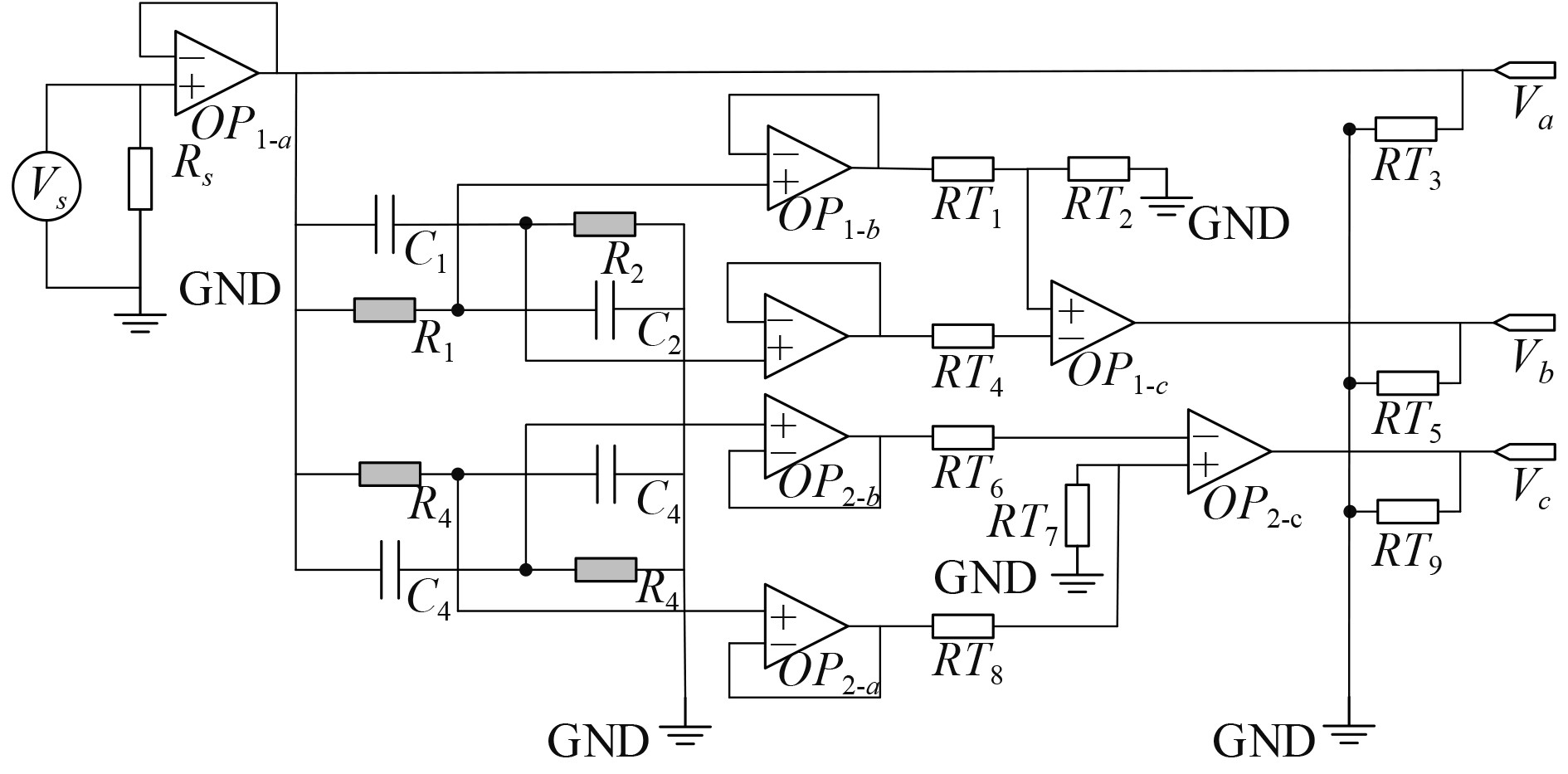
|
图 6 双网络相位控制电路 Fig. 6 Dual network phase control circuit |
| $\begin{aligned} & {\phi _{{{ba}}}} = 2\arctan (\omega {C_{{1}}}{R_{{1}}})\text{,} \\ & {\phi _{{{ca}}}} = 2\arctan (\omega {C_{{3}}}{R_{{3}}})\text{。} \\ \end{aligned} $ | (5) |
取
相比于单移相网络,使用差相移技术可以较好实现宽带信号的
设计并制作相位控制电路进行实验验证,连接信号发生器和示波器输入100 Hz的单频正弦信号,通过调整电位器阻值使得

|
图 7 单网络与双网络相位变化对比 Fig. 7 Comparison of phase change between single network and dual network |
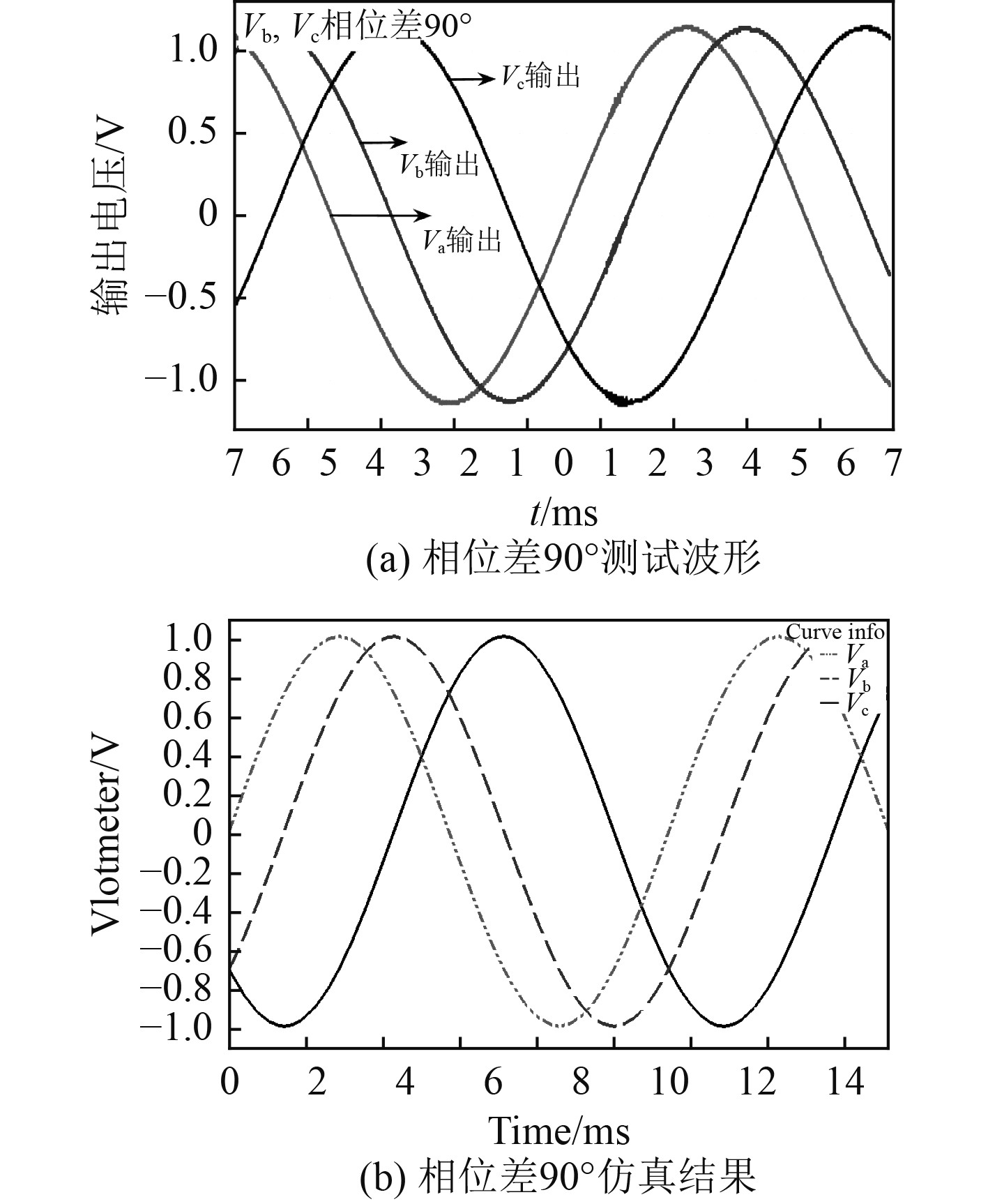
|
图 8 移相电路测试与仿真结果 Fig. 8 Phase shift circuit test and simulation results |
实验对象为2台大功率低音喇叭,其主要参数如表1所示。声场测试设备使用B&K噪声测试系统包括B&K 2270噪声分析仪,B&K3053-B-120数据采集单元、B&K4193传声器及其配套传输线缆,声场分析软件使用B&K PULSE LabShop。
|
|
表 1 扬声器产品参数 Tab.1 Speaker product parameters |
以扬声器锥盆中心为基准放置在圆心处,所在水平面距离地面高度为1.3 m,测量半径为10 m,由信号发生器并通过电路调整相位差输入100 Hz正弦信号,取两锥盆的中心连线正向方向为
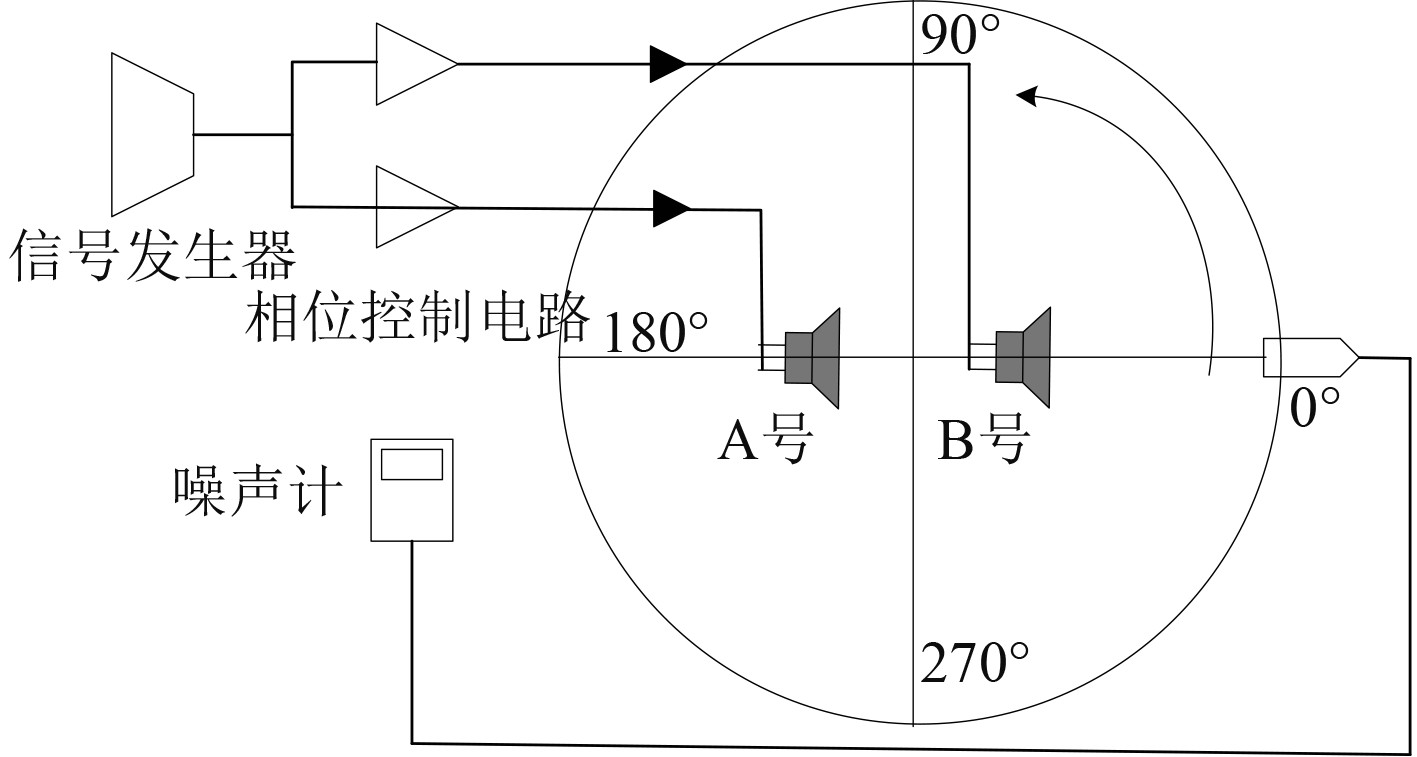
|
图 9 双元扬声器指向性测试布置图 Fig. 9 Arrangement diagram of dual element loudspeaker directivity test |
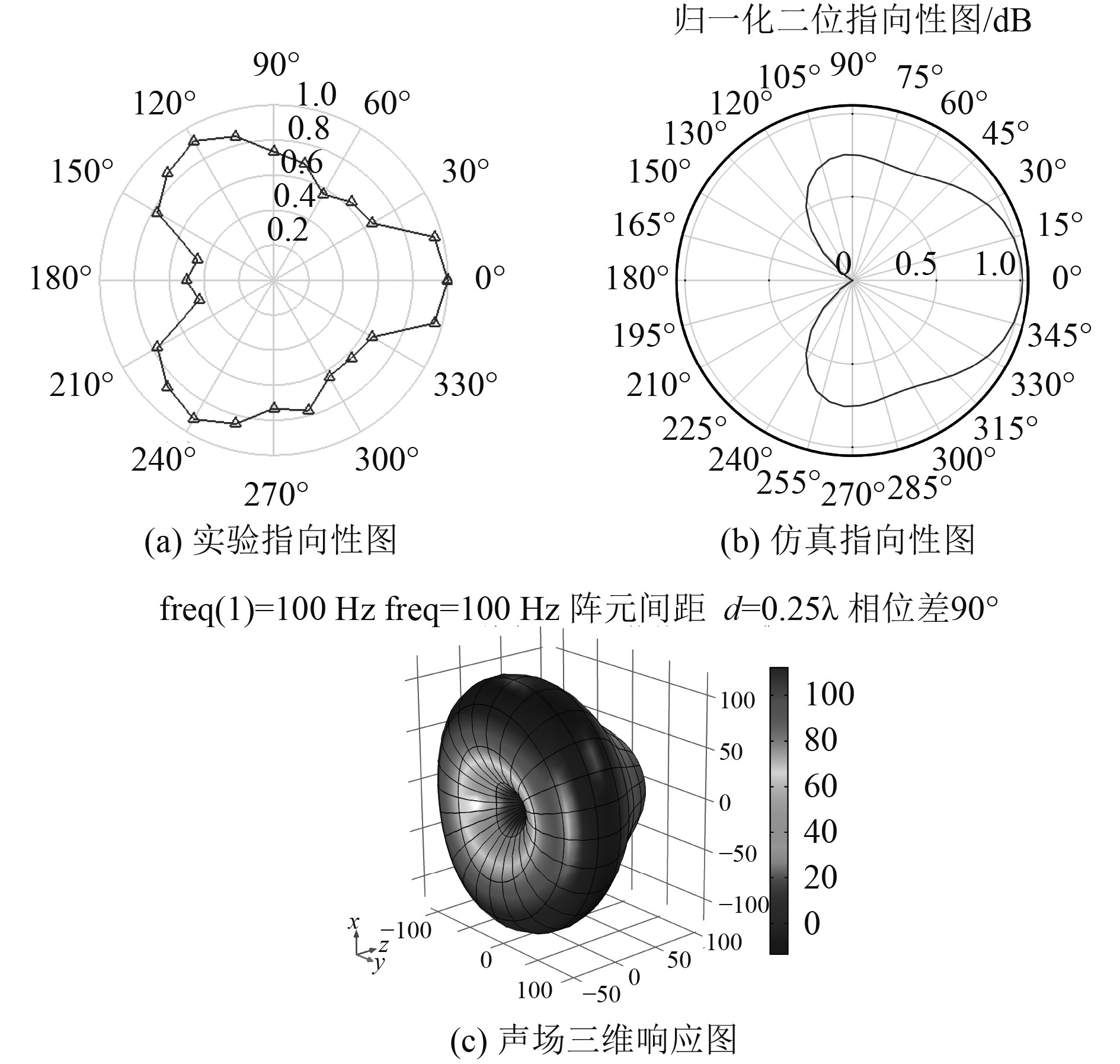
|
图 10 双元扬声器合成声场分布情况 Fig. 10 The distribution of the sound field synthesized by the dual element speaker |
间距与波长比值
由图10可以看出,在
本文基于RC全通桥式电路设计制作了可实现的相位调整控制电路,测试了100 Hz时双元阵列的辐射声场,基本可以实现低频扬声器阵列的指向控制,形成低频声波的单向发射。进一步可采取增加阵元数量、改变阵元排列结构提高指向性,并建立理想的实验条件进行次声波发射的研究与测试。
| [1] |
肖峰. 现场可控非致命的次声武器研究[J]. 兵工学报, 2002(03): 426-429. XIAO Feng. Research on on-site controllable non-fatal infrasound weapon[J]. Acta Armamentarii, 2002(03): 426-429. DOI:10.3321/j.issn:1000-1093.2002.3.037 |
| [2] |
张博, 梁延峰. 非火力打击武器发展研究[J]. 中国电子科学研究院学报, 2015, 10(1): 6-16. ZHANG Bo, LIANG Yan-feng. Research on the development of non-firepower combat weapons[J]. Journal of China Academy of Electronics and Information Technology, 2015, 10(1): 6-16. DOI:10.3969/j.issn.1673-5692.2015.01.002 |
| [3] |
蒋贤沛, 郭三学. 非致命声波武器综合效能评估研究[J]. 应用声学, 2016(2): 122-127. JIANG Xianpei, GUO Sanxue. Research on comprehensive effectiveness evaluation of non-fatal sonic weapons[J]. Applied Acoustics, 2016(2): 122-127. |
| [4] |
张富东, 徐利梅, 陈敏. 相控参量阵波束合成设计[J]. 压电与声光, 2013, 35(2): 282-286. ZHANG Fudong, XU Limei, CHEN Min. Design of phase-controlled parametric array beam synthesis[J]. Piezoelectrics & Acoustooptics, 2013, 35(2): 282-286. DOI:10.3969/j.issn.1004-2474.2013.02.035 |
| [5] |
陈敏, 徐利梅, 黄大贵, 等. 基于MATLAB的换能器阵列指向性分析方法研究[J]. 电声技术, 2006(5): 25-28. CHEN Min, XU Limei, HUANG Dagui, et al. Research on directional analysis method of transducer array based on MATLAB[J]. Electroacoustic Technology, 2006(5): 25-28. DOI:10.3969/j.issn.1002-8684.2006.05.006 |
| [6] |
张亮永, 程章. 空气中相控阵声聚焦仿真研究[J]. 声学技术, 2017, 36(6): 79-82. ZHANG Liangyong, CHENG Zhang. Simulation of phased array sound focusing in Air[J]. Acoustic Technique, 2017, 36(6): 79-82. |
| [7] |
杜功焕, 宋哲民. 声学基础[M]. 第三版. 南京: 南京大学出版社, 2012: 223-226.
|
| [8] |
周福洪. 水声换能器与基阵[M]. 北京: 国防工业出版社, 1984: 235-240.
|
 2020, Vol. 42
2020, Vol. 42
