2. 重庆交通大学 航运与船舶工程学院,重庆 400074
2. School of Shipping and Ship Engineering, Chongqing Jiaotong University, Chongqing 400074, China
实现直流电机运转状态智能监控对推进舰船动力系统智能化具有重要意义。以往曾采用由含有模拟元器件构成的电机控制系统,这种控制电路最大的缺点就是容易产生零点漂移问题,系统的抗扰动性很差[1]。目前舰船直流电机主要采用降压调速和弱磁调速。采用PWM降压调速法的优点在于:能够获得更宽电机调速范围,对同一电机能够更方便的控制其在较大转速范围内稳定运转,同时能实现转速的平滑调速,对电机电枢起到保护作用,此外还有调节功率小,控制方便等特点,并且不必考虑弱磁调速时电机转速高于理想空载转速可能导致飞轮的问题。
本文采用数字增量PID调节器和PWM数字控制技术取代原来由模拟器件完成的直流电机控制系统,通过软件控制解决了电网电压波动和负载变动给电机造成的干扰问题、电机的软启动问题和电机过流保护,并通过改进硬件电路,提升信号采集电路的滤波性能。本文在试验时发现,采用较大的控制量增量时,转速控制稳定性较差,且调节时间较长,针对这种情况,将控制算法进行了优化,对转速控制量增量进行了缩小化处理,使电机转速变化更为平滑。
1 系统硬件结构设计根据电路模块功能和电路工作功率大小,将电机转速控制系统分成控制电路和主功率电路2个主要部分。
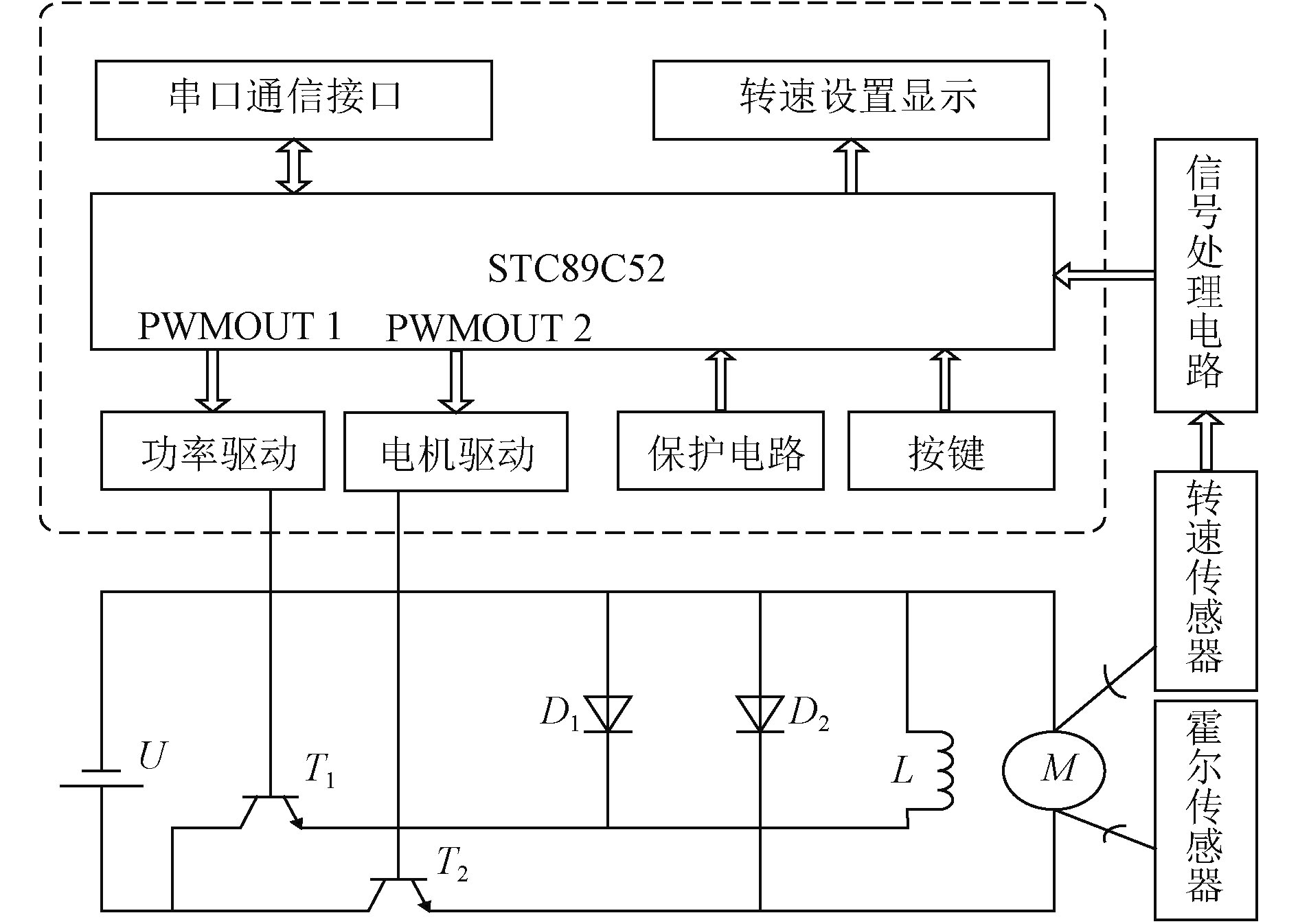
单片机将捕获的采样脉冲转换成电机采样转速,然后将设置的速度与采集速度比较,通过PID控制输出PWM脉冲高电平,结合定时器中断输出PWMOUT2,经驱动放大后输入到T2管的基极。主功率电路部分T1与电动机励磁绕组串联,构成U-T1-L-U励磁控制回路,由于电感L的电气特性,可通过软件不断控制T1的闭合与开断改变L的平均励磁电压和电流,D1为该回路的续流二极管。T2与电枢绕组串联,构成U-T2-M-U电枢电压控制回路,由于电机M属于感性负载,故可以通过PWM调制技术改变加载在电枢两端电压的平均值,与T1不同的是加载到T2管的PWM波占空比可调,实际电枢电压值为:Ua=D*U,其中D为占空比,Ua为电枢电压,当电网电压U发生变化时,若要保持Ua不变,则可通过改变D的大小实现,D2为该回路的续流二极管。
|
图 1 系统框图 Fig. 1 System block diagram |
为避免电机启动时受冲击电流的影响,需要在电机启动时先施加励磁磁场,再施加电枢电压,这就是电机的软启动过程,该过程通过软件时序控制是容易实现的。首先启动励磁回路,方法是控制单片机端口产生一定频率的脉冲信号,通过控制T1的关断实现励磁控制,经短暂延时后,由占空比可变的PWM信号控制
为设计出控制性能较好的PID调节器,选取了一个直流电机样机,根据其铭牌数据和电机拖动与控制理论建立了其频域数学模型,通过分析直流电机在PID调节器作用下的输出响应判断出所设计调节器的可行性。系统数学模型的描述方法分为端部描述法和状态变量描述法[2]。本设计采用解析法建立试验样机的频域数学模型描述系统的端部关系,首先建立直流电机微分方程,然后根据直流电机的等效电路模型和基尔霍夫电压定律得出式(1)并根据力的平衡定律得出直流电机的机械方程式(2),为了方便研究系统的频率响应特性,将式(1)和式(2)进行拉氏变换,得到式(3),本文根据其频率响应特性分析转速调节器的设计。
直流电机电气方程为:
| $ {L_a}\frac{{{\rm d}i}}{{{\rm d}t}} = {u_a} - {i_a}{r_a} - {C_e}\varOmega \left( t \right)\text{,} $ | (1) |
直流电机机械方程:
| $ J\frac{{{\rm d}\varOmega \left( t \right)}}{{{\rm d}t}} = T - {T_L}{\text{,}} $ | (2) |
式中:Ce为电动势系数;La为直流电机等效电路中的电枢电感,H;ua为等效电路的电源,也是加载到电枢两端的等效电压,V;ia为等效电路干路电流,也是电枢电流,A;ra为电机等效电枢电阻,Ω;J为转动惯量;T和TL为电机转矩变量。
| $H(s) = \frac{{\varOmega (s)}}{{{U_a}(s)}} = \frac{{{1 / {{C_e}}}}}{{{T_m}{T_a}{s^2} + {T_m}s + 1}}\text{。}$ | (3) |
式中:Tm和Ta为时间常数。当输入为单位阶跃信号时,得到输出的时域响应曲线特征是随t值增加输出先呈现衰减振荡然后保持稳定。
根据式(3),当确定参数Ce,Tm和Ta的值,可建立样机的传递函数模型,本文通过表1公式计算。
|
|
表 1 模型参数计算公式 Tab.1 Calculation formulas of model parameters |
选用的试验直流电机样机铭牌数据如表2所示。
|
|
表 2 直流电机样机铭牌数据 Tab.2 Nameplate data of DC motor prototype |
根据以上算法算得Ra=0.486 Ω,Ce=0.639 V·s/rad,La=0.022H,Me=7.46 N·m,CT=0.622 N·m/A,Ta=0.045 s,Tm=0.031 s,得到直流电机样机的传递函数为:
| $H(s) \!\!=\!\! \frac{{\Omega (s)}}{{{U_a}(s)}} \!\!=\!\! \frac{{{1 / {{C_e}}}}}{{{T_m}{T_a}{s^2} \!+\! {T_m}s \!+\! 1}} \!=\! \frac{{1.565}}{{0.0014{{\rm{s}}^2} + 0.031s + 1}}\text{。}$ | (4) |
由于单片机只作数字信号处理,故只对数字PID控制算法进行研究。
| $u(k) = {K_p}e(k) + {K_i}\sum\limits_{i = 0}^k {e(k) + {K_d}} \left[ {e(k) - e(k - 1)} \right]\text{。}$ | (5) |
式(5)算法得到的是被控对象的控制量,在运算过程中需要进行偏差信号的累加,单片机处理时容易导致死机,且该算法得到的是控制量,当该控制量较大时很容易引起电机转速发生陡变,使转速不稳定。将式(5)变换得到式(6),该算法输出的是控制量的增量△u(k)(电机转速的变化度),若要获得当前电机稳态转速,可以利用算式u(k)=u(k-1)+△u(k)实现,这种算法明显的特点是不需要对任何偏差变量累加计算,该算法下单片机只需计算前后3次测量的转速偏差值。当确定了控制器的Kp、Ki和Kd3个控制系数,就能够确定转速控制量增量。为提高调节器的控制精度,将式(6)进行改进,对转速控制增量进行缩小50倍处理,提高调速平滑度。
| $\begin{array}{l} \Delta u(k) = u(k) - u(k - 1) =\\ {K_p}\Delta e(k) + {K_i}e(k) + {K_d}[\Delta e(k) - \Delta e(k - 1)] \text{。}\\ \end{array} $ | (6) |
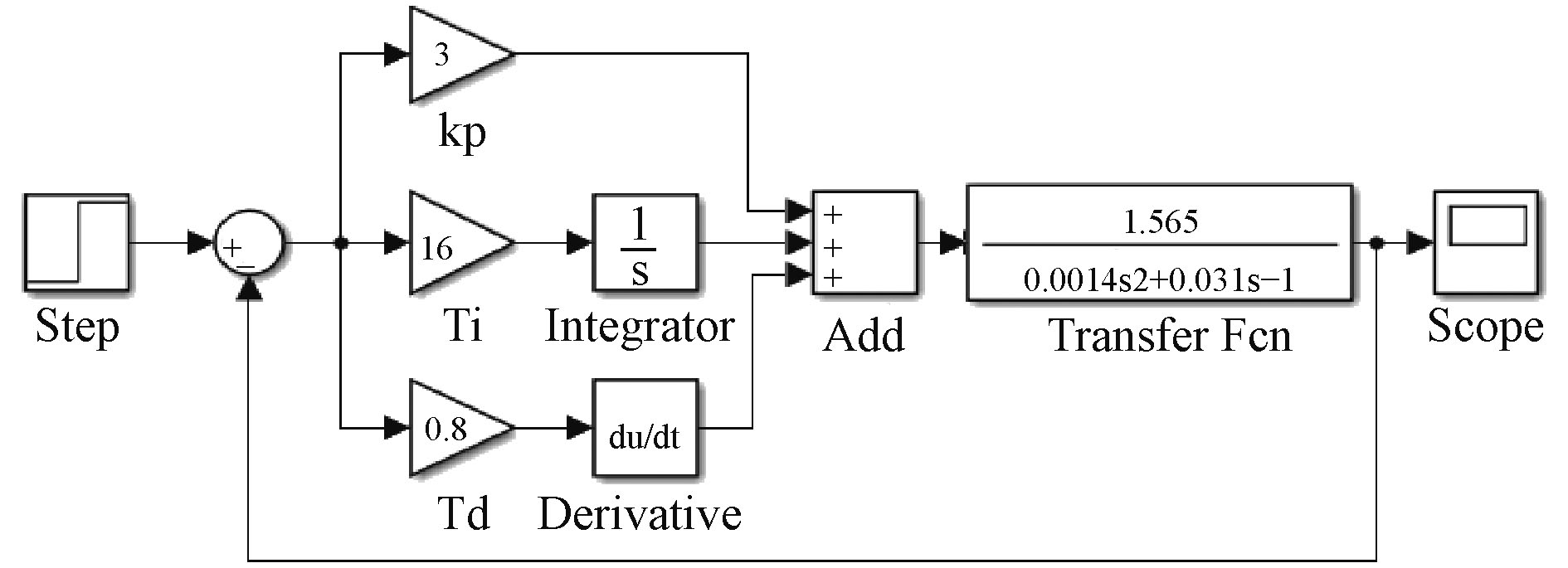
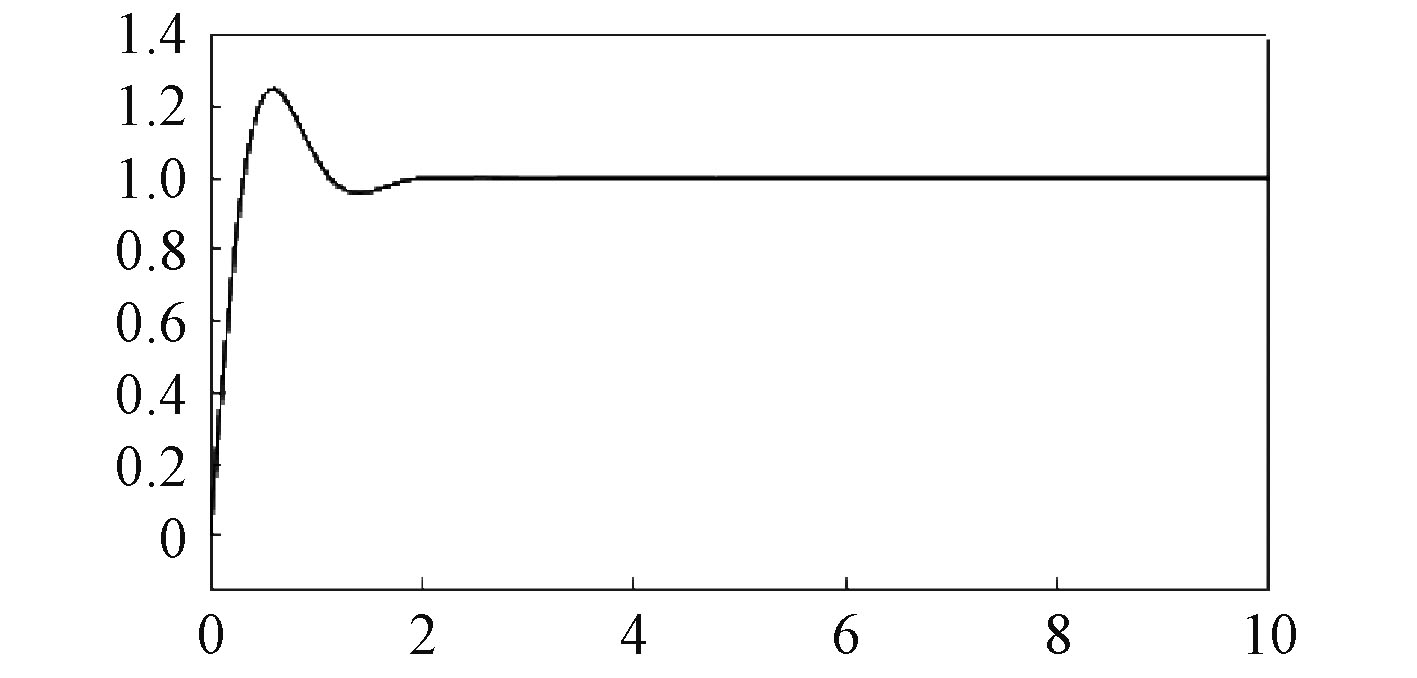
目前关于PID调节器控制系数整定的方法分为依赖于被控制对象数学模型的理论计算法和工程试验经验整定法[3]。本文采用工程试验法,基于Z-N法则和经验公式,结合Matlab软件实现参数整定。该整定方式简单且直观,系统模型框图和输出响应曲线分别如图2和图3所示。
从响应曲线可以看出,系统处于欠阻尼状态,稳态误差几乎为0,最大超调量在22%左右,符合舰船直流电机控制要求,当前输出响应情况下对应的控制器参数匹配为Kp=3,Ki=16,Kd=0.8。
|
图 2 PID参数整定Simulink 模型 Fig. 2 Simulink model of PID parameters tuning |
|
图 3 输出响应曲线 Fig. 3 Output response curve |
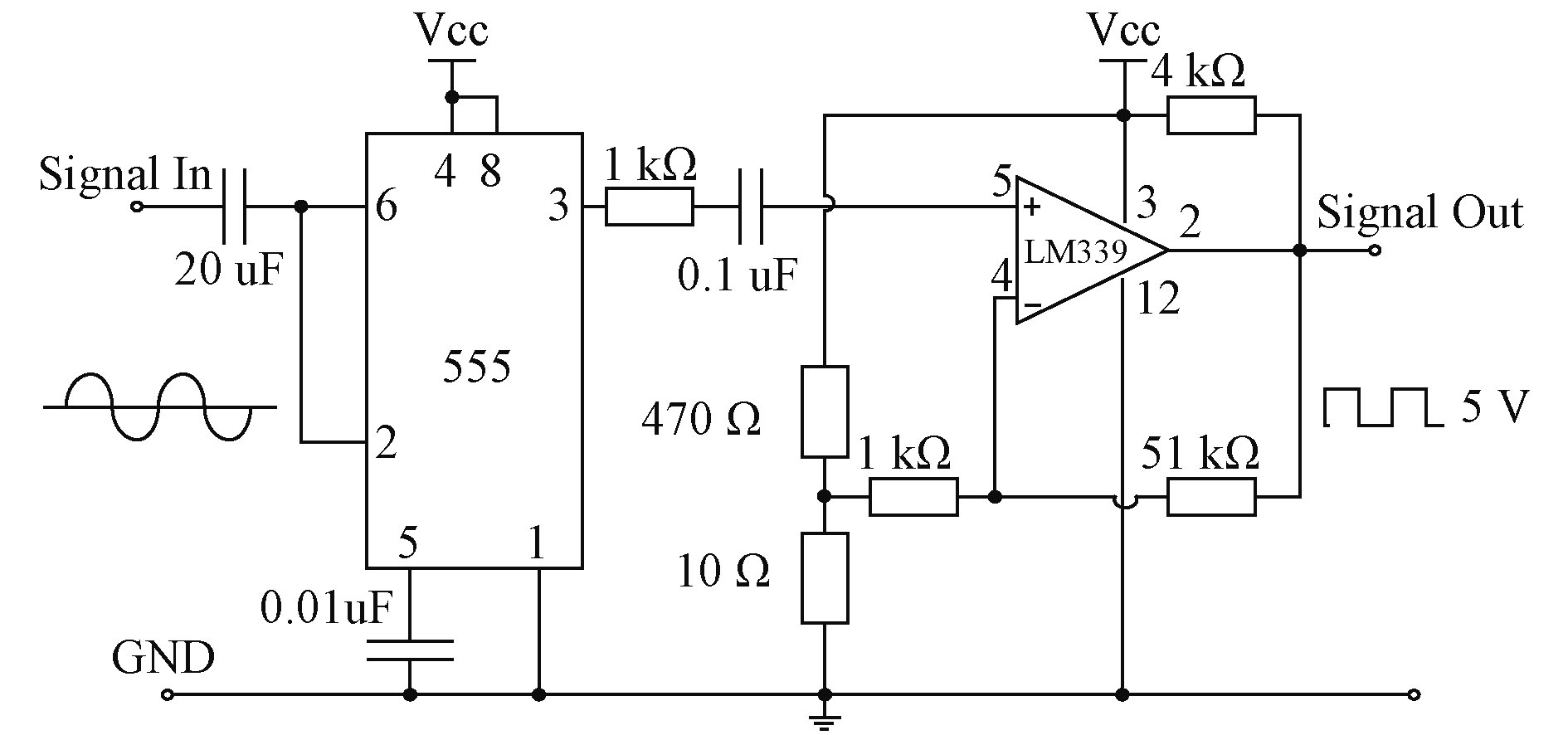
转速传感器采集的转速信号为正弦信号,而单片机只能处理数字信号,本文利用CMOS型555时基芯片5G7556电路先将正弦信号转换成脉冲信号,如图4所示。为提高基准电压的稳定性,将5引脚经0.01uF电容接地。相比分立元器件电路或双极型555构成的信号整形电路而言,该电路连接简单,信号处理能力强,抗扰性更高,即使电机工作在温度变化较大的环境中,温度漂移也不超过500 ppm/℃,而且由于芯片内部的电压正反馈作用,使得整形后的数字信号边沿更陡。该电路两阈值电压为3.33 V和1.66 V,输line-height:16pt出方式具有施密特触发器的回差特性,因而具备很强的抗噪性。
|
图 4 转速信号采集和优化电路 Fig. 4 Speed signal acquisition and optimization circuit |
当电机的电枢电流超出正常工作的限定值时会导致绕组发热,甚至直接烧毁电机,为此需要对电机电枢电流和电压进行实时监控。当电枢电流超出限制时,调用既定的软件控制算法抑制电流的增长。为获取实时电枢电流和电压信号,选用霍尔传感器进行测量[4]。由于舰船直流电机工作环境中干扰噪声较多,为防止谐波分量干扰,将原始采集信号通过阻容滤波电路滤波,然后分别通过由集成运放构成的电压跟随器和电压放大器,反馈到AD转换芯片ADC0804模拟输入引脚,输出按并行连接的方式与单片机相连,单片机通过查询的方式读取电流和电压值。当电流值大于软件设定的限定值,调用电流截止负反馈算法,强行抑制电机电枢电流持续增长,直到电流值小于限定值退出电流负反馈;当不大于限定值,电机正常运行,不调用电流截止负反馈,保证系统能够有较硬静态特性。系统控制原理框图如图5所示。

|
图 5 系统控制原理框图 Fig. 5 System control block diagram |
引入电流截止负反馈是为了保护直流电机。整个控制系统除了需要进行电机保护外,还需要其他硬件设施构成的保护电路保护控制系统,当电机工作在欠压、欠流、超速运行状态时不至于对控制系统和电机产生致命的损害,因而硬件保护电路主要对系统进行过流保护和隔离保护。
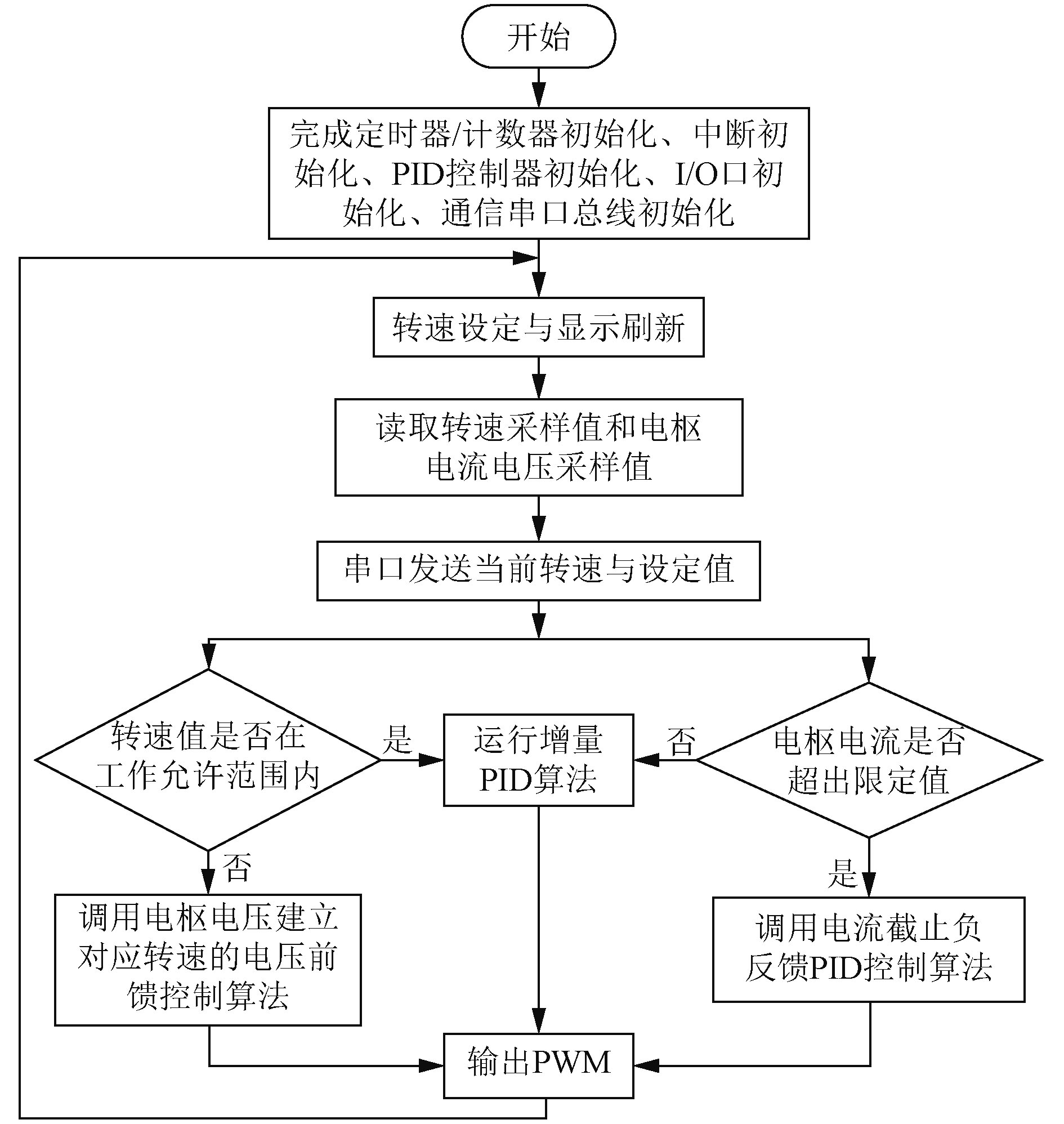
4 系统软件设计利用单片机INT0引脚对传感器反馈的转速脉冲计数,设置IT0=1,即下降沿方式。将定时器T0定时1 s的脉冲计数换算成电机每秒转速,计算当前转速偏差值,采用上述控制器参数,计算控制量增量为△uk=[3*(ek-ek-1)+16*ek+0.8*(ek-2*ek-1+ek-2)]/50,然后换算成当前电机转速控制量。输出由定时器T1的溢出中断控制,设计每隔40 μs进入一次中断,在中断中判断溢出次数计数变量cnt的值与PWMtime(高电平时间)的大小关系并输出PWM。励磁回路的PWM输出占空比是固定的,由软件可改变输出的占空比大小,可通过延时和循环改变单片机输出引脚的电平状态即可实现。系统主程序流程如图6所示。
|
图 6 主程序流程图 Fig. 6 Main program flow chart |
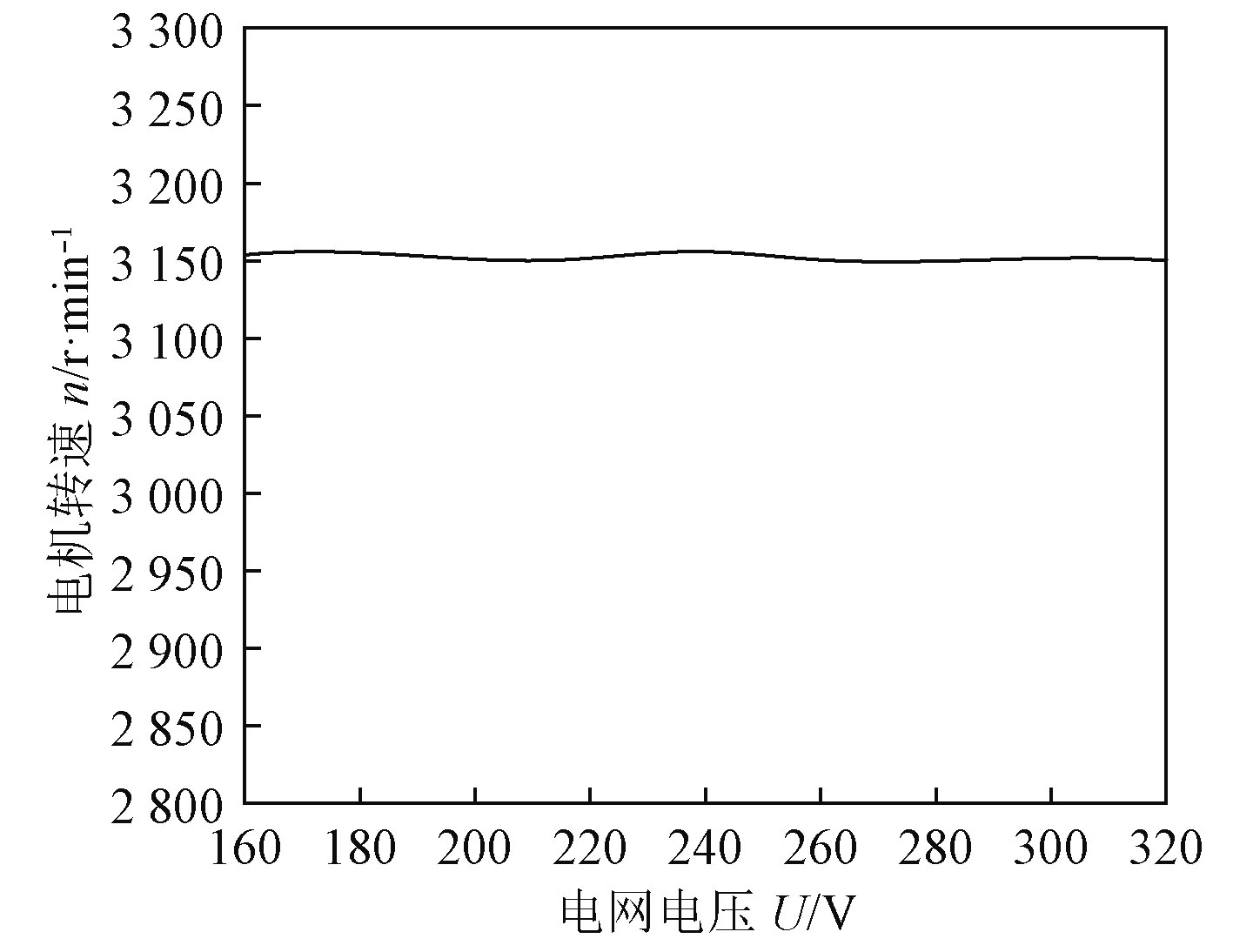
为验证电机转速自稳定性,将样机转速设定为3 150 r/min,改变电网电压大小,使其在160 ~320 V之间波动,观察电机转速变化情况,要求转速误差在±3%内。图7为试验结果,从n-U曲线可看出当给电机施加160 V电源电压使其稳定运行时,转速接近3 150 r/min,转速误差不超过3%。随着电网电压不断增加,电机转速基本保持不变,或沿着设定的3 150 r/min上下波动,但误差均在±3%以内,表明虽然电网电压发生波动,但电机转速仍能够维持在较为稳定的转动状态,满足电机转速自稳定控制要求。
|
图 7 n-U曲线 Fig. 7 n-U curve |
以上研究表明以单片机为主控制芯片构成的舰船直流电机转速自稳定控制系统能保证电机在波动电压下仍然能自行稳定在指定转速状态,证实了该系统是切实可行的。对于一般舰船直流电机控制,微秒级的采样速率已足够满足需求,对于采样要求更高的场合可使用DSP或处理速度更高的数字信号处理芯片。
| [1] |
刘金琨. 先进PID控制MATLAB仿真[M]. 北京: 电子工业出版社, 2016.
|
| [2] |
刘颖. 基于单片机体系的开关磁阻电动机调速系统硬件电路的设计[J]. 煤矿机械, 2013, 11(34): 258-259. |
| [3] |
康凯. 基于MATLAB的数字PID直流电机调速系统的实现[J]. 电脑知识与技术, 2010, 6(22): 6372-6373. DOI:10.3969/j.issn.1009-3044.2010.22.099 |
| [4] |
杨森, 杨杰, 张均东, 等. 基于辩论域模糊PID的船舶柴油发电机调速系统[J]. 中国航海, 2016(1): 16-21. |
| [5] |
Swapnil KHUBALKAR, Amit CHOPADE, Anjali JUNGHARE, et al. Design and Realization of Stand-Alone Digital Fractional Order PID Controller for Buck Converter Fed DC Motor[J]. Springer journal, 2016, V35(6): 2189-2211. |
 2020, Vol. 42
2020, Vol. 42
