2. 海军工程大学 舰船高温复合材料研究所,湖北 武汉 430033
2. Naval University of Engineering, Institute of High Temperature Structural Composite Materials for Naval Ship, Wuhan 430033, China
在国防工业中,汽轮机、柴油机和燃气轮机是现代舰船最主要的三大动力装置,其安全稳定运行对舰船辅助设备以及作战能力至关重要。转子作为动力系统的核心部件之一,运行在高温、高压、强腐蚀等恶劣环境中,长期的交变应力、复杂的载荷等因素会引起转子故障的产生[1]。对于舰船动力装置来说,由于安装质量不高或者机械振动等原因经常会造成机械设备在工作中出现松动故障,而松动会引起系统阻尼和刚度发生变化,造成更进一步加重设备的振动。如果长期运行下去会对机械设备造成严重的伤害,并有可能引起其他故障的产生。常见的松动故障主要包括旋转部件的松动和基础松动[2]。
对于采用汽轮机作为动力装置的舰船来说,在运行过程中会由于汽轮机叶顶间隙不均匀对转轴产生一个横向的激振力。文献[3-6]研究表明,这个激振力会使得转子系统出现失稳,对系统安全稳定运行造成威胁。针对转子基础松动故障已有学者展开了相关研究[7-10],并获得了有价值的成果。而考虑汽轮机汽流激振时转子松动故障特性还未有相关的理论研究,因此很有必要开展考虑汽流激振时转子松动故障振动特性研究。为此,本文建立了考虑汽流激振时具有基础松动故障转子系统分析模型,分析研究系统在不同参数下的非线性振动特性,为舰船汽轮机转子的进一步振动故障诊断提供理论支撑。
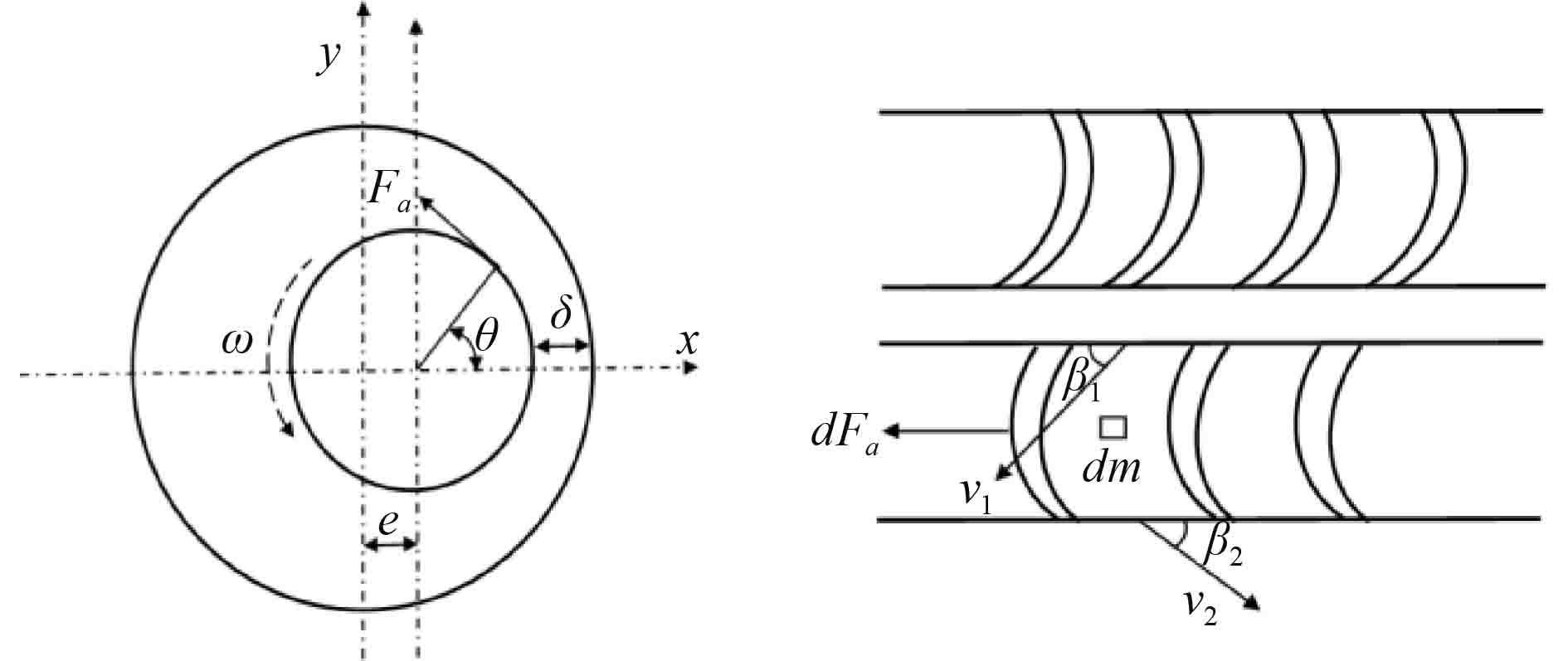
1 汽流激振时转子松动动力学模型 1.1 汽轮机气流激振力模型汽轮机转子系统结构及受力简图如图1所示。
|
图 1 系统受力图及气流在静、动叶片间流动示意图 Fig. 1 Loading diagram of the system |
图中,
| ${F_{\rm{a}}} = {A_1} \cdot \delta \cdot E + {A_3} \cdot {\delta ^3} \cdot {E^3}\text{。}$ | (1) |
式中:
| $\begin{aligned} & {A_1} = \frac{{{{(R_T^2 - R_B^2)}^2}{{\text π}} C{R_T}}}{{{{\left( {R_T^2 - R_B^2 + 2{R_T}\bar \delta } \right)}^2}}},\;\;\;{A_3} = \frac{{3{{(R_T^2 - R_B^2)}^2}{\text π} CR_T^3}}{{{{\left( {R_T^2 - R_B^2 + 2{R_T}\bar \delta } \right)}^4}}}, \\ & E = \sqrt {{x^2} + {y^2}} ,\;\;\;\;\;\;\;\;C = {V^2}\sin {\beta _1}{\rho _0}\left( {\cos {\beta _1} + \varsigma {\beta _2}} \right)\text{。} \end{aligned} $ |
其中:
| $\left( {\begin{array}{*{20}{c}} {{F_{ax}}} \\ {{F_{ay}}} \end{array}} \right) = \left( {{A_1} \cdot \delta \cdot E + {A_3} \cdot {\delta ^3} \cdot {E^3}} \right)\left( {\begin{array}{*{20}{c}} {\cos \theta } \\ {\sin \theta } \end{array}} \right)\text{。}$ | (2) |
式中:
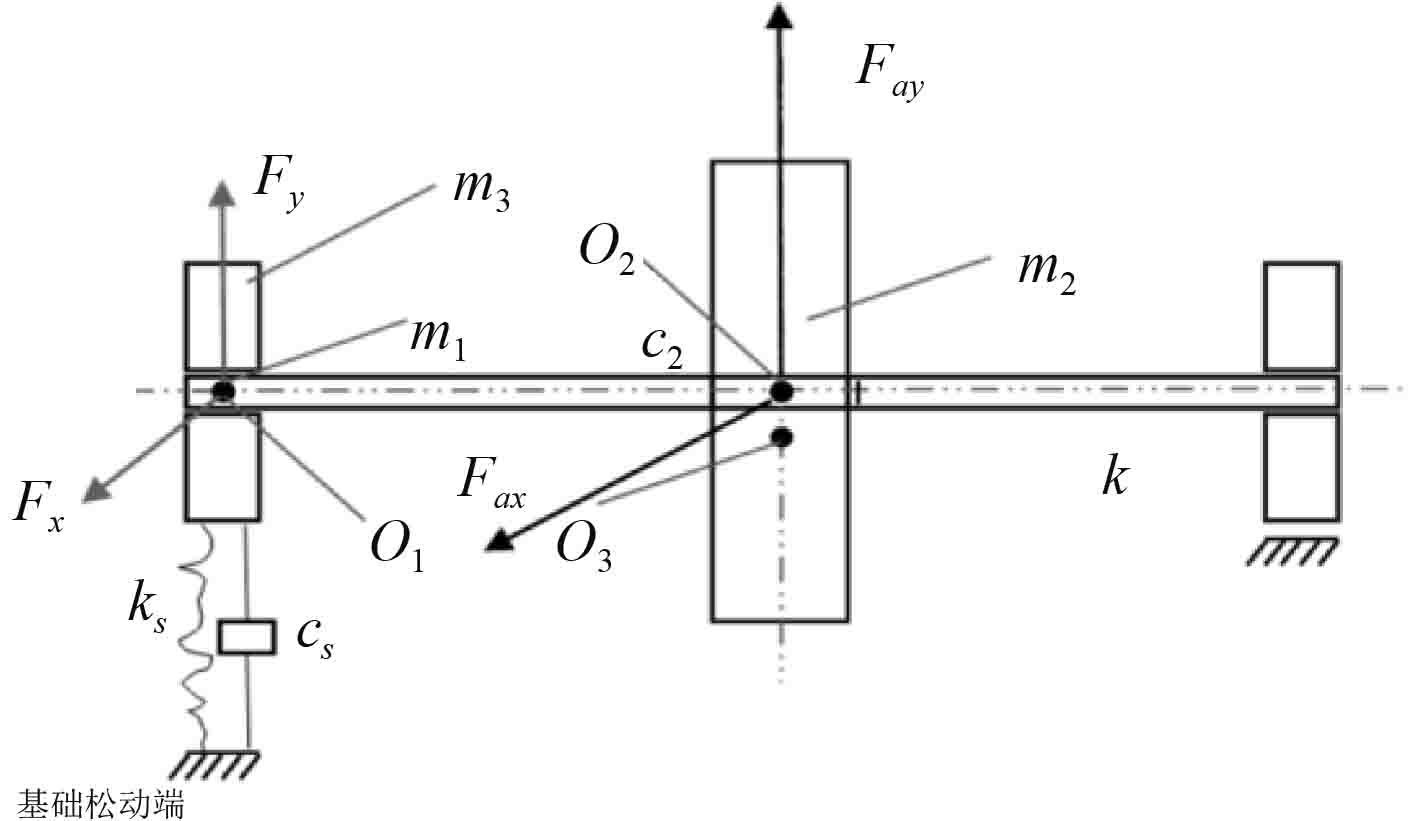
在工程实际中,一般通过螺栓加固轴承座与基础之间的连接,由于安装不良或者长期运行工作都有可能造成若干螺栓出现松动,若汽轮机机组出现较大的振动,轴承座将克服其他螺栓的拉力,暂时部分与基础分离,未松动端的螺栓则受拉力作用,处于弹性变形。具有基础松动故障的转子系统模型及参数如图2和表1所示,松动端轴承座与基础之间的等效刚度为
|
|
表 1 转子模型参数 Tab.1 The parameters of Rotor model |
|
图 2 转子基础松动故障模型 Fig. 2 The rotor system with pedestal looseness fault |
| $ {k_{\rm{s}}} = \left\{ \begin{array}{l} {k_{{\rm{s1}}}}\;\;\;\;{y_4} > {\delta _1} \\ 0\;\;\;\;{\rm{0}} \leqslant {y_4} \leqslant {\delta _1} \\ {k_{{\rm{s2}}}}\;\;\;{y_4} < {\delta _1}{\rm{ }} \\ \end{array} \right.,\;{c_{\rm{s}}} = \left\{ \begin{array}{l} {c_{{\rm{s1}}}}\;\;\;\;{y_4} > {\delta _1} \\ 0\;\;\;\;{\rm{0}} \leqslant {y_4} \leqslant {\delta _1} \\ {c_{{\rm{s2}}}}\;\;\;{y_4} < {\delta _1}{\rm{ }} \\ \end{array} \right.\text{。} $ | (3) |
由于轴承支座一端发生松动,导致转轴两端的运动状态不一致,从而使得两端轴径的油膜力不相等。假设转子未松动端和松动端的轴承油膜力分别为
| $\left\{ \begin{aligned} & {F_{{x_1}}} = sP{f_x}({x_1},{y_1},{{\dot x}_1},{{\dot y}_1}) \\ & {F_{{y_1}}} = sP{f_y}({x_1},{y_1},{{\dot x}_1},{{\dot y}_1}) \\ \end{aligned} \right.\text{,}$ | (4) |
| $\left\{ \begin{aligned} & {F_{{x_3}}} = sP{f_x}({x_3},{y_3} - {y_4},{{\dot x}_3},{{\dot y}_3} - {{\dot y}_4}) \\ & {F_{{y_3}}} = sP{f_y}({x_3},{y_3} - {y_4},{{\dot x}_3},{{\dot y}_3} - {{\dot y}_4}) \\ \end{aligned} \right.\text{。}$ | (5) |
考虑到转子系统含有基础松动故障,依据几何关系,设转子左端轴承处的径向位移为
| $ \begin{aligned} & {{\ddot X}_1} = - \frac{{{c_1}}}{{{m_1}\omega }}{{\dot X}_1} - \frac{k}{{{m_1}{\omega ^2}}}\left( {{X_1} - {X_2}} \right) + \\ & \quad \quad \quad \frac{{sP{f_x}({X_1},{Y_1},{{\dot X}_1},{{\dot Y}_1})}}{{c{m_1}{\omega ^2}}} \text{,}\\ & {{\ddot Y}_1} = - \frac{{{c_1}}}{{{m_1}\omega }}{{\dot Y}_1} - \frac{k}{{{m_1}{\omega ^2}}}\left( {{Y_1} - {Y_2}} \right) + \\ & \quad \quad \quad \frac{{sP{f_y}({X_1},{Y_1},{{\dot X}_1},{{\dot Y}_1})}}{{c{m_1}{\omega ^2}}} \text{,} \\ & {{\ddot X}_2} = - \frac{{{c_2}}}{{{m_2}\omega }}{{\dot X}_2} - \frac{k}{{{m_2}{\omega ^2}}}\left( {2{X_2} - {X_1} - {X_3}} \right) - \\ & \quad \quad \quad \frac{{{F_{ax}}}}{{c{m_2}{\omega ^2}}} + \frac{e}{c}\cos (\tau + \beta ) \text{,}\\ & {{\ddot Y}_2} = - \frac{{{c_2}}}{{{m_2}\omega }}{{\dot Y}_2} - \frac{k}{{{m_2}{\omega ^2}}}\left( {2{Y_2} - {Y_1} - {Y_3}} \right) + \\ & \quad \quad \quad \frac{{{F_{ay}}}}{{c{m_2}{\omega ^2}}} + \frac{e}{c}\sin (\tau + \beta ) - \frac{g}{{c{\omega ^2}}} \text{,} \\ & {{\ddot X}_3} = - \frac{{{c_1}}}{{{m_1}\omega }}{{\dot X}_3} - \frac{k}{{{m_1}{\omega ^2}}}\left( {{X_3} - {X_2}} \right) + \\ & \quad \quad \quad \frac{{sP{f_x}({X_3},{Y_3} - {Y_4},{{\dot X}_3},{{\dot Y}_3} - {{\dot Y}_4})}}{{c{m_1}{\omega ^2}}} \text{,} \\ & {{\ddot Y}_3} = - \frac{{{c_1}}}{{{m_1}\omega }}{{\dot Y}_3} - \frac{k}{{{m_1}{\omega ^2}}}\left( {{Y_3} - {Y_2}} \right) + \\ &\quad \quad \quad \frac{{sP{f_y}({X_3},{Y_3} - {Y_4},{{\dot X}_3},{{\dot Y}_3} - {{\dot Y}_4})}}{{c{m_1}{\omega ^2}}} - \frac{g}{{c{\omega ^2}}} \text{,} \\ & {{\ddot Y}_4} = - \frac{{{c_s}}}{{{m_3}\omega }}{{\dot Y}_4} - \frac{{{k_s}}}{{{m_3}{\omega ^2}}}{Y_4} - \\ & \quad \quad \quad \frac{{sP{f_y}({X_3},{Y_3} - {Y_4},{{\dot X}_3},{{\dot Y}_3} - {{\dot Y}_4})}}{{c{m_3}{\omega ^2}}} - \frac{g}{{c{\omega ^2}}} \text{。} \end{aligned} $ | (6) |
式(6)即为考虑基础松动后汽流激振力作用下转子系统的运动微分方程,在松动端的无量纲油膜力分量分别为
采用Runge-Kutta方法对方程(6)进行求解。为了保证解的收敛性并减少计算误差,计算过程中选用较小的积分步长,同时为了能记录到振动稳定解一般需要舍弃多个周期的瞬态解,本文计算过程中采用积分步长为2π/200,误差为
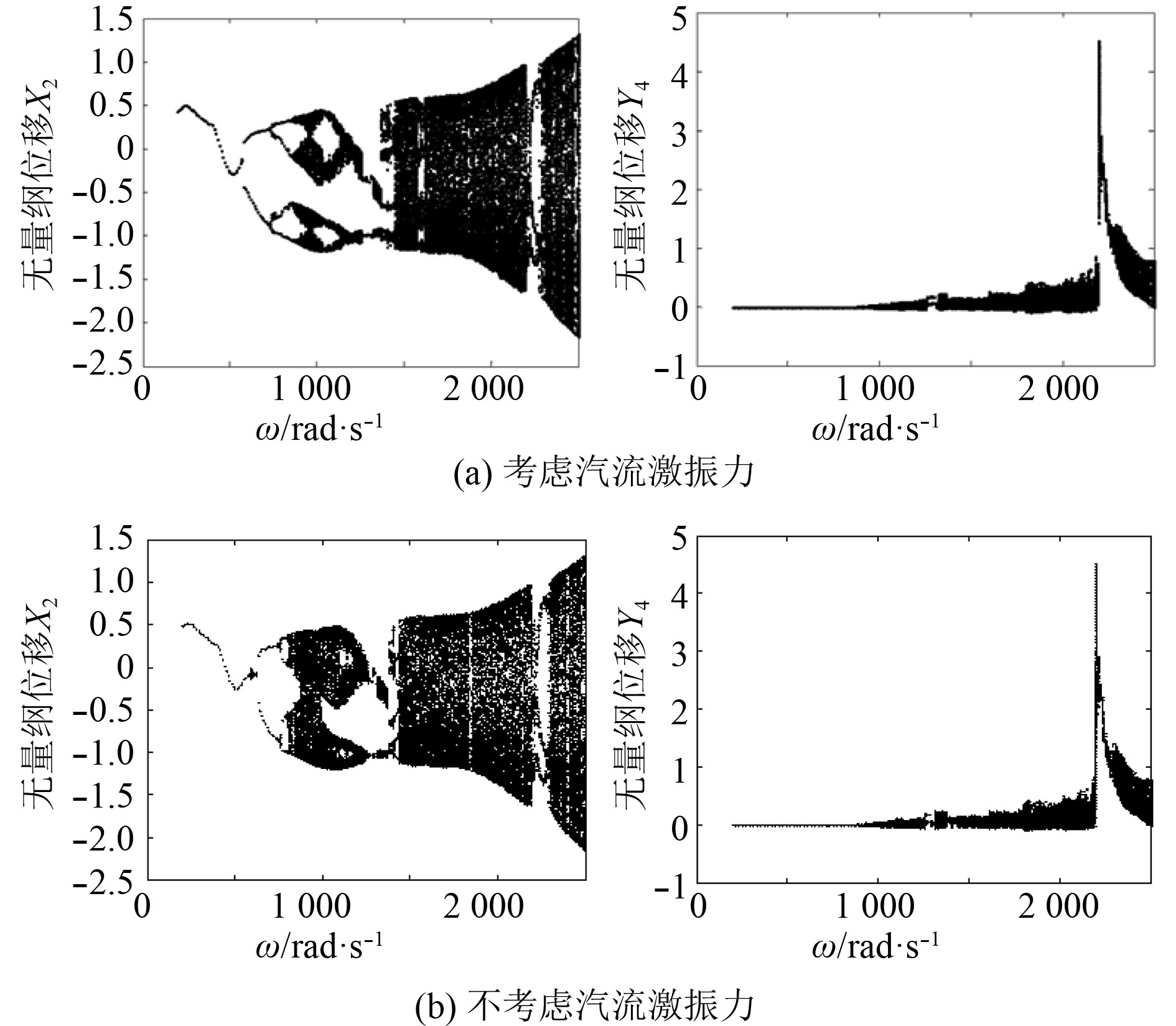
图3分别为在考虑和不考虑汽流激振力时,基础松动转子系统轴心处
|
图 3
系统响应
|
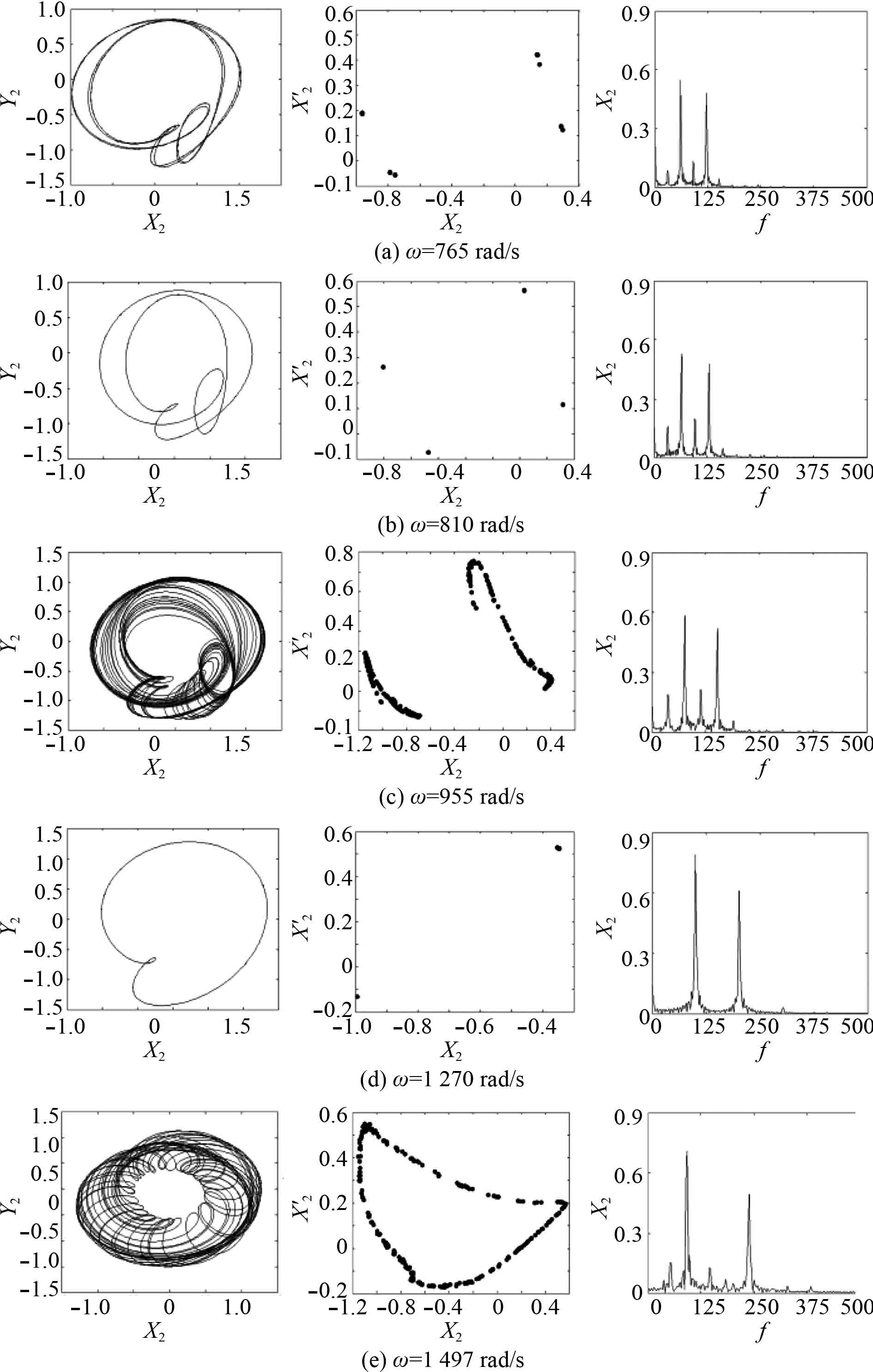
|
图 4 不同转速下基础松动转子系统响应图 Fig. 4 The orbit, poincaré map and frequency spectrums of the rotor system with pedestal |
图3(b)为不考虑汽流激振力时松动转子系统响应分岔图,对比可以看出,汽流激振力的存在使得松动转子系统
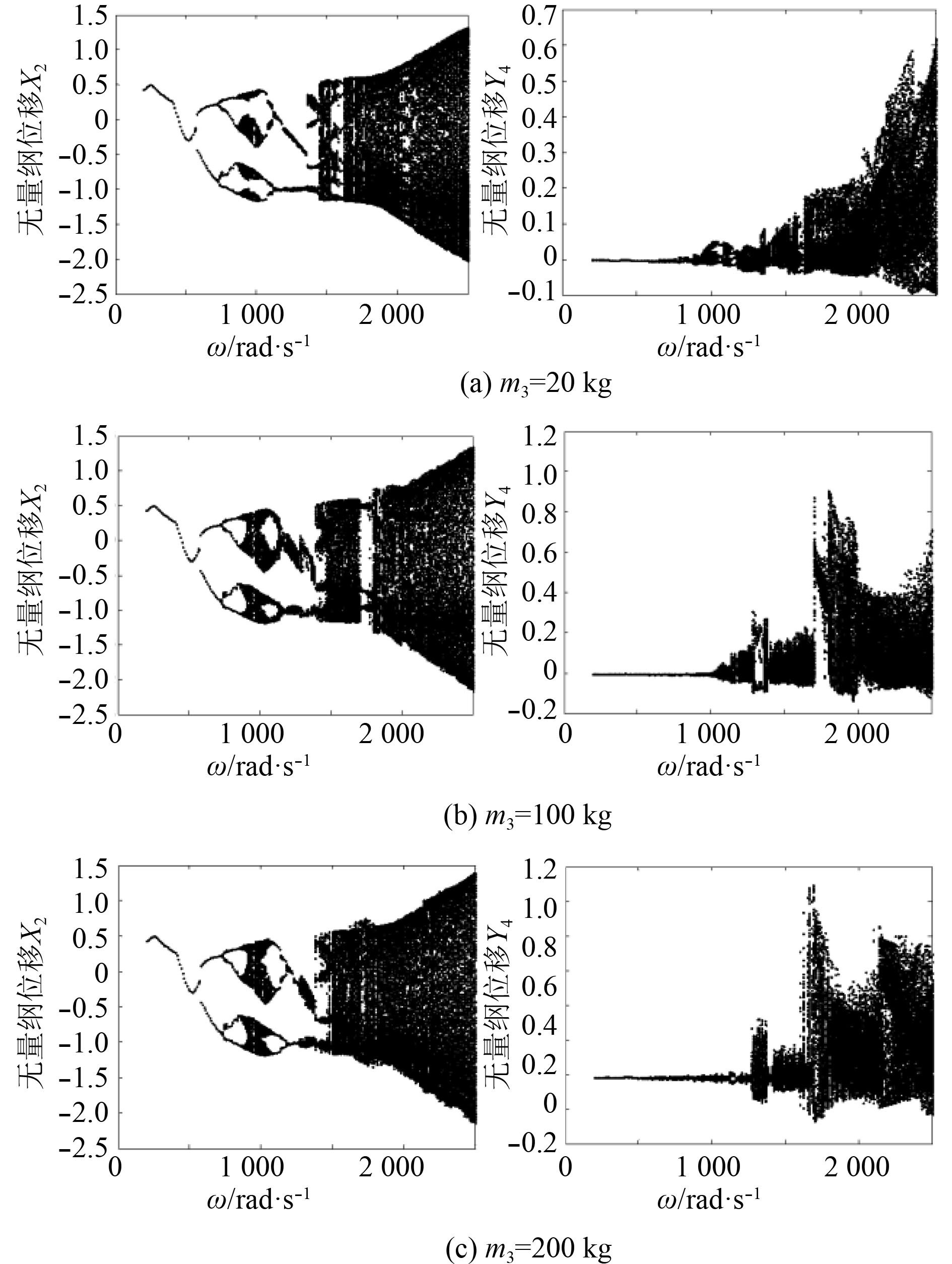
松动端支座质量m3作为系统的一个重要参数,接下来将研究支座质量m3对系统分岔特性的影响。图5分别为系统支座质量m3=20 kg,m3=100 kg和m3=200 kg时,在汽流激振力作用下松动转子系统的分岔图。
图3(a)为m3=50 kg时在汽流激振力作用下响应分岔图,对比图5可以明显看出:松动转子系统轴心处
|
图 5
汽流激振力下松动转子系统
|
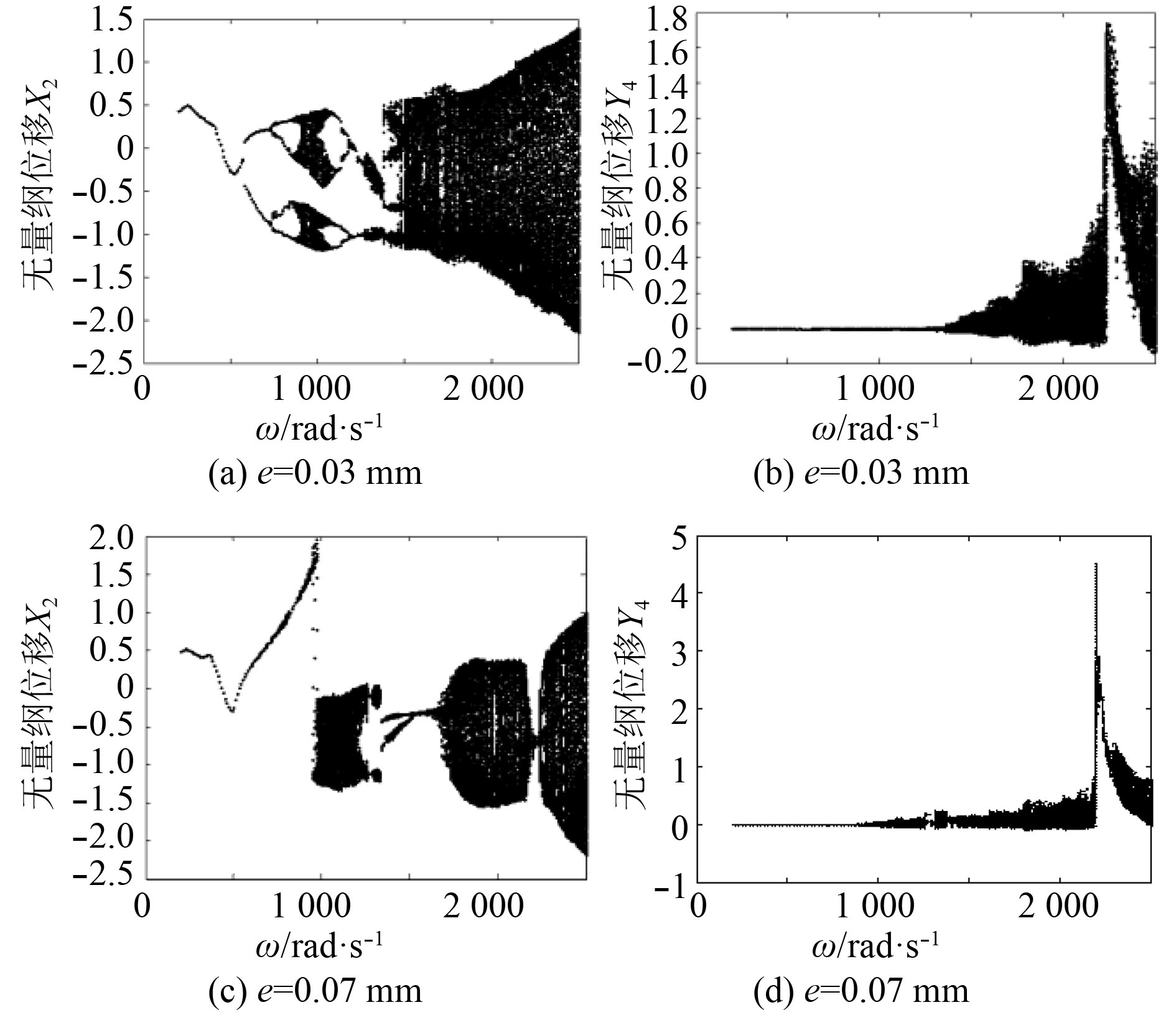
质量偏心作为系统运行稳定性的重要参数,研究其变化对松动转子系统的动力学特性的影响非常有意义。图6分别为质量偏心
|
图 6
e = 0.03 mm和e = 0.07 mm时松动转子系统
|

|
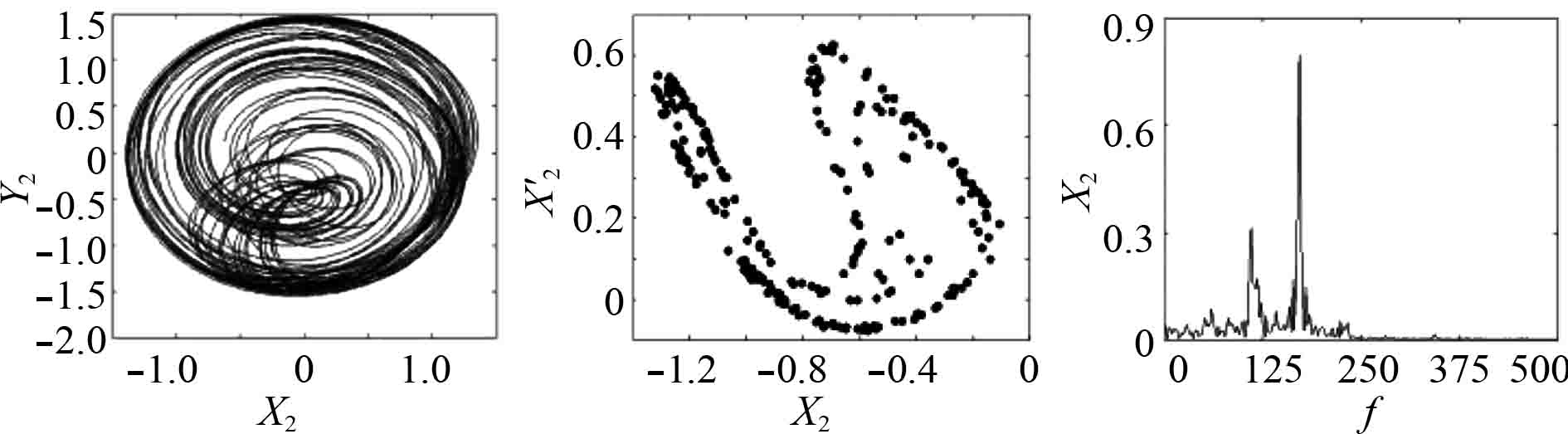
图 7
e = 0.03 mm时松动转子系统响应的轴心轨迹图、Poincaré截面图和频谱图
Fig. 7
The orbit, Poincaré map and frequency spectrums of the rotor system with pedestal when
|
|
图 8
|
1)汽流激振力的存在使得松动转子系统轴心处响应的周期性运动区间变宽,且在临界转速附近的混沌区间变窄,而对支座处响应几乎没有影响。
2)随着支座质量的增加松动转子系统轴心处的响应在临界转速附近的混沌小岛由4个逐渐减小到2个,并且混沌区间变宽;在转速较低时,松动端轴承支座在竖直方向的振动响应几乎为0,在转速升高到临界转速之后的响应才有所增加。
3)质量偏心作为系统的主要参数对系统响应有很大影响,在临界转速以下对系统的响应都不是很大;但当大于临界转速时,系统
| [1] |
瓮雷, 杨自春, 曹跃云, 等. 某船用发电汽轮机转子模态及动力学分析[J]. 舰船科学技术, 2014, 36(3): 62-67. WENG Lei, YANG Zichun, CAO Yueyun, et al. Research on mode and dynamic characteristics of the marine power generation steam turbine rotor[J]. Ship Science and Technology, 2014, 36(3): 62-67. DOI:10.3404/j.issn.1672-7649.2014.03.012 |
| [2] |
蒋勉, 伍济钢, 彭鑫胜, 等. 转子-滑动轴承系统支承松动-碰摩故障动力学行为及评估方法[J]. 动力学与控制学报, 2017, 15(6): 550-557. JIANG Mian, WU Jigang, PENG Xinsheng, et al. Dynamic behaviors and assessment of loose-rubbing faults in rotor-sliding bearing system[J]. Journal of dynamics and control, 2017, 15(6): 550-557. DOI:10.6052/1672-6553-2017-38 |
| [3] |
CHAI Shan, ZHANG Yaoming, ZHAO Youqun, et al. An analysis on the non-linear air exciting-vibration force caused by clearance[J]. Journal of Nonlinear Dynamic in Science and Technology, 2000, 7(1): 25-32. |
| [4] |
柴山, 张耀明, 赵又群, 等. 汽轮机非线性间隙汽流激振力分析(Ⅰ)——相对进气速度沿叶高不变[J]. 非线性动力学学报, 2000, 7(1): 25-32. CHAI Shan, ZHANG Yao-ming, ZHAO Youqun, et al. An analysis on the non-linear air exciting-vibration force caused by clearance[J]. Journal of Nonlinear Dynamic in Science and Technology, 2000, 7(1): 25-32. |
| [5] |
H. S. KIM. Stability analysis of a turbine rotor system with Alford forces[J]. Journal of Sound and Vibration, 2002, 258(4): 777-790.
|
| [6] |
瓮雷, 杨自春, 曹跃云. 汽轮机非线性间隙汽流激振力作用下含裂纹转子的振动特性研究[J]. 振动与冲击, 2016, 35(5): 89-95. WENG Lei, YANG Zichun, CAO Yueyun. Bifurcation characteristic of a cracked rotor-bearing system under air-exciting forces of steam turbine[J]. Journal of Vibration and Shock, 2016, 35(5): 89-95. |
| [7] |
王海飞, 陈果, 廖仲坤, 等. 含支承松动故障的弹用涡轮发动机整机振动建模与机匣响应特征[J]. 航空动力学报, 2015, 30(3): 627-638. WANG Hai-fei, CHEN Guo, LIAO Zhong-kun, et al. Modelling for whole missile turbofan engine vibration with support looseness fault and characteristics of casing response[J]. Journal of Aerospace Power, 2015, 30(3): 627-638. |
| [8] |
王海飞, 陈果, 廖仲坤, 等. 含支承松动故障的航空发动机非同步响应特征[J]. 振动、测试与诊断, 2016, 36(5): 858-864. WANG Hai-fei, CHEN Guo, LIAO Zhong-kun, et al. Characteristics of aero-engine asynchronous response with support looseness fault[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(5): 858-864. |
| [9] |
马辉, 孙伟, 刘杰, 等. 旋转机械支座松动故障实验[J]. 农业机械学报, 2007, 38(6): 134-137. MA Hui, SUN Wei, LIU Jie, et al. Experimental research on rotating machinery with pedestal looseness faults[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(6): 134-137. DOI:10.3969/j.issn.1000-1298.2007.06.033 |
| [10] |
罗跃纲, 闻邦椿. 双跨转子系统裂纹-松动耦合故障的非线性响应[J]. 航空动力学报, 2007, 22(6): 996-1001. LUO Yue-gang, WEN Bang-chun. Nonlinear responses of two-span rotor-bearing system with coupling faults of crack and pedestal looseness[J]. Journal of Aerospace Power, 2007, 22(6): 996-1001. DOI:10.3969/j.issn.1000-8055.2007.06.024 |
| [11] |
曾复, 吴昭同, 严拱标. 裂纹转子的分岔与混沌特性分析[J]. 振动与冲击, 2000, 19(1): 40-42. ZENG Fu, WU Zhaotong, YAN Gongbiao. Analysis of bifurcation and chaos on a cracked rotor[J]. Journal of Vibration and Shock, 2000, 19(1): 40-42. DOI:10.3969/j.issn.1000-3835.2000.01.012 |
 2020, Vol. 42
2020, Vol. 42
