钻井船是能够在海上进行定点勘探钻井作业的海洋工程结构物,具有自航迁移、可变载荷大、适合作业环境条件广等优点。然而,海上勘探钻井作业对钻井船的定位能力[1-3]要求十分苛刻,船体位置必须被限制在较小的区域内才能进行正常作业,否则可能导致作业中断,甚至发生事故,带来巨大的损失。
与频域分析相比,时域分析可得到所模拟物理量的历史记录,并更好地解决瞬态问题和非线性问题,从而做出进一步的统计分析。基于此,本文在时域内对作用于钻井船的风、浪、流联合作用下的漂移载荷进行了分析,为钻井船的定位能力分析提供载荷输入,为改善钻井船的定位能力提供技术支持。
1 风载荷计算原理与普通船舶相比,钻井船甲板上有更加复杂的结构和设备,将受到比普通船舶大得多的风载荷[4-6]。定位分析考虑的是平面内的运动,因此风载荷应包括纵向风力Fxw,横向风力Fyw和绕垂向轴的首摇风力矩Mxyw,分别为:
| $\begin{aligned} & {F_{xw}} = \frac{1}{2}{C_{xw}}{\rho _w}V_{wR}^2{A_T}\text{,} \\ & {F_{yw}} = \frac{1}{2}{C_{yw}}{\rho _w}V_{wR}^2{A_L} \text{,} \\ & {M_{xyw}} = \frac{1}{2}{C_{xyw}}{\rho _w}V_{wR}^2{A_L}{L_{pp}} \text{。} \\ \end{aligned} $ | (1) |
式中:ρw为空气密度;VwR为计算高度处的风速;AT为船舶首向受风面积;AL为船舶侧向受风面积;Lpp为船舶垂线间长;Cxw,Cyw和Cxyw分别为纵向风力、横向风力和首摇风力矩系数,本文依据OCIMF确定。
自然界的风速是一种随机的、具有频谱分布统计特性的规律,本文采用API风谱来描述不规则风场的特性以求解时域内的风载荷:
| $S\left( f \right) = \frac{{{\sigma ^2}\left( z \right)}}{f} \cdot \frac{F}{{{{\left( {1 + F} \right)}^{5/3}}}}\text{。}$ | (2) |
式中:σ(z)=0.15V(z)(z/zs)−0.125,fp=0.025V(z)/z,F=f/fp;V(z)为静水面以上高度为z m处的平均风速,zs=20 mm,称为表面层厚度。
2 流载荷计算原理海流作用于船体上会引起钻井船发生沿流向的漂移运动。同理,作用于钻井船上的流载荷[7~9]包括纵向流力Fxc、横向流力Fyc和首摇流力矩Mxyc,分别为:
| $\begin{aligned} & {F_{xc}} = \frac{1}{2}{C_{xc}}{\rho _c}V_{cR}^2T{L_{pp}} \text{,} \\ & {F_{yc}} = \frac{1}{2}{C_{yc}}{\rho _c}V_{cR}^2T{L_{pp}} \text{,} \\ & {M_{xyc}} = \frac{1}{2}{C_{xyc}}{\rho _c}V_{cR}^2TL_{pp}^2 \text{。} \\ \end{aligned} $ | (3) |
式中:ρc为海水密度;VcR为水表面的平均水流速度,不考虑水流随深度的变化;
不规则波中二阶波浪力[10-12]表现为平均波浪力和低频慢漂力的共同作用,本文采用AQWA软件进行分析,该软件基于Newman近似的近场法预报2阶波浪力,包括时域中的平均波浪力和低频慢漂力。
当组成不规则波的2个规则波相互叠加时,其频率差值可能接近系统的固有频率,从而引起钻井船的低频慢漂振荡,影响钻井船的定位和作业。这种作用于船体的2阶波浪激振力可通过2阶差频波浪力[13-14]传递函数(简称QTF)进行研究:
| $ \begin{split} {F_{sv}} = & \sum\nolimits_{i = 1}^{NSPL} {\sum\nolimits_{j = 1}^{NSPL} {\left\{ {P_{ij}^ - \cos \left[ { - \left( {{\omega _i} - {\omega _j}} \right)t + \left( {{\varepsilon _i} - {\varepsilon _j}} \right)} \right]} \right\}} }+ \\ & \sum\nolimits_{i = 1}^{NSPL} {\sum\nolimits_{j = 1}^{NSPL} {\left\{ {Q_{ij}^ - \sin \left[ { - \left( {{\omega _i} - {\omega _j}} \right)t + \left( {{\varepsilon _i} - {\varepsilon _j}} \right)} \right]} \right\}} }\text{。} \end{split} $ | (4) |
式中:ωi,ωj分别是叠加的2个规则波的圆频率;εi,εj分别是随机相位角;
由NEWMAN近似,
应用傅里叶变换,根据不同浪向、不同频率下的2阶波浪力传递函数,可以得到二次脉冲传递函数g(τ1,τ2),τ1,τ2为时间间隔。于是给定波浪时程η(t),便可以求得2阶波浪力的时程
| $ F_i^{wa\left( 2 \right)}\left( t \right) = \int_0^{ + \infty } {\int_0^{ + \infty } {g\left( {{\tau _1},{\tau _2}} \right)\eta \left( {t - {\tau _1}} \right)} } \eta \left( {t - {\tau _2}} \right){\rm d}{\tau _1}{\rm d}{\tau _2}\text{。} $ | (5) |
根据统计分析方法,对得到的波浪力时程进行处理,得到各项波浪2阶力的最大值。
4 分析模型和参数本文的分析模型为某公司自主研发的钻井船,钻井船的主要参数如表1所示。
|
|
表 1 船型总体参数表 Tab.1 Hull parameters of drill ship |
钻井船在作业工况下的航速为0,吃水为12.0 m,作业水深为3 000 m,分析模型如图1所示。

|
图 1 钻井船漂移载荷计算模型 Fig. 1 Analysis model for drift force of drill ship |
其中:坐标原点位于静水线面上;考虑月池[15]对船体所遭受载荷的影响;考虑钻井船常处于迎浪状态,因此选取的分析浪向为180°,165°和150°。结合作业海域的实际海况,认为波浪为充分发展的随机波浪,分析中采用PM谱,并分解为由多个不同周期、不同随机初始相位的余弦波叠加而成。其中,波浪圆频率范围为0.2~2.4,间隔0.1。风速、波浪参数的取值考虑风生浪因素,波高H与波浪周期T取值符合T=4.1(H)0.4+0.1,选取5组流速、风速和波浪进行计算,具体如表2所示。
|
|
表 2 风、流、波浪输入参数 Tab.2 Environmental parameters of wind,wave and current |
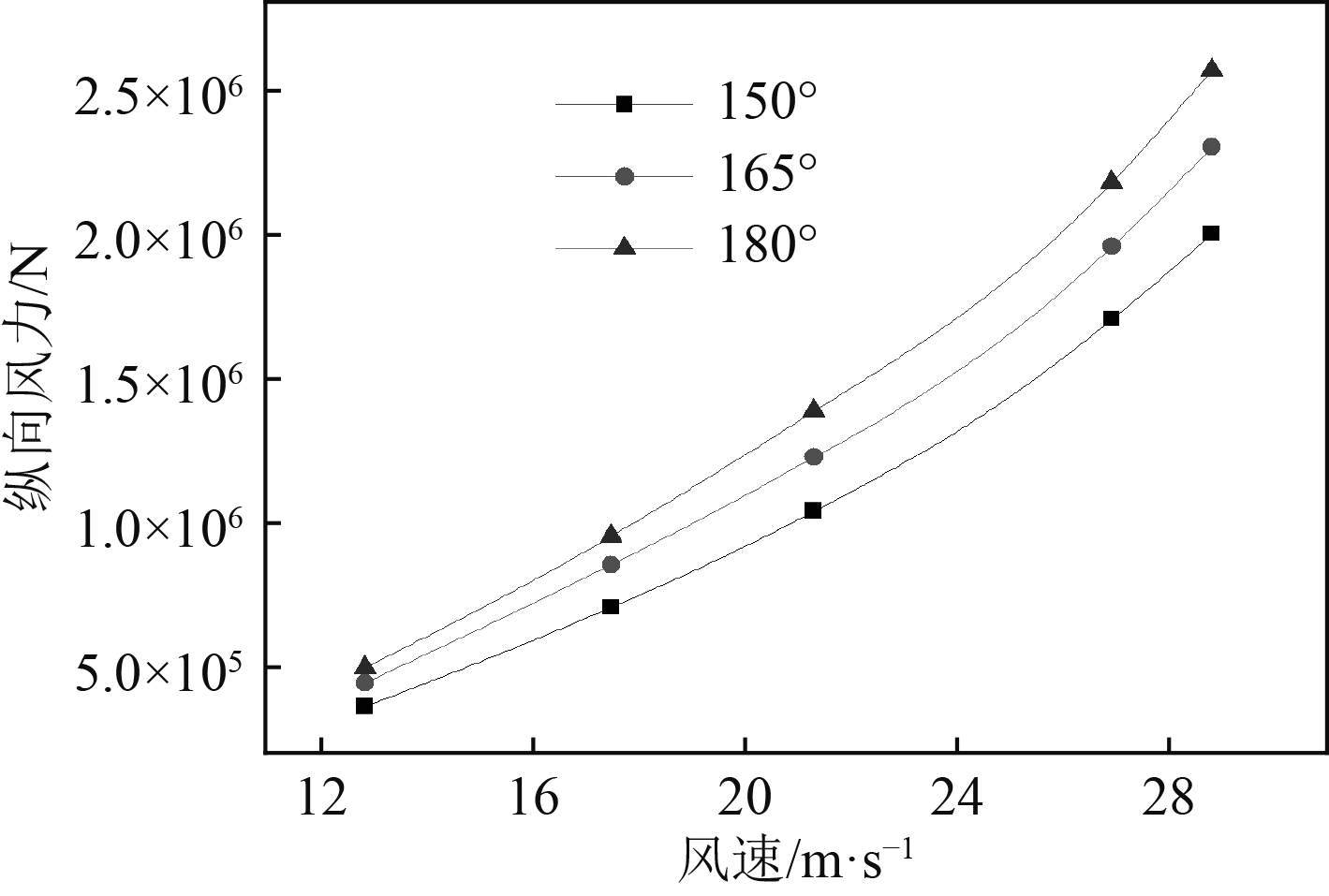
根据前述计算原理,得到150°,165°和180°风向下的风载荷计算结果,分别如图2~图5所示。可以发现,150°风向下的合力和首摇力矩达到最大,因此,图6~图8分别给出了150°风向、风速等于28.78 m/s时,6 000 s时间内的风载荷时间历程曲线。
|
图 2 不同风向、风速下的纵向风力 Fig. 2 Longitudinal wind force under different winds |
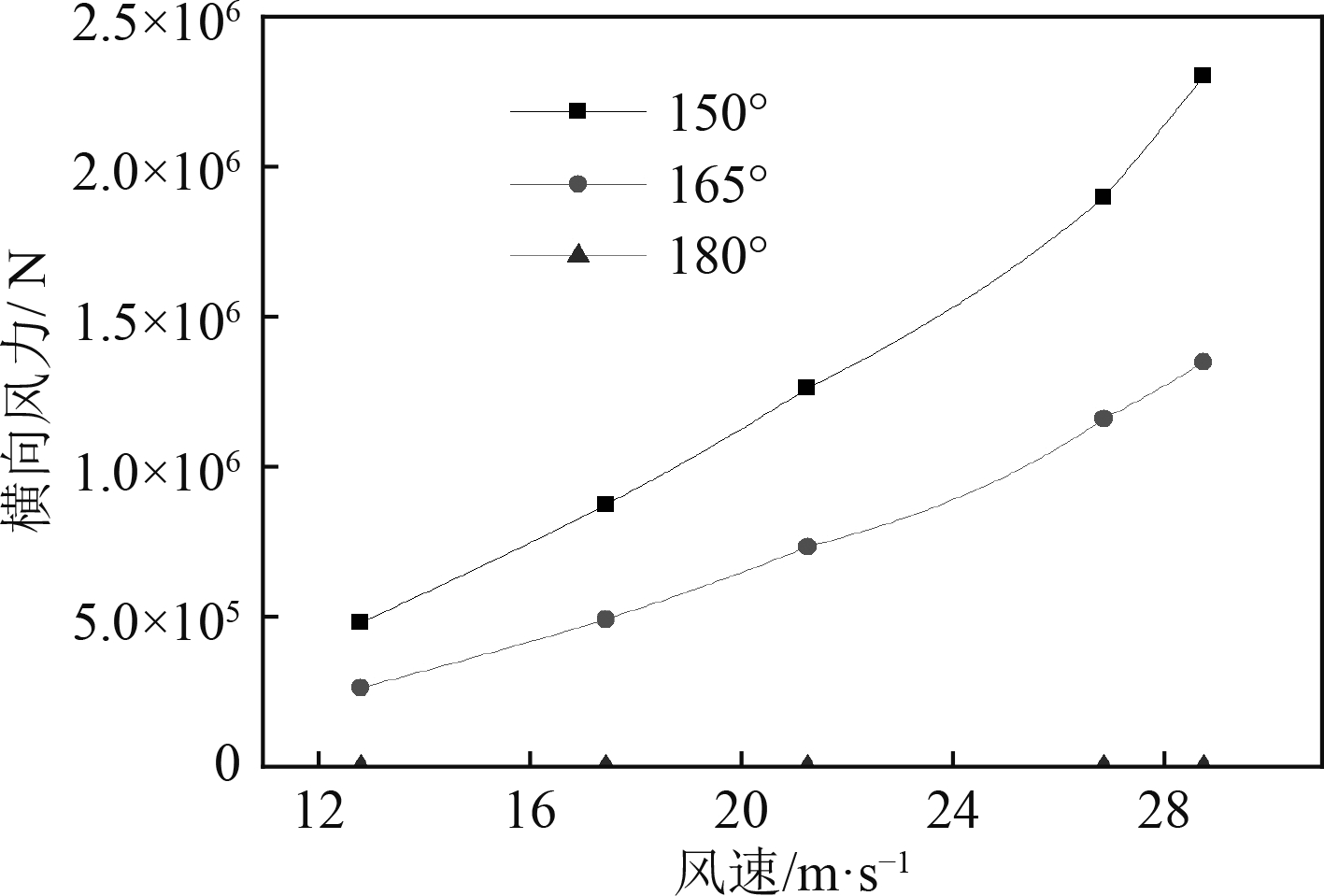
|
图 3 不同风向、风速下的横向风力 Fig. 3 Transverse wind force under different winds |
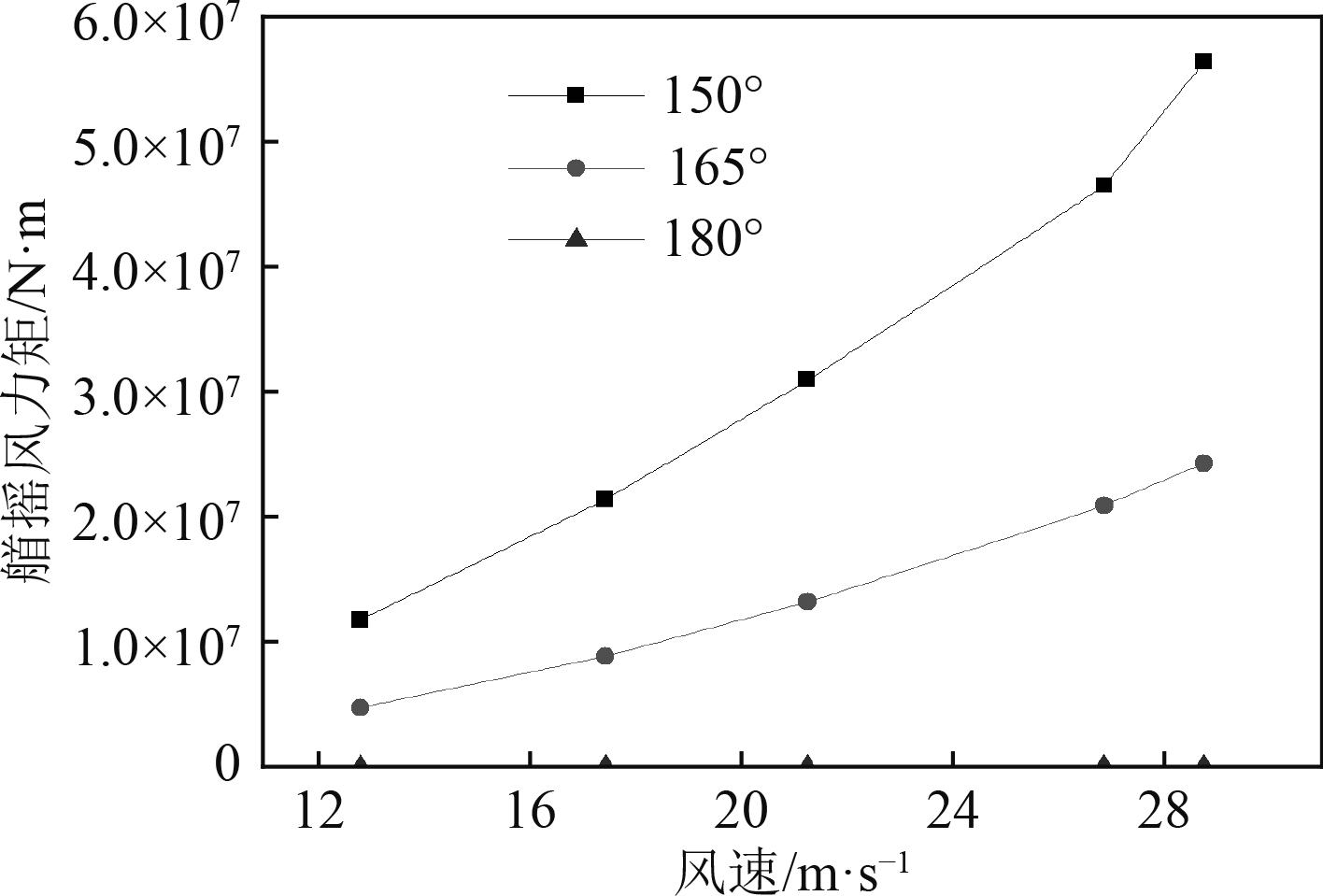
|
图 4 不同风向、风速下的首摇风力矩 Fig. 4 Yaw wind force under different winds |
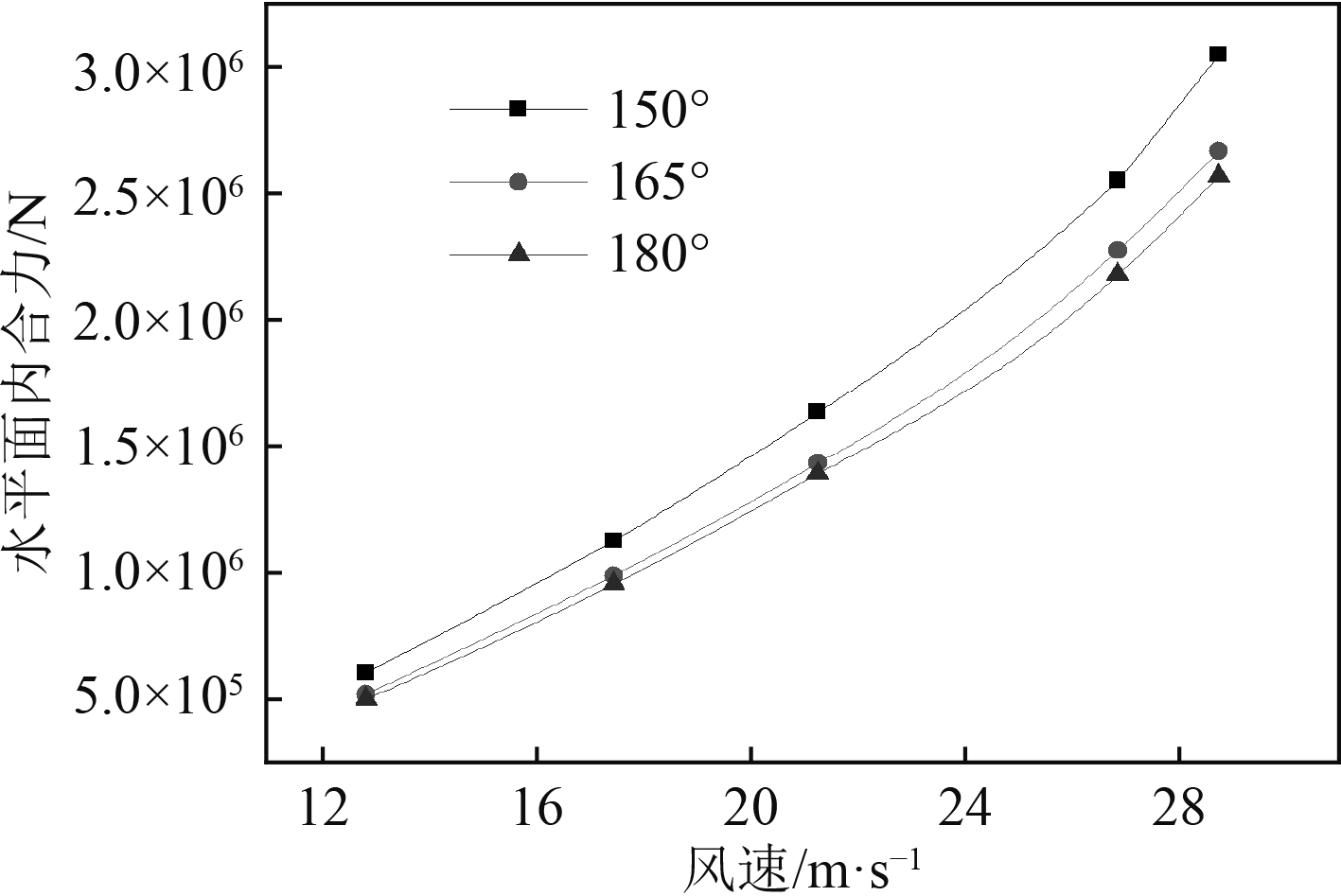
|
图 5 不同风向、风速下的水平面内风合力 Fig. 5 Wind force in horizontal plane under different winds |
|
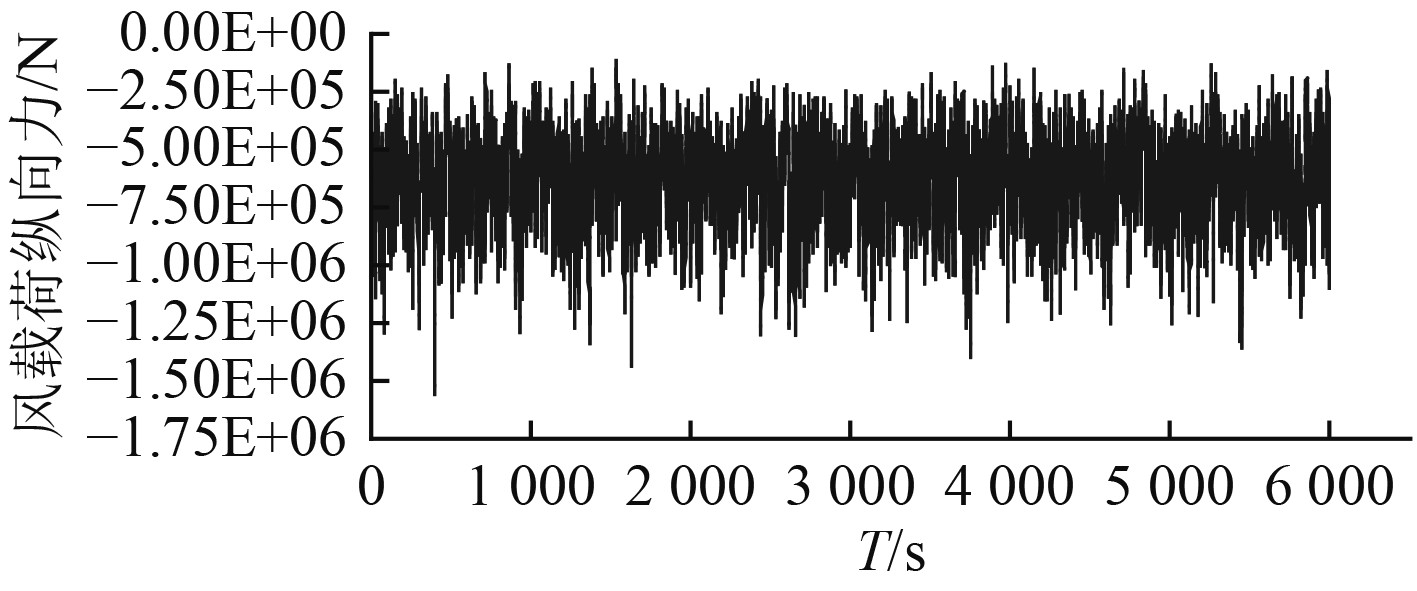
图 6 风载荷纵向力时间历程曲线 Fig. 6 Time history of longitudinal wind force |

|
图 7 风载荷横向力时间历程曲线 Fig. 7 Time history of transverse wind force |
|
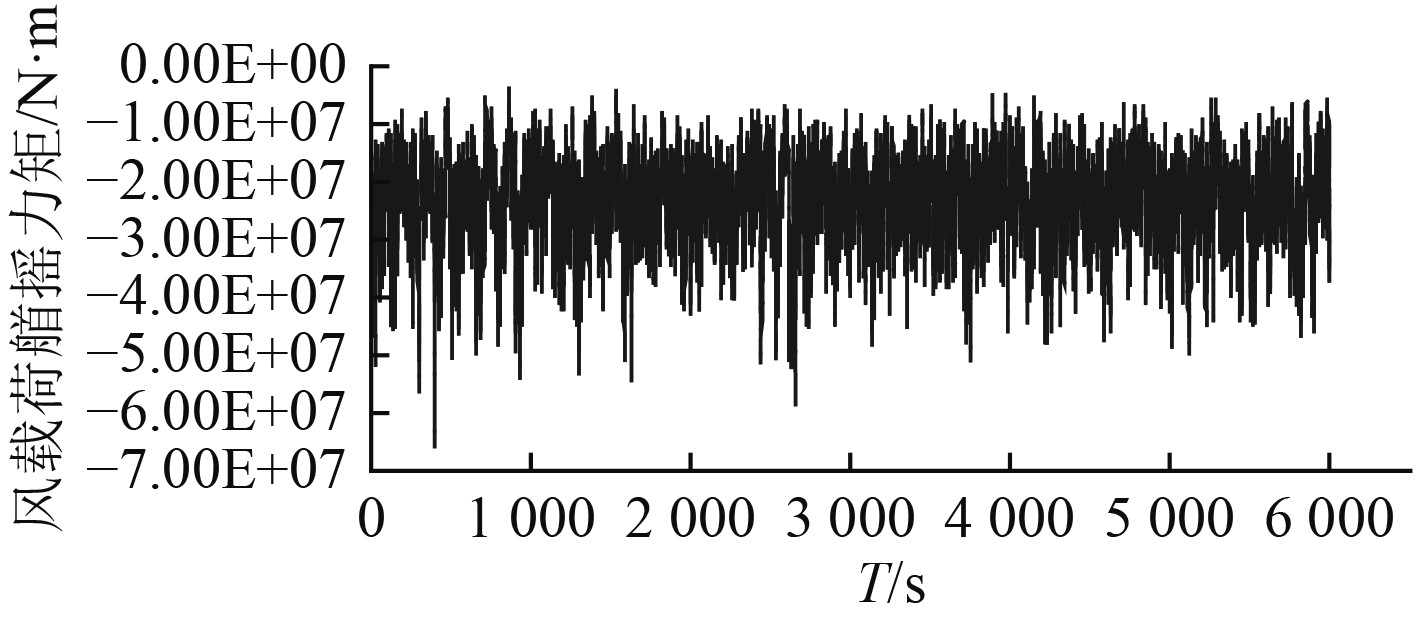
图 8 风载荷首摇力矩时间历程曲线 Fig. 8 Time history of yaw wind force |
由以上计算结果可知,在所考虑的3个风向下:
1)随着风速的增加,纵向风力、横向风力、首摇风力矩和水平面内的风合力均随之增加;
2)风向为150°时,随着风速的增加,横向风力增加的百分比明显大于纵向风力增加的百分比,即横向风力随风速增大而明显增大,随风向偏移顺风状态而明显增大;
3)180°风向(顺风)时,横向风力和首摇风力矩为零,随着风向逐渐变向船舶的横向方向,二者均逐渐增加,这是因为首摇风力矩主要是由横向风力引起的,因此二者的变化趋势是一致的;
4)水平面内的风力合力,即纵向风力和横向风力的合力,在180°风向(顺风)时最小,随着风向逐渐变向船舶的横向方向,风力合力也逐渐增加,150°风向时最大。因此,保持船首处于迎风状态对减小钻井船所承受的风载荷意义重大;
5)在以上计算工况中,风力合力的最大值出现在150°风向、风速为28.78 m/s时,其值为3.05 MN。
5.2 流载荷计算结果根据前述计算原理,得到150°、165°和180°流向下的流载荷计算结果,分别如图9~图12所示。
|
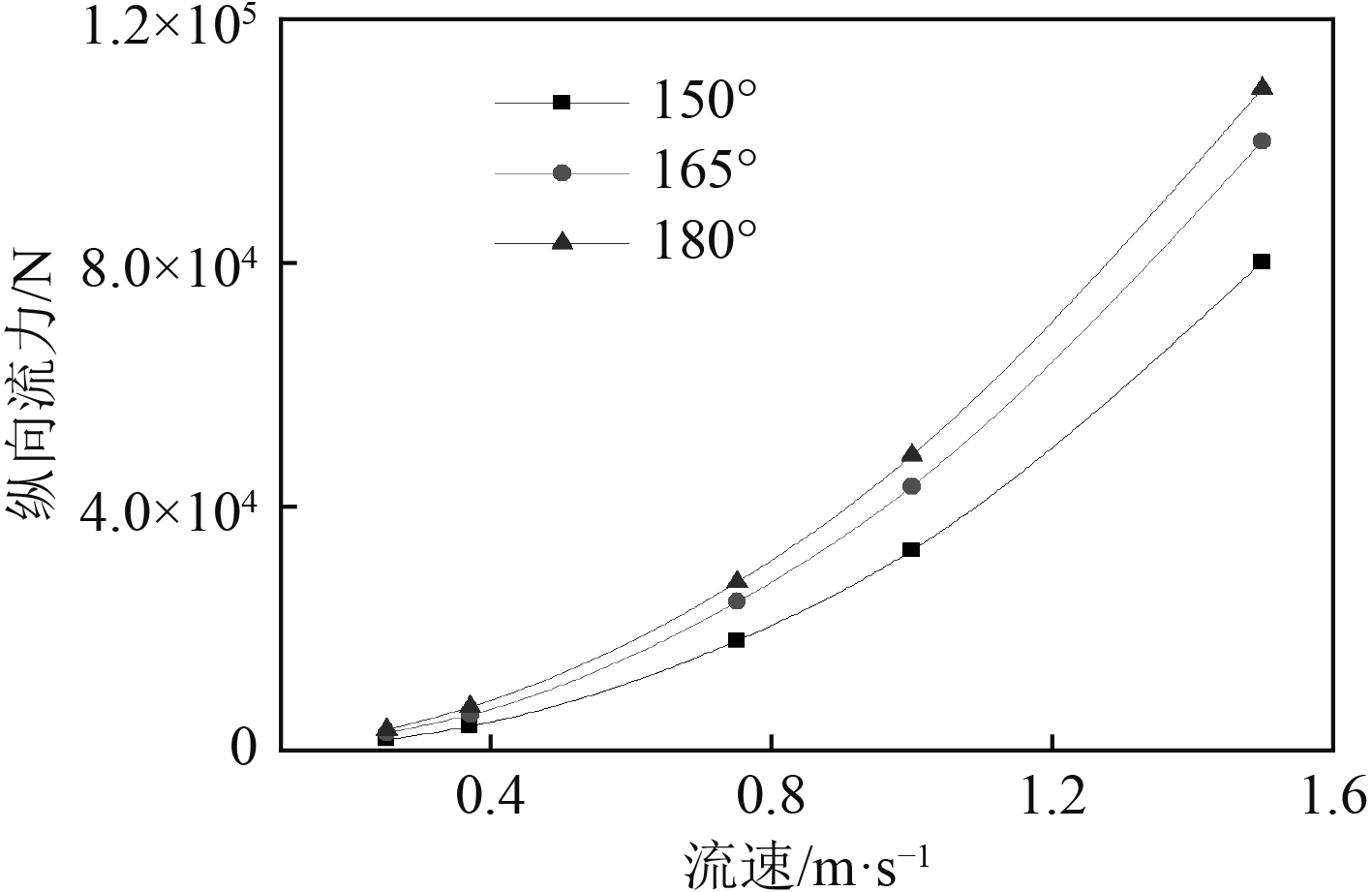
图 9 不同流向、流速下的纵向流力 Fig. 9 Longitudinal wind force under different currents |
|
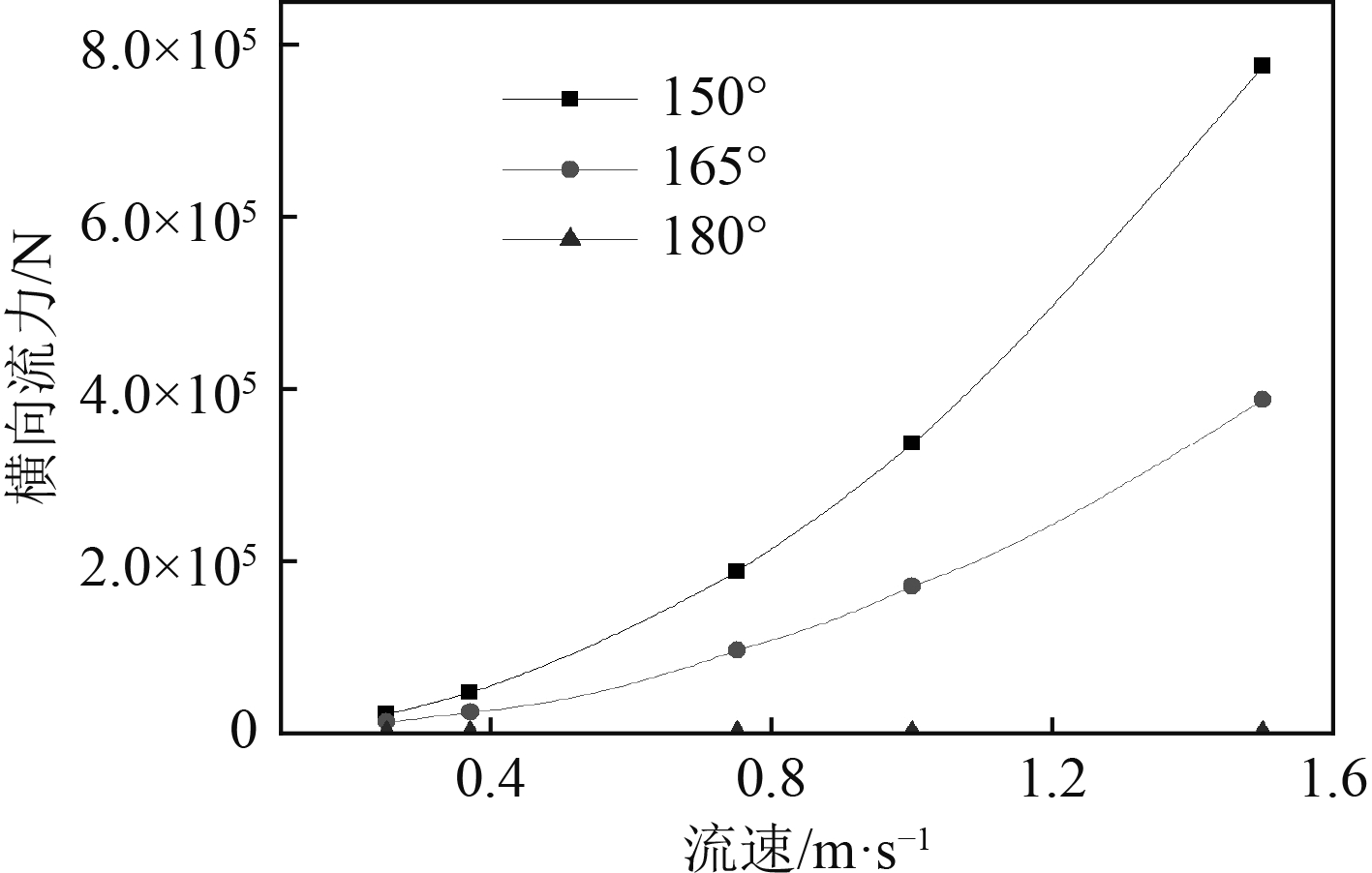
图 10 不同流向、流速下的横向流力 Fig. 10 Transverse wind force under different currents |

|
图 11 不同流向、流速下的首摇流力矩 Fig. 11 Yaw wind force under different currents |
|
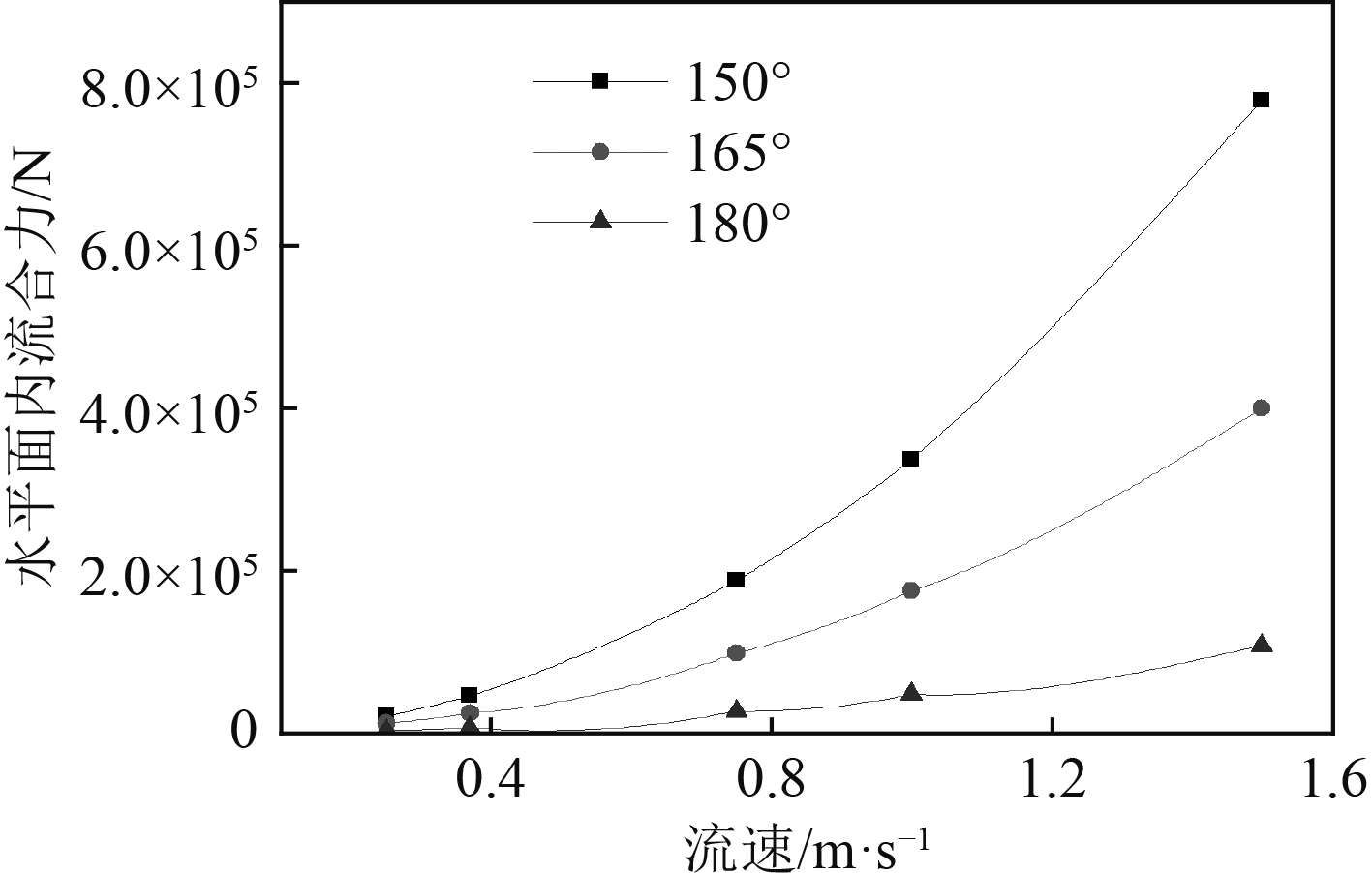
图 12 不同流向、流速下的水平面内流合力 Fig. 12 Current force in horizontal plane under different currents |
以上所有工况中,150°流向下的流合力和首摇流力矩达到最大。因此,图13~图15单独给出150°风向、流速为1.5 m/s时,6 000 s时间内的流载荷时间历程曲线。
由以上计算结果可知,在3个计算流向下:
|
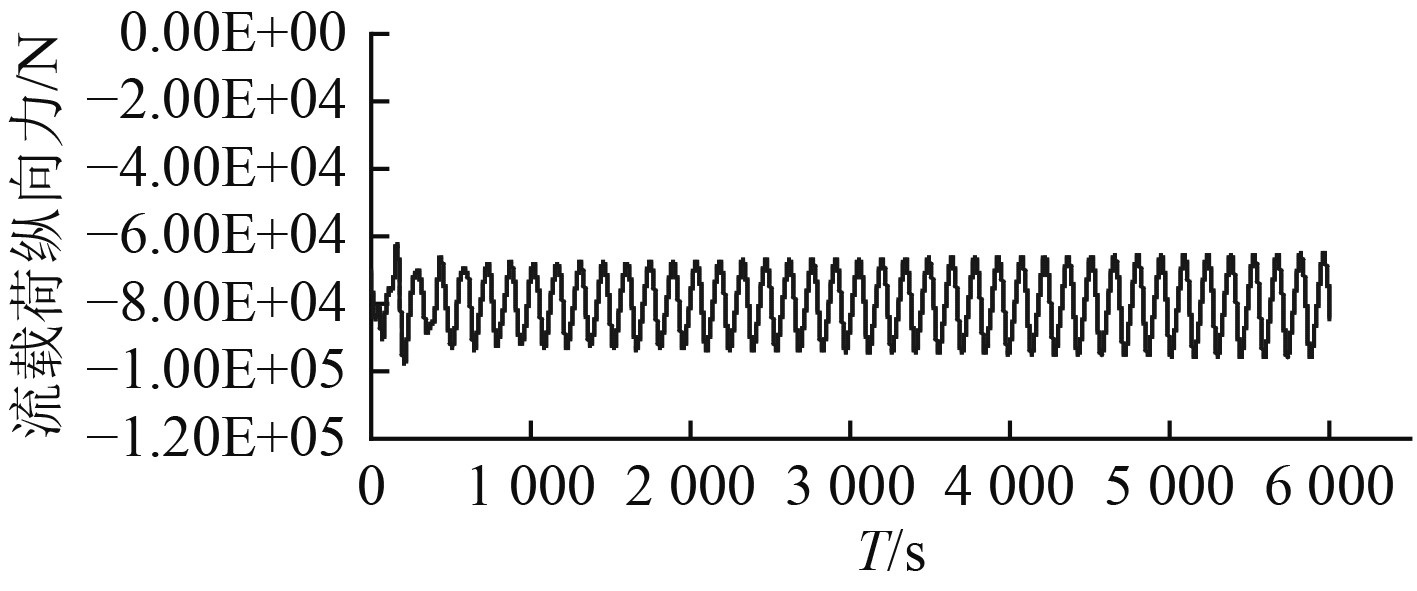
图 13 流载荷纵向力时间历程曲线 Fig. 13 Time history of longitudinal current force |
|
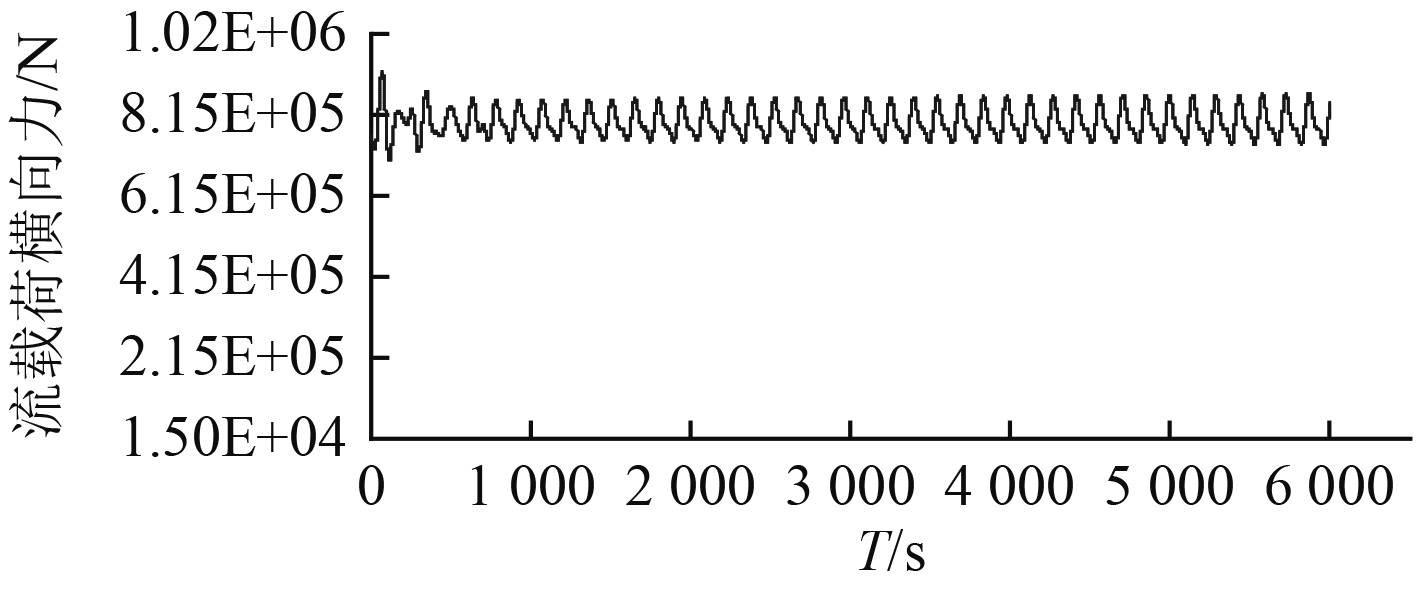
图 14 流载荷横向力时间历程曲线 Fig. 14 Time history of transverse current force |
|
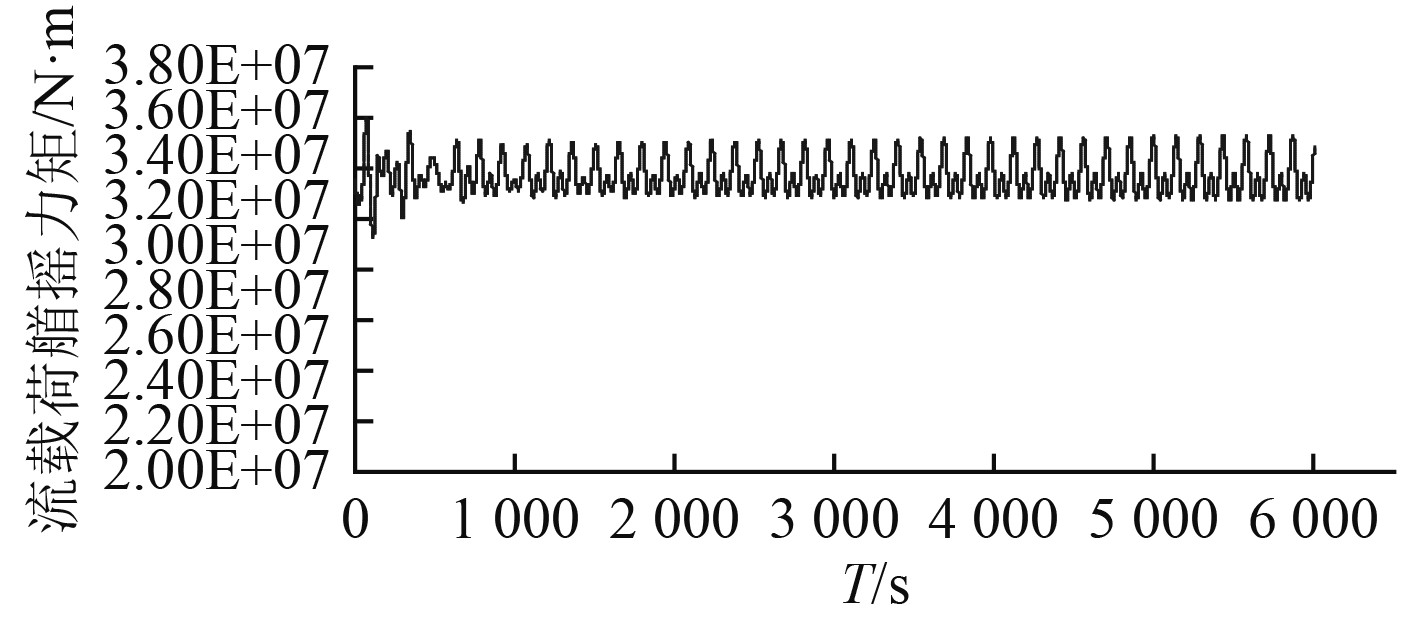
图 15 流载荷首摇力矩时间历程曲线 Fig. 15 Time history of yaw current force |
1)随着流速的增加,纵向流力、横向流力、首摇流力矩和水平面内的流合力均随之增加;
2)150°流向下,随着流速的增加,横向流力增加的百分比明显大于纵向流力增加的百分比,即横向流力随流速增大而明显增大,随流向偏移顺流状态而明显增大;
3)在180°流向时,横向流力和艏摇流力矩均为零,随着流向逐渐变向船舶的横向方向,二者均逐渐增加,这是因为首摇流力矩主要是由横向流力引起的,因此二者的变化趋势是一致的。
4)水平面内的流力合力,即纵向流力和横向流力的合力,在180°流向时最小,随着流向逐渐变向船舶的横向方向,流力合力也逐渐增加,150°流向时最大。因此,保持船首处于顶流状态对减小钻井船所承受的流载荷意义重大。
5)在以上计算工况中,流力合力的最大值出现在150°流向、流速1.5 m/s,其值的大小为779 kN。
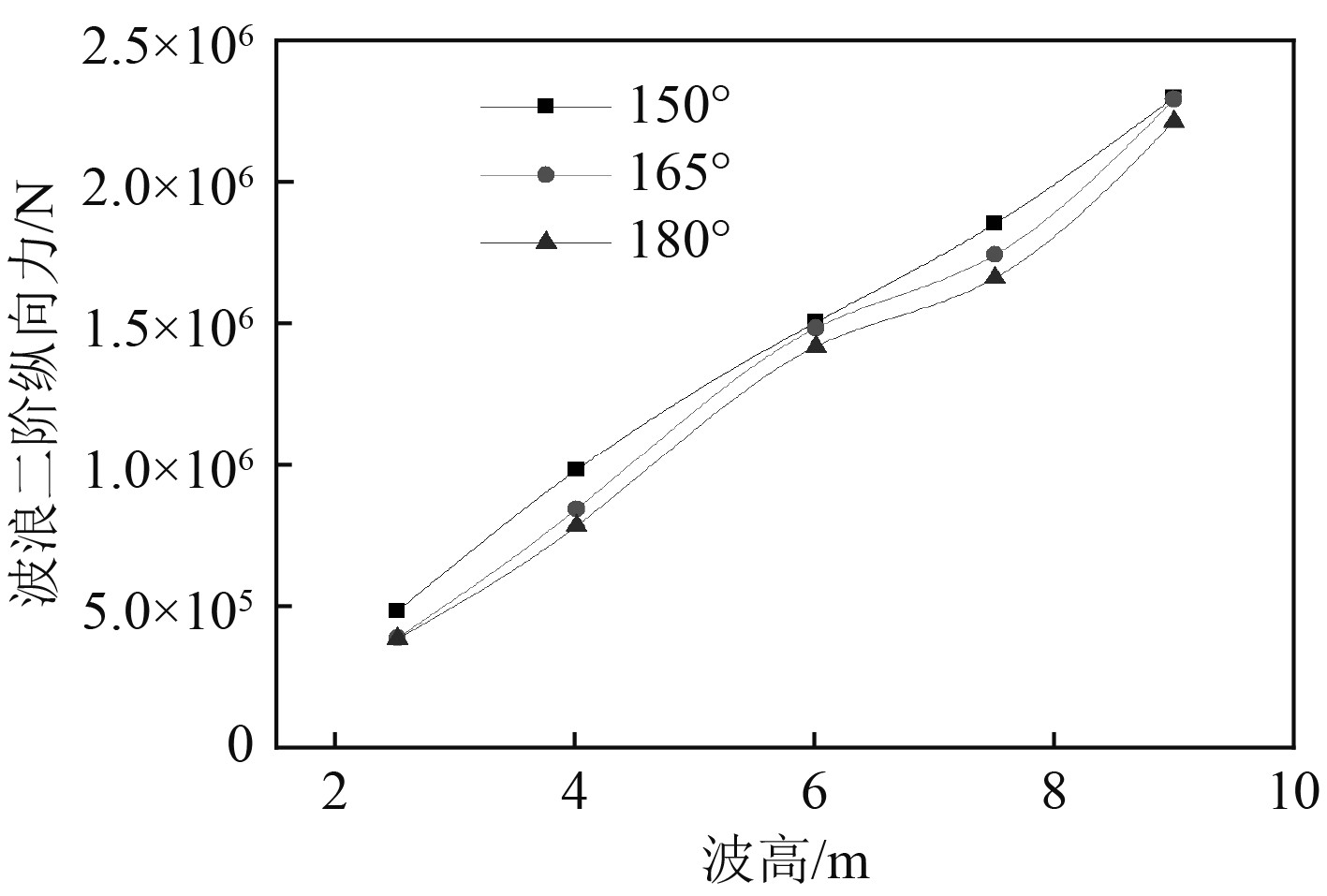
5.3 波浪漂移载荷计算结果根据前述计算原理得到不规则波中波浪2阶力(平均漂移力与低频慢漂力的和)的计算结果,包括不同浪向、波高下的波浪2阶纵向、横向、首摇分力,以及纵向和横向分力的合力,如图16~图19所示。
|
图 16 波浪2阶纵向力 Fig. 16 Longitudinal wave second force under different waves |
|
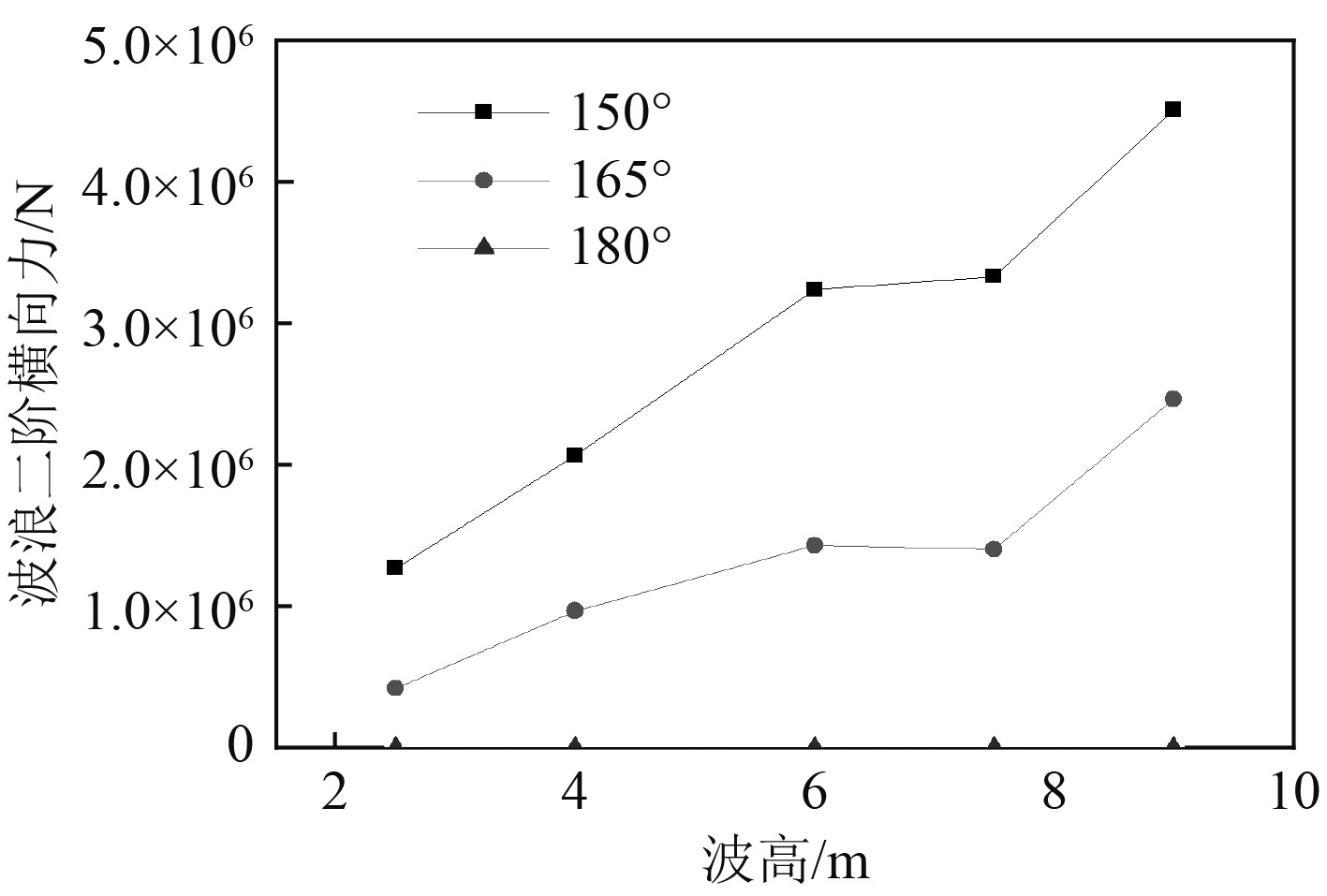
图 17 波浪2阶横向力 Fig. 17 Transverse wave second force under different waves |
|
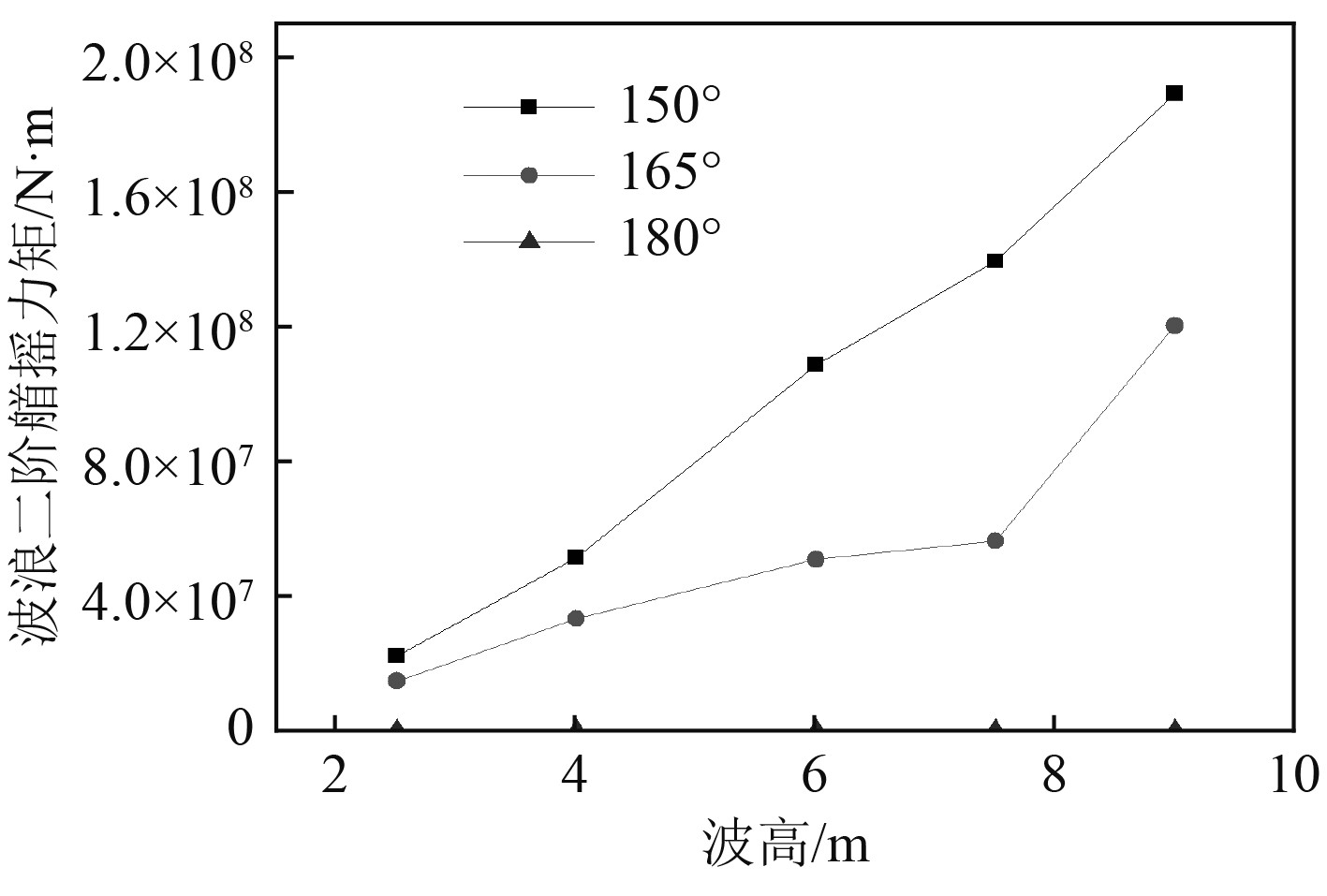
图 18 首摇2阶波浪力矩 Fig. 18 Yaw wave second force under different waves |
|
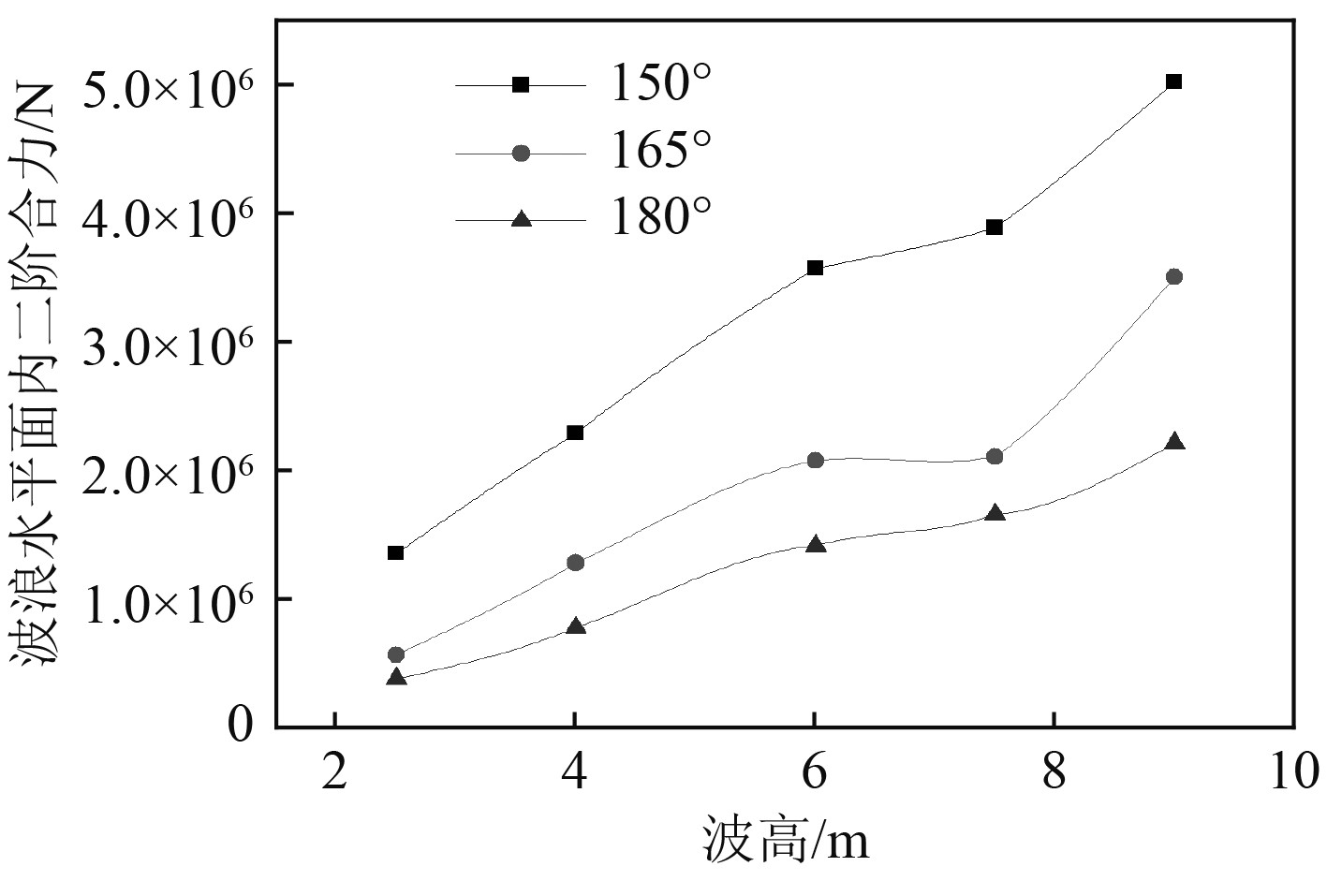
图 19 波浪水平面内2阶合力 Fig. 19 Wave second force in horizontal plane under different waves |
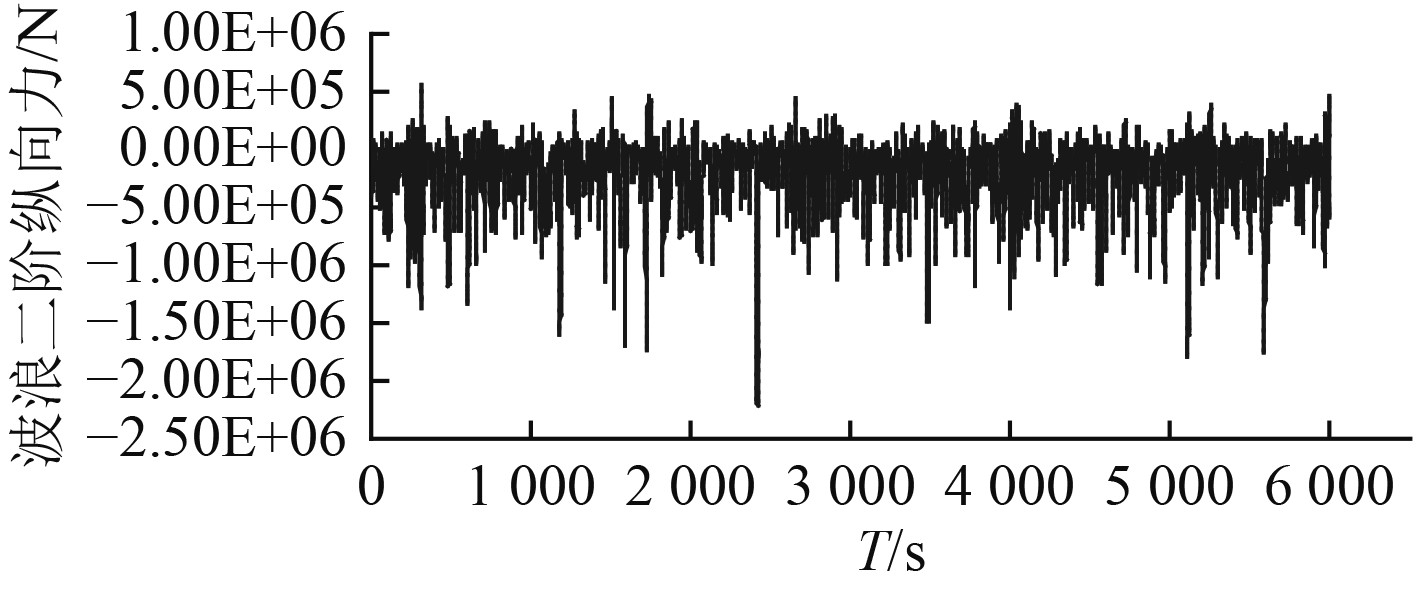
由以上计算结果可知,有义波高为9.0 m时的各项波浪2阶力达到最大,其中各浪向下的2阶纵向力差别不大,150°浪向下的2阶横向力和2阶首摇力矩达到最大。图20~图22分别给出了在6000 s时间内不同浪向β下的波浪2阶力的时域历程曲线。
|
图 20 波浪2阶纵向力时间历程曲线(β=180°) Fig. 20 Time history of longitudinal wave second force |
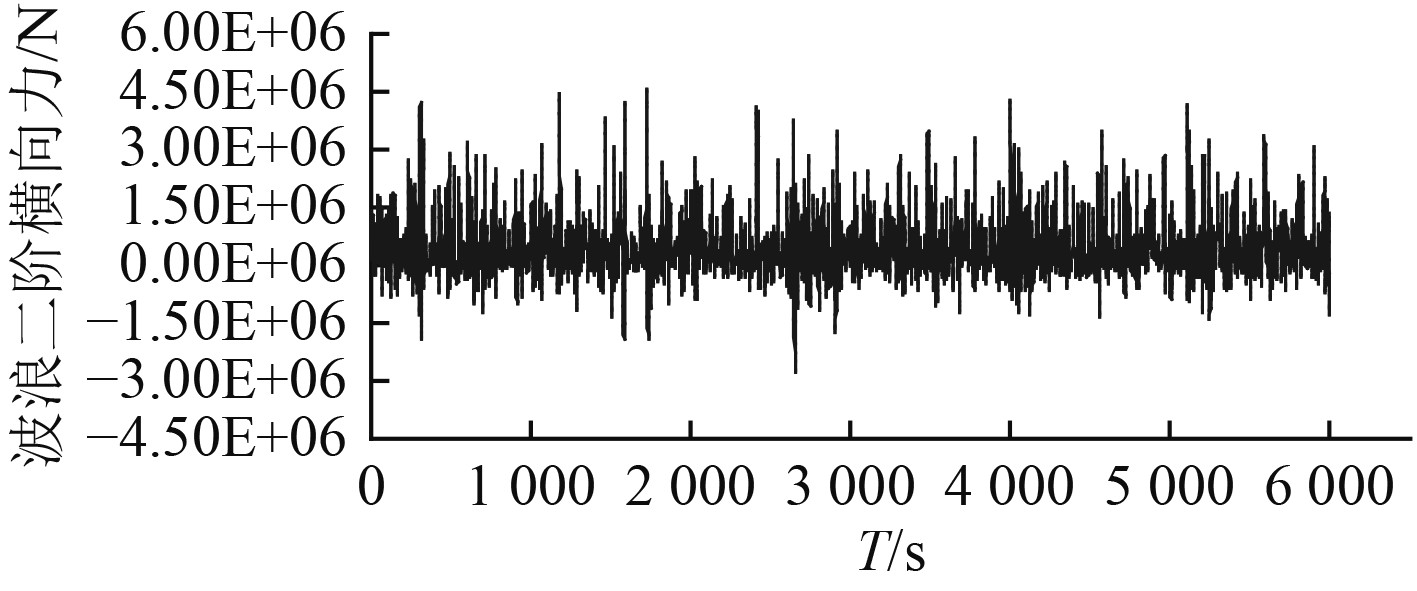
|
图 21 波浪2阶横向力时间历程曲线(β=150°) Fig. 21 Time history of transverse wave second force |
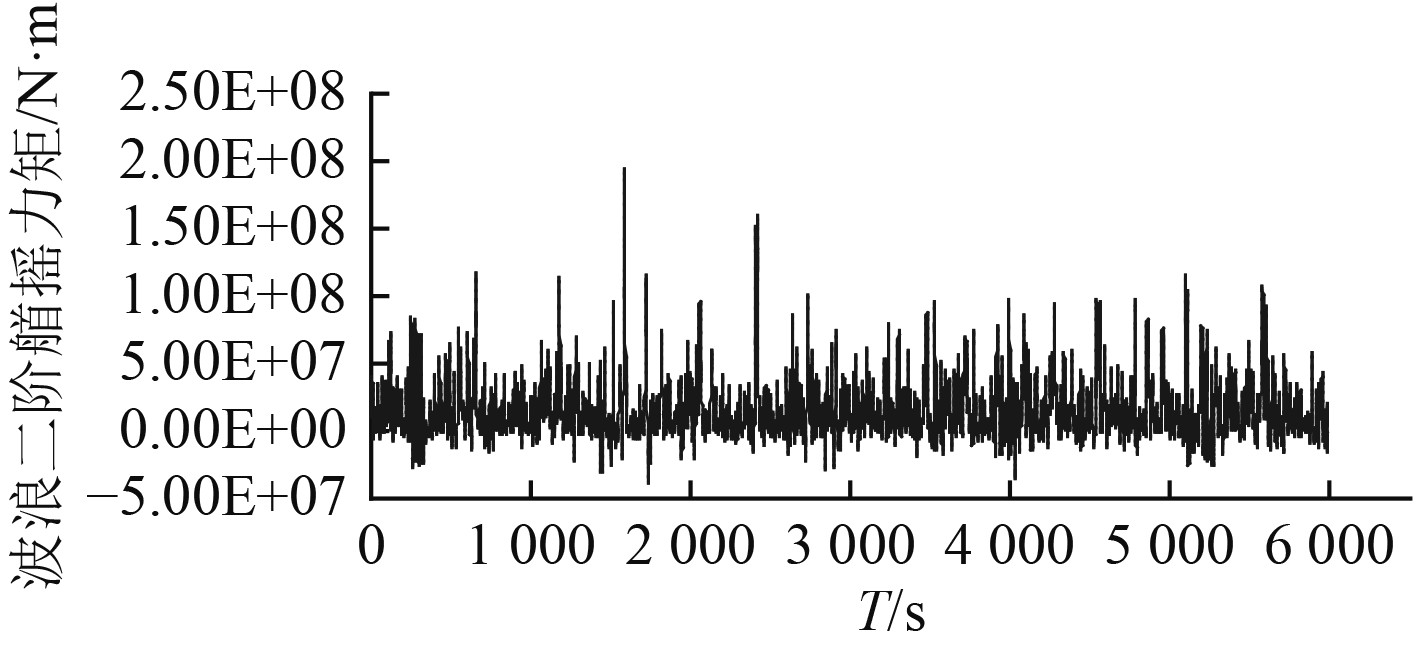
|
图 22 波浪2阶首摇力矩时间历程曲线(β=150°) Fig. 22 Time history of yaw wave second force |
根据以上各图可知:
1)波浪2阶纵向力、横向力、首摇力矩和水平面内的合力均随有义波高的增大而增大。
2)波浪2阶纵向力随浪向的变化不明显.
3)180°迎浪状态下,波浪2阶横向力和艏摇力矩为零,水平面内的波浪2阶力合力最小,随着浪向逐渐向船舶的横向方向偏移而逐渐增大.因此,保持船艏处于迎浪状态对减小钻井船所承受的波浪2阶力有利。
4)在以上计算工况中,波浪2阶力合力的最大值出现在150°浪向、9 m有义波高下,其值的大小为5.02 MN。
5.4 风载荷、流载荷和波浪漂移载荷汇总在本文的计算工况下,风、流和波浪漂移载荷最大值均出现在150°方向,且出现在风速、流速最大和波高最大的工况下。表3为对风、流和波浪漂移载荷最大值进行汇总,包括纵向力、横向力、首摇力矩和平面内的合力。
|
|
表 3 风、流、波浪漂移载荷最大值 Tab.3 Maximum drift force of wind,current and wave |
由表3可知:
1)风、流和波浪的横向力、首摇力矩和水平面内的合力均为波浪力最大,风和波浪的纵向力较为接近,风力次之,流力最小;
2)流力和波浪力的纵向力差值较大,波浪纵向力约为流纵向力的21倍,波浪首摇力矩为流首摇力矩的5.7倍;
3)风、流和波浪产生的漂移载荷共同作用于深水作业钻井船,使其在水平面内发生位移,从而影响钻井船的定位能力。
6 结 语钻井船具备足够的定位能力是保证钻井船正常作业的重要前提条件。本文对带月池的深水作业钻井船所遭受的风、流和波浪漂移载荷进行了数值预报和统计分析,得到如下结论:
1)在时域内对深水作业钻井船漂移载荷进行分析,更加具有真实性,风、流和波浪引起的漂移载荷均随环境条件的增大而快速增加。
2)根据作业海域实际海况设置漂移载荷时域分析的环境参数,并考虑风生浪因素,发现风、流和波浪引起的纵向力、横向力、首摇力矩和水平面内的合力呈波浪力较大、风力次之、流力最小的趋势。
3)180°迎风、顶流、迎浪状态下,钻井船所遭受的水平面内的漂移力最小。根据所模拟的真实海况,作用于钻井船的波浪漂移力、风力、流力呈依次减小趋势。因此,在风向、流向和浪向不同时,使得船艏处于迎浪状态对钻井船的定位有利。
4)对于钻井船而言,波浪漂移力占总漂移载荷的一半以上。因此,为改善其定位能力,最有效的措施为优化船体外型,以降低船体所遭受的波浪漂移力。
| [1] |
ALFHEIM H L, MUGGERUD K, BREIVIK M, et al. Development of a dynamic positioning system for the revolt model ship[J]. IFAC-Papers On Line, 2018, 51(29): 116-121. DOI:10.1016/j.ifacol.2018.09.479 |
| [2] |
HU kaiye, DING Yong, WANG Hongwei, et al. Analysis of capability requirement of dynamic positioning system for cargo transfer vessel at sea[J]. Journal of Marine Science and Application, 2019, 18(02): 205-212. DOI:10.1007/s11804-019-00078-6 |
| [3] |
何进辉, 张海彬, 朱仁传, 等. 某深海钻井船DP3定位能力分析[J]. 船舶, 2018(5): 11-17. DOI:10.3969/j.issn.1007-9750.2018.05.006 |
| [4] |
DAENG P, HARIS M A, SYAMSUL A. Maneuverability of ships with small draught in steady wind[J]. Makara Journal of Technology, 2016, 20(1): 24-30. DOI:10.7454/mst.v20i1.3052 |
| [5] |
林一, 胡安康, 蒋玮. 海洋平台风载荷的数值分析[J]. 船舶工程, 2014, 36(1): 104-108. |
| [6] |
汤晶, 王博, 罗瑞锋. 自升式平台风载荷规范计算方法分析研究[J]. 船舶工程, 2016, 38(S1): 34-38. |
| [7] |
CHEN C, SHIOTANI S, SASA K. Effect of ocean currents on ship navigation in the East China Sea[J]. Ocean Engineering, 2015, 104(4): 283-293. |
| [8] |
JUNG Chang-hyun, NAM Taek-kun. The lateral current force coefficient in the real ship towing test[J]. Journal of the Korean Society of Marine Environment & Safety, 2016, 22(5): 373-379. |
| [9] |
贾宝柱, 纪然, 杨德才. 基于CFD的海洋工程船舶流载荷特性仿真[J]. 舰船科学技术, 2018, 40(10): 82-86, 92. DOI:10.3404/j.issn.1672-7649.2018.10.016 |
| [10] |
王建方, 李辉辉, 徐正强. 两浮体在波浪中二阶漂移力的三维方法研究[J]. 船舶, 2008(2): 18-22. DOI:10.3969/j.issn.1001-9855.2008.02.004 |
| [11] |
金辉, 王腾. 考虑二阶波浪荷载效应的海上TLP浮式风机分析[J]. 海洋技术学报, 2019, 38(1): 66-72. |
| [12] |
GUANGHUA H, MASASHI K. Time-domain analysis of steady ship-wave problem using higher-order BEM[J]. International Journal of Offshore and Polar Engineering, 2014, 24(1): 1-10. |
| [13] |
SUNG K M, JIN P J, KYU A Y, et al. Hydrodynamic Characteristics of Deepwater Drillship for North Sea[J]. Journal of Ocean Engineering and Technology, 2015, 29(4): 300-308. DOI:10.5574/KSOE.2015.29.4.300 |
| [14] |
KIM, BW, HONG, SY, SUNG, HG. Comparison of drift force calculation methods in time domain analysis of moored bodies[J]. Ocean Engineering, 2016, 126(4): 81-91. |
| [15] |
章柯, 杭岑, 施兴华, 等. 含月池开孔的 FPSO 水动力性能及波浪载荷研究[J]. 船舶工程, 2016, 26(S2): 47-52, 266. |
 2020, Vol. 42
2020, Vol. 42
