电容去离子技术(Capacitive Deionization,CDI)类似但又区别于超级电容器[1-3],其在流通模式下运行,并且侧重点在于脱盐而不是电荷存储。作为一种新兴的海水淡化技术,CDI技术在学术研究和工业发展方面受到了越来越多的关注[4-7]。近年来,在电容去离子基础上演变而来的膜电容去离子技术(Membrane Capacitive Deionization,MCDI)也取得了重大进展[8-10]。Porada等[8, 11-12]将电容法脱盐装置组件进行改良制成了中部流入型CDI装置组件,并对其中原水溶液从一侧端板的中间流入,淡化水从组件四周流出的流动方式进行了研究,发现相较于平板式电容法脱盐装置组件,这种新的流动方式会使得流体流动的死区大量减少,更有利于溶液与电极材料的良好接触,离子吸附会更加充分。从已有研究看,目前对于这种新型流动方式的研究主要是基于实验辅以理论方法,而采用数值模拟方法对膜电容法海水淡化装置组件或单元脱盐过程的研究还十分缺乏。
针对一种基于中部流入式的膜电容法脱盐单元,本文建立三维瞬态分析模型,通过对模拟结果进行吸附动力学方程线性回归拟合验证了该模型的正确性后,据此模型分析对比了在2种不同的脱附方式(短接和反接)下,不同入口孔径对该脱盐单元海水淡化过程的影响规律,以及出口浓度,吸、脱附效率随时间变化的规律。
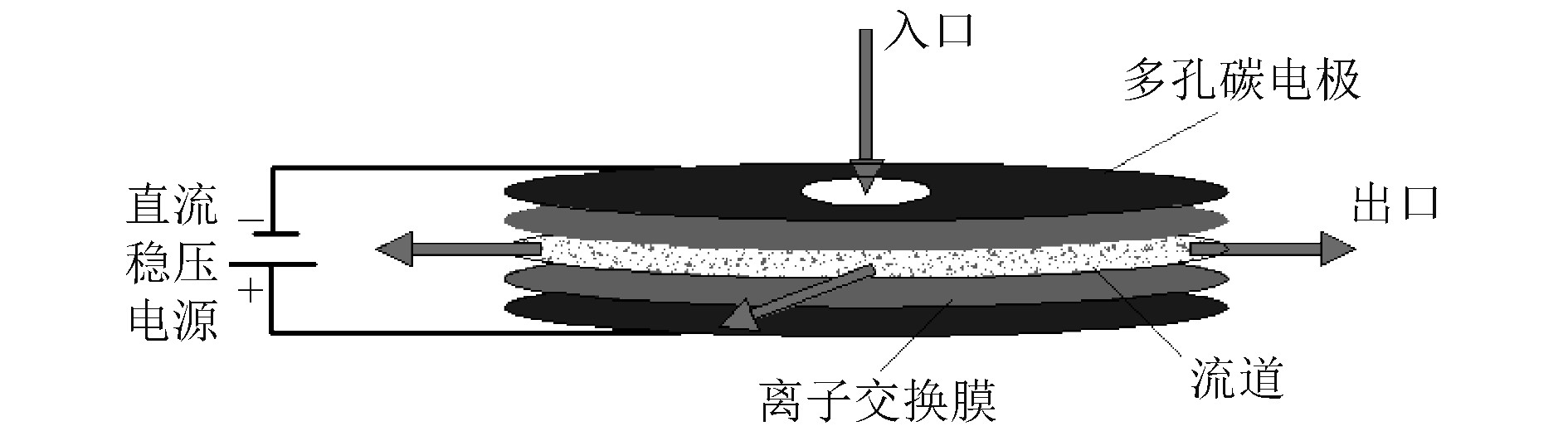
1 模型建立 1.1 MCDI模型几何结构图1为中部流入式膜电容法(MCDI)脱盐模型的几何结构示意图。该模型是在平板式模型基础上,将MCDI模型的矩形改为圆形,并将模型入口区域简化为圆形区域,位于电极一侧中间流入,入口圆孔径设置为2.0 mm,模型出口区域为流道四周;正、负极板为多孔碳材料,单片多孔电极极板厚度约为0.08 mm,且在正、负电极极板内侧两边敷设有一层薄薄的阴、阳离子交换膜,正、负极板之间区域是NaCl溶液流过的流道。
|
图 1 中部流入式MCDI模型几何结构图 Fig. 1 Geometric structure diagram of MCDI model in the middle inflow type |
对于流道,建立盐的质量平衡方程,其中盐的积累是离子由x方向向膜的扩散和迁移以及通过流道的轴向对流流动(或y方向)决定的:
| $\frac{{\partial {c_{sp}}\left( y \right)}}{{\partial t}} = - \frac{{{J_{ion}}\left( y \right)}}{{{\delta _{sp}}}} - {v_{sp}}\frac{{\partial {{\text{c}}_{sp}}\left( y \right)}}{{\partial y}}\text{。}$ | (1) |
式中:
在使用式(1)时,忽略轴向扩散并且认为x方向上的浓度梯度很小。流速
2个膜/溶液的界面上都具有Donnan平衡,且两者分别分布在膜边缘与流道的接触面和膜边缘与电极的接触面。这2个Donnan势如下式:
| ${\Delta {\rm{\phi }}}_{{\rm{d}}{\rm{o}}{\rm{n}}{\rm{n}}{\rm{a}}{\rm{n}}}={\rm{sin}}{{{h}}}^{-1}\frac{\omega {{X}}}{2{{c}}_{{\rm{s}}{\rm{a}}{\rm{l}}{\rm{t}}}}\text{。}$ | (2) |
式中,
膜内电荷平衡由下式
通过膜的线性化的总离子通量
| ${{\text{J}}_{{\text{ion}},{\text{mem}}}}\left( y \right) = - \frac{{{D_{mem}}}}{{{\delta _{mem}}}}\left( {{c_{{\text{T}},{\text{mem}}}}\left( y \right) - \omega X\Delta {\phi _{{\text{mem}}}}\left( y \right)} \right)\text{。}$ | (3) |
对于线性化模型,通过膜的离子通量
通过离散化来解决式(1)中串联的M个理想搅拌体积[14]。在这种情况下,式(1)可以简化为:
| $\frac{{\partial {c_{sp,i}}}}{{\partial t}} = - \frac{{{J_{ion,i}}}}{{{\delta _{sp}}}} - \frac{M}{{{\tau _{sp}}}}\left( {{c_{sp,i}} - {c_{sp,i - 1}}} \right)\text{。}$ | (4) |
式中:
在膜/流道接触面边缘的Donnan电位
| $ \begin{split} & \frac{1}{2}{V_{{\text{cell}}}}/{V_{\text{T}}} = \Delta {\phi _{{\text{sp}},{\text{half}}}} + \Delta {\phi _{{\text{donnan}},{\text{membrane}}/{\text{spacer}}}} + \\ & \Delta {\phi _{{\text{mem}}}} - \Delta {\phi _{{\text{donnan}},{\text{membrane}}/{\text{electrode}}}} + \Delta {\phi _{{\text{elec}}}} + \\ & {{{\left( {\Delta {\phi _{\text{d}}} + \Delta {\phi _{{\text{St}}}}} \right)}_{{\text{micropores}}}}} \;{\text{。}} \end{split}$ | (5) |
上述模型既可用于MCDI,也可用于CDI。可以通过设置膜厚度
MCDI单元模型包含流场、离子浓度场、电场等,因此该模型边界条件如下:
模型入口区域简化为圆形区域,位于电极一侧中间流入,将该圆形区域设置为速度入口,入口圆孔径设置为2.0 mm;模型出口区域为流道四周,出口处设置为压力出口,流体与固体界面采用无滑移边界,各物质在壁处的扩散通量为0。
| $\left\{ {\begin{array}{*{20}{c}} {{{V = }}{{{v}}_{{\rm{in}}}}}\text{,}\\ {{{p = }}{{{p}}_{{\rm{out}}}}}\text{,}\\ {\nabla {{P}} \cdot \overrightarrow {{n}} {\rm{ = 0}}}\text{。} \end{array}} \right.$ | (6) |
式中,
入口流速、入口浓度、温度均为定值:
| $\overrightarrow {{u}} {\rm{ = }}{{{v}}_{{{in}}}}{\rm{, }}{{{c}}_{{i}}}{{ = c}}_{{i}}^{{\rm{ref}}}{{,T = }}{{{T}}_{{{in}}}}\text{。}$ | (7) |
式中,当
| $\overrightarrow {{u}} {\rm{ = 0, }}{{{c}}_{{i}}}{{ = c}}_{{i}}^0\text{。}$ | (8) |
模型计算主要参数取值如表1所示。
|
|
表 1 模型参数 Tab.1 Model parameters |
根据模拟得到中部流入式MCDI脱盐模拟过程中Na+出口浓度的数值结果,利用吸附准一、二级动力学方程对模拟结果进行线性回归拟合,所得线性回归结果如表2所示。
|
|
表 2 模型验证拟合结果 Tab.2 Model fitting results |
Lagergren准一级和准二级动力学方程[15]为:
| $\ln\left(1-\frac{{q}_{t}}{{q}_{e}}\right)=-{K}_{1}t\text{,}$ | (9) |
| $\frac{1}{{{{q}}}_{{{t}}}}=\frac{1}{{K}_{2}{q}_{e}^{2}}\left(\frac{1}{{{t}}}\right)+\frac{1}{{{{q}}}_{{{e}}}}\text{。}$ | (10) |
式中:
综上,可以看出相关系数R2值均接近于1,符合反应动力学方程[15]。因此本文所建立的中部流入式膜电容法脱盐分析模型适用于对MCDI脱盐单元的数值模拟。
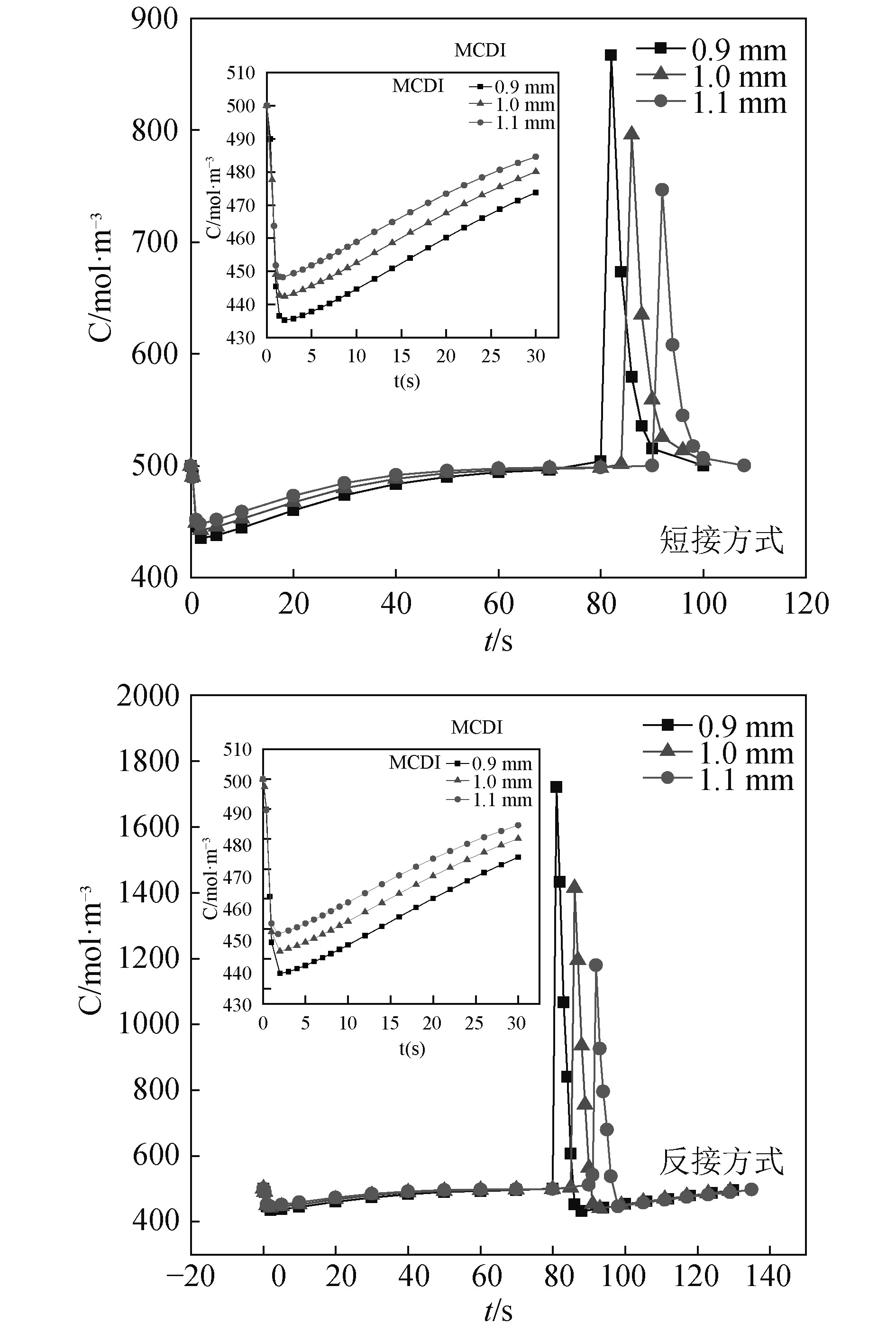
2.2 入口孔径对脱盐性能的影响 2.2.1 两种脱附方式下的结果分析在表1其他条件参数不变的情况下,图2给出了选取不同入口孔径(0.9 mm,1.0 mm和1.1 mm)条件下MCDI脱盐单元在2种脱附方式(短接、反接)下出口浓度变化的脱盐曲线图。
|
图 2 MCDI脱盐单元在不同入口孔径下2种脱附方式的脱盐曲线图 Fig. 2 Desalting curves of MCDI desalting module under different inlet aperture in two desorption methods |
从图2可看出,不同入口孔径下的吸附过程中,吸附达到的最低浓度依次分别为435.23 mol/m3,442.43 mol/m3和448.21 mol/m3,并在分别在80 s,84 s和90 s达到饱和点。因此可得,MCDI脱盐单元的出口最低浓度随入口孔径的增大而增大,且入口孔径越大,其达到吸附饱和的时间越长。不同入口孔径下的脱附过程中,无论脱附方式是短接还是反接,两者存在共同特性:就是入口孔径越小,出口最高浓度越高,脱附时间(即极板再生所需时间)越短,这是因为MCDI脱盐单元中原水溶液是从一侧电极的中部流入,简单来说,就是从一侧电极中间挖一个圆形小孔,让溶液流入,当入口孔径过大时,圆形小孔的面积就会变大,那么电极上除圆形小孔外剩下的用来与溶液接触并从中吸附离子的区域就会变小,因此导致吸附能力减弱和吸附量降低。而两者的不同点在于,同一入口孔径条件下,反接脱附方式下能够达到的最高出口浓度均高于短接脱附方式,是因为相较于电极短接,电极反接会额外提供一个反向电压,脱附时离子受到的电场力增强,其迁移速度相应变快,因此单元出口浓度也会随之增加。并且随着脱附过程出口浓度下降达至初始入口浓度后,在反向电压的作用下,极板开始反向吸附,进入到下一循坏的吸附阶段;反接脱附方式下进入下一循环中吸附达到的最低浓度分别达到431.68 mol/m3,439.7 mol/m3和445.66 mol/m3,这与前一循环的值相差不大。
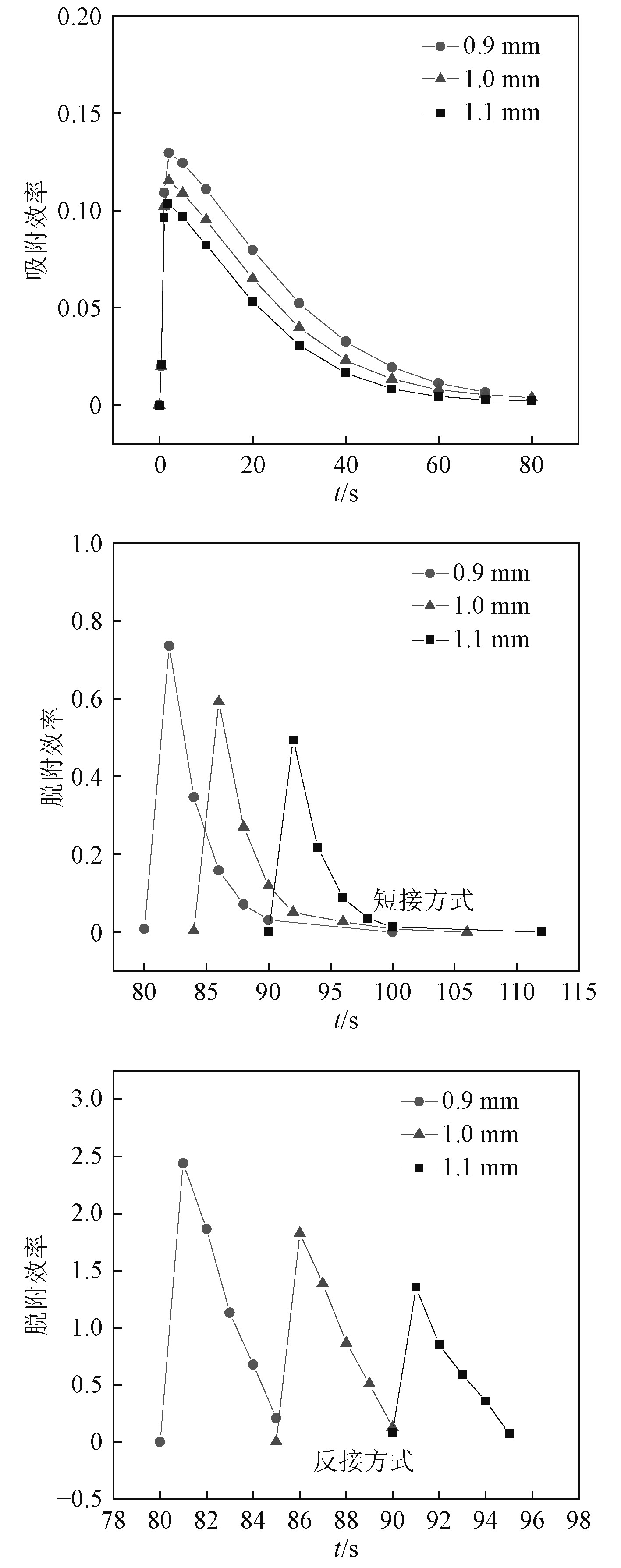
2.2.2 吸、脱附效率图3给出了不同入口孔径下MCDI脱盐单元在2种脱附方式下吸、脱附效率曲线图。
|
图 3 MCDI脱盐单元在不同入口孔径下2种脱附方式的吸、脱附效率图 Fig. 3 Adsorption and desorption efficiency charts of MCDI desalting module under different inlet aperture in two desorption methods |
从图3可以看出,随着吸附过程的进行,吸附效率曲线的趋势大致是先快速上升至峰值,再缓慢下降至0,且入口孔径越大,MCDI脱盐单元的吸附效率越小,当入口孔径为0.9 mm时,单个单元的吸附效率最高可达13%。在不同入口孔径下,脱盐单元在相应吸附饱和时间点开始脱附,且随着入口孔径的增大,脱盐单元能够达到的脱附效率峰值越大;在同一入口孔径下,除反接方式下脱附效率达到的峰值都大于短接方式以外,脱附效率经过峰值之后在短接方式下下降至零点的速度比反接慢,且历时较长,这是由于电极短接后,失去了主要电场力的作用,离子脱附时的速度受到了一些影响。
3 结 语本文在建立了中部流入式膜电容法船用海水淡化装置的三维瞬态分析模型的基础上,考察了2种不同脱附方式(短接和反接)不同入口孔径对该脱盐单元海水淡化过程的影响规律,以及出口浓度,吸、附效率随时间变化的规律,得到如下几点结论:
1)对模拟得到中部流入式MCDI脱盐模拟过程中Na+出口浓度的数值结果进行线性回归拟合研究表明,本文所建立的中部流入式膜电容法脱盐分析模型适用于对MCDI脱盐单元的数值模拟。
2)MCDI脱盐单元的出口最低浓度随入口孔径的增大而增大,且入口孔径越大,其达到吸附饱和的时间越长,但脱盐单元的吸附效率越小;随着入口孔径的增大,出口最高浓度逐渐递减,脱附时间相应增加,脱盐单元能够达到的脱附效率峰值也越大,同一入口孔径条件下,反接脱附方式下能够达到的最高出口浓度均高于短接脱附方式。
| [1] |
BIENER J, STADERMANN M, SUSS M, et al. Advanced carbon aerogels for energy applications[J]. Energy and Environmental Science, 2011, 4(03): 656-667. DOI:10.1039/c0ee00627k |
| [2] |
SIMON P, GOGOTSI Y. Materials for electrochemical capacitors[J]. Nature Materials, 2008, 7(11): 845-854. DOI:10.1038/nmat2297 |
| [3] |
SHPIGEL N, LEVI M D, SIGALOV S, et al. In situ hydrodynamic spectroscopy for structure characterization of porous energy storage electrodes[J]. Nature Materials, 2016, 15(05): 570-575. DOI:10.1038/nmat4577 |
| [4] |
GUYES E N, SHOCRON A N, SIMANOVSKI A, et al. A one-dimensional model for water desalination by flow-through electrode capacitive deionization[J]. Desalination, 2017, 415: 8-13. DOI:10.1016/j.desal.2017.03.013 |
| [5] |
F HE, BIESHEUVEL P M, BAZANT M Z, et al. Theory of water treatment by capacitive deionization with redox active porous electrodes[J]. Water Research, 2018, 132: 282-291. DOI:10.1016/j.watres.2017.12.073 |
| [6] |
JIMOH O, JERINA Z, ABDUL H, et al. A comprehensive review on recently developed carbon based nanocomposites for capacitive deionization: From theory to practice[J]. Separation and Purification Technology, 2018, 207: 291-320. DOI:10.1016/j.seppur.2018.06.046 |
| [7] |
赵飞, 苑志华, 钟鹭斌, 等. 电容去离子技术及其电极材料研究进展[J]. 水处理技术, 2016, 42(05): 38-44. |
| [8] |
BIESHEUVEL P M, ZHAO R, PORADA S, et al. Theory of membrane capacitive deionization including the effect of the electrode pore space[J]. Journal of Colloid and Interface Science, 2011, 360(01): 239-248. DOI:10.1016/j.jcis.2011.04.049 |
| [9] |
HASSANVAND A, CHEN G Q, WEBLEY P A, et al. A comparison of multicomponent electrosorption in capacitive deionization and membrane capacitive deionization[J]. Water Research, 2018, 131: 100-109. DOI:10.1016/j.watres.2017.12.015 |
| [10] |
WANG L, LIN S H. Theoretical framework for designing a desalination plant based on membrane capacitive deionization[J]. Water Research, 2019, 158: 359-369. DOI:10.1016/j.watres.2019.03.076 |
| [11] |
PORADA S, WEINSTEIN L, DASH R, et al. Water desalination using capacitive deionization with microporous carbon electrodes[J]. ACS Applied Materials and Interfaces, 2012, 4(03): 1194-1199. DOI:10.1021/am201683j |
| [12] |
ZHAO R, BIESHEUVEL P M, MIEDEMA H, et al. Charge efficiency: A functional tool to probe the double-layer structure inside of porous electrodes and application in the modeling of capacitive deionization[J]. Journal of Physical Chemistry Letters, 2010, 1(01): 205-210. DOI:10.1021/jz900154h |
| [13] |
BIESHEUVEL P M. Two-fluid model for the simultaneous flow of colloids and fluids in porous media[J]. Journal of Colloid and Interface Science, 2011, 355(02): 389-395. DOI:10.1016/j.jcis.2010.12.006 |
| [14] |
BIESHEUVEL P M, VANDERWAL A. Membrane capacitive deionization[J]. Journal of Membrane Science, 2010, 346(02): 256-262. DOI:10.1016/j.memsci.2009.09.043 |
| [15] |
LI H B, PAN L K, ZHANG Y, et al. Kinetics and thermodynamics study for electrosorption of NaCl onto carbon nanotubes and carbon nanofibres electrodes[J]. Chemical Physics Letters, 2010, 485(1-3): 161-166. DOI:10.1016/j.cplett.2009.12.031 |
 2020, Vol. 42
2020, Vol. 42
