2. 海军工程大学 船舶与海洋学院,湖北 武汉 430033
2. National Key Laboratory on Ship Vibration and Noise, Naval University of Engineering, Wuhan 430033, China
隔振和抗冲击同为舰艇生命力指标的2个重要组成部分[1]。目前,舰船上普遍使用的隔振手段是被动隔振,虽然可以依靠较小的刚度获得比较高的抗冲率,但是同时会造成附属管路的较大相对位移。工程上通常使用限位器来限制相对位移,但由于刚度突变容易带来二次冲击[2]。被动隔振系统自身特性决定了其抗冲击能力的不足,有待于进一步优化。
随着新材料的不断研发,磁流变材料因为其屈服应力高、温度适应性强、响应时间短、稳定性好、需求电压低等优点,已经广泛应用于汽车减振抗冲、房屋桥梁隔振抗冲等方面[3-6]。本文根据最优抗冲击理论,将阻尼可调节的磁流阻尼器(magnetorheological damper,简称MRD)应用于单自由度被动隔振系统,对其冲击隔离性能进行了优化,同时,针对MRD非线性强控制效果差、滑模控制容易抖振影响抗冲击性能等问题,采用模糊滑模控制的方法进行控制,取得了较好的效果。
1 最优抗冲理论针对冲击隔离特点,Sevin和Pilkey[7]提出了冲击隔离过程中抗冲系统的最优控制力模型:假设抗冲系统循序的最大加速度为A,能承受的极限位移为D,被隔离设备的质量为
如果抗冲系统中的阻尼力和弹性力能相互匹配,就可以完全或近似地实现最优抗冲力。但是被动抗冲系统阻尼力往往是恒定的,无法满足最优抗冲要求;而舰船主动隔振系统则需要能同时满足大位移、大功率和小体积等要求的作动器,目前在工程上难以实现。而随着磁流变技术的进一步发展,基于半主动控制的磁流变阻尼器隔振抗冲击系统恰恰为最优抗冲设计的实现提供了新的切实可行的解决方案。
2 隔振抗冲系统优化设计结合冲击隔离过程中各变量的变化对被动隔振系统进行抗冲击优化设计,将隔振器与MRD并联,控制MRD阻尼力输出保证阻尼力与隔振器弹性力之和基本保持恒定,近似达到最优抗冲击效果。抗冲击过程分析如下:
1)初始阶段。
系统相对位移较小但相对速度很大,隔振器弹性力较小,可以控制磁流变阻尼器提供较大的阻尼力,尽可能在冲击响应的初始阶段把抗冲击控制力提高到恒定水平附近。
2)中间阶段。
系统速度不断减小但相对位移不断增加,此时控制MRD产生合适的阻尼力与隔振器弹性力相互匹配,尽可能将抗冲击力保持恒定。
3)结束阶段。
系统速度很小而相对位移接近极大值,此时的抗冲力完全由隔振器提供,保持阻尼力为0即可在结束阶段保持理想的抗冲力。
若冲击输入为

|
图 1 磁流变阻尼器半主动抗冲击系统 Fig. 1 Semi-active shock isolation MRD system |
MRD采用Bingham模型[6]建模,如下式:
| $ f = {f_y}\operatorname{sgn} (\dot x) + {c_0}\dot x\;{\text{。}} $ | (1) |
式中:
采用实验数据进行识别可得:
| $ \begin{array}{l} f = \left( {224.64I + 155.54} \right){\mathop{\rm sgn}} (\dot x)\;+\\ (3941.41 + 2482.21)\dot x\;{\text{。}} \end{array} $ | (2) |
由此即可得到MRD阻尼力表达式,同时可以根据此式反解电流与输出阻尼力表达式。
4 模糊滑模控制器设计由图1可得系统冲击隔离的微分方程为:
| $ m\ddot x + k(x - u) + c(\dot x - \dot u) + f = 0\;, $ | (3) |
若冲击输入
| $m\ddot z + kz + c\dot z + f = - m\ddot u;\;,$ | (4) |
| $\ddot u(t) = \left\{ \begin{array}{l} U\sin ({\rm{{\text{π}}}} t/{t_m}),\\ 0\begin{array}{*{20}{c}} {\text{。}}&{} \end{array} \end{array} \right.$ | (5) |
其中:
令状态变量
| $ \left\{ \begin{array}{l} {{\dot X}} = {{AX}} + {{BU}} ,\\ {{Y}} = {{CX}} + {{DU}} {\text{。}}\\ \end{array} \right. $ | (5) |
其中:
| $ {{A}}=\left[\begin{array}{cccc} 0 & 1 & 0 & 0 \\ -\displaystyle\frac{k_{1}}{m_{1}} & -\displaystyle\frac{c_{1}}{m_{1}} & \displaystyle\frac{k_{2}}{m_{1}} & \displaystyle\frac{c_{2}}{m_{1}} \\ 0 & 0 & 0 & 1 \\ \displaystyle\frac{k_{1}}{m_{2}} & \displaystyle\frac{c_{1}}{m_{1}} & -\displaystyle\frac{k_{1}+k_{2}}{m_{2}} & -\displaystyle\frac{c_{1}+c_{2}}{m_{2}} \end{array}\right]\;{\text{,}} $ | (7) |
| $ {{B}} = {[\begin{array}{*{20}{c}} 0&{ - 1}&0&{ - 1} \\ 0&{ - \displaystyle\frac{1}{{{m_1}}}}&0&{\displaystyle\frac{1}{{{m_2}}}} \end{array}]^{\rm{T}}}\;{\text{,}} $ | (8) |
| $ {{C}} = [\begin{array}{*{20}{c}} { - \displaystyle\frac{{{k_1}}}{{{m_1}}}}&{ - \displaystyle\frac{{{c_1}}}{{{m_1}}}}&0&0 \end{array}]\;{\text{,}} $ | (9) |
| $ {{D}} = [\begin{array}{*{20}{c}} { - 1}&{ - \displaystyle\frac{1}{{{m_1}}}} \end{array}]\;{\text{,}} $ | (10) |
| $ {{U}} = {[\begin{array}{*{20}{c}} {\ddot u}&{{F_M}} \end{array}]^{\rm{T}}}\;{\text{。}} $ | (11) |
定义跟踪误差
| $ J = \int_{{t_0}}^t {\left[ {{{{e}}^{\rm{T}}}{{Qe}} + {{{u}}^{\rm{T}}}{{Ru}}} \right]} {\rm{d}}t\;{\text{。}} $ | (12) |
其中,
为了方便设计滑模控制器,将输出追踪问题转化为等价广义系统的二次型最优调节问题[8]。定义原系统的等价广义系统为:
| $ {\dot {\bar{ X}}} = {\bar{ A}{\bar {{X}}}} + {{\bar{ B}}{{U}}}\;{\text{,}} $ | (13) |
其中,
则式(12)可转化为等价的状态性能指标:
| $ J = \int_{{t_0}}^t {\left[ {{{{\bar{ X}}}^{\rm{T}}}{{\bar{ Q}{\bar {{X}}}}} + {{{u}}^{\rm{T}}}{\bar{ R}}{{u}}} \right]} {\rm{d}}t\;。$ | (14) |
其中,
| $ J = \int_{{t_0}}^t {\left[ {{{{\bar{ X}}}^{\rm{T}}}{{\bar{{ Q}}{\bar {{X}}}}}} \right]} {\rm{d}}t\;{\text{。}} $ | (15) |
此时,若存在非奇异转换矩阵
| $ {{\dot Z}} = {\bar {\bar{ A}}}{{Z}} + {\bar {\bar{ B}}}{{U}} $ | (16) |
其中,
| $ J = \frac{1}{2}\int_{{t_0}}^t {\left[ {{{{z}}_1}^{\rm{T}}{{{\bar{ Q}}}_{11}}{{{z}}_1} + 2{{{z}}_1}^{\rm{T}}{{{\bar{\bf Q}}}_{12}}{{{z}}_2} + {{{z}}_2}^{\rm{T}}{{{\bar{ Q}}}_{22}}{{{z}}_2}} \right]} {\rm{d}}t\;{\text{。}} $ | (17) |
其中,
| $ J = \int_{{t_0}}^t {\left[ {{{{z}}_1}^{\rm{T}}\left( {{{{\bar{ Q}}}_{11}} - {{{\bar{ Q}}}_{12}}{{{\bar{ Q}}}_{22}}^{ - 1}{{{\bar{ Q}}}_{12}}^{\rm{T}}} \right){{{z}}_1} + {{{h}}^{\rm{T}}}{{{\bar{ Q}}}_{22}}{{h}}} \right]} {\rm{d}}t\;{\text{,}} $ | (18) |
则对应的滑模方程为:
| $ {{{\dot z}}_1} = \left( {{{{\bar{ A}}}_{11}} - {{{\bar{ A}}}_{12}}{{{\bar{ Q}}}_{22}}^{ - 1}{{{\bar{ Q}}}_{12}}^{\rm{T}}} \right){{{z}}_1} + {{\bar{ A}}_{12}}{{h}}\;{\text{,}} $ | (19) |
得到滑模面
| $ {{ S}}\left( t \right) = {{{ K} \bar { X}}} = \left( {{{{{\bar { Q}}}}_{22}}^{ - 1}\left( {{{{}}_{12}}^{\rm{T}} + {{{{\bar { A}}}}_{12}}^{\rm{T}}{{ P}}} \right),{{{ I}}_m}} \right){{{ M}}^{ - 1}}{{ \bar { X}}}\;{\text{。}} $ | (20) |
其中,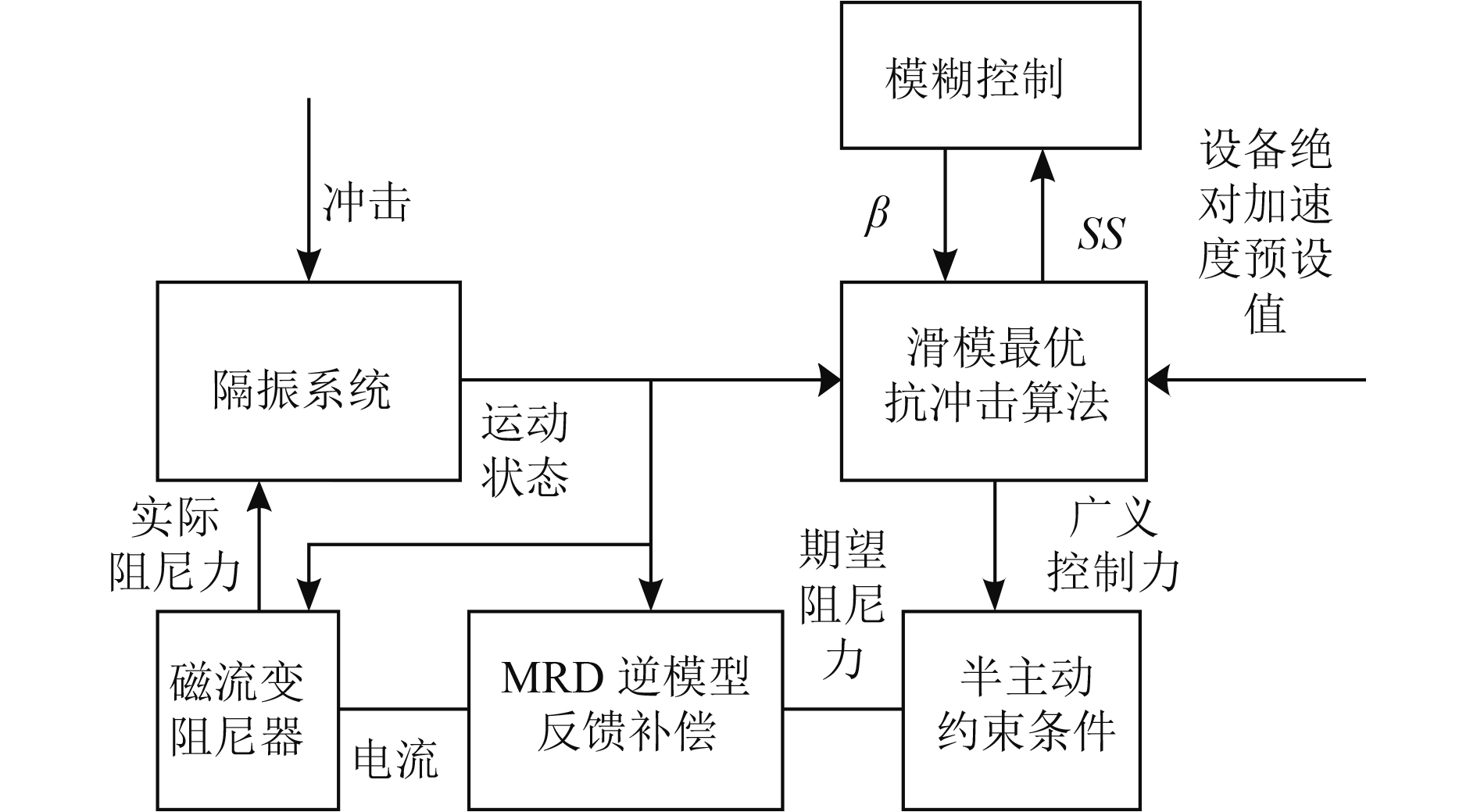 方程的解:
方程的解:
| $ \begin{aligned} & {{P}}\left( {{{{\bar{ A}}}_{11}} - {{{\bar{ A}}}_{12}}{{{\bar{ Q}}}_{22}}^{ - 1}{{{\bar{ Q}}}_{12}}^{\rm{T}}} \right) \;+\\ & \quad \quad {\left( {{{{\bar{ A}}}_{11}} - {{{\bar{ A}}}_{12}}{{{\bar{ Q}}}_{22}}^{ - 1}{{{\bar{ Q}}}_{12}}^{\rm{T}}} \right)^{\rm{T}}}{{P}} \;-\\ & \quad \quad {{P}}{{{\bar{ A}}}_{12}}{{{\bar{ Q}}}_{22}}^{ - 1}{{{\bar{ Q}}}_{12}}^{\rm{T}}{{P}} \;+\\ & \quad \quad \left( {{{{\bar{ Q}}}_{11}} - {{{\bar{ Q}}}_{12}}{{{\bar{ Q}}}_{22}}^{ - 1}{{{\bar{ Q}}}_{12}}^{\rm{T}}} \right) = 0 \end{aligned} $ | (21) |
控制器采用指数趋近方式,即
| $ {{\dot S}}(t) = \alpha {{S}}(t) + \beta sign\left( {{{S}}(t)} \right),\;\;\alpha < 0,\beta < 0\;{\text{。}} $ | (22) |
此时滑模控制率为:
| $ {{u}}\left( t \right) = - {\left( {{{K}}}{\bar {\bar {{B}}}} \right)^{{\rm{ - 1}}}}\left( {{{K}}{{\bar {\bar {{A}}}}{\bar {{X}} }}+ \alpha {{S}}(t) + \beta sign\left( {{{S}}(t)} \right)} \right)\;{\text{。}} $ | (23) |
至此,即可得到基于最优滑模变结构追踪器的控制输出。考虑到滑模控制容易导致系统产生抖振现象,输出控制中的
1)确定输入输出变量
根据滑模到达条件
2)数字量模糊化
输入变量和输出变量的取5个模糊子集{NB,NM,ZO,PM,PB}。按照如下策略选择隶属度函数,在误差较大的地方选用变化较平缓的高斯隶属度函数,保证其稳定性;在误差较小处采用变化较快的三角隶属度函数,保证其灵敏度,如图2所示。
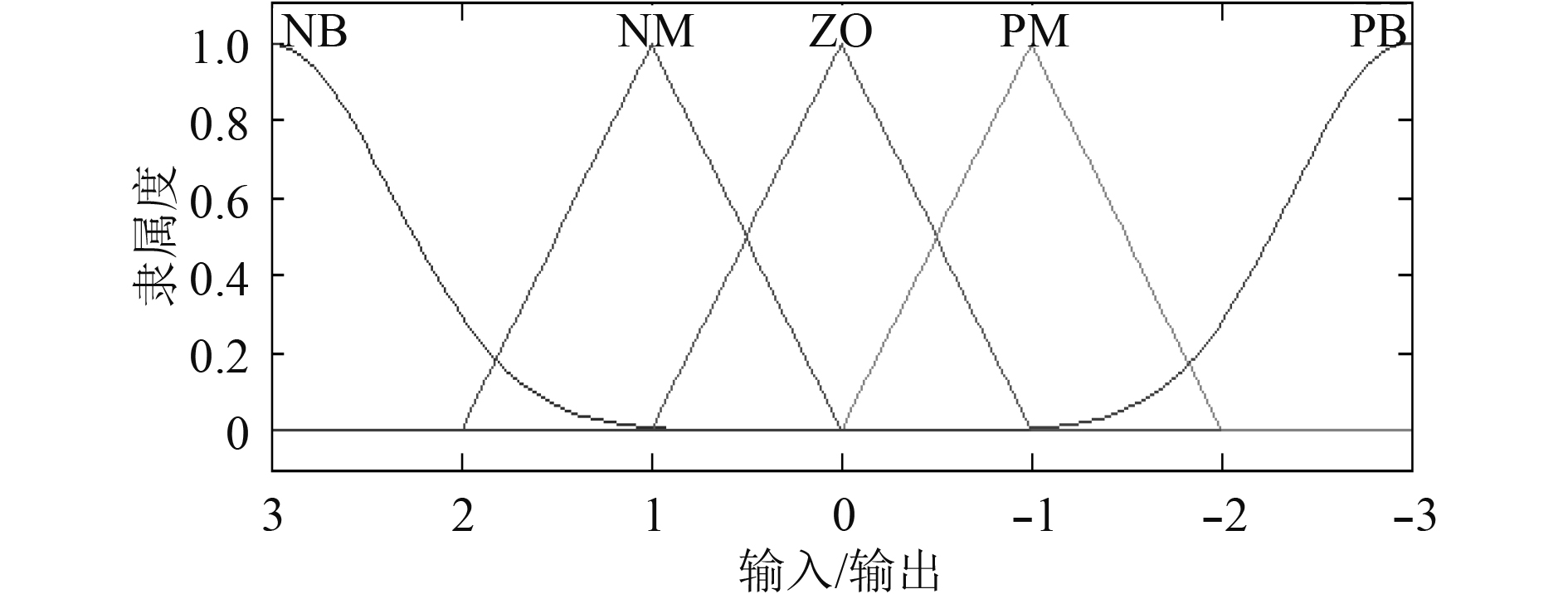
|
图 2 输隶属度函数曲线 Fig. 2 The membership function |
3)利用模糊规则进行模糊推理
模糊推理是利用模糊规则将模糊输入量转化为模糊输出的关键,
|
|
表 1 模糊控制规则表 Tab.1 The form of the fuzzy rules |
4)解模糊还原输出
目前解模糊化的方法主要有3种:最大隶属度法、中位数法和重心法。其中,重心法能使系统输出更为平滑。故本文采用重心法解模糊化,即得到输出

|
图 3 系统控制示意图 Fig. 3 The system control schematic diagram |
分别对单独使用隔振器抗冲、使用隔振器和限位器组合抗冲和采用模糊滑模半主动控制磁流变阻尼器抗冲3种情况进行抗冲击模拟仿真。其中,设备质量m=100 kg,极限加速度A=25 g,极限相对位移D=20 mm,冲击峰值U=200 g,冲击持续时间tm=20 ms,隔振器刚度k1=4×105 N/m,隔振器固有频率ω=10 Hz,隔振器阻尼系数

|
图 4 加速度对比 Fig. 4 Comparison of acceleration |

|
图 5 相对位移对比 Fig. 5 Comparison of relative displacement |
根据仿真结果可以看出,单独使用隔振器的抗冲系统有效地控制了系统的加速度峰值(15 g),但其相对位移却大大增加了(
设备冲击响应过程中,最大加速度
| $ {J_1}{J_2}/{V_0}^2 \geqslant \frac{1}{2}\;{\text{。}} $ | (24) |
通常
分别对单独使用隔振器抗冲、使用隔振器和限位器组合抗冲和采用模糊滑模半主动控制磁流变阻尼器抗冲3种情况进行极限性能的模拟仿真,仿真冲击速度从2~

|
图 6 极限性能对比 Fig. 6 Comparison of limiting performance |
通过对冲击响应和极限性能两者仿真结果的分析可以看出,单独使用隔振器或是采用隔振器和限位器组合均不能满足系统抗冲击要求。前者使得系统相对位移大大增加,后者容易造成二次冲击使得设备加速度增大,反而进一步恶化了冲击隔离环境使得系统极限性能变差。而基于最优抗冲设计的模糊滑模MRD抗冲系统,可以在限制加速度的同时,很大程度地降低相对位移,即便极限冲击情况下,该系统依然具有良好的抗冲击性能。
6 结 语本文依据最优抗冲理论对现有的被动隔振系统进行抗冲击优化,设计了由隔振器和MRD并联的半主动最优抗冲系统,并采用模糊滑模控制器,解决了磁流变阻尼器非线性强难以控制的问题,提升了系统抗冲击效果。通过模拟仿真对比可以看出,相比现有的抗冲击设计,基于模糊滑模控制的MRD半主动最优抗冲设计可以同时抑制冲击加速度和减小设备位移,并且具有更好的极限性能。该研究对于磁流变技术进一步应用于舰船隔振抗冲实践具有较好的指导意义。
| [1] |
汪玉, 华宏星. 舰船现代冲击理论及应用[M]. 北京: 科学出版社, 2005: 1-16, 66-68.
|
| [2] |
胡铂. 基于磁流变阻尼器的半主动悬架控制策略研究[D]. 杭州: 浙江大学, 2017.
|
| [3] |
周文亮, 王强. 冲击隔离发展浅谈[J]. 噪声与振动控制, 2002(5): 22-25. DOI:10.3969/j.issn.1006-1355.2002.05.006 |
| [4] |
陈昭晖, 陈宝春. 斜拉索-磁流变阻尼器系统的频域自适应控制[J]. 福州大学学报(自然科学版), 2017(04): 459-465. |
| [5] |
于漪丁. 小型磁流变飞机起落架建模与缓冲控制研究[D]. 沈阳: 沈阳航空航天大学, 2018.
|
| [6] |
张磊. 基于磁流变阻尼器的飞机起落架控制方法研究[D]. 天津: 中国民航大学, 2017.
|
| [7] |
SEVIN E, PILKEV W D. Optimum shock and vibration isolation[M]. Shock and Vibration Information Analysis Center, Washington, DC, 1971.
|
| [8] |
刘金锟. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005.
|
| [9] |
孙静. 模糊滑模控制的研究[M]. 北京: 北京化工大学, 2003.
|
 2020, Vol. 42
2020, Vol. 42
