0 引　言

推进系统是水下机器人的重要组成部分，对水下机器人的作业具有重要影响。为保障水下机器人的作业安全，需要对推进系统的状态进行在线监测和故障诊断。

通过水下机器人的速度、航向、以及控制量等信息，可以对其运动状态或相关参数进行估计。当推进系统出现故障，会使运动状态的测量值偏离估计值或相关参数的估计值出现异常。上述原理是水下机器人故障诊断算法设计的主要依据之一，相关方法主要包括基于解析模型的观测器^[1-2]、滤波器^[3-5]方法和基于数据模型的神经网络^{[6- 7]}、支持向量机^[8]方法等。在实际应用中，上述方法存在以下问题：

1）基于“故障引起水下机器人的运动发生异常变化”这一现象来诊断故障，而海流等环境因素也会对水下机器人的运动状态造成影响，上述方法难以区分实际故障和海流干扰的影响。

2）一般依赖于精确的系统模型或完备的训练数据。文献[1-2]中观测器的设计、文献[4]中平方根无色卡尔曼滤波的时间更新过程、文献[3-5]中粒子滤波实现过程中状态转移先验概率分布的获取，都需要精确的系统模型。但实际应用中，获取水下机器人精确的数学模型往往较为困难。文献[6-8]中，基于数据对状态估计模型进行训练的过程属于有监督学习，只有当训练数据覆盖足够多的系统状态时，才能够得到满足实际应用需求的结果。

3）一般采用较为固定的算法参数或模型，不具备自适应调整能力。而在实际作业中，水下机器人的作业环境和系统配置都有可能随时间或作业任务而变化^[9-10]，导致新的系统模型和故障类型出现^[11]。因此，有必要在应用中对算法相关参数或模型进行在线调整^[9]。

针对现有方法中存在的不足，本文提出一种具有在线学习和自适应能力的水下机器人推进系统故障诊断方法。该方法基于数据在线建立推进器的转速模型，在建模过程中对模型结构和建模数据进行在线优化，并且在模型残差变大时对模型进行在线更新。该方法对作业环境和系统自身变化的影响具有较强的自适应性，不需要水下机器人的数学模型和系统的详细信息，不需要进行离线训练。此外，该方法还对推进系统的控制时延进行在线识别，有助于在系统存在不确定时延的情况下提高建模精度，进一步提高算法的自适应能力和实用性。

1 推进系统时延估计

时延在机电系统中广泛存在，对于水下机器人来说，在基于数据进行建模或基于残差进行故障诊断时，如果不考虑时延，将对结果造成影响，但目前多数水下机器人故障诊断方法^[1-7]并未对系统中存在的时延进行明确处理。本文通过对控制量和执行机构对应动作测量值之间的相关性变化趋势进行分析，实现时延估计。该方法完全基于数据进行，不需要系统的模型，且能够实现在线估计。

记某时间段内控制系统输出的控制量为 $U = ({u_1},{u_2}, \cdots ,{u_N})$ ，对应时间段内执行机构动作的测量值为 $V = ({v_1},{v_2}, \cdots ,{v_N})$ ，则该时间段内控制量与动作测量值之间的Pearson相关系数为：

$r(U,V) = \frac{{\sum\limits_{i = 1}^N {({u_i} - \bar u)({v_i} - \bar v)} }}{{\sqrt {\sum\limits_{i = 1}^N {{{({u_i} - \bar u)}^2}} \sum\limits_{i = 1}^N {{{({v_i} - \bar v)}^2}} } }}{\text{,}}$

(1)

式中 $\bar u,\bar v$ 分别为该时间段内控制量和测量值的均值。

假设该时间段内，控制量与动作测量值之间的时延为 $\tau $ 个采样周期， $\tau = 0,1, \cdots ,{\tau _{\max }}$ 。按照假设的时延对控制量和动作测量值进行重新对准，从对准后的数据中，分别取 ${U_\tau } = ({u_1},{u_2}, \cdots ,{u_{N - {\tau _{\max }}}})$ 、V_τ= (v_τ+1, v_τ+2, ··· , v_τ+N_−τmax)，计算对应的相关系数：

${r_\tau } = r({U_\tau },{V_\tau }),\tau = 0,1, \cdots ,{\tau _{\max }}{\text{,}} $

(2)

按照上述步骤，依次计算不同假设时延下重新对准后数据的相关系数，当相关系数为极大值时，对应的时延即为控制量与执行机构动作测量值之间时延的估计值 $\hat \tau $ ，即

$\hat \tau = \mathop {\arg \max }\limits_{\tau = 0,1, \cdots ,{\tau _{\max }}} {r_\tau }{\text{。}}$

(3)

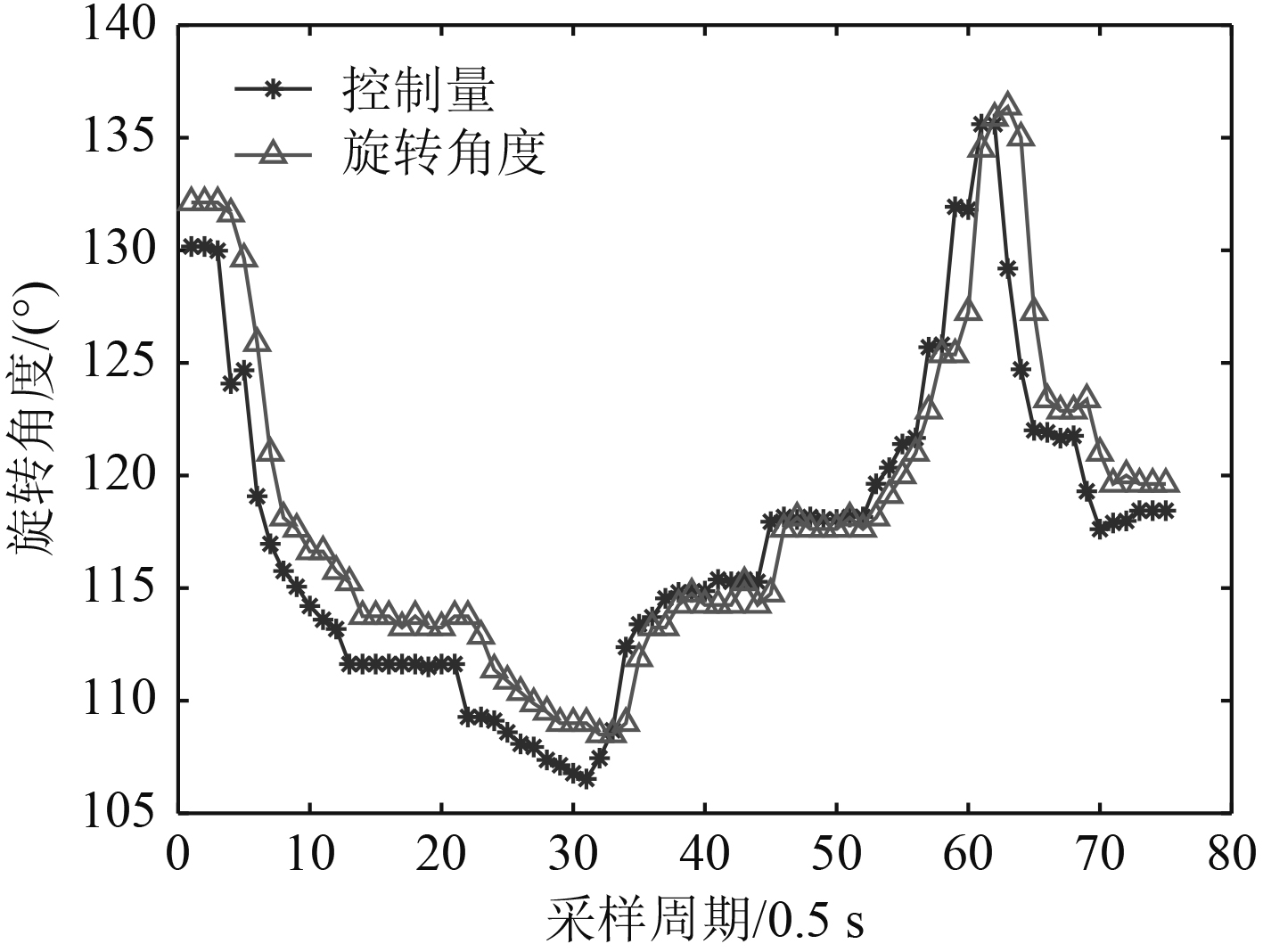
以“海斗”号ARV海试过程中某时间段内的数据为例，对本文时延估计算法进行验证。图1为该时间段内可旋转推进器^[12]旋转电机的控制量与旋转电机角度测量值之间的关系曲线，图2为假为假设时延从0~15变化时相关系数的变化曲线，对应的相关系数在 $\tau = 2$ 时取得极大值，即时延的估计值为2个采样周期。相邻的时间段内，对该旋转电机输入了大幅度阶跃信号，输入阶跃信号前后角度测量值的变化情况如表1所示。由表1可知，在第5个采样周期输入阶跃信号后，旋转电机角度在第7个采样周期开始出现明显的变化，即时延约为2个采样周期，与算法估计结果一致。

2 推进系统在线建模

转速是表征推进器状态的重要参数，对于合理设计的推进器来说，正常工作情况下，海流等环境因素的干扰并不会对推进器的转速造成严重影响。如果以转速的异常变化为依据来设计推进系统故障检测算法，则能够有效排除海流等环境因素的干扰。

受多方面因素影响，推进器控制量与转速之间的关系存在非线性，并且会随作业状态的不同发生变化。因此，本文采用便于在线实现的多项式拟合^[13]来对推进器控制量与转速之间的关系模型。

在多项式拟合过程中，模型的阶次是需要重点考虑的问题。此外，水下机器人作业过程中，作业环境和系统自身会随时间发生一定变化，进而引起系统模型的变化。因此，在进行建模时，还需要选择适当的数据量。本文通过粒子群算法来进行模型阶次和建模数据量的在线优化，推进系统在线建模具体实现流程如下：

步骤1　水下机器人作业过程中，在线获取一定量的推进器控制量和转速数据。为提高建模精度，要求获取的数据中，推进器控制量包含一定的变化。

步骤2　根据获取的数据，采用本文推进系统时延在线估计方法，估计当前状态下推进系统时延。

步骤3　根据时延估计值 $\hat \tau $ ，对推进器控制量和转速数据进行重新对齐：

$\left\{ \begin{array}{l} {U_{\hat \tau }} = ({u_1},{u_2}, \cdots ,{u_{N - \hat \tau }}) \text{，} \\ {V_{\hat \tau }} = ({v_{\hat \tau + 1}},{v_{\hat \tau + 2}}, \cdots ,{v_N}) \text{。} \\ \end{array} \right.$

(4)

步骤4　采用粒子群优化算法，对推进器模型阶次 $q$ 和建模使用的数据量 $w$ 进行优化， $1 \leqslant q \leqslant {q_{\max }}$ ， ${w_{\min }} \leqslant w \leqslant {w_{\max }}$ 。在对粒子的适应度进行评价时，采用数据集：

$\left\{ \begin{array}{l} {U_{\hat \tau ,w}} = ({u_{N - \hat \tau - w + 1}},{u_{N - \hat \tau - w + 2}}, \cdots ,{u_{N - \hat \tau }})\text{，} \\ {V_{\hat \tau ,w}} = ({v_{N - w + 1}},{v_{N - w + 2}}, \cdots ,{v_N})\text{，}\\ \end{array} \right.$

(5)

通过 $q$ 阶多项式拟合建立转速模型 $\hat v = {F_{q,w}}(u)$ ，采用平均绝对百分误差（MAPE）对模型进行评价

$f_{q,w}^{{\rm{MAPE}}}({U_{\hat \tau ,w}},{V_{\hat \tau ,w}}) = \frac{1}{{{N_{\hat \tau ,w}}}}\sum\limits_{i = 1}^{{N_{\hat \tau ,w}}} {\left| {\frac{{{v_i} - {{\hat v}_i}}}{{{v_i}}}} \right|}\text{，} $

(6)

位置在 $(q,w)$ 的粒子适应度取值为：

${f_{q,w}} = \max (f_{q,w}^{{\rm{MAPE}}}({U_{\hat \tau ,w}},{V_{\hat \tau ,w}}),f_{q,w}^{{\rm{MAPE}}}({U_{test}},{V_{test}}))\text{。}$

(7)

其中， $({U_{test}},{V_{test}})$ 为从 $({U_{\hat \tau }},{V_{\hat \tau }})$ 中取的公用测试数据。

步骤5　根据当前数据集下得到的最优建模参数 $({q^*},{w^*})$ ，通过多项式拟合，建立推进器转速模型 $\hat v = {F_{{q^*},{w^*}}}(u)$ 。

通过上述步骤，即可在线建立能够描述当前作业状态下推进器控制量与转速之间关系的推进系统模型，用于推进系统故障的诊断。

3 基于模型在线更新的自适应故障诊断 3.1 推进系统模型在线更新

通过优化在线建立当前作业状态下的推进系统模型之后，接下来的作业过程中，将推进器控制量输入模型，得到转速估计值。将t时刻的推进器转速测量值与对应的转速估计值对比，能够得到推进系统的模型残差

${e_t} = {v_t} - {F_{{q^*},{w^*}}}({u_{t - \hat \tau }})\text{，}$

(8)

水下机器人作业过程中，作业环境和系统自身会随时间发生一定变化，进而引起系统模型的变化。这会导致之前建立的模型与实际系统模型之间出现差异，进而导致模型残差逐渐增大。

得益于本文提出的推进系统建模方法能够在线优化和在线实现的特性，本文设计了一种模型在线更新机制。当模型残差增大到一定程度时，重新启动在线建模过程，利用最新获取的一批数据，建立新的推进系统模型，实现模型的在线更新。

3.2 推进系统故障自适应诊断

水下机器人作业过程中，假设目前正在使用第k次在线建模得到的模型来对推进系统状态进行监测。若在t时刻，发现模型残差

$e_t^k{\rm{ = }}{v_t} - F_{q_k^*,w_k^*}^k({u_{t - {{\hat \tau }_k}}})\text{，}$

(9)

超过限度。此时，对模型进行在线更新，得到新的模型 $F_{q_{k + 1}^*,w_{k + 1}^*}^{k + 1}({u_{t - {{\hat \tau }_{k + 1}}}})$ ，计算t时刻新模型的残差

$e_t^{k + 1}{\rm{ = }}{v_t} - F_{q_{k + 1}^*,w_{k + 1}^*}^{k + 1}({u_{t - {{\hat \tau }_{k + 1}}}})\text{。}$

(10)

模型在线更新过程中，由于对建模参数进行了优化，因此得到的新模型 $F_{q_{k + 1}^*,w_{k + 1}^*}^{k + 1}({u_{t - {{\hat \tau }_{k + 1}}}})$ 能够比原模型 $F_{q_k^*,w_k^*}^k({u_{t - {{\hat \tau }_k}}})$ 更好的拟合建模数据。

在没有出现故障的情况下，可以认为推进系统实际模型在短期内近似不变。可以认为t时刻对应的数据 $({u_{t - {{\hat \tau }_{k + 1}}}},{v_t})$ 与近期获取的其他建模数据来自于同一个系统，都能够较好的符合新模型 $F_{q_{k + 1}^*,w_{k + 1}^*}^{k + 1}({u_{t - {{\hat \tau }_{k + 1}}}})$ 。因此，针对t时刻的数据，新模型的残差应明显小于原模型的残差。

若在t时刻检测到模型残差超过限度，对模型在线更新后，得到的新模型在t时刻的残差明显减小，则说明原模型残差超过限度是由于系统渐变或噪声引起的，系统并未出现故障。

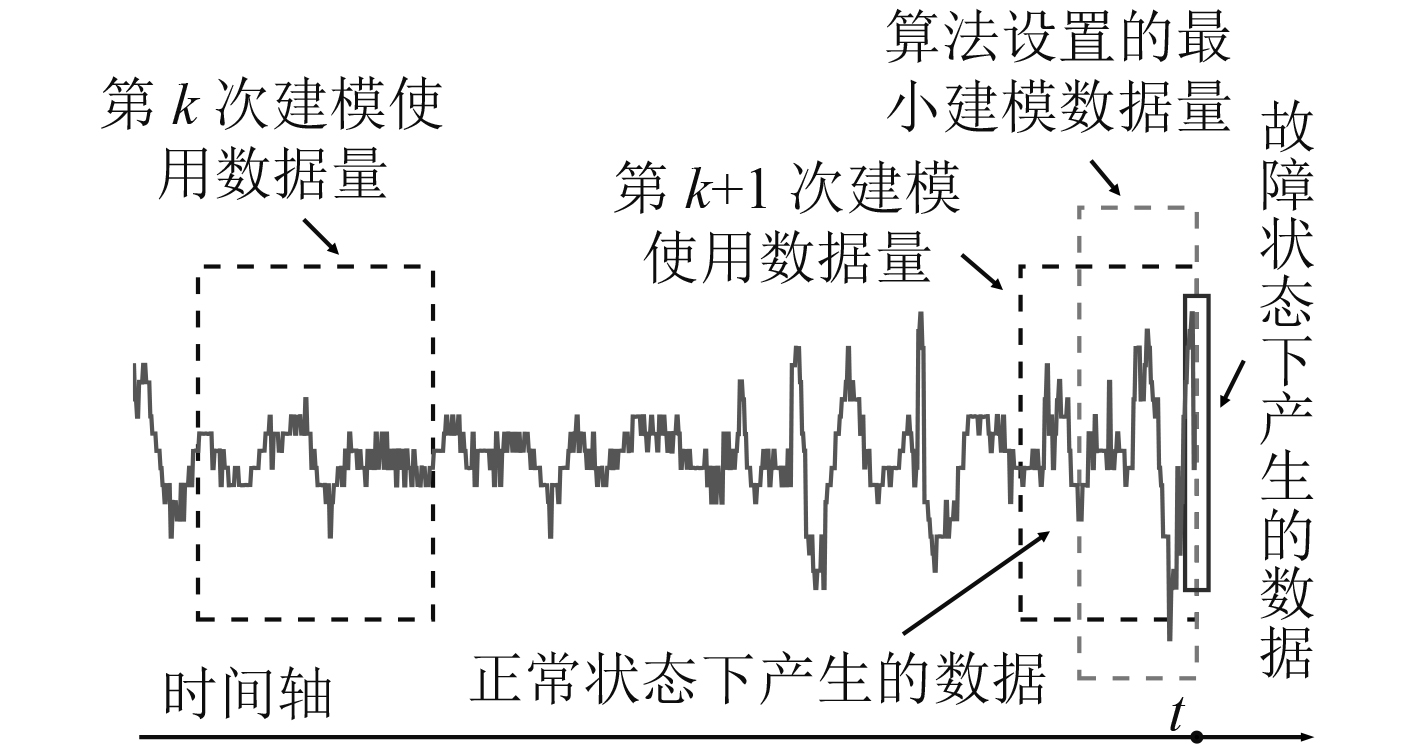
若t时刻推进系统出现了故障，则会导致t时刻故障状态下产生的数据与近期正常状态下获得的数据来自不同的系统。如图3所示，在进行模型更新时，由于算法设置了最小建模数据量 ${w_{\min }}$ ，第k+1次在线建模时，使用的建模数据大部分是正常状态下产生的数据，只有极少部分是故障状态下产生的数据。因此，得到的新模型对正常状态下产生的数据拟合效果较好，对故障状态下产生的数据拟合效果较差。这种情况下，新模型在t时刻的残差相对原模型并不会明显减小，残差仍然会超出限度。

结合以上分析，推进系统故障检测规则如下：

1）若模型残差小于限度，则未出现故障。

2）若t时刻模型残差超出限度，模型在线更新后，新模型在t时刻的残差与原模型相比明显变小，则未出现故障。

3）若t时刻模型残差超出限度，模型在线更新后，新模型在t时刻的残差与原模型相比没有明显减小，则模型仍需要进行在线更新。利用t+1时刻数据对模型在线更新后，若模型残差仍没有明显减小，则判断系统在t时刻出现故障。

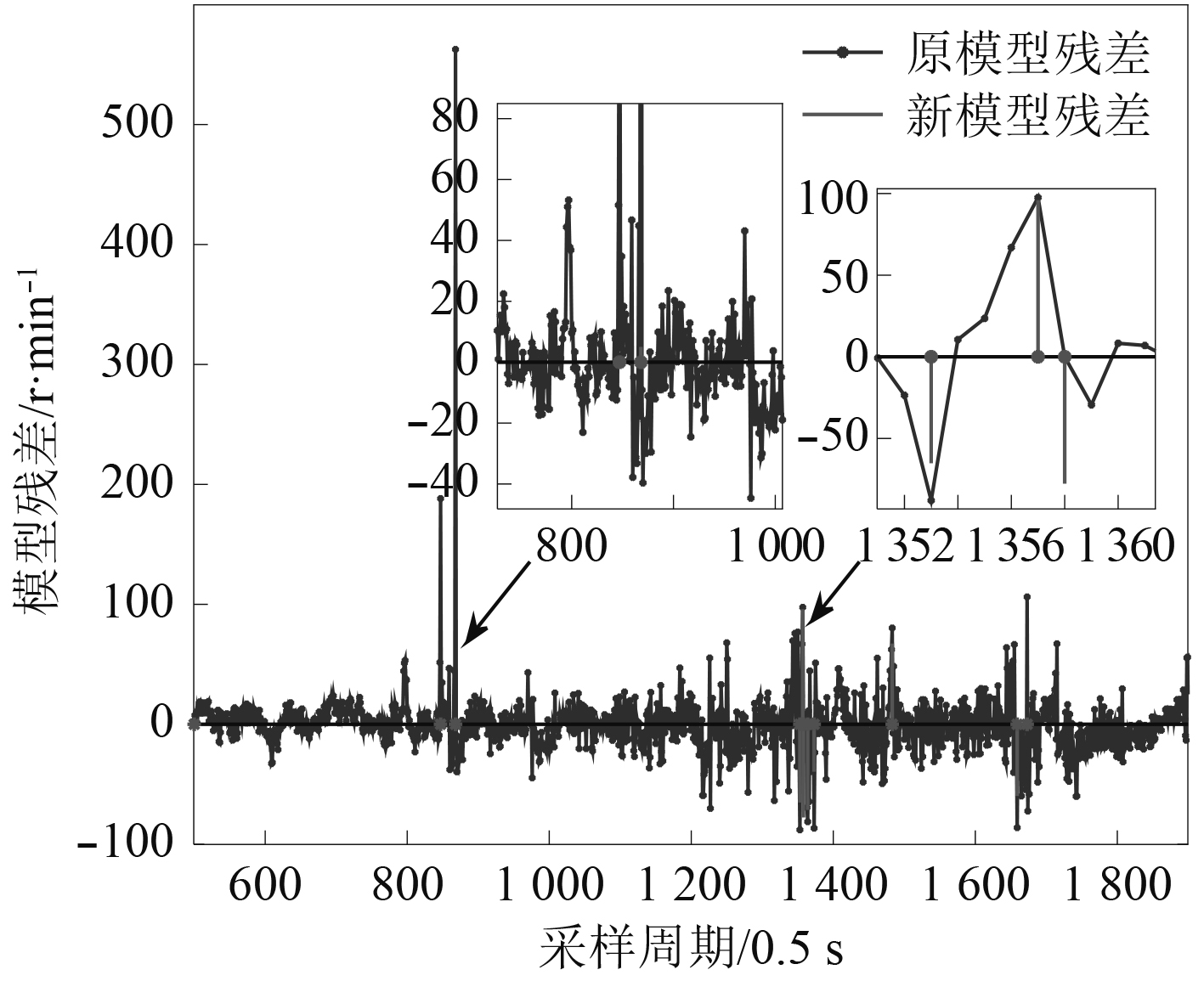
4 实验验证 4.1 海试数据验证

以“深海勇士号”HOV某次海试中采集的数据对本文算法进行测试，得到故障检测过程中某时间段的模型残差如图4所示。由于深海作业过程中干扰因素较多，模型残差波动剧烈，为减少模型在线更新次数降低运算负担，模型残差限度设置为 $\left| {{e_t}} \right| \leqslant 80$ 。算法中设置的建模数据量范围 ${w_{\min }} = 50,{w_{\max }} = 500$ ，作业过程中，采集到500组数据以后，即可以开始进行在线故障检测。

本次海试过程中，推进系统实际上没有故障发生。图4中，第847和第868个采样周期，由于干扰因素影响，模型残差远远超出限度。利用本文提出的模型在线更新机制对模型进行在线更新后，对应时刻新模型的残差都降低到0附近，排除了故障发生的可能。

第1 357个采样周期，检测到模型残差超限，在对模型进行在线更新后，新模型的残差未见明显减小。因此，算法在获得第1 358个采样周期的数据后，第2次对模型进行在线更新。鉴于第1 358个采样周期的残差相比第1 357个采样周期有明显减小，算法排除了故障发生的可能。由于第2次更新后的模型在第1 358个采样周期的残差低于限度，继续采用该模型用于后续的状态监测。在后续的第1 359～1 361个采样周期，模型残差均为较小值，进一步验证了当前无故障发生。

在基于海试数据的故障检测过程中，虽然受作业环境等各方面因素影响导致模型残差波动剧烈，但并没有故障误报的情况发生。

4.2 实际故障验证

海试过程中，实际故障一般难以遇到，而人为制造故障又存在较大安全风险。因此，本文研究过程中，以某推进器为对象，在水池实验中制造实际故障对本文算法进行验证。

水池实验过程中，通过随机拖动实验平台来模拟水下机器人运动状态变化的影响，通过注水和利用池壁反射推进器尾流等方式形成乱流来模拟海流等环境因素影响，通过使推进器吸入布条来模拟作业过程中螺旋桨被渔网、水草等异物缠绕故障。

水池实验过程中通过本文算法进行在线故障检测得到的模型残差数据如图5所示，算法中模型残差限度设置为 $\left| {{e_t}} \right| \leqslant 8$ ，建模数据量范围 ${w_{\min }} = 50, {w_{\max }} = 500$ 。实验开始时，推进系统工作在无故障状态。在第1 280个采样周期附近，使推进器吸入第1批布条，推进系统出现故障。在第1 380个采样周期附近，使推进器吸入第2批布条，推进系统的故障状态发生变化。

由图5可知，从第500个采样周期建立模型进行故障检测开始，到第1 280个采样周期期间，分别在第698和第1 096个采样周期出现了模型残差超限的情况。经模型在线更新后，新模型的残差明显减小，算法判断推进系统未出现故障。

在第1 280个采样周期附近，推进器吸入布条，出现螺旋桨被异物缠绕的故障。由图5可知，在第1 282个采样周期，模型残差超限。此时，算法启动模型在线更新机制对模型进行更新，但新模型的残差仍然超限。因此，算法在得到第1 283个采样周期的数据后，对模型进行第2次在线更新。由图5可知，第2次更新后，在第1 283个采样周期模型残差并未明显减小。至此，算法判断出推进系统在第1 282个采样周期出现故障。

检测到系统出现故障后，由于模型残差持续超限，算法持续对模型进行在线更新。按照本文之前的分析，在出现故障后对模型进行更新时，随着时间的推移，建模数据中故障状态下产生的数据会越来越多，因此在线建立的模型会越来越接近故障状态下的系统模型，进而会使模型残差逐渐减小。观察图5中第1 283～1 324个采样周期对应的新模型残差可以发现，模型残差的变化趋势很好符合了上述分析。在线建模过程直至第1 324个采样周期才结束，共持续了约43个采样周期，与本文算法中设置的最小建模数据量接近。此时，算法已经通过在线学习，建立了一个故障状态下的系统模型。

在第1 380个采样周期附近，推进器吸入第2批布条，推进系统的故障状态发生变化，相当于出现了新的故障。本文算法同样成功检测到了新故障的出现，并在之后的一段时间里基于数据学习到了新故障状态下的模型。本文算法对故障模型的学习，进一步证明了算法的在线学习能力和对作业环境及系统自身状态变化的自适应能力。

5 结　语

本文针对水下机器人推进系统故障诊断中存在的问题，提出了一种具有自适应能力的故障诊断方法，主要成果包括以下几个方面：

1）提出一种基于在线学习的故障检测框架，主要内容包括基于运行数据的在线建模、基于优化的模型在线更新和基于模型在线更新的自适应故障检测。该故障检测框架具有较好的通用性，在基于电流等其他状态参数进行故障检测时同样适用。

2）针对推进系统控制量与转速之间的时间延迟问题，采用一种基于相关性变化趋势分析的时延估计方法。该方法不需要系统详细信息，不影响系统的正常作业，且能够在线运行，因此在系统时延可能随时间变化的场合具有明显优势。