随着人类对海洋资源不断地开发利用,AUV成为探索海洋的重要载体,AUV对接回收是AUV实现工作续航、数据交换的有效方式。通过AUV与水下回收机构的连接,使AUV在能源耗尽前能够及时得到能源补充,并且将采集到的数据及时上传,进行数据交换。2000年,美国Woods Hole海洋研究所研制了第一代REMUS水下对接系统[1];2007年,美国的蒙特利湾海洋研究所研制了Bluefin水下对接基站[2];2012年,挪威康斯伯格海事公司针对其商业化的产品REMUS-100型号AUV设计了拖拽式对接系统[3];国内浙江大学流体动力与机电系统国家重点实验室和杭州电子科技大学联合研制了一种远距离采用声学引导、近距离采用光学引导模型的水下对接系统[4];2015年,哈尔滨工程大学研制了自治式潜器搭载对接基站[5]。
AUV成功对接是AUV续航、数据交换的重要环节。在实际对接过程中,由于水动力的影响,AUV经常在对接时偏离预定对接轨道,与对接装置的导向罩发生碰撞。目前对AUV碰撞的研究较少,文献[6]利用ADAMS软件仿真分析了影响AUV碰撞的不同影响因素。文献[7] 分析了船舶与海洋平台碰撞的外部动力学问题,研究了在水深、风、浪、流联合作用下的碰撞情况。文献[8]对半潜式平台进行合理的简化和假设,分析得到其碰撞力表达式,并研究船舶吸能与平台的吸能情况。文献[9]利用有限元软件Ls-dyna对某半潜式海洋平台在标准船体不同速度下的碰撞进行了分析。文献[10] 针对对接装置中导向罩的形状,建立回收过程中AUV 的接触碰撞模型。
本文以AUV与对接装置发生的碰撞为研究对象,建立AUV的水动力模型及接触碰撞模型,利用ADAMS软件对AUV与导向罩的碰撞过程进行动力学仿真分析,研究AUV初速度、导向罩开口角度、AUV与对接装置的偏心距以及AUV中心与对接装置中轴线的偏角这4个因素对碰撞过程的影响,得到相应的最大碰撞力,并分析实际对接过程需注意的事项。最后根据仿真的数据利用多元非线性回归方程,得出最大碰撞力与AUV初速度、导向罩开口角度、AUV与对接装置的偏心距以及AUV中心与对接装置中轴线的偏角之间的回归方程,为之后实际对接装置优化提供参考。
1 对接过程动力学模型的构建 1.1 AUV水动力建模水下机器人的水动力极其复杂,它的大小与水下机器人的外形,水下机器人的运动速度、加速度,流体介质的物理特性和几何特性与操纵要素有关。水下机器人的水动力主要分为惯性类水动力和粘性类水动力[11],其中惯性类水动力与水下机器人的加速度有关,粘性类水动力与水下机器人的运动速度有关。
1.1.1 惯性类水动力惯性类水动力与载体运行的加速度和角加速度呈线性关系,六自由度的水下机器人,惯性类水动力有36项,表示为:
| ${f_i} = - \sum\limits_{j = 1}^6 {{m_{ij}}{{\dot v}_j}} \text{。}$ | (1) |
其中,
惯性类水动力用加速度系数的有因次形式来表示为:
| $ \begin{gathered} \tiny \left[ {\begin{array}{*{20}{c}} X \\ Y \\ Z \\ K \\ M \\ N \end{array}} \right] = \hfill \\ - \tiny \left[ \!\!\!\!{\begin{array}{*{20}{c}} {\frac{1}{2}\rho {L^3}{{X'}_{\dot u}}}&0&0&0&0&0 \\ 0&{\frac{1}{2}\rho {L^3}{{Y'}_{\dot v}}}&0&0&0&{\frac{1}{2}\rho {L^4}{{N'}_{\dot v}}} \\ 0&0&{\frac{1}{2}\rho {L^3}{{Z'}_{\dot w}}}&0&{\frac{1}{2}\rho {L^4}{{M'}_{\dot w}}}&0 \\ 0&0&0&{\frac{1}{2}\rho {L^5}{{K'}_{\dot p}}}&0&0 \\ 0&0&{\frac{1}{2}\rho {L^4}{{Z'}_{\dot q}}}&0&{\frac{1}{2}\rho {L^5}{{M'}_{\dot q}}}&0 \\ 0&{\frac{1}{2}\rho {L^4}{{Y'}_{\dot r}}}&0&0&0&{\frac{1}{2}\rho {L^4}{{N'}_{\dot r}}} \end{array}} \!\!\!\!\right]\left[ \!\!\!\!{\begin{array}{*{20}{c}} {\dot u} \\ {\dot v} \\ {\dot w} \\ {\dot p} \\ {\dot q} \\ {\dot r} \end{array}} \!\!\!\!\right] \text{。} \end{gathered} $ | (2) |
粘性类水动力与物体的运动速度有关,包括线性和非线性项的粘性类水动力,在水平面和垂直面的运动会相互影响,因而产生耦合的水动力项。
| ${{F}} = [X,Y,Z,K,M,N]'\text{。}$ |
其中:
| $ \begin{split} X = & {X_{uu}}{u^2} + {X_{vv}}{v^2} + {X_{ww}}{w^2} + {X_{rr}}{r^2} + {X_{qq}}{q^2} + \\ & {X_{vr}}vr + {X_{wq}}wq + {X_{pr}}pr + {X_{wp}}wp\text{,} \\ \end{split} $ | (3) |
| $ \begin{split} Y = & {Y_0} + {Y_v}v + {Y_r}r + {Y_{r\left| r \right|}}r\left| r \right| + {Y_p}p + {Y_{p\left| p \right|}}p\left| p \right| + \\ & {Y_{vw}}vw + {Y_{v\left| v \right|}}v\left| {\sqrt {{v^2} + {w^2}} } \right|{\rm{ + }}{Y_{v\left| r \right|}}\frac{v}{{\left| v \right|}}\left| {\sqrt {{v^2} + {w^2}} } \right|\left| r \right|+ \\ &{Y_{vq}}vq + {Y_{wp}}wp + {Y_{pq}}pq + {Y_{wr}}wr + {Y_{qr}}qr\text{,} \end{split} $ | (4) |
| $ \begin{split} Z = & {Z_0} + {Z_w}w + {Z_q}q + {Z_{q\left| q \right|}}q\left| q \right| + {Z_{ww}}{w^2} + {Z_{vv}}{v^2} + {Z_{rr}}{r^2}+ \\ & {Z_{pp}}{p^2} + {Z_{w\left| w \right|}}w\left| {\sqrt {{v^2} + {w^2}} } \right|{\rm{ + }}{Z_{ww}}\left| {w\sqrt {{v^2} + {w^2}} } \right|+ \\ & {Z_{w\left| q \right|}}\frac{w}{{\left| w \right|}}\left| {\sqrt {{v^2} + {w^2}} } \right|\left| q \right| + {Z_{wq}}wq + {Z_{vp}}vp + \\ & {Z_{pr}}pr + {Z_{vr}}vr + {Z_{\left| w \right|}}\left| w \right| \text{,} \\[-13pt] \end{split} $ | (5) |
| $ \begin{split} K = & {K_0} + {K_v}v + {K_r}r + {K_{r\left| r \right|}}r\left| r \right| + {K_p}p + {K_{p\left| p \right|}}p\left| p \right| + \\ & {K_{vw}}vw + {K_{v\left| v \right|}}v\left| {\sqrt {{v^2} + {w^2}} } \right|{\rm{ + }}{K_{vq}}vq + {K_{wp}}wp + \\ & {K_{wr}}wr + {K_{pq}}pq + {K_{qr}}qr \text{,} \end{split} $ | (6) |
| $ \begin{split} M = & {M_0} + {M_w}w + {M_q}q + {M_{q\left| q \right|}}q\left| q \right| + {M_{ww}}{w^2} + {M_{vv}}{v^2}+ \\ & {M_{vr}}vr + {M_{rr}}{r^2} + {M_{pp}}{p^2} + {M_{w\left| w \right|}}w\left| {\sqrt {{v^2} + {w^2}} } \right|+ \\ & {\rm{ }}{M_{ww}}\left| {w\sqrt {{v^2} + {w^2}} } \right| + {M_{w\left| q \right|}}\frac{w}{{\left| w \right|}}\left| {\sqrt {{v^2} + {w^2}} } \right|\left| q \right|{M_{wq}}wq + \\ & {M_{vp}}vp + {M_{pr}}pr + {M_{\left| w \right|}}w \text{,}\\[-13pt] \end{split} $ | (7) |
| $ \begin{split} N = & {N_0} + {N_v}v + {N_r}r + {N_{r\left| r \right|}}r\left| r \right| + {N_p}p + {N_{p\left| p \right|}}p\left| p \right|+ \\ & {N_{vw}}vw + {N_{v\left| v \right|}}v\left| {\sqrt {{v^2} + {w^2}} } \right|{\rm{ + }}{N_{v\left| r \right|}}\frac{v}{{\left| v \right|}}\left| {\sqrt {{v^2} + {w^2}} } \right|\left| r \right|+ \\ & {N_{vq}}vq + {N_{wp}}wp + {N_{pq}}pq + {N_{qr}}qr + {N_{wr}}wr \text{。} \end{split} $ | (8) |
根据经典碰撞理论,对系统作如下假设:
假设1 碰撞时间无限小;
假设2 碰撞过程中AUV及其对接装置位姿保持不变;
假设3 碰撞是点接触;
假设4 碰撞过程中AUV及其对接装置形状和惯量保持不变。
在以上假设的基础上可以认为碰撞过程中产生的冲击力是一个大小和方向一定的量。AUV碰撞力可分为垂直于导向罩接触面的碰撞力
| $F = {F_n} + {F_s}\text{。}$ | (9) |
其中,
两单体间经典的连续接触力模型为Hertz阻尼模型:
| ${F_n} = K{\delta ^n} + \lambda {\delta ^n}\dot \delta \text{,}$ | (10) |
其中,
设牛顿模型定义恢复系数为
| $e = - \frac{{v_1^{} - {v_{10}}}}{{{v_0} - {v_{00}}}}\text{。}$ | (11) |
其中:
| $e = - \frac{{{v_1}}}{{{v_0}}}\text{。}$ | (12) |
AUV对接碰撞过程中能量损失可近似为AUV动能的变化:
| $\Delta E = \frac{1}{2}m({v_0}^2 - {v_1}^2) = \frac{1}{2}(1 - {e^2})m{v_0}^2\text{。}$ | (13) |
由于阻尼的作用,使得AUV在碰撞过程中的动能发生损耗,故损失的动能可以由压缩阶段与恢复阶段产生的滞后环节计算得到,即
| $\Delta E = \oint {\lambda {\delta ^n}\dot \delta } {\rm d}\delta \approx 2\int_0^{{\delta _m}} {\lambda {\delta ^n}\dot \delta } {\rm d}\delta = \frac{{2\lambda m{v_0}^3}}{{3k}}\text{。}$ | (14) |
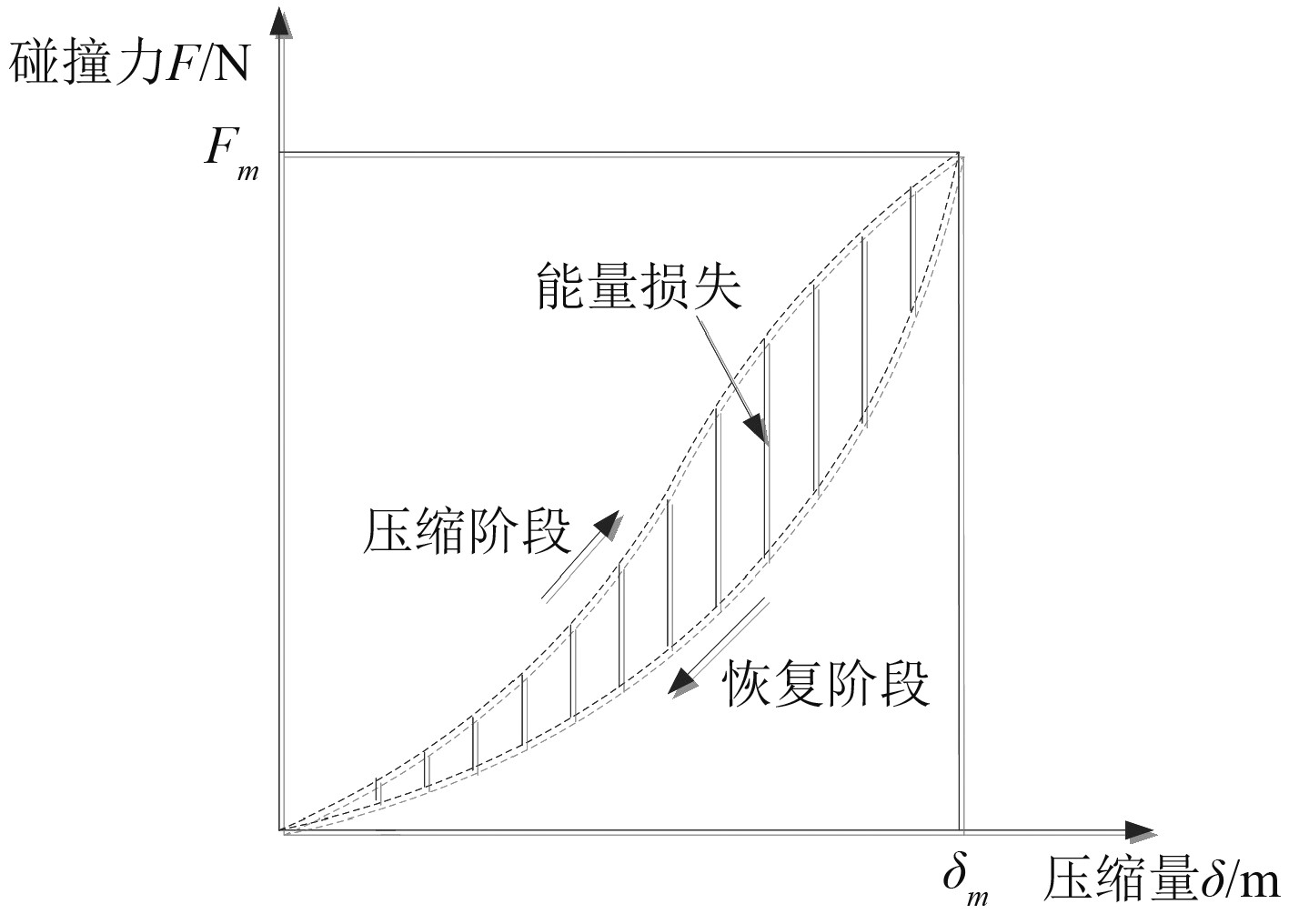
|
图 1 接触中的滞后回线 Fig. 1 Hysteresis loop in contact |
阻尼系数
| $\lambda = \frac{{3k(1 - {e^2})}}{4}\frac{1}{{{v_0}}}\text{,}$ | (15) |
即
| ${F_n} = K{\delta ^n}\left[ {1 + \frac{{3(1 - {e^2})}}{4}\frac{{\dot \delta }}{{{v_0}}}} \right]\text{。}$ | (16) |
由于恢复系数
ADAMS中接触力算法有2种,分别是惩罚函数法和IMPACT冲击函数法。惩罚函数法需要确定惩罚系数和补偿系数2个参数,这2个参数目前没有文献讲述其确切的确定方法,故本文采用IMPACT冲击函数法求解碰撞力。在ADAMS函数库中,IMPACT冲击函数的格式为[12]:
| $ IMPACT = \left\{ {\begin{array}{*{20}{l}} 0, &{{\text{当}}q > {q_1}};\\ {k{{({q_1} - q)}^e} - {c_{\max }}},&{}\\ {\dot q \cdot {\rm step}(q,{q_1}, - d,1,{q_1},0)},&{{\text{当}}q \le {q_1}}\text{。} \end{array}} \right. $ |
式中:
在ADAMS动力学仿真中,参数设置尤为重要,为各参数赋予适当的值是仿真成功的关键。
1)刚度系数
一般来说,刚度值越大,积分求解越困难,两物体渗透的量越小。刚度系数
| $k = \frac{4}{{3{\text π} ({\sigma _1} + {\sigma _2})}}{(\frac{{{r_1}{r_2}}}{{{r_1} + {r_2}}})^{1/2}}\text{,}$ | (17) |
| ${\sigma _i} = \frac{{1 - v_i^2}}{{{\text π} {E_i}}}(i = 1,2)\text{。}$ | (18) |
其中:
2)力指数e
力指数
3)最大阻尼系数
最大阻尼系数定义了接触材料的阻尼属性,通常取其刚度系数的0.1%~1%,本文取最大阻尼系数为
4)渗透量d
渗透量
本次仿真采用的AUV长2 135 mm,直径为20 mm,利用专业模型设计软SolidWorks建立AUV水下对接模型导入ADAMS中,水下对接模型如图2所示。本文中AUV对接碰撞时碰撞力的影响因素为导向罩开口角度
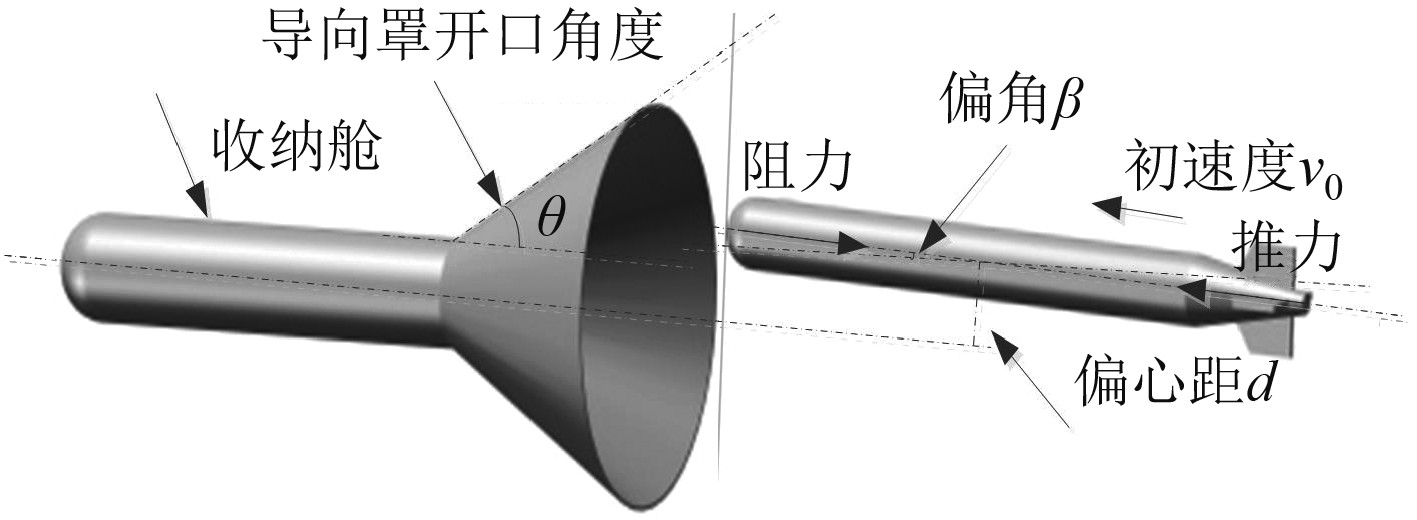
|
图 2 AUV水下对接系统模型 Fig. 2 AUV underwater docking system model |
|
|
表 1 ADAMS中参数设置 Tab.1 Parameter setting in ADAMS |

|
图 3 AUV与导流罩碰撞情况 Fig. 3 AUV with flow deflector |
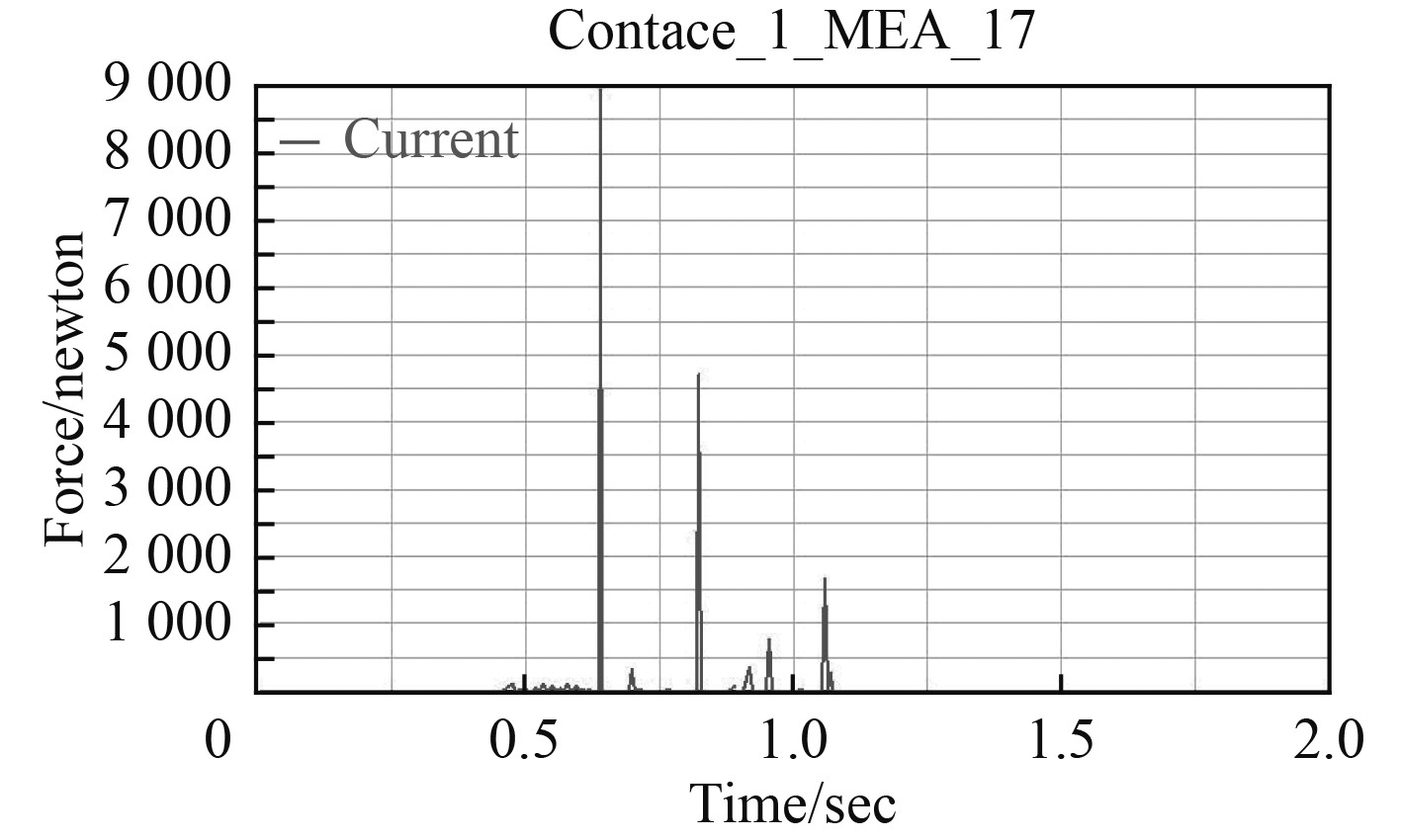
|
图 4 碰撞合力变化图像 Fig. 4 Collision force change image |
本文从导向罩开口角度、AUV初速度、AUV与对接装置的偏心距以及AUV中心与对接装置中轴线的偏角这4个方面分析AUV对接碰撞时的影响因素,对接过程的质量从对接过程中的最大碰撞力
1)不同开口角度对仿真结果的影响
为了研究不同开口角度对AUV对接碰撞的影响,利用SolidWorks建立不同开口角度的导向罩模型,导入到ADAMS中进行仿真分析,表1中得参数为对照组。试验组除开口角度
从表2的数据可以看出,导向罩得开口角度越大碰撞力越大,当开口角度
|
|
表 2 不同开口角度对AUV对接碰撞的影响 Tab.2 Influence of different opening angle on AUV butt collision |
2)不同偏心距对仿真结果的影响
偏心距的不同决定了碰撞区域的不同,偏心距越大,距离收纳舱越远,需要进行较大的姿态调整。为了研究不同偏心距对AUV对接碰撞的影响,在实验中除偏心距外其余的参数和对照组一致,通过不同偏心距的大小导致最大碰撞力的变化来研究不同偏心距对碰撞结果的影响。仿真结果如表3所示。
|
|
表 3 不同偏心距对AUV对接碰撞的影响 Tab.3 Influence of different eccentricities on AUV docking collision |
从表3数据可以看出,随着偏心距
3)不同初速度对仿真结果的影响
为研究不同初速度对AUV对接碰撞的影响,在实验中除初速度外其余的参数和对照组一致,通过不同初速度的大小导致最大碰撞力的变化来研究不同初速度对碰撞结果的影响仿真结果如表4所示。
从表4数据可以看出,随着初速度
|
|
表 4 不同初速度对AUV对接碰撞的影响 Tab.4 Influence of different initial velocity on AUV docking collision |
4)不同偏角
为了研究不同偏角
|
|
表 5 不同偏角对AUV对接碰撞的影响 Tab.5 Influence of different declination on AUV docking collision |
假设AUV首部偏向收纳舱偏角为正,AUV首部偏向导向罩外圈为负,从表5数据可以看出,当AUV头部偏向收纳舱,且偏角越大,碰撞力越小,更容易进入收纳舱,当偏角为负,且角度越大,碰撞力越大,进入收纳舱随着偏角
AUV在对接碰撞的过程中,AUV头部与对接装置的导向罩的接触力大小是评价对接过程稳定性的主要指标之一。AUV与导向罩的接触力越大,越不利于AUV与回收装置的对接,AUV与导向罩的接触力越小,则对接的成功率越高。本文以偏心距
多元线性回归模型的一般表现形式为:
其中
| $\begin{aligned} F = & - 2005 + 16889d + 184\theta + 1210\beta + 258{v_0} - \\ & 18902{d^2} + 4915{v_0}^2 - 16{\beta ^2} \text{。} \\ \end{aligned} $ |
图6为回归方程的残差图,从图6可以看出,数据的残差离零点均较近,零点均被包含在残差的置信区间,这说明Matlab中得出的回归模型能很好地反映碰撞力与其影响因素之间的关系。
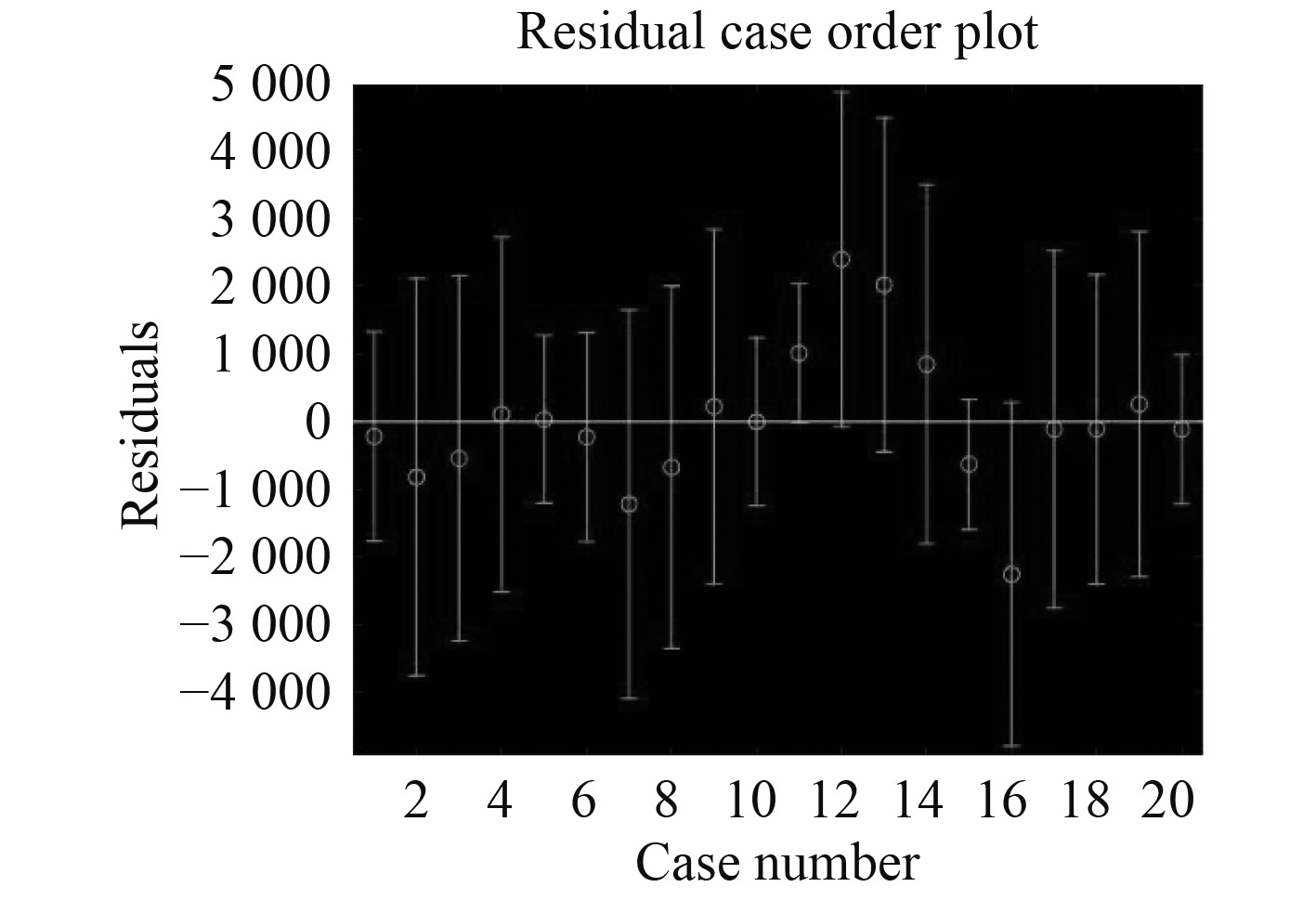
|
图 6 残差图 Fig. 6 Residual map |
利用Matlab中优化工具箱中提供的fmincon函数对回归方程中的约束优化问题进行求解。约束条件为对接实验中参数变化范围。通过仿真可以得出当对接初速度越小、导向罩开口角度越小、偏角越偏向收纳舱及开口角度越小,越有利于AUV对接回收,产生的碰撞力也越小。
4 结 语本文针对水下机器人回收过程中因路径跟踪的误差及外部干扰而导致AUV与对接装置的导向罩发生碰撞的过程进行仿真分析,建立AUV动力学模型和碰撞力模型,利用SolidWorks软件对AUV及其对接装置进行建模,将模型导入ADAMS软件中,利用ADAMS软件对整个过程进行仿真,继而得出AUV初速度、导向罩开口角度、AUV与对接装置的偏心距以及AUV中心与对接装置中轴线的偏角对碰撞过程的影响,最后将所得到的数据进行分析,利用多元非线性回归得出影响碰撞的因素与最大碰撞力之间的回归模型。通过对仿真结果的分析为之后实际对接提供参考。
| [1] |
MILLER A. B., B. M. Miller. Determination of the AUV velocity with the aid of seabed acoustic sensing[J]. Journal of Communications Technology and Electronics, 2018, 63(6). |
| [2] |
ROBERT S, McEwen, MEMBER, etal. Docking control system for a 54-cm-diameter(21-in)AUV. IEEE Journal of Oceanic Engineering. 2008, 33(4): 550-562P.
|
| [3] |
KONGSBERG S I H O. Underwater mobile docking of autonomous underwater vehicles. Oceans 12 MTS/IEEE Conference, Hampton Roads, VA. 2012: 1-15.
|
| [4] |
TANG J. YU Y, NIE Y. An autonomous underwater vehicle docking system based on optical guidance[J]. Ocean Engineering, 2015, 104(6): 639-648. |
| [5] |
李开飞. AUV水下对接关键技术及对接碰撞问题研究[D]. 哈尔滨: 哈尔滨工程大学, 2017.
|
| [6] |
张医博, 唐元贵, 要振江. 便携式AUV水下对接过程中的碰撞分析与罩式对接平台优化设计[J]. 海洋技术学报, 2017, 36(05): 27-31. |
| [7] |
袁培银, 刘俊良, 雷林, 等. 船舶与海洋平台碰撞的动力响应研究[J]. 舰船科学技术, 2018, 40(03): 27-32+45. |
| [8] |
王林, 王强强. 半潜式海洋平台与供应船碰撞的理论方法研究[J]. 中国水运(下半月), 2016, 16(11): 20-23. |
| [9] |
刘平, 王林. LS-DYNA软件对某半潜式海洋平台发生碰撞的分析[J]. 解放军理工大学学报(自然科学版), 2015, 16(05): 465-470. |
| [10] |
赵国良, 许可, 赵春城, 等. 导向喇叭口剖面半径对AUV回收的影响[J]. 水下无人系统学报, 2018, 26(02): 166-173. |
| [11] |
WANG S, SUN X J, WANG Y H, et al. Dynamic modeling and motion simulation for a winged hybird-driven underwater glider[J]. China Ocean Engineering, 2011, 25(1): 97-112. DOI:10.1007/s13344-011-0008-7 |
| [12] |
史剑光, 李德骏, 杨灿军, 等. 水下自主机器人接驳碰撞过程分析[J]. 浙江大学学报(工学版), 2015, 49(03): 497-504. |
 2020, Vol. 42
2020, Vol. 42
