0 引　言

水下无人航行器的路径规划是在复杂的水下环境中, 按照一定的评价标准, 为水下无人航行器寻找一条从起始点到达目标点的无障碍路径^[1]。水下无人航行器路径规划包括全局路径规划和局部路径规划。全局路径规划是根据水下环境信息规划出一条从起始点到达目标点的无障碍全局路径^[2-3]。

通常情况下，最短航行路径是很有优势的，可以使航行时间和能源消耗最小化。对于水下无人航行器，除了确定路径点外，还需确定水下无人航行器在该点的方向。在规划中还需要考虑水下无人航行器航行时的约束条件，其中最主要的约束就是曲率或转弯半径^[4]。

2个位姿点间的最短路径是Dubins路径，Dubins 路径由 Dubins 在 1957 年完成数学证明^[5]。Dubins路径被定义为：在最大曲率限制下，平面内2个有方向的点间的最短可行路径是CLC路径或CCC路径，或是它们的子集，其中C表示圆弧段，L表示与C相切的直线段^[6]。Dubins路径的几何特性简单，但是当路径由圆弧段过渡到直线段或由直线段过渡到圆弧段时，路径上曲率变化不连续，会使水下无人航行器的路径跟踪产生较大误差。曲率随路径长度线性变化的Clothoid 曲线可使路径在直线段与圆弧段间有平滑的过渡，所以基于Clothoid 曲线的复合路径更易于水下无人航行器实现紧密跟踪^{[7 − 8]}。

1 传统Clothoid复合路径避障算法的设计

Clothoid 曲线是一种螺旋曲线，通过计算Fresnel积分得到，路径的曲率随曲线弧长线性变化。路径的方向需要沿路径长度对曲率积分：

$\phi (q) = \int_0^q {\kappa \frac{k}{h}} {\rm{d}} k = \frac{\kappa }{{2h}}{q^2}\text{，}$

(1)

式中： $q$ 为沿弧段路径的长度变量； $h$ 为总弧段长； $\kappa $ 为在 $h$ 处的曲率。

终点位置的 $x$ 与 $y$ 为L：

$\left\{ {\begin{aligned} & {x(h) = \int_0^h {\cos (\frac{\kappa }{{2h}}{q^2}){\rm{d}}q} }\text{，}\\ & {y(h) = \int_0^h {sin(\frac{\kappa }{{2h}}{q^2}){\rm{d}}q} }\text{。} \end{aligned}} \right.$

(2)

从Clothoid曲线的表达式可以看出，该曲线的最大特点就是曲率连续。

为了能够在充满障碍物的环境中航行，水下无人航行器需要在避开障碍物的环境中计算路径并按路径航行到目的地，这要求计算得到的复合Clothoid路径包含障碍物回避运动。

在障碍物周围画一个障碍物圆，将障碍物都包含在障碍物圆内。复合Clothoid路径与障碍物圆的相交存在下面2种情形：

1）路径的直线段与一个障碍物圆相交

当直线段与障碍物相交时：

$\frac{{{d_n}}}{{{r_o}}} < 1,{\rm{ }}{d_n}{\kappa _o} < 1\text{。}$

(3)

式中： ${d_n}$ 为障碍物中心圆点到该直线段的垂直投影线； ${r_o}$ 为障碍物圆的半径； ${\kappa _o}$ 为障碍物圆的曲率。

避障方法：调整起始运动弧和终止运动弧使直线段与障碍物圆相切，此时Clothoid路径由5部分组成：初始弧、中间弧、终止运动弧以及2条直线段。这就会产生2种可行解：绕障碍物圆正向旋转或负向旋转路径。因此对于每个障碍物需要计算2条避障路径。

2）路径的弧线段与障碍物圆相交

当弧线段与障碍物圆相交时：

$ \left\{ \begin{aligned} & \frac{1}{{{\kappa _{\rm{S}}}_1}}{\rm{ + }}\frac{1}{{{\kappa _{\rm{o}}}}} > {d_{\rm{c}}} > \frac{1}{{{\kappa _{\rm{S}}}_1}} - \frac{1}{{{\kappa _{\rm{o}}}}}\text{，}\\ & \frac{1}{{{\kappa _{\rm{S}}}_2}}{\rm{ + }}\frac{1}{{{\kappa _{\rm{o}}}}} > {d_{\rm{c}}} > \frac{1}{{{\kappa _{\rm{S}}}_2}} - \frac{1}{{{\kappa _{\rm{o}}}}}\text{。} \end{aligned} \right.$

(4)

式中： ${\kappa _{{\rm{S1}}}}$ 与 ${\kappa _{{\rm{S2}}}}$ 分别为弧线段与障碍物圆的2个交点处的曲率； ${\kappa _{\rm{o}}}$ 为障碍物圆的曲率； ${d_{\rm{c}}}$ 为弧线段圆心到障碍物圆圆心的距离。

避障方法：调整与障碍物圆相交的弧段的曲率，得到的弧线段与障碍物圆相切。

传统的Clothoid路径避障算法存在以下问题：

1）当Clothoid路径与障碍物圆相交时，不一定与障碍物本身相交，如果按相交情况处理，就需要重新画避障路径，不仅增加了计算量，而且还增加了Clothoid路径的长度；

2）当Clothoid路径直线段与障碍物相交时，障碍物圆的曲率不一定满足水下无人航行器的运动约束，此时按原障碍物圆设计的Clothoid避障路径不满足运动约束，在实际情况中无法实现。

2 对Clothoid路径避障算法的改进

针对传统的Clothoid路径避障算法存在的问题，做出以下改进：

1）当Clothoid路径与障碍物圆相交时，检测与障碍物边界是否相交。

当检测到生成的Clothoid路径与某障碍物圆相交时，计算与障碍物圆的交点。

当直线段与障碍物圆相交时，交点到直线段起始点的距离分别为：

$\left\{ \begin{aligned} & {d_{ip}} = {d_o}\cos {\theta _o} + \sqrt {{d_o}^2({{\cos }^2}{\theta _o} - 1) + \frac{1}{{{\kappa _o}^2}}}\text{，} \\ & {d_{im}} = {d_o}\cos {\theta _o} - \sqrt {{d_o}^2({{\cos }^2}{\theta _o} - 1) + \frac{1}{{{\kappa _o}^2}}} \text{。} \end{aligned} \right.$

(5)

式中： ${d_o}$ 为障碍物圆心到起始点的距离， ${\theta _o}$ 为直线段与障碍物圆心到起始点线段的夹角。

当弧线段与障碍物圆相交时，可以得到：

$\left\{ \begin{aligned} & {\left( {{x_1}({h_1}) - {x_z}} \right)^2}{\rm{ + }}{\left( {{y_1}({h_1}) - {y_z}} \right)^2} = \frac{1}{{{\kappa _o}^2}}\text{，}\\ & {\left( {{x_2}({h_2}) - {x_z}} \right)^2}{\rm{ + }}{\left( {{y_2}({h_2}) - {y_z}} \right)^2} = \frac{1}{{{\kappa _o}^2}}\text{。} \end{aligned} \right.$

(6)

式中： ${h_1}$ ， ${h_2}$ 分别为弧线段与障碍物圆的2个交点处的弧长；（ ${x_1}({h_1})$ ， ${y_1}({h_1})$ ），（ ${x_2}({h_2})$ 、 ${y_2}({h_2})$ ）分别为2个交点处的坐标； $({x_z},{y_z})$ 为障碍物圆的圆心坐标。

检测与障碍物圆相交的2个交点间的直线段或弧线段是否与障碍物的边界线相交。如果检测到与边界线没有相交，就不需要画避障路径。这样就减少了计算量，且路径比避障路径更短。

2）当Clothoid路径直线段与障碍物相交时，如果障碍物圆的曲率不满足运动约束，按照运动约束重新画障碍物圆。

首先计算起始弧与原障碍物圆的公切线，得到障碍物圆上的切点为（ ${x_q},{y_q}$ ），然后设计过（ ${x_q},{y_q}$ ）点的新障碍物圆，新障碍物圆具有以下特点：

①将原障碍物圆全部包括在内；

②与原障碍物圆内切；

③满足运动约束曲率。

生成的新障碍物圆为：

$\left\{ \begin{aligned} & {({x_q} - {x_0})^2} + {({y_q} - {y_0})^2} = \frac{1}{{{\kappa _n}^2}}\text{，}\\ & {(x - {x_0})^2} + {(y - {y_0})^2} = \frac{1}{{{\kappa _n}^2}}\text{，}\\ & \frac{{{x_0} - {x_z}}}{{{y_0} - {y_z}}} = - \frac{{{y_{{P_X}}} - {y_q}}}{{{x_{{P_X}}} - {x_q}}}\text{。} \end{aligned} \right.$

(7)

式中： $({x_0},{y_0})$ 为新障碍物圆的圆心坐标； $({x_z},{y_z})$ 为原障碍物圆的圆心坐标； $({x_{{P_{\rm{X}}}}},{y_{{P_{\rm{X}}}}})$ 为直线段起始点； ${\kappa _n}$ 为新障碍物圆的曲率（满足运动约束）； $(x,y)$ 为新障碍物圆上的点。

式（7）的解包括外切圆解与内切圆解，这里只保留内切圆解。那么根据原路径可生成2组内切圆解。然后根据生成的新障碍物圆设计Clothoid避障路径。

这样改进后具有以下优点：

1）生成的新障碍物圆将原障碍物圆全部包括，确保了生成的新路径不会与原障碍物圆内的障碍物相交；

2）改进的新路径不改变起始弧线段的曲率，直线段起始点和起始点到障碍物圆的直线段与使用原障碍物圆时相同，减少了计算量。

3 Clothoid路径规划方法仿真

在Matlab中对改进的Clothoid路径规划方法进行仿真验证，仿真结果如下：

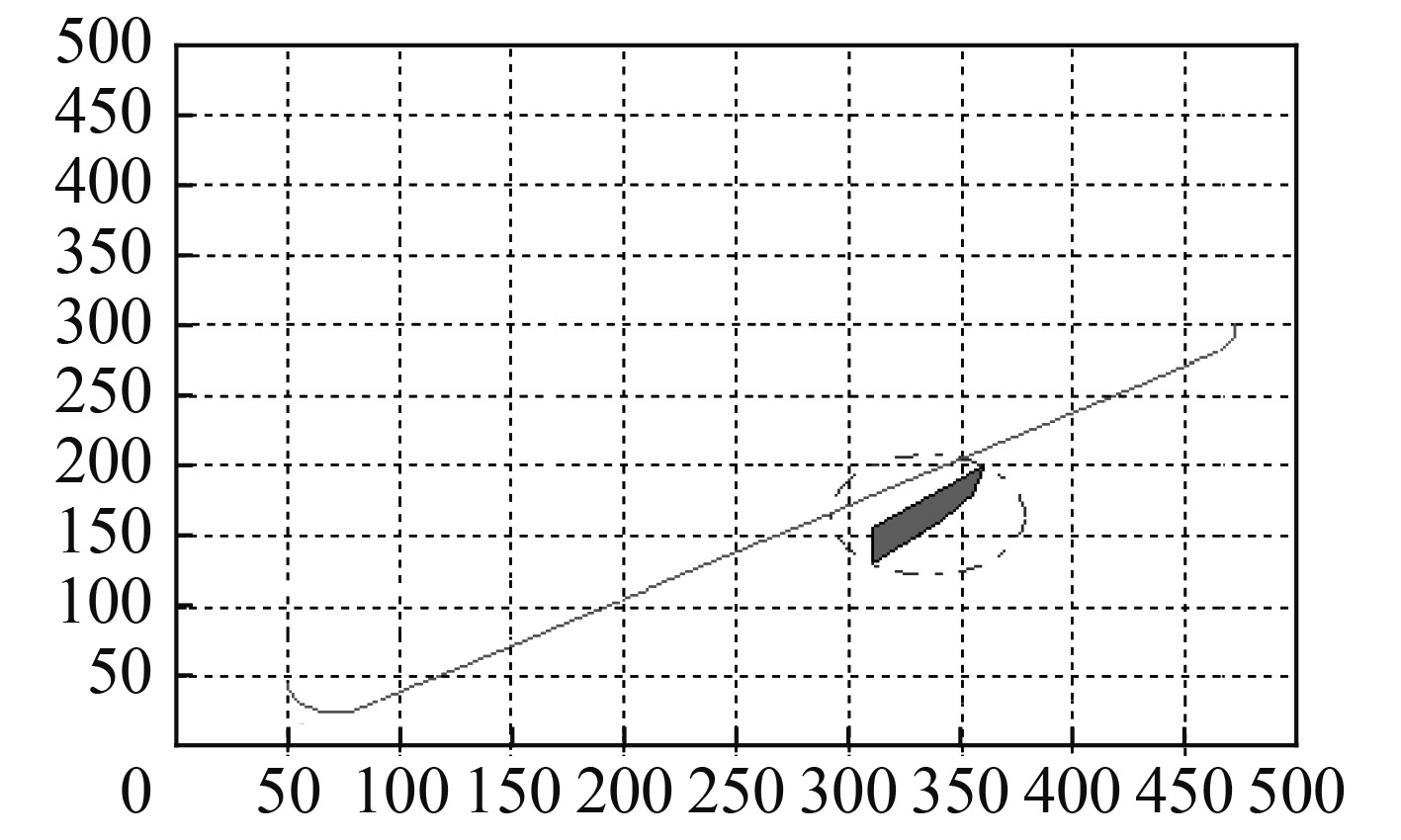
1）水下无人航行器从起始位姿点[50, 48, 90°]以2 kn的速度航行到终止位姿点[472, 300, 90°]。从图1可以看出，起始位姿点与终止位姿点的连线与1个障碍物圆相交，但是没有与障碍物圆内的障碍物边界相交，因此根据检测结果不需要重新画Clothoid路径（由于横坐标与纵坐标显示比例不一致，障碍物圆显示结果呈椭圆形）。

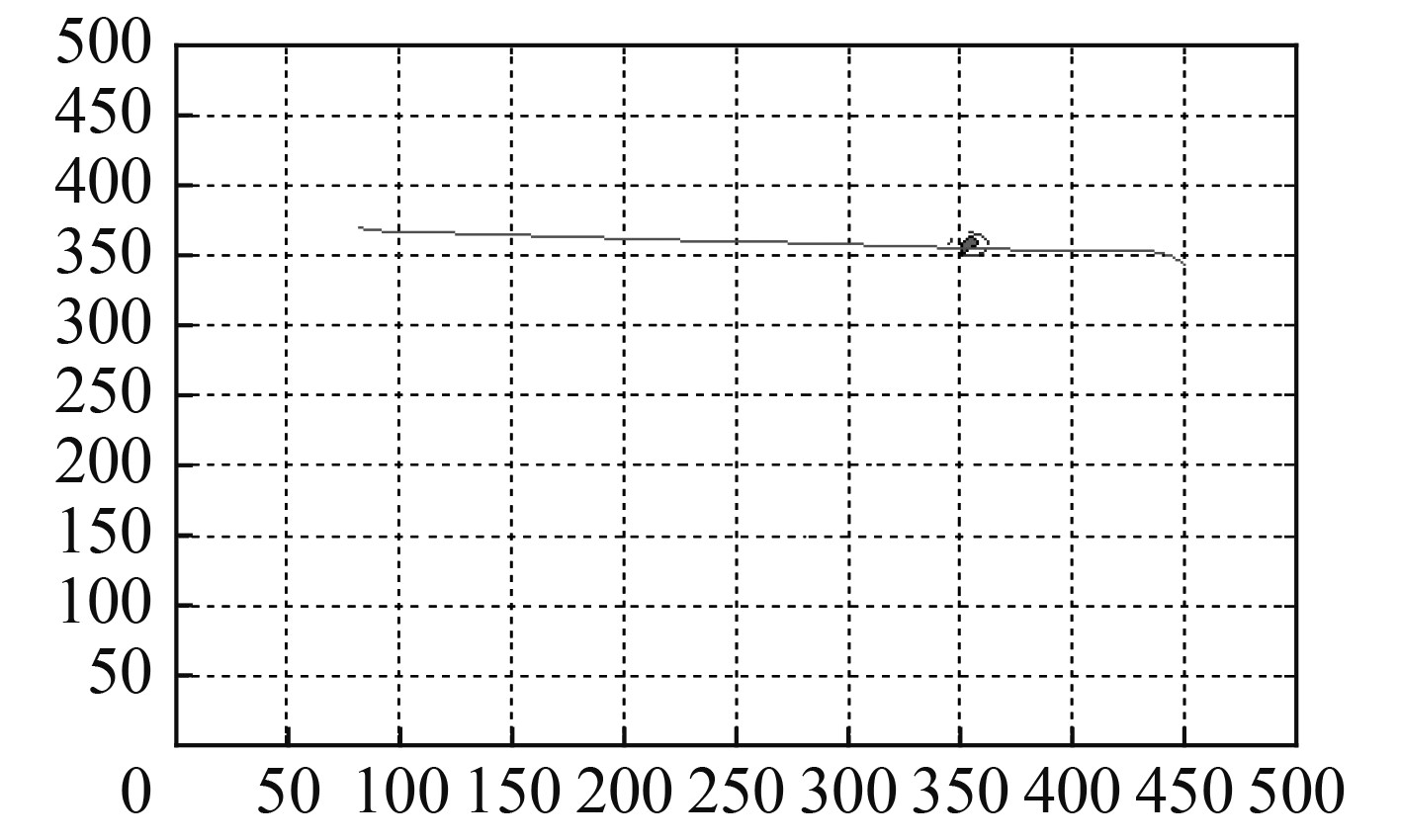
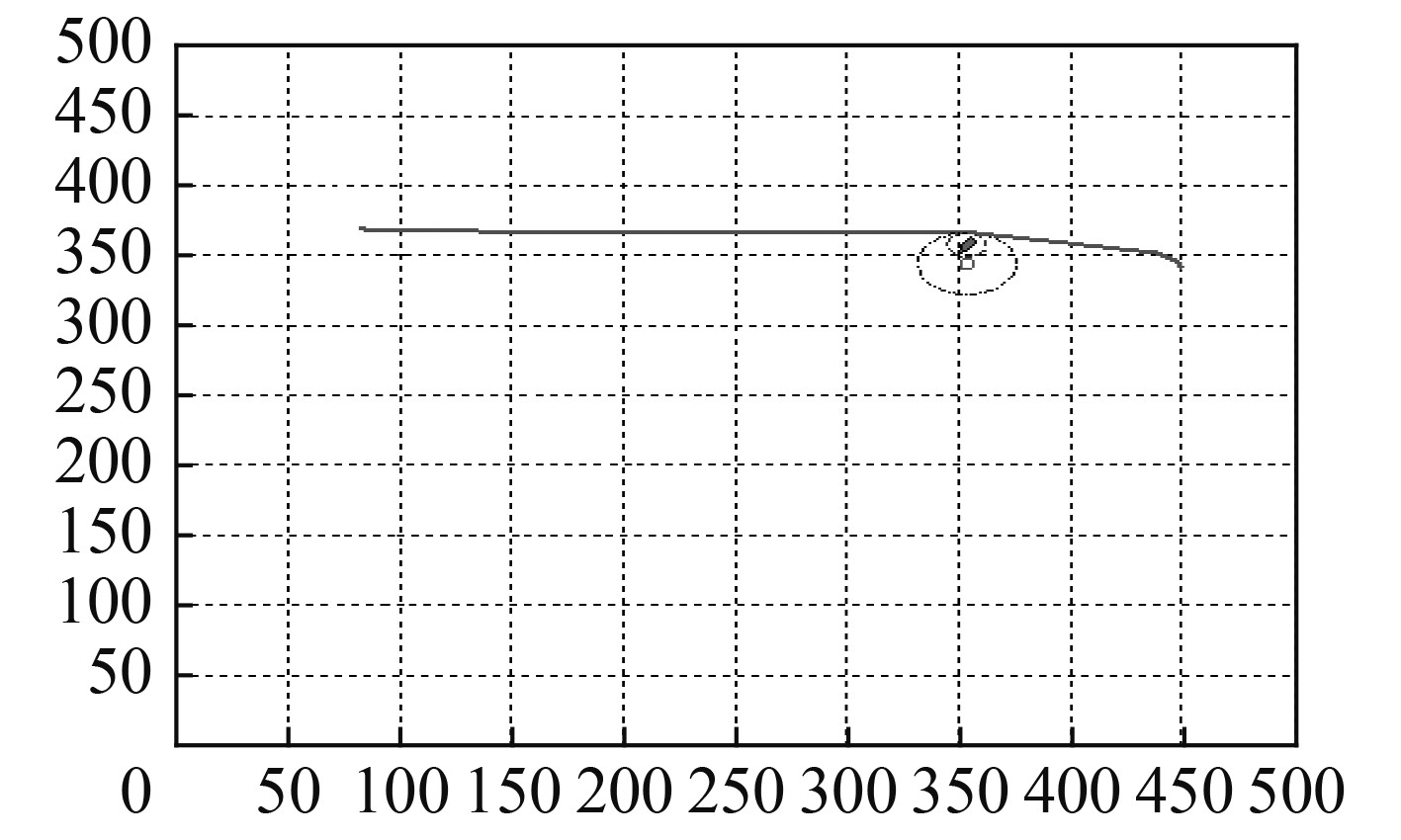
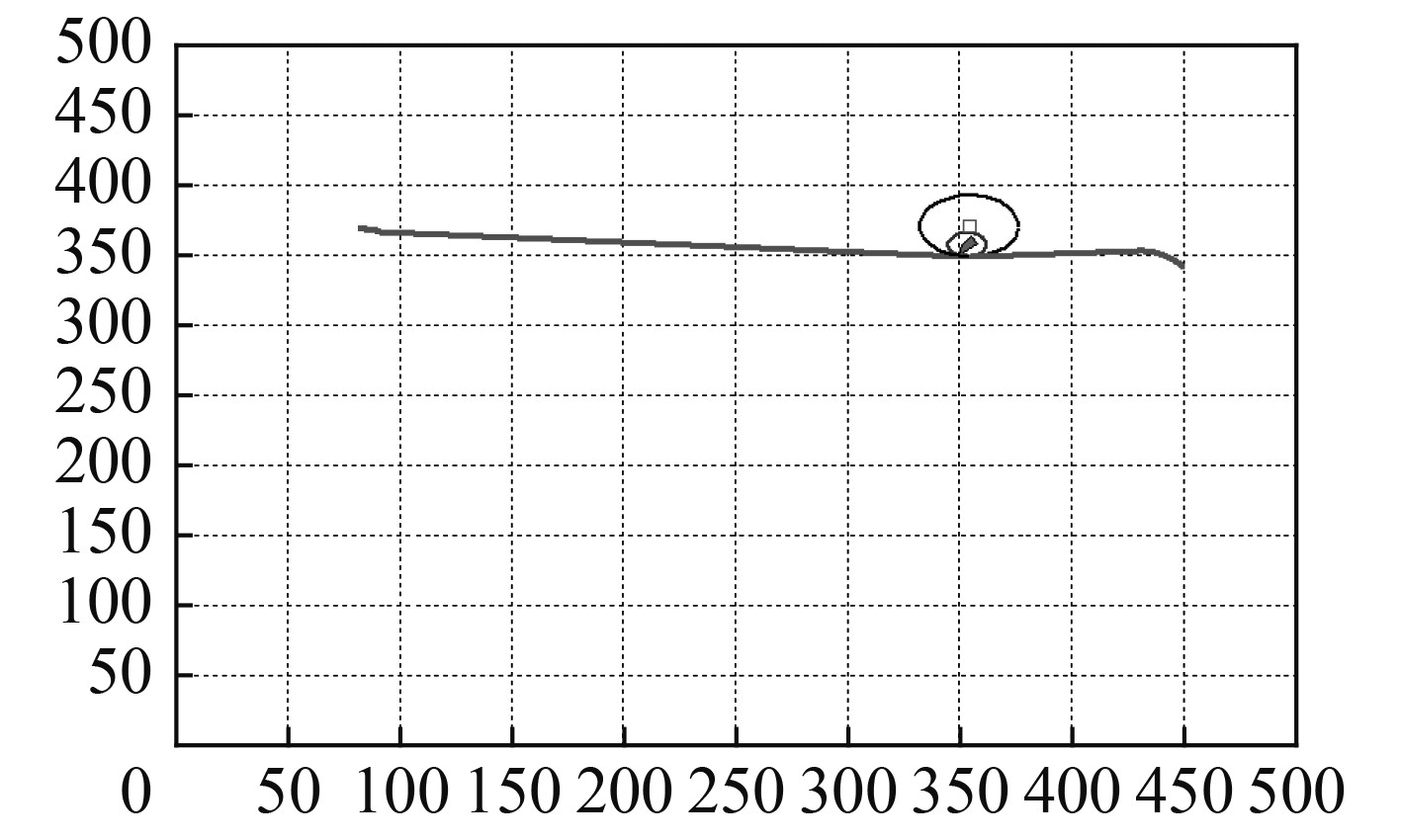
2）水下无人航行器从起始位姿点[82, 370, 50°]以4 kn的速度航行到终止位姿点[450, 341, 80°]。从图2可以看出，起始位姿点与终止位姿点的原始路径与1个障碍物圆相交，障碍圆的半径小于水下无人航行器的转弯半径，因此根据水下无人航行器的运动约束运用改进的Clothoid路径规划方法生成避障路径。生成的2条避障路径分别如图3和图4所示。图3中的公切圆为顺时针旋转生成，图4中的公切圆为逆时针旋转生成。

4 结　语

本文针对传统Clothoid路径避障算法存在的问题，提出了2种改进措施：

1）当Clothoid路径与障碍物圆相交时，计算与障碍物圆的交点，然后检测与障碍物圆相交的2个交点间的直线段或弧线段是否与障碍物的边界线相交，如果没有相交，就不需要画避障路径。

2）当Clothoid路径直线段与障碍物相交时，如果障碍物圆的曲率不满足水下无人航行器的运动约束，按照运动约束生成将原障碍物圆全部包括的内切障碍物圆。

理论分析与仿真结果表明，按照改进措施生成新Clothoid避障路径，避免了画一些不必要的避障路径，减少了计算量，使路径更短，并且新路径满足水下无人航行器的运动约束条件，实用性更强。