0 引　言

轴系校中状态对轴承载荷分配、轴系运转稳定性有重要影响，从最早的直线校中法到后来的负荷校中法、合理校中法和动态校中法等，这些校中方法对轴系校中的影响因素考虑得越来越全面，校中结果也越来越接近轴系布置的真实情况。但对于这些校中方法的研究，多数集中于校中方法本身，对于轴系校中之后振动特性的改变研究较少^[1-2]。

国内外学者在轴承标高变化对轴系振动和稳定性影响方面做了一些工作。崔颖^[3]认为轴承的油膜失稳特性与轴承的标高抬起引起的轴承动态平均载荷降低密切相关。马斌^[4]提出抬高尾轴承标高可以使尾轴承的承载更加均匀，并研究了抬高尾轴承标高对尾轴承处轴心振动的影响。刘金林比较了直线状态和轴承变位后轴系横向振动和回旋振动响应特性。刘荣强^[5]通过传递矩阵法研究了多跨轴系各轴承标高变化对轴系失稳转速的影响。刘学伟^[6]比较了直线校中和以尾轴后轴承静载最小的优化校中2种情况下的轴承力传递特性。Lee^[7-8]认为轴承不校中引起的轴承刚度变化将显著影响转子系统的不平衡响应和临界转速。Matthew^[9]通过研究发现在风机中齿轮箱与发电机的联接之间给予一定的不校中量有利于延长风机的寿命。上述研究对深入了解轴系振动特性有重要意义，但主要考虑的是轴承标高变化时轴系的振动特性，没有将校中方法与轴系振动结合起来考虑，缺乏轴系校中对其振动特性影响的研究。

本文首先对某船推进轴系进行负荷校中，通过求解雷诺方程实现轴系校中振动计算的轴承变位处理，然后研究轴系校中状态对轴承的油膜特性和轴系横向振动传递特性的影响，最后通过试验对上述有限元分析结果进行验证。

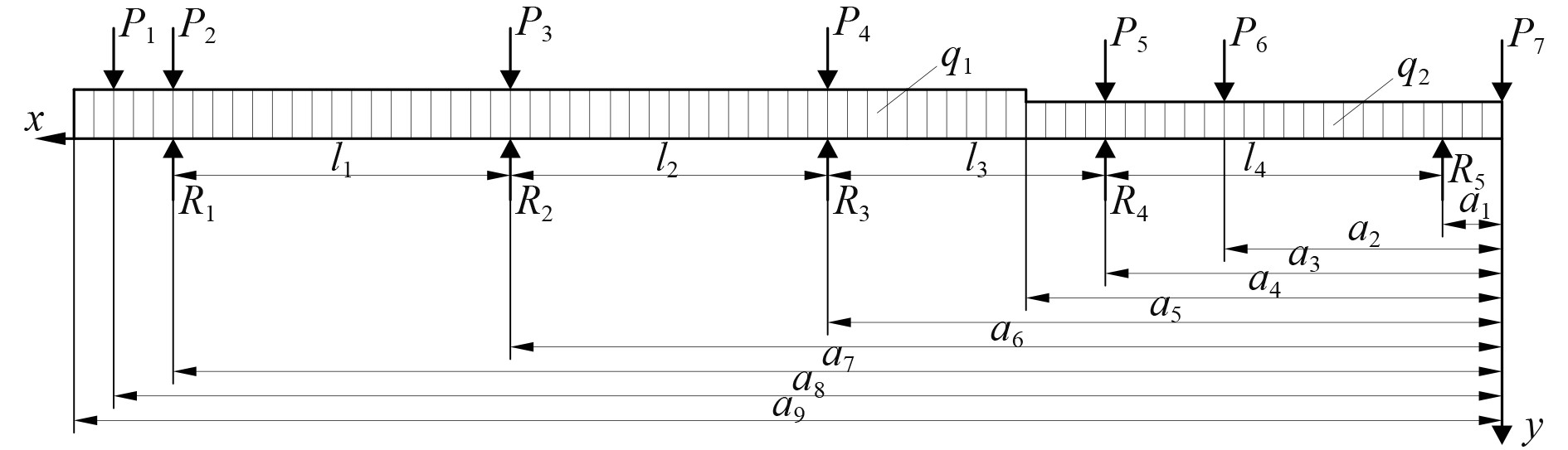
1 某船推进轴系负荷校中 1.1 轴系简化模型及参数

在进行轴系校中时，将推进轴系在弹性联轴器处断开，只考虑弹性联轴器输出端至螺旋桨的推进轴系简化模型如图1所示。轴系有5个轴承支承，从螺旋桨端至弹性联轴器端依次为尾后轴承、尾中轴承、尾前轴承、推力轴承和中间轴承，将其依次编号为1#～5#轴承。为了计算方便，将轴颈一些位置的突起简化成集中载荷处理。推进轴系载荷分布如图2所示。

推进轴系参数如表1所示。校中过程中力的单位采用吨力， $1{\rm tf} = {10^4}{\rm N}$ 。由于精度对负荷校中计算结果影响较大，各参数均精确到小数点后四位。

1.2 轴系负荷校中 1.2.1 轴系负荷校中

将1#，4#和5#轴承布置在一条在直线上，通过改变2#和3#轴承的标高来实现轴系的负荷校中。负荷校中前后各轴承的支反力和轴承标高如表2所示，这里轴承标高以重力的反方向为正向。

从表2可以看到，直线校中状态下，1#轴承的承载最大，明显大于其他各轴承，2#轴承承载很小，有脱空的可能。进行负荷校中后1#轴承的承载相对减小，2#轴承的承载明显增大，各轴承的支反力分布更加均匀，这有利于减小1#轴承的磨损和损坏的几率，对延长轴承寿命和保证轴系运行安全有利。

1.2.2 轴承变位的处理

运转工况下，轴颈与轴承之间形成润滑油膜，轴承对轴系的支撑刚度实际上是油膜刚度、轴承机械结构刚度和轴承基座刚度的串联。由于轴承油膜刚度远小于机械结构刚度，因此轴承对轴系的支撑刚度主要取决于油膜刚度。轴系与轴承之间通过油膜进行力和振动的传递，轴承变位不仅会导致轴承载荷和轴颈倾斜角度的改变，同时还会改变轴承的油膜刚度和分布，对轴系的振动特性产生影响。当然，轴承油膜特性还会受到温度、润滑油粘度等因素的影响，这里主要考虑轴承变位的影响，其他因素保持不变。

以轴颈靠近螺旋桨一端几何中心为原点，轴颈与轴承截面中心连线为 $y$ 轴方向，轴承轴线方向为 $z$ 轴正向建立直角坐标系如图3所示。

图中， ${O_1}$ ， ${O_2}$ 分别为零截面轴承内径和轴颈的几何中心，偏心距 $e = {O_1}{O_2}$ ， $h$ 为偏角 $\theta $ 处的油膜厚度， $L$ 为轴承长度， $\alpha $ 为轴颈倾斜角，定义轴颈向零截面倾斜时轴颈倾斜角为正。

根据流体动力润滑理论，轴承油膜压力分布与油膜厚度和轴颈转速的关系可以用雷诺方程表示如下：

$\frac{\partial }{{\partial x}}(\frac{{{h^3}}}{\eta } \cdot \frac{{\partial p}}{{\partial x}}) + \frac{\partial }{{\partial z}}(\frac{{{h^3}}}{\eta } \cdot \frac{{\partial p}}{{\partial z}}) = 6U\frac{{\partial h}}{{\partial x}} + 6V\frac{{\partial h}}{{\partial z}} + 12V\text{。}$

(1)

式中： $p$ 为油膜压力， $h$ 为油膜厚度， $\eta $ 为润滑剂动力粘度， $x$ 为轴颈旋转方向， $z$ 为轴承轴向， $U$ 为轴颈切向速度分量， $V$ 为轴颈径向速度分量。

当轴系在稳定工况下运行时，径向速度分量 $V$ 为零，上式可简化为：

$\frac{\partial }{{\partial x}}(\frac{{{h^3}}}{\eta } \cdot \frac{{\partial p}}{{\partial x}}) + \frac{\partial }{{\partial z}}(\frac{{{h^3}}}{\eta } \cdot \frac{{\partial p}}{{\partial z}}) = 6U\frac{{\partial h}}{{\partial x}}\text{。}$

(2)

Reynolds边界条件认为液膜在轴承间隙内不是连续的，液膜在轴承扩散区的某处随着负压的增大而自然破裂，其边界条件为：

$ \left\{ {\begin{array}{*{20}{c}} {\varphi = 0,p = 0};\\ {\varphi = [{\varphi _2},2{\text π} ],p = 0,\displaystyle\frac{{\partial p}}{{\partial \varphi }} = 0}\text{。} \end{array}} \right. $

(3)

式中：φ₂为油膜破裂终止角。

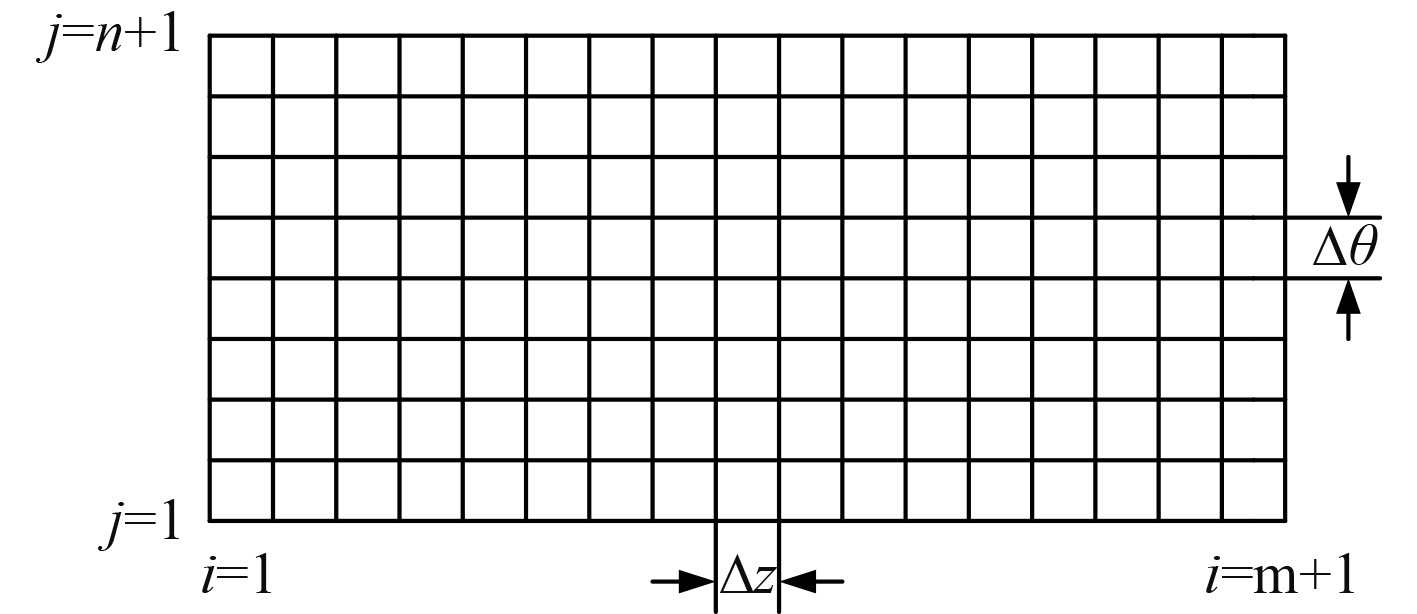
这个椭圆形的偏微分方程仅对特殊间隙形状才可能求得解析解，而对于复杂的几何形状问题，无法用解析方法求得精确解，因此采用数值算法成为求解润滑问题的有效途径。将滑动轴承油膜的求解域进行离散化处理，等距离网格划分如图4所示。

不考虑轴颈偏移，当轴颈倾斜角 $\alpha $ 为正时，在任一截面 $z = (i - 1)\Delta z$ ，（ $i = 1, \cdots ,m + 1$ ）处轴颈的偏心距：

$e' = e + (i - 1)\Delta z \cdot \cos \alpha \text{，}$

(4)

当轴颈倾斜角 $\alpha $ 为负时，在任一截面 $z = (i - 1)\Delta z$ ，（ $i = 1, \cdots ,m + 1$ ）处轴颈的偏心距：

$e' = e - (i - 1)\Delta z \cdot \cos \alpha \text{，}$

(5)

任一截面轴颈偏心率：

$\varepsilon ' = \frac{{e'}}{C}\text{。}$

(6)

式中， $C$ 为半径间隙。

在任一截面 $z$ 处偏角为 $\theta $ 位置的轴承油膜厚度可表示为：

$h = C(1 + \varepsilon '\cos \theta )\text{。}$

(7)

有限差分法将各节点 $P(i,j)$ 的1，2阶偏导数用其周围的节点变量值来表示。利用有限差分法求解雷诺方程的具体过程在滑动轴承润滑的相关文献和书籍中均有介绍，这里不再赘述。求得油膜压力后，利用摄动法取一个小扰动量 $\Delta x$ ，根据式（8）可求得轴承在各个方向的油膜刚度。

$K = \frac{{\partial F}}{{\partial x}} = \frac{{\Delta F}}{{\Delta x}} = \frac{{F' - F}}{{\Delta x}}\text{。}$

(8)

2 校中状态对轴系振动传递特性影响研究 2.1 校中状态对轴承油膜特性的影响

轴系校中状态的改变将导致轴系轴承油膜刚度、分布和轴颈倾斜角的改变，从而影响轴系的振动传递特性。为了研究校中状态对轴系振动特性的影响，必须首先了解校中状态对轴承油膜特性的影响。

2.1.1 校中状态对轴承油膜刚度及轴颈倾斜角的影响

两种校中状态下，推进轴系各轴承的油膜刚度和轴颈在各轴承位置的倾斜角如表3所示。

可以看到，与直线校中状态相比，负荷校中状态下1#和2#轴承的油膜刚度变化较大，3#～5#轴承油膜刚度变化相对较小。除了1#和2#轴承油膜刚度减小外，其他轴承的油膜刚度均增大。与直线校中状态相比，负荷校中状态下除2#轴承处轴颈倾斜角减小外，其他轴承位置的轴颈倾斜角均增大，即轴承内油膜的厚度更加不均匀。

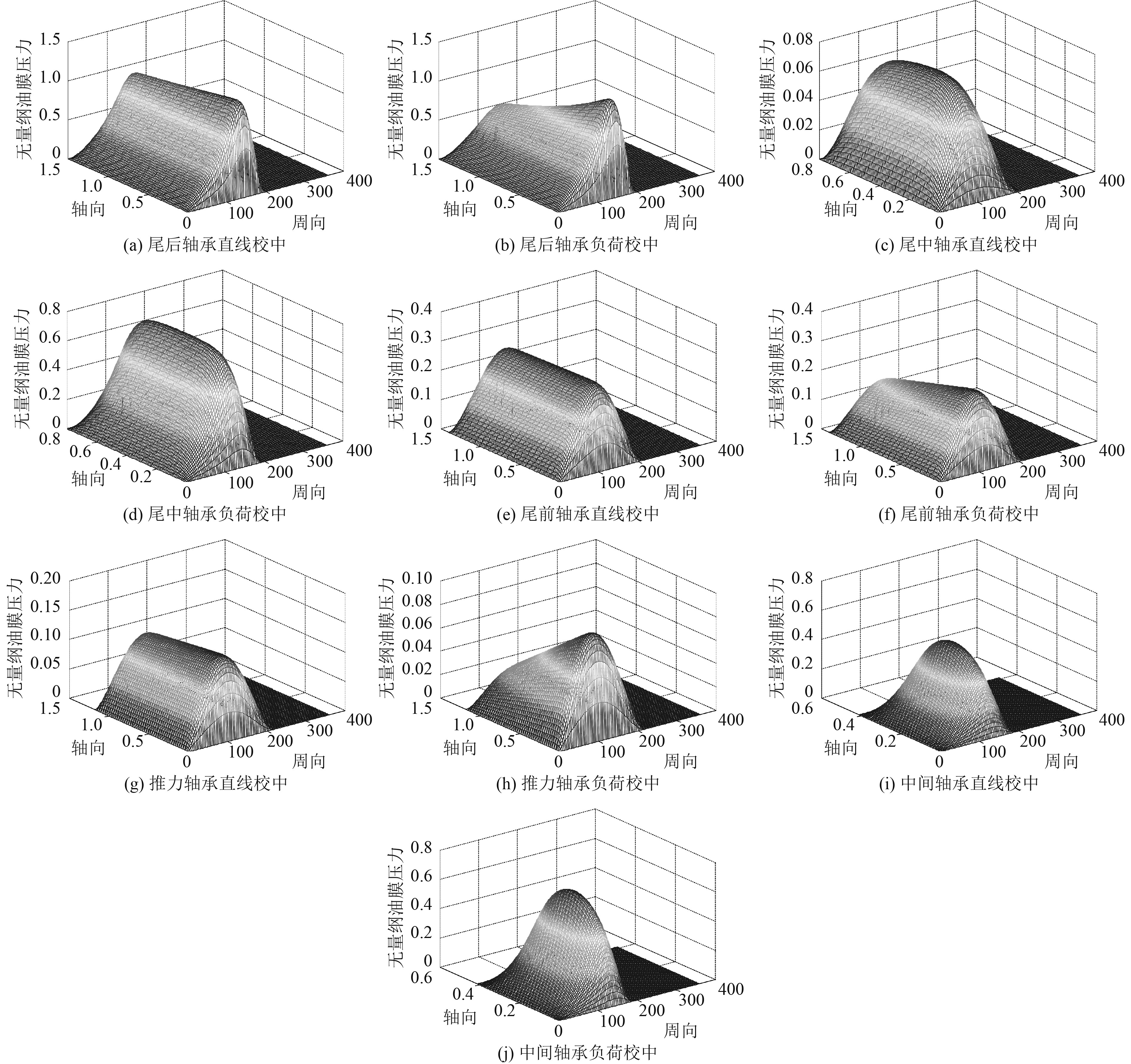
2.1.2 校中状态对油膜分布的影响

轴承均有一定的承载比压，当油膜比压过大，将导致轴承磨损加重甚至损坏。轴承油膜作为轴系的支撑边界条件，其分布对轴系振动也有一定影响。负荷校中前后，各轴承油膜压力分布如图5所示。

从图中可以看到，负荷校中前后，各轴承的油膜压力分布在周向变化不大；在轴向，尾后轴承、尾前轴承和推力轴承的油膜压力分布均向尾轴端倾斜，油膜分布更加不均匀，尾后轴承和尾前轴承远离螺旋桨一端的油膜压力明显减小，靠近螺旋桨一端的油膜压力变化不大；推力轴承的油膜压力分布在校中后虽然很不均匀，但压力值明显减小；尾中轴承的油膜压力增大，轴向分布也更加均匀；中间轴承的油膜压力变化不大，压力值有所增加。

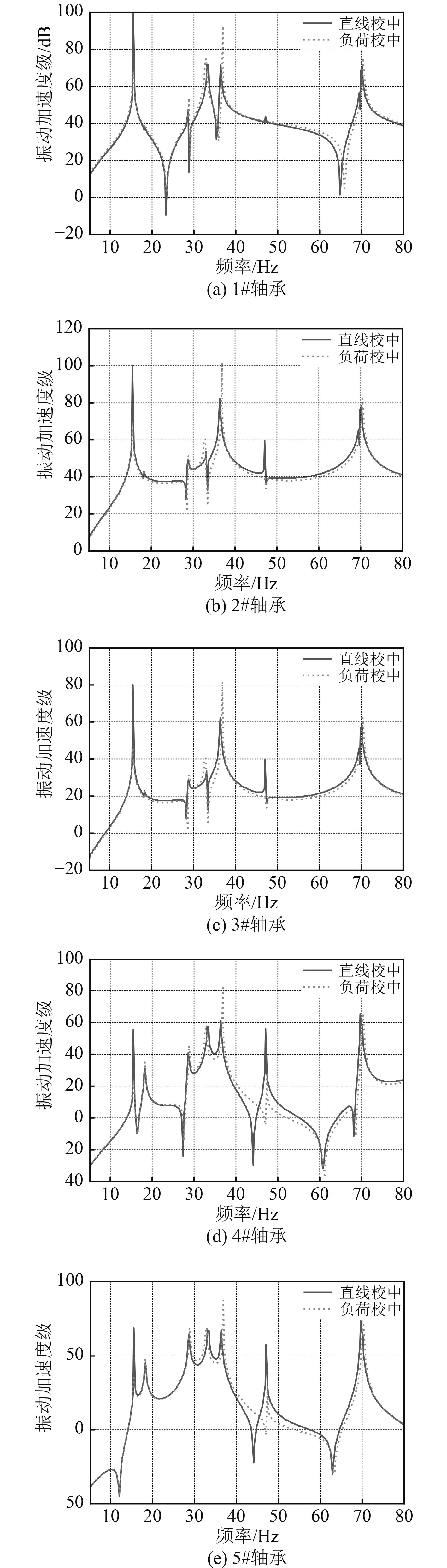
2.2 校中状态对轴系横向振动传递特性的影响

分别以2.1节轴系不同校中状态下轴承油膜特性为边界条件，在螺旋桨位置施加单位横向激励力，得到2种校中状态下轴系在各轴承位置的振动加速度传递函数频谱如图6所示。

从图中可以看出，5～80 Hz范围内，与直线校中状态相比，负荷校中状态下轴系在各轴承位置的振动加速度传递函数在轴系尾部1阶弯曲振动固有频率15 Hz和局部弯曲振动固有频率47 Hz处的峰值显著减小，在37 Hz频率处的传递函数峰值增大，其他各阶弯曲振动频率处的峰值变化不大。可见，采用负荷校中法能够有效抑制轴系在一些频率点的横向振动传递。

3 试验研究 3.1 试验台设计

在满足试验要求的基础上，尽量简化试验台的结构。试验台由电机、变频器、减速器、中间轴、弹性联轴器、尾轴、轴承及基座和质量盘组成。尾轴上装有3个轴承，尾轴尾端装有用于模拟螺旋桨的质量盘。在中间轴承的基座上装有顶伸螺钉，用于调整中间轴承的高度。在中间轴承一侧的轴上安装百分表，用于观测中间轴承标高的变化量。轴系试验台如图7所示。

由于尾轴上只有3个轴承，因此负荷校中时保持前后2个轴承的高度不变，仅调节中间轴承的高度。对试验轴系进行负荷校中，得到直线校中和负荷校中状态下各轴承的支反力和中间轴承标高如表4所示。

3.2 试验结果分析

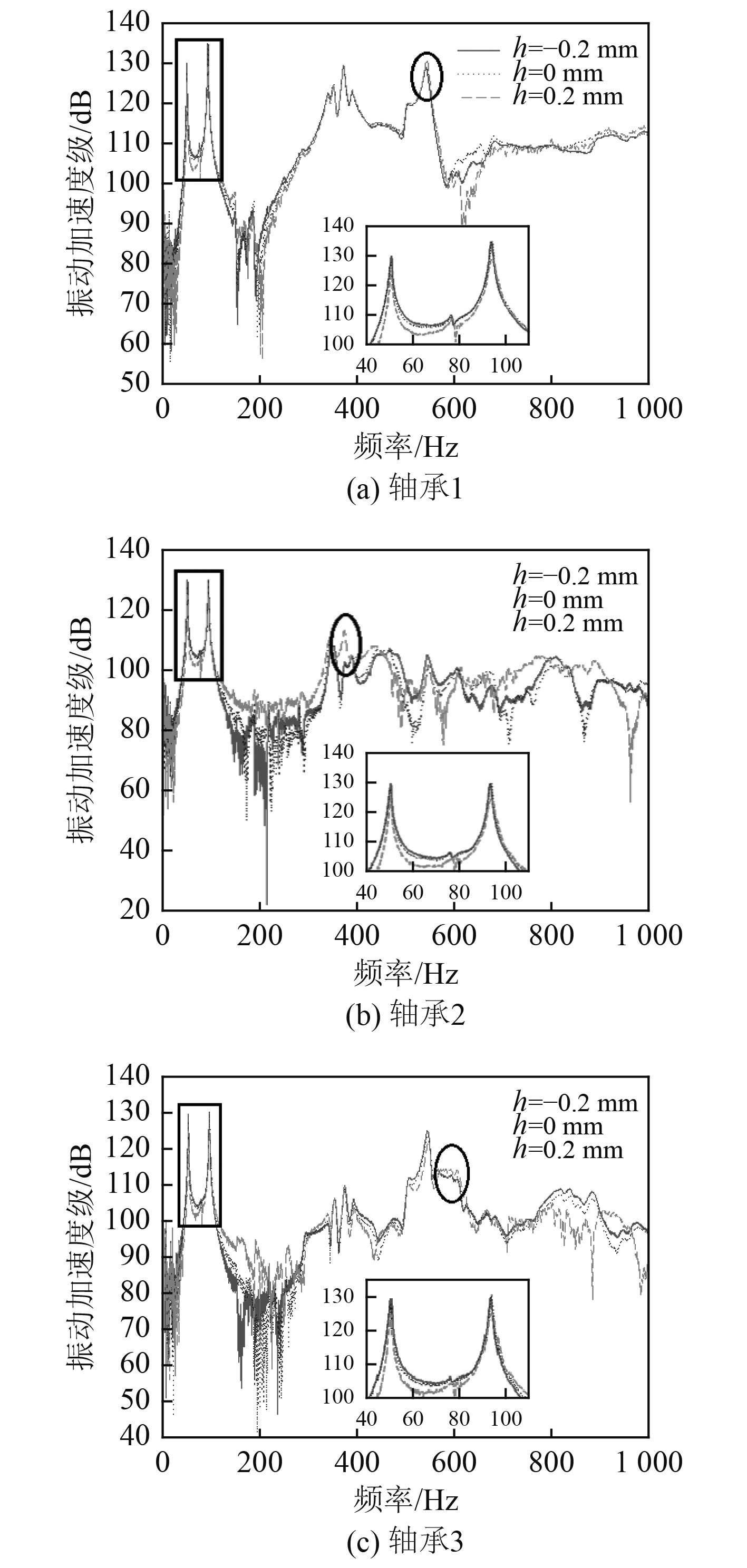
根据负荷校中结果，分别测试h=−0.2 mm，0，0.2 mm 3种轴系校中状态时各轴承基座处的振动加速度。螺旋桨横向激励力作用下，测得螺旋桨至3个轴承基座的振动加速度传递函数如图8所示。

从图中可以看出，螺旋桨横向激励力作用下，与直线校中状态相比，当h=−0.2 mm时，轴系在3个轴承处的加速度传递函数峰值增大，这是因为中间轴承向下移动导致该轴承的承载进一步减小，对轴系的支撑作用减弱，轴系在该轴承位置接近于脱空状态；按照负荷校中结果，当h=0.2 mm时，轴系在3个轴承处的加速度传递函数减小，这是因为直线校中状态时，由于螺旋桨的悬臂作用，导致中间轴承的承载较小，中间轴承向上移动增强了该轴承对轴系的约束，可见轴系负荷校中能够降低轴系对某些频率的振动传递。同时从图中椭圆形标示可以看到，在一些局部振动频率点，轴系的振动传递函数有所增大，这是因为轴承标高变化改变了轴系的支撑状态，导致轴系局部模态发生改变。这与2.2节中的分析结论相一致，说明轴系校中状态对螺旋桨横向激励力的传递有较大影响，整体上来说负荷校中比直线校中能取得更好的振动控制效果。

4 结　语

本文首先对某船推进轴系进行了负荷校中，重点研究了轴承变位对轴承油膜特性和校中状态对轴系横向振动传递特性的影响，最后通过缩比模型试验对仿真分析结论进行验证。试验结果与仿真分析结论基本一致，轴系横向振动对校中状态比较敏感，负荷校中能够有效抑制轴系尾部的1阶弯曲振动。总的来说，负荷校中比直线校中法能取得更好的振动控制效果，对轴系进行负荷校中十分必要。