2. 海军工程大学动力工程学院,湖北 武汉 430033
2. College of Power Engineering, Naval Universitg of Engineering, Wuhan 430033, China
供水管路系统对舰船的重要性毋庸置疑,然而由于空间限制,舰船上的管道有很大一部分布置在人员难以检查的区域,一旦发生泄漏不易被及时发现导致舰船续航力下降。因此研究舰船管道泄漏的识别与定位方法具有较大的实用价值。普通的管道泄漏检测方法主要有听音法、示踪法、压力/流量检测、探地雷达、红外检测、管道机器人检查、光纤/电缆检测法、超声检测法、漏声/振动信号检测等[1]。其中,基于声振信号的相关检测法具有较高的泄漏识别定位能力,成为供水管道泄漏检测的重要方法之一[2],而且此方法在舰船环境中适用性强。基于此,本文主要研究管道泄漏振动信号产生原因及其影响因素,为舰船管道泄漏检测奠定基础。
1 泄漏管道振动产生机理供水管道泄漏振动主要是由泄漏处湍流及空化现象产生,水中产生的振动耦合到管壁上,使管道也产生并传播振动,因此可以利用管壁上采集的振动信号进行泄漏识别与定位。
1.1 空化现象产生的振动空化现象描述的是液体中气泡的产生、发展及溃灭的过程。当液体中局部压力下降到空气分离压,甚至降到液体饱和蒸汽压力以下时,液体中溶解的气体析出或液体汽化都会产生气泡,当气泡随水流运动至压力较大区域,气泡会迅速缩小直至溃灭,在空泡消失的瞬间,四周的水流向空泡中心冲击,产生强烈的振动。
荷兰科学家Minnaert提出了气泡脉动理论[3],得出单个气泡溃灭产生的振动频率f为:
| $f = \frac{1}{{2{\text{π}} r}}\sqrt {\frac{{3\gamma P}}{\rho }} \text{。}$ | (1) |
其中:ρ表示液体密度,
| ${r_{\max}} = \sqrt {\frac{{2P}}{{3\rho }}{t_g}}\text{。} $ | (2) |
其中:
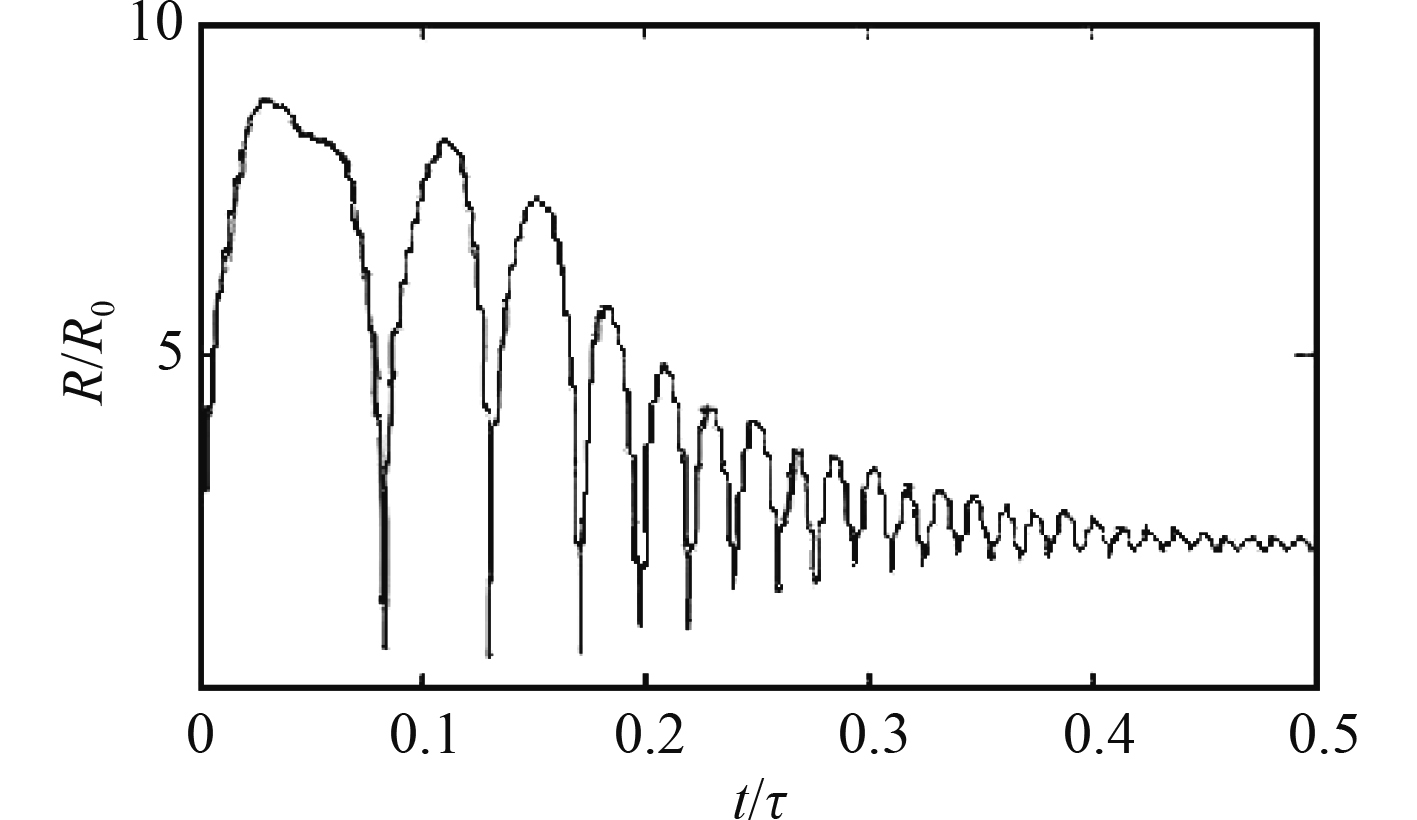
|
图 1 气泡溃灭阶段半径随时间的变化情况 Fig. 1 The variation of the radius of the bubble collapse phase with time |
黄景泉[7]研究了空泡溃灭产生的声压p,在距离空泡为l的某点,由空泡溃灭产生的声压表达式为:
| $ \begin{aligned} & p\left( {r,l} \right) = \frac{\sigma }{l}\left[ {{{\left( {\frac{{{R_0}}}{r}} \right)}^2} - 3} \right] + \frac{{{p_\infty } - {p_v}}}{l}\left\{ {\frac{{4r}}{3}\left[ {{{\left( {\frac{{{R_0}}}{r}} \right)}^3} - 1} \right] - \frac{{R_0^3}}{{{r^2}}}} \right\} - \\ & \frac{{{P_1}}}{{\left( {1 - \gamma } \right)l}}\left\{ {\frac{{4r}}{3}\left[ {{{\left( {\frac{{{R_0}}}{r}} \right)}^3} - {{\left( {\frac{{{R_0}}}{r}} \right)}^{3\gamma }}} \right] - \frac{{R_0^3}}{{{r^2}}} + \frac{{\gamma R_0^{3\gamma }}}{{{r^{\left( {3\gamma - 1} \right)}}}}} \right\} \text{。} \\[-17pt] \end{aligned} $ | (3) |
其中:R0是空泡溃灭时的起始半径,
实际情况中,空泡并不是单独出现的,在管道泄漏口附近的低压区域会有大量的气泡产生,研究空泡溃灭对管道的影响要研究其总声压对管道的作用,即所有空泡溃灭产生的声压之和。
空化数cv是描述空化程度的量,其表达式为:
| ${c_v} = \frac{{{P_\infty } - {P_v}}}{{\rho v_\infty ^2/2}}$ | (4) |
式中:
总结以上各表达式可以得到,由单个空泡溃灭产生的振动与空泡半径和来流压力有关:空泡半径越大,产生的振动幅值越大,但频率越小;反之空泡小,产生的振动幅值小,但频率高;来流压力越大,溃灭产生的声压越强,相应的振动幅值越大。从整个空化区域考虑,产生的空泡数目越多,产生的声压越大,振动越强。
1.2 湍流产生的振动湍流边界层是随机变化的,并且会产生脉动压力,进而产生振动。有研究表明脉动压力起伏程度与流速有关,在湍流中,因速度场变化而产生声压是随机函数,根据Mani[8]的研究,湍流区产生的声压近似为:
| $p \approx C\frac{{\rho {v^8}{L^2}}}{{2{c^5}}}\text{。}$ | (5) |
其中:C正比于湍流体积,L为涡流的特征长度,通过上式可以得到,湍流声的功率与流体流速及特征涡流的大小成正相关的关系。
2 管壁上测点的振动响应方程在管壁上采集的振动信号是泄漏振动源的响应和传递。流场中湍流、空泡产生的声压引起管道的振动,且振动强度与声压成正相关的关系。
将管道上某点采集的泄漏振动信号可用傅里叶级数形式表示为:
| $ x\left( t \right) = \mathop \sum \limits_{i = 1}^{{\rm{i}} \to \infty } {a_i}\sin \left( {2{\text{π}} {f_i}t + {\theta _i}} \right) $ | (6) |
其中fi表示第i个频率,ai为其振幅,
| $ x\left( t \right) = \mathop \sum \limits_{i = tl}^{tg} {a_{ti}}\sin \left( {2{\text{π}} {f_{ti}}t + {\theta _{ti}}} \right) + \mathop \sum \limits_{i = kl}^{kg} {a_{ki}}\sin \left( {2{\text{π}}{f_{ki}}t + {\theta _{ki}}} \right) + y\left( t \right)\text{。} $ | (7) |
其中
| ${a_{ti}} = {b_{ti}}C\rho {v^8}{L^2}/2{c^5} = {C_t}{b_{ti}}{d_i}{v^8}\text{。}$ | (8) |
其中:Ct为常量,与水的物理属性有关;bti代表声压与管道的耦合系数,与管道材质尺寸有关;di是与湍流区大小有关的量。
对于气泡而言,由式(3)可知,单个气泡产生的声压与管内压力、气泡初始溃灭半径等有关,而由式(2)可知,气泡半径与压力有关。由式(4)可知,空化数与来流压力、速度有关,故气泡溃灭产生的振动幅值aki可以简化为:
| ${a_{ki}} = {C_k}{b_{ki}}{p_{ki}}/{v^2}\text{。}$ | (9) |
其中Ck为常量,bki同样是声压与管道的耦合系数,pki是与来流压力大小有关的量。将式(8)和式(9)代入式(7)中,可得管道上振动信号的数学表达式为:
| $ \begin{split} & x\left( t \right) = \mathop \sum \limits_{i = tl}^{tg} {C_t}{b_{ti}}{d_i}{v^8}\sin \left( {2{\text{π}} {f_{ti}}t + {\theta _{ti}}} \right)+ \\ & \mathop \sum \limits_{i = kl}^{kg} \left( {{C_k}{b_{ki}}{p_{ki}}/{v^2}} \right)\sin \left( {2{\text{π}}{f_{ki}}t + {\theta _{ki}}} \right) + y\left( t \right)\text{。} \end{split} $ | (10) |
假设产生振动的湍流和空化区域大小远远小于泄漏点与检测点的距离,则在管道上距离泄漏点距离为l的某点的振动响应方程可表述为:
| $ \begin{split} & x\left( {l,t} \right) = \mathop \sum \limits_{i = tl}^{tg} {C_t}{b_{ti}}{d_i}{v^8}sin\left[ {2{\text{π}}{f_{ti}}\left( {t + \frac{l}{c}} \right) + {\theta _{ti}}} \right] + \\ & \mathop \sum \limits_{i = kl}^{kg} \left( {{C_k}{b_{ki}}{p_{ki}}/{v^2}} \right)\sin \left[ {2{\text{π}} {f_{ki}}\left( {t + \frac{l}{c}} \right) + {\theta _{ki}}} \right] + y\left( {t + \frac{l}{c}} \right) \text{。} \end{split} $ | (11) |
其中c表示信号传播速度。由此可知,管内压力、流速、湍流区域大小等因素会对湍流和空泡引起的振动起到不同的影响。
3 管道泄漏仿真分析为验证上述方程的正确性,应用计算流体力学软件对管道泄漏情况进行仿真。为简化计算,以长直管道上的泄漏故障作为仿真研究对象。在仿真计算时选用k-ε模型,选用的管道为管内径20 mm,厚度为3 mm的不锈钢管,长度200 mm,图2即为泄漏管道三维模型,设置初始条件为:流速1.5 m/s,管内压力0.2 MPa(此为相对压力,以大气压力作为参考值,下文中若无特殊说明皆为相对压力),模拟泄漏的小孔直径为3 mm,泄漏孔出口压力设为0 MPa。
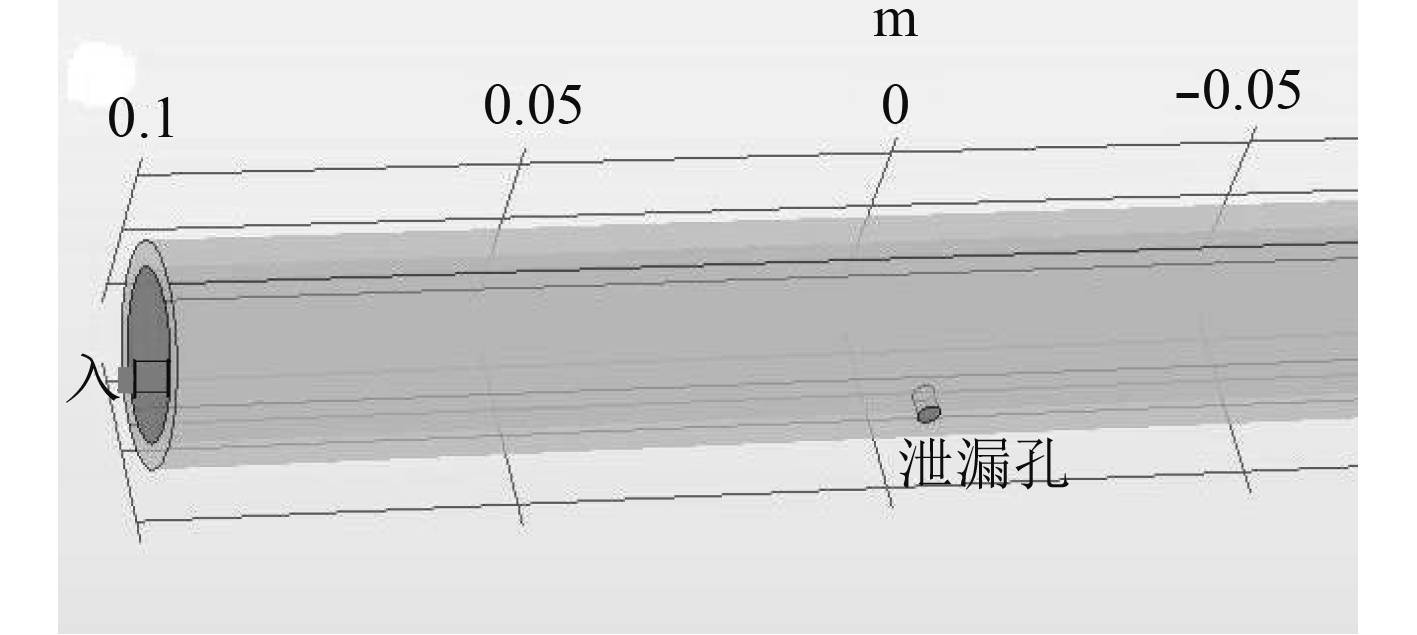
|
图 2 泄漏管道三维模型 Fig. 2 Three-dimensional model of leaking pipeline |
分别将管内压力调整为0.1 MPa,0.2 MPa,0.4 MPa进行仿真计算,结果如图3和图4所示。
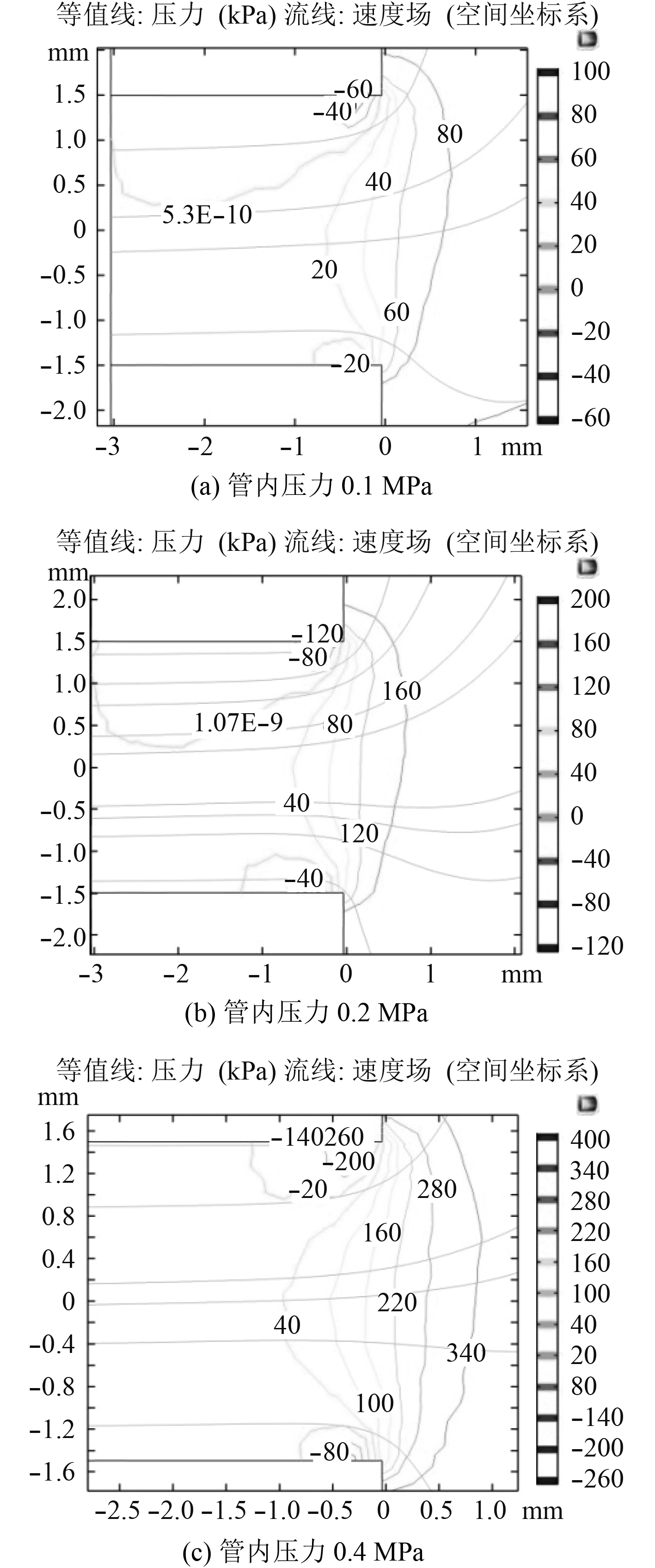
|
图 3 不同管内压力情况下泄漏处流场压力分布 Fig. 3 Flow field pressure distribution at the leak in different tube pressures |
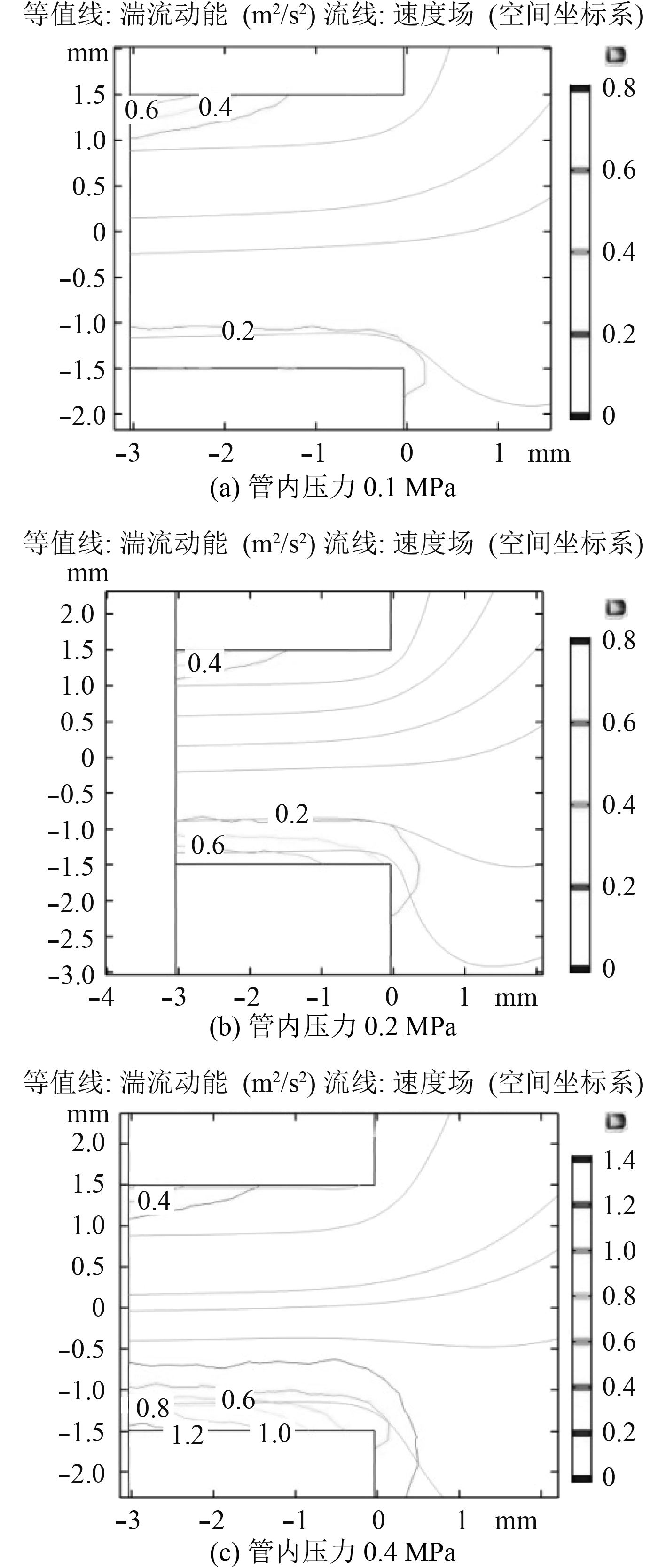
|
图 4 不同管内压力情况下流场湍流动能等值线 Fig. 4 Flow field turbulent energy contours under different tube pressures |
图3为泄漏处切面的流场等压力线分布图,各图中均形成了两个低压区,分别在泄漏口与主管交接处的上、下游两侧,上游的低压中心压力分别为:–60,–120,–260 kPa,下游的低压中心压力分别为:–20,–40,–100 kPa。比较3幅图中的压力分布情况可以得出:随着主管内压力的增加,低压区中心压力更低、低压区域更大,这些都有利于气泡的产生。根据上文关于空化气泡最大半径式(2)的表述,来流的压力高会导致空泡的半径较大[9],由式(3)可知气泡溃灭起始半径大则空泡产生的声压高,而且更大的低压区会使气泡产生数目增加,故耦合到管道上使其振动强度增大。即管内压力越大,泄漏处气泡的产生与溃灭导致的振动更强,符合式(11)的表述。
湍流动能的表达式为式(12),其值的大小可体现湍流引起振动的程度。
| $k = \frac{1}{2}m\left( {{{\overline {u'} }^2} + {{\overline {v'} }^2} + {{\overline {w'} }^2}} \right)\text{。}$ | (12) |
| $\overline {u'} = \frac{1}{T}\int_{{t_0} - \frac{T}{2}}^{{t_0} + \frac{T}{2}} {\left( {u - \bar u} \right){\rm d}t}\text{。} $ | (13) |
其中
| $\overline u = \frac{Q}{{A'}} = \frac{{\sqrt {\Delta P/\rho gSL} }}{{A'}}\text{。}$ | (14) |
其中:
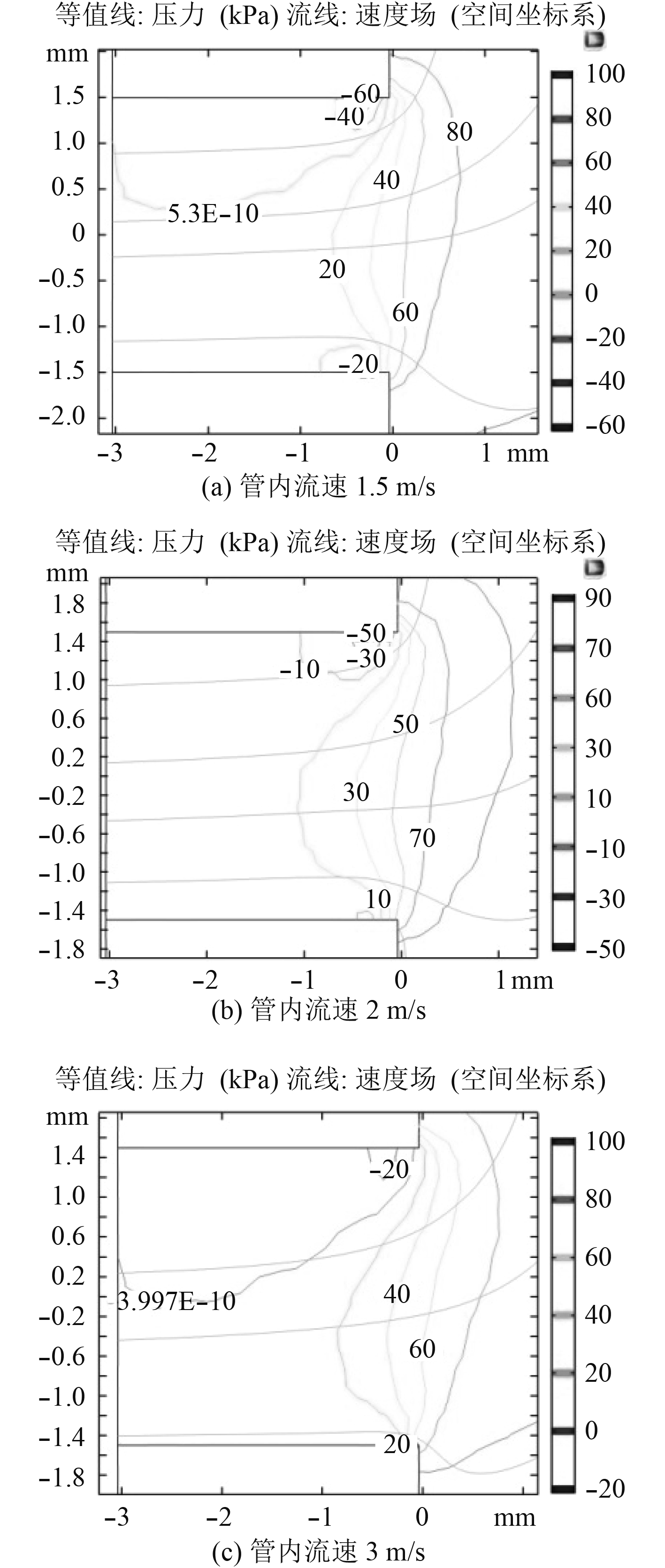
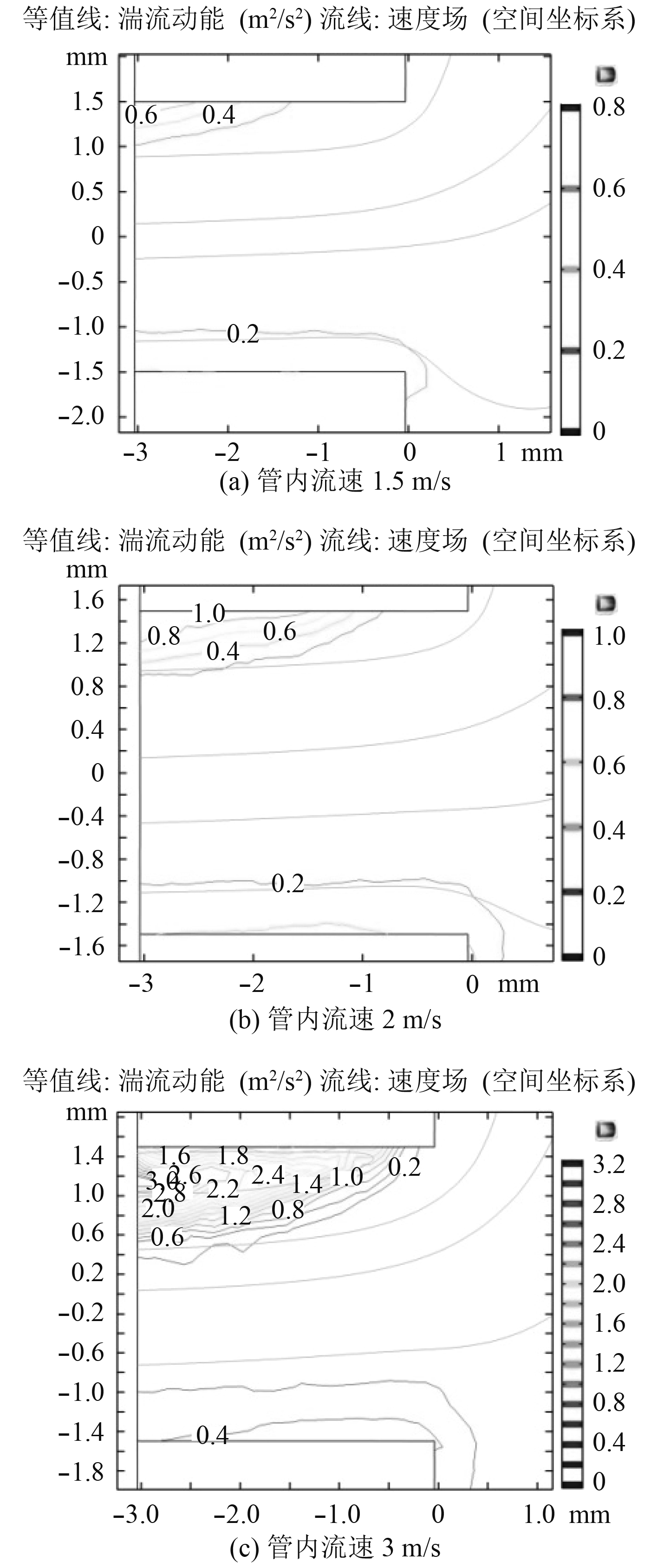
选用同样的管道模型,设置管内压力为0.1 MPa,分别将流速从1.5 m/s调整到2 m/s,3 m/s进行仿真计算,得到的压力分布,速度分布与湍流强度分布结果如图5和图6所示。
|
图 5 不同管内流速情况下流场压力等值线 Fig. 5 Flow field pressure contours for different flow rates |
|
图 6 不同管内流速情况下流场湍流动能等值线 Fig. 6 Flow field turbulent energy contours in different tube flow rates |
由图5(a)可以观察到,管内压力不变的情况下随着主体流速的增加,低压区的中心压力在升高,分别为–60,–50,–20 kPa,均在水的饱和蒸汽压力以上,故没有汽化产生的气泡,只有溶解的空气析出而产生的气泡,低压区压力在升高,由式(2)可知气泡半径会减小,则由式(1)可知气泡溃灭产生的频率会升高,但引起的振动幅值会降低,即高频部分的振动幅值将减小。
观察图6可知随着流速的增加,上游湍流动能较大的区域在逐渐增大,湍流动能也在增大,而下游的湍流区域则变化不大。随着主管中流体流速的增加,湍流动能迅速增大的区域,其流速也有所增加,符合式(11)的描述。
由上述分析可得:在管内压力不变的情况下,随着管内流体流速的增加,低压区压力上高,气泡产生的振动频率升高,幅值减小;湍流区域增大、湍流动能变大导致湍流引起的振动强度增加。
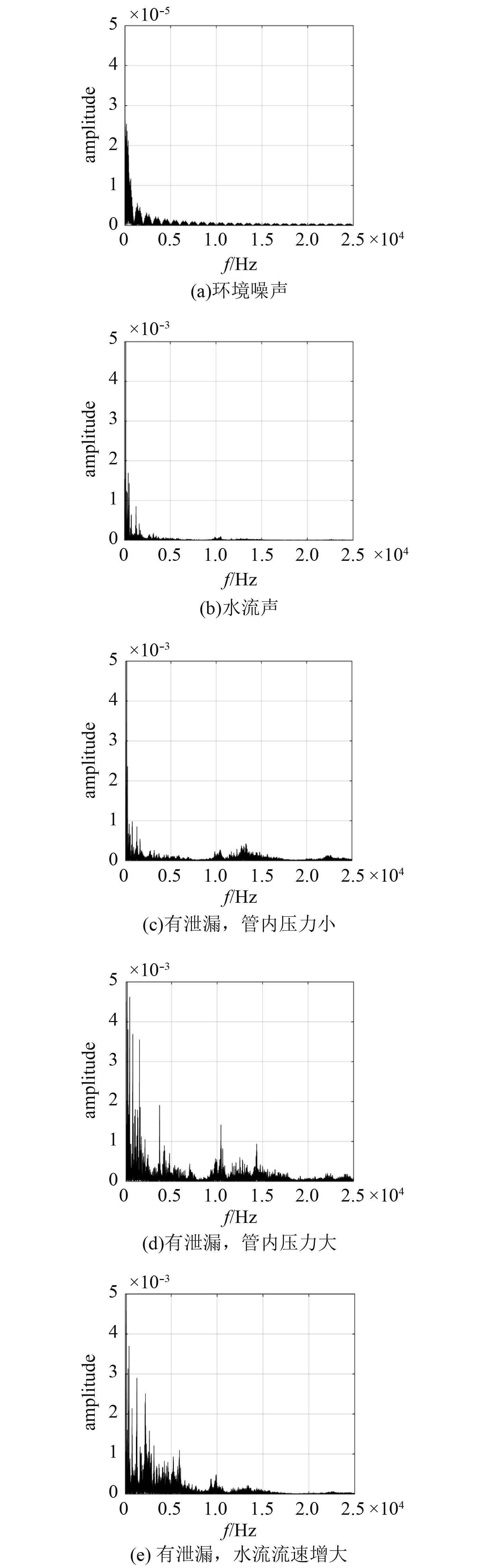
4 实 验图7为实验室采集的管道振动信号的频谱图,其中图7(a)采集的是空水管的信号,代表环境噪声,图7(b)为水管内有水流但管道无泄漏情况,图7(c)~图7(e)为管道有泄漏时采集的信号,其中图7(d)情况中管内压力比图7(c)大。图7(e)与图7(c)压力同,但图7(e)流速高。由图7(a)可以看到环境噪声幅值比其余信号幅值小100倍以上,且主要分布在较低频段。由图7(b)可以看到,实验室管道中水流动引起的管道振动主要集中在0-2kHz范围内。由图7(c)~图7(e)可以发现,泄漏振动信号在低频和高频部分都存在,其中10-18kHz部分与文献[6]的实验相符,可以认为主要由是空泡溃灭引起的振动,而频率较低部分则可以认为主要是由湍流引起的。图7(d)中空泡溃灭引起的高频振动部分幅值比图7(c)大,且频段稍有偏移,即压力的增加导致空泡溃灭振动增强。而在湍流主要起作用的低频段,图7(d)中的低频部分比图7(c)中相应部分幅值高。这些情况与式(11)相符,比较图7(c)~图7(e)可以发现,随着流速的增加,振动信号的低频部分幅值增幅较大,而高频部分幅值反而减小,符合式(11)的描述,由此可证实本文所建管道上测点的振动响应数学表达式符合实际情况。
|
图 7 不同情况下在管壁采集的振动信号 Fig. 7 Vibration signals collected by the pipe wall under different circumstances |
本文根据管道泄漏处湍流、空化引起的振动特性,建立了管壁上某点的振动响应方程,讨论了影响泄漏振动信号的因素,并通过仿真及实验验证了该方程的正确性。为进一步研究舰船环境中管道泄漏识别与定位奠定了一定的基础。
| [1] |
刘景斌, 王基, 刘树勇. 基于振动分析的损伤识别方法综述[C]. 全国声学设计与噪声振动控制工程学术会议.2017.
|
| [2] |
杨进, 文玉梅, 李平. 泄漏声振动传播信道辨识及其在泄漏点定位中的应用[J]. 振动工程学报, 2007, 20(3): 260-267. DOI:10.3969/j.issn.1004-4523.2007.03.010 |
| [3] |
MINNARERT M. Musical air-bubbles and the sound of running water[J]. Philosophical Magazine, 1933, 16. |
| [4] |
RAYLEIGH L. Pressure Developed in a Liquid During the Collapse of a Spherical Cavity[J]. Philosophical Magatine, 1917, 34(199): 94-98. |
| [5] |
陶跃群, 蔡军, 刘斌, 等. 湍流作用下空化泡的动力学分析和溃灭瞬间自由基产量计算[J]. 中国科学院大学学报, 2017, 34(2): 191-197. |
| [6] |
王国玉, 曹树良, 赵令家, 等. 高速水流中旋涡空化所引起的空蚀和振动[J]. 工程热物理学报, 2002, 23(6): 707-710. DOI:10.3321/j.issn:0253-231X.2002.06.014 |
| [7] |
黄景泉. 空泡起始和溃灭阶段的噪声[J]. 应用数学和力学, 1990, 11(8): 725-730. |
| [8] |
MANI R. The influence of jet flow on jet noise. Part I. The noise of unheated jets[J]. Journal of Fluid Mechanics, 1976, 73(4): 753-778. DOI:10.1017/S0022112076001602 |
| [9] |
黄继汤. 空化与空蚀的原理及应用[M]. 北京: 清华大学出版社, 1991.
|
 2020, Vol. 42
2020, Vol. 42
