2. 上海海事大学 附属职业技术学校,上海 200137;
3. 上海岽俊船舶工程有限公司,上海 200137
2. Shanghai Maritime University Affihiated Vocational and Technical School, Shanghai 200137, China;
3. Shanghai Donjun Ship Engineering Co., Ltd., Shanghai 200137, China
船舶在海上航行时,受风浪干扰,船体产生摇晃,其中横摇的危险性最高,除了加剧船舶负荷以及加重船员的疲惫感,当波倾角过大可能会导致船体倾覆,减摇鳍就是一种在海洋航行中能高效减少船体摇晃的装置。实际中,船舶结构复杂,很难基于力学原理建立精确的数学模型,所以针对控制对象变化,PID的动态调节性能变差,所以控制器的动态性能急需提高。
模糊控制是一种不需要依赖于精确控制模型的算法,它是用计算机来模拟实现人的思维方式,对于像船舶减摇鳍这类的变参数、非线性对象有很好的控制效果。将模糊控制与PID结合,实现在不同变化条件下PID三个参数实时整定,使得控制器性能极大优化。免疫系统抵御外界变化的能力十分明显,本文以模糊推理近似拟合免疫调节器,实现模糊控制和免疫算法的结合,设计一种适应性能力更高的减摇鳍模糊免疫控制系统。经仿真验证,该系统控制效果较传统PID显著提高。
1 海浪模型海浪的形成是由于风能的传递,使得海浪达到一种稳定发展的状态,基于随机性和不规则性的存在,无法将海浪波近似于任何规则波,实际建模中将长峰波海浪等效为多个波长、相位,以及波幅相互独立的规则波叠加而成。根据线性水波理论,在某一固定点的长峰不规则浪表达式为:
| $ \zeta (t) = \sum\limits_{n = 1}^\infty {{\zeta _{an}}\cos ({\omega _n}t + {\varepsilon _n})} {\text{。}} $ | (1) |
式中:
目前广泛采用海浪谱来模拟长峰不规则海浪,已有的海浪波能谱公式有PM谱、单参数波能谱(ITTC)、双参数波能谱(ISSC)、JONSWAP波谱[1]。选取ITTC谱,其公式为:
| $ {S_\zeta }(\omega ) = \frac{{0.008\,1{g^2}}}{{{\omega ^5}}}\exp \left( - \frac{{3.11}}{{h_{\frac{1}{3}}^2{\omega ^4}}}\right){\text{。}} $ | (2) |
式中:g为重力加速度,m2/s;
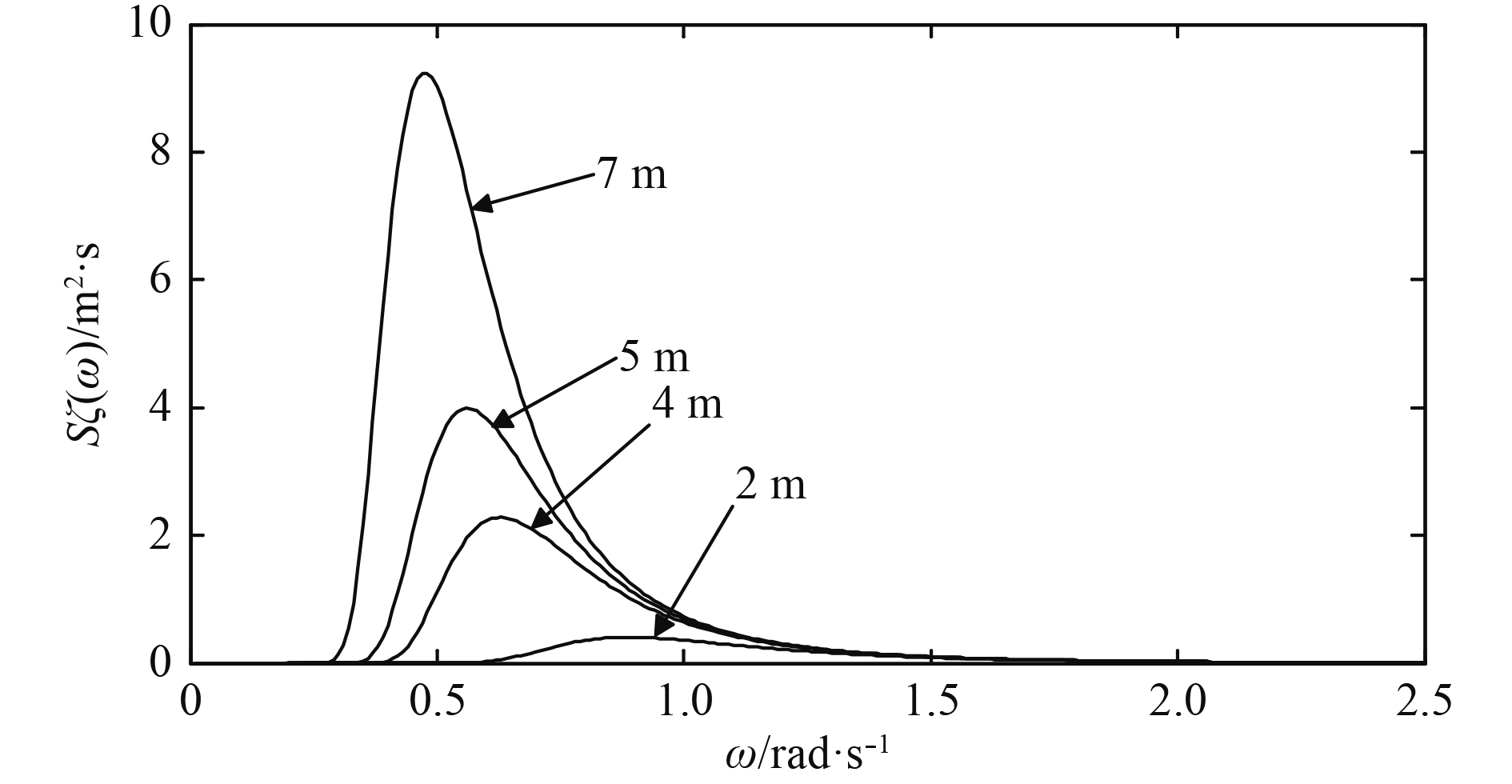
选取有义波高2 m,3 m,5 m和7 m,绘制其P-M谱,波谱如图1所示。
|
图 1 不同有义波高下波能谱密度图 Fig. 1 Waveform density map of different sense wave heights |
可以看出,海浪谱频率集中分布在
| $ {\alpha _\omega }{\rm{ = }}\frac{{\omega _n^2}}{g}\sum\limits_{n = 1}^{25} {\sqrt {2{S_\zeta }({\omega _n})\Delta \omega } } \cos ({\omega _n}t + {\varepsilon _n}){\text{。}} $ | (3) |
海浪传播方向和船舶航行方向之间的夹角称为遭遇角,遭遇角直接影响海浪对船的作用效果。当遭遇角一定时,船舶航行过程中受到海浪的作用频率就变为遭遇频率[2]:
| $ {\omega _e} = \omega \left(1 - \frac{{\omega V}}{g}\cos {\mu _e}\right){\text{。}} $ | (4) |
式中:g为重力加速度,V为船舶航行速度,
| $ \begin{split} &{\alpha _{\omega e}} = {K_B}{K_T}{\alpha _\omega }{\text{,}}\\ &{K_B} = 1 - \sqrt {{C_\omega }} {(B/\lambda )^2}{\text{,}}\\ &{K_T} = {e^{ - kd/2}}{\text{。}} \end{split} $ | (5) |
式中:
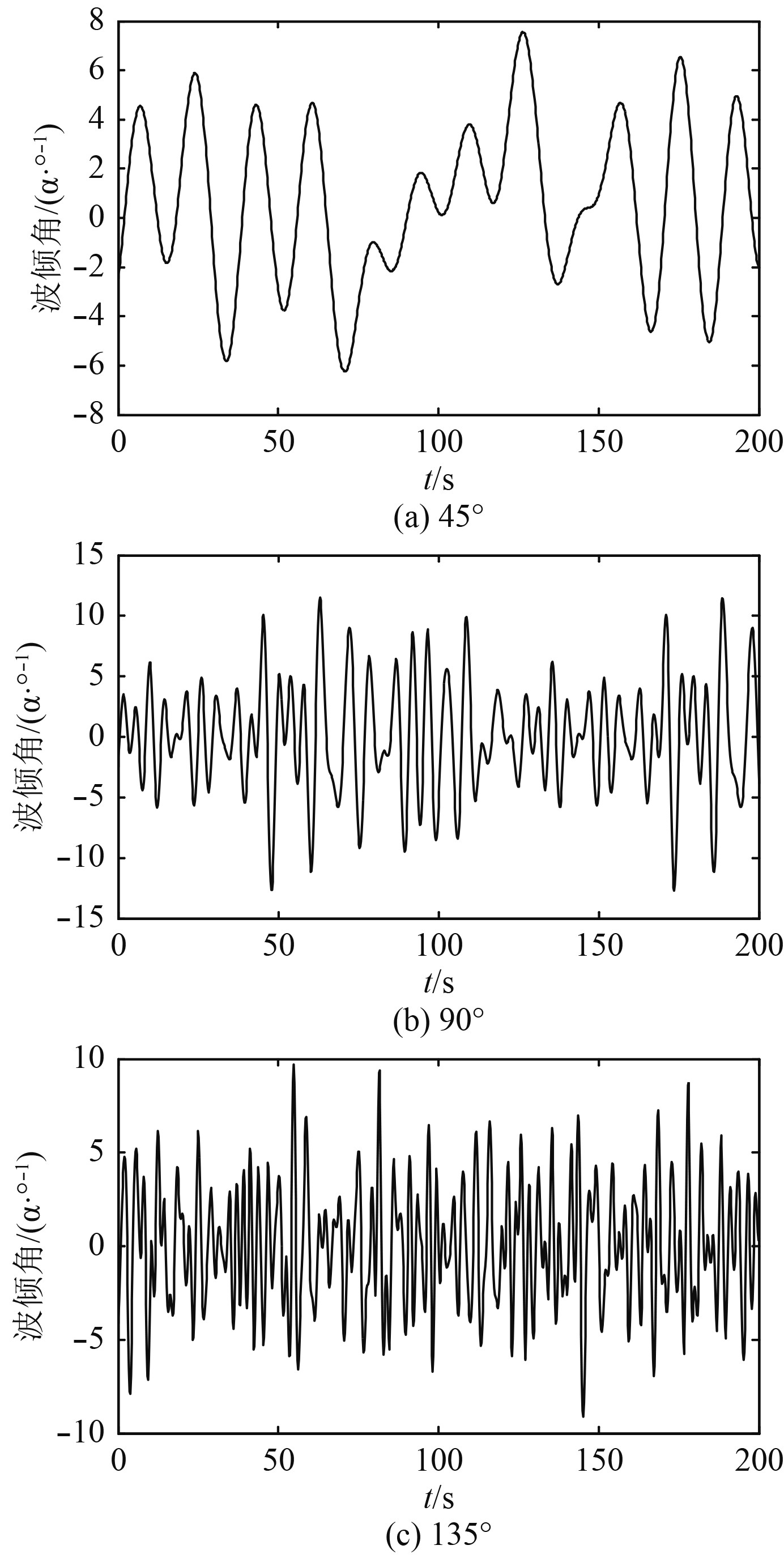
图2为45°,90°和135°遭遇角下的海浪波倾角曲线。
|
图 2 遭遇角分别为45°,90°,135°时的波倾角曲线 Fig. 2 Wave inclination curve of the encounter angles of 45°,90° and 135° |
船舶参数采用中谷2 500集装箱船,船宽B=16 m,吃水深度T=3 m,水线面系数为
依据Conolly理论,在船舶横摇角度较小的情况下,船舶横摇模型可近似表示为一二阶线性微分方程:
| $ ({J_\phi } + \Delta {J_\phi })\ddot \phi + 2{N_\phi }\dot \phi + Dh\phi = - Dh{a_e}{\text{。}} $ | (6) |
式中:
假设初始条件均为0,对上式微分方程进行拉氏变换,得到船舶横摇模型的传递函数:
| $ {G_\phi }(s) = \frac{{\phi (s)}}{{{a_e}(s)}} = \frac{1}{{T_\phi ^2{s^2} + 2{T_\phi }{\zeta _\phi }s + 1}}{\text{。}} $ | (7) |
式中:船舶固有周期
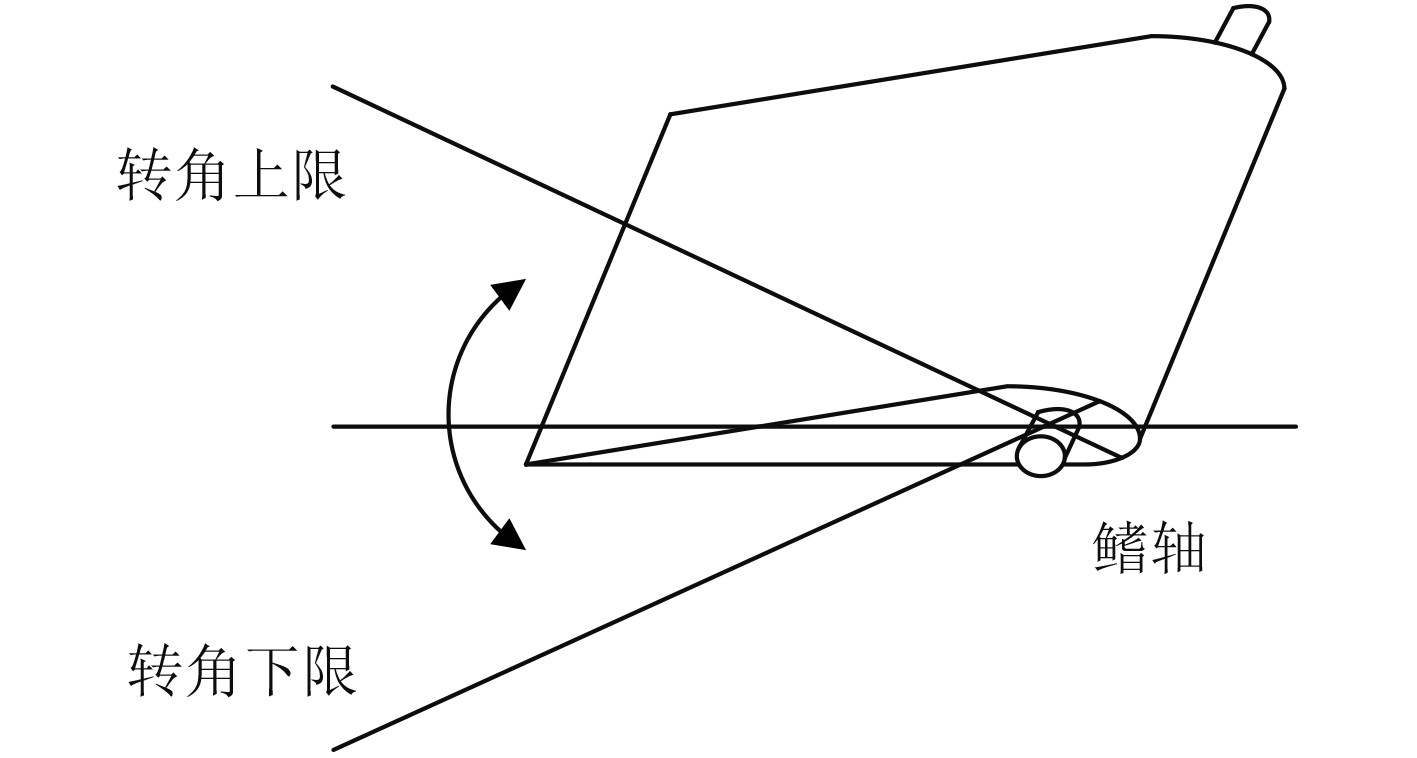
减摇鳍是仿生学在船舶上的一个成功应用实例。图3为减摇鳍的工作方式,他通过改变鳍轴转动的攻角从而减小船舶在海浪影响下的摇晃程度,鳍设置有转角的上下限。
|
图 3 减摇鳍工作方式 Fig. 3 Fins work mode |
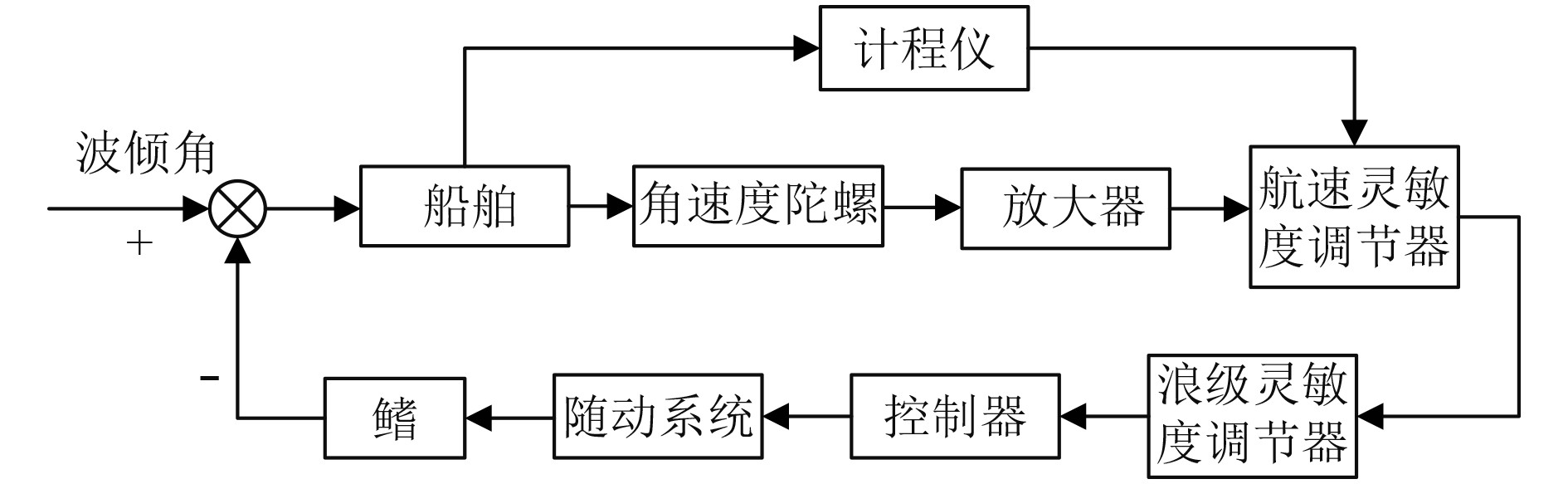
系统通过传感器检测得到船的倾斜角信息,利用液压等动力驱动减摇鳍转动,整个控制系统的作用是随着横摇角的变化改变鳍角,从而利用减摇鳍产生抵抗海浪干扰的稳定力矩,达到稳定船体的目的[4],如图4所示。
|
图 4 减摇鳍系统原理图 Fig. 4 Schematic diagram of the fin stabilizer system |
1)角速度陀螺仪
角速度陀螺仪能够测量船舶横摇角度及角速度变化,输出电压信号[5],传递函数为:
| $ {G_a}(s) = \frac{{400s}}{{{s^2} + 80s + 4\;000}}{\text{。}} $ | (8) |
2)放大器
对横摇角以及角速度信号进行放大,用以驱动下一级调节器,其传递函数为:
| $ {G_Q}(s) = {K_Q} = 40{\text{。}} $ | (9) |
3)航速调节器和浪级调节器
航速灵敏度调节器调节规律是根据最大以及最低航速来设定比例系数的;浪级调节器是为了在海情状况较严重的情况下,调节减摇鳍使其工作在线性,这里设定系数为:
| ${G_H} = {G_L} = 1\text{。}$ | (10) |
4)控制器
大多数减摇鳍采用PID控制,由于传统PID控制容易受外界干扰,实际应用中,往往会做一些改进,微分环节易被高频干扰,积分环节存在漂移,因此,控制器传递函数为:
| $ \begin{split} & {W_{PID}}(s) = {K_P} + \frac{{{K_I}}}{{{T_I}s + 1}} + \frac{{{K_D}{T_{d1}}s}}{{({T_{d1}}s + 1)({T_{d2}}s + 1)}} =\\ & {K_P} + \frac{{{K_I}}}{{24.607s + 1}} + \frac{{0.064{K_D}s}}{{(0.064s + 1)(0.18s + 1)}} {\text{。}} \end{split} $ | (11) |
5)随动系统
根据输入信号大小,将反馈电压放大送入异步电机控制绕组,利用液压调速系统驱动减摇鳍转动,使鳍能旋转对应角度。其数学模型近似等效为二阶振荡环节,传递函数如下:
| $ {G_s}(s) = \frac{{550}}{{{s^2} + 15s + 225}}{\text{。}} $ | (12) |
6)鳍角转换
鳍转动的角度到影响船的波倾角的转换近似为一比例环节,对于NJ5型减摇鳍,其转换系数为:
| $ {K_a} = 0.256\;4 {\text{。}} $ | (13) |
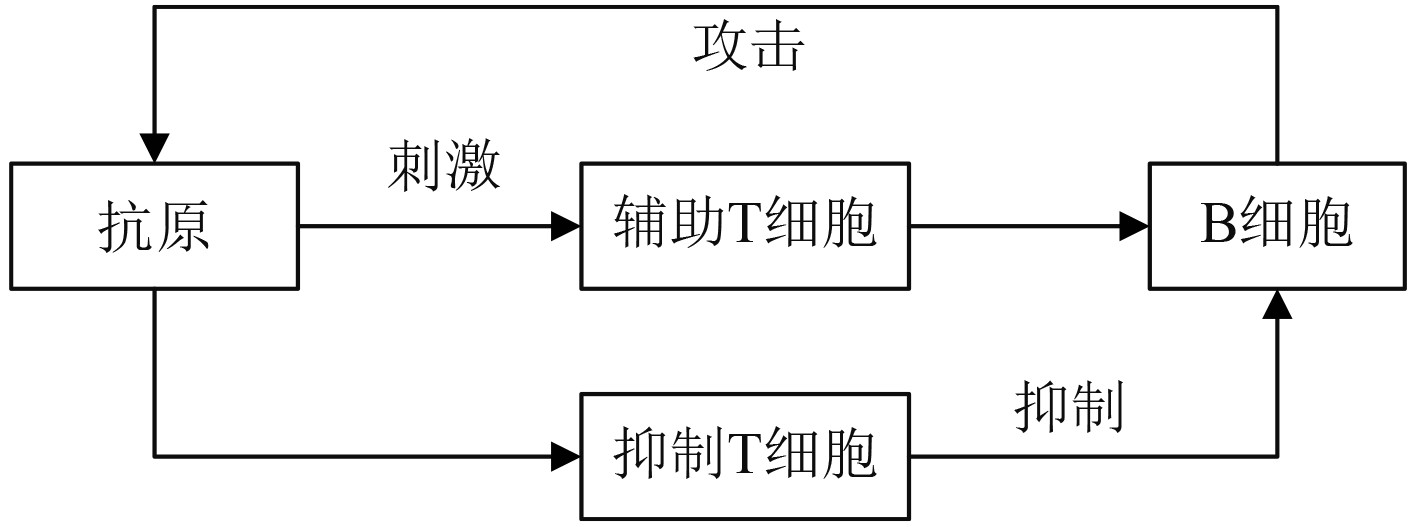
人体免疫系统中,T淋巴细胞和B淋巴细胞起主要作用。当体内出现抗原,B细胞会产生相应抗体与抗原特异性结合并消除。B淋巴细胞产生于骨髓,T淋巴细胞则由胸腺分泌,其中,T细胞有2种类型,一种是辅助性T细胞,能促进B细胞生成,另一种是抑制性T细胞,用以抑制B细胞分泌[6]。
|
图 5 免疫系统原理 Fig. 5 Principle of the immune system |
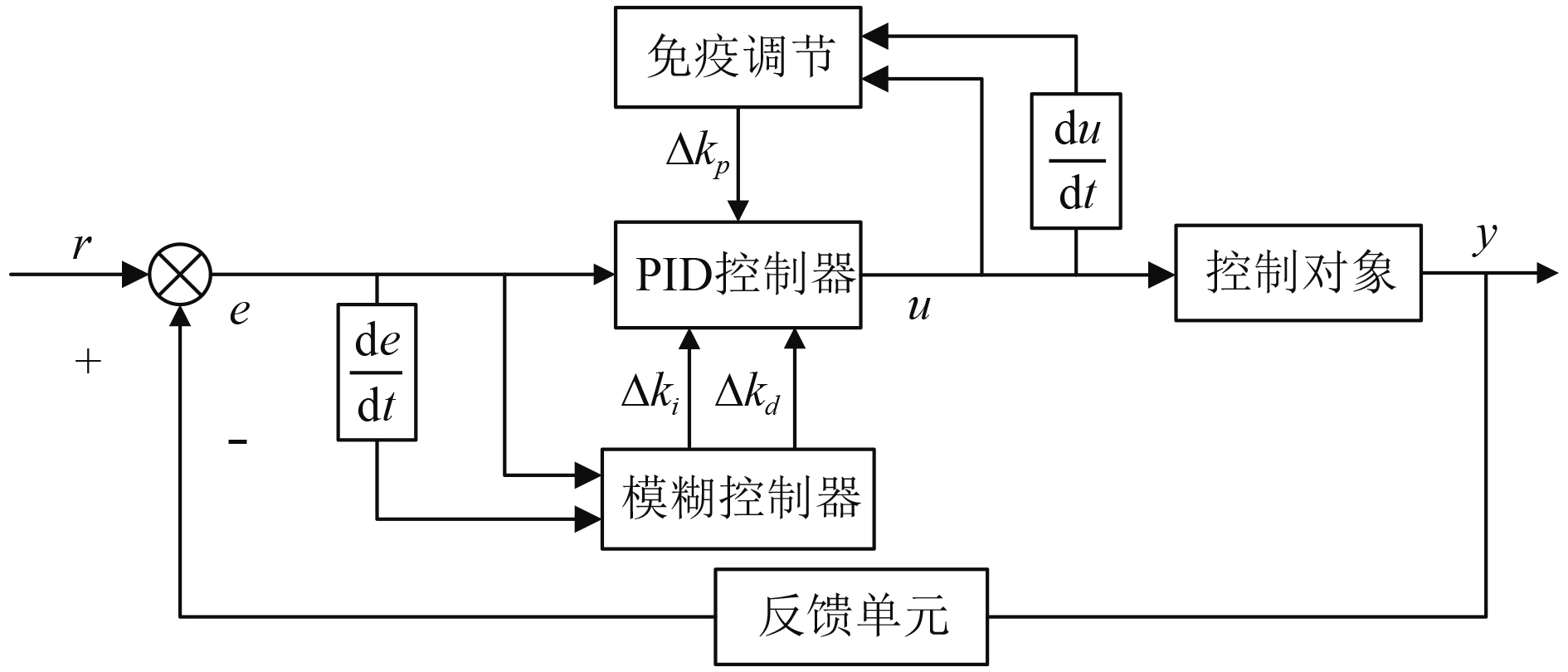
当体内抗原数量增多时,辅助性T细胞增多,抑制性T细胞减少,从而对B细胞的刺激作用增强,B细胞数量增加;抗原数量减少的情况下,抑制性T细胞增多,辅助性T细胞减少,对B细胞的抑制作用增强,B细胞数量减少。免疫细胞数量的动态变化使得免疫系统处于一个高效稳定的运行状态[7]。如图6所示,虚线代表抑制作用,实线代表促进作用。
|
图 6 模糊免疫原理图 Fig. 6 Fuzzy immune schematic |
假定第K代抗原数量为ε(k),辅助性T细胞数量为
| $ S(k) = {T_H}(k) - {T_S}(k){\text{。}} $ | (14) |
式中:
| $ u(k) = {k_1}[1 - \eta f(u(k),\Delta u(k))]e(k) = {k_p}e(k) {\text{。}} $ | (15) |
式中:
根据控制经验,有如下一些规则可以参考[9]:
1)当船体向左偏角及角速度均较大,左鳍需要快速转一较大正攻角,右鳍转相同大小的负攻角;
2)当船体向左偏角较大,角速度向左且偏小,左鳍需要转一较小的正攻角,右鳍转同一角度负攻角;
3)当船体向左偏角较小,角速度向右且偏小,此时使鳍在零位,即不转攻角;
4)当船体向左偏角较小,角速度向右且较大,右鳍转一正攻角,左鳍转一同角度负攻角。
模糊论域的划分对控制影响精度较大,这里采用经典的论域划分方式,控制规则采用49条,为
|
|
表 2 Δkd模糊规则 Tab.2 Table 1 Δkd fuzzy rules |
|
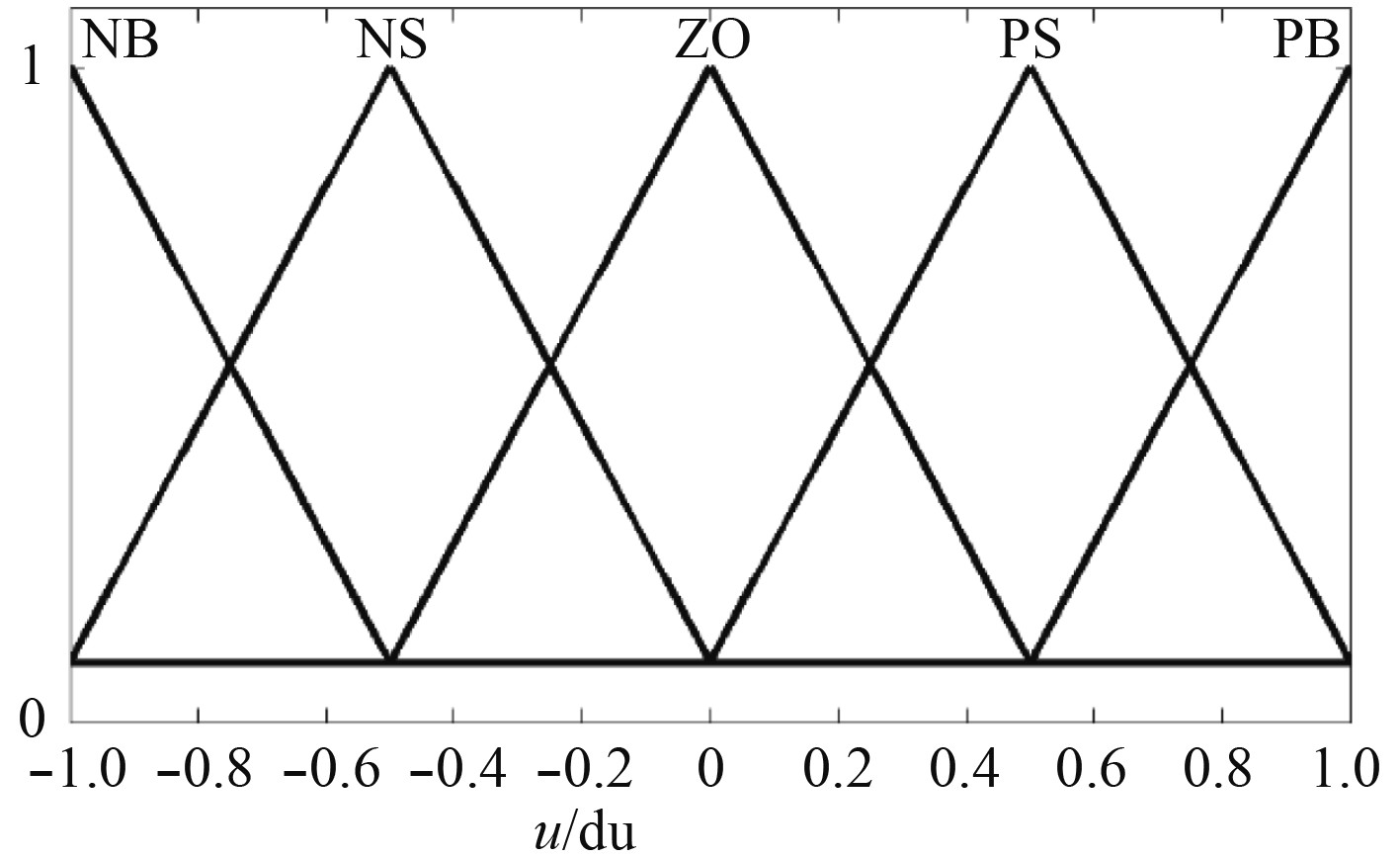
图 7 免疫输入隶属度 Fig. 7 Immunological input membership |
|
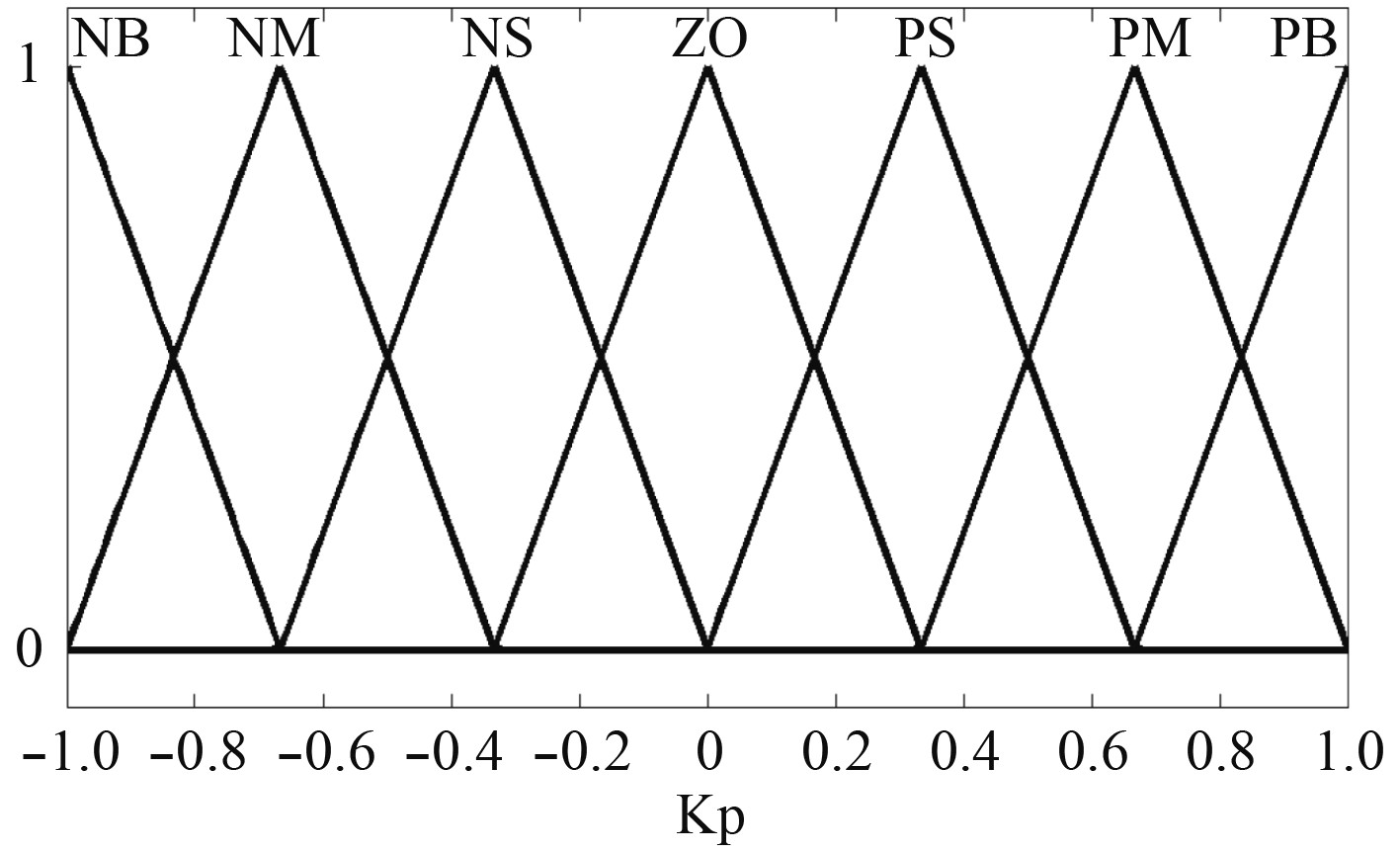
图 8 免疫输出隶属度 Fig. 8 Immunity output membership |
免疫控制的核心环节的是设计合适的非线性函数
依据免疫调节对抗原的特异性反应过程,建立模糊规则如表1~表3所示。
|
|
表 1 Δki模糊规则 Tab.1 Δki fuzzy rules |
|
|
表 3 免疫推理规则 Tab.3 Immune inference rules |
在Simulink环境下建立仿真,仿真输入信号为图2中的波倾角信号,波倾角在Matlab中利用m文件编程实现,减摇鳍完整仿真模型在Simulink中搭建,波倾角信号通过工作区数据传递到Simulink,有义波高为4 m。仿真时间为200 s,PID初始参数为4.2,3.5和0.6,e和ec的量化因子分别为0.5和0.3,微分积分的输出比例因子为0.6和0.5,模糊免疫调节中u和du的量化因子为0.08和0.001 5,
图9~图11为遭遇角分别为45°,90°和135°时横摇角变化曲线,单纯使用PID控制,动态特性较差,减摇鳍达到最大鳍角的可能性增加,减摇作用变差,对减摇鳍机械磨损加剧。模糊免疫控制使得船舶横摇角显著减小,同时应对不同海况,模糊免疫控制下减摇鳍工作饱和率更加平稳,减摇性能更加优越。
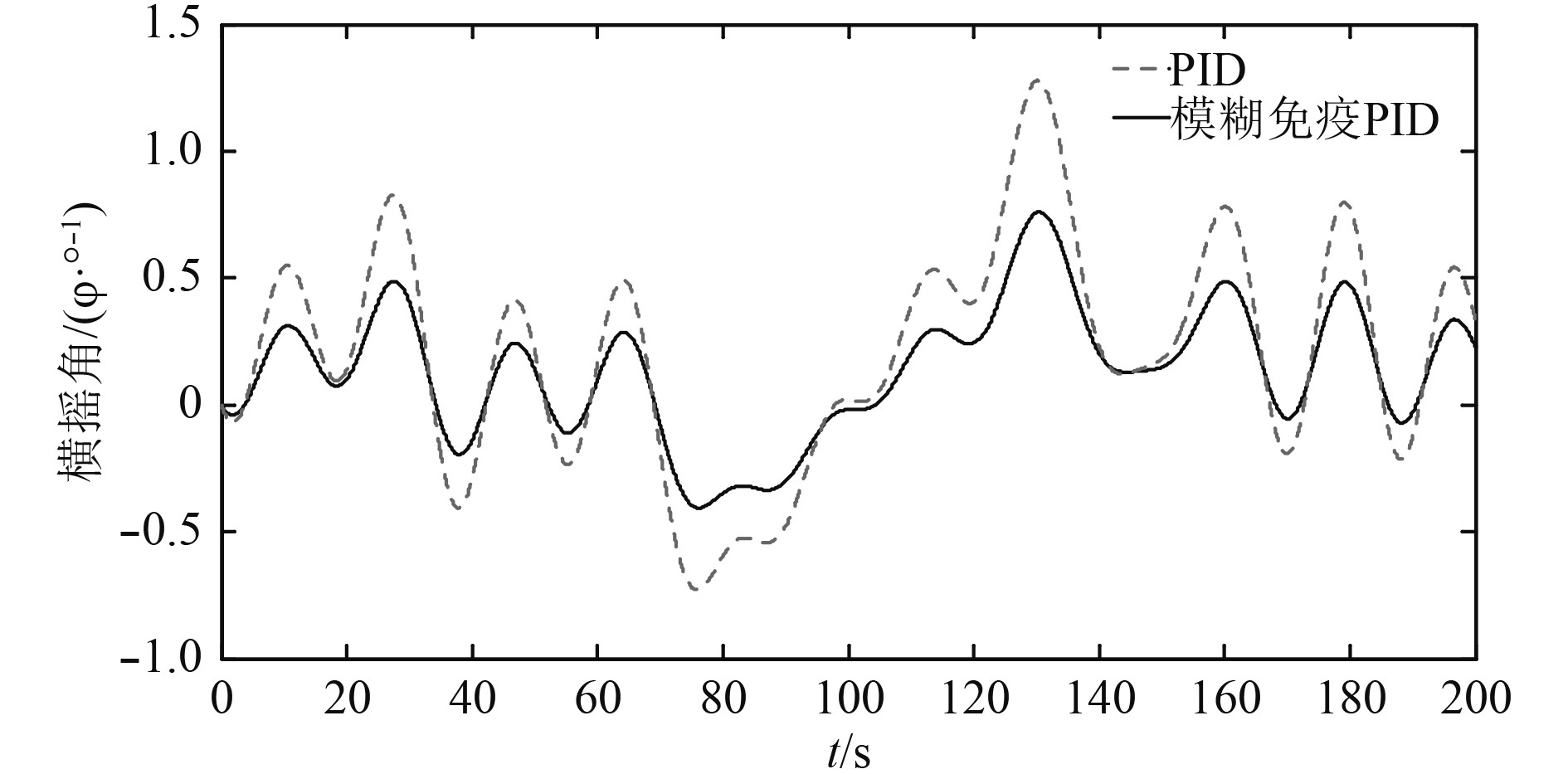
|
图 9 遭遇角为45°横摇角变化曲线 Fig. 9 The rolling angle curve of encounter angle 45° |
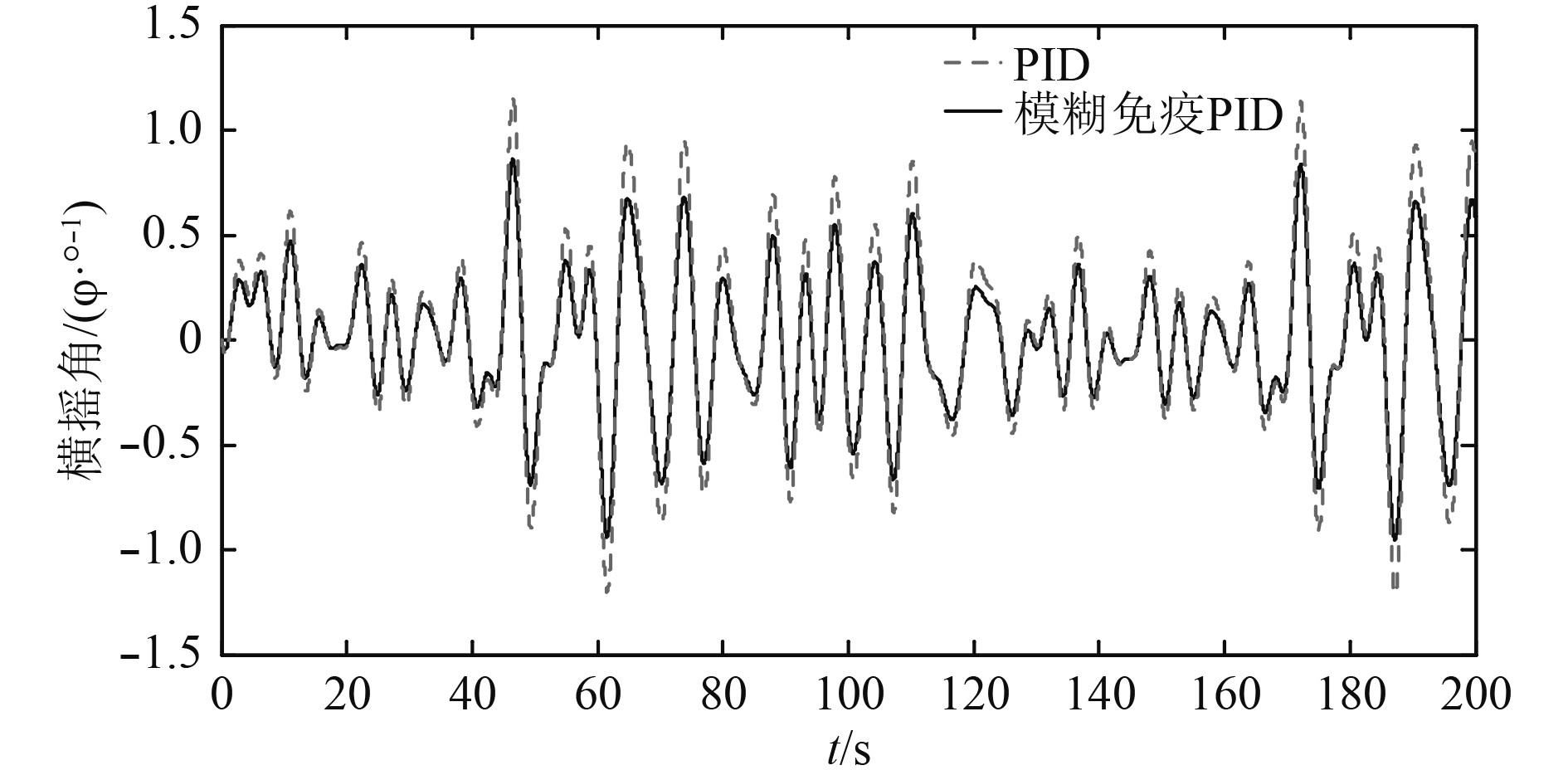
|
图 10 遭遇角为90°横摇角变化曲线 Fig. 10 The rolling angle curve of encounter angle 90° |
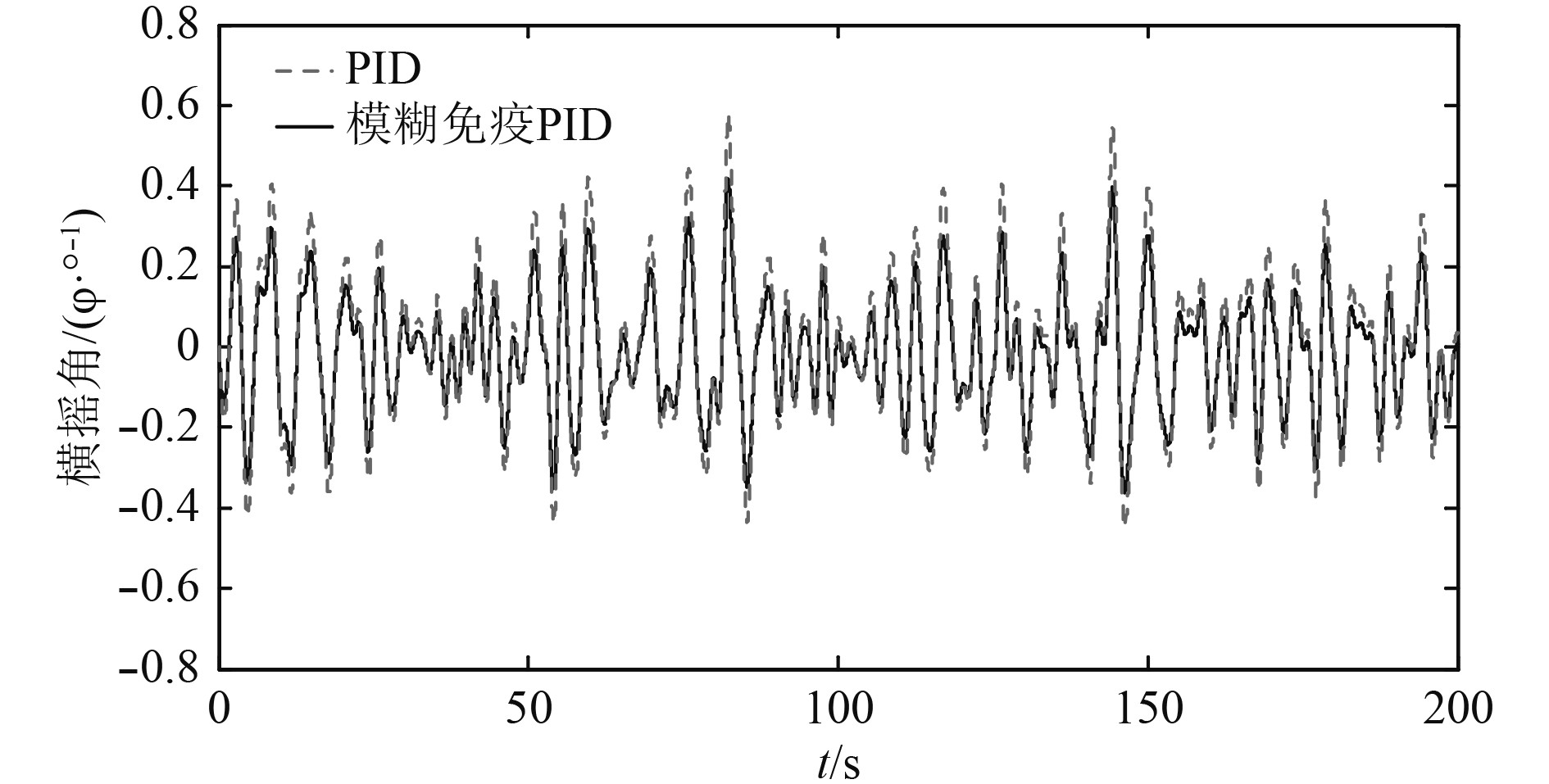
|
图 11 遭遇角为135°横摇角变化曲线 Fig. 11 The rolling angle curve of encounter angle 135° |
本文延续PID控制基础,设计了一种模糊免疫算法的船舶减摇鳍控制系统。模糊控制实时调整控制器积分和微分系数,免疫调节实时修正PID比例系数,利用模糊推理近似拟合免疫调节中的非线性函数,使得系统控制效果良好。Simulink仿真验证了所设计方案的可行性,模糊免疫控制使得减摇鳍能够较好地适应海洋环境变化,有效抑制海浪干扰,维持船体稳定。
| [1] |
郑则炯, 梁文祯. 基于变结构鲁棒性控制的船舶减摇鳍非线性系统研究[J]. 舰船科学技术, 2017, 39(22): 46-48. |
| [2] |
刘志全, 金鸿章. 基于航速保持的舵减摇控制方法[J]. 中国舰船研究, 2017, 12(1): 128-133. DOI:10.3969/j.issn.1673-3185.2017.01.019 |
| [3] |
张树豪. 基于自抗扰控制的船舶横摇控制研究[D]. 大连: 大连海事大学, 2016.
|
| [4] |
田军. 舵鳍联合控制参数优化及仿真[J]. 自动化技术与应用, 2015, 34(7): 9-13. |
| [5] |
Q. Zhigang, L. Yanwen J. Hong, Research on the lift characteristic of morphing bionic fin stabilizer at zero/low speed[C]// 2015 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, 2015, 1374-1378.
|
| [6] |
闫爱平, 王帆. 减摇鳍系统自适应反演滑膜控制的设计及仿真研究[J]. 舰船科学技术, 2016, 38(12): 16-18. |
| [7] |
王辉, 王科俊, 于立君. 减摇鳍模糊免疫自适应PID控制器设计及仿真研究[J]. 海军工程大学学报, 2007(4): 17-21+29. DOI:10.3969/j.issn.1009-3486.2007.04.005 |
| [8] |
段玉波, 马杰. 模糊免疫PID控制器设计及其仿真研究[J]. 自动化技术与应用, 2017, 36(4): 106-110. |
| [9] |
梁利华, 赵朋, 张松涛, 等. 基于相位匹配的零航速减摇鳍控制策略研究[J]. 哈尔滨工程大学学报, 2018, 39(9): 1539-1545. |
 2020, Vol. 42
2020, Vol. 42
