2. 中国船舶及海洋工程设计研究院,上海 200011;
3. 喷水推进技术重点实验室,上海 200011
2. Marine Design and Research Institute of China, Shanghai 200011, China;
3. Science and Technology on Water Jet Propulsion Laboratory, Shanghai 200011, China
前置导叶喷水推进轴流泵是近年来随潜艇降噪技术发展而产生的一种新泵型,与传统的后置导叶喷水推进轴流泵相比,前置导叶喷水推进轴流泵将导叶安装在动叶轮前的低压区,脉动压力低,水流经过前置导叶,产生一个与叶轮旋向相反的负预旋,抵消了由于动叶轮旋转产生的周向诱导速度。前置导叶优化了叶轮进流,激振力减小,水动力噪声会大大减小。此外,前置导叶还充当了叶轮轴的前支架,简化了推进泵的结构,缩短了轴向尺寸。前置导叶喷水推进轴流泵的这些优点契合了军用舰船对结构尺寸紧凑和噪声低等性能的要求,因此,前置导叶喷水推进轴流泵已经被越来越多的国家重视,并应用于潜艇、扫雷艇等军用船舶上。
1 与常规轴流泵的对比常规喷水推进轴流泵基本为卧式布局,水从船底进口吸入,经弯曲的进水流道进入到动叶轮,旋转的动叶轮把机械能转换成水的位能、动能和压力能。动能表现为液流的轴向速度和周向诱导速度,前者是喷水推进泵追求的指标,后者只会是损失消耗能量,为此在动叶轮后设置导叶,将周向诱导速度转化为有用的压力能,从而提高泵效率。最终以无旋转的水流从喷口高速喷出,以获得船艇前进的推力。从水动力状态仔细分析不难发现,后置导叶喷水推进轴流泵,水流经过动叶轮后,以较大流速和压力进入到导叶体,在叶轮和导叶之间的区域会引起较大的压力脉动,易形成振动和噪声。也就是说从降噪的角度考虑,这种布局有它的先天不足。
20世纪80年代,中国船舶及海洋工程设计研究院(MARIC)开发了外置式喷水推进组合体,其是一种浸没式喷水推进装置,可装用于大型重负荷船舶、工程船和潜艇。这也是典型的后置导叶轴流泵,所不同的是它有前支架,前支架内布置有轴承,这是为了轴系布置而设置的。对于这种外置式喷水推进器,如果取消后置导叶,将前支架改成前置导叶,可以大大简化装置结构,减轻重量并降低造价。
基于上述2个实际问题,将后置导叶改为前置导叶,似乎可以带来2个好处。首先可以减小流场的脉动压力,降低水动力噪声;其次可以简化轴流泵的结构,减轻装置重量,降低装置成本。
常规喷水推进轴流泵的工作原理是前方的叶轮通过旋转运动,给水流增压的同时,还造成叶轮出口水流的周向诱导速度,此速度方向与叶轮旋转方向相同,此速度如果不回收,意味着这部分能量损失掉,效率会降低。叶轮后方配置导叶的目的是通过导叶片回收此部分旋转动能,并将其转化为压力能,提高效率。
而前置导叶轴流泵型在结构上主要由前置导叶、动叶轮、泵壳和轴系组成。前置导叶与泵壳连成整体,是固定不动的,动叶轮在其后,通过泵轴传递动力使叶轮旋转做功。其工作原理为:前方的导叶通过安放角的变化,将沿轴向流动的水流偏转,诱导水流产生周向速度的同时压力降低,诱导的周向速度即为预旋,由于其方向与后方的叶轮旋转方向相反,称之为反预旋(Pre-swirl),即负的周向速度Vu。由伯努利方程可知,此时绝对速度增加,但静压比导叶进口处低。带反预旋的水流离开导叶进入叶轮后,通过叶轮的旋转运动及叶轮叶片安放角度的变化,充分吸收此预旋并增压,使叶轮出口水流无旋,叶轮后水流与导叶前水流压力的变化量即为前置导叶轴流泵的扬程。实际上前置导叶起到了整流的作用。
后置导叶轴流泵水流进入动叶轮理论上是没有预旋的,即ω = 0。从泵的基本方程可知,在相同功率下,前置导叶较后置导叶的理论扬程HT相对较低,因而前置导叶轴流泵的比转速相对较高,一般应在1 000以上。从泵的基本方程还可看出,在相同几何尺寸和相同扬程下,前置导叶轴流泵消耗的功率相对较高,其泵效率相对低一些。
从以上分析可见,2种泵的工作原理完全不同,后置导叶的作用是回收叶轮诱导的周向旋转动能,而前置导叶的作用是诱导负的预旋。从压力沿流线变化看,后置导叶轴流泵的水流经叶轮增压后以较高的压力状态流入导叶,导致叶轮与导叶间的区域压力脉动大,噪声大;而前置导叶泵的水流流出导叶后,由于产生了负的预旋,导叶后的水流压力较低,导叶出口与叶轮进口区域的水流相对压力脉动小,噪声低。
另外,在喷水推进泵降噪研究中发现,推进泵正常运转的主要噪声是旋转叶轮与静止导叶之间水流相互扰动、周期性压力脉动引起的。如果将常规喷水推进泵高压区的后导叶取消,在叶轮前低压区安装前置导叶,这样压力脉动会大幅度降低,水力噪声也会大大减小,这将是很好的降噪措施。
2 数学模型 2.1 基本假设前置导叶喷水推进轴流泵内部是非常复杂的三元非定常流动,描述这样流动的基本方程组包括运动方程(N-S方程)、能量方程、连续性方程。直接利用这样的方程组来研究叶轮机械的原理过于复杂,为简化设计有利于计算求解,对流动做如下的假定:
1)叶轮的叶片数为无穷多,叶片无限薄。因此叶轮内的流动可以看成轴对称,并且速度方向与叶片表面相切;
2)相对流动是定常的;
3)无径向速度即Vr = 0;
4)液体质点在以泵轴线为中心线的圆柱面上流动,且相邻各圆柱面上的液体质点的运动互不相关,不存在径向分速度,即Vr= 0,也就是说圆柱面即流面。
2.2 数学模型1)进出口速度三角形
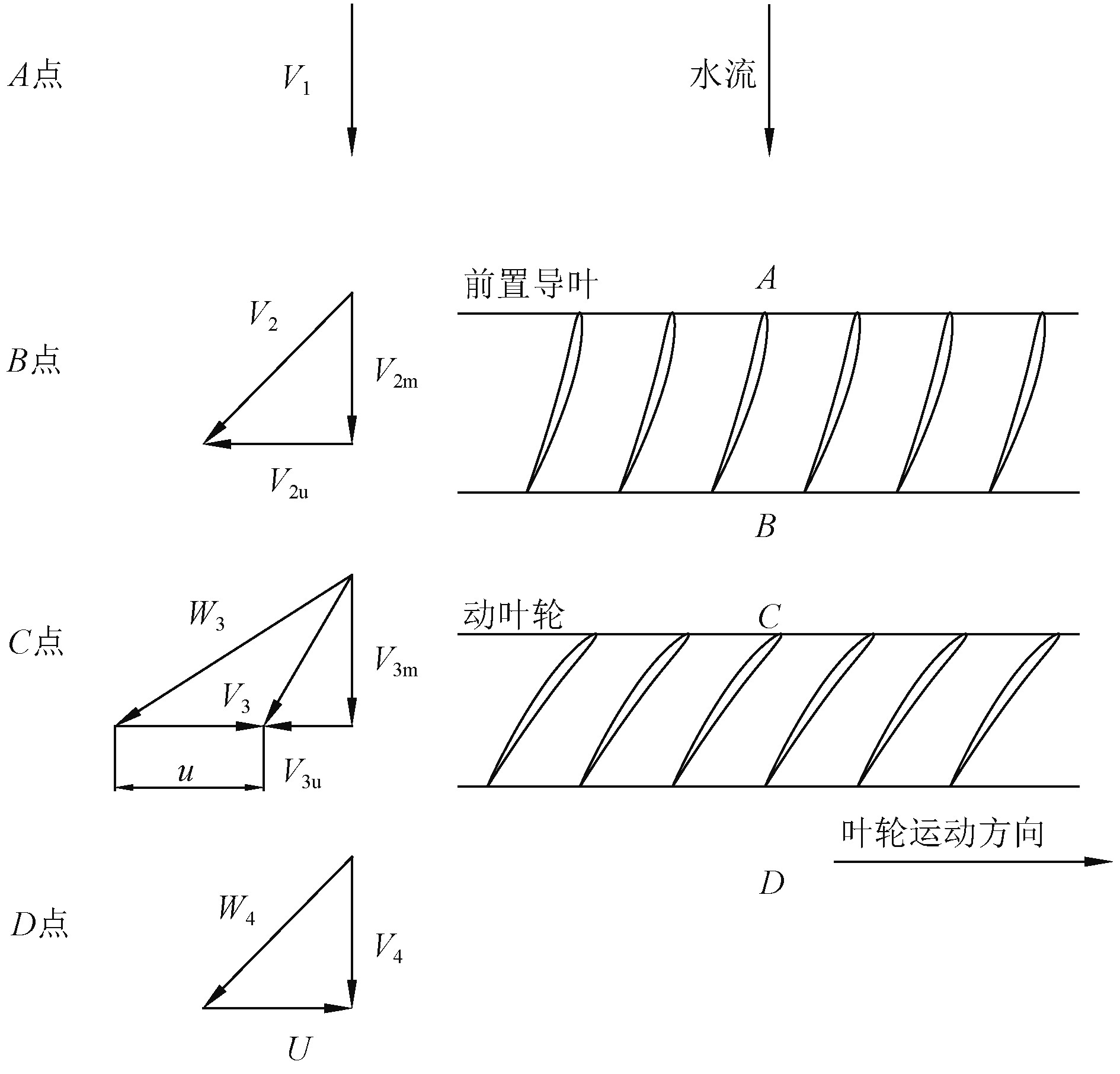
为了研究叶片与介质的能量交换,应研究叶片进出口的流动情况,为此给出前置导叶喷水推进轴流泵进出口处的速度三角形,如图1所示。
2)基本方程
在给出的前置导叶喷水推进轴流泵基本假设前提下,根据相对运动的欧拉方程均可推导出前置导叶喷水推进轴流泵的基本方程。
将动量矩定理应用于叶轮内的流体,则可求得叶轮与流体相互作用的力矩。根据图1所示的速度三角形,单位时间流出叶轮出口边的动量矩为
| $M = \frac{{{\rm d}L}}{{{\rm d}t}} = {q_m}({V_{4u}}{r_4} - {V_{3u}}{r_3})\text{。}$ | (1) |
|
图 1 前置导叶喷水推进轴流泵速度三角形 Fig. 1 Speed Triangle of water jet axial flow pump with front guide vane |
式中,M由叶片对流体作用力和粘性摩擦产生的切应力对轴的力矩组成,粘性摩擦产生的力矩通常小,在不考虑损失时可认为该力矩M的功率即为流体从叶片获得的功率P。
对于前置导叶喷水推进轴流泵,叶轮进口的速度周向分量V3u与叶轮旋转的周向速度U方向相反;而叶轮出口圆周速度为0,即V4u=0;r3=r4=r因而有
| $P = M\omega = \omega {V_{3u}}{r_3}{q_m} = g{q_m}{h_{th}}\text{。}$ | (2) |
整理得前置导叶喷水推进轴流泵的基本方程:
| ${H_T} = \frac{{\omega r{V_{3u}}}}{g} = \frac{{u{V_{3u}}}}{g}\text{。}$ | (3) |
式中,HT为理论扬程,u为在半径为r剖面的圆周速度。
3 设计方法 3.1 环量分布环量就意味着扬程(理论扬程,包括位能、静压能和动能),是能量的概念。关于环量沿半径分布的问题,许多学者已经进行了深入的研究探索。MARIC从1976年开始参照升力线理论,吸取螺旋桨设计的经验,发展了沿径向变环量分布的轴流泵设计方法。这种环量分布经过30年设计、实践,证明对提高泵的效率和抗空泡能力非常有效,此种方法也逐渐为水泵界所接受,设计出了很多好的水力模型。
对于前置导叶喷水推进轴流泵动叶轮,围绕翼型剖面的速度环量为:
| $ \varGamma = \frac{{2{\text{π}} r}}{z}\left( {{V_{4u}} - {V_{3u}}} \right)\text{,} $ | (4) |
代入式(3),得到环量与扬程的关系式如下:
| ${H_T} = u\frac{{{V_{4u}} - {V_{3u}}}}{g}\text{。}$ | (5) |
其中
设环量
| $ {H_T}(r) = \frac{\omega }{{2{\text{π}} g}} \cdot \varGamma (r) = \frac{\omega }{{2{\text{π}} g}}k(r) \cdot \overline \varGamma = k\left( r \right){H_T}\text{。} $ | (6) |
对于前置导叶方案的动叶轮欧拉方程为:
| ${H_T} = u \cdot \frac{{{V_{4u}} - {V_{3u}}}}{g}\text{。}$ | (7) |
将式(6)从根部到梢部积分,
| $\int_{\overline {{r_h}} }^1 {k\left( {\overline r } \right)} {\rm d}\overline r = 1 - \overline {{r_h}}\text{。} $ | (8) |
具体计算可采用辛浦生积分法:
| $\frac{1}{3}\Delta \overline r \sum {f\left( {k\left( {\overline r } \right)} \right)} = 1 - \overline {{r_h}} \text{。}$ | (9) |
如取毂径比
|
|
表 1 不同的环量分布系数表 Tab.1 Different circulation distribution coefficients |
|
|
表 2 环量分布积分计算表 Tab.2 Integral calculation table of circulation distribution |
|
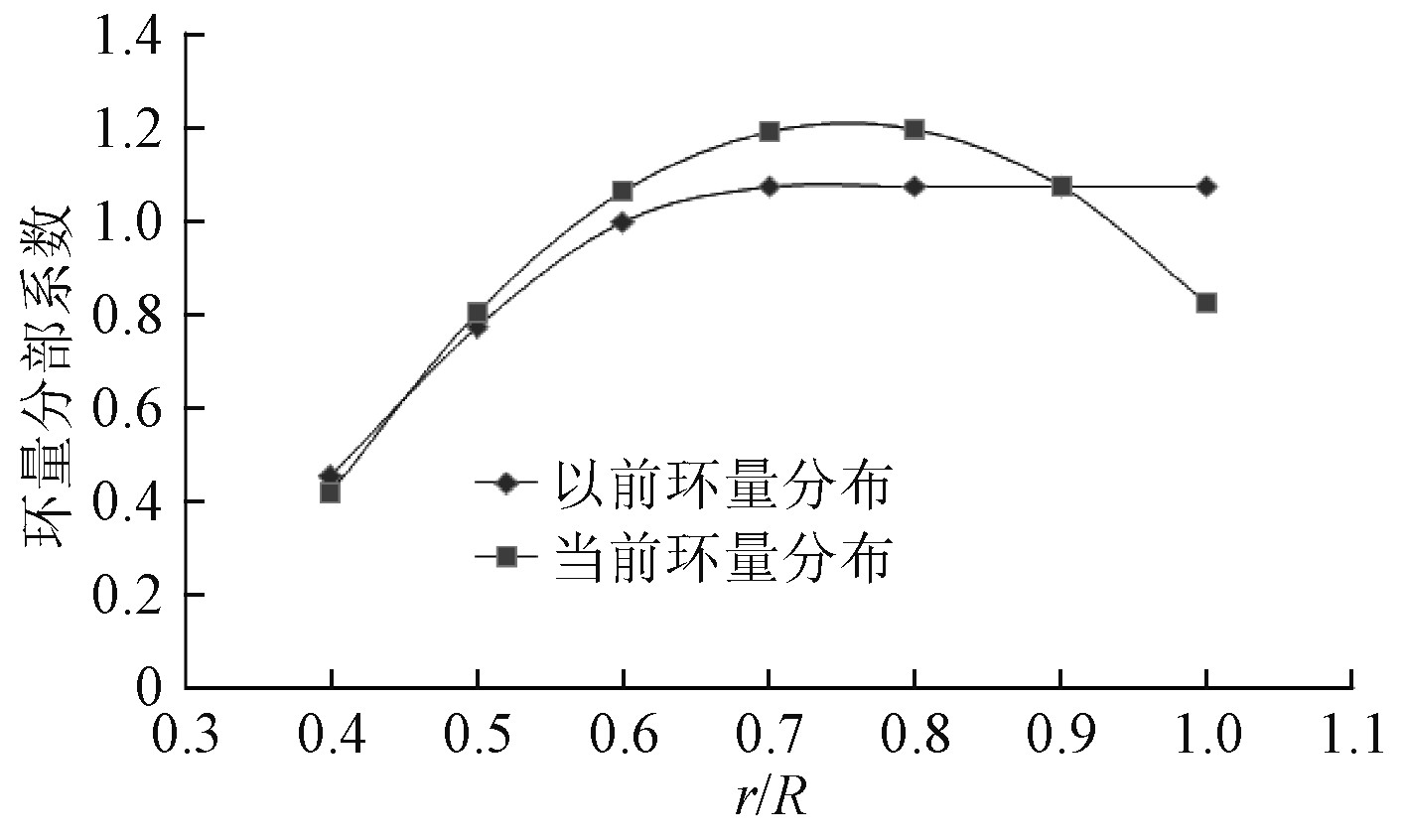
图 2 环量分布图 Fig. 2 Figure of circulation distribution |
根据环量分布校核公式:
左边=
右边=
在以往的轴流式叶轮设计处理中,“变环量等轴面速度”的假定有相当的近似性,在工程应用上是可行的,不但简化了设计过程,而且也可得到较佳的效果,但严格讲这并不符合实际情况。由理论推导的公式和实测的结果可知轴面速度也是沿径向变化的,并且与环量分布存在内在的函数关系,对于前置导叶出口处也是如此。如果环量分布是沿径向分布变化的,那么轴面速度也应该是沿径向随之改变。
|
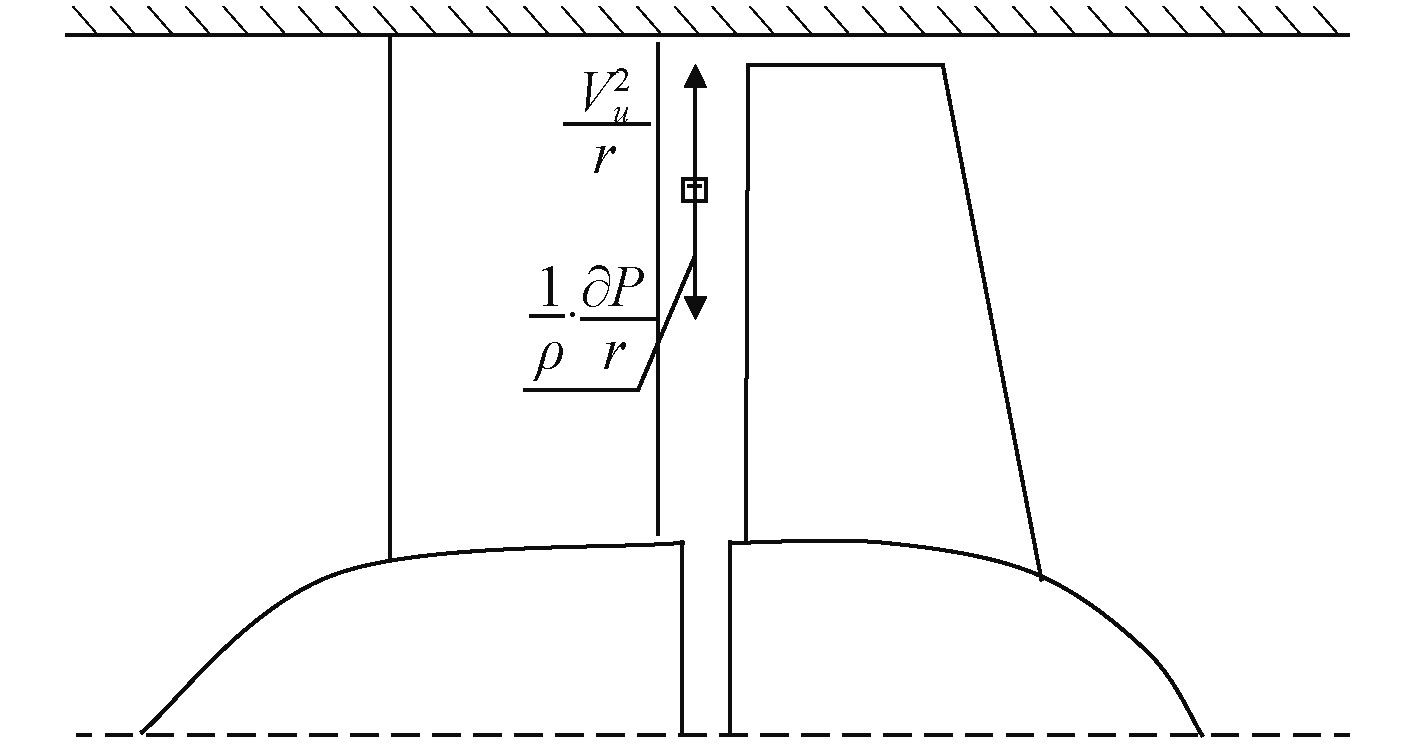
图 3 前置导叶喷水推进轴流泵示意图 Fig. 3 Sketch of water jet propulsion axial flow pump with front guide vane |
对于叶片泵内部流动,在流体是理想、不可压缩的假设下,可由柱坐标形式下欧拉运动方程来描述,即
| $ \left\{ \begin{array}{l} \dfrac{{{\rm{d}}{V_r}}}{{{\rm d}t}} - \displaystyle\frac{{V_u^2}}{r} = - \frac{1}{\rho } \cdot \dfrac{{\partial P}}{{\partial r}} + {F_r} \text{,}\\ \dfrac{{{\rm{d}}\left( {{V_u}r} \right)}}{{{\rm d}t}} = - \frac{1}{\rho } \cdot \dfrac{{\partial P}}{{r\partial \theta }} + {F_\theta } \text{,}\\ \dfrac{{{\rm{d}}\left( {{V_z}} \right)}}{{{\rm d}t}} = - \frac{1}{\rho } \cdot \dfrac{{\partial P}}{{\partial z}} + {F_z}\text{。} \end{array} \right. $ | (10) |
式中:Fr,Fθ,Fz是质量力
| $ \left\{ \begin{array}{l} {F_r} = 0 \text{,} \\ {F_\theta } = 0 \text{,} \\ Fz = - g \text{。} \\ \end{array} \right. $ |
对任何函数的全导数为:
| $\frac{\rm d}{{{\rm d}q}} = \frac{\partial }{{\partial r}}\frac{{{\rm d}r}}{{{\rm d}q}} + \frac{\partial }{{\partial \theta }}\frac{{{\rm d}\theta }}{{{\rm d}q}} + \frac{\partial }{{\partial z}}\frac{{{\rm d}z}}{{{\rm d}q}}\text{,}$ | (11) |
这样对压力P的全导数应为:
| $ - \frac{1}{\rho }\frac{{{\text{d}}P}}{{{\text{d}}q}} = - \frac{1}{\rho }\left( {\frac{{\partial P}}{{\partial r}}\frac{{{\text{d}}r}}{{{\text{d}}q}} + \frac{{\partial P}}{{\partial \theta }}\frac{{{\text{d}}\theta }}{{{\text{d}}q}} + \frac{{\partial P}}{{\partial z}}\frac{{{\text{d}}z}}{{{\text{d}}q}}} \right)\text{。}$ | (12) |
把式(10)对应的项分别代入上式,可得
| $ - \frac{1}{\rho }\frac{{{\text{d}}P}}{{{\text{d}}q}} = \left( {\frac{{{\text{d}}{V_r}}}{{{\text{d}}t}} - \frac{{V_u^2}}{r}} \right)\frac{{{\text{d}}r}}{{{\text{d}}q}} + \frac{{{\text{d}}\left( {{V_u}r} \right)}}{{{\text{d}}t}}\frac{{{\text{d}}\theta }}{{{\text{d}}q}} + \left( {\frac{{{\text{d}}{V_z}}}{{{\text{d}}t}} + g} \right)\frac{{{\text{d}}z}}{{{\text{d}}q}}\text{,} $ | (13) |
对轴流式叶片泵,沿径向变化,即dr=dq时
| $ \frac{{{\text{d}}r}}{{{\text{d}}q}} = 1;\frac{{{\text{d}}\theta }}{{{\text{d}}q}} = 0;\frac{{{\text{d}}z}}{{{\text{d}}q}} = 0\text{,} $ |
根据圆柱层无惯性假设,Vr=0,故式(12)简化为:
| $\frac{1}{\rho }\frac{{{\text{d}}P}}{{{\text{d}}r}} - \frac{{V_u^2}}{r} = 0\text{,}$ | (14) |
再列出导叶上沿流线的柏努利方程:
| $\frac{P}{\rho } + gz + \frac{{{V^2}}}{2} = {(g{H_D})_{in}}\text{,}$ | (15) |
对r求导,得
| $\frac{1}{\rho }\frac{{{\text{d}}P}}{{{\text{d}}r}} + g\frac{{{\text{d}}z}}{{{\text{d}}r}} + {V_m}\frac{{{\text{d}}{V_m}}}{{{\text{d}}r}} + {V_u}\frac{{{\text{d}}{V_u}}}{{{\text{d}}r}} = \frac{{{\text{d}}{{(g{H_D})}_{in}}}}{{{\text{d}}r}}\text{。}$ | (16) |
因为
则上式可写为:
| $\frac{1}{\rho }\frac{{{\text{d}}P}}{{{\text{d}}r}} = - {V_m}\frac{{{\text{d}}{V_m}}}{{{\text{d}}r}} - {V_u}\frac{{{\text{d}}{V_u}}}{{{\text{d}}r}}\text{。}$ | (17) |
由式(14)和式(15)整理得:
| ${V_m}\frac{{{\text{d}}{V_m}}}{{{\text{d}}r}} = - \frac{{V_u^2}}{r} - {V_u}\frac{{{\text{d}}{V_u}}}{{{\text{d}}r}} = \left( { - \frac{{{V_u}}}{r}} \right)\frac{{{\text{d}}\left( {{V_u}r} \right)}}{{{\text{d}}r}}\text{。}$ | (18) |
任意变环量形式有很多种,根据实践,假定导叶出口处环量分布为:
| $ {V_u}r = \frac{{\varGamma \left( r \right)}}{{2{\text{π}} }} = \frac{{\overline \varGamma }}{{2\pi }}k\left( r \right) = \frac{{\overline \varGamma }}{{2{\text{π}} }}\left( {{a_0} + {a_1}r + {a_2}{r^2}} \right)\text{。} $ | (19) |
式中:
将上式代入式(18)解该全微分方程可得:
| $ \begin{split} &{V_m} = \\ &\sqrt {\frac{{\overline \varGamma }}{{\text{π}} }\left[ { - \frac{{\overline \varGamma }}{{2{\text{π}} }}a_2^2{r^2} \!\!-\!\! \frac{{3\overline \varGamma }}{{2{\text{π}} }}{a_1}{a_2}r \!\!-\!\! \frac{{\overline \varGamma }}{{2{\text{π}} }}(a_1^2 \!\!+\!\! 2{a_0}{a_2})\ln r \!\!+\!\! \frac{{\overline \varGamma }}{{2{\text{π}} }}{a_0}{a_1}\frac{1}{r}} \right]\!\! +\!\! c} \text{。} \end{split} $ | (20) |
调整C值使得连续性方程成立,即lic>值使得连续性方程成立,即
| $ Q = \int_{{r_h}}^R {2{\text{π}} \cdot {V_m}} \left( r \right) \cdot r{\rm d}r\text{。} $ | (21) |
由上可计算得出沿径向分布的变轴面速度(叶轮进口处导=叶出口处)。
|
|
表 3 变环量变轴面速度分布表 Tab.3 Velocity distribution of variable circulation and axial velocity |
按升力设计理论,叶栅稠密度l/t的合理选取非常关键。如果l/t选取过大,即叶栅稠密度增加,则叶栅影响增大并且摩擦损失增加,水力效率必然降低;如果l/t选取过小,则升力系数Cy较大,这就要求剖面的拱度或者攻角较大,同时厚度比也较大,增加了空泡发生的危险。由于在叶梢处相对流速最大,最易发生空化,因而叶梢处叶栅稠密度l/t的选择主要考虑空泡要求,在保证空泡数的条件下,尽量选择较小的l/t;叶根处则主要考虑强度的要求来选取适当的厚度及弦长以保证低阻性能。中间剖面处的弦长按下式确定:
| $ l = {l_h} + \left( {\overline r - \overline d } \right) \times \left( {{l_R} - {L_h}} \right)/\left( {1 - \overline d } \right)\text{。} $ |
叶根剖面的厚度按照强度的要求计算决定,安全系数取7。叶梢剖面的厚度按工艺要求而定,由于厚度比
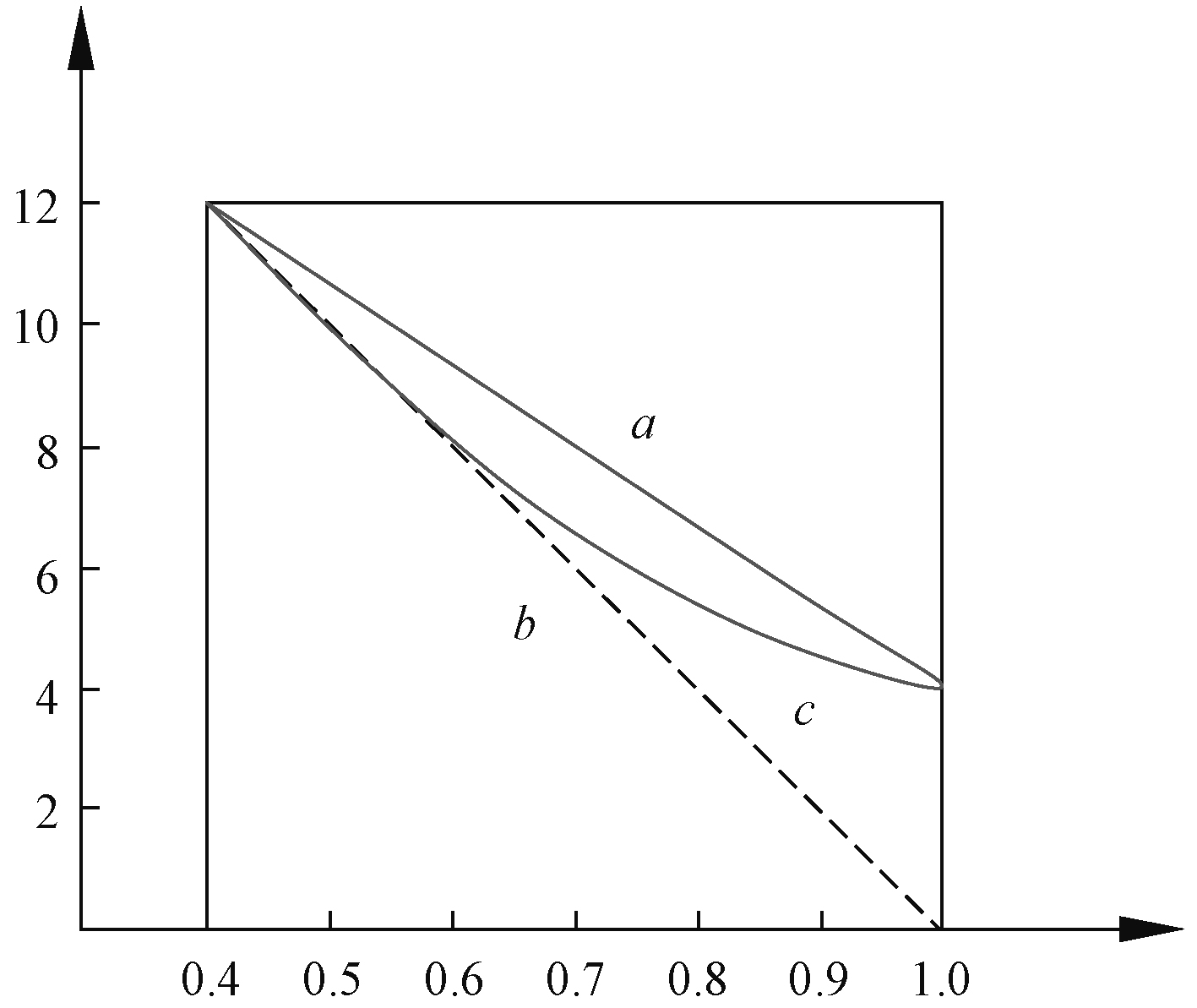
叶根和叶梢的厚度决定后,中间各剖面的厚度一般是按直线进行分布,如图4中的曲线a,这是一种简单的处理方法,这样决定的厚度分布导致中间剖面的厚度往往偏大,使得中间剖面翼型的升阻比过小,影响效率,实际选取中按照等强度要求从根部开始与曲线b相切的内凹曲线c作为厚度分布较为合理。
3.5 翼型选择在翼型的选择上需要兼顾性能与汽蚀,对空泡要求不高的泵可以选择低阻翼型,如哥丁根和NACA44系列翼型,最大厚度位置在离导边0.3~1/3l处,对空泡要求高的泵可采用抗空泡性能好的翼型,如NACA16α=0.8 和NACA66α=0.8翼型。设计中也可在各剖面选择不同翼型,如在根部选择低阻翼型,梢部选择抗空泡好的翼型,但中间存在过渡问题。
|
图 4 叶片厚度分布曲线 Fig. 4 Curve of blade thickness distribution |
考虑到前置导叶喷水推进轴流泵应用的特殊性,本文选用NACA16α=0.8,该翼型的特点是在冲角为0时,翼型上的压差分布均匀,汽蚀性能优良。
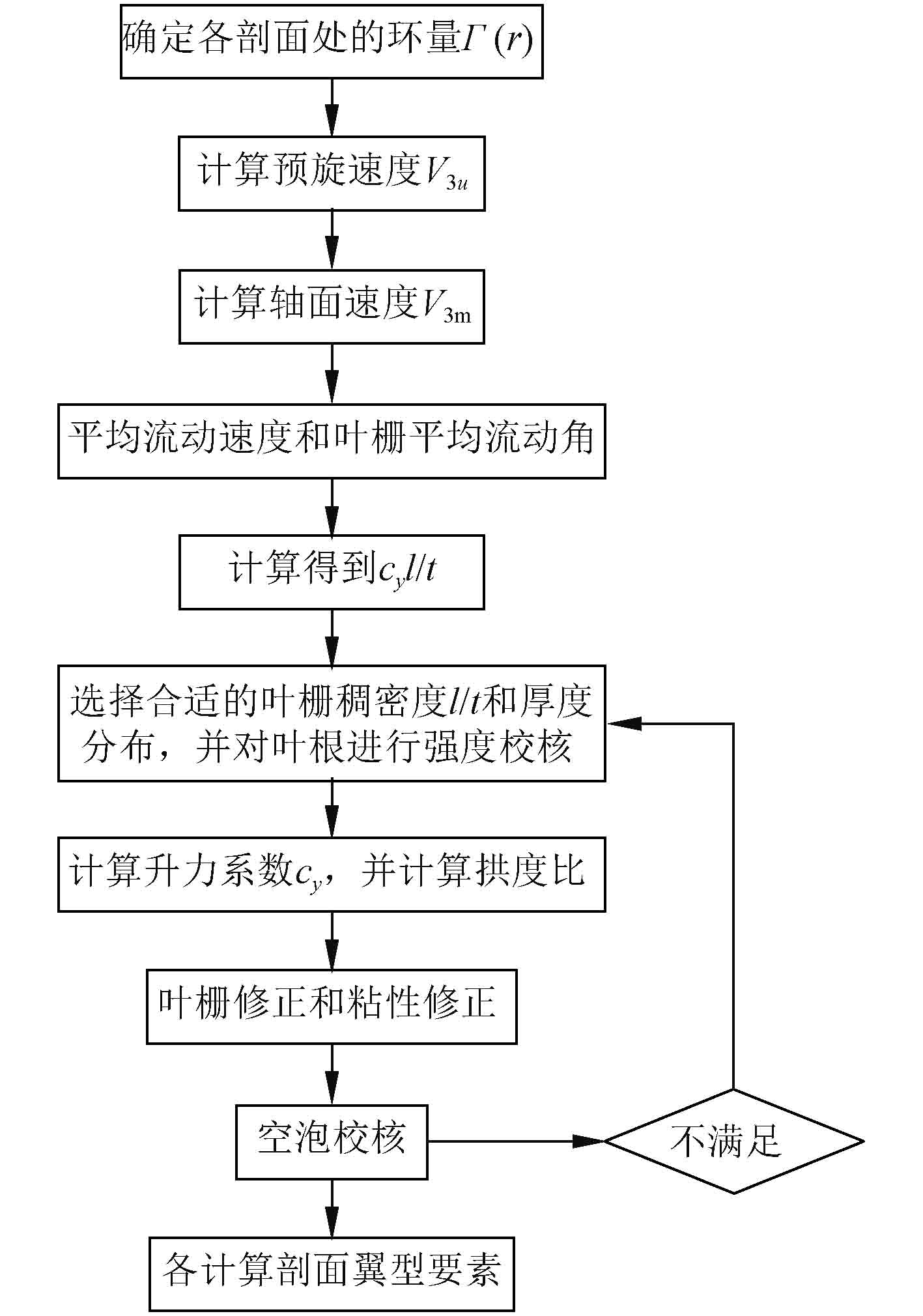
4 设计步骤根据上节所述可以总结处前置导叶喷水推进轴流泵的叶轮设计步骤如下:
1)采用变环量分布法确定各计算剖面处的环量Γ(r);
2)根据前置导叶喷水推进轴流泵的基本方程式(3)和绕翼剖面的速度环量式(4),计算预旋速度V3u;
3)联立变轴面速度法确定的轴面速度V3m,计算得到平均流动速度W∞和叶栅平均流动角β∞;
4)根据前置导叶喷水推进轴流泵中扬程与升力系数的关系式确定
5)选定翼型,并根据翼型的升力特性,选择合适的叶栅稠密度l/t和厚度分布,并同时对叶根部进行强度校核;
6)确定升力系数cy并计算拱度比
7)进行叶栅修正和粘性修正对拱度比和安放角进行修正;
8)校核空泡数,不满足则重新调整叶栅稠密度l/t和厚度。具体步骤如图5所示。
|
图 5 动叶轮的设计计算步骤 Fig. 5 Design and calculation process of rotor |
通过建立前置导叶轴流泵的数学模型和基本方程,结合变环量的轴流泵设计方法,分析总结出适用于前置导叶轴流泵叶轮的设计方法和步骤,相关研究工作将进一步向工程应用方面拓展。与常规后置导叶型喷水推进轴流泵对比,前置导叶泵在结构布置和噪声性能方面具有明显的优势,应用前景广阔。
| [1] |
王立祥, 朱为民, 王泽群. 带前置或后置导叶的轴流泵性能试验研究[C]//第五届亚洲流体机械国际会议论文集, 1997(10): 207.
|
| [2] |
金平仲, 曾松祥, 沈奉海, 等. 轴流泵的变环量设计方法[J]. 水泵技术, 1985(2): 14-20. |
| [3] |
张新, 轴流泵设计中的环量分布与轴面速度分布, 水泵技术, 1984, 1.
|
| [4] |
吴刚. 前置导叶喷水推进轴流泵的研究与设计[D]. 2003.
|
| [5] |
HUTTON S. P., Three-dimensional motion in axial flow impellers, Report of the Institution of British Mechanical Engineering[J], 1955, 10.
|
| [6] |
HU, P., ZANGENEH, M.. CFD Calculation of the flow through a waterjet pump[C]//International Conference on Waterjet Propulsion III, RINA, Gothenborg, 2001
|
 2020, Vol. 42
2020, Vol. 42
