2. 喷水推进技术重点实验室,上海 200011
2. Science and Technology on Water Jet Propulsion Laboratory, Shanghai 200011, China
“泵喷”(pump jet)和“喷水推进”(water jet)均是由外文直接翻译过来的,water jet一词大致在1661年出现,pump jet一词出现于20世纪20年代,两者原理是一致的,技术核心是“水泵”与“喷射”,都是用泵这种水力机械把水流向后喷射,利用进出流的动量差产生推力。泵喷与我国20世纪广泛应用的喷水推进组合体类似。学术界关于泵喷与喷水推进关系的争论一直存在,王立祥等研究认为:喷水推进和泵喷推进均属泵类推进,都是通过管道内叶轮和导叶的流场匹配设计在喷口产生轴向射流而获得推进作用;喷水推进的第一设计指标是高效率、首要保证快速性,相应的设计结果是喷水推进器;泵喷推进的第一设计指标是低噪声、首要保证声隐身性,相应的设计结果是泵喷推进器。泵喷与喷水推进作用机理和原理一致,技术体系与范畴相同,只是由于应用平台或者设计要求差异带来称谓的不同[1-2]。
泵喷已经发展成为安静型核潜艇和水下航行器首选推进方式[3-4],目前有2种设计思路,一种是从推进泵的设计角度出发,另一种是导管桨的设计思路,且以第2种设计方法居多。本文旨在从喷水推进理论出发,结合推进泵模型试验,预报泵喷的推进特性,为泵喷设计提供一种新的技术路径。
|
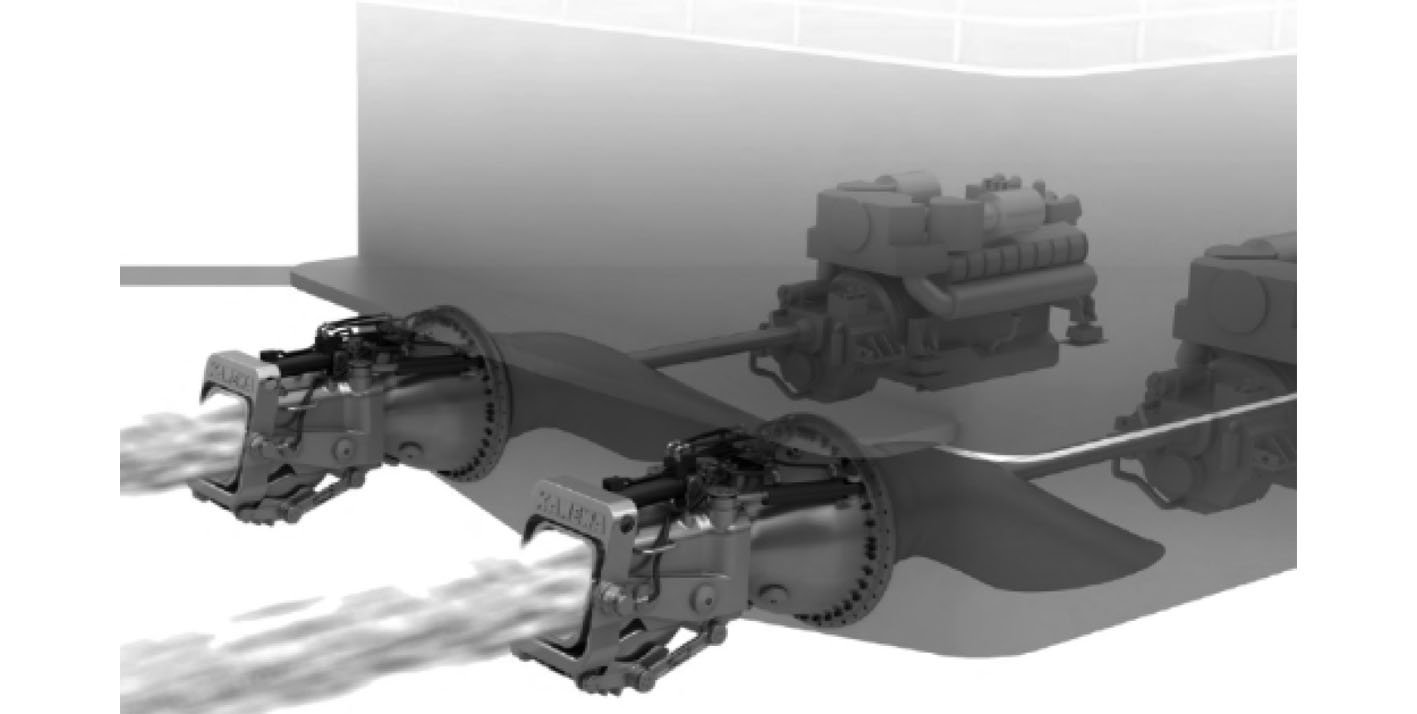
图 1 内置式喷水推进装置 Fig. 1 Internal-mounted water jet unit |
|
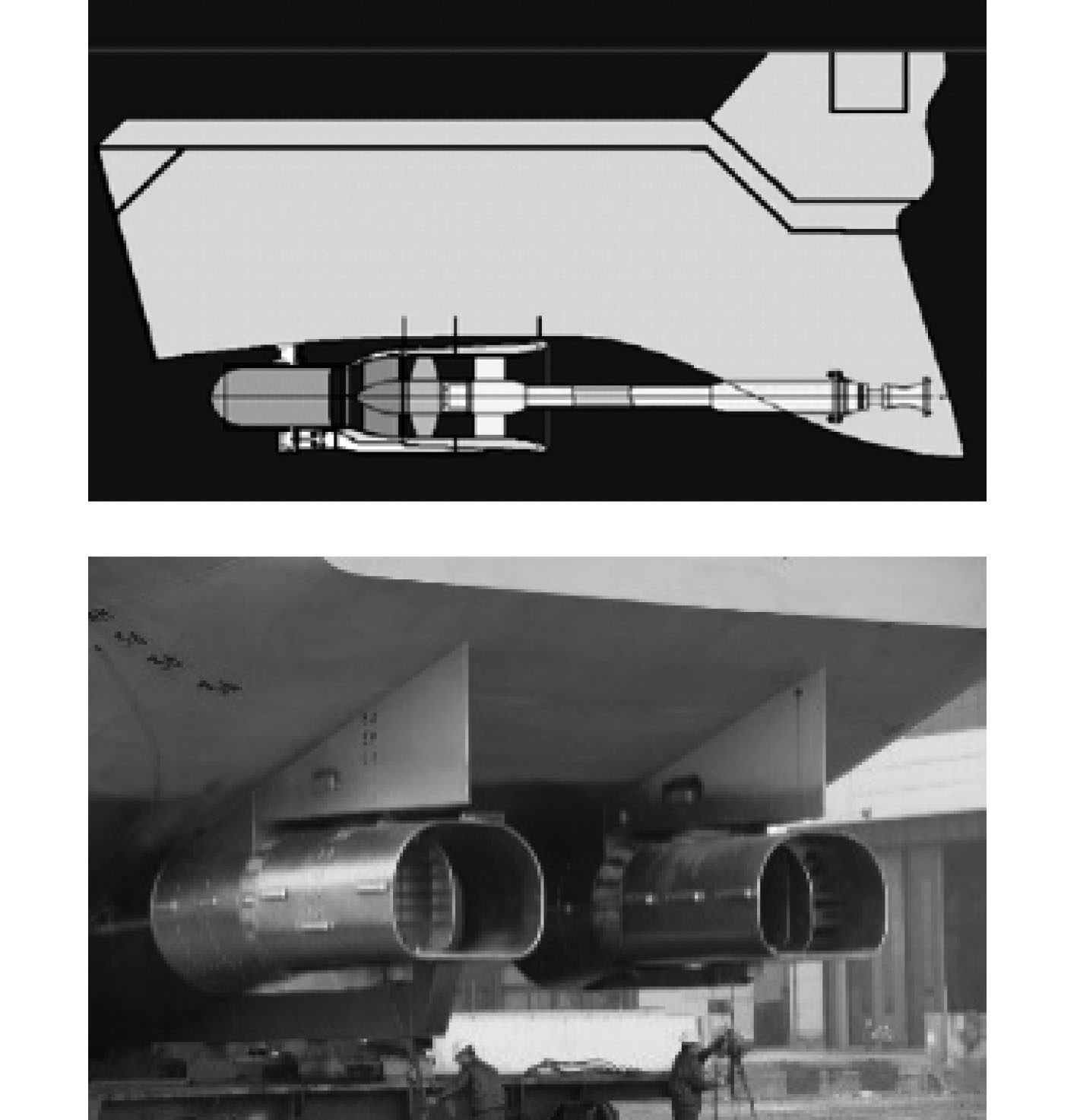
图 2 喷水推进组合体(外悬式) Fig. 2 Outer-mounted water jet unit |

|
图 3 泵喷推进 Fig. 3 Pump jet |
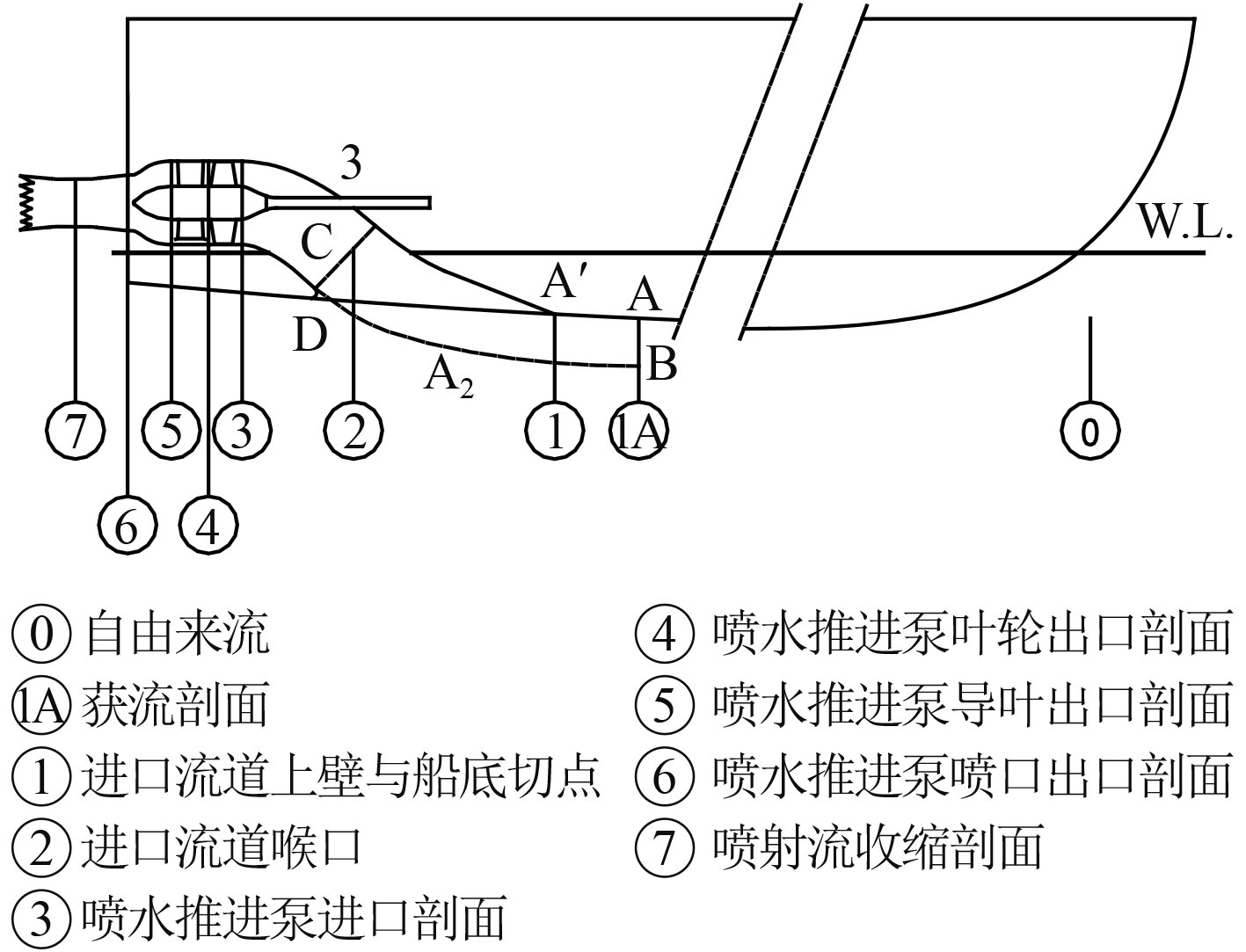
喷水推进应用动量定理分析推力的研究方法称为“动量通量法”,这是目前较为流行且被普遍认可的方法。ITTC第21-24届会议[5-7]提出了喷水推进系统控制体概念,如图4所示。
|
图 4 喷水推进系统水动力模型的控制体 Fig. 4 The control volume system of the water jet |
喷水推进装置可以被细分为泵(③,⑤位置之间的区域)和管道系统(①,③和⑤、⑥位置之间的区域)。将
 站至⑦站之间流管区域定义为控制体,该流管一部分由装置实体边界来定义,一部分由实体进口A/D前分割的流面BC来定义。这个分割流面(指A2)是在流动中的一个假想的表面,其定义为流动中没有任何质量通过该表面。假想的获流区
站至⑦站之间流管区域定义为控制体,该流管一部分由装置实体边界来定义,一部分由实体进口A/D前分割的流面BC来定义。这个分割流面(指A2)是在流动中的一个假想的表面,其定义为流动中没有任何质量通过该表面。假想的获流区
 站一般取进口前一倍叶轮直径的位置,以减小由于进口几何带来的流动变形。喷水推进在设计时一般取喷口处曲线2阶偏导数为0,以便出流平直,使得最小收缩口⑦处的直径与喷口⑥处直径相当,流速相等,减小喷射损失。
站一般取进口前一倍叶轮直径的位置,以减小由于进口几何带来的流动变形。喷水推进在设计时一般取喷口处曲线2阶偏导数为0,以便出流平直,使得最小收缩口⑦处的直径与喷口⑥处直径相当,流速相等,减小喷射损失。
1)力平衡方程
假定控制体进出口静压差可忽略不计,其⑦站与
 站的动量差即为喷水推进产生的推力为:
站的动量差即为喷水推进产生的推力为:
| $ {T}=\Delta {{M}{x}}_{(7-1{A})}=\rho {Q}{{V}}_{{j}}-\rho {Q}{{V}}_{1{A}}{\text{=}} $ |
| $ \rho {Q}{ ({V}}_{{j}}-\alpha {{V}}_{0}){\text{。}} $ | (1) |
式中:ρ为流体密度,
 处获流区面积。
处获流区面积。
| $ \mathrm{\alpha }=\frac{1}{{V}_{0}}\frac{{\int }_{1A}^{}{V}^{2}{\mathrm{d}}A}{{\int }_{1A}^{}V{\mathrm{d}}A}{\text{,}} $ | (2) |
| $ \mathrm{Q}={\int }_{1A}^{}V{\mathrm d}A \text{。}$ | (3) |
考虑推进器与平台间的推力减额t后,推力与阻力平衡如下式:
| $ R = \left( {1 - t} \right)T \text{。} $ | (4) |
式中:t为推力减额;R为平台的阻力,N。
2)功率平衡方程
推进泵的有用功率为
| $ {\mathrm{N}}_{\mathrm{e}}=\mathrm{\rho }{g}{Q}{H}/{\eta }_{{p}} $ | (5) |
式中:g为重力加速度,
(3)损失平衡方程
喷水推进泵扬程必须与推进系统的损失相平衡。
| $ {H}=\frac{(1+{k}_{j})}{2g}{{V}_{j}}^{2}+({K}_{1}-\mathrm{\beta })\frac{{{\mathrm{V}}_{0}}^{2}}{2g}+{h}_{c}\text{。} $ | (6) |
式中:kj为5站至7站的水力损失系数;
| $ \mathrm{\beta }=\frac{1}{{{V}_{0}}^{2}}\frac{{\displaystyle\int }_{1A}^{}{V}^{3}\mathrm dA}{{\displaystyle\int }_{1A}^{}V\mathrm dA}\approx {\alpha }^{2} \text{。} $ | (7) |
如前所述,泵喷与喷水推进工作机理具有一致性,本节基于喷水推进动量通量理论,定义泵喷控制体及其基本方程。
|
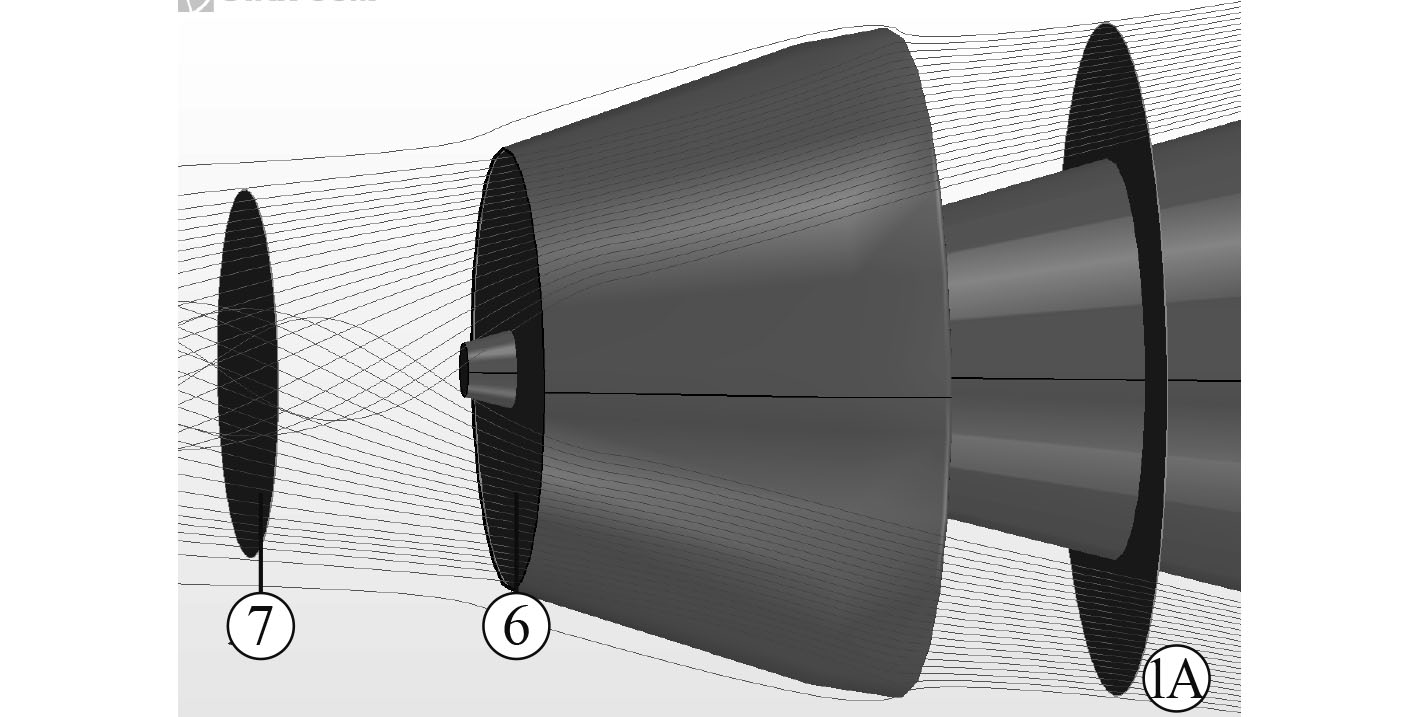
图 5 泵喷水动力模型的控制体 Fig. 5 The control volume system of the pumpjet |
定义入流
 站至喷流⑦站之间流管区域为控制体,
站至喷流⑦站之间流管区域为控制体, 站取在推进器与操纵面间适当位置,⑦站为喷射流最小收缩断面。该流管一部分由导管内壁实体边界来定义,一部分由进流和喷流的虚拟流管来定义,并遵循质量守恒。
站取在推进器与操纵面间适当位置,⑦站为喷射流最小收缩断面。该流管一部分由导管内壁实体边界来定义,一部分由进流和喷流的虚拟流管来定义,并遵循质量守恒。
上述控制体受到泵的作用,其动量差产生的推力定义为T:
| $ {{T}}'=\Delta {{M}{x}}_{(7'-1\mathrm{A}')}=\rho {Q}{ ({V}}_{{j}}-\alpha {{V}}_{0})\text{。} $ | (8) |
整套泵喷产生的推力T为控制体推力T与导管外表面受力
| $ {T}={{T}}'+{T}_{duct}=\rho {Q}{ ({V}}_{{j}}-\alpha {{V}}_{0})+{T}_{\begin{array}{c}duct \\ \end{array}} \text{。}$ | (9) |
泵喷相对于喷水推进,由于增加了导管外表面的作用力,其推力方程增加了导管外表面受力项。
推力与阻力平衡、功率平衡、损失平衡方程与式(3)~式(5)相同。
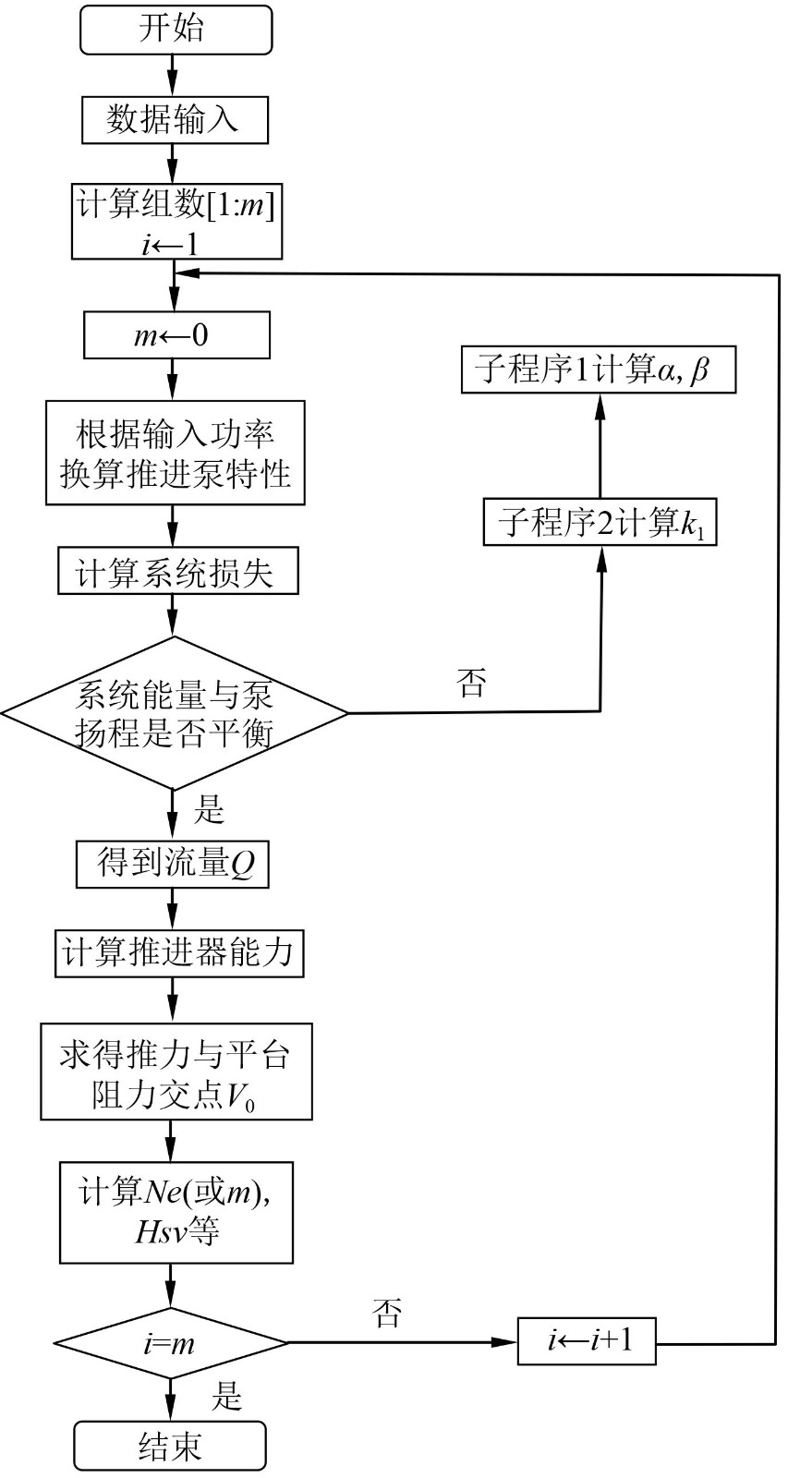
3 喷水推进推进性能预报技术应用于泵喷的差异与修正针对喷水推进试验的方法,ITTC发布了标准试验程序,包含喷水推进泵模型试验、系统试验和自航试验[5-7]。国内已具备完善的喷水推进泵模型试验条件,并建立了基于推进泵模型试验的推进性能预报方法,用数据和图表曲线表示各种转速(或功率)下功率(或转速)、推力与航速的关系,在船舶和两栖车辆等载体上大量应用和优化,其核心流程如图6所示。
|
图 6 喷水推进性能预报流程 Fig. 6 The procedure of the performance prediction of the waterjet |
1)根据推进泵模型试验数据,基于相似准则,确定直径并换算至不同转速n(或功率Ne)下的扬程H与流量Q、效率
2)按式(5)计算不同航速下的系统损失特性。
3)将不同转速(或功率)下推进泵扬程与不同航速下系统特性(水力损失)的平衡点作为计算依据,按式(3)式、(4)求得不同转速(或功率)下对应的航速、推力和推进泵收到功率(或转速),导入阻力曲线,形成一系列推力与阻力平衡点,对应的H、Q和
4)形成喷水推进性能和船舶阻力性能交汇的特性图表[1]。
在实践中发现,喷水推进推进性能预报技术应用于泵喷是可行的,但需根据两者的差异性开展相应的修正。
3.1 推进泵模型试验数据应用修正应用于泵喷的推进泵属于前置导叶、高比转速范畴,具有大流量、小扬程的特点。国家标准GB3216规定,模型泵试验测量扬程时取压点设置在被试泵前后各2倍直径处,这段管路的摩擦损失,对于泵喷扬程和效率的影响可达5%以上,因此必须对泵的通用特性曲线加以修正[10]。
管路摩擦损失:
| $ {{H}}_{j}=\mathrm{\lambda }\frac{{L}}{d}\displaystyle\frac{{(\frac{4Q}{\text{π} {d}^{2}})}^{2}}{2g}\text{,}$ | (10) |
| $ \frac{1}{\sqrt{\lambda }}=-2{\mathrm{log}}_{10}\left[\frac{2.51}{Re\sqrt{\lambda }}+\frac{1}{74}\right]\text{。} $ |
式中:L为拟计算的管长,m;d为拟计算的管路内径,m。
利用式(9),计算出各测试流量Q下的管路摩擦损失
模型的雷诺数一般均小于实尺度,且过流部件表面相对粗糙度高于实尺度,这两点均导致实尺度比模型效率高,需对效率进行修正。泵效率
喷水推进泵水力效率换算一般采用Moody 2公式:
| $ \frac{{1-{\eta }}_{{h}{s}}}{{1-\mathrm{\eta }}_{{h}{m}}}={\left(\frac{{{D}}_{{m}}}{{{D}}_{{s}}}\right)}^{0.2}\text{,} $ | (11) |
式中:D为直径;下标m,s分别发表模型和实尺度,
流量、扬程由式(11)、式(12)相似换算获得,随后由式(4)计算获得实尺度功率。
| $\frac{{{Q_s}}}{{{Q_m}}} = \left( {\frac{{{n_s}}}{{{n_m}}}} \right){\left( {\frac{{{D_s}}}{{{D_m}}}} \right)^3}\text{,}$ | (12) |
| $\frac{{{H_s}}}{{{H_m}}} = {\left( {\frac{{{n_s}}}{{{n_m}}}} \right)^2}{\left( {\frac{{{D_s}}}{{{D_m}}}} \right)^2}\text{。}$ | (13) |
经工程应用检验,上述方法应用于喷水推进是成功的。但研究发现,国内喷水推进项目实尺度相对于模型或中间尺度放大一般不大于3,而泵喷的尺度放大往往超过10倍以上,现有方法存在局限性,换算至实尺度的效率仍偏低、流量和扬程偏小,致使推进器负荷偏轻,工况点偏离。
通过试验分析,泵喷推进遵循功率相似:
| $N{e_s} = \frac{{{\gamma _s}}}{{{\gamma _m}}}{\left( {\frac{{{n_s}}}{{{n_m}}}} \right)^3}{\left( {\frac{{{D_s}}}{{{D_m}}}} \right)^5}N{e_m}\text{,}$ | (14) |
效率换算采用Moody 3公式:
| $ \frac{{1-\mathrm{\eta }}_{\mathrm{h}\mathrm{s}}}{{1-\mathrm{\eta }}_{\mathrm{h}\mathrm{m}}}={\left(\frac{{{D}}_{{m}}}{{{D}}_{{s}}}\right)}^{0.25}{\left(\frac{{H}_{m}}{{H}_{s}}\right)}^{0.1}\text{。} $ | (15) |
流量和扬程引入修正系数
| $ \frac{{{Q_s}}}{{Q{}_m}} = {C_Q}\left( {\frac{{{n_s}}}{{{n_m}}}} \right){\left( {\frac{{{D_s}}}{{{D_m}}}} \right)^3}\text{,} $ | (16) |
| $\frac{{{H_s}}}{{{H_m}}} = {C_H}{\left( {\frac{{{n_s}}}{{{n_m}}}} \right)^2}{\left( {\frac{{{D_s}}}{{{D_m}}}} \right)^2}\text{。}$ | (17) |
式(14)~式(16)与式(4)迭代求解。
3.3 其他差异性1)推力
比较式(1)与式(8),泵喷推力比喷水推进多出导管外表面推力项
2)空泡
喷水推进以快速性为首要目标,重点关注对推进性能产生影响的空泡,模型试验参照GB3216标准,以各流量点扬程下降3%作为空泡评判准则。
泵喷以噪声为重要指标,关注空泡起始,特别是梢涡空泡。为此,模型泵试验中的评判标准相应进行调整,通过观测各类型空泡起始,获得各流量点起始空泡数,且需注意从模型至实尺度换算时的空泡尺度效应修正问题。
3)边界层影响系数
从式(1)与式(8)分析,
针对喷水推进,国内外关于进流对边界层影响的研究众多,一般假定
 站获流区为半椭圆形[11],据不完全统计,
站获流区为半椭圆形[11],据不完全统计,
泵喷应用于回转体艇尾,可360°吸入边界层, 站获流区近似圆环形,根据现有泵喷方案分析,
站获流区近似圆环形,根据现有泵喷方案分析,
以某泵喷为对象,采用喷水推进技术重点实验室推进泵试验台完成模型试验,应用本文介绍之方法完成推进性能预报。
输入数据需包括:
|
|
表 1 推进泵模型试验数据(归一化) Tab.1 The model hydrodynamic performance of the waterjet pump(unitary) |
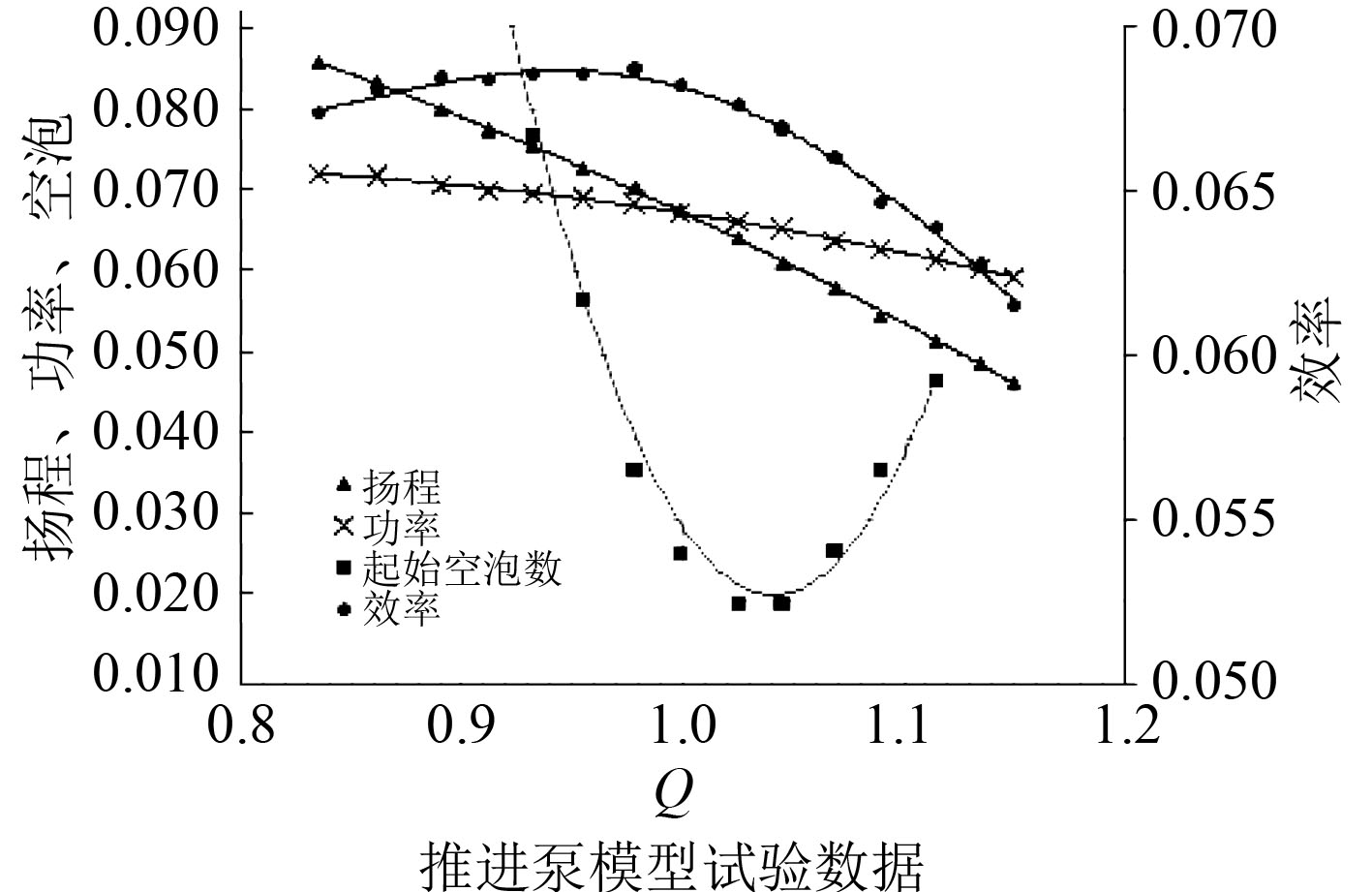
|
图 7 推进泵模型试验曲线 Fig. 7 The model hydrodynamic performance of the waterjet pump |
2)艇体阻力曲线;
3)泵喷导管外表面推力曲线;
4)推进性能计算输入参数(见表2)。
|
|
表 2 泵喷推进性能计算输入参数表 Tab.2 The input forthe prediction of propulsion performance of pumpjet |
输出数据为:以航速为自变量,推力、转速为因变量的曲线,汇入阻力和功率曲线,即可完成匹配转速、航速的预报,形成泵喷推进特性曲线。最后,根据工作流量点空泡数校核其空泡临界航速。
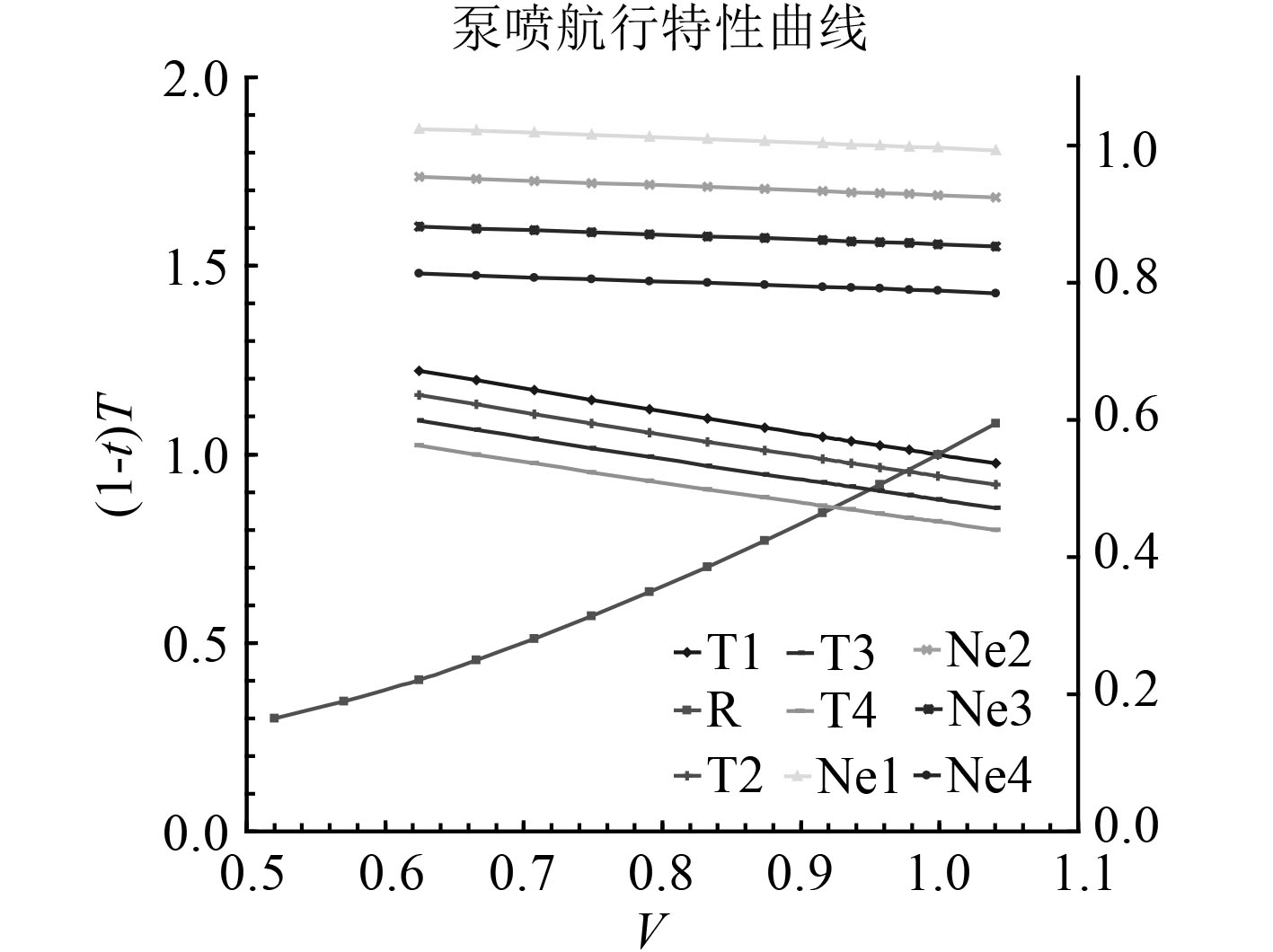
|
图 8 泵喷推进特性曲线(归一化) Fig. 8 The propulsion performance of the pumpjet |
上述性能预报结果与泵喷自航试验和艇后空泡试验结果比对情况见表3,匹配转速偏差−0.1%,最高航速偏差−1.6%,空泡临界航速偏差−1.2%。
|
|
表 3 推进性能预报与自航试验结果偏差表 Tab.3 The comparison between theperformanceprediction and self-propulsion test |
1)本文从喷水推进理论出发,基于动量通量方法,建立了泵喷研究控制体和基本方程;与喷水推进相比,泵喷推力方程增加了导管外表面受力项。
2)泵喷属于高比转速泵范畴,模型泵试验数据应用时需采用测压段管路损失修正扬程和效率曲线;采用Mody3公式换算水力效率、引入流量和扬程修正系数,解决从模型放大至实型时的尺度效应问题。
3)以模型泵试验数据为基础,完成了某泵喷推进性能预报,与泵喷自航试验和艇后空泡试验结果比对显示:匹配转速偏差−0.1%,最高航速偏差−1.6%,空泡临界航速偏差−1.2%,验证了基于喷水推进理论的泵喷推进性能预报方法的可行性和有效性,对泵喷性能预报和设计方法拓展和具有重要意义。
| [1] |
王立祥、蔡佑林. 喷水推进及推进泵设计理论和技术[M]. 上海: 上海交通大学出版, 2018: 1-12, 73-90.
|
| [2] |
王永生. 喷水推进和泵喷推进的概念: 共性、特性及区别[J]. 中国舰船研究, 2019, 5: 1-10. |
| [3] |
王天奎, 唐登海. 泵喷推进器—低噪声的核潜艇推进方式[J]. 现代军事, 2006(7): 52-54. |
| [4] |
魏以迈. 潜艇低噪声推进器技术研究与进展[C]//第十届船舶水下噪声学术讨论会论文集. 2005: 15-18.
|
| [5] |
KRUPPA, C. (Chairman). Report of the specialist committee on waterjets[C]//21st ITTC, Bergen and Trondheim, 1996.
|
| [6] |
HOYT III, J. G. (Chairman). Report of the specialist committee on waterjet[C]//22nd ITTC, Seoul/Shanghai, 1999.
|
| [7] |
VAN TERWISGA, T. J. C. (Chairman). Report of the specialist committee on validation of waterjet test procedures[C]//23rd-24 rd ITTC, Venice, Volume II,2002-2005.
|
| [8] |
金平仲. 船舶喷水推进[M]. 北京: 国防工业出版社, 1986: 67-104.
|
| [9] |
陈松山, 严登丰, 葛强. 泵及泵装置效率换算方法研究[J]. 农业机械学报, 2006, 37: 52-55, 59. DOI:10.3969/j.issn.1000-1298.2006.08.013 |
| [10] |
戴原星, 王立祥. 基于CFD的前置导叶轴流泵通用特性曲线预报较[J]. 船舶, 2013, 10: 1-5. DOI:10.3969/j.issn.1001-9855.2013.04.001 |
| [11] |
孙存楼, 王永生. 喷水推进推力预报的两种不同方法比较[J]. 船舶力学, 2010, 11: 1208-1212. DOI:10.3969/j.issn.1007-7294.2010.11.003 |
 2020, Vol. 42
2020, Vol. 42
