2. 中国船舶科学研究中心,江苏 无锡 214082
2. China Ship Scientific Research Center, Wuxi 214082, China
螺旋桨根部负荷对于其推进效率的影响一直是螺旋桨设计研究的重要内容之一。Lerbs[1]最早提出求解最佳径向环量分布的变分法时认为叶根处某一桨叶压力面与相邻桨叶吸力面发生压力中和,造成叶根处升力为零。Kerwin[2]采用镜像涡的办法近似处理桨毂,并认为螺旋桨根部存在环量。孙文愈[3]将面元法计算的桨毂诱导速度加入变分法求解最佳环量中,得到的最佳环量分布在叶根处存在负荷,Brizzolara[4]的计算结果也得到了相同的结论。Hong[5]和Shin[6]采用CFD数值模拟技术分析了螺旋桨环量分布形式,结果均显示桨叶根部存在负荷。Jessup[7]应用LDV流场测量技术分析了该问题,证实了螺旋桨根部的环量是真实存在的,并通过与Wang[8]的计算结果对比,阐述了桨毂对于螺旋桨根部环量存在重要影响。
直接针对螺旋桨毂涡结构进行研究的论文并不多见。Kumar[9]采用大涡模拟(LES)方法进行螺旋桨尾流场不稳定性研究时简要分析了毂涡的流动特点。Felli[10-11]通过高速摄影进行了梢涡和毂涡空泡流动显示观测对螺旋桨尾涡的不稳定性进行细致分析,认为螺旋桨的梢涡和毂涡的相互干扰是尾涡不稳定的重要原因。此外,回收利用螺旋桨毂涡能量的节能装置研究也是毂涡结构研究的一个重要延伸。李鹏程等、李鑫、高德宝等[12-14]学者对于毂帽鳍、舵球、消涡轮等不同种类的毂涡节能装置进行过分析研究。
本文基于粘流CFD技术进行螺旋桨尾流场的数值模拟,并将数值模拟结果与LDV流场测量结果进行了对比,验证了其可靠性。通过对不同根部负荷螺旋桨毂涡结构的对比分析,描述了根部负荷对毂涡结构的影响,这对于螺旋桨设计中桨毂影响分析及毂涡节能装置设计具有一定的参考意义。
1 CFD模拟方法 1.1 数值方法本文螺旋桨水动力性能及尾流场的数值模拟以连续性方程和三维不可压缩雷诺应力(RANS)方程为控制方程,并以SST k-ω二方程湍流模型确保方程封闭,方程离散采用有限体积法进行。对流项和耗散项的离散分别应用2阶迎风格式和2阶中心差分格式。求解过程基于Simple算法,离散方程采用Gauss-Seidel进行迭代求解。
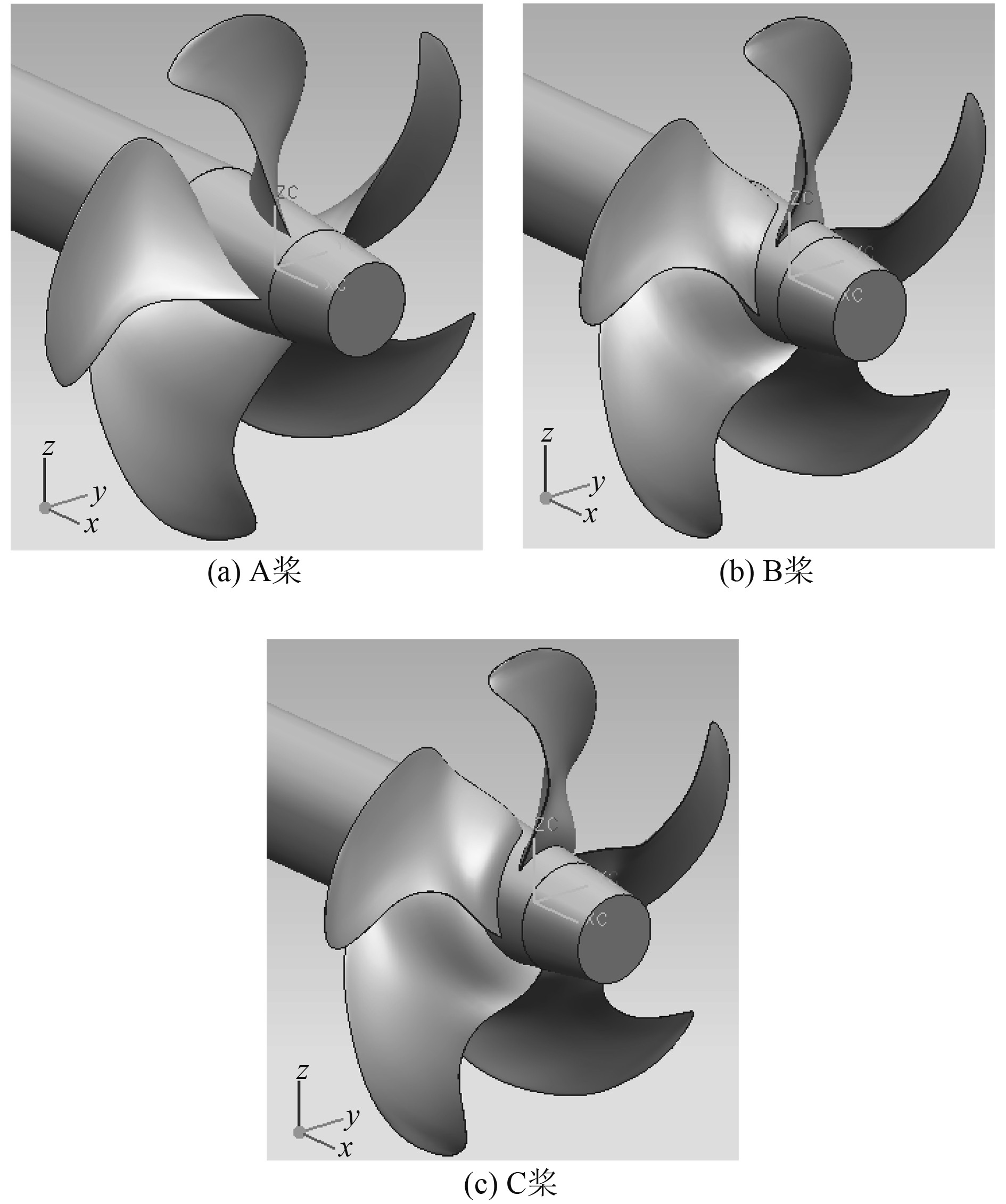
1.2 计算模型和边界条件计算模型均为5叶螺旋桨,半径R为125 mm,除径向环量分布差异引起的螺距和最大拱度分布存在区别外,其余主参数及剖面型值均相同,三维模型如图1所示。螺旋桨前方为延伸至计算域入口的与桨毂大端等直径的圆柱。数值模拟计算域为圆柱形区域,入口位于螺旋桨盘面上游4R,出口位于螺旋桨盘面下游16R,计算域半径为6R。本文直角坐标系x沿螺旋桨轴线向下游为正,y、z方向符合右手法则,螺旋桨参考线与y轴正向重合;柱坐标系轴向a向下游为正,径向r向外为正,切向t逆时针为正,参考线位置为0相位。螺旋桨旋转方向为右旋,旋向为负。
|
图 1 螺旋桨三维模型 Fig. 1 3D model of the propeller |
计算域入口V0为3 m/s的等值速度进口边界,出口为压力出口边界,螺旋桨、桨毂及桨轴表面为无滑移边界。进速系数
数值模拟计算网格总数约为18M,桨叶区域采用非结构化网格,叶根和桨毂壁面网格为0.002R;桨叶以外区域采用六面体结构化网格,网格增长率为1.05。
本文所列结果速度以来流速度V0,长度以螺旋桨半径R,压力以
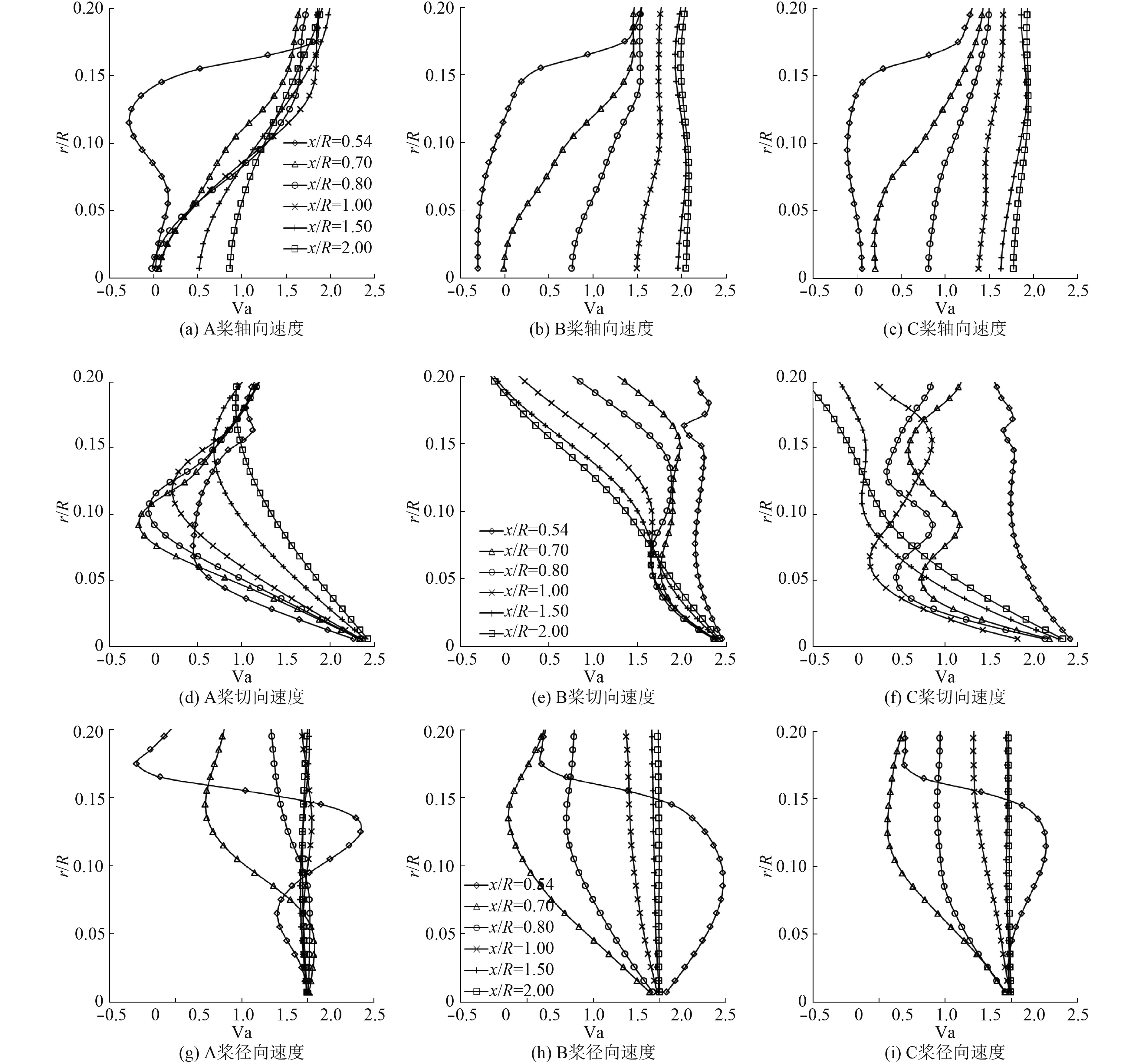
该螺旋桨曾经应用LDV流动测试技术进行过尾流场速度测量[15],本文CFD数值模拟得到的螺旋桨尾流场与之进行了对比。在轴向x/R=0.54位置的周向平均速度沿径向分布的对比结果如图2所示,径向位置r/R=0.36和0.096(毂涡区域内)的流场周向速度分布对比结果如图3所示。从图2的对比结果可以看出,LDV与CFD得到的周向平均速度差异在大部分区域内吻合良好。从图3(a)结果看出CFD模拟较准确地描绘了桨叶尾流区速度峰值的位置和大小。螺旋桨毂涡区域湍动能较强[9],流场脉动较大,这从图3(b)中波动较大的LDV测试结果也可以看出。本文CFD模拟得到的速度场在毂涡区域与LDV测试结果吻合程度相对毂涡外的螺旋桨尾流区为低,但是仍可以得到正确的周向平均切向速度峰值出现的径向位置周向速度分布的趋势也与LDV结果相符。因此,采用本文的数值模拟结果进行螺旋桨尾涡系分析是可行的。

|
图 2 螺旋桨尾流场CFD模拟与LDV测量周向平均速度结果对比 Fig. 2 Comparison of propeller circumferential average velocity between CFD |

|
图 3 螺旋桨尾流场CFD模拟与LDV测量周向速度分布结果对比 Fig. 3 Comparison of propeller circumferential velocity distribution between CFD simulation and LDV measurement |
螺旋桨的环量分布采用斯托克斯定理,通过对桨后流场中的切向速度进行周向积分得到,其计算方法见式(1)。Hong[5]通过CFD数值模拟分别采用该方法和绕叶片直接速度积分进行径向环量分布计算,除叶梢区域外,2种方法得到的结果吻合很好。图4为计算结果。

|
图 4 归一化的径向环量分布(x/R=0.16) Fig. 4 Normalized radial circulation distribution (x/R=0.16) |
| $Z\varGamma = r\oint {{v_t}\mathrm d\theta }\text{。} $ | (1) |
式中,Z为螺旋桨叶数,Γ为桨叶环量。
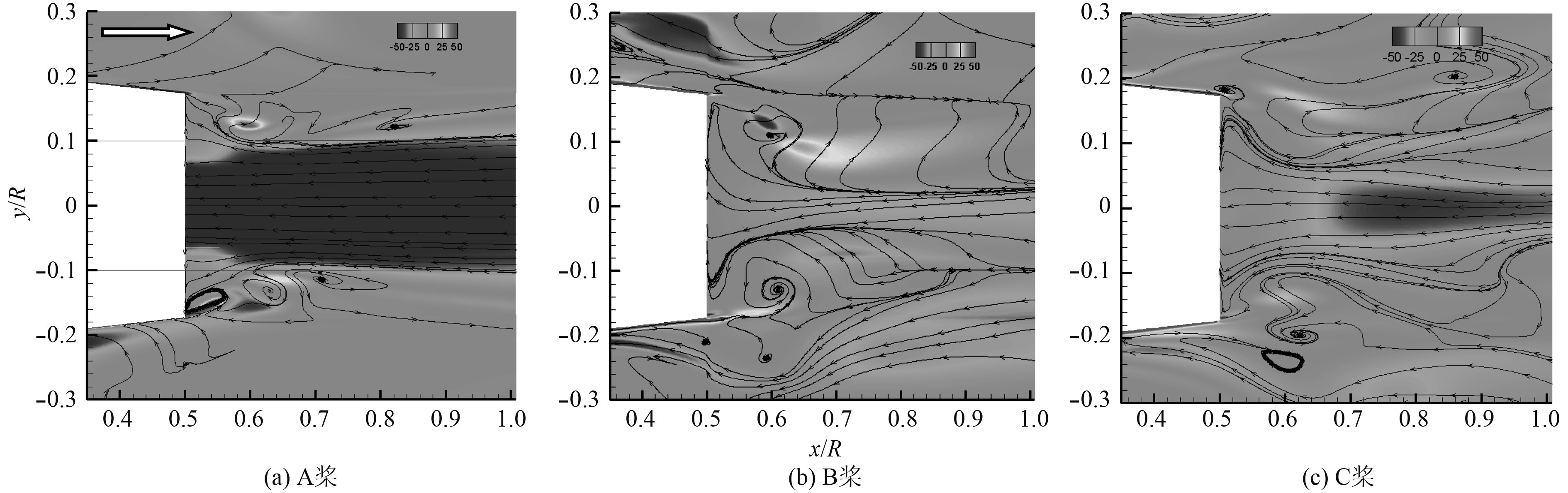
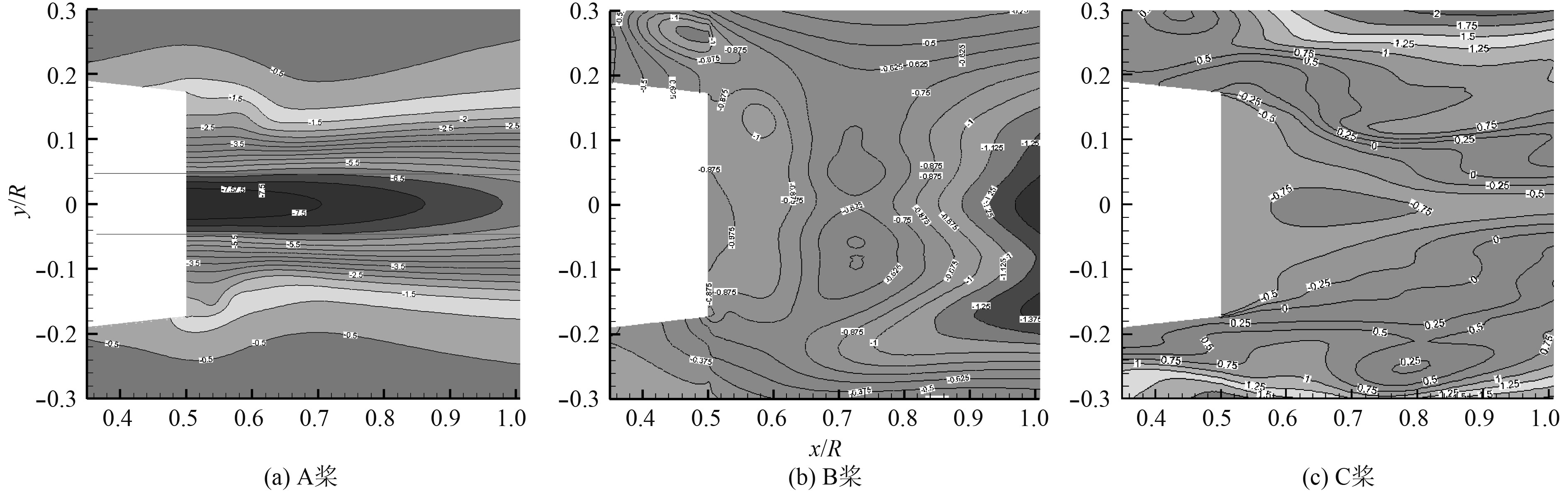
4 结果分析 4.1 毂涡形态图5和图6分别为中纵剖面轴向涡量分布、涡线图和压力分布图。从图5可以看出,A桨毂涡轴向涡量集中,且均为轴向涡,B桨毂涡微弱,除轴线附近区域外以径向涡为主,C桨毂涡强度和轴向涡区域的直径大小均居中;A桨在桨毂端面壁面附近的涡线指向外半径,而B桨和C桨则指向内半径,说明A桨毂涡区壁面附近的切向速度已经高于壁面当地旋转线速度。从图5和图6三桨的对比可以发现,随着螺旋桨根部负荷的增加,毂涡强度增强,毂涡区域压力越低,从桨毂端面引出的涡线锥度越小,轴向涡占优明显。
|
图 5 中纵剖面(Z=0)轴向涡量Ωa分布及涡线 Fig. 5 Axial vorticity Ωa distribution and vortex line in the middle section (Z=0) |
|
图 6 中纵剖面(Z=0)压力分布 Fig. 6 Pressure distribution in the middle section (Z=0) |
A桨根部负荷很重,毂涡及低压区均从桨毂端面处产生,B桨桨毂区域基本不存在毂涡及低压区,而C桨的根部负荷居中,也更接近普通民船螺旋桨,此时的低压区距离壁面存在一定距离,这一现象应该是由旋转速度、桨叶根涡和端面分离流动共同作用导致的。
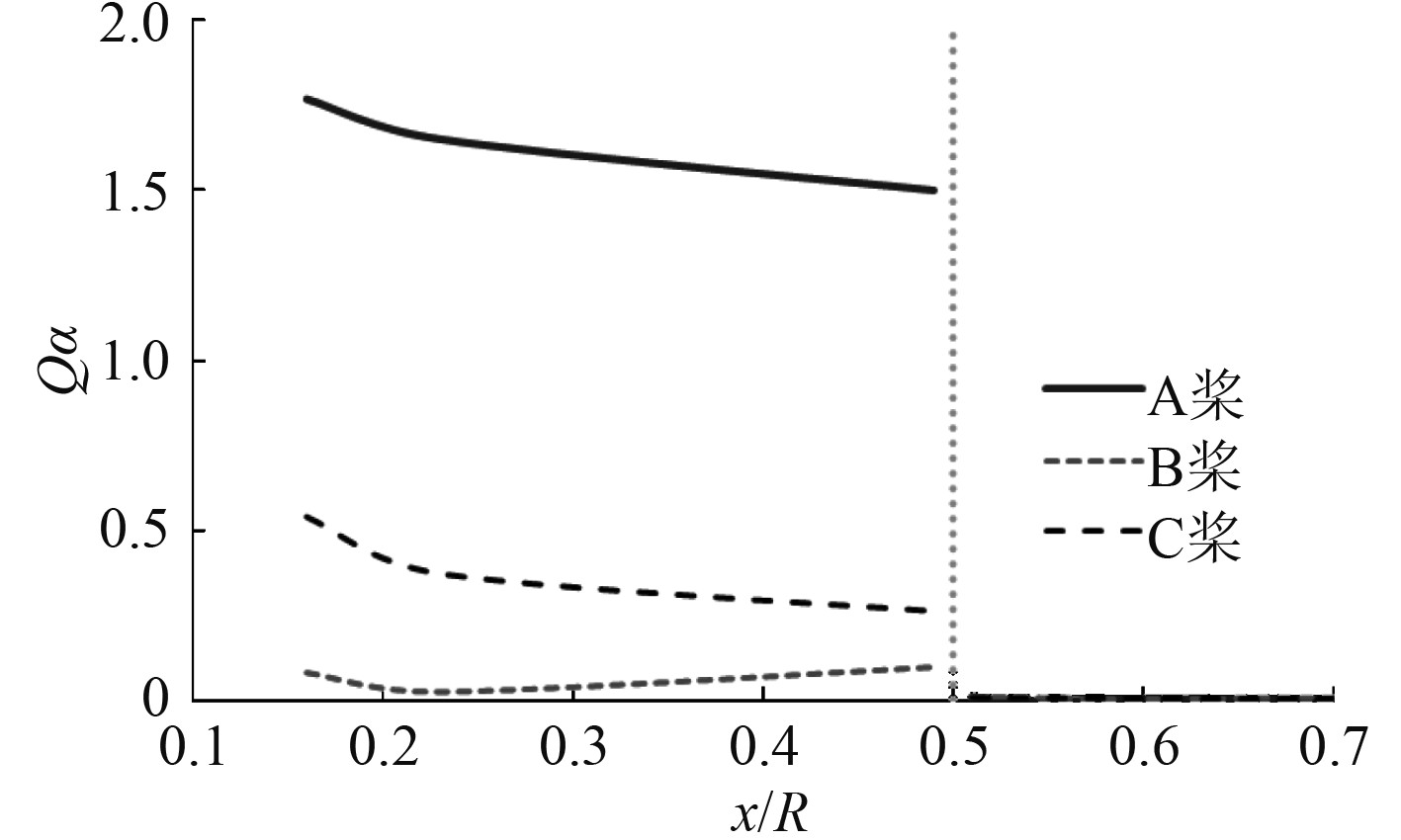
4.2 轴向涡通量发展为进一步研究毂涡结构,对不同轴向断面分别进行轴向涡通量Qa计算,计算方法见式(2),在桨毂区域(x/R<0.5)径向积分范围为桨毂壁面边界层外至半径R,图7为计算结果。从图中可以看出,由于涡量耗散,在桨毂端面之前的轴向涡通量呈现不断缓慢下降的趋势,而在桨毂端面以后位置,轴向涡通量降至零。由于在r/R=1.0位置的切向速度已经降至0,由斯托克斯定理即式(3)易得,不同轴向断面半径r/R=1.0以内的轴向涡通量同样为0。因此,桨毂环量与图7中x/R<0.5的部分大小相等,正负相反。而在离开桨毂以后,对于根部存在负荷的螺旋桨,从桨毂环量发展成为由桨毂端面产生的一根轴向涡,使得斯托克斯定理得以继续满足。图8为端面后方该轴向涡直径大小沿轴向位置变化,即与桨毂环量相等时的轴向涡通量积分区域半径大小。
|
图 7 轴向涡通量沿轴向位置的变化 Fig. 7 Variation of axial vortex flux along axial position |

|
图 8 与毂涡环量相等的轴向涡直径变化 Fig. 8 Variation of axial vortex diameter the vortex flux of which equal to hub vortex ring |
| ${Q_a} = \int\nolimits_s {{{\varOmega }} \cdot {\rm d}{{s}}} = \int\nolimits_0^1 {\int\nolimits_0^{2{\text{π}} } {{\varOmega _a}} } {\rm d}\theta {\rm d}r \text{,}$ | (2) |
| $\int\nolimits_S {{{\varOmega }} \cdot {\rm d}{{s}}} = \int\nolimits_L {{{v}} \cdot {\rm d}{{l}}}\text{。} $ | (3) |
图9为螺旋桨后方根部周向平均速度分布图。A桨切向速度明显大于C桨,轴向速度亏损随着x/R的增加恢复较慢,径向收缩较快,而B桨均处于A桨、C桨之间,这与4.1中涡量的分析结果相对应。根部负荷较重的A桨毂涡很强,切向速度大、压力低,这抑制了轴向速度亏损的恢复和加快了桨毂端面后方的收缩流动。而根部零负荷的B桨与其相反,不存在低压区,因此桨毂后方的轴向速度亏损很快恢复,径向收缩较缓慢。
|
图 9 桨毂后方周向平均速度分布 Fig. 9 The average circumferential velocity distribution behind the propeller hub |
本文采用CFD技术对螺旋桨尾流场进行数值模拟,并与LDV流场测量结果进行对比,验证了计算结果的可靠性。通过对3个不同负荷形式的螺旋桨毂涡流动的数值模拟结果对比分析,研究了根部负荷对毂涡结构的影响。结果表明,螺旋桨毂涡环量向下游发展形成了轴向集中涡,其强度与根部负荷呈现正相关,重负荷桨毂涡直径更大,毂涡区域压力更低,这造成了桨毂端面后方的收缩速度更快,轴向速度亏损恢复也更慢。
本文计算仅为定常流动模拟,并未针对后端面的分离流动影响详细分析,这有待将来开展进一步的研究工作。
| [1] |
LERBS H W. Moderately loaded propellers with a finite number of blades and an arbitrary distribution of circulations[J]. Transactions - Society of Naval Architects and Marine Engineers, 1952, 60: 73-123. |
| [2] |
KERWIN J E, LEOPOLD R. A design theory for subcavitaing propellers[C]// SNAME 1964.
|
| [3] |
孙文愈. 螺旋桨性能分析与优化设计中桨毂的影响分析[J]. 中国造船, 2016, 57(1): 19-29. DOI:10.3969/j.issn.1000-4882.2016.01.003 |
| [4] |
BRIZZOLARA S, GAGGERO S, GRASSI D. Hub effect in propeller design and analysis [C]// Third International Symposium on Marine Propulsors, Australia, 2013.
|
| [5] |
HONG FANGWEN, DONG SHITANG. Numerical analysis for circulation distribution of propeller blade[J]. Journal of Hydrodynamics, 2010, 22(4): 488-493. DOI:10.1016/S1001-6058(09)60080-9 |
| [6] |
SHIN K W, ANDERSEN P. CFD study on effective wake of conventional and tip-modified propellers [C]// 31st Symposium on Naval Hydrodynamics, America, 2016.
|
| [7] |
JESSUP S D. An experimental investigation of viscous aspects of propeller blade flow[D]. The Catholic University of America, 1989.
|
| [8] |
WANG M H. Hub effects in propeller design and analysis[D]. Cambridge: Massachusetts Institute of Technology, 1985.
|
| [9] |
KUMAR P, MAHESH K. Large eddy simulation of propeller wake instabilities[J]. Journal of Fluid Mech, 2017, 814: 361-396. DOI:10.1017/jfm.2017.20 |
| [10] |
FELLI M, ROBERTO C, GUJ G. Experimental analysis of the flow field around a propeller-rudder configuration[J]. Exp Fluids, 2009, 46: 147-164. DOI:10.1007/s00348-008-0550-0 |
| [11] |
FELLI M, CAMUSSI R, DIFELICE F. Mechanisms of evolution of he propeller wake in the transition and far fields[J]. Journal of Fluid Mech, 2011, 682: 5-53. DOI:10.1017/jfm.2011.150 |
| [12] |
李鹏程, 邓丽丽, 韩用波. 螺旋桨毂帽鳍设计新方法[J]. 船海工程, 2011(6). DOI:10.3963/j.issn.1671-7953.2011.06.036 |
| [13] |
李鑫. 桨后节能舵球的水动力性能分析[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
| [14] |
高德宝. 消涡轮节能装置的机理分析及效果论证评估[D]. 无锡: 中国船舶科学研究中心, 2015.
|
| [15] |
LI PENGCHENG, ZHANG GUOPING, ZHOU WEIXIN. LDV measurements of flow field of propeller with PBCF for CFD validation [C]// Advanced Maritime Engineering Conference, Taipei, 2012: GT-12.
|
 2020, Vol. 42
2020, Vol. 42
