0 引　言

对于船体振动计算时的舱内液体模拟，目前通常的处理方法并不考虑附连水质量，而采用以下2种方法：1）将液体质量用质量单元模拟并均布在舱内强构件上（避免出现较多局部模态），或者通过改变舱室的结构单元材料密度来模拟液体质量，并确保重心位置的准确（以下简称“质量分布法”）；2）在液舱体积中心位置添加质量单元，并使用MSC/Nastran中多点约束单元RBE3^[7]将其与液舱强构件连接模拟（以下简称“多点约束法”）。

由于质量分布法和多点约束法都涉及人为节点选择与RBE3主节点定义，这会导致有限元模型中的质量分布与实际附加质量分布不符。虽然质量点可以通过调整不同区域的质量点疏密调节质量分布，RBE3单元也可以通过调整主节点及其权重因子达到调节质量分布的目的，可是这种方法无法对不同的振动模态进行动态调整。

与舷外水相比，在实船领域采用边界元法模拟舱内液体附加质量的实例相对较少。本文以文献[1]中的实验船模为研究对象，采用与舷外水相同的处理方法，对其舱内液体使用虚拟质量模拟^[2-3]（以下从质量模拟的角度简称“虚拟质量法”），并将结果与上述2种方法的结果进行对比。验证其准确性，并采用这3种方法分析某型油船的振动模态并对其结果进行对比分析。

1 虚拟质量法基本原理

基于Nastran软件平台，使用边界元法在湿表面上分布一系列的源汇来求解拉普拉斯方程。通过匹配相应的边界条件，可以求解以源强为未知数的线性方程组，进而得到面元上的压力。

假设边界上某面元的源强为 ${\sigma _j}$ ，面元的面积为 ${A_j}$ ，位置向量为 ${r_j}$ ，则任意位置 ${r_i}$ 处诱导速度 ${\dot u_i}$ 为：

${\dot u_i} = \sum\nolimits_j {\int_{{A_j}} {\frac{{{\sigma _j}{e_{ij}}}}{{\left| {{r_i} - {r_j}} \right|}}} } {\rm d}{A_j}\text{。}$

(1)

式中， ${e_{ij}}$ 为从j点指向i点的单位矢量，该点的压力为：

${\dot p_i} = \sum\nolimits_j {\int_{{A_j}} {\frac{{\rho {{\dot \sigma }_j}{e_{ij}}}}{{\left| {{r_i} - {r_j}} \right|}}} } {\rm d}{A_j}\text{。}$

(2)

式中， $\rho $ 为流体的密度。将方程离散后，可写成矩阵形式，分别为：

$\left\{ {{\dot u}} \right\} = \left[ \chi \right]\left[ \sigma \right]\text{，}$

(3)

$\left\{ { F} \right\} = \left[ \Lambda \right]\left[ {\dot \sigma } \right]\text{。}$

(4)

式中， $ F$ 为节点列阵， $\Lambda $ 为式（2）积分而得。将式（3）和式（4）联立可得：

$\left\{ { F} \right\} = \left[ {{{ M}^f}} \right]\left[ {{\ddot u}} \right]\text{。}$

(5)

式中， ${M^f}$ 为虚拟流体质量矩阵，ü为加速度矩阵，由此可求得：

$\left[ {{{ M}^f}} \right] = \left[ \Lambda \right]{\left[ { \chi} \right]^{ - 1}}\text{。}$

(6)

需要注意的是，如果 $\left[ \chi \right]$ 是奇异矩阵或者接近奇异矩阵，求解虚拟质量矩阵时会产生奇异性问题。这种情况只有在流体被结构完全包围（封闭结构）并且有对称运动平面时才会发生。上述情况会导致计算结果失真。

当 $\left[ \chi \right]$ 可能是奇异矩阵时，需在靠近各个流域体积中心的地方增加额外的源，或者采用以下避免矩阵奇异性的方法：

1）通过从ELIST卡片中移除一个在不重要面上的单元，使边界上产生一个或多个孔；

2）在靠近液舱顶部定义一个自由面，并通过改变ELIST来移除这个面以上的单元；

3）约束结构以消除封闭体积的任何净变化，即产生一个MPC方程，使得：

$\sum\limits_i {{A_i}{{\overline n }_i} \cdot {{\overline u }_i}} = 0\text{。}$

式中， $i$ 为边界上的节点， ${A_i}$ 和 ${\overline u _i}$ 分别为有效面积和法向速度矢量。

由于船舶舱室通常是封闭结构，如果不作处理，在求解时会产生奇异性。本文采用方法1从ELIST卡片中去除舱室最顶部的一个单元，来消除奇异性。

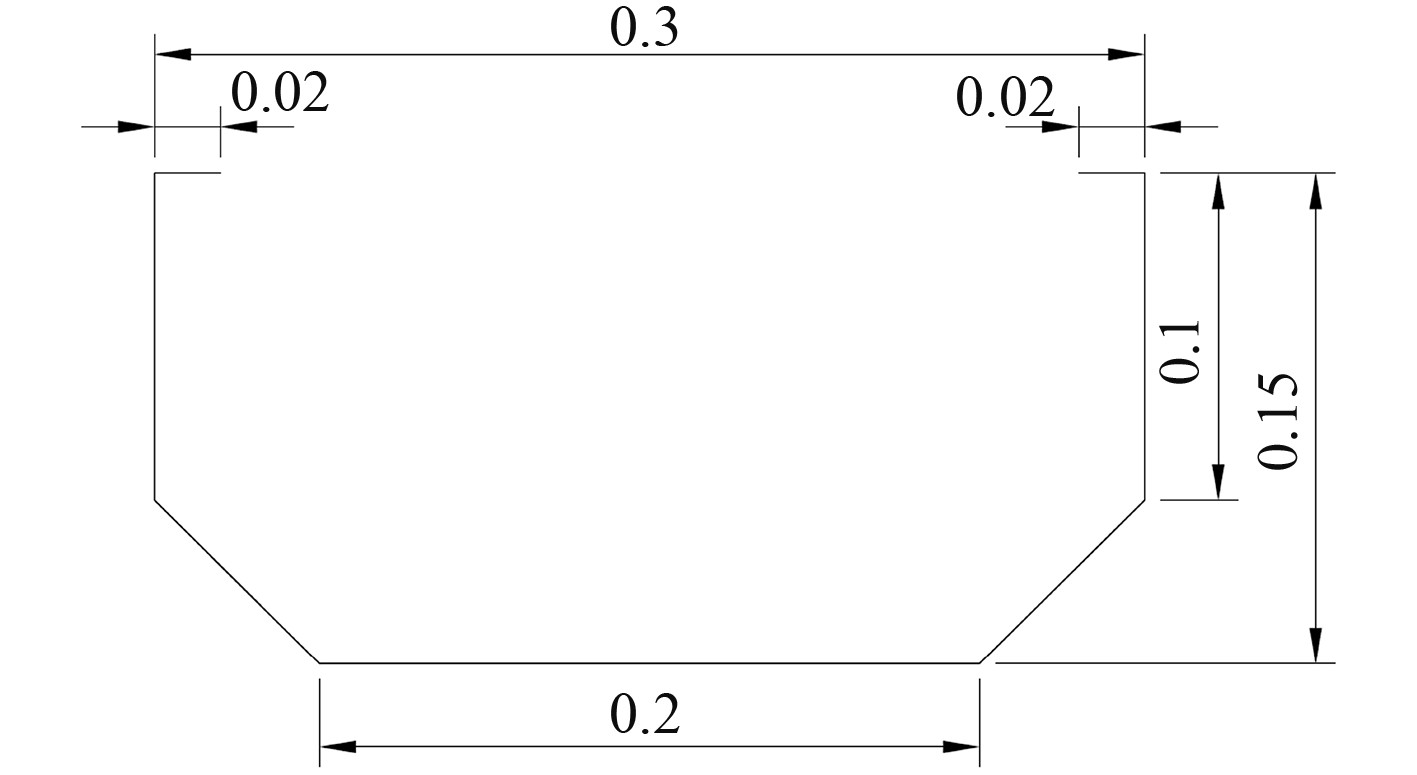
2 船模实例计算 2.1 船模参数及有限元模拟

本节选取文献[1]中所述的船模，分别使用质量分布法，多点约束法以及虚拟质量法计算其1阶垂向固有频率，并将其与实验值进行对比。船模共有6个舱，各舱及船模横剖面的尺寸分别如图1和图2所示。

船模的物理参数如表1所示。

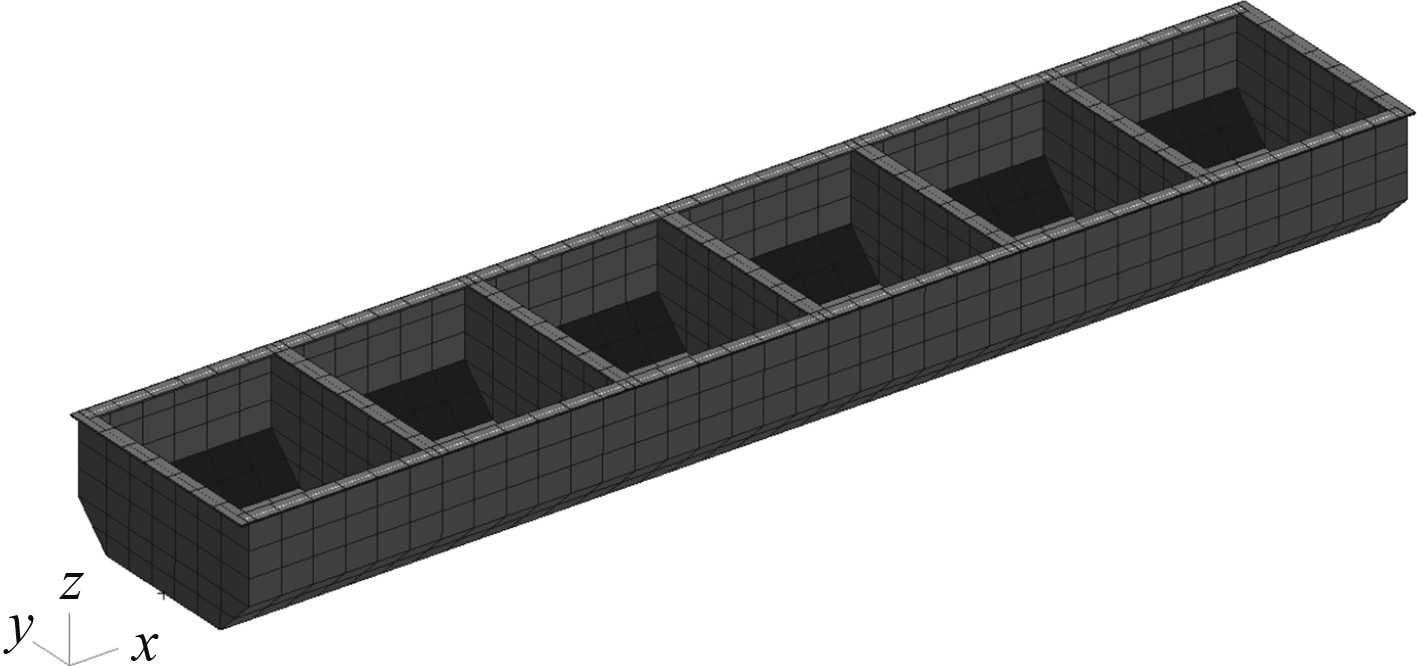
船模有限元模型如图3所示。

船模空船状态下（干模态）1阶垂向振动固有频率实验值与有限元数值计算结果如表2所示。

由表2可知，有限元计算结果与实验值很接近，说明船模结构有限元模型的模拟是准确的。

2.2 装载实验结果与有限元计算值比较

在舱内装水并计算装载状态下的船模1阶垂向振动固有频率。选取实验中5种装载状态，分别为10.5 kg，15 kg，30 kg，39 kg和48 kg。使用分布质量法，多点约束法，以及虚拟质量法对舱内的水进行模拟。

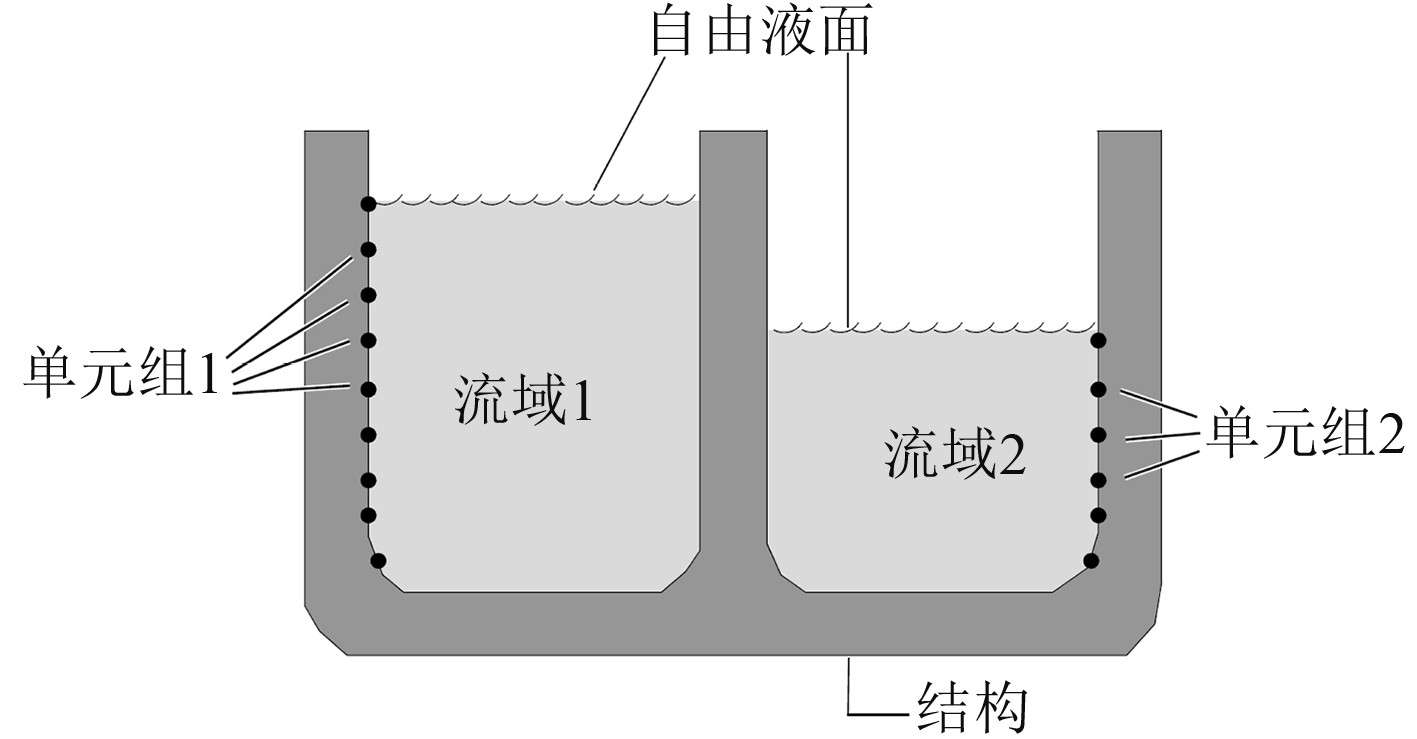
虚拟质量使用MSC/Nastran中MFLUID卡片^[5]进行定义。图4展示了定义MFLUID卡片时对应的模型示意图。

每个流域由一张MFLUID卡片单独定义，其中包含了液体密度，自由面高度，液体和结构之间交界面等信息。液体和结构的交界面使用ELIST卡片定义，ELIST卡片中包含由一组三角形和四边形单元组成的湿单元，而湿单元的法向确定了流域的位置。在同一个流域中湿单元的法向应保持一致。

使用质量分布法的有限元模型如图5所示，使用多点约束法的有限元模型如图6所示。

表3给出了不同装载量下船模1阶垂向振动固有频率实验值，以及采用虚拟质量法、质量分布法、多点约束法船模1阶垂向振动固有频率有限元数值计算结果，表4给出了各有限元数值计算与实验值之间的偏差情况。

图7为不同装载工况下实验值和3种舱内液体模拟方法下有限元计算结果之间的关系和趋势。

由表3、表4和图7可以发现：

1）与另外2种模拟方法相比，使用虚拟质量法计算得到的船模1阶垂向固有频率与实验值最为接近；

2）当舱内装载率逐渐增加时，虚拟质量法与实验值之间的误差逐渐减小，而其他2种变化不大；

3）5种装载工况下，虚拟质量法的平均计算误差为11.12%，在装载率较高的情况下，虚拟质量法的计算误差小于10%；

4）多点约束法与质量分布法的计算结果与实验值偏差比虚拟质量法大，其中多点约束法的偏差普遍大于40%。

在实际船舶装载过程中，满舱和空舱情况较多。空舱情况无需模拟液体质量，而对于满舱，相比质量分布法与多点约束法，虚拟质量法具有更高的精度。

3 实船计算

以某型油船为例，在满载出港工况下使用虚拟质量法计算该型油船低阶固有频率，并以此为基准，将其与使用质量分布法和多点约束法的计算值进行对比，考察不同舱内液体模拟方法对计算结果的影响。

3.1 全船有限元模型

所选船型主参数如表5所示。

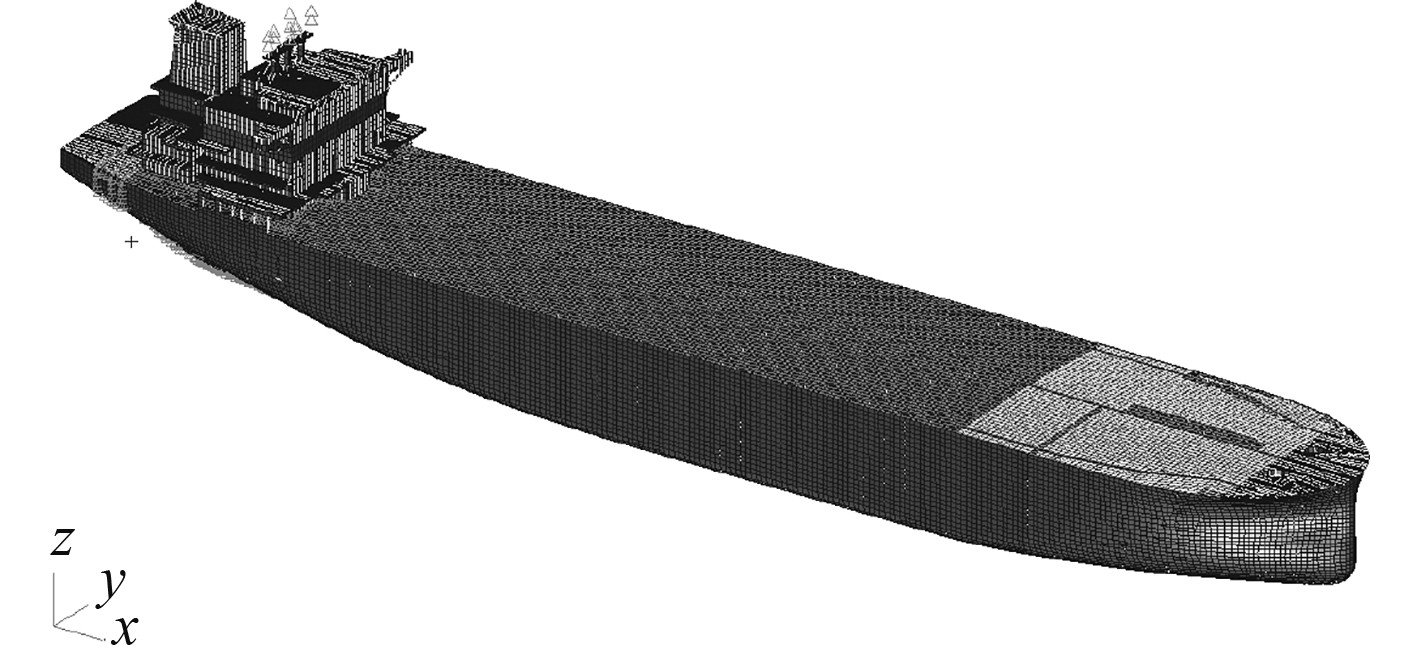
全船结构有限元模型如图8所示。3种方法的模型除货舱区舱内液体质量模拟方式不同外，其余模型完全一致。

3.2 模态计算结果

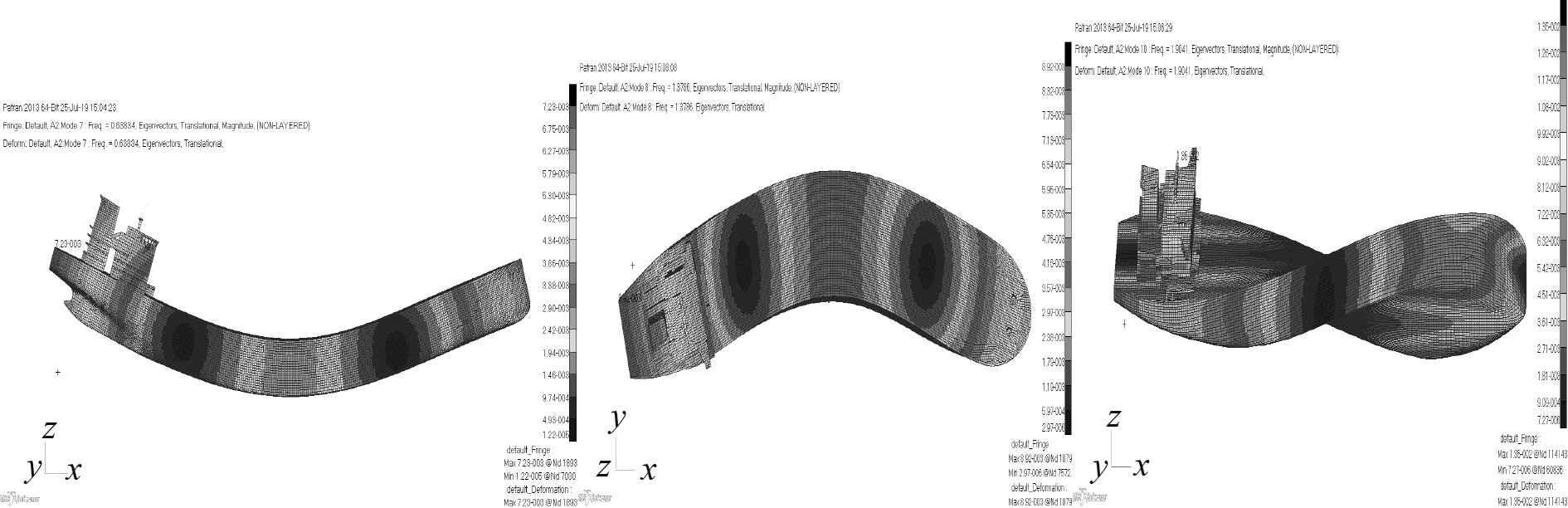
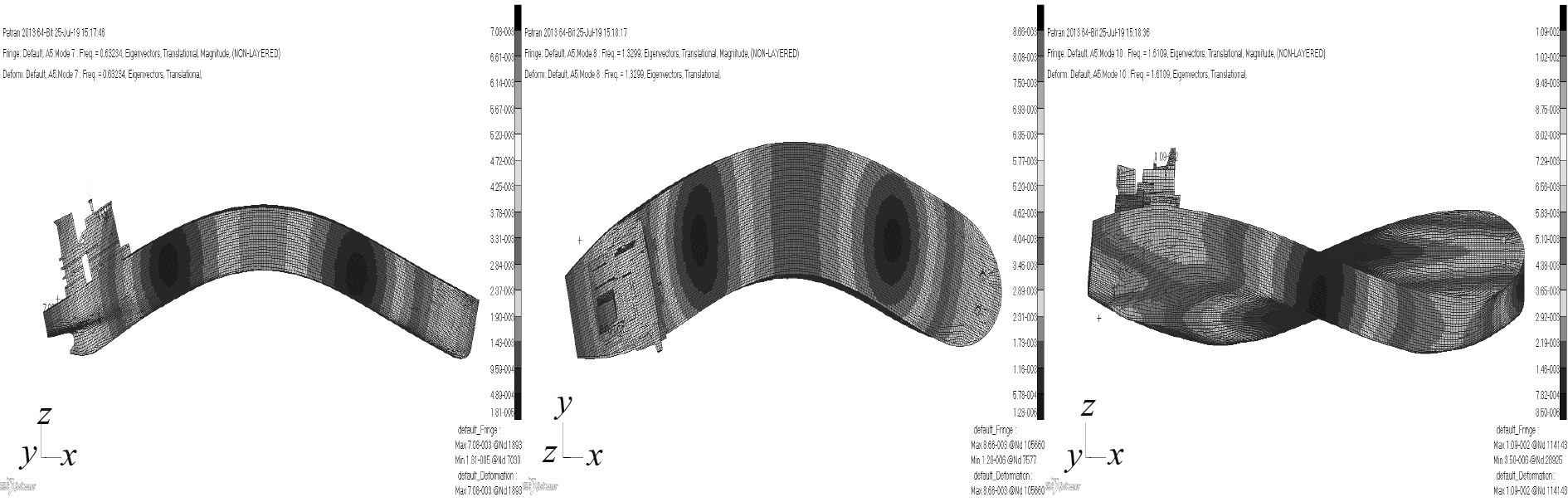
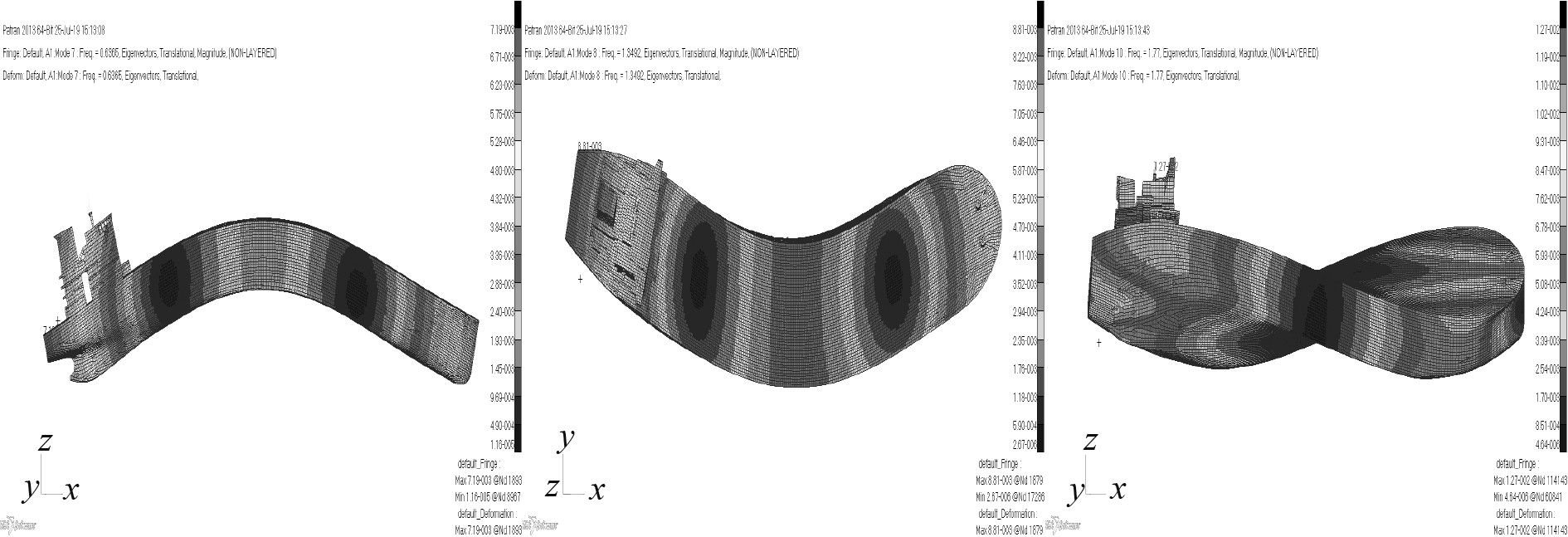
3种不同模拟方法的有限元数值计算结果如表6所示，其1阶垂向/横向/扭转振动模态如图9～图11所示。

表7计算了使用质量分布法、多点约束法时与使用虚拟质量法时的偏差情况。

由表6和表7对比结果可以发现：

1）使用虚拟质量法计算的船体梁扭转固有频率与使用另外2种方法计算的扭转固有频率差异较大；

2）使用虚拟质量法与使用另外2种方法计算第4阶垂向固有频率较前3阶垂向固有频率偏差显著增大；

3）使用虚拟质量法计算的船体梁1阶垂向固有频率与使用另外2种方法计算的1阶垂向固有频率差异较小。

3.3 计算结果分析

上述船型的扭转固有频率在使用虚拟质量法时的计算值较高且与使用另外2种方法计算的扭转固有频率差异较大，这说明此时的附加质量与液舱中液体的总质量相比较少或者质量分布不是均布。

但是在使用质量分布法时，由于仅考虑舱内液体重心位置的准确，舱内液体质量一般是平均添加到模型中相应各节点上的，且一经确定，无法根据不同的振动模态进行动态调整。

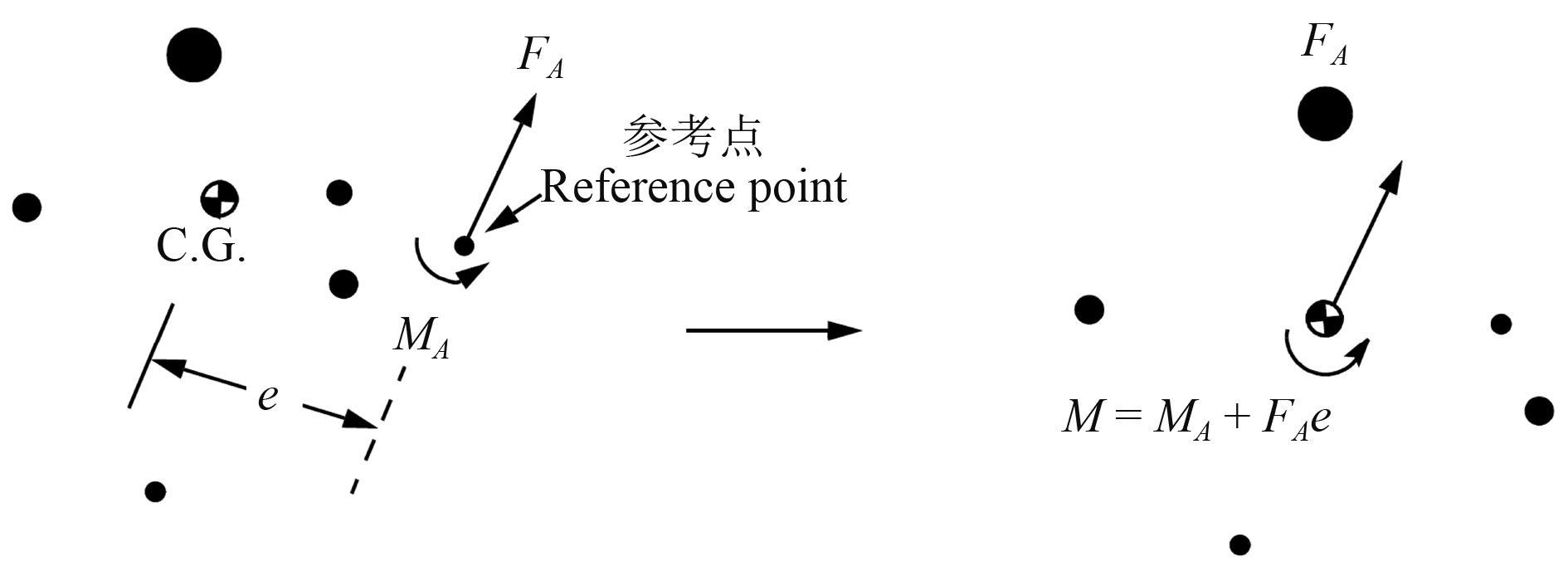
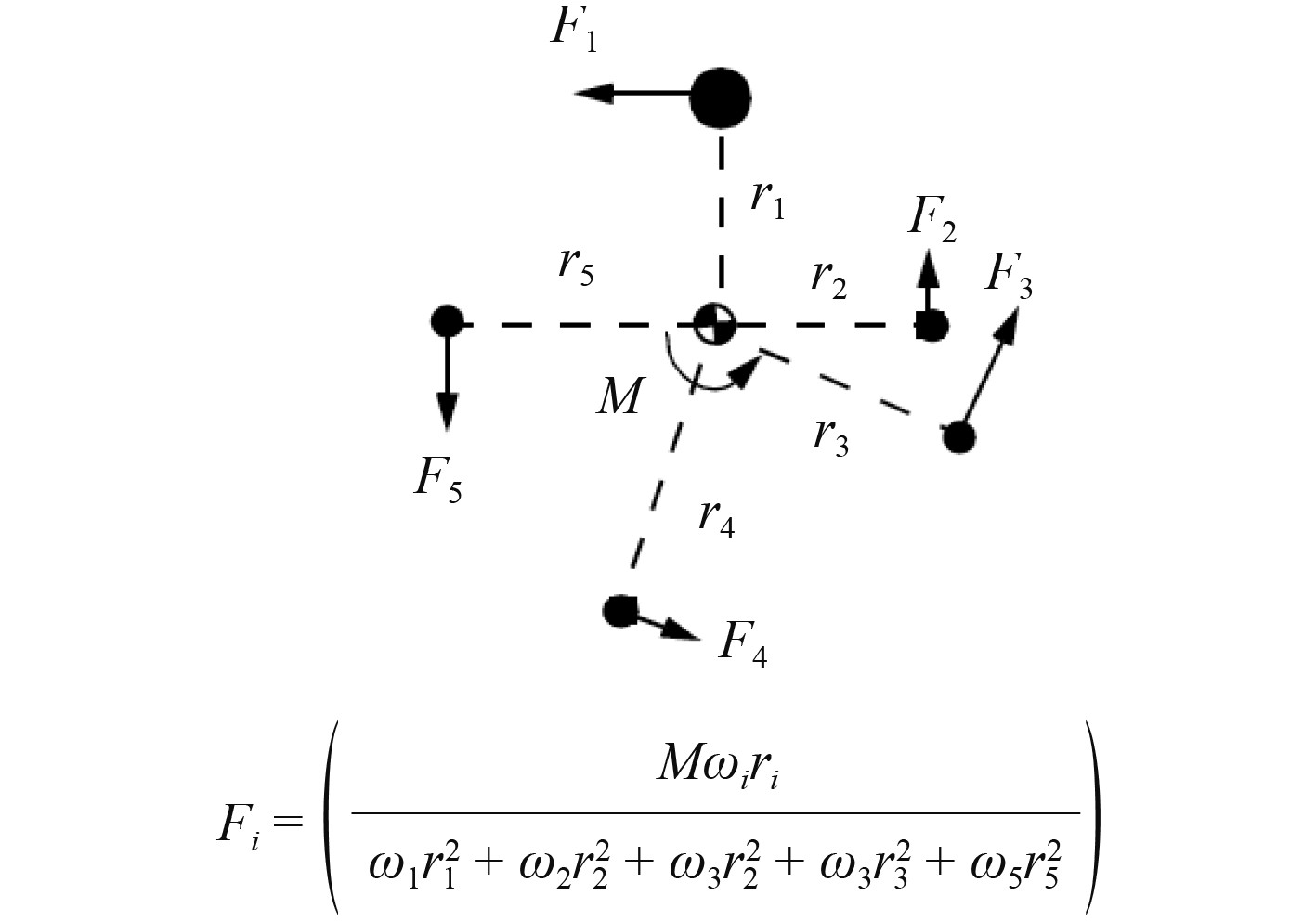
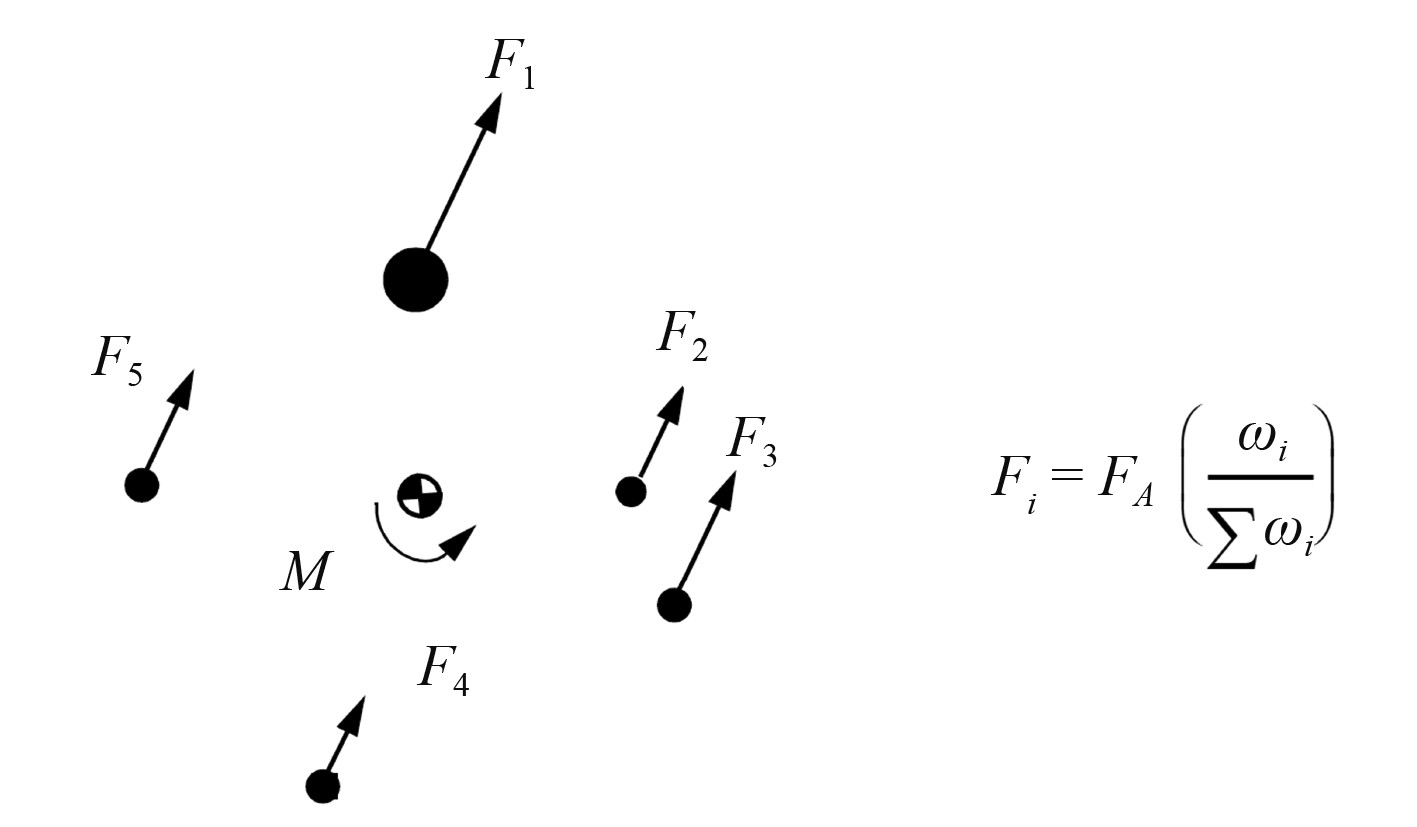
图12～图14显示了使用多点约束法时RBE3单元如何计算参考点上作用的力和力矩在节点组重心处的等效力和力矩，以及在节点组重心处等效力和力矩的一般分配方法。图中 ${\omega _i}$ 为力或力矩在 $i$ 点的权重系数^[9]。

若未手动设置权重系数（即 ${\omega _i} = 1$ ），惯性力将平均分配到RBE3的各个主节点上，而惯性力矩将根据与节点组重心的距离远近将惯性力分配到RBE3的各个主节点上^[9]。当主节点设置的位置、数量和权重选择不当，质量分布将与实际存在一定的差异，并且，无法根据不同的振动模态进行合理的动态调整。

垂向振动、水平振动、扭转振动模式下，船体传递给舱内液体的能量是不同的，其不同阶模态对应的虚拟质量是不相同的。虚拟质量法针对不同形式的振动模态，通过源汇分布法求解各阶振动模态下流体速度势进而求得流体的虚拟质量，这与分布质量法和多点约束法相比更加合理。

3.4 其他影响

船模数值计算中，虚拟质量法、质量分布法和多点约束法计算的1阶垂向固有频率结果有一定的偏差，而实船计算中3种计算方法的1阶垂向固有频率结果偏差较小，这是由于除了质量模拟的方法不同外，还与舱室形状和船体梁刚度等其他因素有关。

4 结　语

由于质量分布法和多点约束法在模拟舱内液体时存在一定的缺陷，而且与舷外水相比，采用边界元法模拟舱内液体附加质量的实例较少，所以本文分别使用质量分布法、多点约束法以及虚拟质量法模拟小型实验船模和某型油船舱内液体的附加质量，计算了低阶固有频率并对比分析，得到以下结论：

1）与质量分布法、多点约束法相比，采用虚拟质量法模拟舱内液体附加质量时的固有频率数值计算结果从理论角度较为严谨，通过对实验船模的数值分析对比，具有更高的精度。

2）若通过3种方法计算的固有频率差异较大，说明其舱内液体质量分布差异较大，应将虚拟质量法的模态与响应计算结果纳入减振的考虑范围。