2. 哈尔滨工程大学 船舶工程学院 黑龙江 哈尔滨 150001;
3. 蓬莱中柏京鲁船业有限公司,山东 烟台 265601
2. College of shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China;
3. Penglai Zhongbai Jinglu Ship Industry, Co. Ltd, Yantai 265601, China
船舶砰击响应是船舶结构设计中需考虑的重要方面。为保证频繁遭受砰击的船首结构的安全,各船级社规范也给出了船首底部和外飘区域的加强设计要求,但目前不同规范的要求仍存在着较大的差别[1]。尽管足够多的加强可以保证砰击载荷作用下船首的安全,但也会导致船体过重,影响其营运效率。因而,为实现船首结构的合理设计,学者们在船首砰击载荷与结构响应计算方面进行了许多研究。
于鹏垚等[2]利用三维势流理论预报船首与波浪间的相对速度,并结合任意欧拉-拉格朗日算法[3]预报了船首入水冲击的强非线性载荷。砰击载荷预报的目的是为了实现结构响应的计算。Yu等[4]结合半解析砰击模型和有限元方法实现了船体板架入水冲击响应的分析。Ren等[5]利用船体外飘区域的砰击压力载荷分布实现了外飘板架结构的动力响应分析。于鹏垚等[6]参考ABS船级社的计算指南[7],采用静力分析方法实现集装箱船首部砰击响应的计算。王辉等[8]利用楔形板架的落体砰击载荷试验获得了板架入水的动力响应,并通过与静力分析方法的应力结果对比,给出了用于肋骨响应分析的等效静压力。
可以看出,当采用动力分析方法进行局部结构砰击响应计算时,计算对象多数为船体的板架结构,而局部板架边界的设置对结构响应影响很大,如何合理地确定边界条件是利用板架模型分析时的难点。若对整船模型或船首模型进行动态响应计算,通常耗时较长,因而,耗时较短的静力分析方法在工程中被普遍采用。但是,关于如何评估砰击载荷作用下的船首局部强度,各船级社尚未给出统一的方法[1]。本文系统地分析了各参数对等效静力系数的影响,进而建立砰击载荷作用下结构响应的等效静力方法,实现了船首外飘结构的屈服强度评估。
1 等效静力方法的建立通过对入水砰击过程中三维板架动态和静态响应的比较分析,引入等效静力系数的概念,进而建立砰击载荷作用下局部板架的等效静力分析方法。
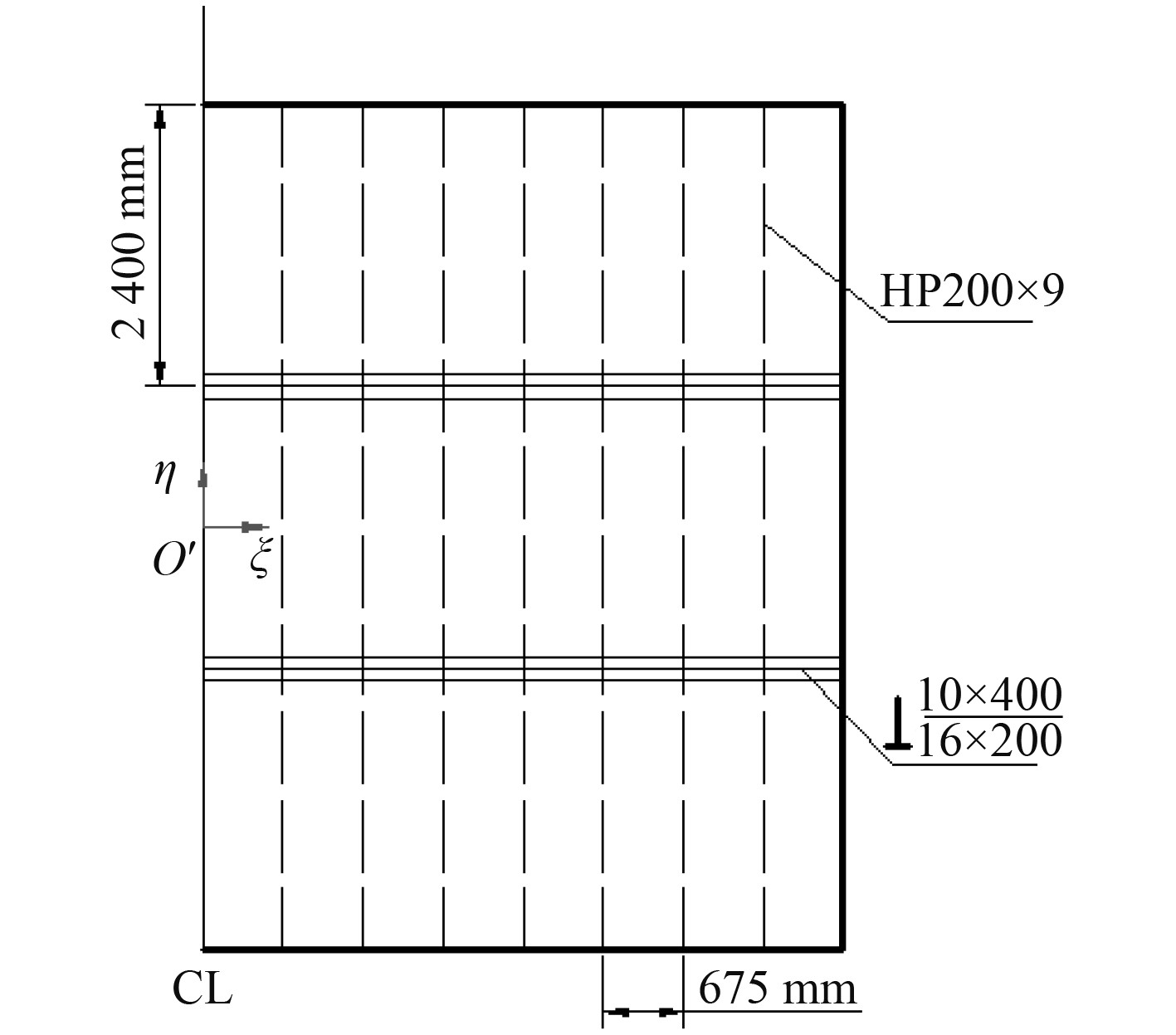
1.1 计算模型的构建楔形体入水砰击研究的有关结论在船体砰击载荷与局部结构响应的研究中常被采用[11]。这里将船体板架结构看作楔形体的一侧,进行砰击载荷作用下船体板架等效静力方法的研究。板架的具体形式如图1和图2所示。其中
|
图 1 楔形体的横剖面 Fig. 1 Transverse section of the wedge |
|
图 2 板架模型的尺寸 Fig. 2 Dimensions of the grillage |
|
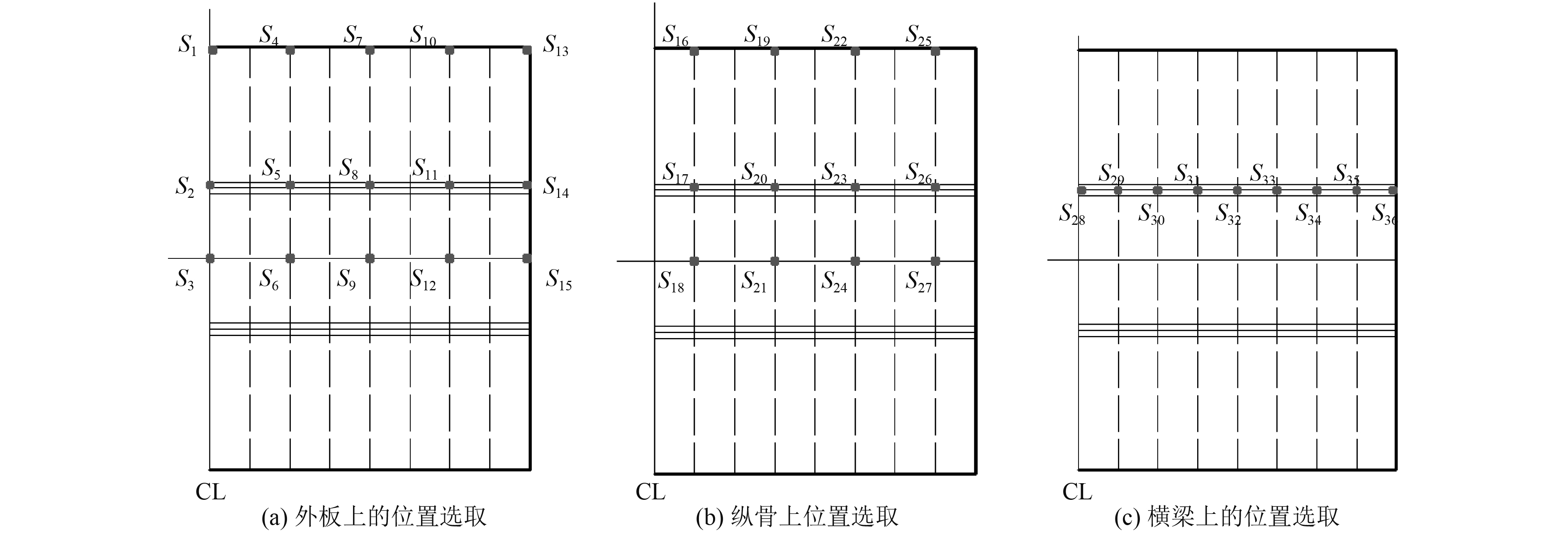
图 3 板架上的位置选取 Fig. 3 Selected locations of the grillage |
参考相关文献[8-9]或规范[7, 10],对等效静力系数进行如下定义:在某一工况下,采用板架入水冲击的动力响应分析方法,得到位置动态应力峰值;在同一工况下,加载板架上各位置压力峰值,得到静态应力;动态应力峰值与静态应力值的比值,为等效静力系数。
当采用直接计算方法或规范方法确定波浪中船首砰击载荷峰值后,可以利用上述介绍的等效静力系数进行船首砰击响应的等效静力分析。具体的操作为:选取各位置上的砰击压力峰值,将其加载到模型上进行分析,将得到的静力响应与前文定义的等效静力系数相乘,其值即为实际结构响应。
在下述条件下,5 m/s的砰击速度、35°的斜升角、50 mm的网格尺寸,板架四周为自由支持,计算得到高应力位置点的等效静力系数,如表1所示。入水砰击时板架结构的动态应力峰值,可利用Lsdyna[11],Dytran[12]或相关数值算法[4]求解。由表1发现,各构件各位置的等效静力系数并不相同,说明采用一个固定的等效静力系数进行结构分析并不合理。
|
|
表 1 高应力处的等效静力系数 Tab.1 Equivalent static coefficients of high stress locations |
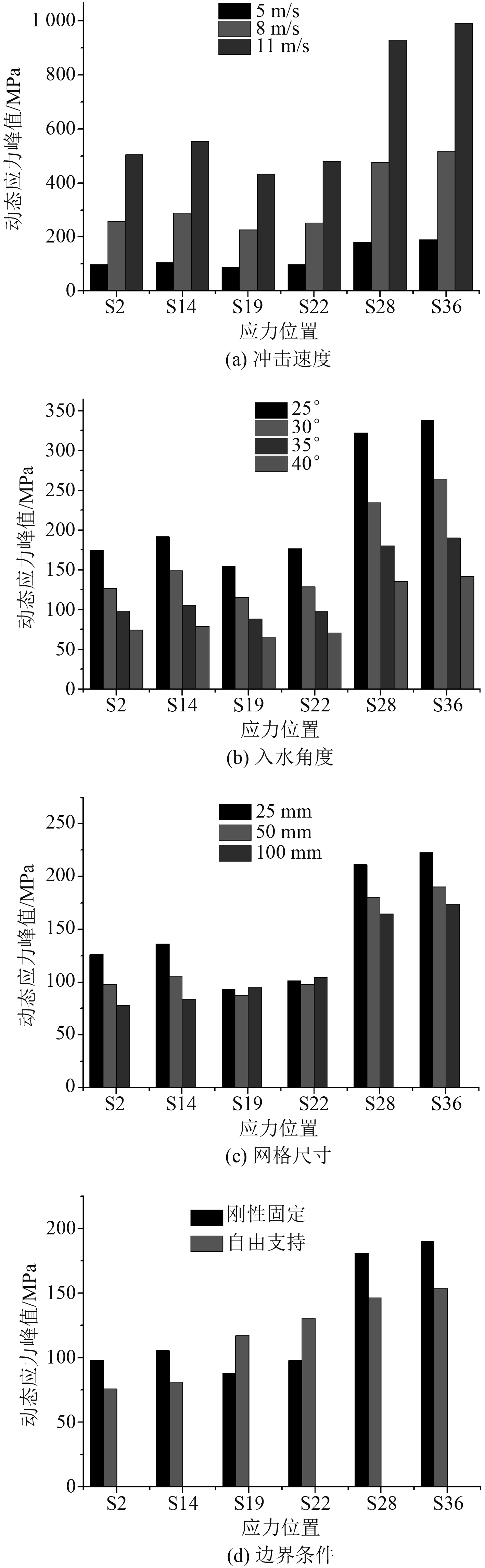
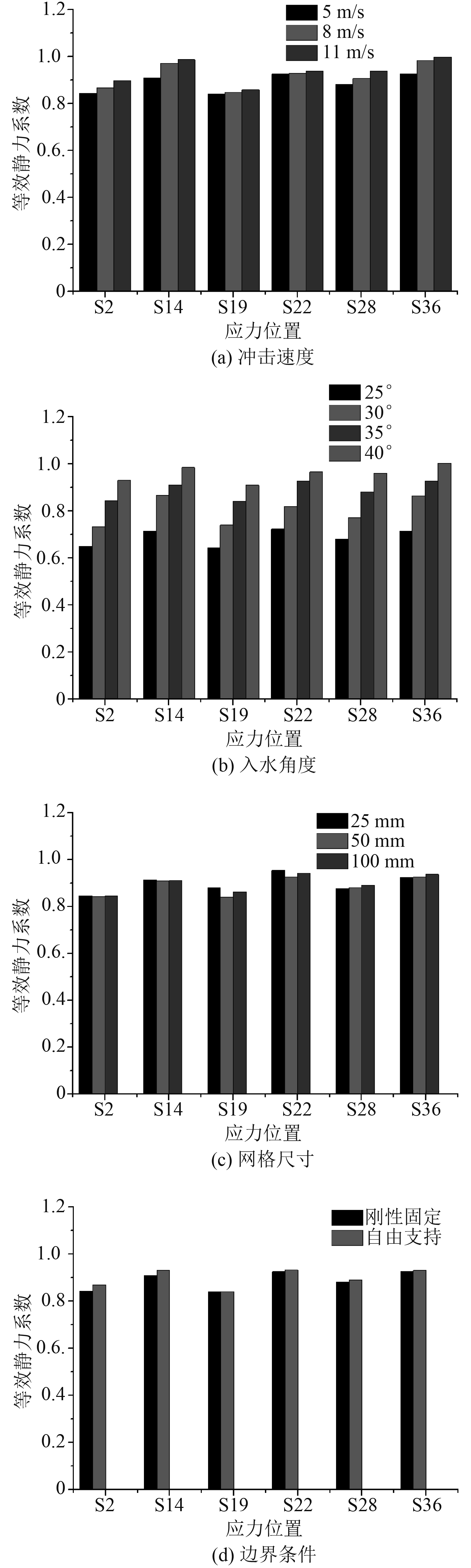
通过改变计算工况中的计算参数,分析了板架结构在各影响因素作用下的动态应力响应峰值以及等效静力系数。分析时所用的不同参数组合见表2。通过不同组合的计算,得到的不同计算参数下动态应力响应峰值和等效静力系数的比较如图4和图5所示。
|
|
表 2 不同参数的组合 Tab.2 Groups of different parameters |
|
图 4 不同计算参数对动态应力响应峰值的影响 Fig. 4 The influence of different parameters on the dynamic stress response |
|
图 5 不同计算参数对等效静力系数的影响 Fig. 5 The influence of different parameters on the equivalent static coefficient |
通过组合1的计算,可以看出,随着入水砰击速度的增大,各位置的动态应力峰值明显增大,但各位置的等效静力系数稍有增大。通过组合2的计算,可以看出,随着入水角度的增大,各位置的动态应力峰值减小,但各位置的等效静力系数增大。通过组合3的计算,可以看出,不同网格尺寸下,个别位置的动态应力峰值差别较大,但各位置的等效静力系数变化不大。通过组合4的计算,可以看出,不同边界条件下,各位置的动态应力峰值差别较大,但各位置的等效静力系数变化不大。
2 船首砰击强度的评估 2.1 评估方法的介绍借鉴疲劳强度研究中节点应力集中系数和节点S-N曲线的研究思路[13],对入水砰击载荷作用下的局部模型的砰击响应进行分析,计算得到等效静力系数。其中,局部模型的结构形式与实船结构相似,入水速度和砰击角度取值应与设计状态下实船砰击的情况相近。网格尺寸可以依据相关规范对局部强度评估的模型要求来确定。由于等效静力系数受边界条件影响较小,因此,在等效静力系数计算时,局部模型的边界条件选取四周刚性固定或四周自由支持均可。
综合分析,采用如下步骤进行船首关注构件的砰击强度:1)利用与实船构件布置相近的局部模型进行等效静力系数的计算。2)建立船首结构,将各砰击压力峰值加载于构件所在板架上的关注位置,并对其分析。3)提取关注构件的应力响应,并与等效静力系数相结合得到实际砰击状态下的动态应力响应峰值,从而实现关注构件的屈服强度评估。下面针对具体的实船首部外飘结构进行砰击强度的评估。
2.2 等效静力系数的计算局部模型的边界条件如图6所示。选取各构件上可能产生高应力的一系列位置,并计算所对应的等效静力因子,详细位置如图7所示。等效静力系数的结果如表3所示,表中仅列出少数的几个位置作为代表,实际分析时,计算了更多位置的等效静力系数。

|
图 6 板架模型的边界条件 Fig. 6 Boundary conditions of the grillage model |

|
图 7 计算位置 Fig. 7 Calculated position |
|
|
表 3 等效静力系数的计算值 Tab.3 Values of equivalent static coefficients |
由图8可以看出,在粗网格模型中其骨材端面对应的仅是一个节点,而纵骨和横框架的面板在细网格模型中用板单元模拟,本文使用多点约束的方法来处理粗细网格间的过渡。

|
图 8 板架模型网格的过渡 Fig. 8 Processing of the grillage model grid |
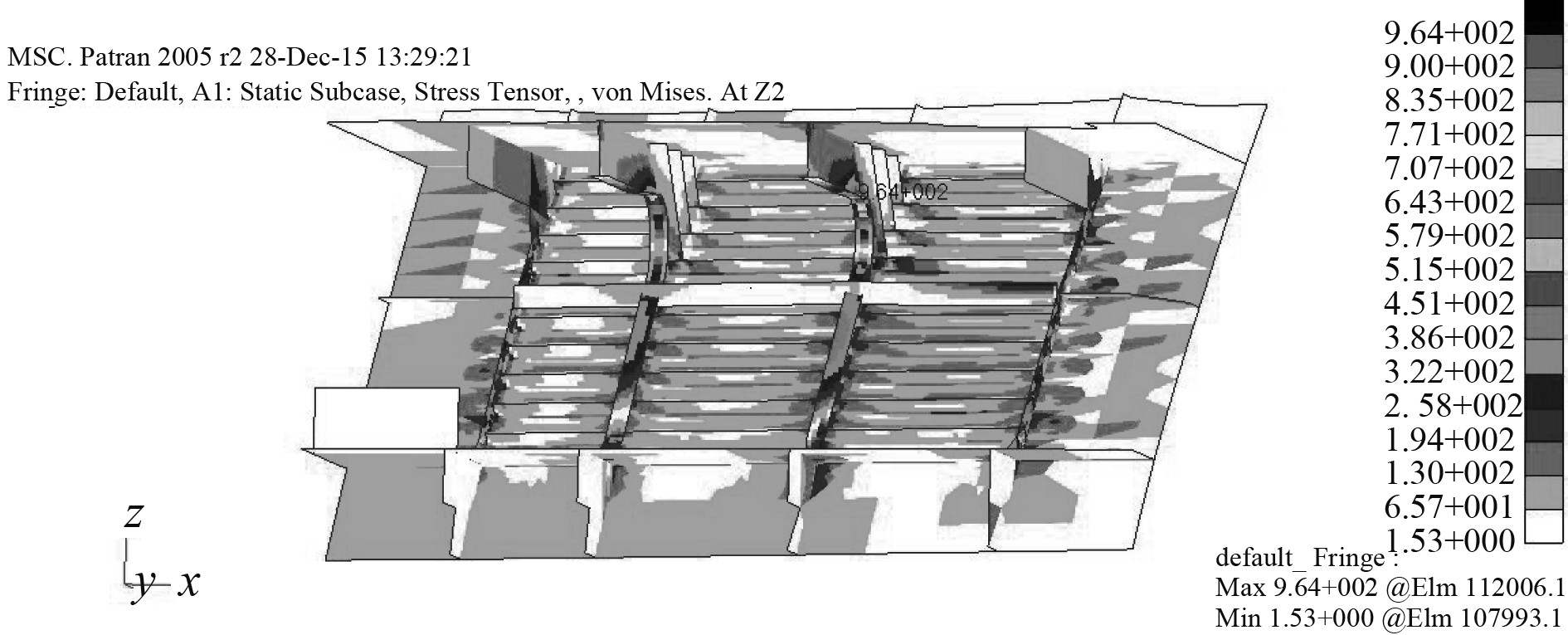
在上述边界条件以及载荷的作用下,对模型进行静力分析,图9为静力分析后得到的细网格关注区域的应力云图。各关注区域加载砰击压力峰值时的应力
|
图 9 加载砰击压力峰值时各作用点处的应力云图 Fig. 9 Stress cloud loading the peak of slamming pressure at different locations |
| ${\lambda _f} \leqslant {\lambda _{fperm}}\text{。}$ | (1) |
其中,
| ${\lambda _f} = \frac{{k \cdot {\sigma _{vm}}}}{{235}}\text{。}$ | (2) |
其中:
各个作用点的对应评估结果如表4所示,其中采用屈服极限为355 Mpa的钢材。大部分评估位置的强度满足要求,横框架上位置6附近的强度不满足要求,有待于加强。
|
|
表 4 屈服强度的评估值 Tab.4 Evaluations of yield strength |
本文通过对三维板架入水砰击响应的分析,建立了砰击载荷作用下板架结构响应的等效静力分析方法,并进一步实现了船首外飘区域局部结构的砰击强度分析,具体结论包括以下几方面:
1)通过分析计算参数对板架结构响应和等效静力系数的影响,发现边界条件对高应力位置的等效静力系数影响较小,但对板架结构的应力响应影响较大。说明在等效静力系数计算时,边界条件取为刚性固定或自由支持均可。然而,在结构响应计算时,应合理地考虑关注构件周围的边界。
2)基于三维板架的入水砰击分析,建立了船首外飘结构砰击强度评估的静力分析方法,并以实船船首为例,将板架分析的结论推广应用到实船模型中,合理地实现了砰击载荷作用下关注构件的屈服强度评估。该方法可为船首砰击强度相关的规范或指南的编写提供参考。
| [1] |
ISSC. Impulsive pressure loading and response assessment[R]. Rostock, Germany, 2012.
|
| [2] |
于鹏垚, 任慧龙, 李陈峰, 等. 船首外飘砰击设计载荷直接计算[J]. 船舶力学, 2016, 20(5): 566-573. DOI:10.3969/j.issn.1007-7294.2016.05.007 |
| [3] |
YU, P LI, H; ONG, M C. Numerical study on the water entry of curved wedges[J]. Ships and Offshore Structures, 2018, 13(8): 885-898. DOI:10.1080/17445302.2018.1471776 |
| [4] |
YU, P LI, H; ONG, M C. Hydroelastic analysis on water entry of a constant-velocity wedge with stiffened panels[J]. Marine Structures, 2019, 63: 215-238. DOI:10.1016/j.marstruc.2018.09.007 |
| [5] |
REN H, YU P, WANG Q, et al. Dynamic Response of the bow flare structure under slamming loads[C]// Asme International Conference on Ocean. 2015.
|
| [6] |
于鹏垚, 任慧龙, 冯国庆, 等. 船首外飘砰击强度直接计算[J]. 中国造船, 2015, 56(1): 61-68. DOI:10.3969/j.issn.1000-4882.2015.01.007 |
| [7] |
American Bureau of Shipping. Guide for Slamming Loads and Strength Assessment for Vessels[S]. 2011.
|
| [8] |
王辉, 顾学康, 祁恩荣, 等. 砰击载荷作用下船底肋骨等效设计压力的确定[J]. 舰船科学技术, 2010, 32(3): 10-15. WANG Hui, GU Xuekang, QI Enrong, et al. The equivalent design pressure of ship frame structures under bottom slamming loads[J]. Ship Science and Technology, 2010, 32(3): 10-15. |
| [9] |
于鹏垚. 船舶局部砰击载荷与结构响应计算方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [10] |
中华人民共和国国家军用标准 GJB/Z-1999, 水面舰艇结构设计计算方法[S]. 国防科学技术工业委员会 1999.
|
| [11] |
骆寒冰, 董德龙, 季红叶, 等. 基于ALE 算法的无转角和有转角铝制加筋板楔形体水弹性砰击的数值模拟研究[J]. 船舶力学, 2017, 21(2): 175-183. DOI:10.3969/j.issn.1007-7294.2017.02.007 |
| [12] |
陈震, 肖熙. 空气垫在平底结构入水砰击中作用的仿真分析[J]. 上海交通大学学报, 2005, 39(5): 670-673. DOI:10.3321/j.issn:1006-2467.2005.05.002 |
| [13] |
冯国庆. 船舶结构疲劳强度评估方法研究[D]. 哈尔滨, 哈尔滨工程大学, 2006.
|
 2020, Vol. 42
2020, Vol. 42
