随着全球气候变暖,北极冰层逐年消融,各国对连接欧洲、亚洲和北美的北极航线的探索不断深入。与此同时,对北极地区天然资源的关注也不断升温[1]。北极地区的探测、建设和通航都需要利用冰区航行船舶进行,因此对冰区船在有冰区域航行性能的模拟预报具有重要意义。
冰区船的航行性能受许多因素的影响,包括海冰的力学特性、海冰的密集度、波浪以及覆雪与否等,其中对于航行影响最大的即为破冰过程中的冰阻力。船舶在冰区航行的过程中,海冰在船舶的挤压作用下发生变形,产生环向与径向裂纹,随着裂纹的逐渐拓展,引起海冰的断裂破坏[2]。受海冰物理和力学性质、船体结构和航行环境的影响,海冰与船舶相互作用的过程十分复杂[3]。在船舶冰阻力的研究过程中,通常采用现场试验、模型试验、经验模型和数值模拟计算的方式来探究海冰与船舶的作用机理[2][4]。数值计算方法参数设置灵活、模拟准确度较高,可以对船-冰相互作用的阻力进行初步的预报,为现场试验和室内模型试验的设计和测量提供依据,是十分重要的研究途径。
近年来,数值模拟方法在模拟冰-船相互作用方面逐渐发展完善,其中以有限元方法和离散元方法最为成熟。由于冰-船相互作用的过程中,会呈现出由连续体向离散块体转变的过程,离散元模型在计算船体冰阻力和准确模拟破冰模式方面具有明显的优势[3]。Hopkins[5]发现离散元方法在确定结构-海冰相互作用方面具有明显的计算优势;Shen[7]最早将基于颗粒理论的离散元方法应用于海冰动力学,建立了海冰碰撞流变学;Yue and Bi、季顺迎[8-9]等利用离散元方法对海冰与海洋平台作用的冰载荷和破坏模式进行了研究;季顺迎等[10]将基于GPU的高性能计算方法引入离散元数值模拟中,可显著提高颗粒规模和计算效率;季顺迎、李紫麟等[11]利用球体单元、拓展圆盘单元和拓展多面体单元构造海冰,并应用于船舶冰阻力的研究。离散元方法不但可以模拟海冰的碰撞特性和流变特征,还可对冰-船相互作用时的破坏模式进行合理的数值分析,确定作用过程中的冰阻力。
本文针对冰-船相互作用的特性,利用离散元方法对冰区船破冰过程的破冰模式和冰阻力进行数值计算,研究海冰物理和力学特性以及船舶航行速度对冰阻力的影响,同时与Lindqvist模型估算的冰阻力进行分析比较,为冰区航行船舶冰阻力的预报提供参考。
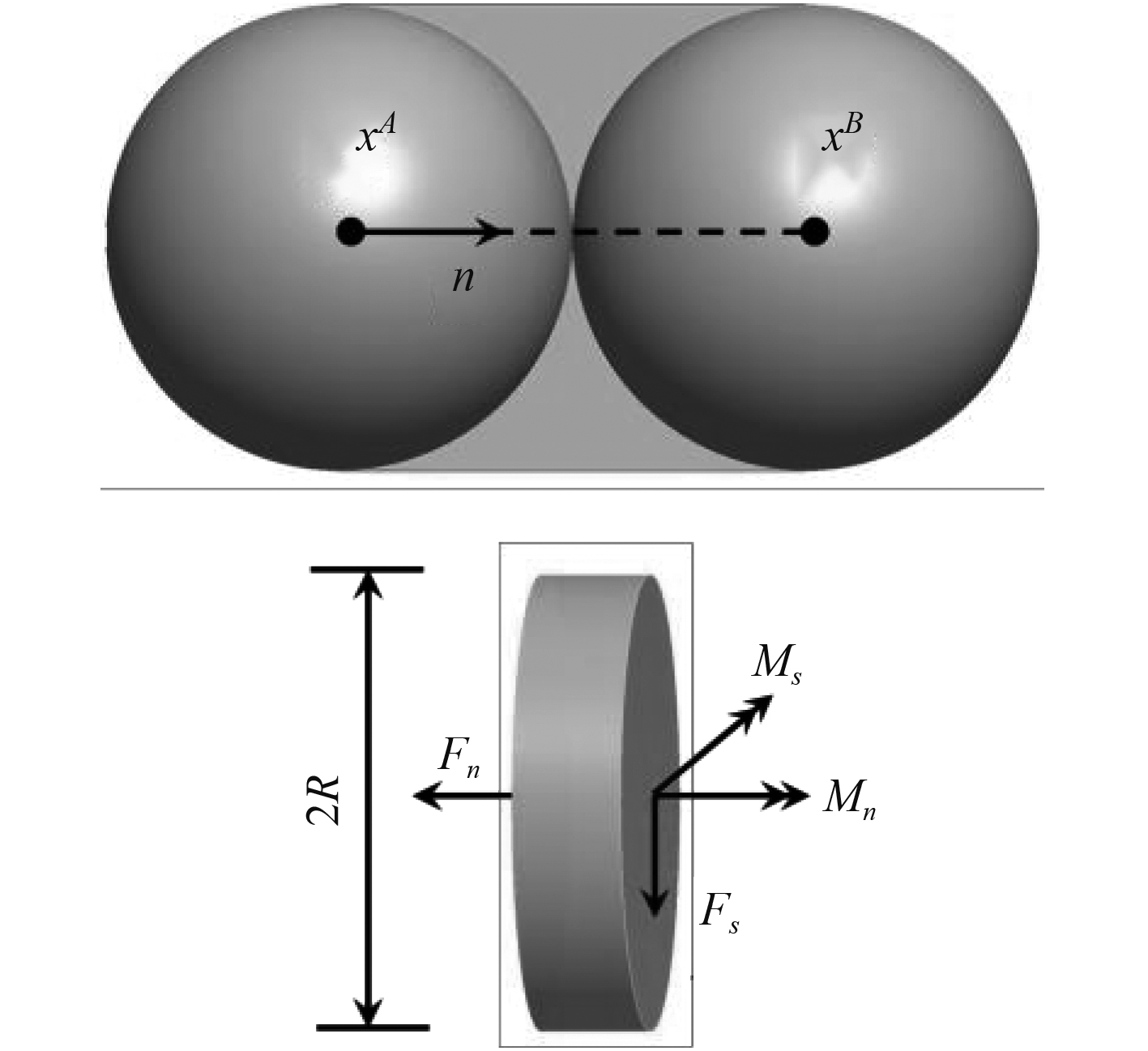
1 海冰和船体结构的离散元方法 1.1 海冰的离散元方法在海冰离散元模型中,利用具有一定质量和大小的均匀球体单元构造海冰,并按照最密堆积的方式将颗粒单元进行规则排列。为模拟海冰的连续体特性,对相邻颗粒单元进行粘结处理。单元之间的粘结方式包括点接触模型和平行粘结模型。点粘结模型只作用在相邻颗粒单元很小区域内,只能通过接触点传递单元间的粘结力,无法传递粘结力矩。而另一种粘结模型则是在2个单元的相邻区域内假设一个以接触点为中心的粘结圆盘,可通过该粘结圆盘同时传递单元间的粘结力和粘结力矩(见图1)。图中
|
图 1 颗粒之间的平行粘结模式 Fig. 1 Parallel bonding mode between particles |
| ${\sigma _{\rm max}} = \frac{{ - {F_n}}}{A} + \frac{{\left| {{M_s}} \right|}}{I}R\text{,}$ | (1) |
| ${\tau _{\rm max}} = \frac{{{F_s}}}{A} + \frac{{\left| {{M_n}} \right|}}{J}R\text{。}$ | (2) |
式中:
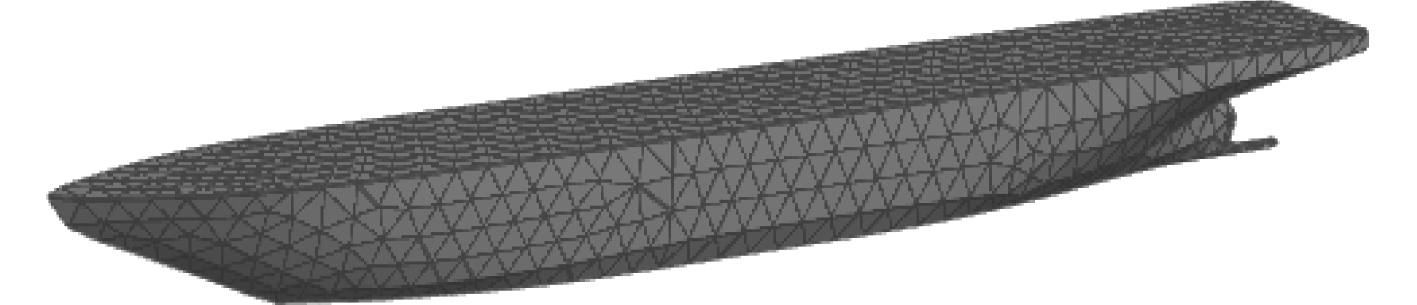
本文利用我国某型号的科学考察船进行数值计算,缩尺比λ=30,具体船型参数见表1。针对该考察船的船型特点,采用三角形单元构建船模船体结构的离散元模型。同时根据冰船接触位置,建立面网格,将船体离散化,共采用1 839个三角形单元,如图2所示。在船-冰相互作用过程的离散元模拟中,是根据给定速度计算船体在冰区中的运动情况。为了能够更好地对船体的运动受力情况进行研究,规定x轴正方向指向船首,y轴正方向指向左舷,z轴正方向垂直向上。
|
|
表 1 船模船型参数 Tab.1 Ship type parameters of ship model |
|
图 2 船体的离散元方法 Fig. 2 The discrete element model of ship |
在船-冰相互作用的数值计算中,将冰层离散为4层均匀排列的球形颗粒,且对平整冰的边界进行固定。模拟中的主要计算参数见表2。在模拟过程中,船舶以恒定的航速在平整冰层中航行,破坏冰层,并留下一条狭长的航道,如图3所示。从图中可以看出,在冰船相互作用的过程中,船首首先与冰层发生接触,当垂向破冰力达到一定程度时,冰层开始发生弯曲破坏,此时在船体首柱附近产生半径较小的楔形碎片,主要发生挤压和弯曲破坏。随着船舶的行进,船身进入冰层,船体两侧的冰层开始出现以弯曲破坏为主的径向和环向裂纹。破碎后的海冰会沿船侧滑动或滑入船体底部,均会与船体产生摩擦阻力。
|
|
表 2 离散元模拟的主要参数 Tab.2 Main parameters of discrete element simulation |

|
图 3 船体在平整冰中航行的过程 Fig. 3 Process of hull sailing through flat ice |
|
|
表 3 冰厚变化时的计算结果 Tab.3 Calculation results when thickness changes |
|
|
表 4 弯曲强度变化时的计算结果 Tab.4 calculation results when flexural strength changes |
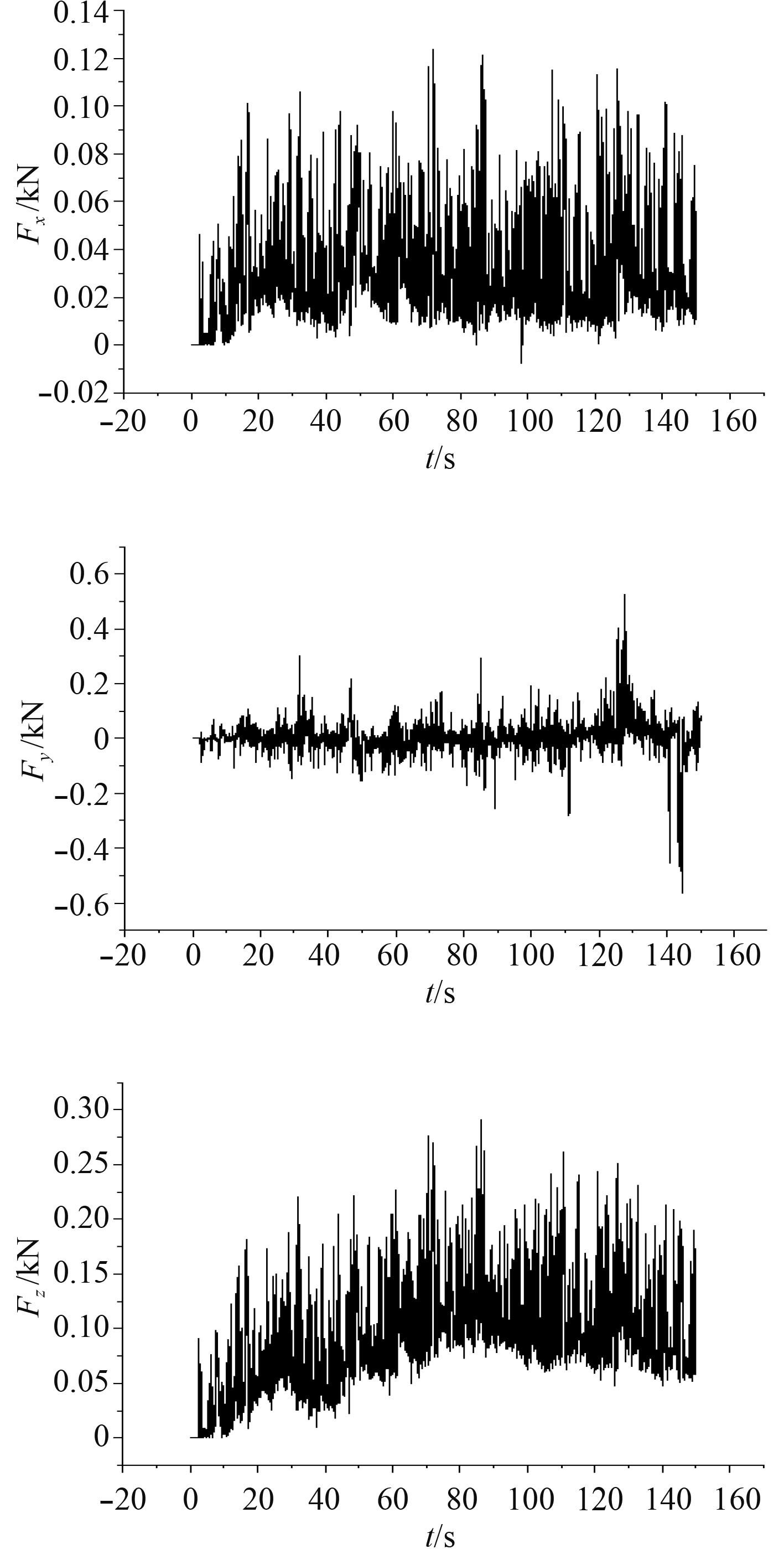
船舶在航行过程中,X,Y,Z三个方向的冰阻力变化如图4所示。可以看到,当船体进入冰区时,冰阻力随着船体进入冰层的长度增加而增加;当船体整体进入冰区后,船体受到的冰阻力达到最大,并且在一定的范围内呈现出很强的脉动特性。在分析比较过程中,冰阻力F取X方向冰阻力的平均值。由于边界设置为三面固定边界,未模拟船体驶出冰区时的冰阻力变化。
|
图 4 X,Y,Z方向冰阻力曲线 Fig. 4 Ice resistance curve in X direction, Y directionand Z direction |
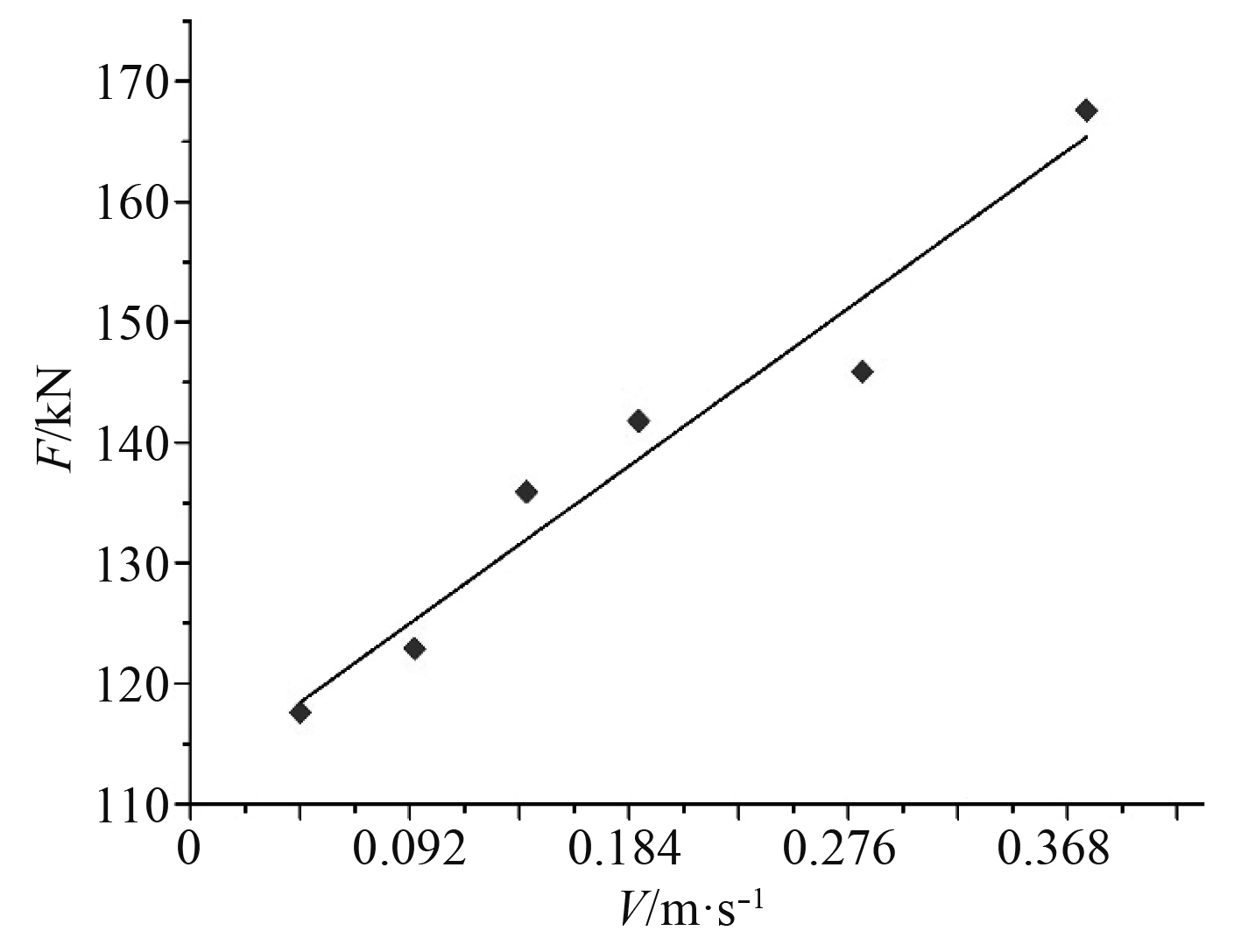
为分析破冰过程中航速的影响,分别将航速设置为0.046 m/s,0.094 m/s,0.141 m/s,0.188 m/s,0.282 m/s和0.376 m/s,冰厚为0.032 m,弯曲强度为25 kPa。在不同航速下,计算得到的冰阻力如图5所示。
|
图 5 冰阻力随航速的变化 Fig. 5 Variation of ice resistance with speed |
船舶航速的大小决定了冰船相互作用的速度和频率,是影响船体总冰阻力的一个重要因素。由图5可知,随着航速的增加,船体受到的冰阻力逐渐增加,破冰效率得到提升,同时海冰对船体的损伤也逐渐增加,船体结构更易受到破坏;如果航行速度减小,则使破冰效率降低,影响经济性。因此,在航速选择时要综合考虑经济性与海冰对船体的损伤两方面因素,根据不同冰况合理地选择船舶航速。
2.2 冰厚对冰阻力的影响海冰条件对冰区航行船舶冰阻力的影响,以冰厚最为显著。为了分析冰厚对冰阻力的影响,将冰厚分别设定为为0.016 m和0.032 m进行比较,其他参数不变。图6为船体进入冰层时船首破冰的情况,图7为冰阻力随冰厚的变化情况。
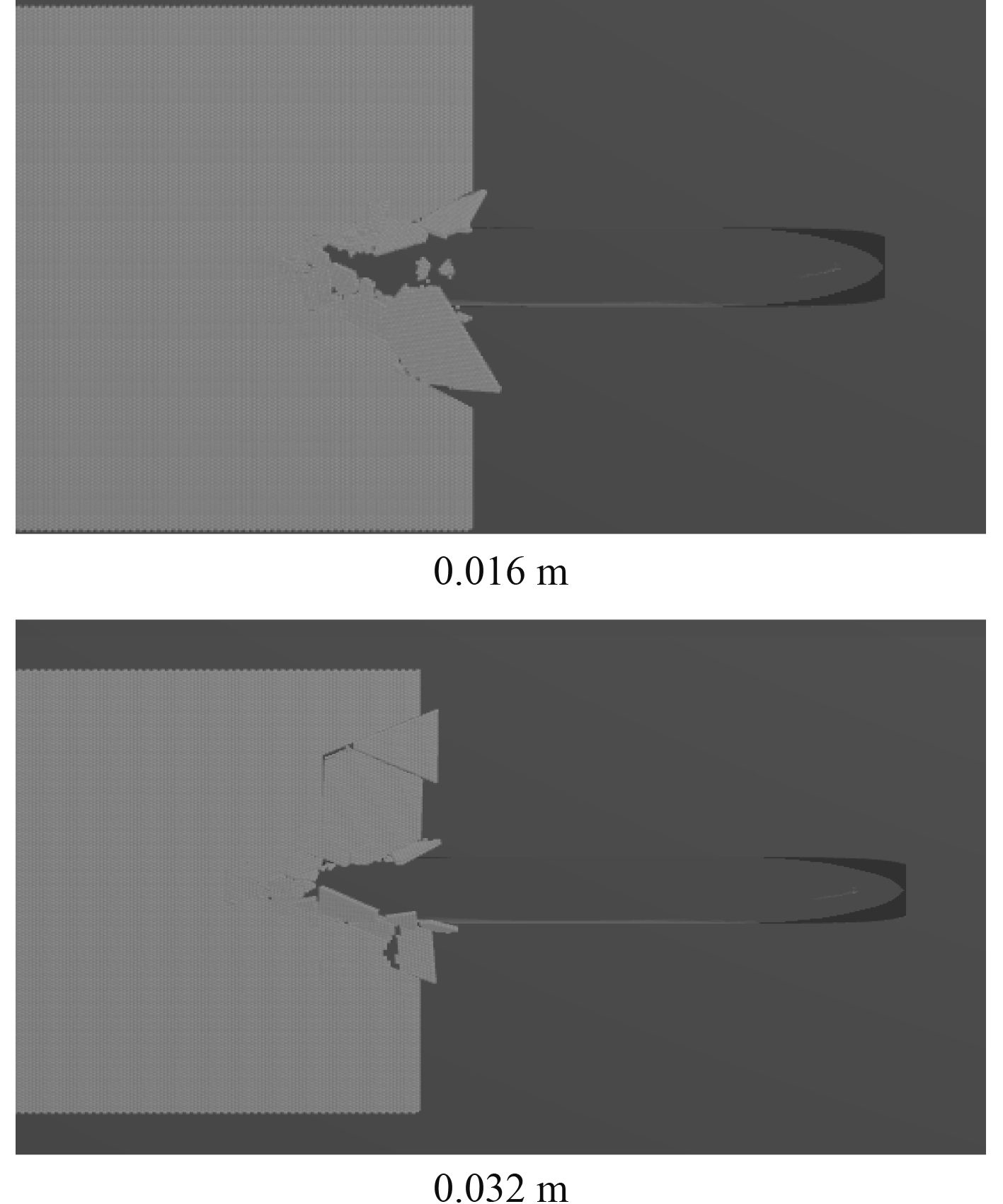
|
图 6 在不同冰厚情况下的破碎形式 Fig. 6 Crushing forms under different ice thickness |

|
图 7 冰阻力随冰厚的变化 Fig. 7 variation of ice resistance with ice thickness |
在模拟过程中可以观察到,随着冰厚的增加,船体受到的冰阻力也逐渐增加,同时冰的破碎尺寸也在逐渐增大。这意味着,当冰区航行船舶航行区域冰况发生变化时,不仅要考虑冰的物理力学特性的变化,而且要考虑破坏模式的变化。
2.3 弯曲强度对冰阻力的影响通过对船舶海冰作用的过程进行分析,破冰过程可分为挤压、弯曲和旋转滑移3个阶段,其中弯曲破坏为主要的破坏模式。为了研究海冰弯曲强度的变化对船体受到的冰阻力的影响,分别选取16 kPa和25 kPa两种不同弯曲强度的冰层,其他实验参数不变。图8为不同弯曲强度情况下冰阻力随航速的变化。结果显示,在同一航速下,冰阻力随着弯曲强度的增加而增加。
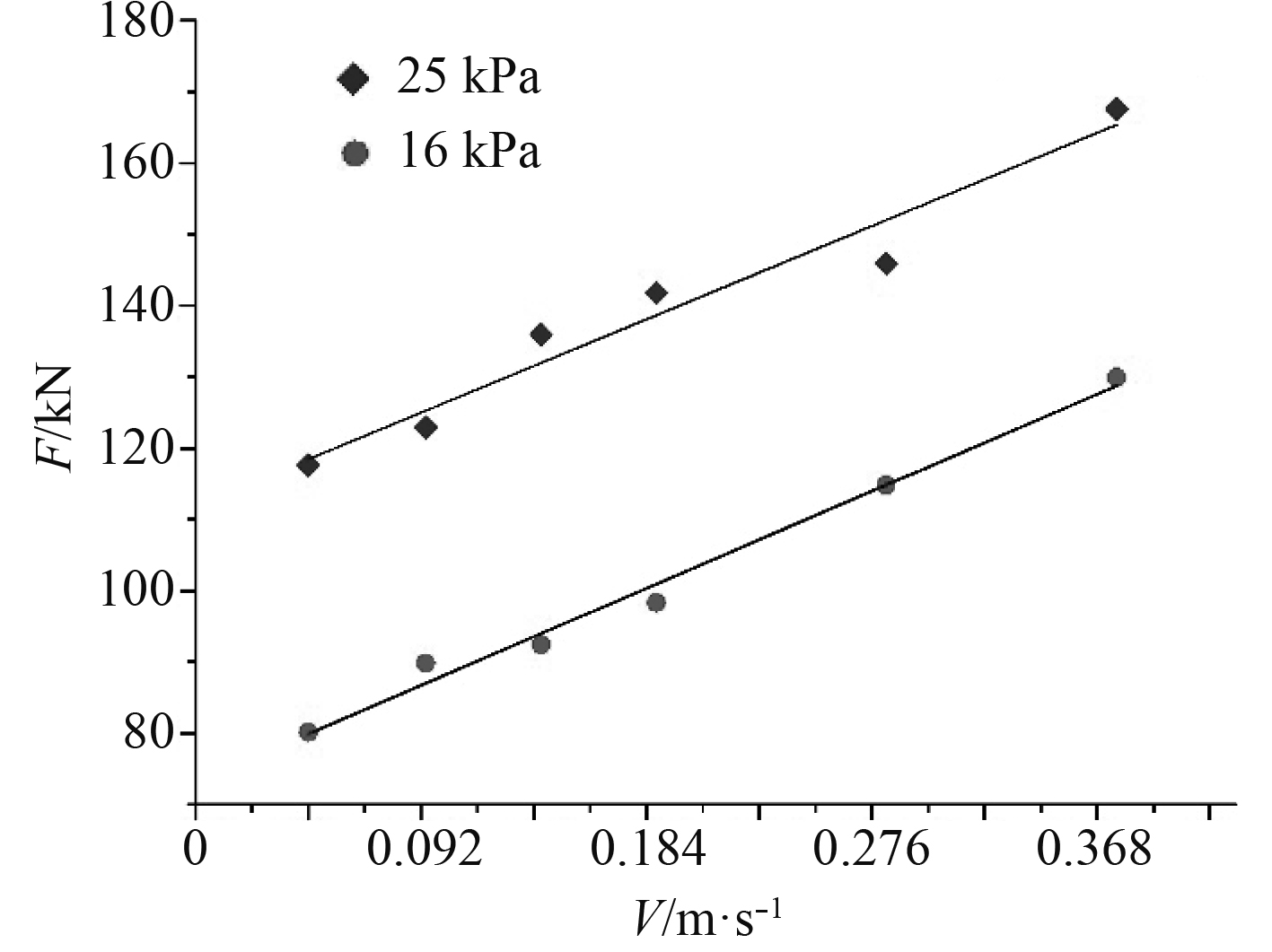
|
图 8 冰阻力随弯曲强度的变化 Fig. 8 variation of ice resistance with flexural strength |
Lindqvist[14]公式是根据在波罗的海波的尼亚湾进行的实船实验总结出来的经验模型。该模型阐述了一种简单的方式来预报船舶的冰阻力,能够快速对冰阻力进行简单的预报。
3.1 Lindqvist模型介绍Lindqvis模型将冰阻力分解为挤压冰阻力、破冰阻力和浸没阻力3部分,并给出了与船舶主尺度、船型角度、速度、冰厚、摩擦系数及弯曲强度等参数相关的冰阻力表达式。Lindqvist经验公式表达式为:
| $ {R}_{i}\left(v\right)=\left({R}_{c}+{R}_{b}\right)\left(1+1.4\frac{v}{\sqrt{gh}}\right)+{R}_{s}(1+9.4\frac{v}{\sqrt{gL}})\text{,} $ | (3) |
| $ {R}_{c}=0.5{\sigma }_{b}{h}^{2}\frac{{\rm tan}\varphi +\mu {\rm cos}\varphi /{\rm cos}\psi }{1-\mu {\rm sin}\varphi /{\rm cos}\psi } \text{,}$ | (4) |
| $ {R}_{b}=\frac{27}{64}{\sigma }_{b}B\frac{{h}^{1.5}}{\sqrt{\frac{E}{12\left(1-{\nu }^{2}\right)}}}\frac{{\rm tan}\psi +\mu {\rm cos}\varphi }{{\rm cos}\varphi {\rm sin}\alpha }(1+\frac{1}{{\rm cos}\psi }) \text{,}$ | (5) |
| $\begin{split} {R_s} = & \left( {{\rho _w} - {\rho _i}} \right)ghB\left( {T\frac{{B + T}}{{B + 2T}} + \mu \left( {0.7L - \frac{T}{{{\text{tan}}\varphi }} - } \right.} \right. \\ & \left. {\left. {\frac{B}{{4{\text{tan}}\alpha }} + T{\text{cos}}\varphi {\text{cos}}\psi \sqrt {\frac{1}{{{\text{sin}}{\varphi ^2}}} + \frac{1}{{{\text{tan}}{\alpha ^2}}}} } \right)} \right] \end{split}\text{。} $ | (5) |
式中:
利用Lindqvist公式对考察船的冰阻力进行模拟,并将离散元方法计算得到的结果通过一定的比例换算到实船,两者进行分析比较,计算结果如图9和图10所示。计算结果对比如表5和表6所示。
|
|
表 5 冰厚变化时的计算结果对比 Tab.5 Comparison of result when ice thickness changes |
|
|
表 6 弯曲强度变化时的计算结果对比 Tab.6 Comparison of result when flexural strength changes |
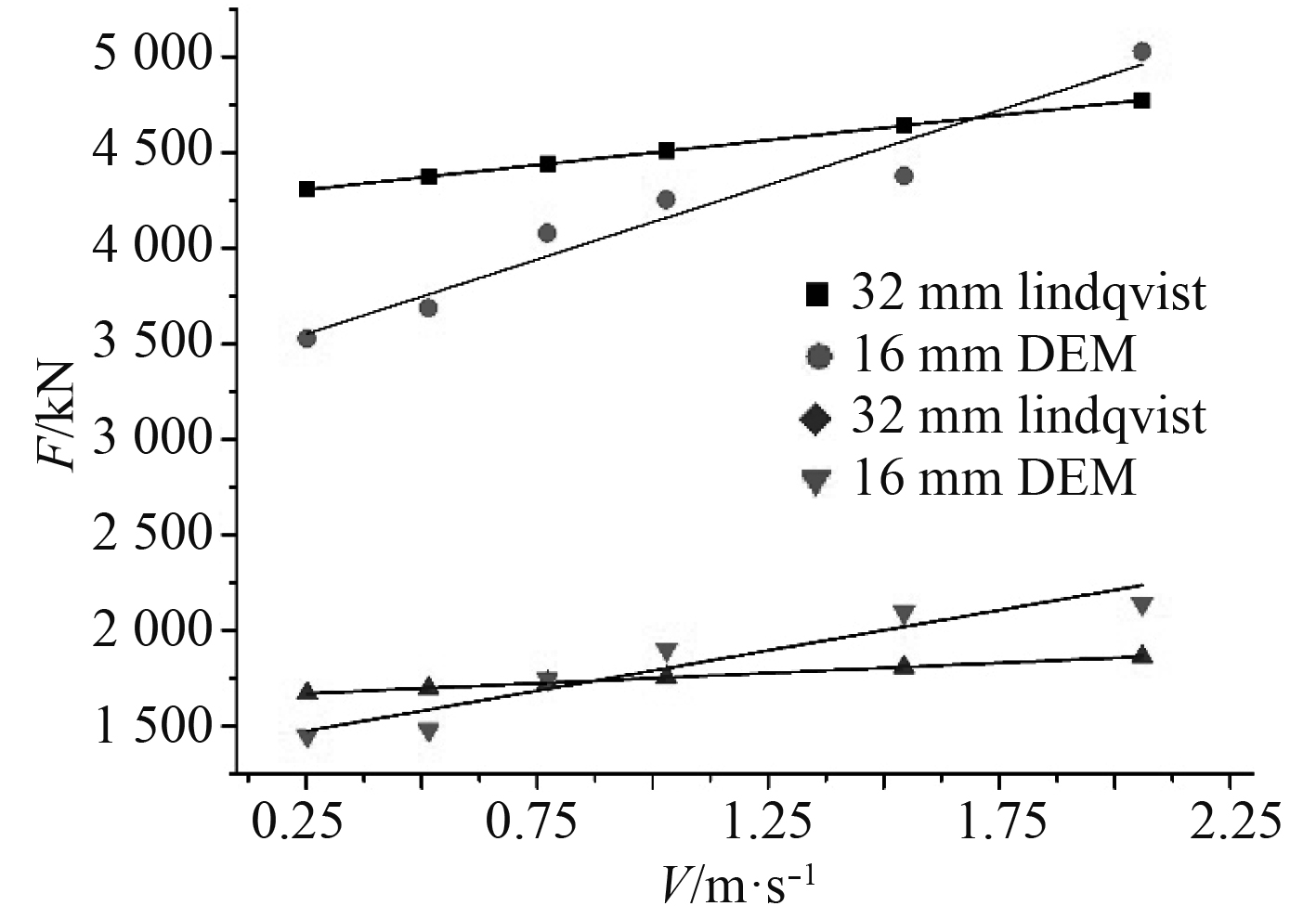
|
图 9 冰厚变化时的计算结果 Fig. 9 Calculation results when thickness changes |
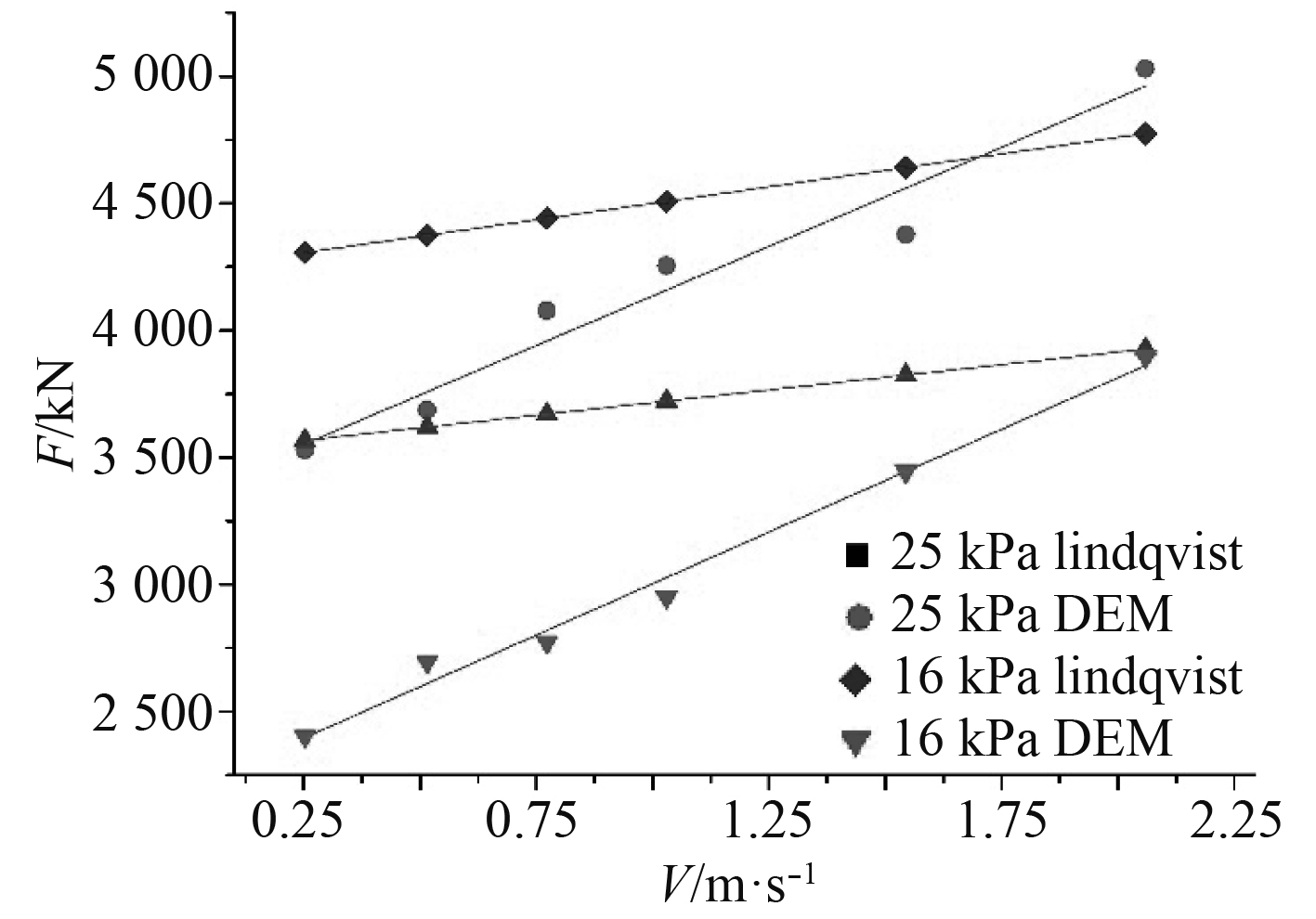
|
图 10 弯曲强度变化时的计算结果 Fig. 10 Calculation results when flexural strength changes |
从图中可以看出,Lindqvist经验模型计算得到的结果与速度呈线性变化,而离散元方法得到的结果具有一定的离散性,但两者求得的冰阻力的变化趋势是相同的,即冰阻力随航速、冰厚和弯曲强度的变化而产生了相同的变化。由表中的数据可以看出,离散元方法计算得到的船体冰阻力值和Lindqvist经验模型得到的值相比,二者相差不大,这说明离散元方法可以对船舶在平整冰中航行的冰阻力进行较为准确的模拟,可以为冰阻力的预报提供初步的参考。
4 结 语本文采用离散元方法对冰区航行船舶航行的冰阻力和破冰模式进行数值计算,分析了海冰厚度、海冰弯曲强度和航行速度对船舶冰阻力的影响,得到冰阻力随上述因素的变化趋势,同时也得到了船体受到的冰阻力。研究表明,离散元方法可以较为准确地预报冰区航行船舶在有冰区域的航行性能,但该方法未考虑单元尺寸、接触模型和破碎准则对船体冰阻力产生的影响,需要在后续工作中进一步完善,同时应考虑船体与海冰接触时的水动力特性,以便更精确地模拟船舶的破冰过程及冰阻力的变化。
| [1] |
龚榆峰, 张正艺, 刘敬喜, 等. 基于ABAQUS的海冰单元开发及冰载荷直接计算法[J]. 中国舰船研究, 2017, 12(3): 75-85. GONG Y F, ZHANG Z Y, LIU J X, et al. Development of sea ice element and direct analysis method of predicting ice loads based on ABAQUS[J]. Chinese Journal of Ship Research, 2017, 12(3): 75-85. DOI:10.3969/j.issn.1673-3185.2017.03.011 |
| [2] |
吴炜. 考虑不同漂角的船舶冰阻力模型试验研究[D]. 天津: 天津大学, 2019, 11. WU wei. Model tests on ice resistance of an icebreaking ships with different ice drift angles[D]. Tianjin: Tianjin Univercity, 2016, 11. |
| [3] |
狄少丞, 季顺迎, 薛彦卓. 船舶在平整冰行进过程的离散元分析[J]. 海样工程, 2017, 35(3): 59-69. DI S C, JI S Y, XUE Y Z. Discrete element analysis of ship moving on flat ice[J]. The Ocean Engineering, 2017, 35(3): 59-69. |
| [4] |
GAGNON R, CUMMING D, RITCH R, et al. Overview accompaniment for papers on the barge bit impact trials[J]. Cold Regions Science and Technology, 2008(52): 1-6. |
| [5] |
RALPH F, MCKENNA R, GAGNON R. Iceberg characterization for the barge bit impact study[J]. Cold Regions Science and Technology, 2008(52): 7-28. |
| [6] |
HOPKINS M A. Onshore ice pile-up: a comparison between experiments and simulations[J]. ColdRegions Science and Technology, 1997, 26(3): 205-214. |
| [7] |
SHEN H H, HIBLER W D., LEPPARANTA M.. The role of floe collisions in sea ice rheology[J]. Journal of Geophysical Research, 1987, 92(C10): 7085-709. |
| [8] |
YUE Q, BI X. Ice-induced jacket structure vibrations in Bohai Sea[J]. Journal of Cold Regions Engineering, 2000, 14(2): 81-92. DOI:10.1061/(ASCE)0887-381X(2000)14:2(81) |
| [9] |
季顺迎, 王安良, 车啸飞, 等. 椎体导管架海洋平台冰激结构振动响应分析[J]. 海洋工程, 2011, 29(2): 32-38. JI S Y, WANG A L, CHE X F, et al. Vibration response analysis of ice induced structures on cone jacket platform[J]. The Ocean Engineering, 2011, 29(2): 32-38. DOI:10.3969/j.issn.1005-9865.2011.02.005 |
| [10] |
季顺迎, 狄少丞, 李正, 等. 海冰与直立结构相互作用的离散单元数值模拟[J]. 工程力学, 2013, 30(1): 463-469. JI S Y, DI S C, LI Z, et al. Discrete element numerical simulation of interaction between sea ice and vertical structures[J]. Engineering Mechanicals, 2013, 30(1): 463-469. |
| [11] |
JI shum Ying. Discrete element model and ice load analysis for ship sailing in broken ice area[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(6): 868-877. |
| [12] |
JI S Y, DI S C, LONG X. DEM simulation of uniaxial compressive and flexural strength of sea ice: parametric study[J]. Journal of Engineering Mechanics, 2016. |
| [13] |
JI S, SUN, S, LONG, X, et al. Discrete element modeling of ice loads on ship and offshore structures[C]//The 7th International Conference on Discrete Element Methods, Dalian, China 2016.
|
| [14] |
LINDQVIST G. A straightforward method for calculation of ice resistance of ships[C]//Proceedings of the Tenth International Conference on Port and Ocean Engineering under Arctic Conditions. Lulea, Sweden, 1989: 722-735.
|
 2020, Vol. 42
2020, Vol. 42
