船舶工业是我国实施海洋强国和"一带一路"倡议的重要支撑,是《中国制造 2025》制造强国战略的重要组成部分。船舶工业目前正处于转型升级期,在船舶工业智能化建设过程中,工业互联网建设占据重要地位,工业信息安全防护尤为重要。目前,船舶工业面临的工业互联网入侵手段层出不穷,检测困难导致防护系统易受攻击。因此,为确保船舶工业互联网的安全运行,网络入侵检测至关重要[1]。
目前,针对船舶工业网络入侵检测的方法主要有,基于主元分析、反向传播(back propagation,BP)神经网络、极限学习机、粒子群等方法[2-3]。随着船舶智能化的不断提升,网络环境更加复杂,遭受网络入侵的风险逐步增加,上述方法在遇到新型入侵时,检测准确度不够好,且不具有无标签网络数据的学习能力,造成了极大的数据浪费。针对上述问题,提出基于深度学习的船舶监控网络入侵检测系统设计方法,并进行了仿真测试,本文方法提高了船舶网络入侵检测鲁棒性和准确性。
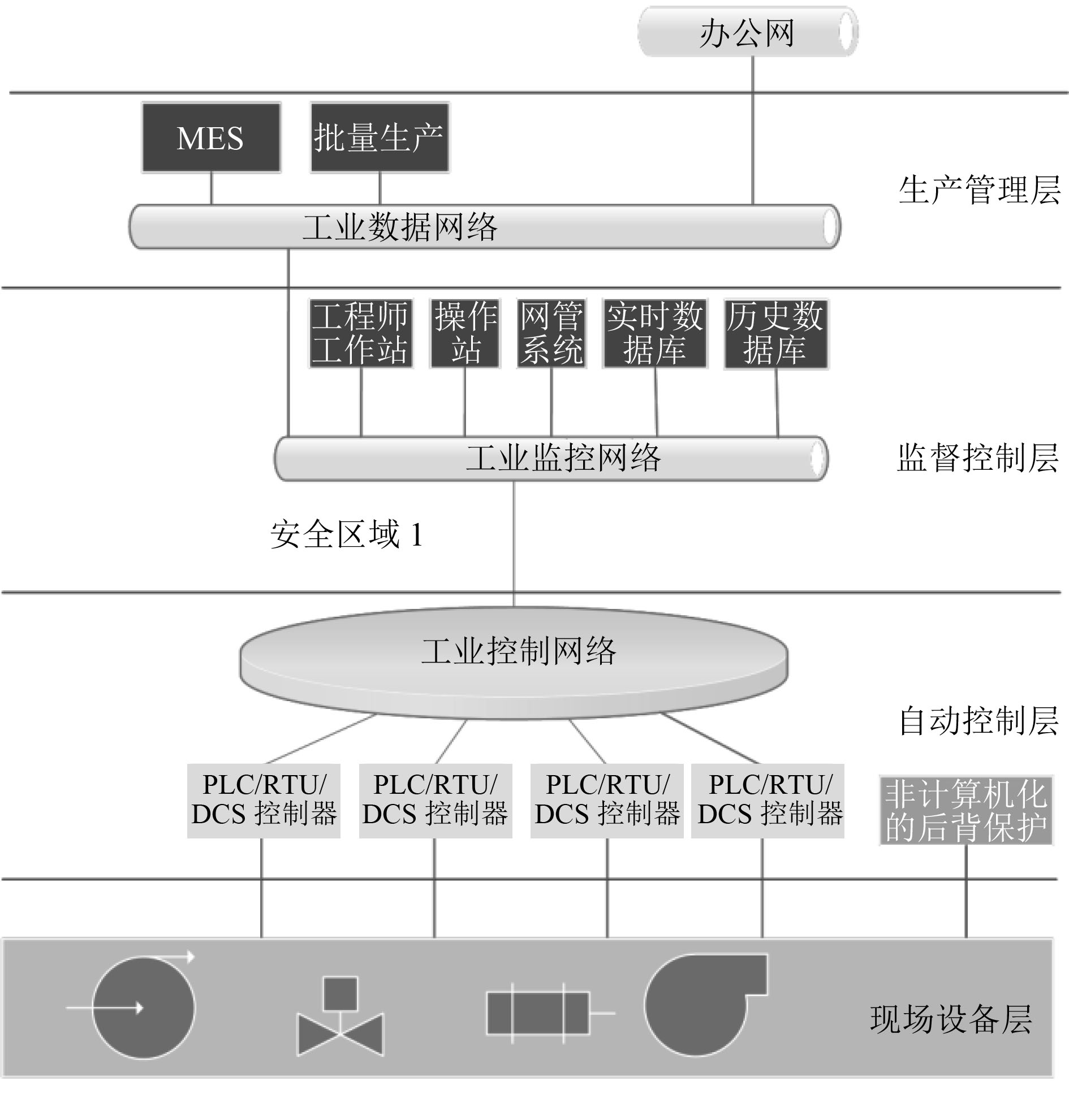
1 船舶工业网络入侵风险评估 1.1 船舶工业网络系统船舶工业中的网络系统包括:工业控制网络、工业监控网络、工业数据网络和办公网络,如图1所示。各网络之间协同作业,确保船舶的安全运行与正常通信。
|
图 1 船舶工业网络系统 Fig. 1 Ship industry network system |
该系统通过工业控制网络与现场设备连接,并把信息传递到工作站,以便工程师了解现场状况,更加准确迅速地下达指令。数据库用来存放船舶各系统的状态数据以及船舶与外部的通信数据、航海日志等信息。
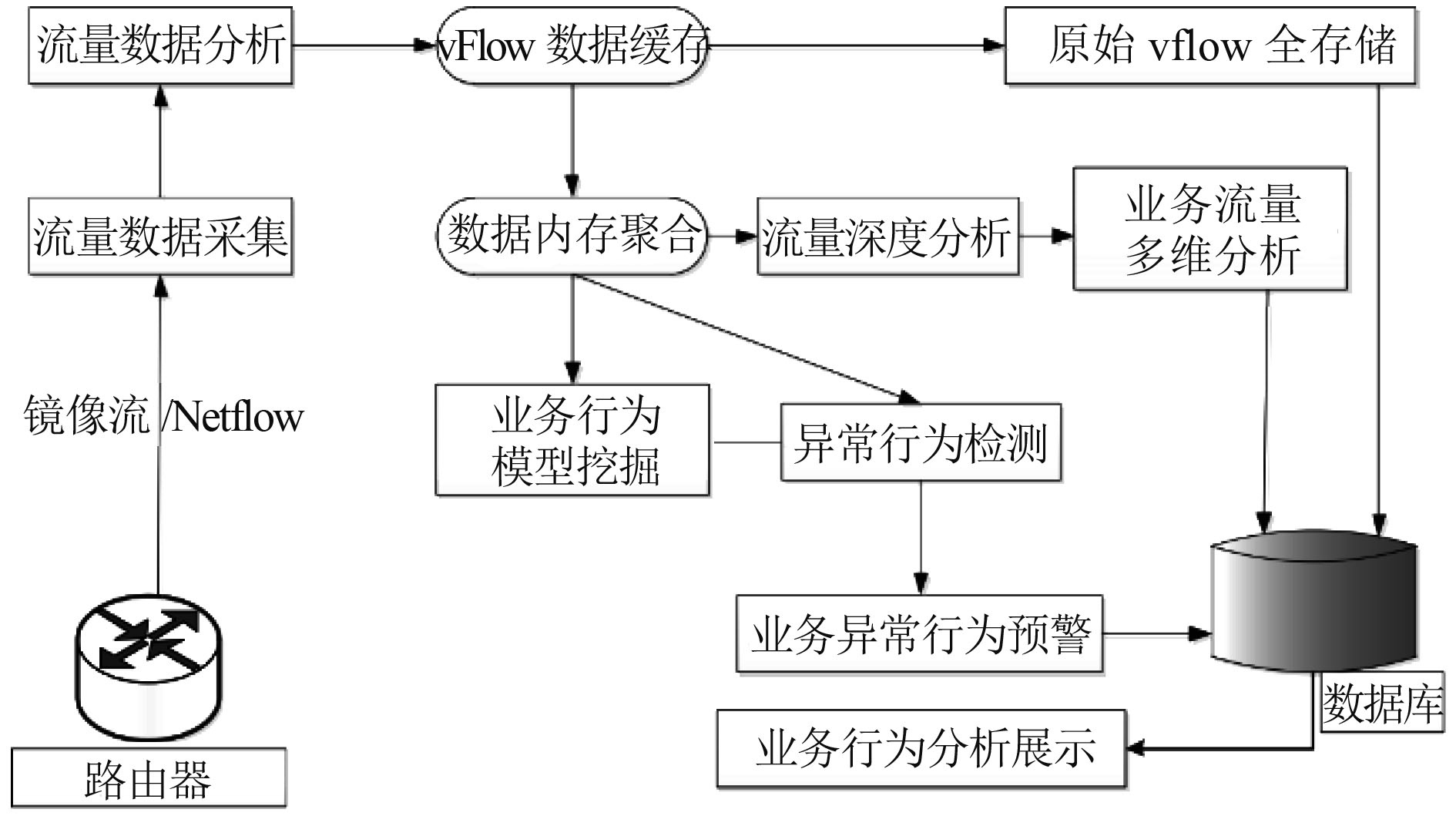
1.2 风险评估架构船舶工业网络入侵数据的确定主要是指在未授权情况下,对网络进行违背安全要求的访问行为[4]。未经授权的访问,易导致非法外联控制、不良访问等情况。船舶工业网络由于其独立性、复杂性、庞大性不同于其他网络结构,为此,本文采用工控网络流秩序行为分析法建立针对船舶工业网络的风险评估系统,解决入侵检测设备对工业控制领域中业务安全分析针对性不强、有效性差的问题,如图2所示。工控网络流秩序行为分析技术需要设计与之对应的复合流量采集器、业务交互行为挖掘、业务行为规则体系、业务异常预警和建立业务健康度指标体系等。
|
图 2 网络安全评估框架 Fig. 2 Network security assessment framework |
传统的方法对已知入侵方式检测具有很好的效果,但对检测未知网络入侵能力不足。深度学习算法具有很好的自学习能力,能够弥补传统算法中的对未知方式入侵检测能力不足的缺点。
深度学习源于人工神经网络,并通过反向传播自我修正[5]。其原理为:假设在一个系统

|
图 3 深度学习基本结构图 Fig. 3 Basic structure of deep learning |
算法工作流程为:1)输入训练集;2)隐含层进行特征提取;3)每一层把上一层的输出作为输入继续提取特征值;4)提取最后两层特征进行特征融合,经过分类器进行分类。
2.2 Softmax分类器在深度学习算法特征提取的基础上,需要结合分类器进行入侵等级划分。Softmax分类模型是Logistic回归模型在多分类问题上的推广,可以同时输出多类别的匹配概率。因此,本文选用softmax进行分类,划分为3个危险等级:低危、中危、高危3种情况。
训练集
| $ { {h_\theta} }\left( {{x^{\left( i \right)}}} \right) = \left[ {\begin{array}{*{20}{c}} {p\left( {{y^{\left( i \right)}} = 1|{x^{\left( i \right)}};\theta } \right)}\\ {p\left( {{y^{\left( i \right)}} = 2|{x^{\left( i \right)}};\theta } \right)}\\ \vdots \\ {p({y^{\left( i \right)}} = k|{x^{\left( i \right)}};\theta )} \end{array}} \right]= \frac{1}{{\sum _{j = 1}^k{e^{\theta _j^{\rm T}{x^{\left( i \right)}}}}}}\left[\!\!\!\! {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{e^{\theta _1^{\rm T}{x^{\left( i \right)}}}}}\\ {{e^{\theta _2^{\rm T}{x^{\left( i \right)}}}}} \end{array}}\\ \vdots \\ {{e^{\theta _k^{\rm T}{x^{\left( i \right)}}}}} \end{array}} \!\!\!\!\right]\text{,} $ | (1) |
其中,
| $ p\left({y}^{\left(i\right)}=1|{x}^{\left(i\right)};\theta \right)=\frac{{e}^{{\theta }_{j}^{{\rm T}}x\left(i\right)}}{{\sum }_{l=1}^{k}{e}^{{\theta }_{l}^{{\rm T}}x\left(i\right)}} \text{。}$ | (2) |
式中:
| $ I\left\{ {\rm expression} \right\} = \left\{ {\begin{array}{*{20}{l}} 0\text{,}&{{\rm if}\;{\rm expression} = {\rm false}}\text{,}\\ 1\text{,}&{{\rm if}\;{\rm expression} = {\rm true}}\text{,} \end{array}} \right. $ | (3) |
代价函数
| $ J\left( \theta \right) = - \frac{1}{m}\left[ {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^k I } \{ {y^{\left( i \right)}} = j\} log\frac{{{e^{\theta _j^{\rm T}x\left( i \right)}}}}{{\sum _{l = 1}^k{e^{\theta _l^{\rm T}x\left( i \right)}}}}} \right]\text{,} $ | (4) |
为解决式(4)中的参数冗余和解不唯一的问题,加入权重衰减项,则代价函数变为:
| $ \begin{split} J\left( \theta \right) = & - \frac{1}{m}\left[ {\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^k I } \{ {y^{\left( i \right)}} = j\} log\frac{{{e^{\theta _j^{\rm T}x\left( i \right)}}}}{{\sum _{l = 1}^k{e^{\theta _l^{\rm T}x\left( i \right)}}}}} \right]+\\ & \frac{\lambda }{2}\sum\limits_{i = 1}^k {\sum\limits_{j = 0}^n {\theta _{ij}^2} } \text{。} \end{split} $ | (5) |
式中:n为输出数据个数,当参数值过大时,权重衰减项将对其惩罚。最小化
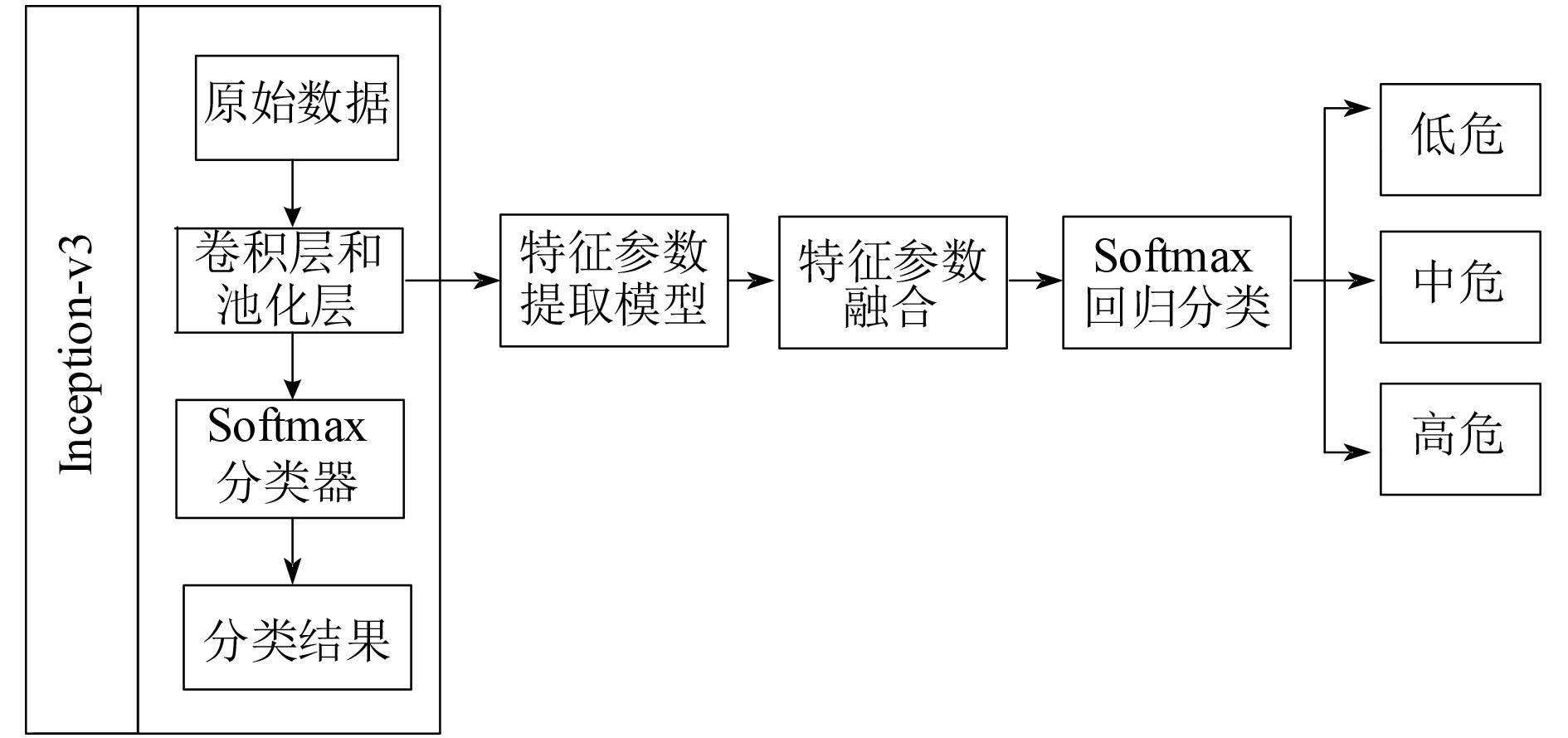
基于深度学习的船舶工业网络入侵检测模型构建分为4个步骤:Inception-v3模型在前端用来提取入侵数据集中的有效信息,保存最后2层池化层中的特征,用做Softmax分类器的输入,用来对危险等级分类。基于深度学习的船舶工业网络入侵检测模型如图4所示。
|
图 4 基于深度学习的船舶工业网络入侵检测模型 Fig. 4 Intrusion detection model of ship industry network based on deep learning |
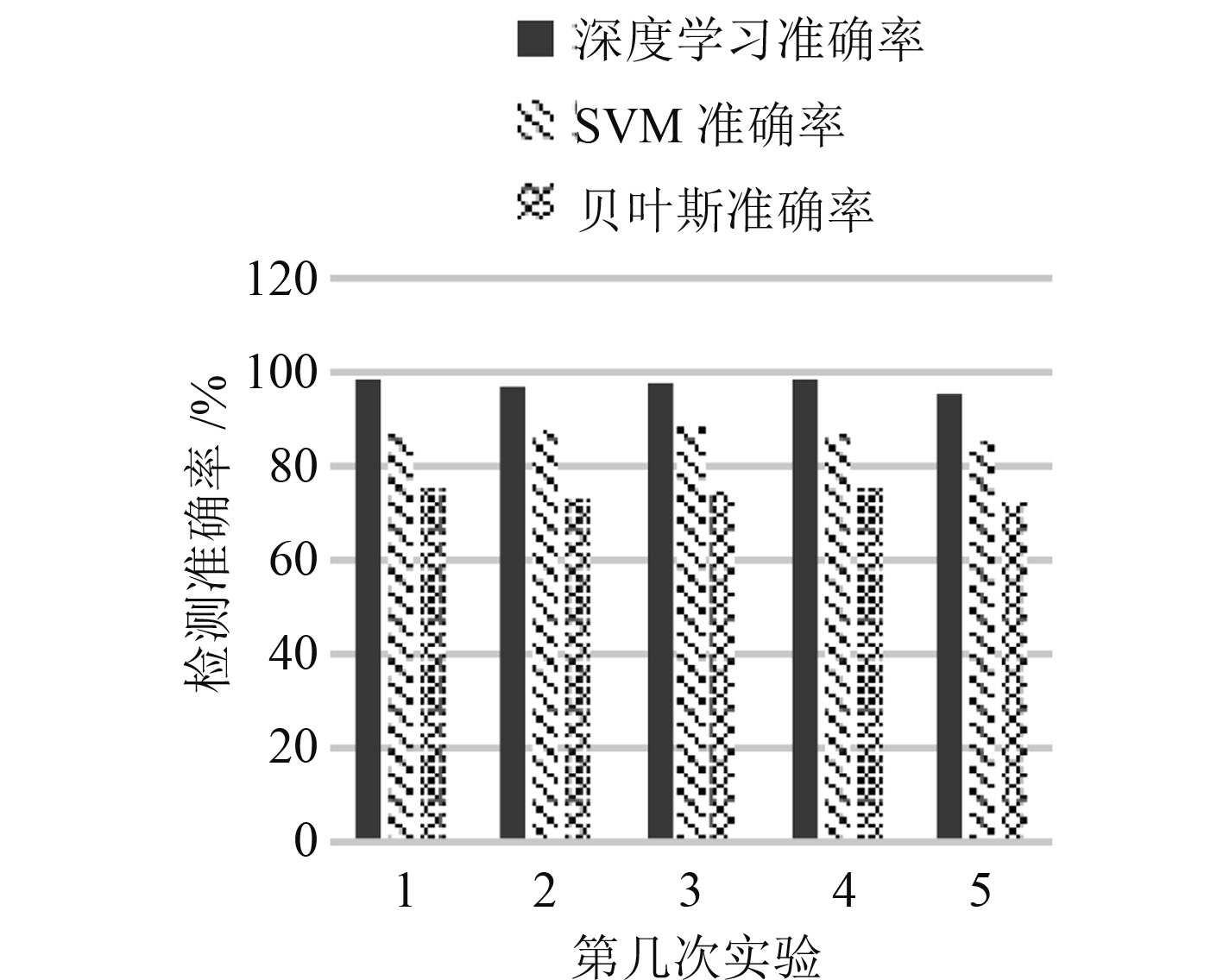
为评估基于深度学习的船舶工业网络入侵模型的入侵检测性能,本文选用支持向量机(SVM)和贝叶斯算法进行对比分析。船舶工业网络入侵的检测准确率、检测时间作对比标准。其准确率和检测时间对比如图5和图6所示。
|
图 5 入侵检测准确率对比 Fig. 5 Comparison of intrusion detection accuracy |
|
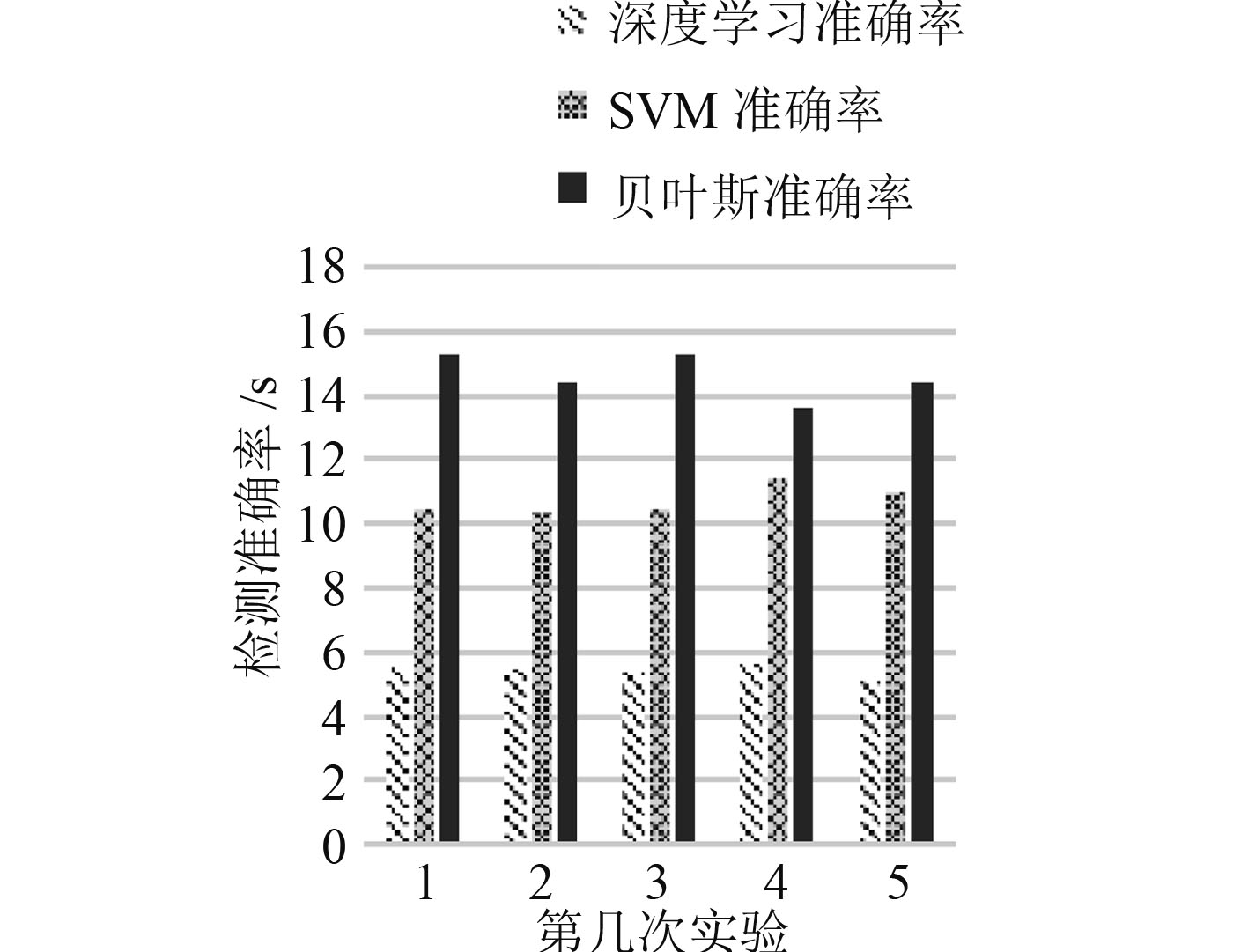
图 6 入侵检测时间对比 Fig. 6 Intrusion detection time comparison |
从图5可以看出,深度学习模型的网络入侵检测准确率都在95%以上,而SVM入侵检测准确率最高到86%,贝叶斯算法最高到75%。相较于SVM和贝叶斯算法,本模型准确率有较大改进。这表明从检测时间来看,图6可以看出深度学习模型的网络入侵检测时间最高为5.95s,可以较好满足工业网络入侵检测的响应时间。相较于SVM和贝叶斯算法,本模型检测时间平均快5.32s,实验对比结果说明了本文基于深度学习的船舶工业网络入侵检测方法的优越性。
4 结 语本文针对传统算法在网络入侵检测中的响应速度慢、检测不准确、无法检测未知入侵等问题,提出基于深度学习的船舶工业网络入侵模型,结果显示相比传统算法,该模型能够快速准确的检测船舶工业网络的入侵信息,鲁棒性较好。
| [1] |
李聪, 贾红军. 船舶网络入侵风险等级估算研究[J]. 舰船科学技术, 2018, v. 40(12): 56-58. |
| [2] |
章昱, 李腊元. 网络入侵检测系统的设计与实现[J]. 武汉理工大学学报(交通科学与工程版), 2004, 28(5): 657-660. DOI:10.3963/j.issn.2095-3844.2004.05.008 |
| [3] |
李辉, 管晓宏, 昝鑫, 等. 基于支持向量机的网络入侵检测[J]. 计算机研究与发展, 2003, 40(6): 799-807. |
| [4] |
支持向量机算法及其在网络入侵检测中的应用[D]. 大连: 大连海事大学, 2004.
|
| [5] |
尹宝才, 王文通, 王立春. 深度学习研究综述[J]. 北京工业大学学报, 2015(1): 48-59. |
 2020, Vol. 42
2020, Vol. 42
