为解决资源短缺困境,我国必须大力发展深海开发技术用以勘探深海石油与天然气[1]。导管架与重力式平台因造价与自重的原因,已不再满足现今的要求,半潜式平台逐渐将其取而代之[2]。
目前,国内外对半潜式平台的研究主要集中于其水动力性能特性研究,对于波浪爬升的研究较少。波浪爬坡现象最初由近口和海岸工程的学者Galvin和Hallermeier[3]提出,堤坝、桥墩等周围频繁出现波浪爬升现象。Mericier等[4]1994年首次对波浪爬升的谐频成份开展试验研究,发现KA对波浪爬升的低阶谐频值影响很弱。Lwanowski等[5]采用粘流软件Comflow针对平台立柱周围的波浪爬升效应进行理论研究。单铁兵、杨建民等[6-8]采用CFD方法研究多立柱间的水动力干扰与其间距的关系,分析立柱间距等参数对柱体之间波面影响和波浪爬升规律。Nielsen[9]首次对不同截面形状的类圆柱进行试验研究,探讨立柱横剖面形状对波浪爬坡效应和其周围波面分布的影响。
本文基于粘流理论对半潜式平台立柱波浪爬升进行数值模拟研究,深入讨论不同模式下立柱波浪爬升的一般规律以及相关参数对波浪爬升的影响,讨论波浪发生非线性时各波频导致的波浪爬升比重大小,为今后半潜式平台立柱波浪爬升研究提供参考价值。
1 数值计算方法自然界中的流体运动要遵循三大基本守恒定律,分别为质量守恒定律、动量守恒定律以及能量守恒定律。
当流体为粘性不可压缩,在运动过程中由于流体的密度为定值,
| $\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0\text{,}$ | (1) |
式中:ρ为流体密度u,v,w为流场中流体质点速度V在x,y,z三个方向上的分量
流体为粘性流体,当其运动时,ρ为定值,对于粘性不可压缩流体,N-S方程表示为:
| $ \begin{split} & \frac{{\partial {u_i}}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {{u_i}{u_j}} \right) = \\ & - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + v\frac{\partial }{{\partial {x_j}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) \text{,} \end{split} $ | (2) |
式中:
对湍流瞬态N-S方程作平均时间处理,即
| $ \left\{ \begin{aligned} & u = \overline u + {u^{,}};v = \overline v + {v^{,}};w = \overline w + {w^{,}}\text{,} \\ & p = \overline p + {p^{,}} \text{。} \end{aligned} \right. $ | (3) |
忽略质量力后,动量守恒方程表示为:
| $ \left\{ \begin{aligned} & \frac{{\partial u}}{{\partial t}} + \frac{{\partial \left( {uu} \right)}}{{\partial x}} + \frac{{\partial \left( {uv} \right)}}{{\partial y}} + \frac{{\partial \left( {uw} \right)}}{{\partial z}}=\\ & - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + \frac{1}{\rho }\left( {\frac{{\partial {\sigma _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{yx}}}}{{\partial y}} + \frac{{\partial {\tau _{zx}}}}{{\partial z}}} \right)\text{,}\\ & \frac{{\partial v}}{{\partial t}} + \frac{{\partial \left( {uv} \right)}}{{\partial x}} + \frac{{\partial \left( {vv} \right)}}{{\partial y}} + \frac{{\partial \left( {vw} \right)}}{{\partial z}}=\\ & - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + \frac{1}{\rho }\left( {\frac{{\partial {\tau _{xy}}}}{{\partial x}} + \frac{{\partial {\sigma _{yy}}}}{{\partial y}} + \frac{{\partial {\tau _{zy}}}}{{\partial z}}} \right)\text{,}\\ & \frac{{\partial w}}{{\partial t}} + \frac{{\partial \left( {uw} \right)}}{{\partial x}} + \frac{{\partial \left( {vw} \right)}}{{\partial y}} + \frac{{\partial \left( {ww} \right)}}{{\partial z}}= \\ & - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} + \frac{1}{\rho }\left( {\frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial y}} + \frac{{\partial {\sigma _{zz}}}}{{\partial z}}} \right)\text{。} \end{aligned} \right. $ | (4) |
联立式(3)和式(4),并对两边取时间平均值,有
| $\overline {{u^{,}}} = 0;\overline {{v^{,}}} = 0;\overline {{w^{,}}} = 0;\overline {{p^{,}}} = 0\text{,}$ | (5) |
| $\frac{{\partial \overline u }}{{\partial x}} + \frac{{\partial \overline v }}{{\partial y}} + \frac{{\partial \overline w }}{{\partial z}} = 0\text{。}$ | (6) |
式(4)是Reynolds湍流方程,与式(5)质量守恒方程构成湍流平均运动的方程式。其中Reynolds应力
| $\left( {\begin{array}{*{20}{c}} { - \rho \overline {{u^{,}}{u^{,}}} }&{ - \rho \overline {{u^{,}}{v^{,}}} }&{ - \rho \overline {{u^{,}}{w^{,}}} } \\ { - \rho \overline {{v^{,}}{u^{,}}} }&{ - \rho \overline {{v^{,}}{v^{,}}} }&{ - \rho \overline {{v^{,}}{w^{,}}} } \\ { - \rho \overline {{w^{,}}{u^{,}}} }&{ - \rho \overline {{w^{,}}{v^{,}}} }&{ - \rho \overline {{w^{,}}{w^{,}}} } \end{array}} \right)\text{。}$ | (7) |
在实际深海环境中,为精确模拟波浪环境,需要考虑波浪的非线性问题,则运用2阶斯托克斯波理论。下面依次为2-stokes波的势函数、波面方程以及水质点运动速度的方程。
势函数:
| $ \begin{split} & \phi = \frac{{{\text{π}} H}}{{kT}}\frac{{\cosh k\left( {z + h} \right)}}{{\sinh kh}}\sin \theta + \\ & \frac{3}{8}\frac{{{{\text{π}} ^2}H}}{{kT}}\left( {\frac{H}{L}} \right)\frac{{\cosh 2k\left( {z + h} \right)}}{{{{\sinh }^4}kh}}\sin 2\theta \text{,} \end{split} $ | (8) |
波面方程:
| $ \eta = \frac{H}{2}\left[ \begin{array}{l} - \dfrac{{Hk}}{{4\sinh 2kh}} + \cos \theta + \\ \dfrac{{Hk}}{8}\dfrac{{\cosh kh\left( {2{{\cosh }^2}kh + 1} \right)}}{{{{\sinh }^3}kh}}\cos 2\theta \end{array} \right]\text{,}$ | (9) |
质点水平速度:
| $ u = \frac{H}{2}\omega \left[ \begin{array}{l} \dfrac{{\cosh k\left( {z + h} \right)}}{{\sinh kh}}\cos \theta + \\ \dfrac{3}{8}Hk\dfrac{{\cosh 2k\left( {z + h} \right)}}{{{{\sinh }^4}kh}}\cos 2\theta \end{array} \right]\text{。} $ | (10) |
上述方程中
本文采用的半潜式平台是由4根立柱、2根横撑及2个下浮箱组成。平台相关几何参数详见表1。
|
|
表 1 平台相关尺度参数 Tab.1 Platform related scale parameter |
平台工作水深为250 m,平台布置及入射波方向如图1所示。在立柱的迎浪面设置4个观测点,取编号为1~4,距离立柱近壁面距离分别为0.006 25 R、0.2 R、0.6 R,R(R为立柱的特征半径)。另外绕立柱一周取7个观测点,距离立柱近壁面距离为0.006 25 R。入射波为规则波,相关参数见表2。在计算域的远场处设立一个远场观测点,以检验入射波是否为所设定规则波,如图2所示。

|
图 1 观测点布置示意图 Fig. 1 Observation point arrangement diagram |
|
|
表 2 计算工况 Tab.2 Calculation condition |

|
图 2 远场规则波时历曲线 Fig. 2 Far-field regular wave time history curve |
数值计算中平台设定为固定模式与系泊模式,运用HEXPRESS模块对其进行网格划分,运用软件内部网格品质检查功能检查网格质量显示良好,计算域整体网格划分如图3所示,平台有限元网格划分如图4所示。

|
图 3 计算域整体网格示意图 Fig. 3 Computational domain overall grid diagram |

|
图 4 平台网格划分 Fig. 4 Platform meshing |
一般对于波浪爬升现象的研究,为方便分析波浪爬升的特性,通常采用无量纲参数对其进行分析对比。本文定义Ar/(H/2)为波浪爬升无因次量,即波浪爬升高度与波幅的比值,其中Ar为波浪爬升高度,H为入射波的波高。
图5给出半潜式平台在固定模式和系泊模式下前立柱迎浪面的波浪爬升在不同计算工况下的变化图。从图中可以看出,固定模式和系泊模式下半潜式平台前立柱迎浪面的波浪爬升变化规律一致,即立柱迎浪面的波浪爬升高度随着距立柱距离的减小而增大,波浪在立柱的近壁面达到最大值。入射波与立柱相遇时,一部分水体从立柱的两侧流走,一部分水体停留在立柱迎浪面并继续往上爬升,水体的动能转化为势能,并在立柱表面爬升至最高处。
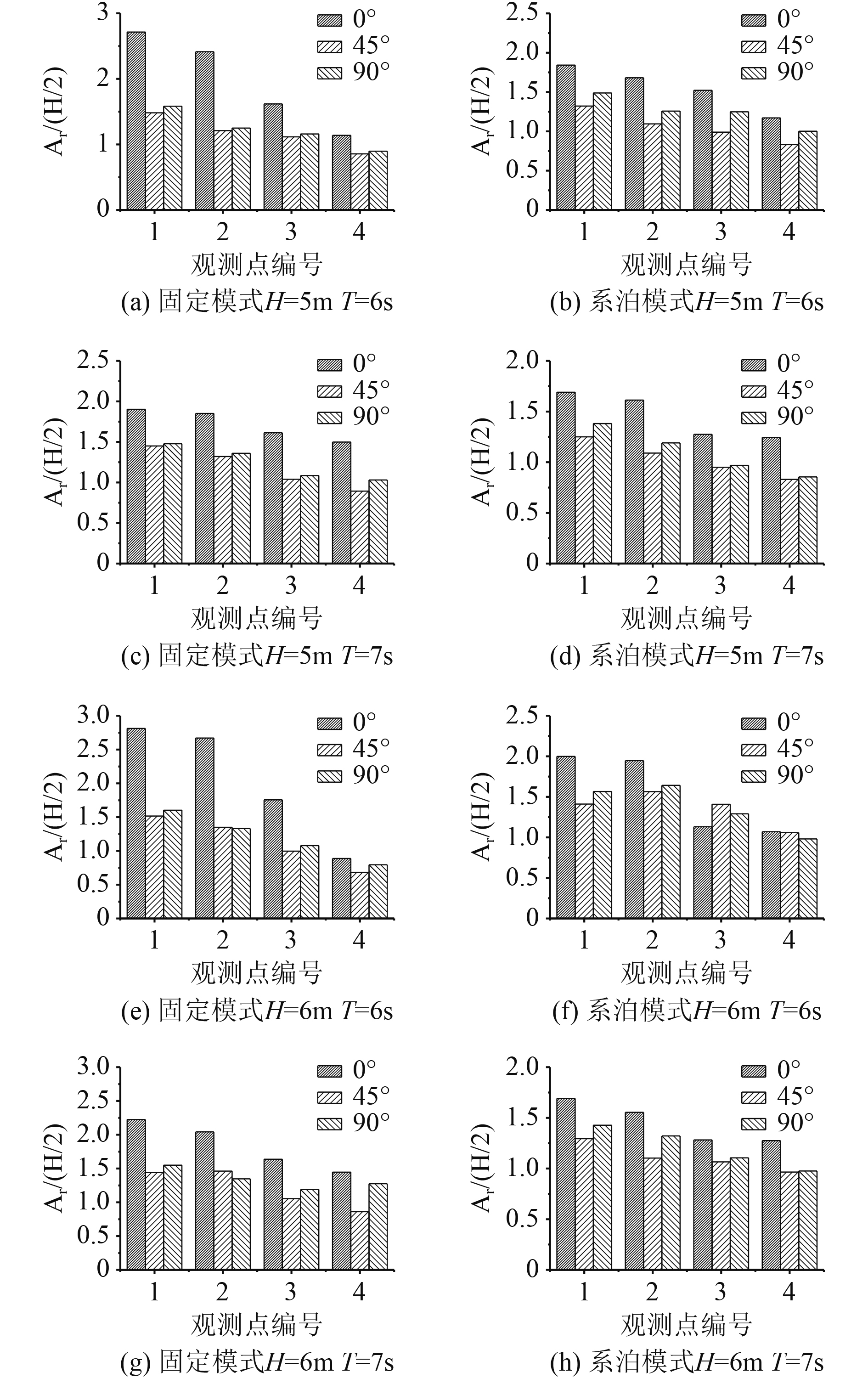
|
图 5 两种模式下前立柱迎浪面波浪爬升变化 Fig. 5 Change of wave run-up on the front column under two modes |
通过对比发现,固定模式下立柱迎浪面的波浪爬升大于系泊模式下的立柱迎浪面的波浪爬升。除此之外,距立柱表面距离越远波浪爬升呈现下降趋势,固定模式下波浪爬升下降趋势相较于系泊模式下波浪爬升下降趋势较为陡峭。原因在于当入射波与半潜式平台相遇时,系泊模式下的平台会随着水体一起运动,减缓了立柱的波浪爬升幅度。
3.2 立柱一周波浪爬升分布特征由于波浪爬升效应一般在立柱近壁面处效果明显,所以针对立柱一周进行波浪爬升数值模拟预报分析。为深入分析立柱周围的波面分布情况,图6给出半潜式平台在固定模式和系泊模式下,入射波浪向角β分别为0°,45°和90°时,半潜式平台前立柱近壁面波面分布曲线图。横坐标为θ/2π(θ为沿立柱逆时针旋转角度),纵坐标为波浪爬升无因次量Ar/(H/2)。可以看出:3种入射角下立柱周围波浪爬升变化曲线大致呈现“W”型。波浪与立柱相遇,一部分水体沿着立柱的迎浪面产生爬坡效应,另一部分水体沿着平台立柱的两侧向前继续传播,两侧的边波和后立柱的反射波在前立柱的背浪面处产生波浪叠加现象,形成波峰。入射角不同时,波浪入射角β=0°下波浪爬升效应最为剧烈。
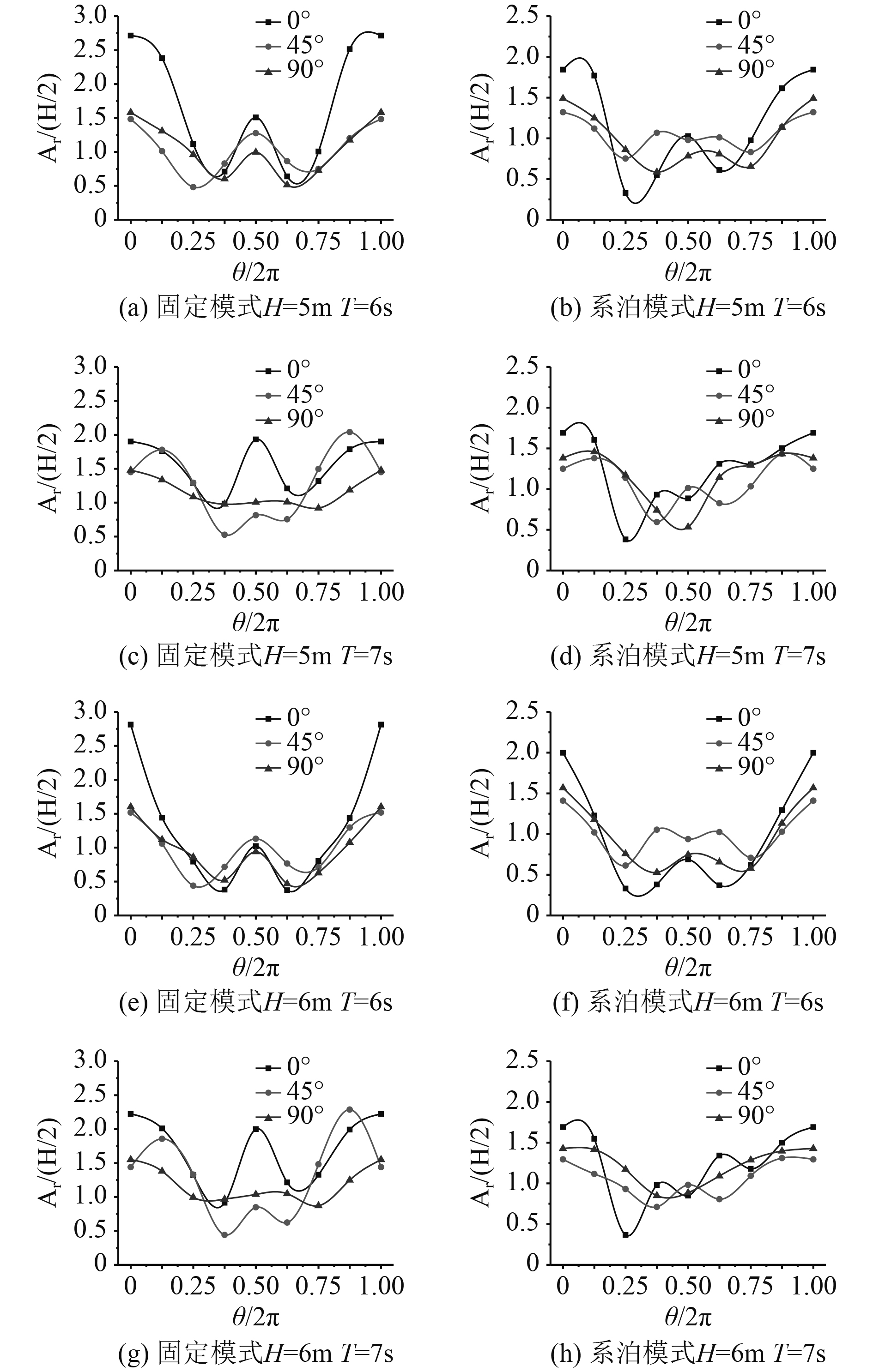
|
图 6 两种模式下立柱一周波浪爬升变化曲线 Fig. 6 Wave run-up curves around columns under two modes |
入射波波高一定,随着周期增大,立柱周围波浪爬升变化幅度趋于平缓。当平台处于不同模式时,立柱周围的波浪爬升相差较为明显,原因在于系泊模式下平台随水体运动,减弱波浪爬升能力。
当入射角β=45°时,立柱周围的波浪爬升趋势波动较为复杂,这是由于此时的近场干涉效应严重,从而影响立柱周围的波面分布。
3.3 波浪散射与爬升特性研究为便于分析立柱的波浪爬升规律,引入波陡参数KA(
由图7可以看出,同一散射参数下,随着波陡参数KA减小,前立柱迎浪面的波浪爬升幅度越来越小。这表明波陡参数越小,波浪的非线性越小,波浪爬升效应越不明显。随着波陡参数的减小,随距立柱表面距离越远前立柱迎浪面的波浪爬升呈现的下降趋势越发平缓。当入射波的波陡参数越来越小时,对波浪爬升的影响逐渐减小,入射波的非线性特性越来越弱,导致波浪的爬升能力越弱,即波浪爬升效应不明显。
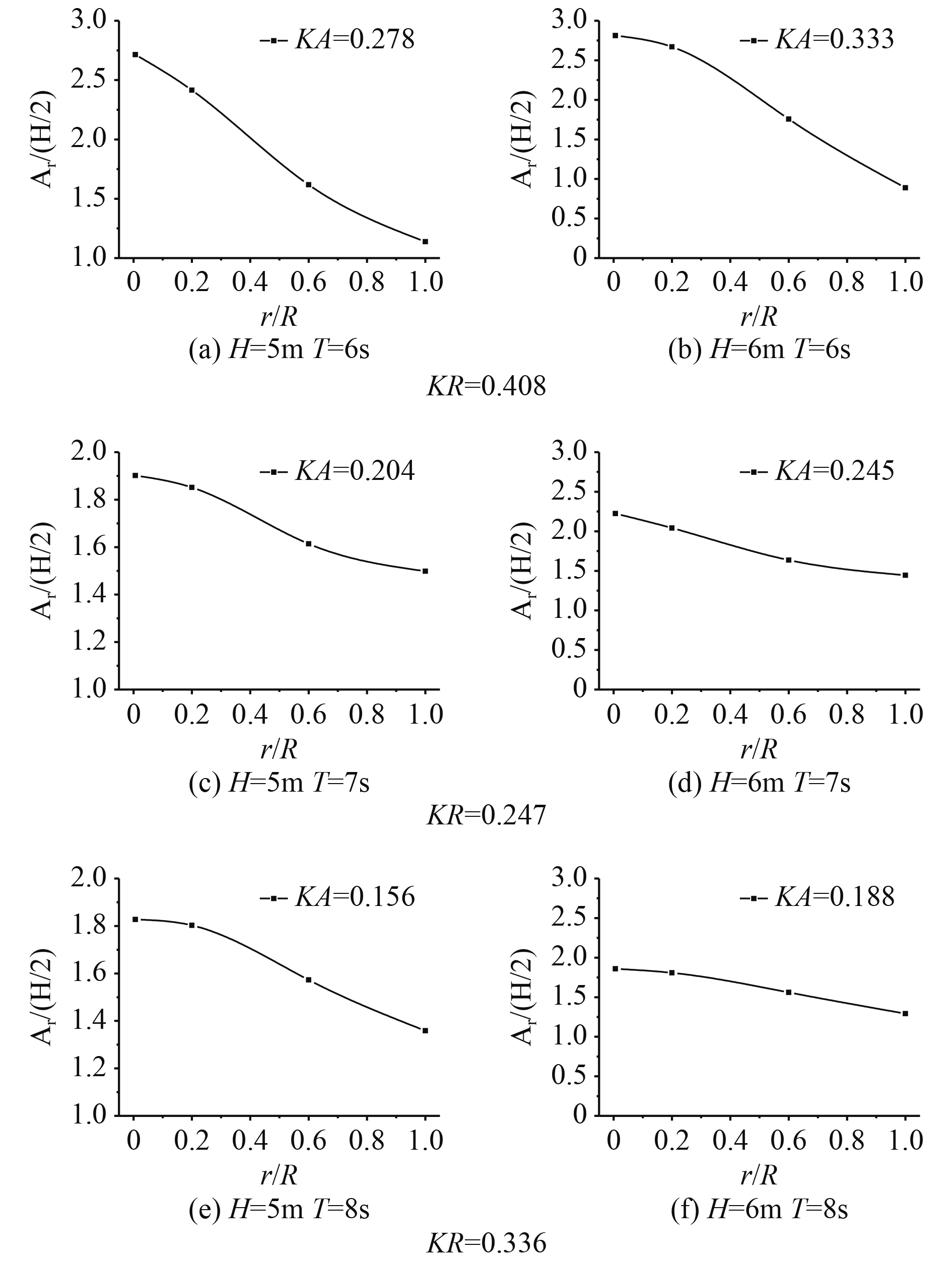
|
图 7 不同波陡参数下前立柱迎浪面波浪爬升分布特征 Fig. 7 Distribution characteristics of wave run-up in front of front column under different wave steepness parameters |
图8给出半潜式平台处于固定模式时,同一波陡参数不同散射参数下前立柱近壁面的波浪爬升无因次值对比图。可以发现,当入射波的波陡参数一定时,波浪的散射参数越大,则波浪爬升的无因次值越大,波浪的爬升效应越明显。随着入射波的散射参数KR增大,波浪爬升幅度增大。原因在于入射角不同时,可供波浪爬升的立柱平面投影不同,这导致水体与立柱相遇时停留在立柱迎浪面的那一部分水体多少不同,平面大的停留的水体多,则波浪能量大,波浪的动能转化为势能,则波浪爬升幅度大。
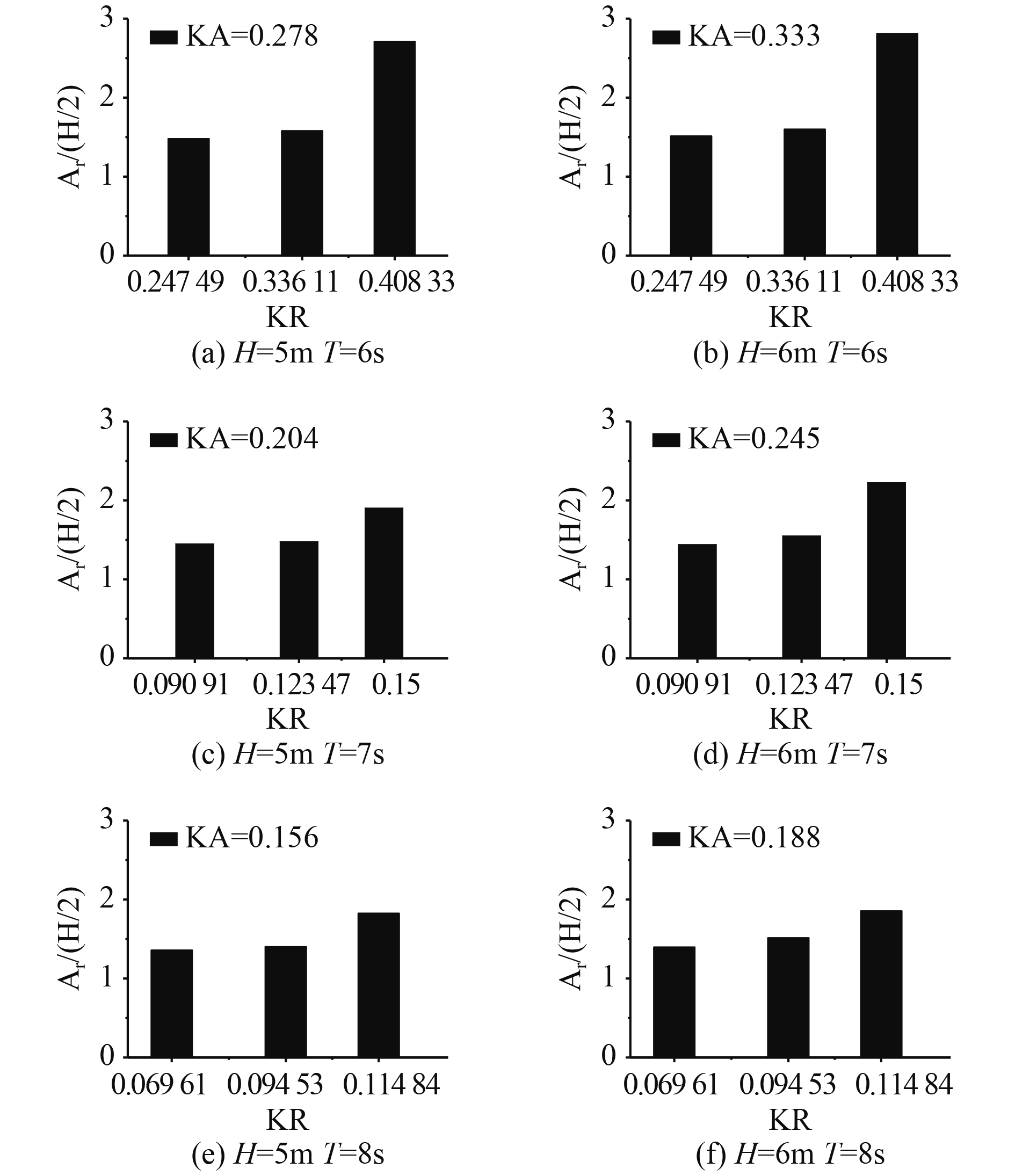
|
图 8 不同散射参数下前立柱迎浪面近壁处波浪爬升特征 Fig. 8 Wave run-up characteristics of the front wall near the wall of the front column with different scattering parameters KR |
通过对比左右2组图可以发现,随着入射波的波陡参数KA减少,散射参数KR对立柱近壁面的波浪爬升效应的影响越来越小。图8(c)中散射参数KR为0.15时所对应的波浪爬升无因次值为1.902,散射参数KR为0.09091时所对应的波浪爬升无因次值为1.45,两者相差0.452;图8(d)中散射参数KR为0.15时所对应的波浪爬升无因次值相差0.794。
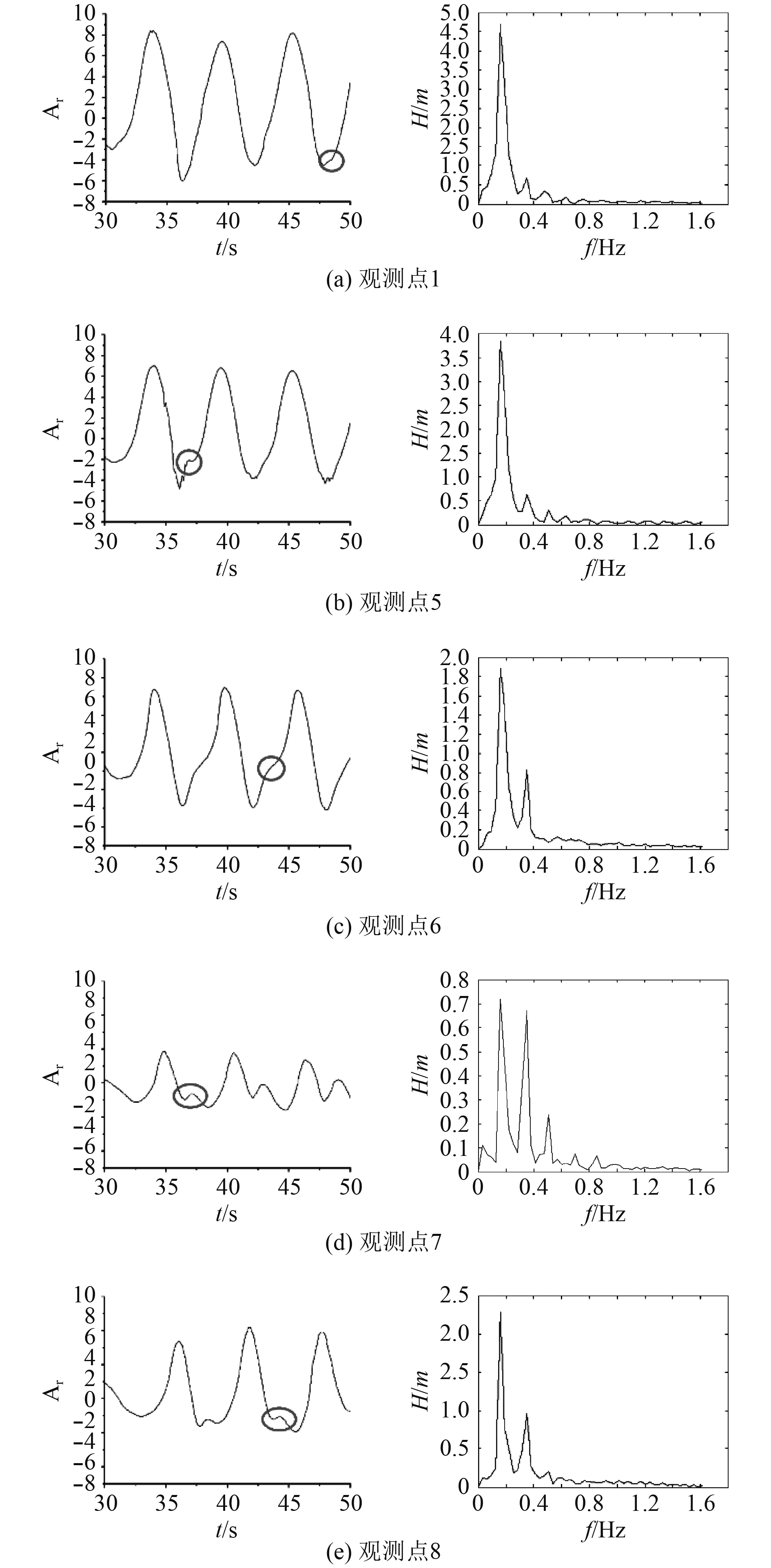
3.4 波浪绕立柱过程中的非线性特征运用自编程后处理软件Matlab对观测点波浪爬升时历曲线进行处理,得到各观测点波浪爬升的频谱分析图。图9给出前立柱半周的5个观测点的波浪爬升时历曲线图(Ar为波浪爬升高度)和频谱分析图(H是各谐频成分导致波浪爬升的高度)。可以看出:对比左侧观测点的波浪爬升时历曲线,1号观测点的波浪爬升最显著,之后观测点的波浪爬升在不断减弱,但在8号观测点处的波浪爬升有着小幅度的提高。波峰在不断变瘦,且波浪爬升的时历曲线中二次波峰的现象愈发明显,这表面波浪的非线性特性在不断地增强。
|
图 9 立柱近壁面处波浪爬升时历曲线和相应频谱分析图 Fig. 9 Wave run-up time curve and corresponding spectrum analysis diagram of the column near the wall |
对比右侧的频谱分析图,随着观测点的推移,观测点1处只有一处明显峰值,而观测点4处有着两处明显的峰值,二次波峰现象十分明显,表明波浪爬升中的低阶谐频成分不断降低,高阶谐频成分不断增多,波浪的非线性特征不断增强。原因在于结构物对波浪的扰动以及回流的叠加。从图中还可以发现,波浪的非线性先增强,在立柱后倒角处的波浪非线性最显著,然后在立柱的背浪面处回落,前者是由于立柱倒角的缘故,后者则是因后立柱的回流与多种波浪(如入射波、边波等)的叠加效应而导致的。
4 结 语本文基于粘流理论,通过商业软件FINE/Marine建立数值水槽,针对平台立柱的波浪爬升进行数值模拟,研究不同模式下立柱迎浪面以及立柱一周的波浪爬升规律,讨论波陡参数与散射参数对波浪爬升的影响,分析波浪各频谱导致波浪爬升的比重。研究结果表明:
固定模式与系泊模式下,半潜式平台立柱迎浪面的波浪爬升高度随距立柱距离增大而减小;固定模式下的立柱迎浪面的波浪爬升大于系泊模式下的立柱迎浪面的波浪爬升。立柱周围波浪爬升变化曲线大致呈现“W”型。随着波陡参数和散射参数的减小,前立柱迎浪面的波浪爬升幅度越来越小。随着波浪经过立柱时,立柱近壁面的波浪非线性特征先增大后减小,位于前立柱后倒角处最为显著。
| [1] |
李清平. 我国海洋深水油气开发面临的挑战[J]. 中国海上油气, 2006, 18(2): 130-133. DOI:10.3969/j.issn.1673-1506.2006.02.013 |
| [2] |
姜哲, 谢彬. 新型深水半潜式生产平台发展综述[J]. 海洋工程, 2011, 29(3): 132-138. DOI:10.3969/j.issn.1005-9865.2011.03.020 |
| [3] |
GALVIN CJ, HALLERMEIer RJ. Wave run-up on vertical cylinders[C]// Proc. 13th International Conference on Coastal Engineering, Vancouver, Canada, 1972, pp1955-1974.
|
| [4] |
MERCIER R S, NIEDZWEEHI J M. Experimental measurements of second. order diffraction by a truncated vertical cvlinder in m0no-chromatic waves[C]// 7th International Conference on the Behavior of Ofshore Structures. 1994, 2: 265-287.
|
| [5] |
LWANOWSKI B, MARC L, Wemmenhove R. CFD simulation of wave run-up on a semi-submersible and comparison with experiment[C]// Proceedings of the 28th International Conference on Ocean, Offshore and Arctic Engineering, OMAE2009-79052.
|
| [6] |
单铁兵. 波浪爬升的机理性探索和半潜式平台气隙响应的关键特性研究[D]. 上海: 上海交通大学. 2013.
|
| [7] |
单铁兵, 杨建民, 李欣. 深海平台立柱周围波浪非线性爬升研究进展[J]. 海洋工程, 2012, 30(1): 151-160. DOI:10.3969/j.issn.1005-9865.2012.01.022 |
| [8] |
单铁兵, 杨建民, 李欣. 水流对立柱周围波浪爬升特性的影响[J]. 上海交通大学学报, 2014, 48(1): 116-124. |
| [9] |
NIELSEN FG. Comparative study on airgap under floating platforms and run-up along platform columns[J]. Marine Structures, 2003, 16(2): 97-134. DOI:10.1016/S0951-8339(02)00023-0 |
 2020, Vol. 42
2020, Vol. 42
