2. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110016;
3. 中国科学院大学,北京 100049
2. Institute for Robotics and Intelligent Manufacting, Chinese Academy of Sciences, Shenyang 110016, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
自主水下机器人(Autonomous Underwater Vehicle,AUV)是探索海洋空间的有力工具之一,在海洋科学考察和海底资源勘测等领域获得广泛应用。利用水下对接平台对AUV进行自主对接,可以实现AUV能源补充、数据上传和使命下载,从而增强AUV的续航力与作业能力,降低AUV的应用成本。而AUV与移动对接平台之间的实时路径规划技术,是AUV与水下对接平台自主对接的使能技术之一。
Ken T等[1-2]提出一种基于TSK模糊理论的AUV对接控制方法,利用AUV与水下固定式对接平台之间的横向误差、纵向误差、AUV的期望纵向速度和艏向角建立相应的模糊策略,通过仿真实验和实际实验结果证明,该方法可使AUV在没有障碍物和海流未知的情况下回收到水下固定对接平台内;Jantapremjit P等[3-4]将对接阶段分为2个阶段,利用切换加权系数的人工矢量场法,使AUV沿着水下固定对接平台的中轴线运动,达到对接所需方向和位置最终实现AUV的安全对接;李晔和姜言清等[5-6]提出一种基于3次B样条和遗传算法的AUV小范围静态路径规划方法,该方法满足AUV对接过程中所需的终端约束和运动约束。上述方法都是AUV与水下固定对接平台之间的路径规划方法,存在容易陷入局部极值或运算复杂规划时间长等缺点,无法满足环境未知的情况下,AUV与水下移动平台对接的实时性需求。
本文针对复杂动态环境下AUV与水下移动平台对接的实时性和终端姿态需求,研究了一种基于混合整数线性规划[7](Mixed Integer Linear Programming,MILP)的AUV与水下移动平台对接路径规划方法,根据对接阶段的需求设计了不同的目标优化函数,实现了移动对接目标函数建模,对障碍物约束和AUV本体约束进行了相应的线性化,建立起由线性化约束和目标函数组成的线性规划模型,在相对速度坐标系下实现对AUV加速度的优化,实时规划出AUV相应的纵向速度和艏向角,并充分考虑AUV实际的动力学模型,最终在AUV与水下移动平台之间得到满足所有约束且目标函数最优的实时优化路径,利用仿真实验验证该方法的有效性。
1 问题描述本文将对接过程分为2个阶段:归航阶段和终端导引阶段[8-9]。第1阶段,AUV通过超短基线等传感器快速到达对接平台前方一定距离位置[10];第2阶段,AUV通过高精度传感器(声、光、磁等)进行精确导航定位,根据当前的位置和艏向,以及水下对接平台的位置及艏向,最终以期望的航向姿态完成欠驱动AUV与水下移动对接平台之间的精确移动对接。

|
图 1 AUV与水下移动平台对接过程示意图 Fig. 1 Diagram of docking process between AUV and underwater mobile platform |
MILP是在线性规划(Linear Programming,LP)的基础上发展而来的一种优化方法,它融入了整数变量,可以解决具有复杂逻辑关系的实数-整数混合优化问题。为了利用MILP优化方法更好地解决AUV与水下移动平台之间的实时优化路径规划问题,在此,进行相关假设和简化:
1)设AUV、障碍物和水下对接平台的当前时刻的相对位置和相对速度已知,且下一时刻的相对位置和相对速度未知;
2)设在极小时间周期内,障碍物和水下移动平台的速度保持不变;
3)设对接阶段水下对接平台航行速度小于AUV的速度;
4)设水下对接平台沿着水下移动平台的中轴线方向移动。
2 约束建模 2.1 障碍物约束的线性化如图2所示,设
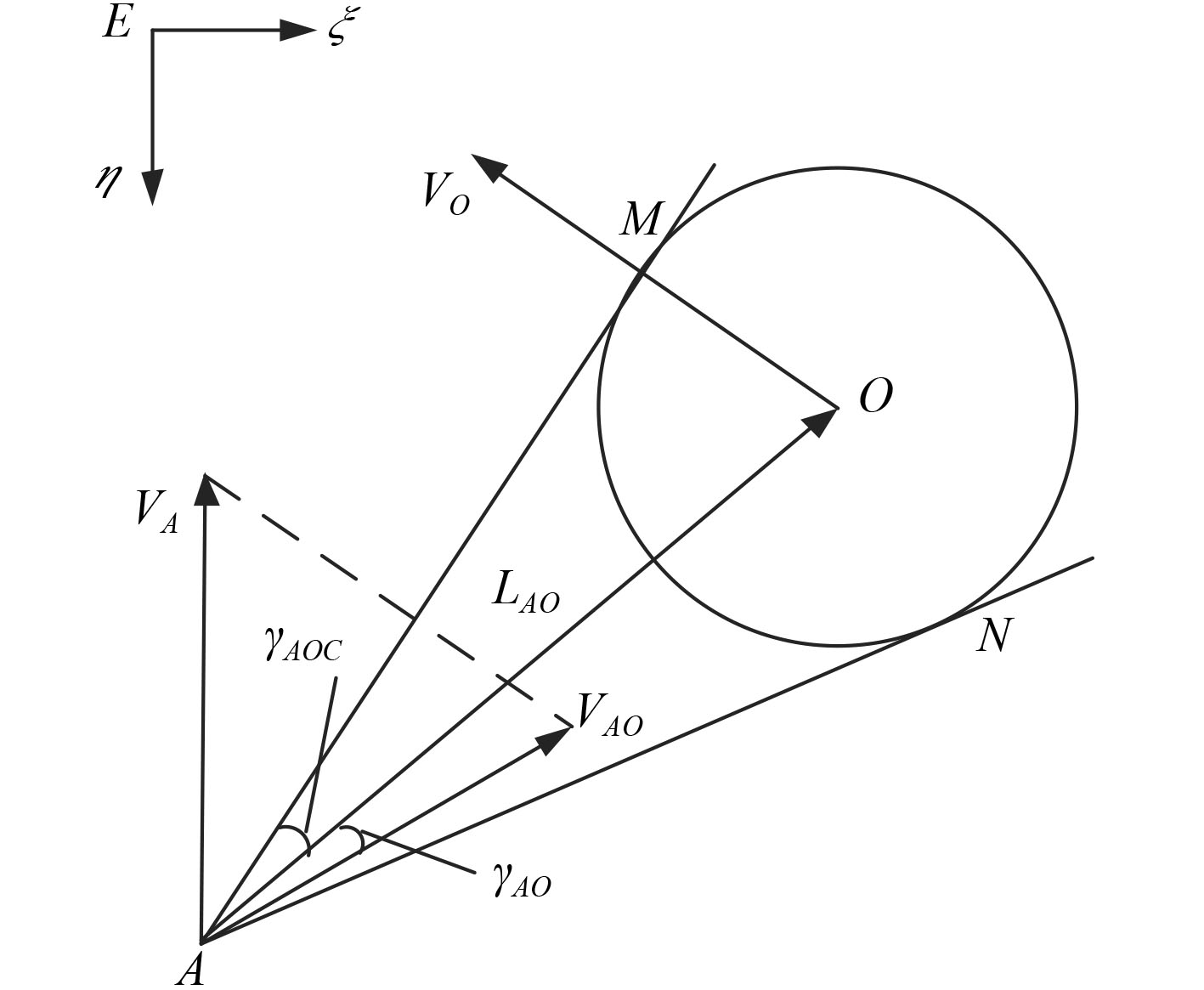
|
图 2 AUV-障碍物示意图 Fig. 2 Diagram of AUV-obstacle |
关于
| $ \begin{aligned} \Delta {\gamma _{{{AO}}}}_{{C}} = & - \frac{1}{{\sqrt {|{{{V}}_{{{AO}}}}{|^2}|{{{L}}_{{{AO}}}}{|^2} - {P_{{{AO}}}}^2} }} \times \\ & {{ }}\left( {{{{L}}_{{{AO}}}} - \frac{{{P_{{{AO}}}}}}{{|{{{V}}_{{{AO}}}}{|^2}}}{{{V}}_{{{AO}}}}} \right) \cdot \Delta {{V}}_{{{AO}}}^{{\rm T}}\text{,} \end{aligned} $ | (1) |
其中,
为了使AUV可以避开多个障碍物,障碍物约束的线性化模型可以写成:
| ${\gamma _{{{AO}}i}} + \Delta {\gamma _{{{AOi}}}} \geqslant {\gamma _{{{AO}}}}_{{{Ci}}}{\text{或}}{\gamma _{{{AOi}}}} + \Delta {\gamma _{{{AOi}}}} \leqslant {{ - }}{\gamma _{{{AO}}}}_{{{Ci}}}\text{,}$ | (2) |
其中:
为了解决AUV避开障碍物时的转向问题,可以将式(2)写成:
| $\left\{ \begin{array}{l} {\gamma _{{{AOi}}}} + \Delta {\gamma _{{{AOi}}}} \leqslant {\text{π}} + {a_i}\kappa \text{,} \\ {\gamma _{{{AOi}}}} + \Delta {\gamma _{{{AOi}}}} \geqslant {\gamma _{{{AO}}}}_{{{Ci}}} - {a_i}\kappa \text{,} \\ {\gamma _{{{AOi}}}} + \Delta {\gamma _{{{AOi}}}} \geqslant - {\text{π}} - {b_i}\kappa \text{,} \\ {\gamma _{{{AOi}}}} + \Delta {\gamma _{{{AOi}}}} \leqslant - {\gamma _{{{AO}}}}_{{{Ci}}} + {b_i}\kappa \text{。} \end{array} \right.$ | (3) |
其中
当
当
考虑 AUV动力学模型,由于螺旋桨的转速极限约束,欠驱动AUV航速不会太大,由AUV操纵性知识可知,过低的航速会导致方向舵失效。假设在单个采样周期
| $\left\{ \begin{array}{l} {{{V}}_{\min }} \leqslant {{V}} \leqslant {{{V}}_{\max }} \text{,} \\ - \Delta {{{V}}_{\max }} \leqslant \Delta {{V}} \leqslant \Delta {{{V}}_{\max }} \text{。} \end{array} \right.$ | (4) |
其中,
由速度约束
| ${{{V}}_{\min }} \leqslant {{V}} + \Delta {{V}} \leqslant {{{V}}_{\max }}\text{,}$ | (5) |
联立式(4)和式(5)得加速度分量约束如下:
| $ \begin{split} &\max \left\{ { - \Delta {{{V}}_{\max }},{{{V}}_{\min }} - {{V}}} \right\} \leqslant \Delta {{V}} \leqslant \\ &\min \left\{ {\Delta {{{V}}_{\max }},{{{V}}_{\max }} - {{V}}} \right\}\text{。} \end{split} $ | (6) |
目标函数是根据AUV与水下移动平台对接的任务需求来确定的。在AUV回收的第1阶段,目的是尽快缩短AUV与水下移动平台的距离,并快速到达大致预定位置,这里与其他AUV路径规划问题类似,只需要解决目标点的到达问题;第2阶段,目的是AUV以期望的航向姿态尽快与水下移动平台完成对接,这里与其他AUV路径规划问题不同的是,不仅需要解决目标点的到达问题,还要保证AUV是以期望方向到达目标点。
3.1 距离收敛为了使AUV与水下移动平台之间的距离越来越近(见图3),即
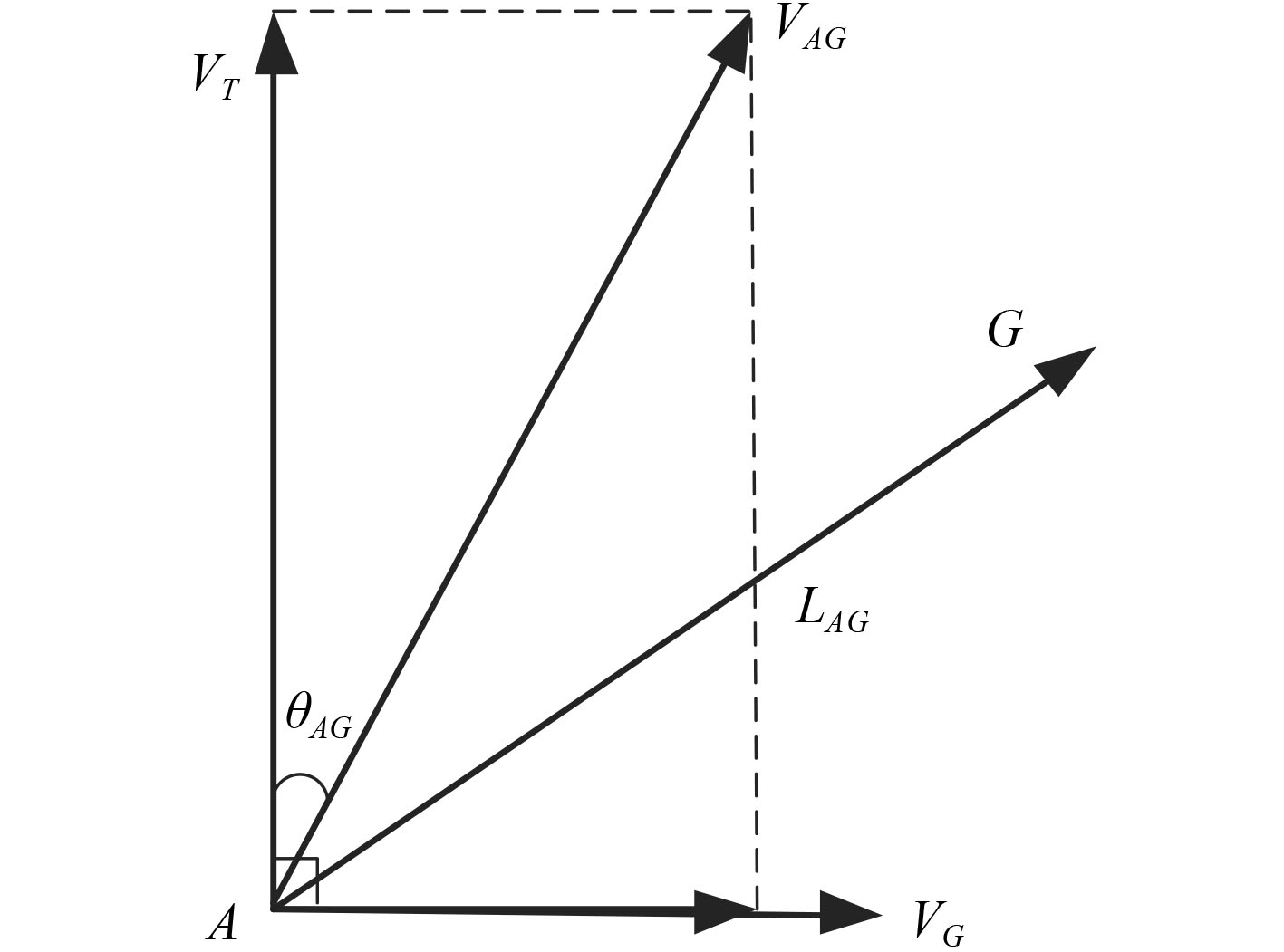
|
图 3 相对速度的速度分解 Fig. 3 Velocity decomposition of relative velocity |
| $\min :|{{{L}}_{{{AG}}}} - ({{{V}}_{{{AG}}}} + \Delta {{{V}}_{{{AG}}}})\Delta t|\text{。}$ | (7) |
其中,
为了方便计算,式(7)写作:
| $\min :{J_j} = |{l_j} - ({v_j} + \Delta {v_j})\Delta t|,j = 1,2 \text{。}$ | (8) |
其中,
为了尽快缩短AUV与水下移动对接平台之间的相对距离
| $\max :|{{{V}}_{{C}}}| = |{{{V}}_{{{AG}}}}{{|cos}}{\gamma _{{{AG}}}}\text{,}$ | (9) |
其中,
经过线性化[11]以及为了与距离收敛目标函数式(8)相对应,式(9)最终为:
| $\min :{J_{v1}} = - \frac{{{P_{{{AG}}}}}}{{|{{{L}}_{{{AG}}}}|}} - \frac{{{{{L}}_{{{AG}}}}}}{{|{{{L}}_{{{AG}}}}|}} \cdot \Delta {{V}}_{{{AG}}}^{\rm{T}}\text{。}$ | (10) |
其中,
为了使AUV以期望的航向姿态与水下移动平台完成对接,AUV与目标的相对速度
| $\max :|{{{V}}_{{T}}}| = |{{{V}}_{{{AG}}}}|\cos {\theta _{{{AG}}}}\text{,}$ | (11) |
其中,
设
| ${{n}} = \frac{{{{{V}}_{{G}}} \times {{{L}}_{{{AG}}}} \times {{{V}}_{{G}}}}}{{|{{{V}}_{{G}}} \times {{{L}}_{{{AG}}}} \times {{{V}}_{{G}}}|}}\text{,}$ | (12) |
令
| $\begin{array}{l} {\rm{f}}({{{V}}_{{{AG}}}}{{) = |}}{{{V}}_{{T}}}{{|}} = {{|}}{{{V}}_{{{AG}}}}{{|}}\cos {\theta _{{{AG}}}}=\\ {{ }}{{{V}}_{{{AG}}}} \cdot {{n}}\text{。} \end{array}$ |
根据泰勒公式可知:
| $\Delta {\rm{f}}({{{V}}_{{{AG}}}}) = \nabla f \cdot \Delta {{V}}_{{{AG}}}^{{\rm T}} + o(||\Delta {{{V}}_{{{AG}}}}||)\text{,} $ |
其中,
忽略高阶项,以及为了与距离收敛目标函数式(8)相对应,式(11)最终为,
| $\min :{J_{v2}} = - (f + \Delta f){{ = - }}{{{V}}_{{{AG}}}} \cdot {{n}} - {{n}} \cdot \Delta {{V}}_{{{AG}}}^{{\rm T}}\text{。}$ | (13) |
在AUV与水下移动平台对接的第1阶段,只需要考虑目标点到达问题;在第2阶段,不仅需要考虑目标点达到问题,还要保证AUV是以期望方向到达目标点。同时根据子目标函数的分析,可得总的目标函数:
| $ \min :J = \left\{ \begin{aligned} & {J_{\rm{I}}} = \sum\limits_i^M {{\omega _i}{J_i}} + {\omega _{v1}}{J_{v1}}\text{,}{\rm{ |}}{{{L}}_{{\rm{AG}}}}| \geqslant {d_{\min }}{\text{或}}{\phi _{{\rm{AG}}}} \leqslant {\phi _{\min }}\text{,}\\ & {J_{{\rm{II}}}} = \sum\limits_i^2 {{\omega _i}{J_i}} + {\omega _{v2}}{J_{v2}}\text{,}{\text{其他}}\text{。} \end{aligned} \right. $ | (14) |
其中,i=1,2,…M,表示维数,这里取M=2,表示二维平面,
AUV与水下移动对接平台的精确对接系统的实时路径规划流程图如图4所示。具体的算法流程如下:
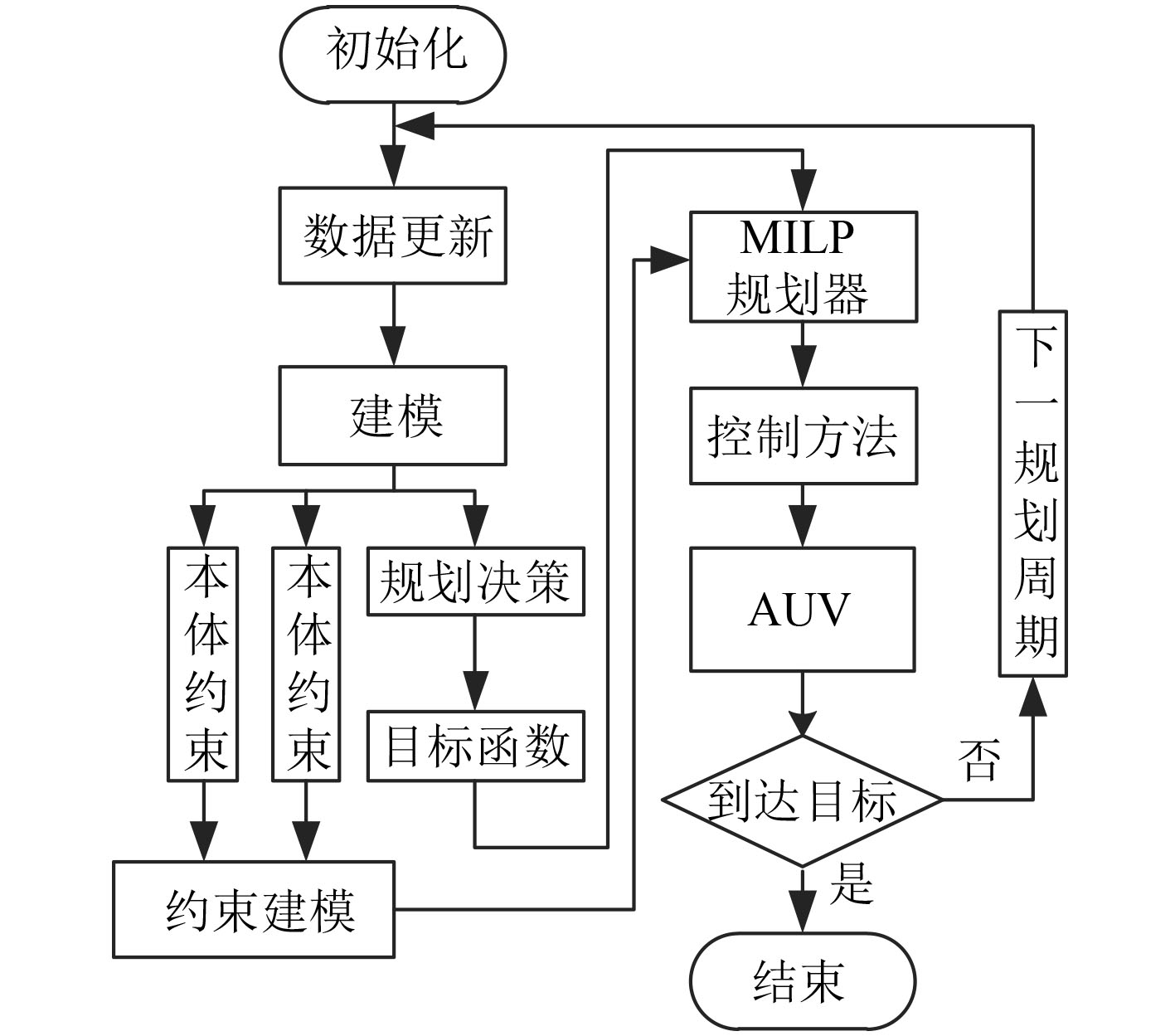
|
图 4 算法流程图 Fig. 4 Flow diagram of algorithm |
1)通过传感器数据获得水下移动平台和障碍物的位置信息和速度信息;
2)对传感器约束和本体约束进行线性化,获得相应模型;
3)根据规划策略公式(14)设计相应的目标函数;
4)利用MILP规划器实现对AUV加速度的优化,并得到期望的速度
| $ \begin{array}{l} {u_{{d}}} = |{{V}} + \Delta {{V}}\Delta t| \text{,}\\ {\psi _{{d}}} = {{arctan}}\frac{{{{({{V}} + \Delta {{V}}\Delta t)}_\eta }}}{{{{({{V}} + \Delta {{V}}\Delta t)}_\xi }}} \text{,} \end{array} $ | (15) |
其中,
5)将航行控制器作用于AUV的实际动力学模型上,得到实际的速度
6)根据实际的速度
| $\begin{split} & \xi (t + \Delta t) = \xi (t) + u \cdot \Delta t \cdot \cos \psi \text{,} \\ & \eta (t + \Delta t) = \eta (t) + u \cdot \Delta t \cdot \sin \psi \text{。} \end{split} $ | (16) |
7)判断AUV是否到达水下移动对接平台位置,如果到达,则规划算法结束,否则返回步骤2进行下一周期规划。
5 仿真实验仿真实验在Matlab R2015b下进行,采用PID控制器对某型AUV进行航行控制。MILP的规划周期
|
|
表 1 仿真实验初始值 Tab.1 Initial value of simulation experiment |
根据仿真结果可知,MILP单步规划时间约为0.18 s,可以满足AUV与水下移动平台之间路径规划的实时性需求。由图5可知,AUV可以有效避开障碍物O1和障碍物O2,AUV在位置

|
图 5 实时规划路径图 Fig. 5 Real-time path planning map |

|
图 6 AUV速度曲线 Fig. 6 The velocity curve of AUV |

|
图 7 AUV航向曲线 Fig. 7 The heading curve of AUV |
以往的大多数路径规划算法只考虑目标点的到达问题,没有考虑AUV到达目标点的姿态需求。本文针对复杂动态环境下AUV与水下移动对接平台的实时性和终端姿态需求,提出一种基于MILP的实时路径规划方法。充分考虑了障碍物约束、AUV本体约束,根据多个对接阶段的需求设计了距离收敛、时间最优和姿态最优等不同的目标优化函数,建立了移动对接目标函数,形成相应的多约束线性规划模型,实现对AUV加速度优化。仿真结果表明,该算法能满足AUV与水下移动对接平台的实时性和终端姿态需求。
AUV的期望航向在路径规划的后半程存在剧烈变化,分析可知,这是由于AUV参数的设计不太恰当导致的,需要进一步改进。下一步需要考虑海流对AUV和水下移动对接平台运动的影响,以便更好地满足实际工程需要。
| [1] |
TEO K, AN E, BEAUJEAN P. A robust fuzzy autonomous underwater vehicle (AUV) docking approach for unknown current disturbances[J]. IEEE Journal of Oceanic Engineering, 2012, 37(2): 143-155. DOI:10.1109/JOE.2011.2180058 |
| [2] |
TEO K, GOH B, CHAI O K. Fuzzy docking guidance using augmented navigation system on an AUV[J]. IEEE Journal of Oceanic Engineering, 2012, 40(2): 349-361. |
| [3] |
JANTAPREMJIT P, WILSON P A. Optimal control and guidance for homing and docking tasks using an autonomous underwater vehicle[C]//Mechatronics and Automation, 2007. ICMA 2007. International Conference on. IEEE, 2007: 243-248.
|
| [4] |
JANTAPREMJIT P, WILSON P A. Guidance-control based path following for homing and docking using an autonomous underwater vehicle[C]//Oceans 2008-MTS/IEEE Kobe Techno-Ocean. IEEE, 2008: 1-6.
|
| [5] |
姜言清. 约束条件下欠驱动AUV的路径规划问题研究[D]. 哈尔滨: 哈尔滨工程大学, 2013: 16-36. Jiang Y Q. Research on path planning of underactuated auv under constraints[D]. Harbin: Harbin engineering university, 2013: 16-36. |
| [6] |
李晔, 姜言清, 张国成, 等. 考虑几何约束的AUV回收路径规划[J]. 机器人, 2015, 37(04): 478-485. LI Y, JIANG Y q, ZHANG G c, et al. AUV recovery path planning considering geometric constraints[J]. Robot, 2015, 37(04): 478-485. |
| [7] |
ZU D, HAN J D, TAN D L. Acceleration space lp for the path planning of dynamic target pursuit and obstacle avoidance[C]//The 6th World Congress on Intelligent. Control and Automation.Dalian, 2006: 9084-9088.
|
| [8] |
STOKEY R, PURCELL M, FORRESTER N, et al. A docking system for REMUS, an autonomous underwater vehicle[C]//OCEANS'97. MTS/IEEE Conference Proceedings. IEEE, 1997, 2: 1132-1136.
|
| [9] |
MCEWEN R S, HOBSON B W, MCBRIDE L, et al. Docking control system for a 54-cm-diameter (21-in) AUV[J]. IEEE Journal of Oceanic Engineering, 2008, 33(4): 550-562. DOI:10.1109/JOE.2008.2005348 |
| [10] |
STOKEY R, ALLEN B, AUSTIN T, et al. Enabling technologies for REMUS docking: an integral component of an autonomous ocean-sampling network[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 487-497. DOI:10.1109/48.972082 |
| [11] |
程大军. AUV环境建模及行为优化方法研究[D]. 北京: 中国科学院大学, 2011: 44-46. CHENG D J. Research on auv environmental modeling and behavior optimization[D]. Beijing: University of chinese academy of sciences, 2011: 44-46. |
 2020, Vol. 42
2020, Vol. 42

