2. 中国海洋大学 信息科学与工程学院,山东 青岛 266100
2. School of Information Science and Engineering, Ocean University of China, Qingdao 266100, China
随着科学社会的快速发展,人口、环境和资源已经成为全球性问题,随着资源的日渐减少,人类已经将目光投向海洋世界。自主水下航行器(Autonomous Underwater Vehicle,AUV)作为一种新型海洋环境移动监测平台,具有灵活性高、自身作业能力强、下潜深度大、使用成本低及测量范围大等特点,已逐步成为全球海洋探测领域技术研究的重点和热点之一[1-3]。
水下航行器的姿态控制主要是通过尾舵的转动提供升力。尾舵具有控制简单,造价低,具有一定的稳定性等优点成为大多数水下航行器采用的控舵方式[4]。大多数的AUV设计都是将全动舵作为AUV的尾舵,但是考虑到水下环境复杂多变,本文在全动舵的正前方设计一个固定不动的舵以保证全动舵的安全,此固定舵的增加使AUV外形变复杂,必将会引起尾舵水动力性能的变化[5-7]。本文通过计算流体力学的方法对固定舵增加后会对水动力特性造成的影响,固定舵与全动舵之间的缝隙,铰链力矩大小等关键的问题进行分析。
1 计算模型 1.1 数学模型所有不可压缩流体流动都遵循质量守恒定理和动量守恒定理,本文针对不可压缩流体采用RANS方程,其中连续性和RANS方程[8-10]为:
| $\frac{{\partial {u_i}}}{{\partial {x_i}}} = 0\text{,}$ | (1) |
| $ \begin{split} & \rho \frac{{\partial \overline {{u_i}} }}{{\partial t}} + \rho \frac{\partial }{{\partial {x_j}}}(\overline {{u_i}} \overline {{u_j}} ) = - \frac{{\partial \overline P }}{{\partial {x_i}}} + \rho \mu \frac{{{\partial ^2}\overline {{u_i}} }}{{\partial {x_i}\partial {x_j}}} - \\ & \rho \frac{\partial }{{\partial {x_j}}}(\overline {{u_i}^{'}{u_j}^{'}} ) + \rho \overline {{f_i}} \text{。} \end{split} $ | (2) |
式中:
本文选取的全动舵剖面形状为一对对称翼型。NACA-4数字系列翼型是美国NACA最早建立的一个低速翼型系列。这类翼型具有较高的最大升力系数和较低的最小阻力系数。由于NACA系列具有升力大、阻力小的特点而被广泛使用。本文仿真实验用的全动舵翼型为NACA0012,前2位“00”表示对称翼型,后2位“12”表示厚度比的百分比。对于该种翼型的升力系数
| ${{C}_{L}}=\frac{L}{{}^{1}\!\!\diagup\!\!{}_{2}\;\rho {{v}^{2}}C}\text{,}$ | (3) |
| ${{C}_{D}}=\frac{D}{{}^{1}\!\!\diagup\!\!{}_{2}\;\rho {{v}^{2}}C}\text{,}$ | (4) |
| ${{C}_{M}}=\frac{M}{{}^{1}\!\!\diagup\!\!{}_{2}\;\rho {{v}^{2}}Ca}\text{。}$ | (5) |
式中:
|
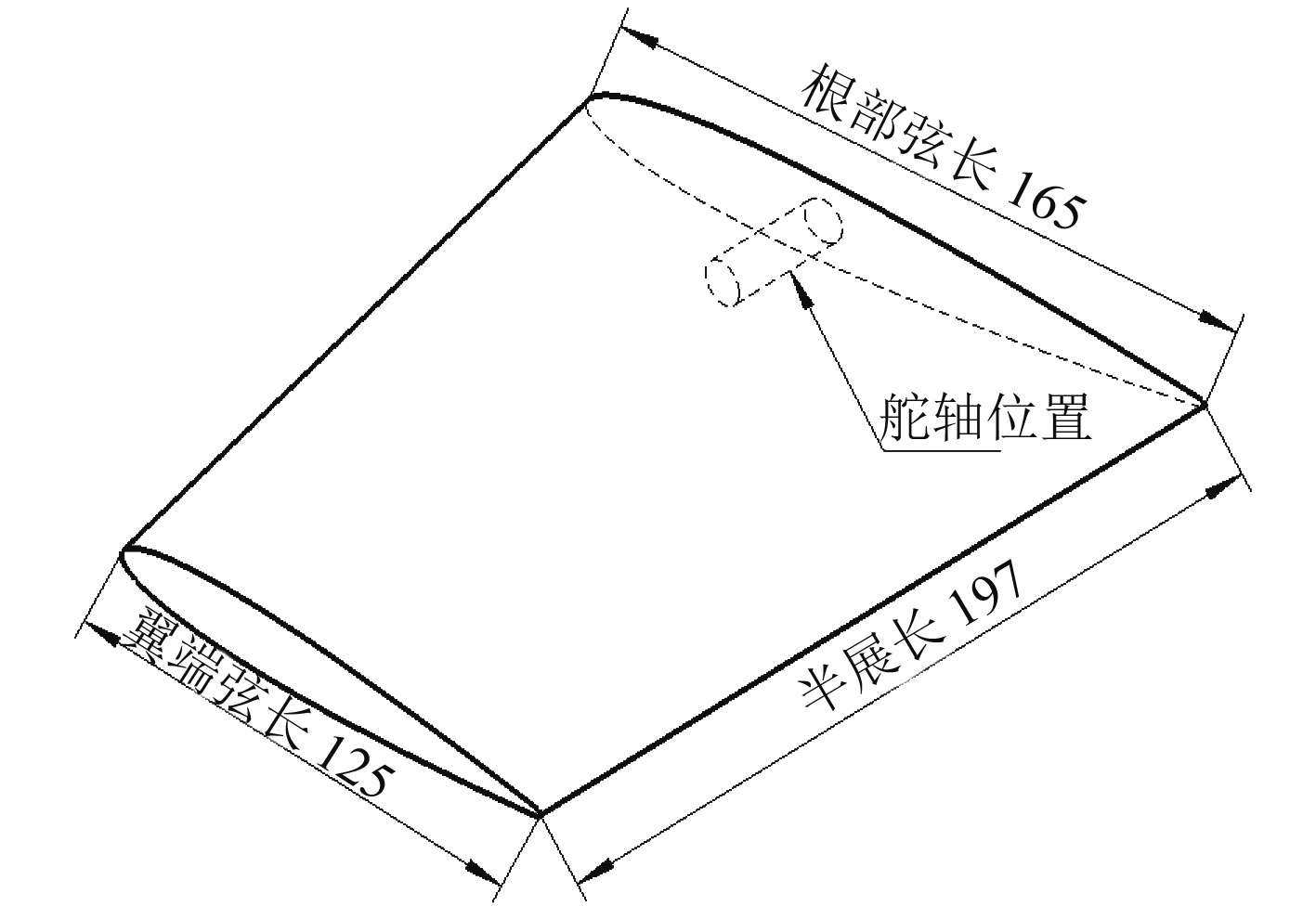
图 1 全动舵结构参数图 Fig. 1 Structural parameters of the all-movable rudder |
|
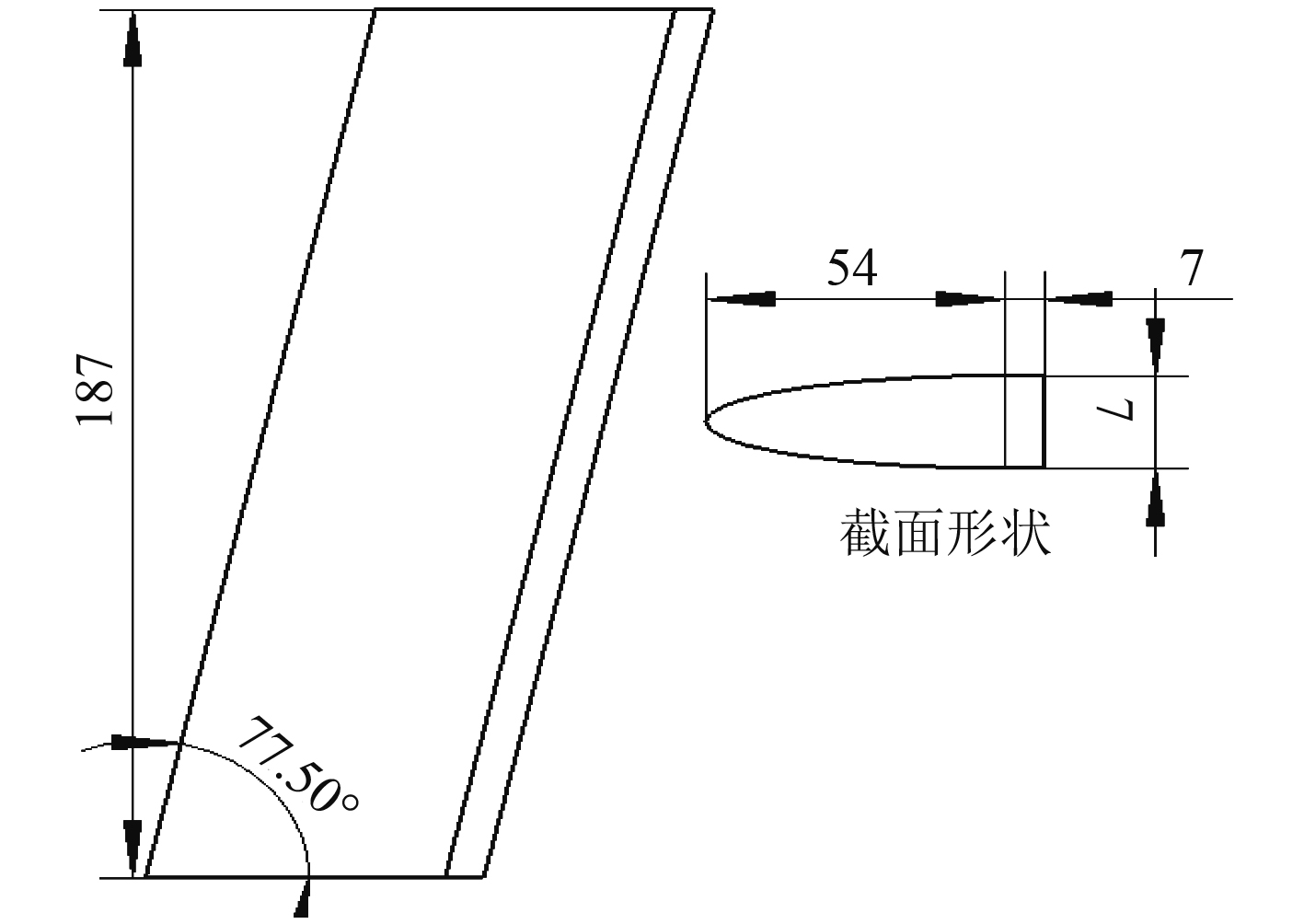
图 2 固定舵结构参数图 Fig. 2 Structural parameters of the fixed rudder |

|
图 3 AUV实物图 Fig. 3 Appearance of the AUV |
本文通过ICEM对尾舵部分进行网格划分,选择的流域为底面直径400 mm,长度为750 mm的圆柱型流域。本文采用非结构化网格对尾舵模型进行网格划分,表面的网格类型为三角形网格,体网格类型为Tetra/Mixed,AUV舵片的整体网格模型图如图4所示。

|
图 4 AUV舵片的整体网格模型图 Fig. 4 Overall mesh model of AUV rudder |
本文利用三维CFD方法模拟了不同来流速度,不同攻角尾舵的水动力特性。由于标准k-ε模型主要针对湍流发展比较充分的湍流流动建立的高雷诺数湍流计算模型,而RNG k-ε模型关注平均流动中的旋转和旋流流动,比标准模型更具优越性[12-13],所以本文湍流方程选取RNG k-ε模型。进口条件设定为速度入口,出口条件设定为压力出口,模型表面采用固定无滑移壁面设计。
3 全动舵与固定舵缝隙本文通过改变固定舵与全动舵模型之间的缝隙大小,对不同缝隙不同攻角的尾舵在同一速度2 m/s状态下进行网格划分与水动力性能分析,得到的升力阻力与升阻比的关系如图5~图7所示。

|
图 5 不同攻角下的升力变化曲线 Fig. 5 Lift curve at different angles of attack |
|
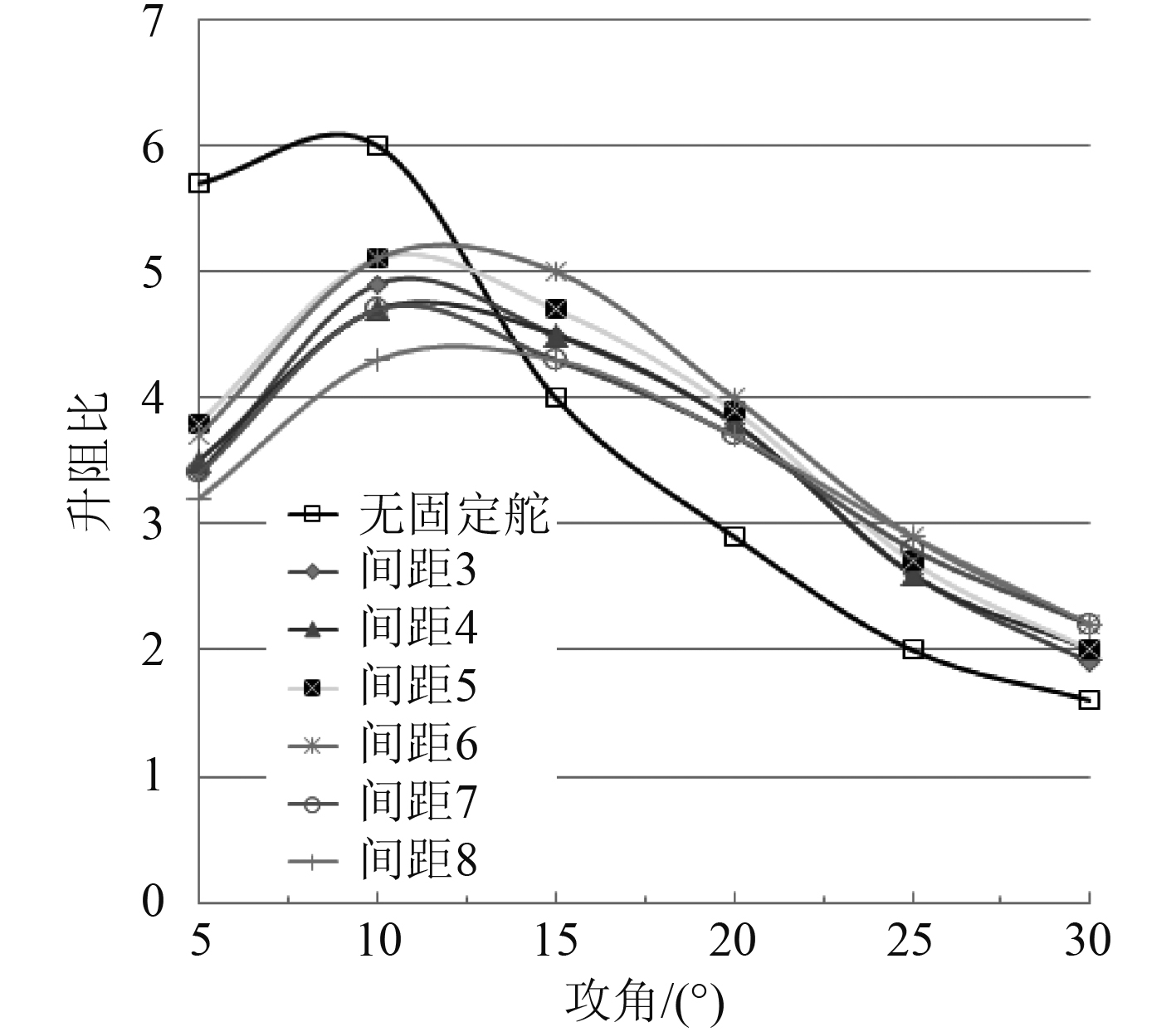
图 7 不同攻角下的升阻比变化曲线 Fig. 7 Lift-to-drag ratio curve at different angles of attack |
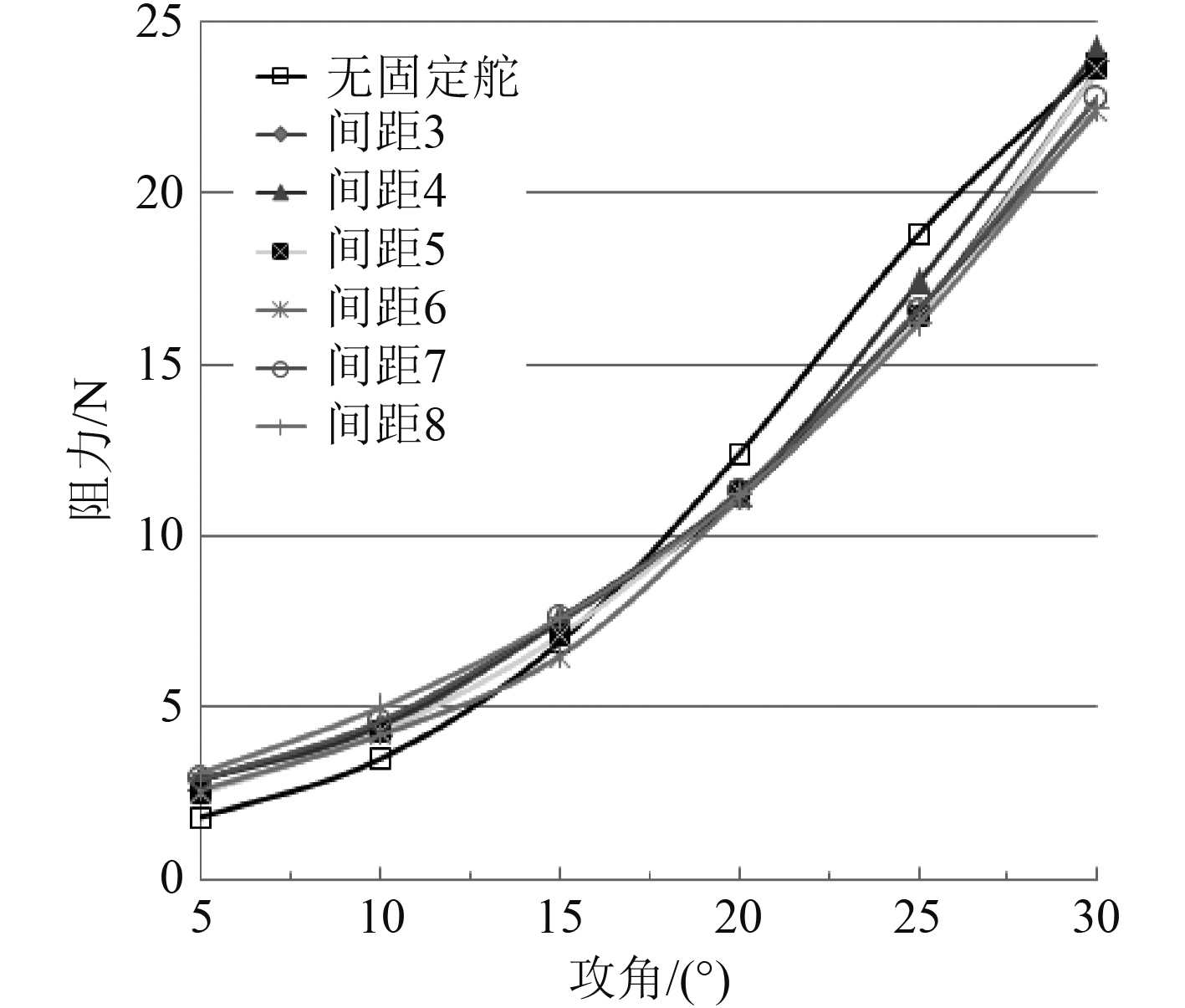
图7为升阻比随攻角的变化曲线。由图可知,无固定舵片时尾舵能达到最大的升阻比,且最大的升阻比出现在攻角8°左右。结合图5不同缝隙尾舵升力随攻角变化曲线图以及图6不同缝隙尾舵阻力随攻角变化曲线图,可以看出攻角12°之前有无固定舵片及固定舵与全动舵片之间缝隙大小对尾舵的升力没有产生明显影响,但是固定舵的增加却增加了舵片的阻力从而使安装固定舵的尾舵升阻比在攻角12°之前小于单一全动舵的升阻比。故对于一些长期工作在低攻角状态下的AUV或是对AUV升阻比要求较高的,不适于采用增加固定舵的方式保护全动舵。随着攻角的增大,无固定舵片的全动舵升阻比在攻角12°之后开始小于有固定舵片的尾舵。攻角在15°之后无固定舵的尾舵阻力一直大于安装固定舵的尾舵,升力曲线中也可以看出升力远小于安装固定舵的尾舵。
|
图 6 不同攻角下的阻力变化曲线 Fig. 6 Resistance curve at different angles of attack |
对于安装固定舵的尾舵模型,分别取两舵间距3,4,5,6,7,8作为研究对象,分析出6种间距模型在不同状态的升阻比。可以看出两舵间距对舵升阻比的影响较明显,而且两舵间距为6 mm的舵片模型升阻比一直高于其他间距的升阻比。所以对于安装固定舵保护全动舵的AUV建议将固定舵与全动舵之间的间隙保持6 mm。
图8为单一全动舵压强分布云图,图9为两舵间距6 mm时压强分布图,两图都是全动舵攻角为15°时的压强云图。从图8可以看出舵片前缘迎流面与背流面两侧的压力分布相反且压强值较大,而到了尾舵后缘背流面出现了较大压强值说明尾舵后缘出现绕流现象。

|
图 8 全动舵压强分布云图 Fig. 8 Pressure distribution of all-movable rudder |
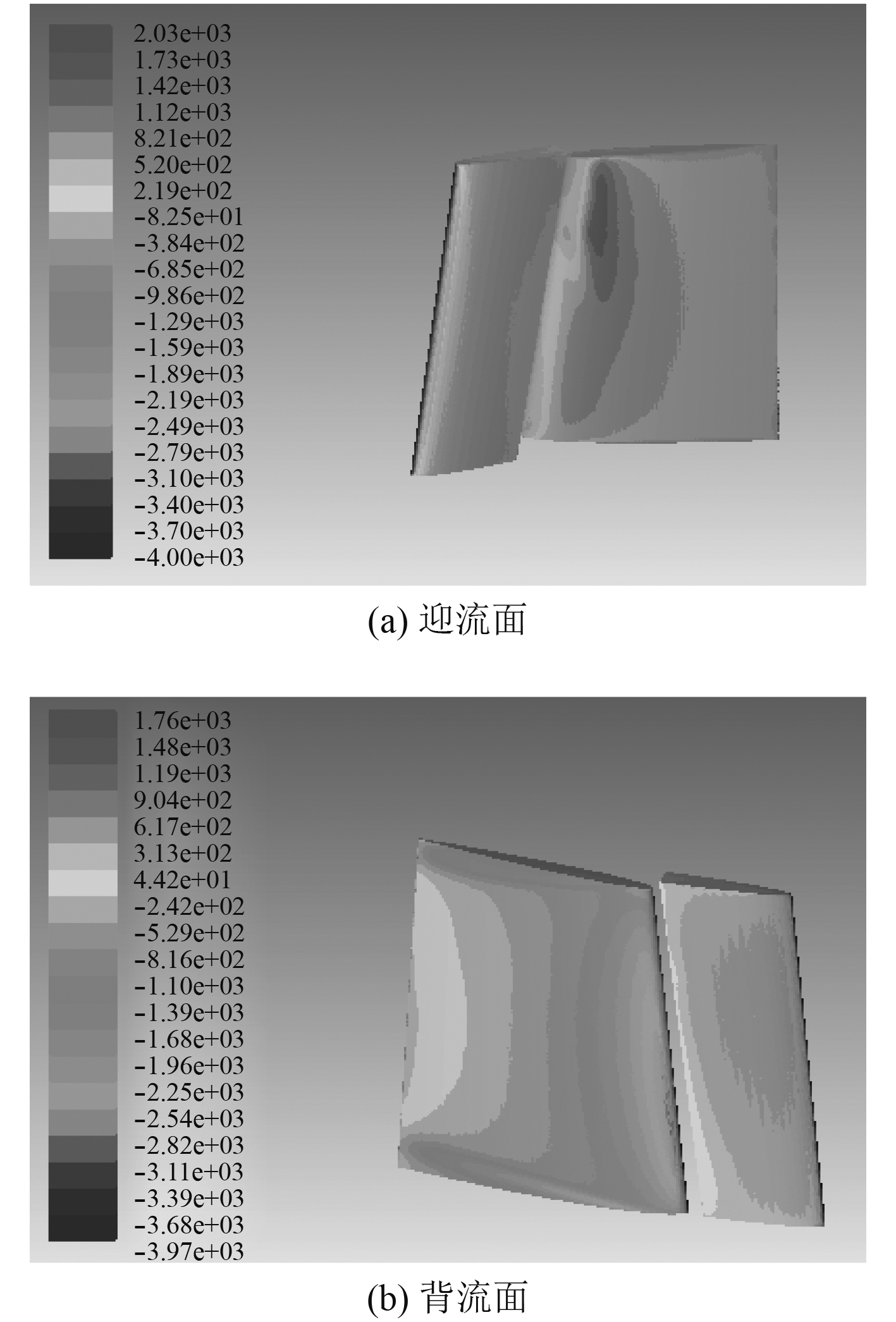
|
图 9 两舵间距6 mm时压力分布云图 Fig. 9 Pressure distribution at a distance of 6 mm between the two rudders |
综合以上可知,单一全动舵的最大压强值出现在舵片前缘而安装固定舵片的模型在固定舵的前缘出现了最大压强值而不是全动舵的前缘。固定舵前缘的大压力导致了大阻力的产生。安装有固定舵片的尾舵迎流面压强较大,而且固定舵片的迎流面压强也大于背流面,说明此时的固定舵片也可以提供一部分升力。
为了确认固定舵片的增加对整个系统的影响是否和速度有关,本文对舵片攻角20°的2种模型(单一全动舵模型和安装固定舵且固定舵与全动舵间距为6 mm的模型)在不同速度下进行了对比分析得到数据如表1所示。
|
|
表 1 两种舵片模型在不同速度下的升阻比对比表 Tab.1 Comparison of lift-drag ratio of two rudder blade models at different speeds |
可以看出,单一全动舵的升阻比随着速度升高略有升高,安装固定舵片的升阻比也随着速度的升高略有升高且始终大于单一全动舵升阻比。由图可知,整个系统的升阻比只和是否增加固定舵片以及全动舵的攻角大小有关,故固定舵片引起的升阻比升高和速度无关。
4 铰链力矩分析铰链力矩是指流过片的流体对舵轴形成的力矩。执行机构一般是通过机械传递控制舵片的偏转,为了使舵面偏转到需要的位置,必须克服作用在舵轴上的铰链力矩。铰链力矩越大则舵的偏转速度越小,航行器对控制的反应越慢[14]。为了研究保护舵的增加对铰链力矩的影响,本文选取无保护舵模型和间距为6 mm的两舵模型进行对比分析,结果如图10所示。
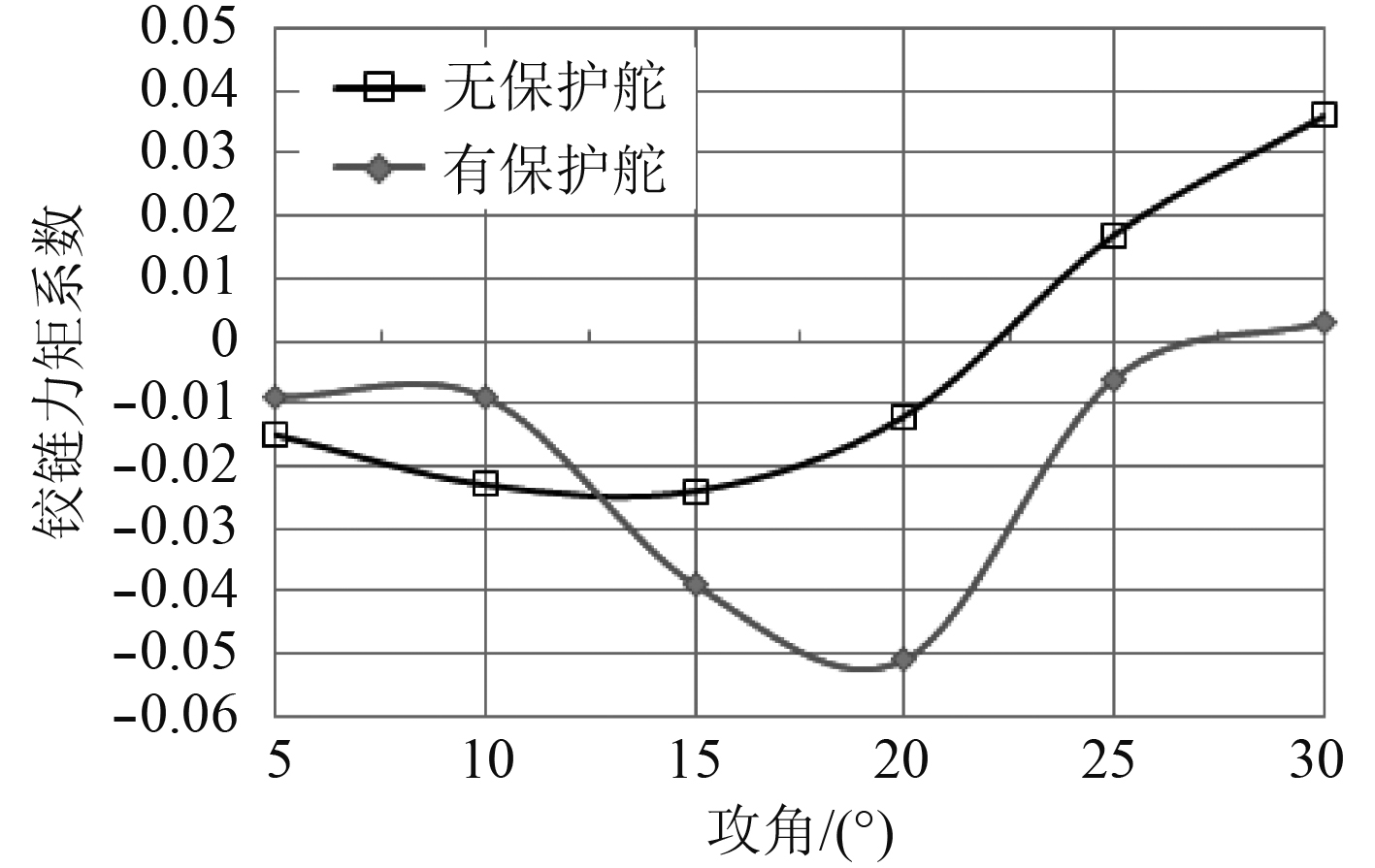
|
图 10 不同攻角下的铰链力矩系数变化曲线图 Fig. 10 Hinge moment coefficient curve under different angles of attack |
可以看出,单一全动舵的铰链力矩系数变化较平稳,约22°以后出现随攻角快速增大现象。有保护舵的模型铰链力矩系数约在12°~25°之间大于无保护舵模型,且变化率较为明显。最大铰链力矩系数出现在20°左右。综上所述,保护舵片的增加增大了系统的铰链力矩且在15°~25°之间变化较大。
5 结 语本文运用CFD数值计算方法对固定舵片与全动舵片的不同安装缝隙进行研究,分析了在2 m/s的速度下固定舵片与全动舵片之间的缝隙大小对整体升力、阻力以及升阻比的影响,进而分析出固定舵片与全动舵的最佳安装缝隙,为AUV设计保护舵片提供一定的参考。通过仿真数据比对两舵片的不同安装缝隙以及不同的攻角得出以下结论:
1)当全动舵片攻角小于12°时,固定舵片的增加虽没有对全动舵的升力产生影响却导致全动舵的阻力增加,故安装固定舵片系统在全动舵攻角小于12°时会降低系统整体性能。
2)当全动舵片攻角大于12°时,安装固定舵片的模型升力开始大于单一全动舵模型,且在15°之后阻力开始小于单一全动舵,使得整个系统的升阻比大幅提升,所以安装固定舵片系统在全动舵攻角大于12°时有利于提高系统性能。
3)对于需安装固定舵片保护全动舵的AUV建议将两舵片的缝隙定为6 mm,6 mm的间距使得大部分攻角的升阻比都大于其他间距。
4)保护舵片的增加增大了系统的铰链力矩,最大铰链力矩出现在20°左右。
| [1] |
BLIDBERG D R. The development of autonomous underwater vehicles(AUV). A brief summary[C]//International Conference rob. Autom. (ICRA), seoul, 2001.
|
| [2] |
陈强, 张林根. 美国军用UUV现状及发展趋势分析[J]. 舰船科学技术, 2010, 32(7): 129-134. DOI:10.3404/j.issn.1672-7649.2010.07.026 |
| [3] |
MEAHMED A. DUAN W. Overview on the development of autonomous underwater vehicles (AUVs)[J]. Journal of Ship Mechanics, 2016, 20(6): 768-787. |
| [4] |
张铭钧, 张仁存, 李广君, 等. 水下机器人[M]. 北京: 海洋出版社, 2000.
|
| [5] |
王鹏, 宁腾飞, 杜晓旭, 等. 带复杂外形附体的AUV流体动力数值计算[J]. 兵工学报, 2013, 34(2): 223-228. |
| [6] |
CHYBA M. Autonomous underwater vehicle[J]. Ocean Engineering, 2009, 36(1): 1. DOI:10.1016/j.oceaneng.2008.12.005 |
| [7] |
王鹏, 翟继莹, 宁腾飞. 带复杂外形附体的AUV悬臂水池数值计算[J]. 西北工业大学学报, 2013, 315(5): 764-769. DOI:10.3969/j.issn.1000-2758.2013.05.017 |
| [8] |
刘江波, 周玉龙, 李密, 等. 敞水舵水动力学的数值模拟[J]. 船舶工程, 2008, 30(1): 8-10. DOI:10.3969/j.issn.1000-6982.2008.01.008 |
| [9] |
马玉成, 林俊兴, 赵阳. 敞水舵水动力数值计算及分析[J]. 中国水运, 2008, 8(12): 1-4. DOI:10.3969/j.issn.1006-7973-B.2008.12.001 |
| [10] |
谢俊超. 襟翼舵设计计算及水动力性能仿真研究[D]. 武汉: 武汉理工大学, 2011: 8-10.
|
| [11] |
武建国, 张宏伟. 小型自主水下航行器尾舵设计与研究[J]. 海洋技术, 2009, 28(3): 5-8. DOI:10.3969/j.issn.1003-2029.2009.03.002 |
| [12] |
CHEN C W, JIANG Y, HUANG H C, et al. Computational fluid dynamics study of motion stability on an autonomous underwater helicopter[J]. Ocean Engineering, 2017(43): 227-239. |
| [13] |
ZHENG H B, WANG X, XU Z B. Study on hydrodynamic performance and CFD Simulation of AUV[C]//IEEE International Conference on Information and Automation(ICIA). 2017.
|
| [14] |
李军. 鱼雷舵铰链力矩计算[J]. 鱼雷与发射技术, 2004, 1: 30-32. |
 2020, Vol. 42
2020, Vol. 42
