2. 船舶振动噪声重点实验室,湖北 武汉 430033;
3. 海军驻大连四二六厂军事代表室,辽宁 大连 116000
2. National Key Laboratory on Ship Vibration and Noise, Wuhan 430033, China;
3. Navy Force Representative Bueau in Dalian 426 Factory, Dalian 116000, China
随着舰船减振需求的不断提高,具有强大的位移补偿能力,小尺寸和优异的性能挠性接管被大量使用于船上[1]。其中弧形管指一种管体呈弧形的挠性接管,它在较小的空间内具有更强的位移补偿能力。疲劳破坏是弧形管损坏的一种失效方式,它指的是弧形管在外界应力或应变作用下伴随着疲劳过程的不断加深最终出现橡胶管体损伤的现象。在现有工程实践中,采用的疲劳可靠性评估方法一般为从一批成管中抽取几根进行给定次数的疲劳试验若为出现破坏则认为其具有一定可靠性,此法试验时间长并且因为其未从机理上分析疲劳失效原因,可置信性比较差。在汽车行业中,裂纹萌生法因其简单快速的特性而广泛用于橡胶疲劳寿命研究,该方法基于连续介质力学,从橡胶裂纹产生的机理出发,解释了疲劳失效的机理[2,3],即橡胶产品本身存在很多内部缺陷,在疲劳载荷的作用下,内部缺陷逐渐扩展至一定程度出现破坏,宏观上表现为橡胶制品出现裂纹。同时该方法将有限元方法和材料级别的拉伸疲劳试验结合起来直接预测得到弧形管的疲劳寿命,大幅减少元器件级别的疲劳试验时间,具有简便快捷,易于计算的优点。
本文对以弧形管为研究对象,采用裂纹萌生法研究探索了一种弧形管疲劳寿命预测方法,研究结果可用于指导弧形管疲劳可靠性设计。
1 橡胶材料本构模型为了建立准确可靠的有限元模型,需要对弧形管用橡胶材料的本构力学行为进行研究。针对橡胶材料复杂的力学行为,国内外学者利用应变能函数来表征橡胶材料的本构行为。在连续介质力学理论中,橡胶材料被认为是各项同性的超弹性材料,确定应变能和伸长率的关系,便可确定应力-应变关系。Ogden是一种常用的本构模型[4]:
| $ W \!=\! \sum\limits_{i = 1}^N {\frac{{2{\mu _i}}}{{{\alpha _i}^2}}} \left( {{\lambda _1}^{\overline {{\alpha _i}} } + {\lambda _2}^{\overline {{\alpha _i}} } + {\lambda _3}^{\overline {{\alpha _i}} } - 3} \right) \!+\! \sum\limits_{i = 1}^N {\frac{1}{{{D_i}}}{{\left( {J - 1} \right)}^{2i}}}\text{。} $ | (1) |
式中:
本文弧形管用橡胶进行了单轴条件下、等双轴条件下、平面条件下3种拉伸本构试验。
利用Abaqus有限元软件自带的拟合功能,发现Ogden三阶模型具有最佳的拟合效果(见图1),因此选择它作为本橡胶材料的本构模型。该模型的拟合参数为:
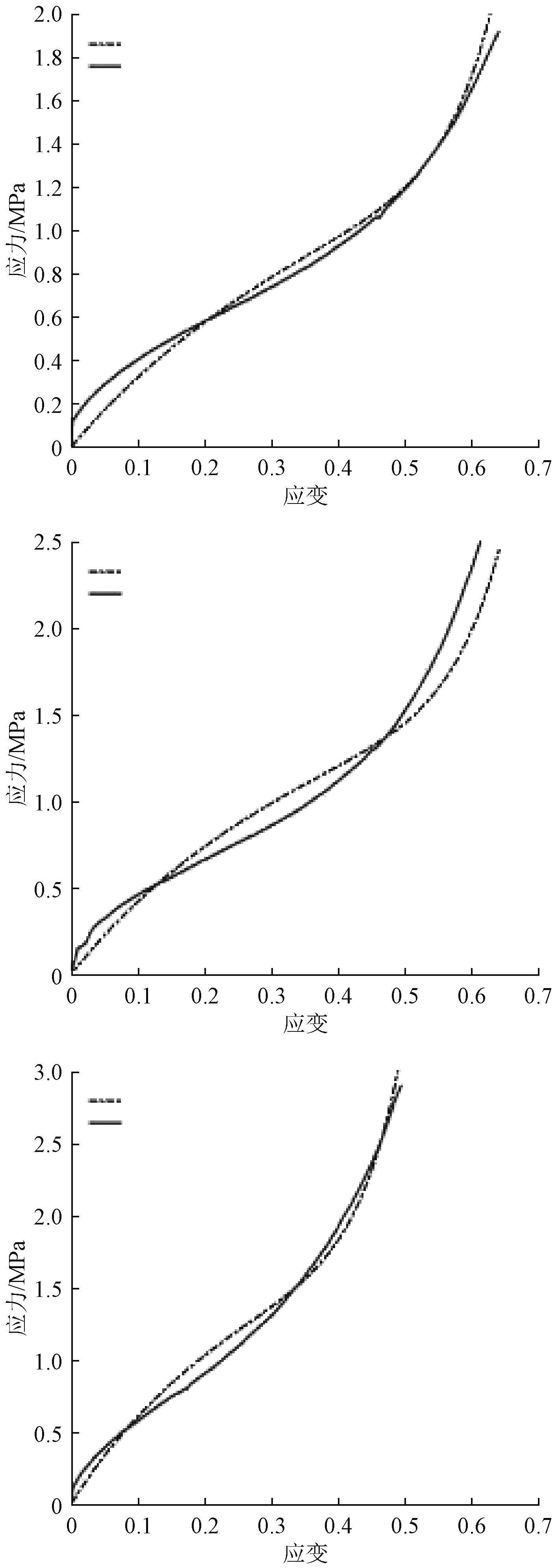
|
图 1 三阶Odgen模型拟合结果 Fig. 1 Fit result by 3 order Odgen model |
在裂纹萌生法中,疲劳寿命通常是通过疲劳损伤参量表征的,疲劳损伤参量一般可以基于应变:应力和能量给出,其表征了初始裂纹的产生是否苛刻。
2.1 基于应变的疲劳损伤参量以图2的均匀拉伸橡胶杆件为例,杆件未拉伸前的初始长度记为L,拉伸后的长度为

|
图 2 单轴应力状态的橡胶杆件 Fig. 2 Rubber rod in uniaxial tension deformation state |
| $ \lambda = \frac{l}{L},{x_2} = {\lambda ^{ - \frac{1}{2}}}{X_2},{x_3} = {\lambda ^{ - \frac{1}{2}}}{X_3}\text{。} $ | (2) |
其中,
最大主Green-Lagrange应变
| $ {\varepsilon }_{A}={e}_{11}=\frac{{\lambda }^{2}-1}{2{\lambda }^{2}} \text{,}$ | (3) |
| $ {\varepsilon }_{G}={E}_{11}=\frac{{\lambda }^{2}-1}{2} \text{。}$ | (4) |
其中:
工程应变
| $ {\varepsilon }_{E}=\lambda -1\text{,} $ | (5) |
主对数应变
| $ {\varepsilon }_{L}={\int }_{L}^{l}\frac{{\rm d}l}{l}=ln\left(\frac{l}{L}\right)=ln\left(\lambda \right)\text{,} $ | (6) |
八面体切应变
| $ {\varepsilon }_{o}=\frac{\sqrt{2}}{3}\left|{\lambda }^{2}-{\lambda }^{-1}\right|\text{。} $ | (7) |
应变能密度的峰值也常被用来选作橡胶材料的疲劳损伤参量。应变能密度(W)的定义式为:
| $ {\rm d}W=\sigma \cdot {\rm d}\varepsilon $ | (8) |
其中,σ和ε为一组共轭且功能完全确定一点应力和应变状态的应力张量和应变张量。
对于单轴应力状态,上式为
| $ W={\int }_{0}^{{\varepsilon }_{E}}{\sigma }_{E}{\rm d}{\varepsilon }_{E} \text{,}$ | (9) |
其中,
Mars[6]通过研究发现应变能密度峰值与工程应变峰值之间存在着幂函数关系。本文测试了4种工程应变水平下的应力应变曲线,在经过5次循环后取最后一个循环加载段的曲线。将试验数据导入Matlab中,通过梯形数值积分函数TRAPZ对其进行积分求得对应的应变能密度峰值。基于非线性最小乘法得到的拟合模型如图3所示,其数学表达式为:
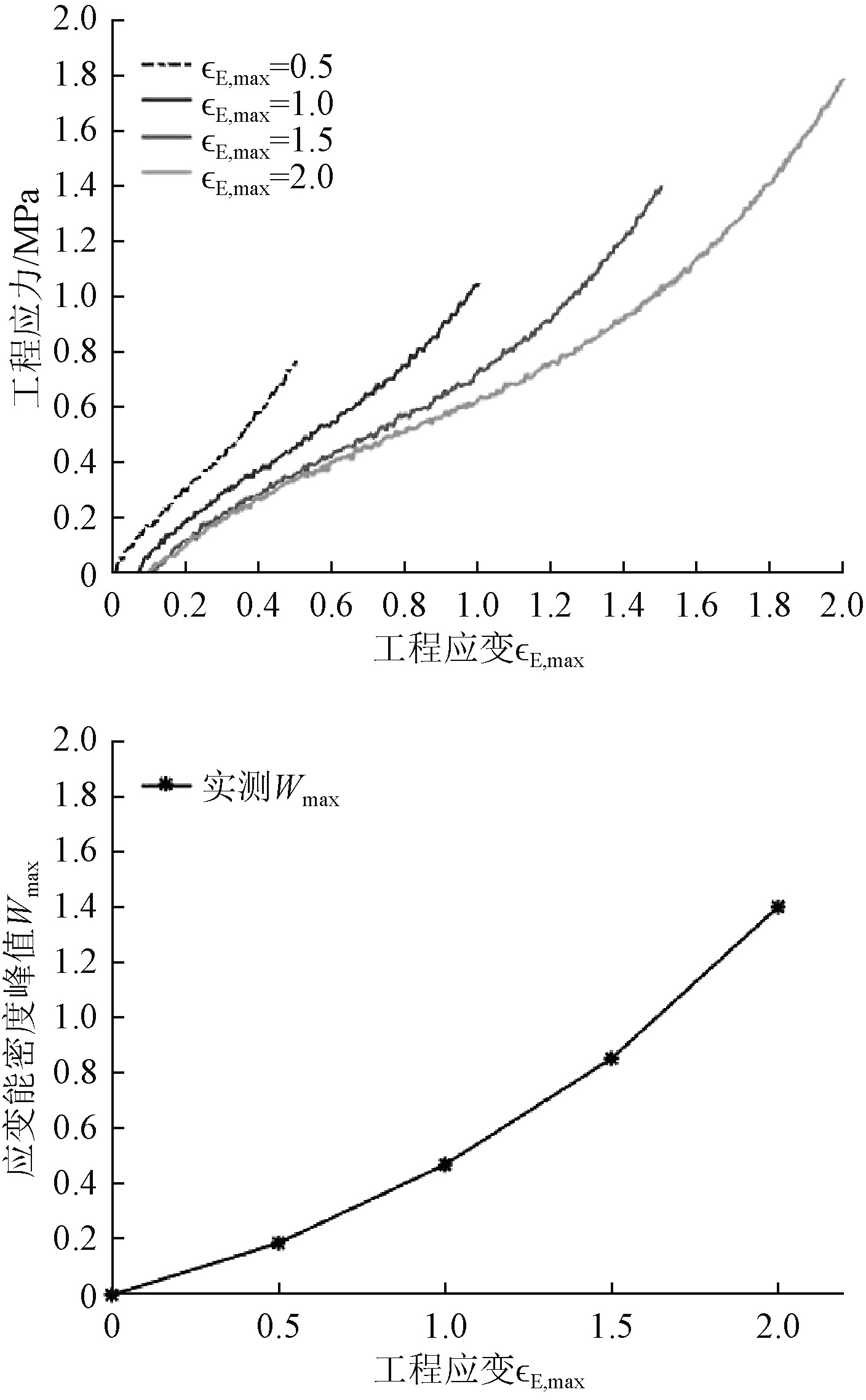
|
图 3 单轴拉伸试验结果及拟合结果 Fig. 3 Strain energy density experimental data |
| ${W_{\max }} = 0.4671{({\varepsilon _{E,\max }})^{1.57}}{\text{。}}$ | (10) |
式(10)的拟合精度为0.998 5,较为接近1,说明该模型精度较高,是可取的。
3 疲劳寿命预测模型的建立在裂纹萌生法中,为了构建疲劳损伤参量与疲劳寿命之间的关系,需要对橡胶材料哑铃型试片进行单轴拉伸疲劳试验。拟合得到疲劳损伤参量与疲劳寿命之间的数学关系,即疲劳寿命预测模型。
3.1 单轴拉伸疲劳试验本次橡胶材料的疲劳性能的试验研究参照《GT/T 1600-2008 硫化橡胶伸张疲劳的测定》,试验试样为哑铃型试片。在单轴循环应变载荷的作用下,将样品反复拉伸至断裂。样品循环的应变比为0,样品断裂时记录的循环次数为疲劳寿命。本次试验一共开展了5种不同拉伸载荷工况下的疲劳试验,应变幅值分别为80%,100%,120%,140%,160%,各个工况下测试试片数量为12片。记录每一组中哑铃型试样中间狭长部位断裂时试验的循环次数,若试件在非狭长部分断裂,则剔除此样件。
根据ASTM标准,橡胶材料的疲劳寿命服从对数正态分布,平均寿命的计算公式为:
| ${\log _{10}}({N_e}) = \sum\limits_{i = 1}^n {{{\log }_{10}}({N_i})/n} \text{。}$ | (11) |
式中:n为相同载荷工况的一组数据经去除离散数据后剩余的个数;
|
|
表 1 橡胶哑铃型试件片拉伸疲劳试验结果 Tab.1 Tensile fatigue results of rubber |
表中Nf,max,Nf,min表示每种载荷条件下测量的12个橡胶试样的最大值和最小值。Nf,min/Nf,max的大小体现试验结果的分散性。从试验结果可以看出,橡胶拉伸疲劳试验的分散度在(2.38,6.71)之间,基本满足橡胶材料疲劳寿命分布要求。
3.2 疲劳寿命预测模型根据相关文献,疲劳裂纹萌生寿命与疲劳损伤参量之间通常满足幂律[7]:
| $P = K{({N_f})^b}\text{。} $ | (12) |
其中:
|
|
表 2 疲劳寿命模型拟合结果 Tab.2 Fitting results of fatigue life model |

|
图 4 寿命预测模型拟合结果 Fig. 4 Life prediction model fitting result |
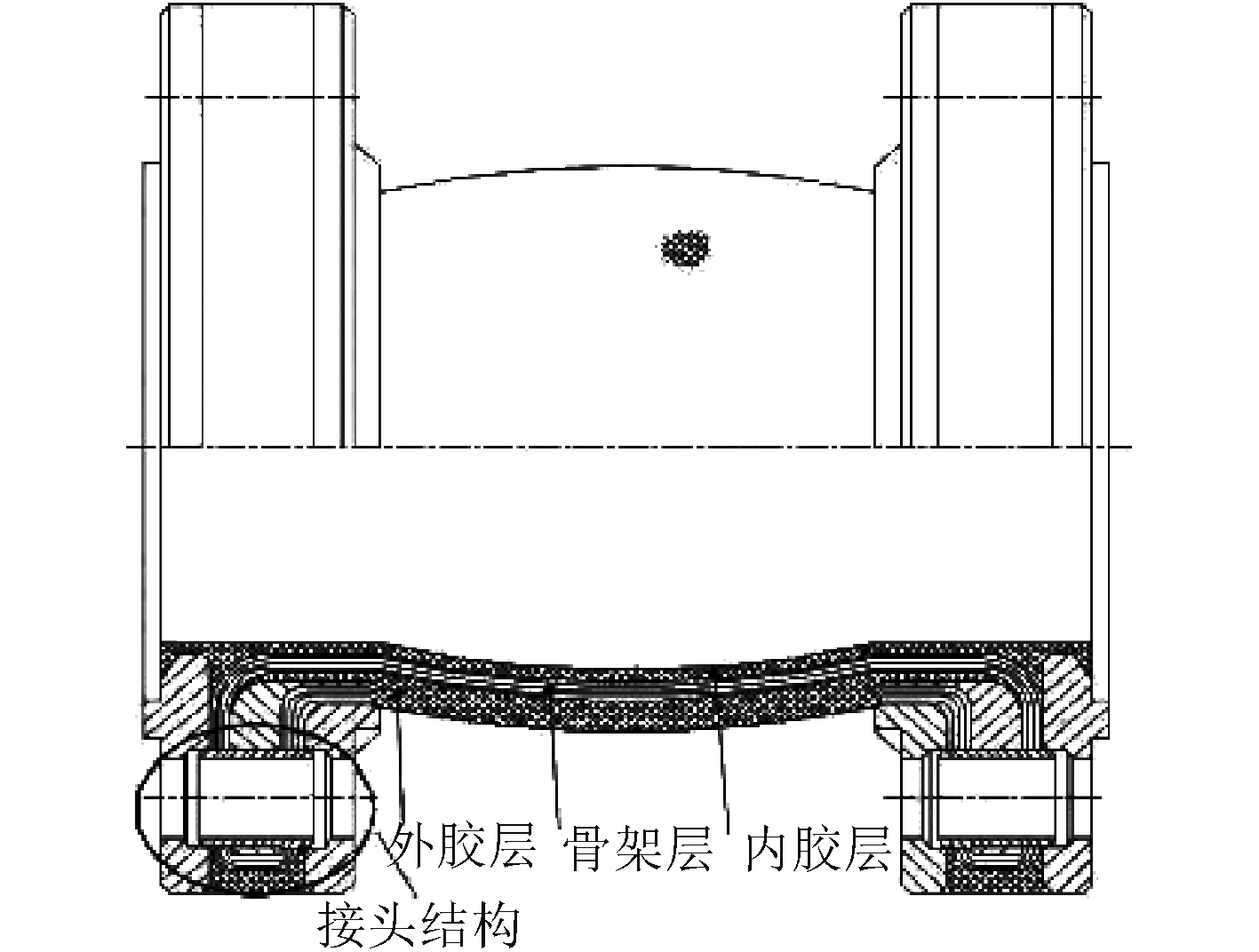
|
图 5 弧形管结构和管体模型 Fig. 5 Flexible pipe structure and model |
可以看出,不同的疲劳损伤参量拟合得到的寿命预测模型大相径庭,其中
弧形体挠性接管主要由內胶层,芳纶帘线骨架层,外胶层和法兰接头4个部分组成[8-9]。骨架层是由芳纶帘线组成,是主要的承载部件,包在内外胶层之间,分为多层,各层严格按照一定角度交叉包覆,呈现出各向异性的特点。各胶层使用的橡胶是含有各种填料的氯丁橡胶。
在有限元软件Abaqus中选用Rebar单元M3D4R来模拟帘线、三维应力单元C3D8RH来模拟橡胶、三维应力单元C3D8R来模拟上下盖板。帘线材料按照刚性材料定义,杨氏模量为33.882 GPa,泊松比为0.3。缠绕角度理论缠绕等效缠绕平衡角度52°进行布置,在此缠绕角度下,仅受内压时,弧形管将不会产生轴向力和位移,具有较好的平衡性。因为帘线层包络在内外橡胶层中,所以在Abaqus中采取内置区域定义橡胶层和帘线层之间的关系。橡胶材料选用超弹性本构模型,本构模型参数按选用前文建立的本构模型——三阶Odgen模型中的参数。由于本文不考虑盖板的影响,故将上下盖板都设置为刚体。
将该有限元模型的刚度仿真结果与刚度特性试验结果进行比较发现相对误差不超过5%,一致性较好,故仿真可代替试验进行下一阶段研究。
有限元仿真模型的精度决定了仿真结果是否可信,其影响因素有很多如网格划分的质量,本构模型的选用等。通过橡胶本构试验拟合得出的Odgen三阶模型大大提高了有限元模型精度,刚度试验与仿真值的对比也反映出此现象。
4.2 基于有限元的寿命评估对DN80弧形管拉压载荷工况下的疲劳特性进行了预测。本文主要考虑橡胶部分的疲劳失效,提取出橡胶部分拉压疲劳应变云图如图6所示,将提取出的应变代入前文所求寿命预测模型,得到了寿命预测值(见表4)。
|
|
表 4 拉压疲劳寿命预测值 Tab.4 Predicted value of fatigue life |

|
图 6 拉压疲劳应变云图 Fig. 6 Tensile fatigue strain cloud |
|
|
表 3 载荷工况 Tab.3 Load condition |
由上述结果可见,在采用不同的疲劳损伤参量对目标工况进行寿命评估时,实验结果出现一定的分散性。尽管各个疲劳损伤参量拟合精度都达到了0.97以上,但是由于单轴拉伸试验的最低工程应变量仅为0.8,而上述目标工况的最小的工程应变峰值可达到0.352,这可能是导致分散性的原因之一。
4.3 验证试验为缩短试验时长,节省试验成本,选择载荷幅值作为加速因子进行加速拉压疲劳试验,位移载荷幅值为30 mm,内压为0 MPa。当进行了3.3万个加载循环后,弧形管外胶层与法兰连接处的橡胶层出现破坏,破坏位置与仿真结果基本相同。
通过有限元仿真可知在该载荷条件下的最大主应变为1.365,选用表2中拟合效果最好的最大主伸长率
1)针对以往弧形管可靠性检测中存在的试验成本高,置信度差的缺点,且未从失效机理进行分析探索的缺点,本文将汽车行业橡胶志平中常用的裂纹萌生法用于弧形管寿命预测,成功预测了弧形管拉压疲劳寿命,并通过加速试验验证了该试验方法的正确性。
2)由于寿命预测模型在进行实际预测时外推范围较大,因此本文为了减少因外推带来的误差选择了拟合程度最高的最大主伸长率作为疲劳损伤参量。没有具体理论支撑应如何选择疲劳损伤参量才能较好进行寿命预测,这是值得进一步探索的。
| [1] |
赵应龙, 何琳. 橡胶挠性接管特性研究[J]. 海军工程大学学报, 2001(1): 15. ZHAO Yin-long, HE-Lin. A study of the characteristics of rubber flexible pipes[J]. Journal of naval university of engineering, 2001(1): 15. |
| [2] |
王小莉. 防振橡胶材料疲劳寿命研究方法综述[J]. 河北科技大学学报, 2016, 37(3). WANG Xiaoli. A review on fatigue life prediction methods for anti-vibration rubber materials[J]. Journal of Hebei University of Science and Technology, 2016, 37(3). |
| [3] |
上官文斌, 李明敏, 段小成, 等. 动力总成橡胶悬置高温疲劳特性的预测与试验研究[J]. 振动与冲击, 2015, 34(15): 66-71. SHANGGUAN Wen-bin, LI Ming-min, DUAN Xiaocheng, et al. Fatigue life prediction and tests for rubber mounts under high temperature[J]. Journal of vibration and shock, 2015, 34(15): 66-71. |
| [4] |
BONET J, WOOD R D. Nonlinear continuum mechanics for Finite Element Analysis[M]. Cambridge: Cambridge University Press, 1997.
|
| [5] |
王小莉. 橡胶隔振器多轴疲劳寿命预测方法研究[D]. 广州: 华南理工大学, 2014.
|
| [6] |
MARS W.V, FATEMI A. Factors that affect the fatigue life of rubber: A literature survey[J]. Rubber Chemistry and Technology, 2004, 76: 391-412. |
| [7] |
帅长庚. 肘形挠性接管设计理论、试验方法及工艺研究[D]. 武汉: 海军工程大学, 2005.
|
| [8] |
何琳, 帅长庚, 周炜. JYXR系列舰用挠性接管研究[J]. 舰船科学技术, 2006, 28(S2): 121. HE Lin, SHUAI Changgeng, ZHOU Wei. Study on flexible pipe of JYXR series used in ship[J]. Ship Science and technology, 2006, 28(S2): 121. |
| [9] |
金著, 赵应龙, 何琳. 膜式气囊隔振器帘线缠绕角研究[J]. 舰船科学技术, 2015, 37(12): 63-67. JIN Zhu, ZHAO Ying-long, HE Lin. Research on the cord′s wound angle in reversible sleeve air spring[J]. Ship Science and technology, 2015, 37(12): 63-67. DOI:10.3404/j.issn.1672-7649.2015.12.013 |
 2020, Vol. 42
2020, Vol. 42
