0 引　言

舰炮发射率高，发射时后坐部分的后坐行程相对短，后坐复进时间短，后坐阻力相对较大。发射瞬时后坐部分能量通过反后坐装置提供的后坐阻力做功吸收，而反后坐装置产生的后坐阻力则经由摇架、耳轴传递到炮架上，并经过对炮架的冲击作用后传递到舰艇甲板基座。炮架作为舰炮的主承力结构，上部支撑发射系统等部组件，下部通过转盘轴承与舰艇甲板基座固连。炮架在舰炮发射时后坐阻力激励下的动态应力、动态变形对舰炮射击精度具有一定影响，动态加速度对安装在炮架上的电子元器件、机构、零件等的抗加速度冲击有着一定影响，后坐阻力通过炮架弹性变形吸能进而传递到甲板基座对舰炮的适装性有着一定影响。因此，舰炮炮架在舰炮总体设计中占有重要位置，设计之初即分析后坐阻力激励下舰炮炮架的响应对实现舰炮的技术指标、提供甲板基座受力等安装要素具有重要意义。因使用环境、使命任务、使用方式等方面的不同，舰炮炮架设计与陆炮炮架有着较大差异。当前对于舰炮炮架的设计研究大多集中在静力分析方面，动态分析研究的文献尚不多见。文献[1-2]仅对舰炮炮架模态进行了分析，文献[3]基于Ansys软件对某舰炮托架的模态进行了分析，对后坐阻力激励下托架的动态响应进行了仿真。总体来看，对于后坐阻力激励下，整个舰炮炮架的响应分析工作很少涉及，对于后坐阻力传递到甲板基座上的作用力尚未见到研究文献。本文通过对舰炮炮架在后坐阻力激励下的响应分析，可以让设计人员加深对传统上视炮架为刚体、以最大后坐阻力校核设计带来的不足。同时，可以让设计人员对后坐阻力传递到甲板基座后的力的分布及其幅值提供途径，有助于对舰炮最大后坐阻力的理解与认识。

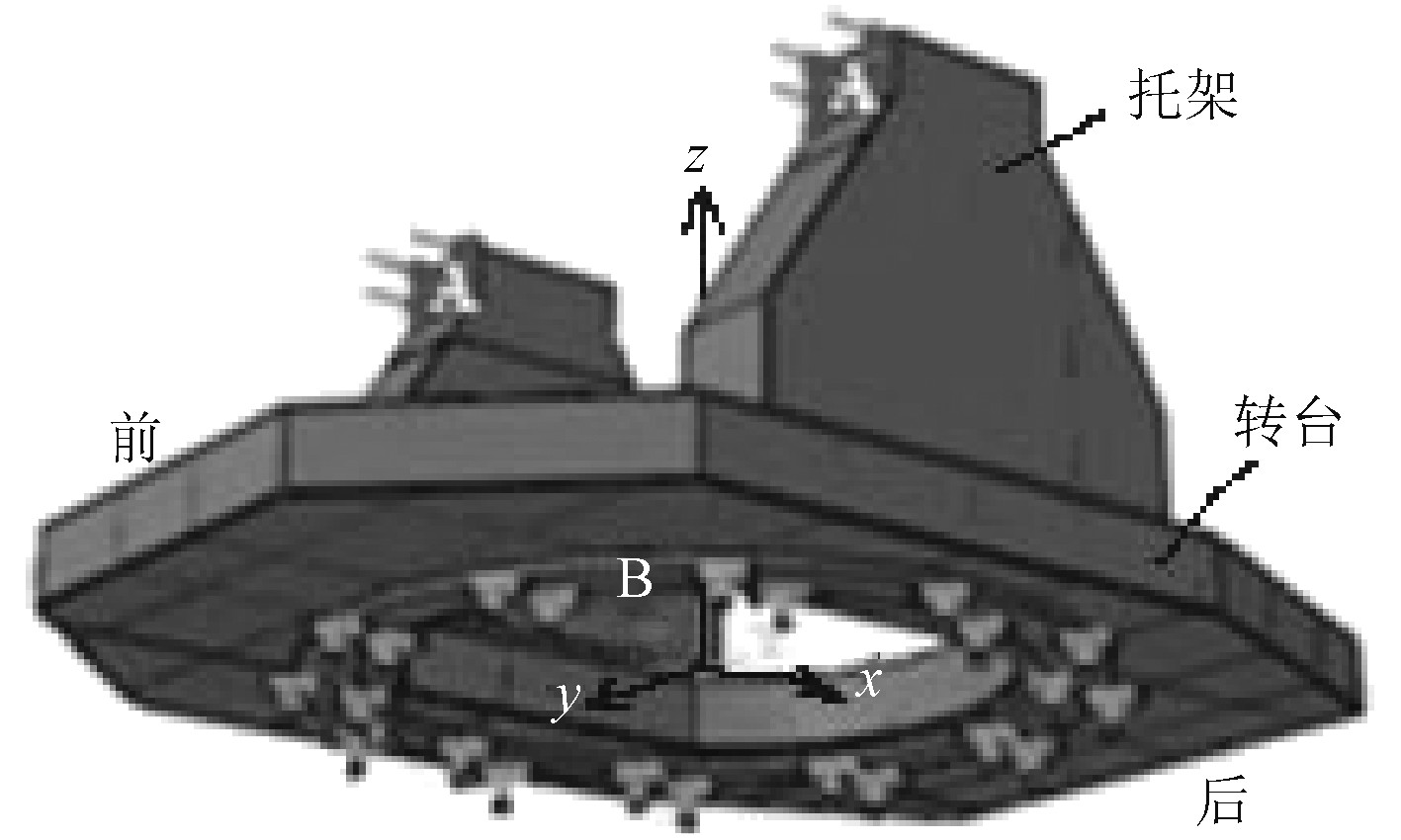
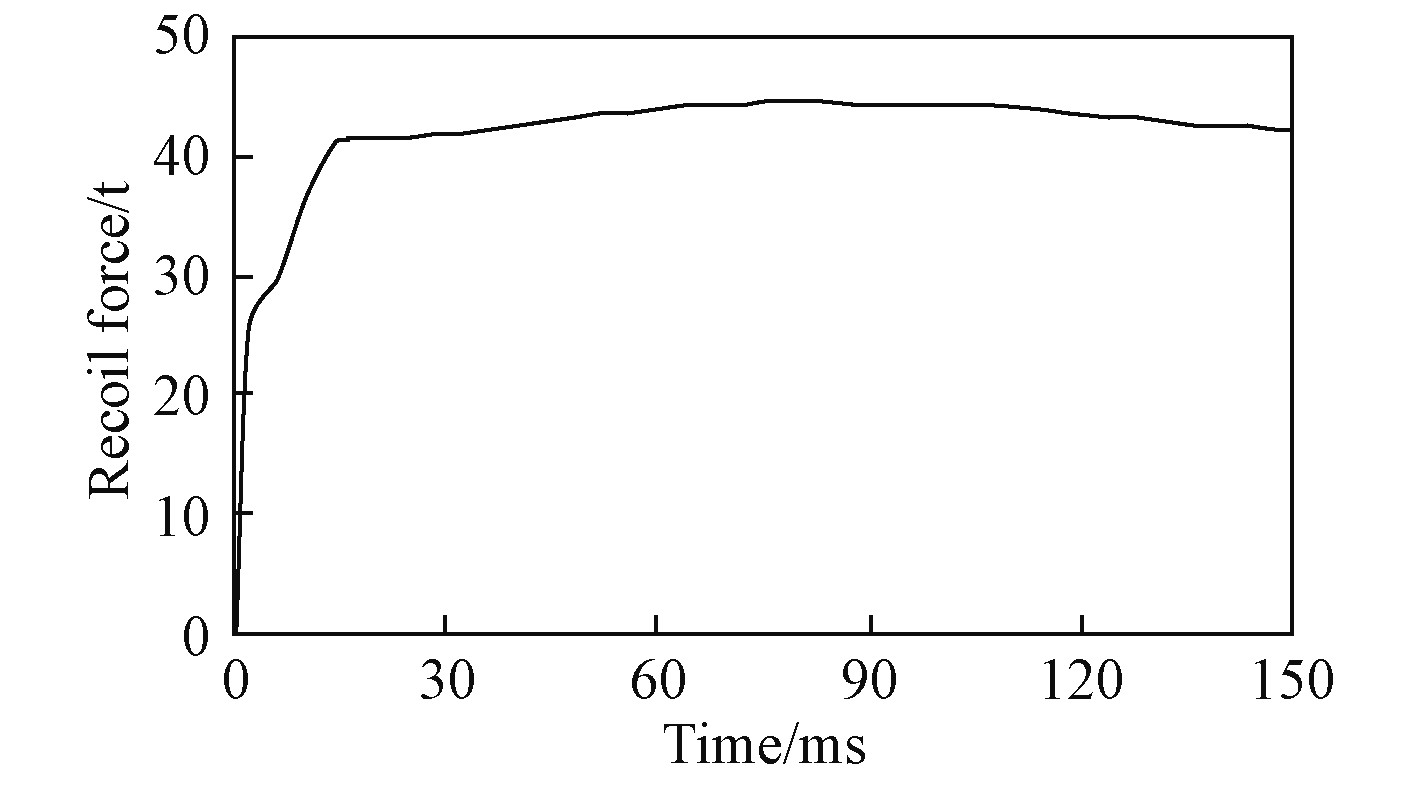
1 炮架模型与后坐阻力

炮架结构是根据舰炮总体功能、性能要求进行设计的。图1是其三维模型，以B面中心为坐标原点，垂直A面为x轴方向（等同1方向），平行于A面为y轴方向（等同2方向），垂直于B向上为z轴方向（等同3方向）。为研究方便对炮架模型进行了一定的简化处理，忽略了部分小尺寸结构，并将转盘轴承等效成结构体成为炮架的一部分。整个炮架材料为Q345，质量5.82 t。A面为水平射击时炮架承受后坐阻力的受力面，B面为与甲板基座配合的安装面。炮架长4 m，宽3 m，高1.74 m。A面总面积为0.08 m²，B面为一外径为Φ2.6 m、内径为Φ2.2 m的圆环。初始边界条件为水平射击，B面固支，A面受到随时间变化的后坐阻力，如图2所示。后坐总时间0.15 s，最大后坐阻力45 t。

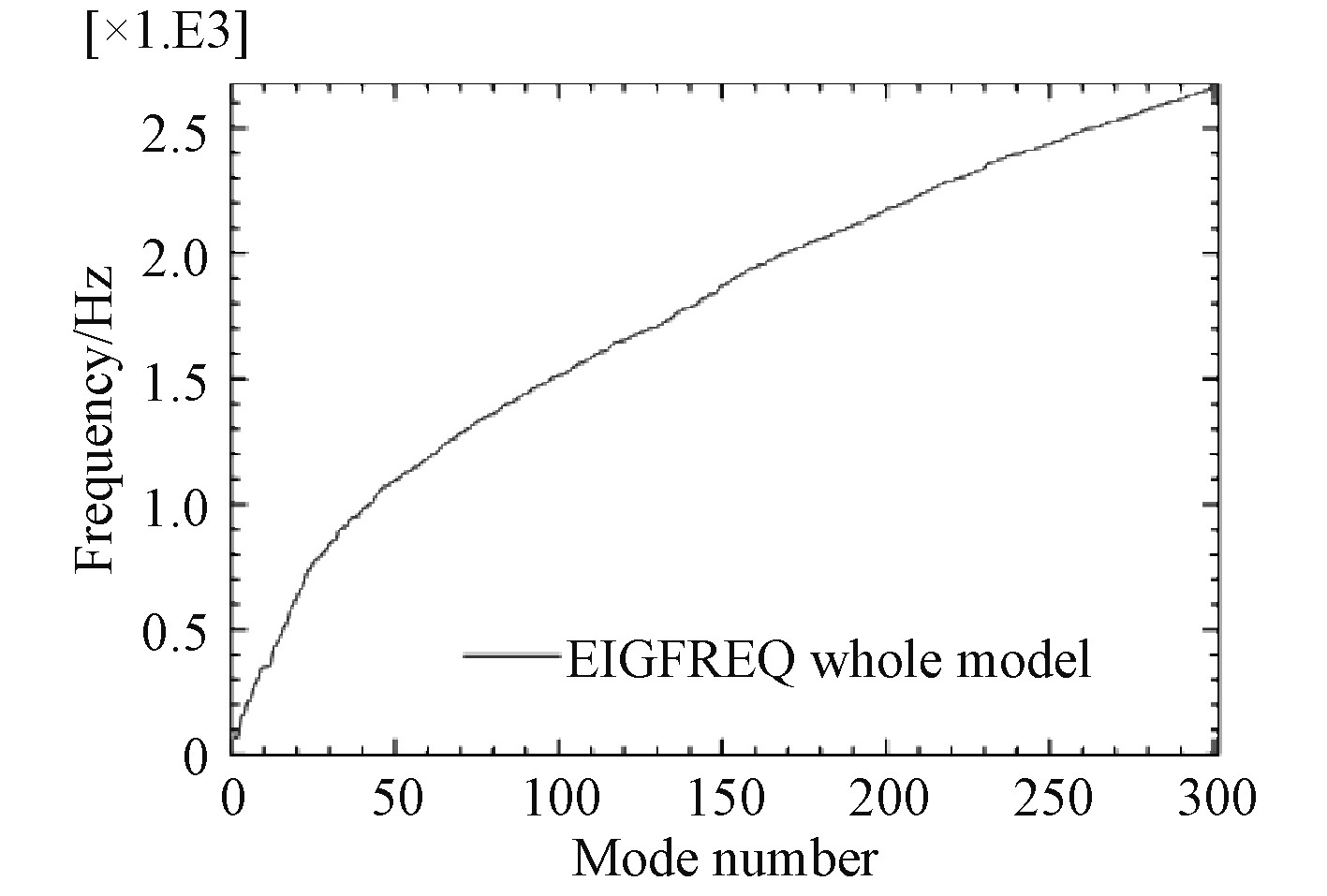
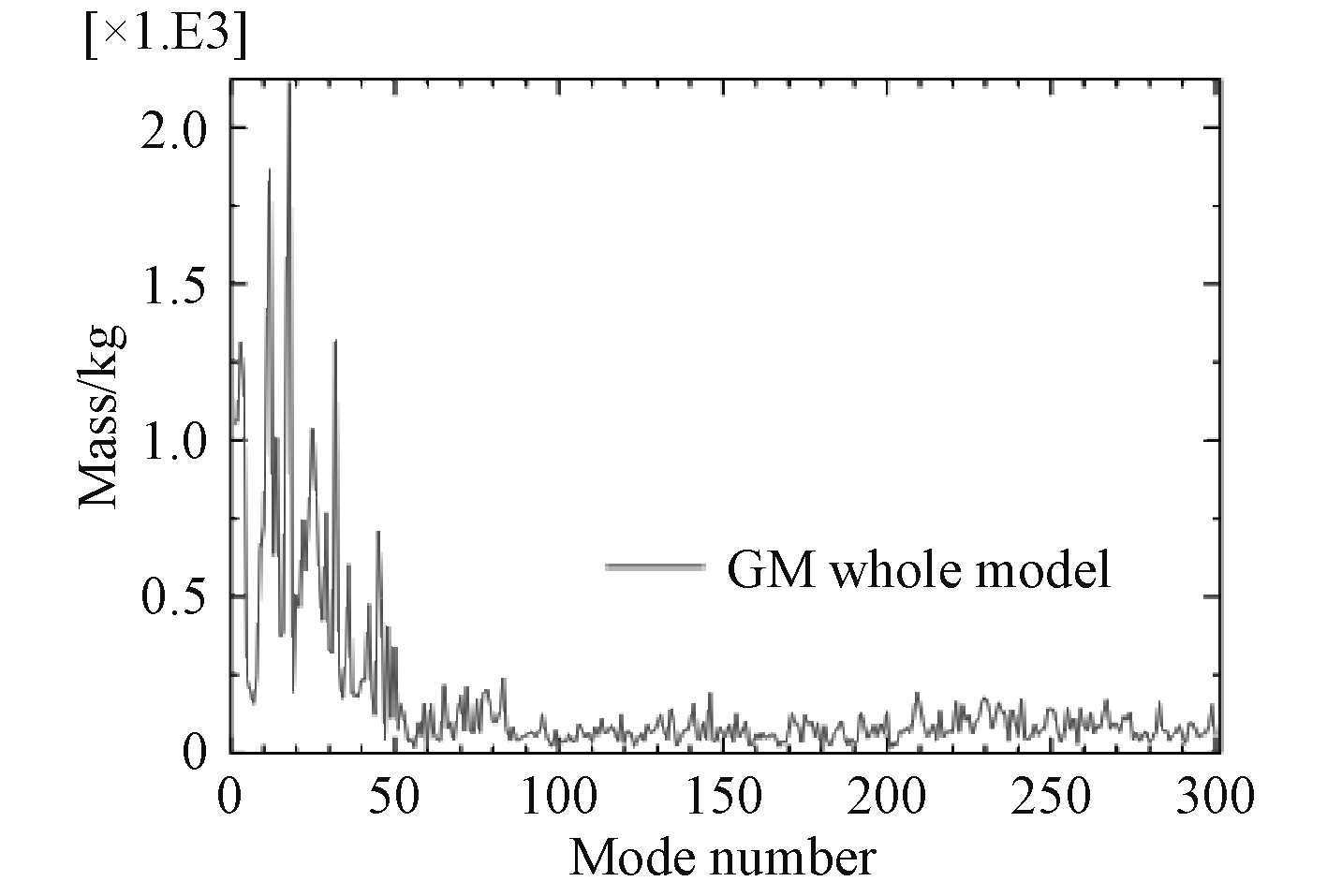
2 炮架模态分析

在对后坐阻力激励时炮架响应分析之前必须首先对炮架的固有模态进行分析。在确定结构的炮架模型及B面约束条件下，采用有限元软件的振型叠加法进行分析，为保证在频率提取分析步中提取了足够数量的模态，先按照300阶进行计算。分析得到的300阶固有频率曲线如图3所示，炮架前10阶固有频率依次为69.149，69.761，156.89，160.31，212.35，226.15，278.62，295.62，42.79，349.07 Hz，第43阶固有频率为1 004.4 Hz，第170阶固有频率为2 004.7 Hz，第300阶固有频率为2 662.8 Hz。图4为炮架固有频率阶次与有效质量的关系图，从中可以看出，前50阶固有频率对总有效质量超过了炮架模型可运动质量的85.6%以上，因此取50阶模态已足够使用振型叠加法求解炮架的动态问题。

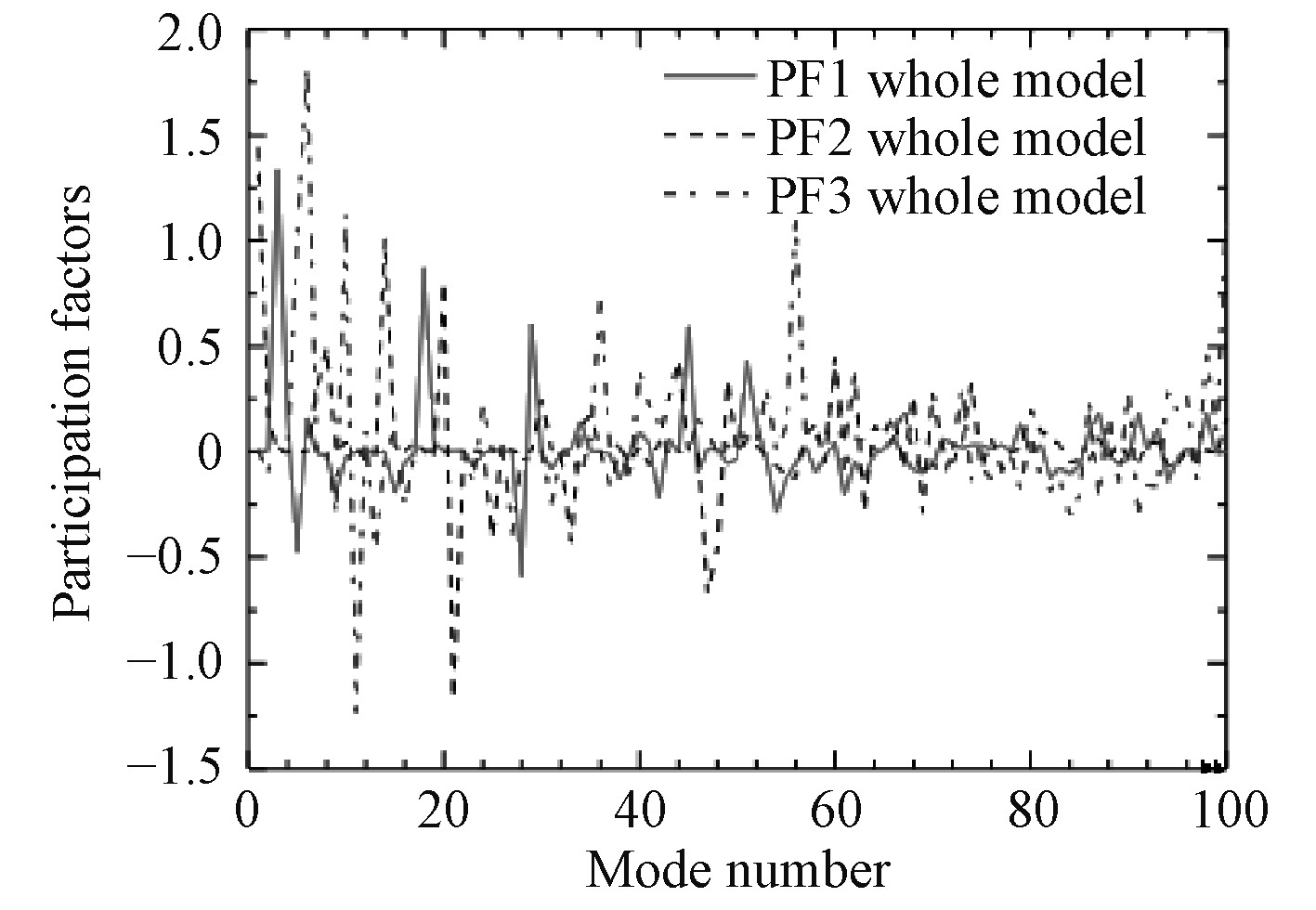
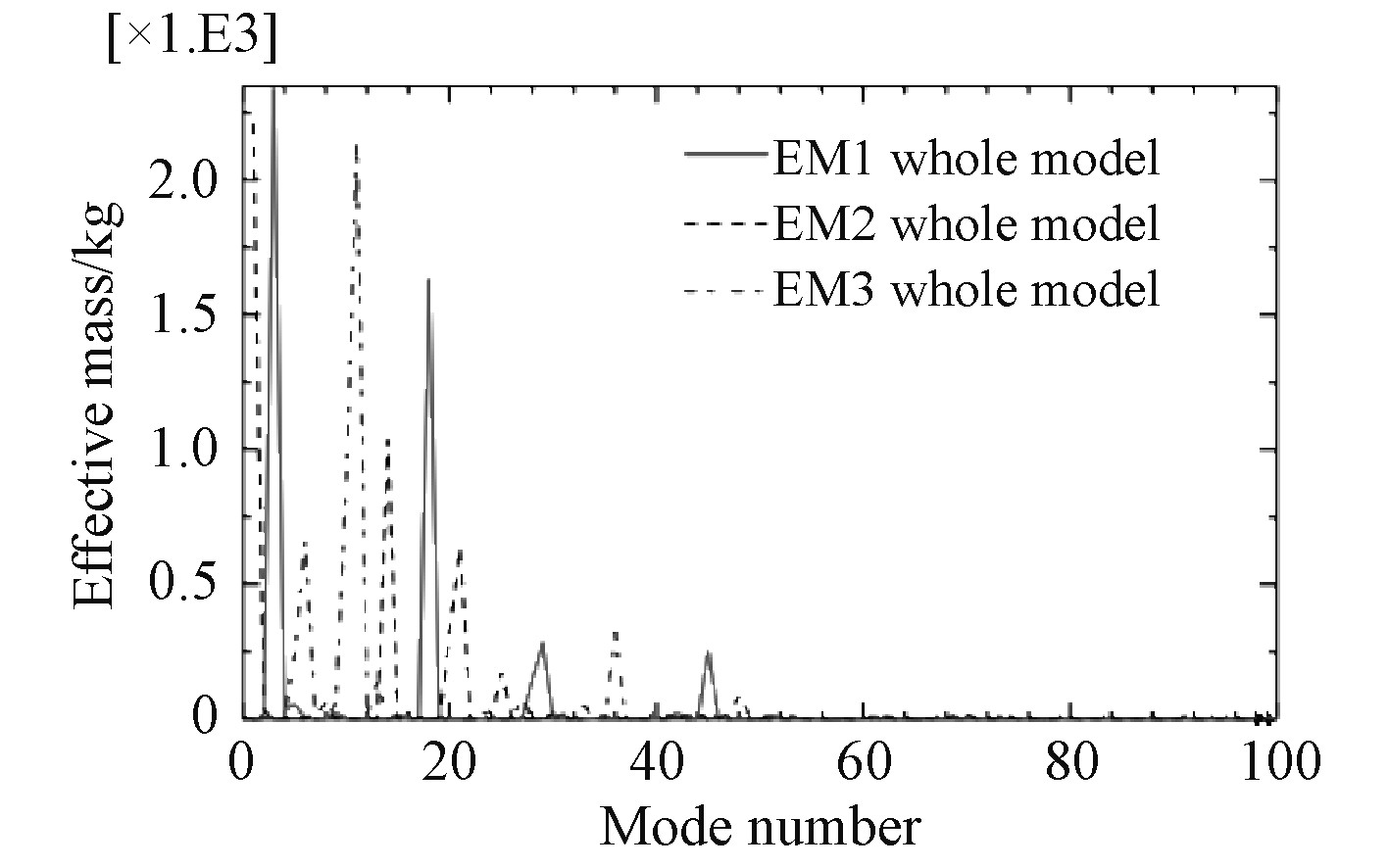
图5为前100阶次振型在1，2，3方向的参与系数仿真曲线图，图6为前100阶次振型在1、2、3方向的有效质量曲线图。根据仿真结果，50阶以上的振型在3个平动自由度上的参与系数与激活的有效质量都相对较小，进一步说明实际研究时取前50阶模态确实是可行的。为说明问题，取前100阶模态进行分析。第3，5，18，28，29，45阶振型在x方向起主导作用，第1，8，14，20，21，47阶振型在y方向起主导作用，第6，10，11，36，56，100阶振型在z方向起主导作用；第3，18阶振型在x方向激活的有效质量起主导作用，第1，14，21阶振型在y方向激活的有效质量起主导作用，第6，11阶振型在z方向激活的有效质量起主导作用。综合而言，第1，3，11，18阶振型所激活的有效质量最为显著，分别达到2 213 kg，2 337 kg，2 132 kg，1 631 kg，分别占炮架总质量的38%，40%，36%，28%，因此工程中需要重点关注。尽管56、100阶振型在z方向上的参与系数较高，但由于固有频率已高达1 146 Hz，1 512 Hz，振型所激活的有效质量仅有21 kg，24 kg，对炮架的动态效应所起的作用已不大。

图7～图10分别为炮架第1，3，11，18阶振型对应的位移云纹图。从图中可见，1阶频率下，炮架的左右托架上部朝左右（近似垂直纸面方向）的变形趋势最大，说明左右托架更易于在左右方向产生振动弹性变形，而炮架下部的转台基本处于深色区域，不容易受到该阶频率时的振动影响；3阶频率下，炮架的左右托架上部朝炮架前后方向（纸面的左右方向）的变形趋势最大，同时炮架的转台前后部也呈现出前后方向的变形趋势；11阶频率下，炮架的左右托架上部朝上下方向的变形趋势最大，转台的左右两侧部呈现出向上、向下的变形趋势；18阶频率下，炮架的左右托架呈现出的变形趋势与3阶频率下相似，炮架下部转台的变形则由前后部向左右部分转移。综合而言，在有显著质量的激励的4个频率时，炮架的托架更易于产生振动变形，这也是需要炮架设计必须重点关注的地方。

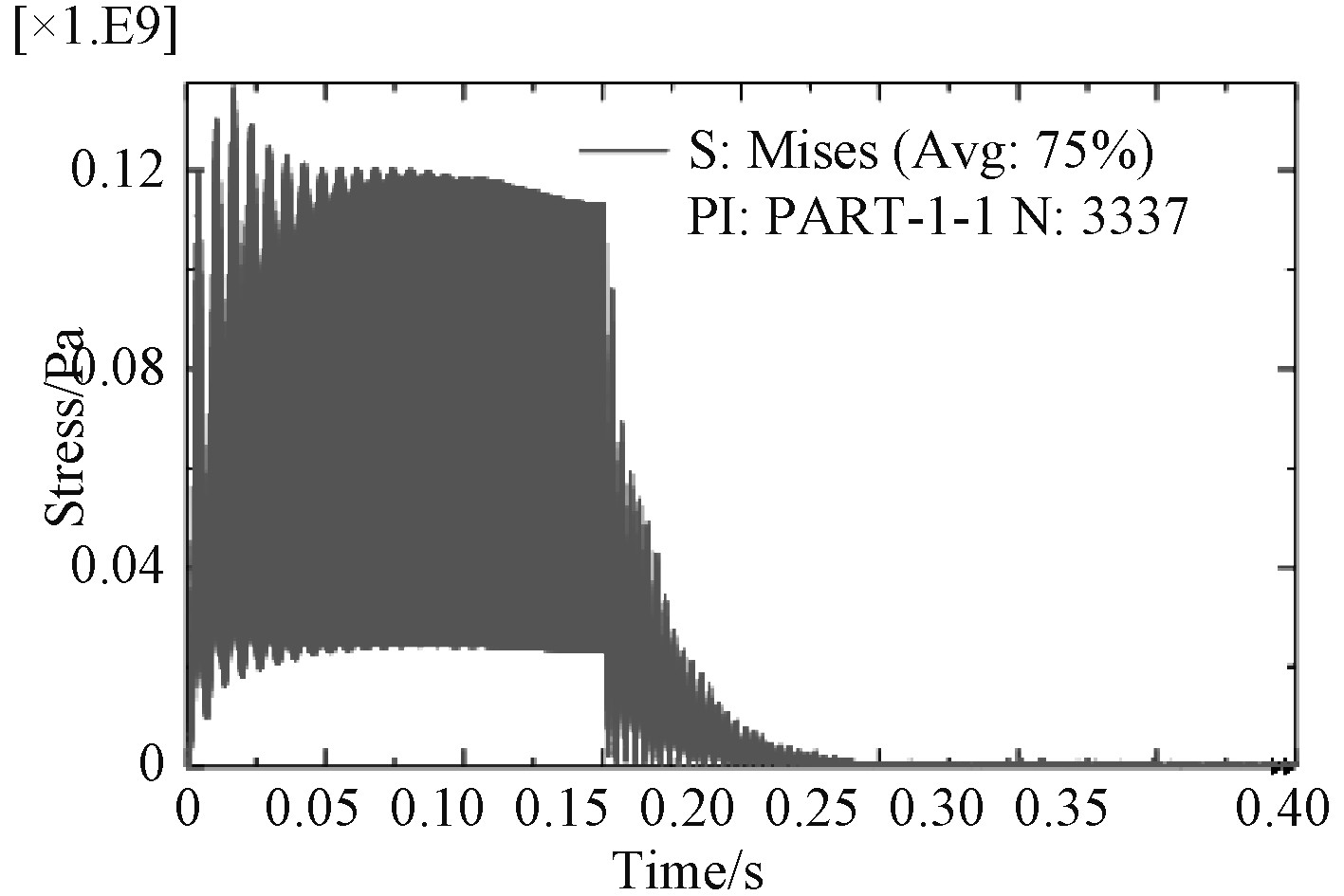
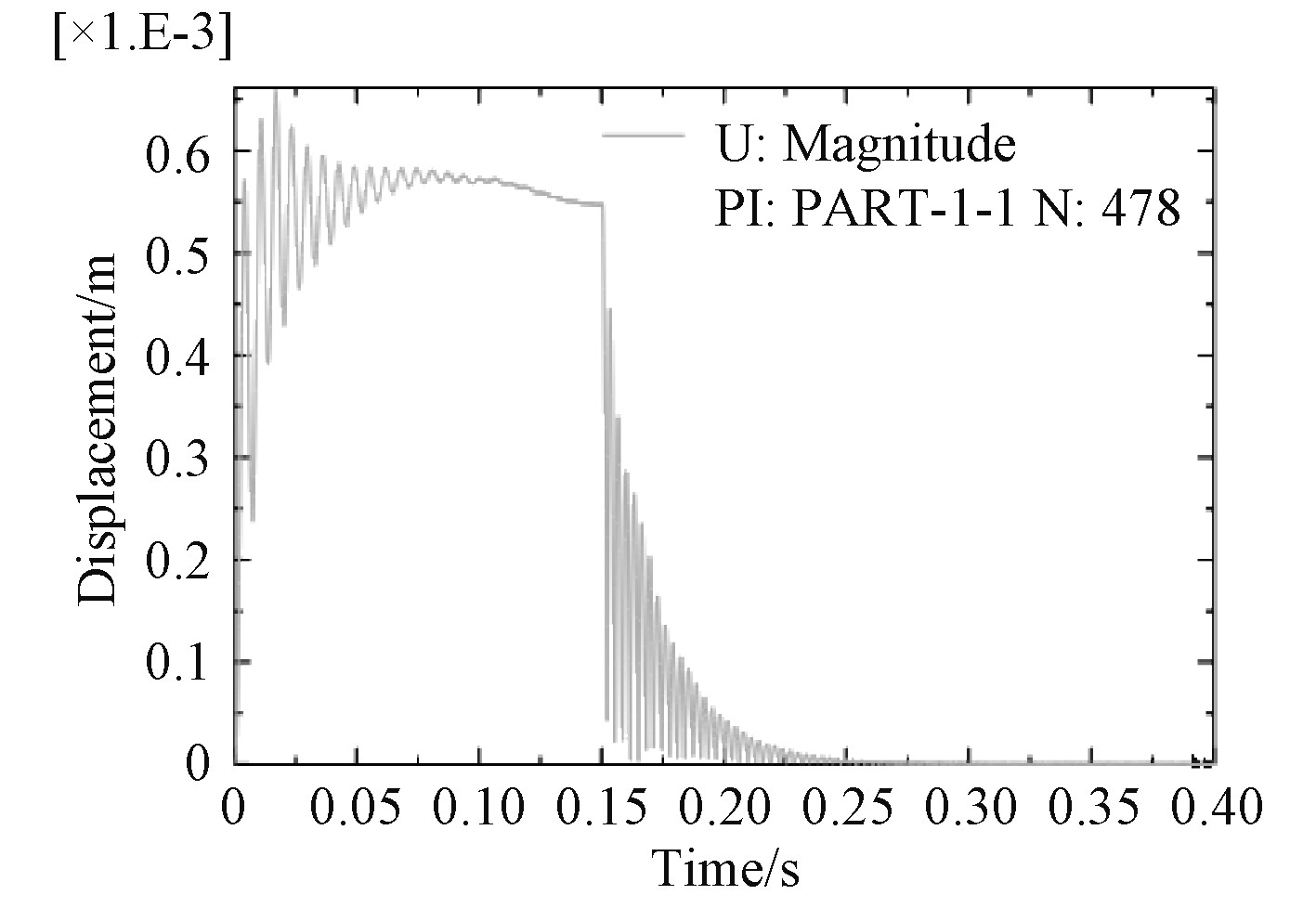
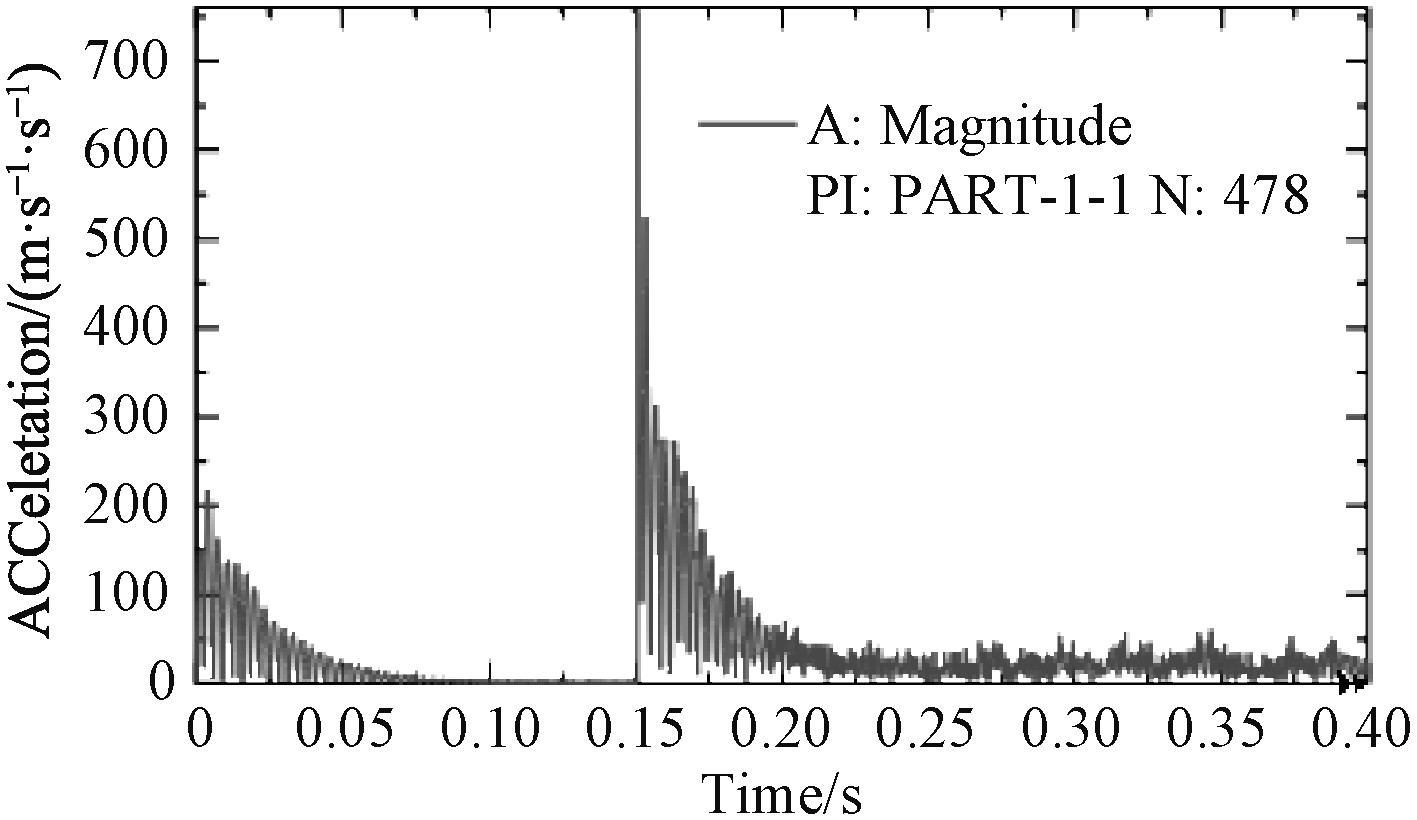
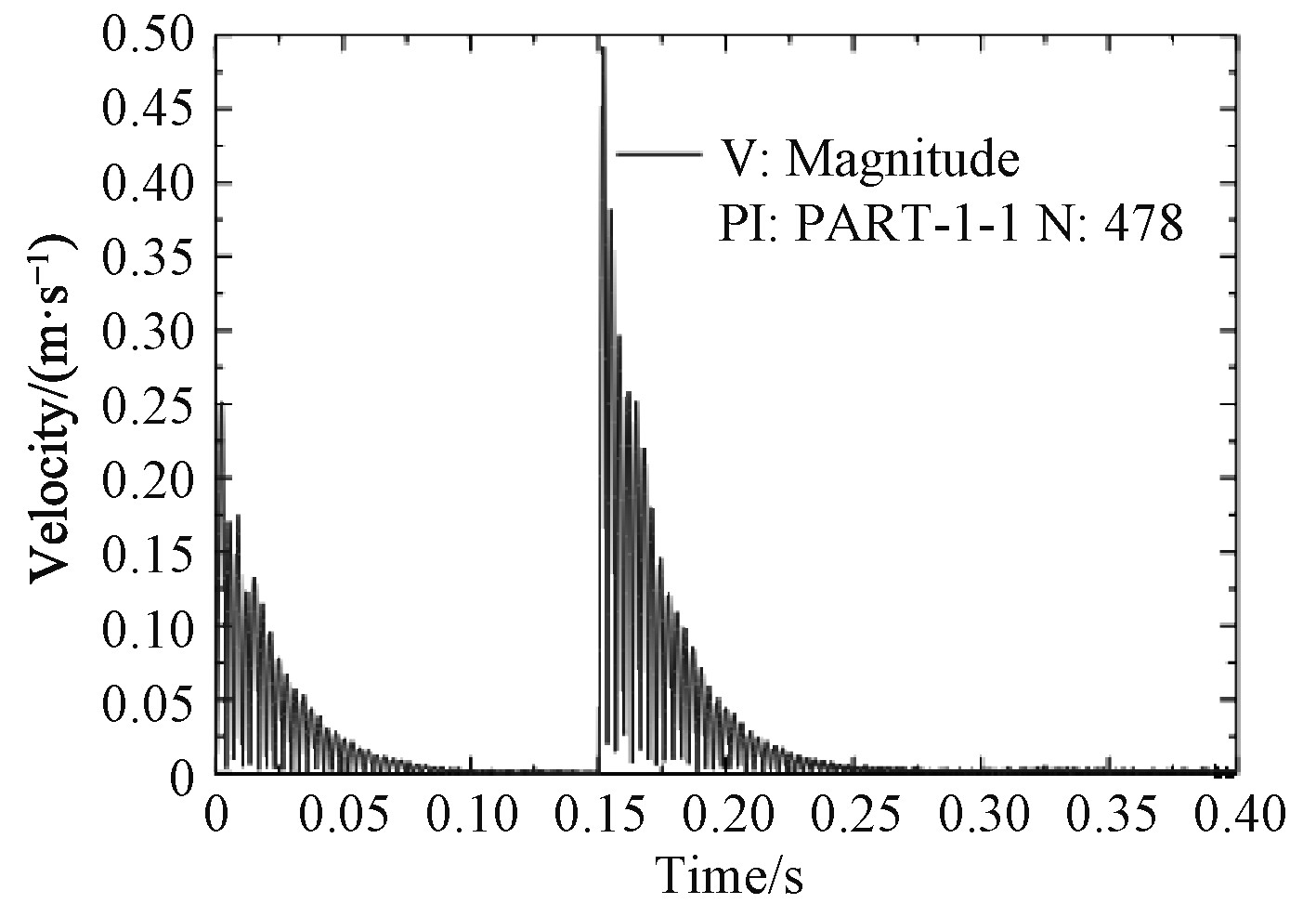
3 炮架瞬时模态动态分析

在炮架模态分析基础上，通过在A面施加随时间变化的后坐阻力，可以得到炮架的瞬时模态动态响应数据。后坐总时间为0.15，为观察炮架在后坐阻力激励后的响应，设定分析步时间为0.4 s，B面固支约束。后坐阻力瞬时作用时，最大应力出现在转台底部、正对托架与转台交接的竖里面位置，并与B面外圆柱面相交的节点（编号3337），该节点的Mises应力随时间变化曲线如图11所示。最大应力136.8 MPa，出现在0.017 s时刻。而以最大后坐阻力加载到同样模型进行静力学分析，最大应力同样出现在节点3337号，幅值为59.5 MPa，动态与静态分析结果比值为2.3:1。最大加速度、最大速度、最大变形的节点编号为478，位于托架顶面四边形的顶点部位，其中最大变形0.63 mn，出现在0.0108 s时刻，而以最大后坐阻力加载到同样模型进行静力学分析，最大变形同样出现在节点478，幅值为0.29 mn，动态与静态分析结果比值为2.17:1。最大速度0.493 m/s，出现在0.152 s时刻，最大加速度756.4 m/s²，出现在0.150 6 s时刻。最大加速度、最大速度出现的时刻符合运动学规律，尽管加速度很大，但由于时间短暂，仅有0.000 5 s左右，因此节点产生的速度并不大。图12～图14给出节点478的位移、速度、加速度的绝对幅值随时间的变化关系，从图中可以看出，在后坐阻力突然增加、突然撤销时，节点的位移、速度、加速度都有一个突然变化，这是动态分析与静态分析的最大不同，幅值仿真曲线与节点x，y，z单向仿真曲线可以为实际测试提供依据。

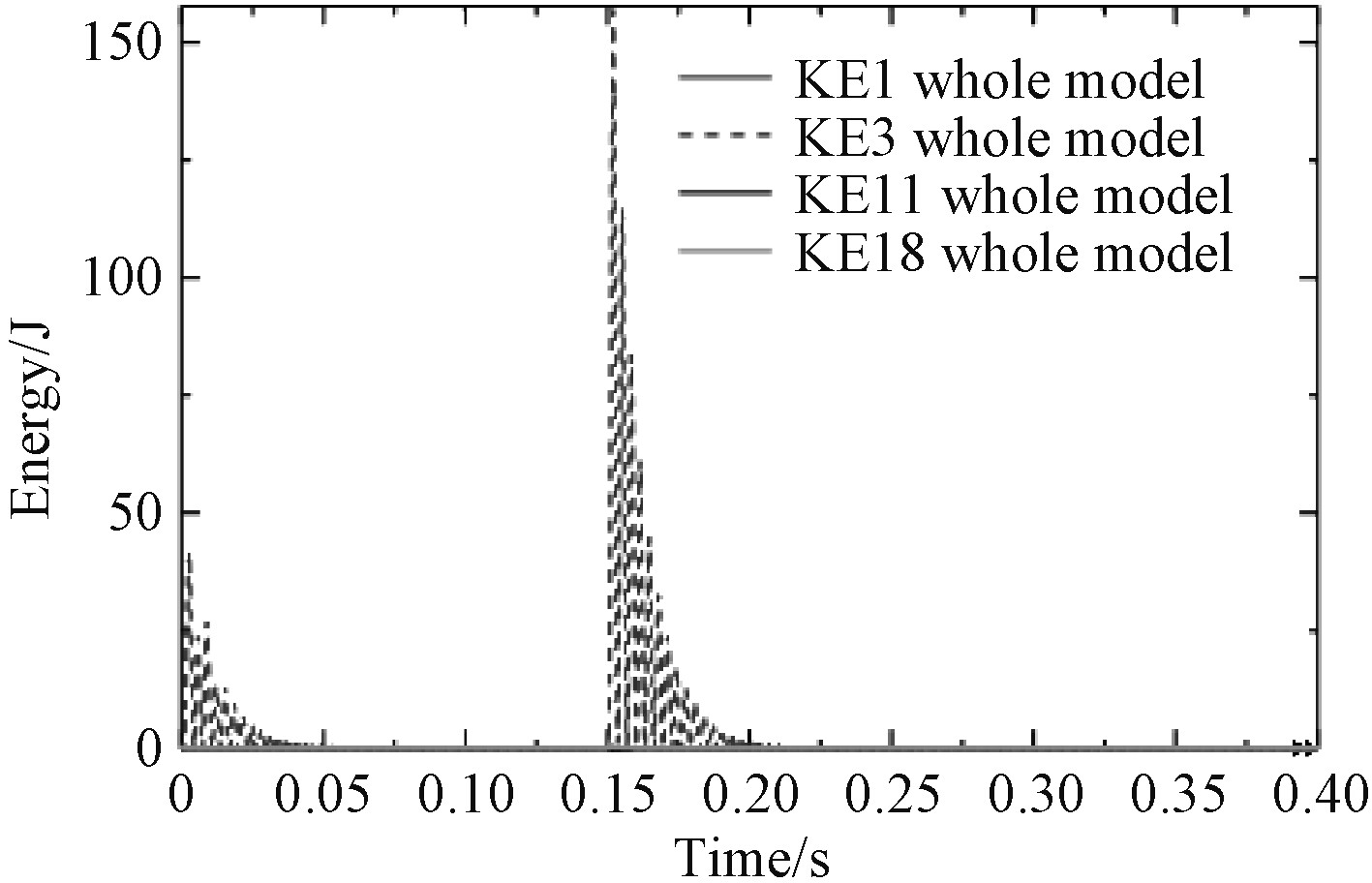
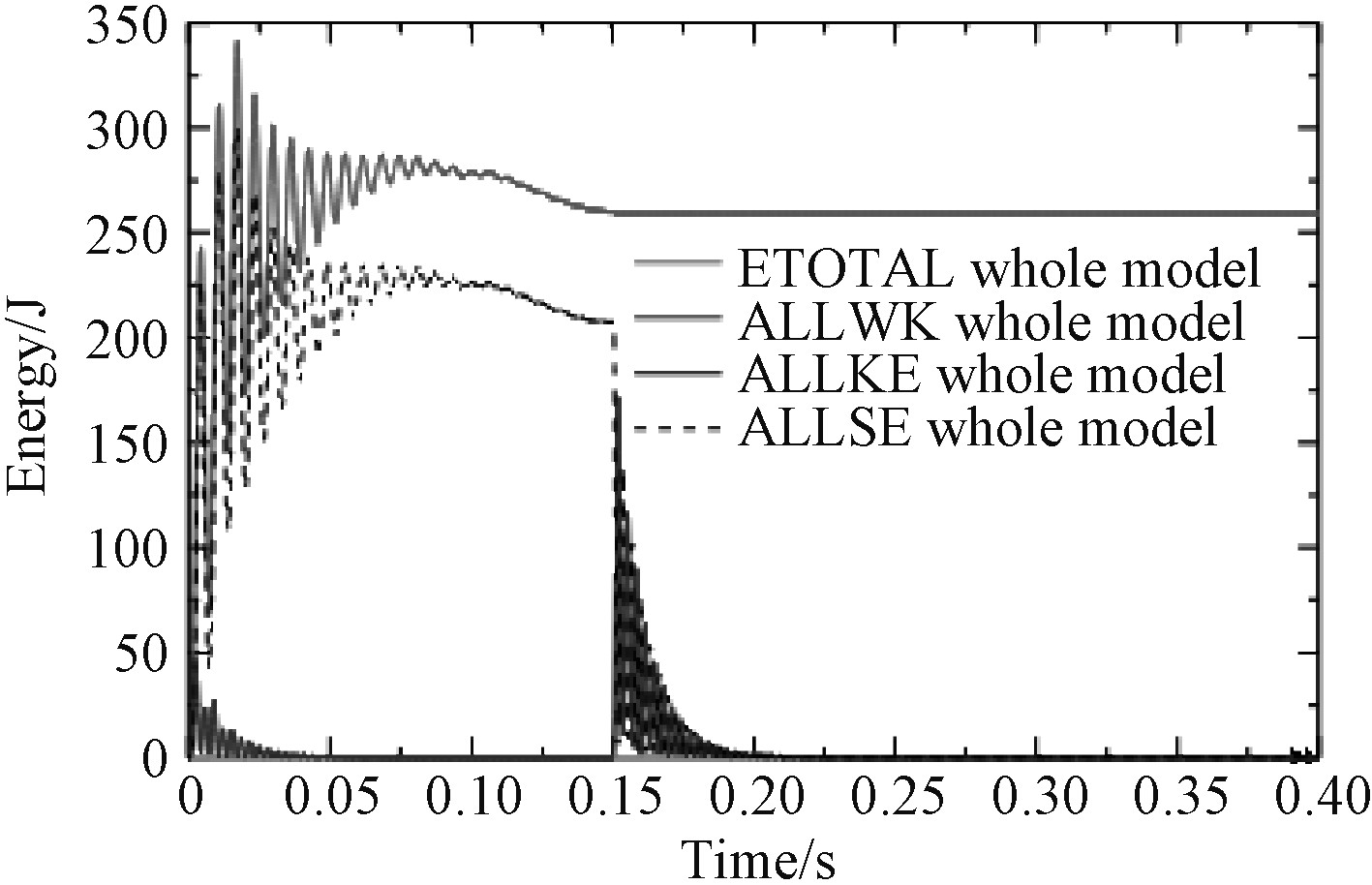
后坐阻力对炮架的激励过程是被离散化成有限个质量单元的炮架的各个网格单元运动状态发生连续变化的动态过程，网格单元产生加速度，随着时间的持续，网格单元具有了一定的速度进而带来各节点位移的变化。因此，后坐阻力对炮架的激励过程，实际上是按照各阶振型不断振动的过程，激励过程为0.15 s，振动在0.275 s时刻完全结束。振动过程伴随着能量的消耗，前文已明确在1，3，11，18阶振型时激活的有效质量最为显著。真实激励加载后，这4阶振型各自所激起的动能随时间曲线如图15所示。从图中可以看到，第3阶振型下激起的瞬时最大动能达156.9 J，而1，11，18阶振型下激起的动能极小，基本都不超过1 J。由此可以判断，对于该炮架需要重点关注第3阶振型，即平行于后坐阻力方向的振型。图16为炮架振动过程中的主要能量随时间变化的曲线图，整个模型的总平衡能量（ETOTAL）始终为0，表明计算过程稳定，结果比较可信。后坐阻力做功（ALLWK）最大峰值341.4 J，能量平衡后保持259.1 J不变。后坐阻力持续做功期间，伴随着炮架单元弹性应变能（弹性势能）和动能的产生，会抵消一部分后坐阻力做功。最大弹性应变能（ALLSE）299.6 J，后坐阻力突然撤销时为207.2 J，上之后到0.25 s时衰减到0；最大动能（ALLKE）171.6 J，后坐阻力突然撤销时为171.6 J，之后到0.25 s衰减到0。

4 后坐阻力传递到甲板基座的支反力分析

最大后坐阻力是舰炮的一个装舰要素。长期以来，很多人认为多达几十吨的后坐阻力对甲板基座的刚强度影响很大，甚至影响到舰炮的适装性。但通过前文仿真分析可知，舰炮后坐阻力实际上是一个瞬时过程，炮架相当于刚度系数较高的弹性体，后坐阻力激励的过程伴随着炮架各网格单元的弹性应变能和动能的能量耗散，传递到甲板基座时的能量必然会有一定幅度的损耗。而后坐阻力传递到甲板基座的力，即炮架B面相配合的甲板基座表面对炮架B面提供的支反力，必然会比将炮架视为绝对刚体传递时的有所减小。同时，由于炮架B面、甲板基座安装面的接触面积更大，甲板基座受力后的应力应变会有显著改善，远较舰炮耳轴座受力后的状态要好。

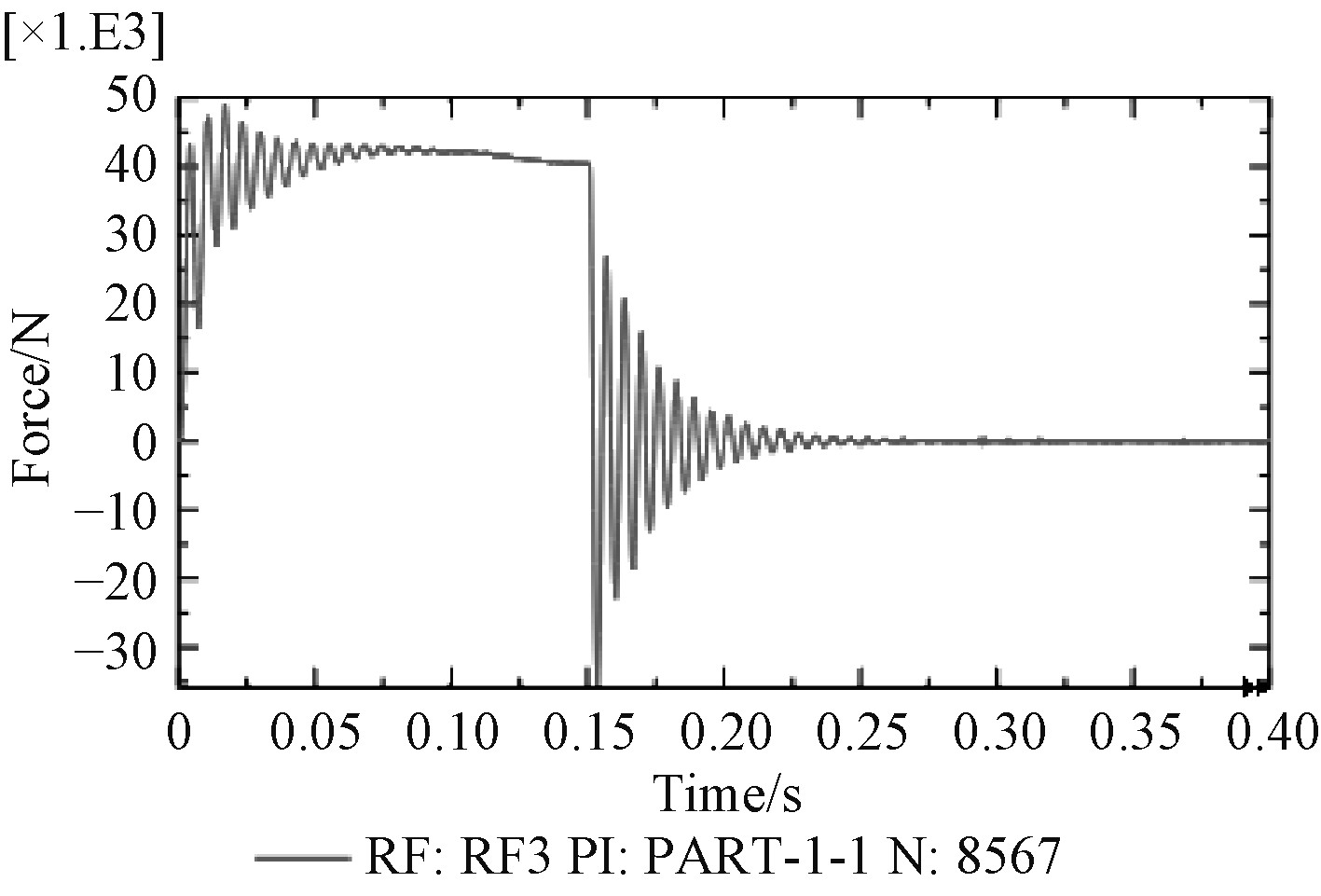
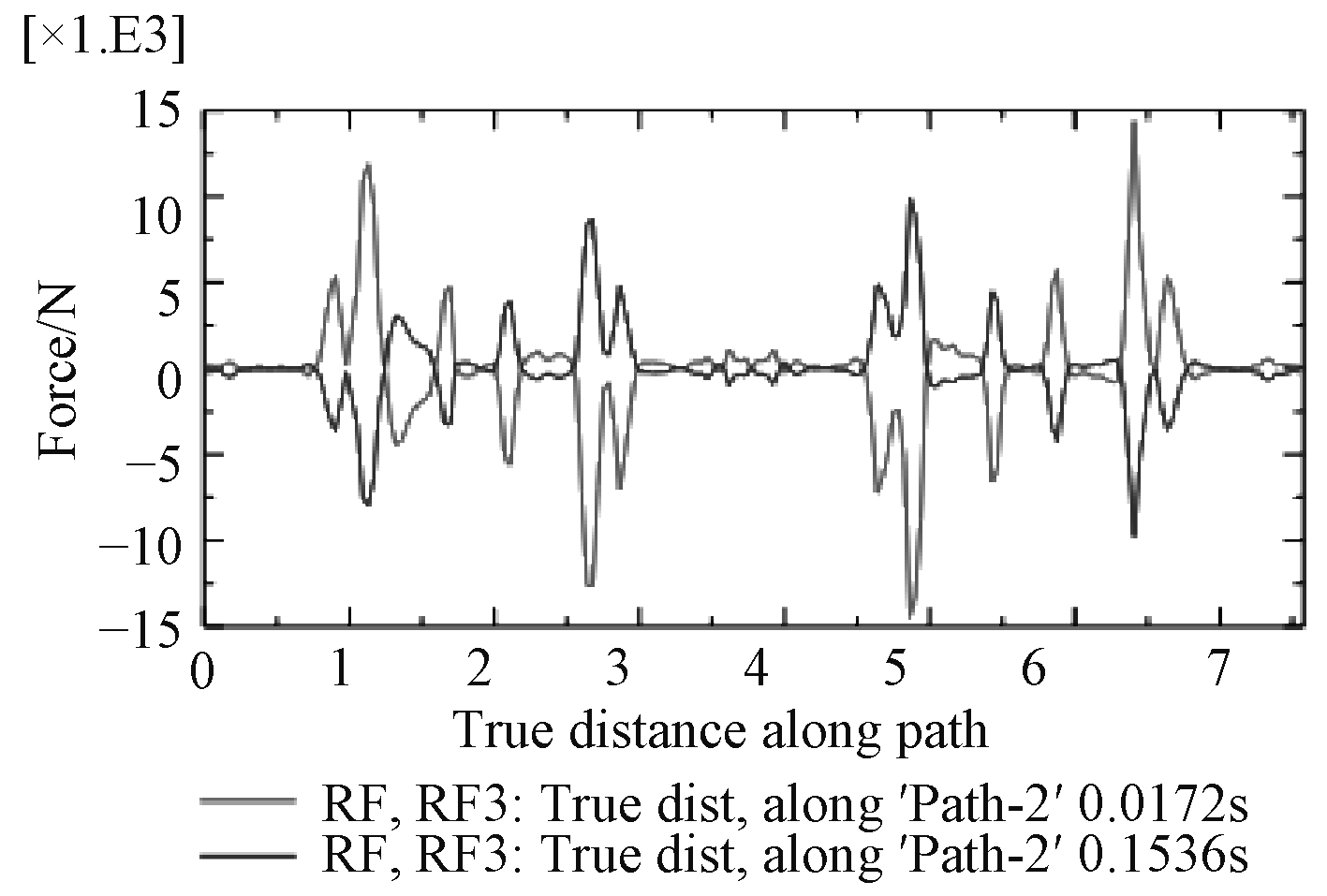
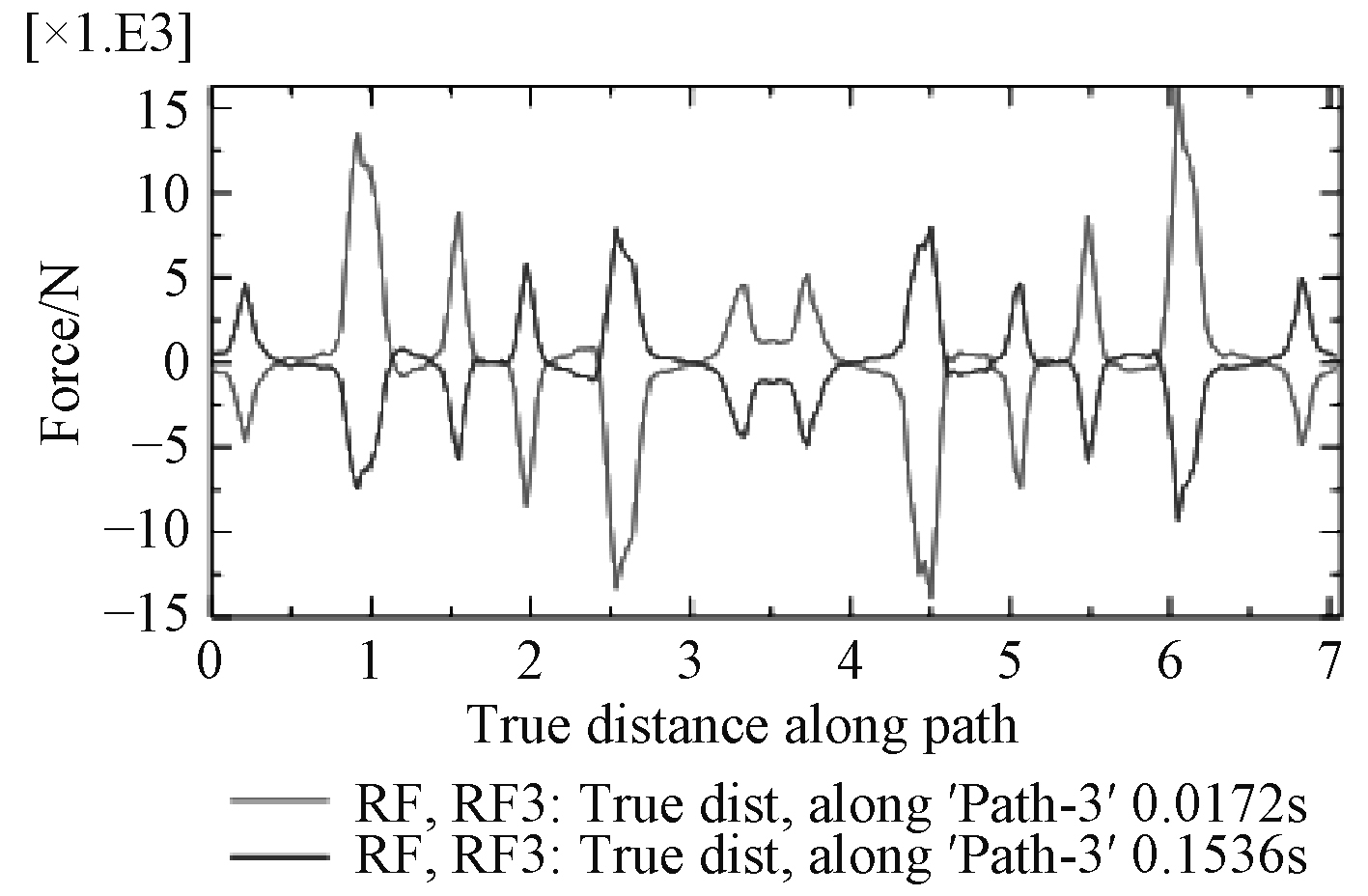
B面受到最大支反力的节点位于B面最大外圆部位并正对托架后部底部位置，节点编号8567，在z向上的支反力随时间变化如图17所示。该节点在受到突然施加的后坐阻力作用时，产生了突然增大然后波动、最后趋于稳定的向上的支反力，0.017 2 s时支反力最大到4.9 t，到0.15 s时支反力降到4.04 t，而以最大后坐阻力加载到同样模型进行静力学分析，最大支反力同样出现在节点8 567，幅值为2.11 t，动态与静态分析结果比值为1.91:1。在后坐阻力撤销瞬时该节点的支反力突然换向，最大值达到负向3.54 t，之后在阻尼作用下逐渐衰减并在0.25 s时到0值。这一过程反映了B面最大支反力点的反力是一个动态、方向变化的事实。为进一步考察炮架B面支反力的整体情况，在环形B面上设定3条圆形路径，半径分别为1 280，1 200，1 120 mn，分别命名为path1，path2，path3路径。参考最大支反力点出现最大力值的时刻，探求在0.017 2 s，0.153 6 s时刻3条路径上的支反力情况。

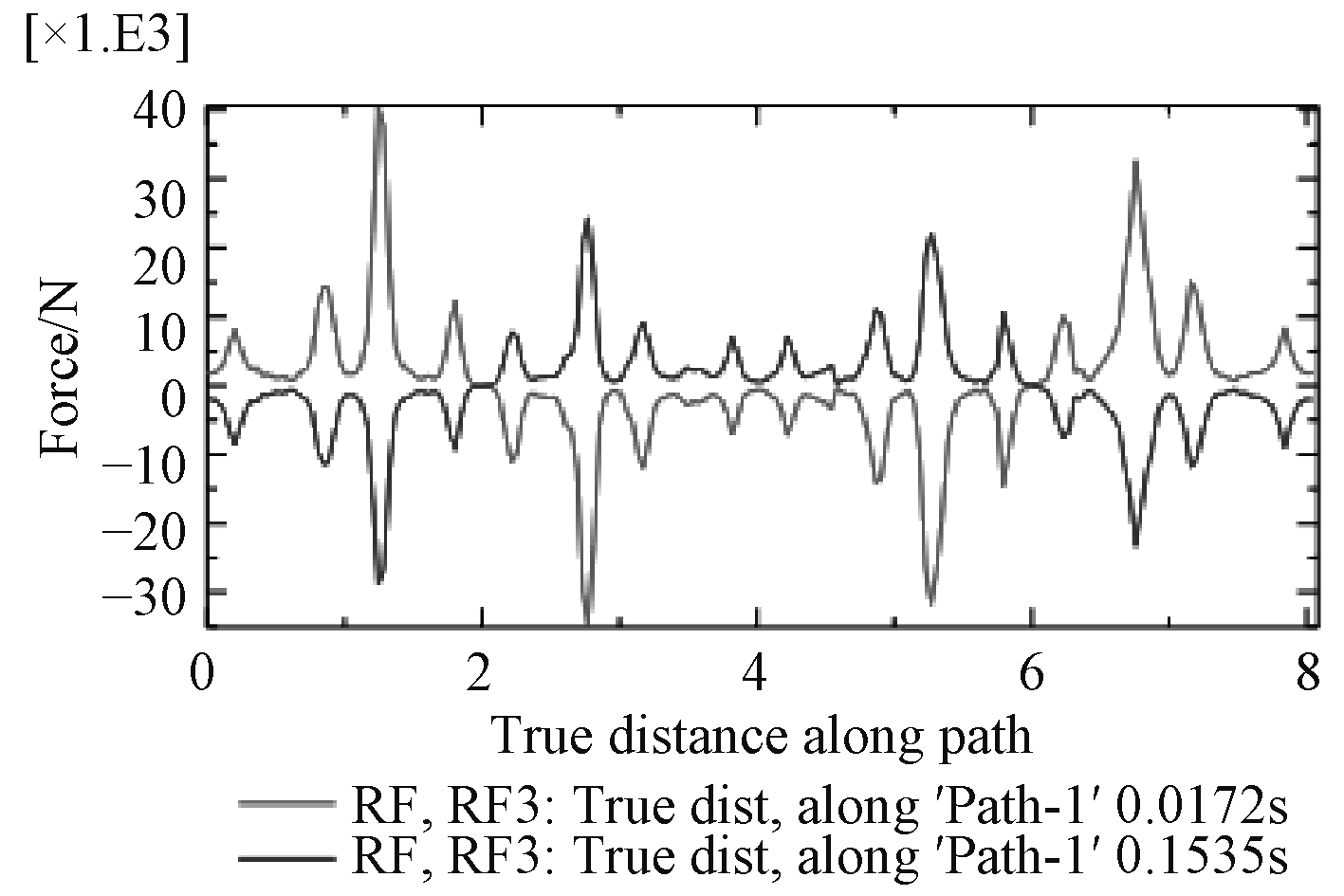
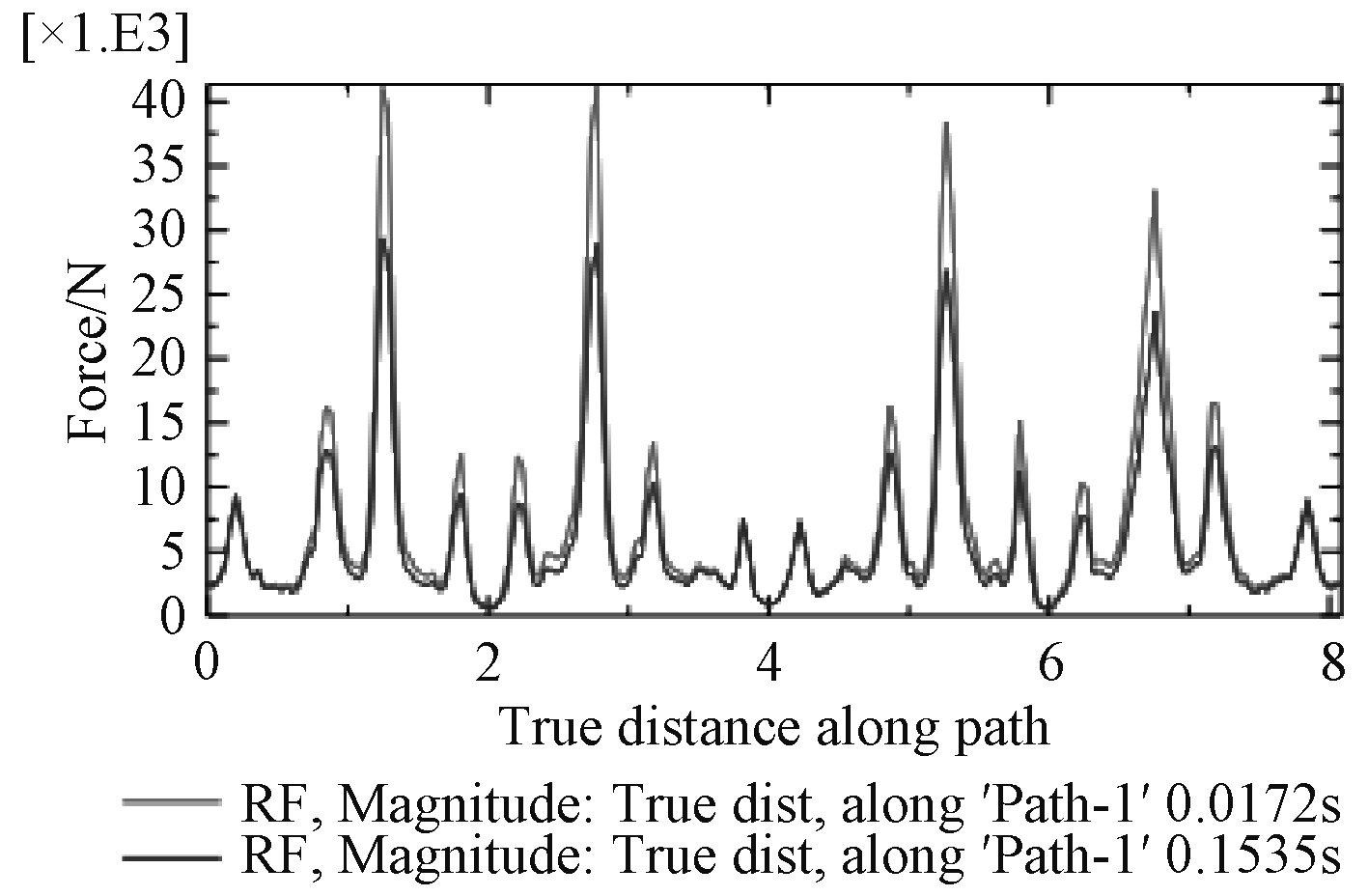
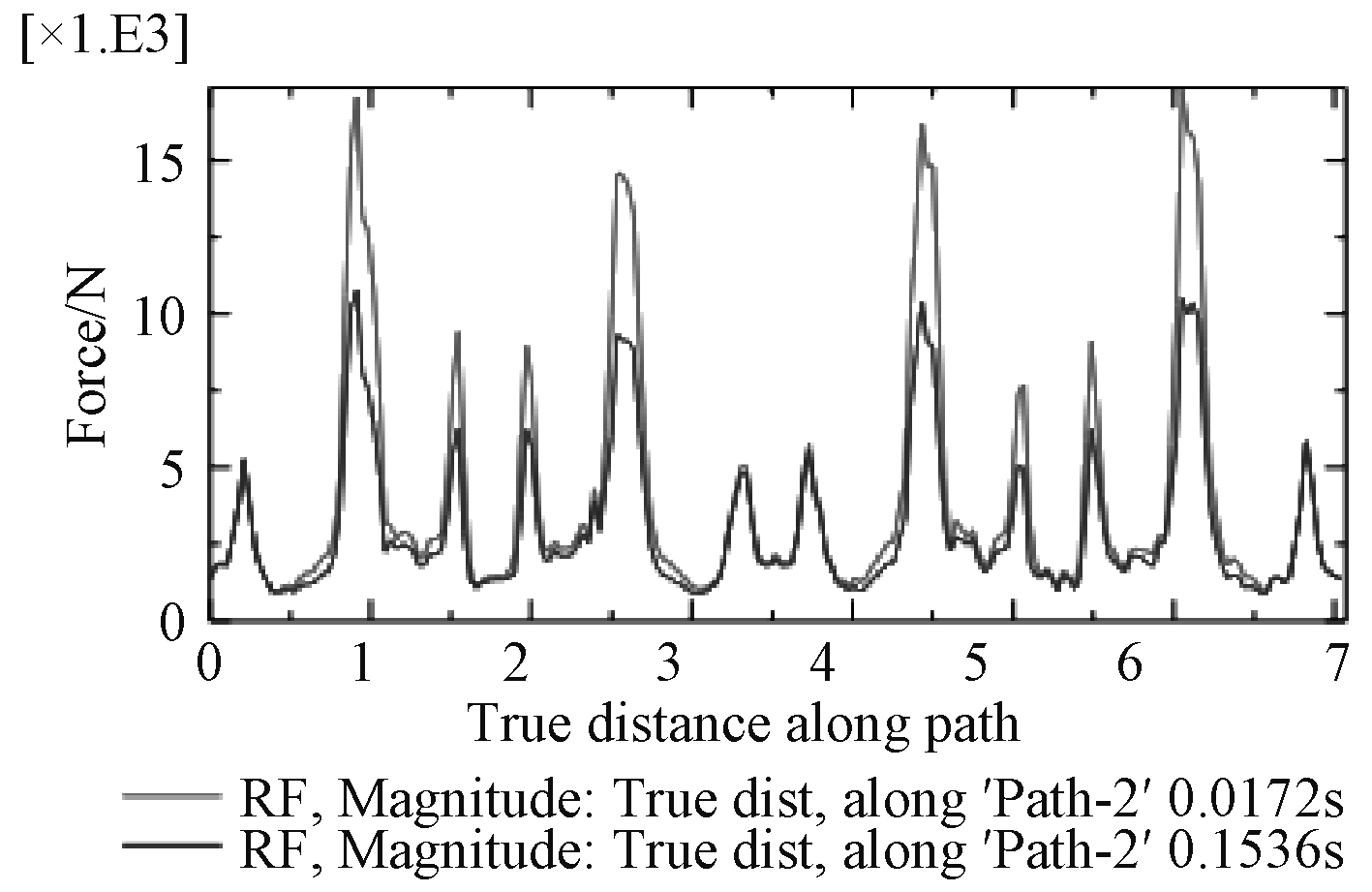
图18～图23为在0.017 2 s、0.153 6 s两特征时刻path1，path2，path3路径上的垂向支反力、支反力幅值曲线图。分析曲线图可知，2个特征时刻各路径上的垂向支反力方向刚好相反，绝对值不同；从环向看，路径半径越大，同一时刻垂向支反力越大；同一时刻同一路径上各点的支反力大小不同，从模型坐标系来看，x轴正半轴与负半轴方向的垂向支反力刚好相反；垂向支反力4个最大值点刚好位于B面正对托架底部最前、最后部位；path2路径可视为炮架与甲板基座连接螺栓分布圆的直径，path2路径上垂向支反力四个峰值均在1.5 t以下，作为静不定结构，大部分点位上的支反力在0 t附近波动，仅仅考虑后坐阻力影响，不仅甲板基座结构设计能够轻易实现较高刚度，连接螺栓同样能够达到极高安全系数。对于支反力幅值，包含了垂向、横向、纵向分力，从绝对值来看支反力的幅值与垂向支反力绝对值相差很小，因此垂向支反力对于甲板基座刚强度起显著作用，而横向、纵向分力（最大值1.09 t）主要是对连接螺栓的剪切强度有影响。

5 结　语

本文同时对不同射角时后坐阻力的动态问题进行了分析。通过数值仿真，得出如下结论：

1）炮架结构设计确定后，应综合考虑约束条件、振型激活总质量、各方向参与系数确定欲进行瞬时模态动态分析需要的固有频率阶数，确定哪阶或哪几阶振型对炮架动态分析起决定性影响；

2）在后坐阻力激励下，炮架的应力、变形、速度、加速度、支反力等都呈现出动态变化趋势，其峰值应力、变形、支反力等较传统静力分析结果要高，炮架在外力激励下的响应仅靠静力计算不够准确，实际安全系数偏小；

3）后坐阻力激励的过程，实际上也是炮架自身单元弹性应变能、动能的不断消耗过程，后坐阻力做功传递过程也是一个能量逐渐减小的过程，甲板基座安装面单个螺栓连接部位不能简单地以最大后坐阻力进行施加校核，安装面所承受的垂向力沿圆周方向的分布值可以通过仿真得到，应重点关注安装面正对托架底部前后结构对应部位的四处最大支反力，但单个幅值仅约为最大后坐阻力1/10；

4）炮架动态分析是设计趋势，文中分析步骤对于舰炮动态分析具有指导作用。