2. 海军工程大学 振动与噪声研究所,湖北 武汉 430033
2. Institute of Noise and Vibration, Naval University of Engineering, Wuhan 430033, China
凯夫拉增强型挠性接管(FW-FP)大量应用在船舶管路的减振降噪领域[1],其工作状态正常与否直接影响船舶设备的安全性能。对FW-FP进行实时状态监测和工作寿命评估,是提高其安全性、可靠性的重要手段之一。
挠性接管在使用过程中,管体会产生4种类型的变形,第1种是管体充压时产生的变形;第2种是由于轴向力作用导致管体的轴向变形;第3种是由于剪切力作用导致管体的径向变形。这3种变形都属于管体正常的整体性变形。第4种是管体的局部异常变形,它是由于管体内部流体压力变化而产生的一种疲劳变形[2],这种局部异常变形会使管体局部区域应力集中,会加速管体破裂失效。Aaron等[2-6]提出电阻感应原理用来识别橡胶管体的局部异常变形,可以实现管体变形的全局监测,对管体的寿命进行评估。这种方法存在2个缺点:一是该检测方法具有开关特性,当管体临近损坏时,电流信号才有明显的变化,不能实现管体全寿命周期内的变形监测;二是测量精度相对较低,对于管体局部敏感部位不能实现有效的变形监测。光纤布拉格光栅(in-fiber bragg grating, FBG)技术是一种新型的结构内部应变分布式监测技术[7],可将多个光纤光栅传感器埋入复合材料结构中,实现复合结构中多个局部敏感区域的实时变形监测,具有测量精度高、连续性的优点,同时对于管体变形的敏度度更高,能够较早识别出管体的异常变形。
本文针对上述问题,考虑挠性接管的复合材料结构特点,融合电阻感应原理和光纤布拉格光栅传感原理,提出一种基于管体变形实时监测的挠性接管寿命评估方法。通过建立管体变形监测模型,采用数值计算和有限元仿真方法进行分析,提取出可区别管体正常变形和局部异常变形的特征阈值。该方法可有效识别管体的局部异常变形,实现挠性接管工作寿命的评估。
1 管体变形监测原理 1.1 FBG传感原理基本原理:当具有一定波长的宽带入射光进入光纤光栅时,当外界的参数(应变、温度)发生变化时,其背向反射光的中心波长会发生漂移,而其中心波长的漂移量
| $\Delta \lambda = \lambda (1 - {\rho _\alpha })\Delta \varepsilon \text{。}$ | (1) |
式中:
对式(1)化简可得:
| $\Delta \lambda = k\Delta \varepsilon\text{。} $ | (2) |
式中:
Aaron等[2-6]学者提出可以将金属导线传感器埋入橡胶层内,通过检测金属导线阻值的变化来得到管体橡胶层的变形量,公式为:
| $R = \rho \frac{l}{S}\text{。}$ | (3) |
式中:
挠性接管由内胶层、骨架层、外胶层组成,骨架层由4~6层凯夫拉纤维帘布缠绕而成,可将2种传感器分别埋入骨架层的不同帘布层。采用光纤光栅传感原理可以对管体局部敏感区域的变形进行监测,采用电阻感应原理可以对管体的全局变形进行监测,通过融合这2种传感原理,实现管体变形全方位、针对性的实时监测。
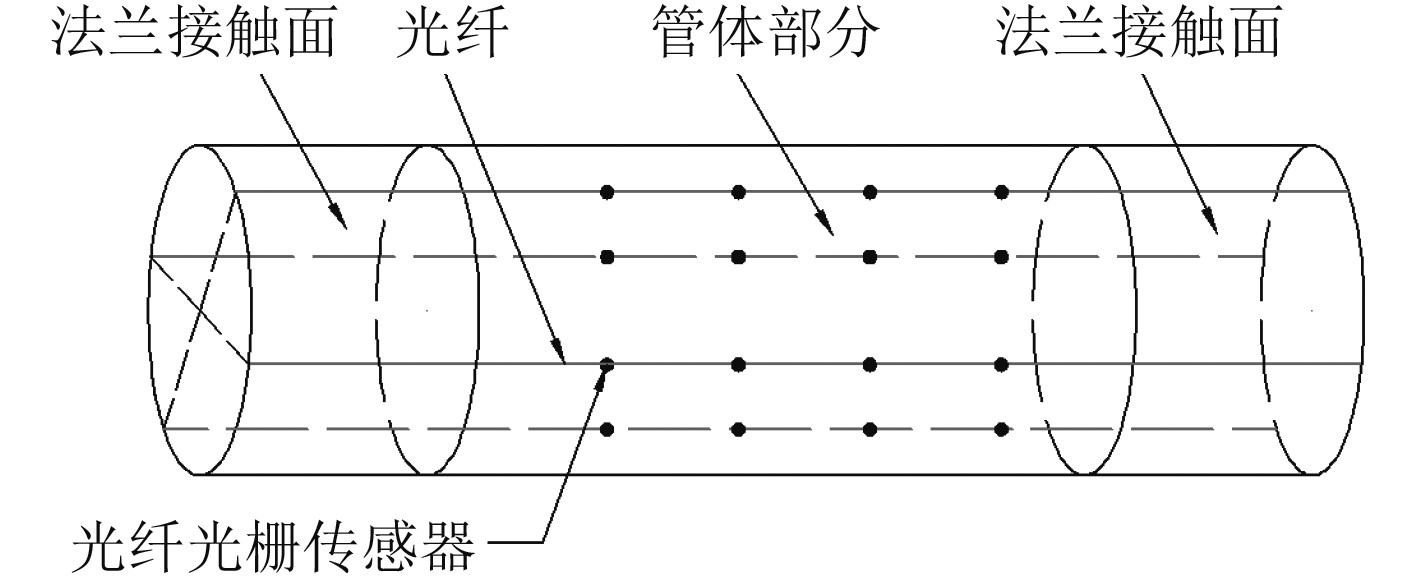
挠性管体部分是挠性接管易损坏的薄弱部位,将光纤光栅传感器的测点布置在挠性管体中。由于光纤光栅传感器测量被测物的纵向应变,将光纤沿管体径向按照一定角度均匀布置在挠性接管骨架层内的四周,根据不同型号管体的尺寸来确定光纤光栅测点的个数和布置的位置,如图1所示。
|
图 1 光纤光栅传感器布置 Fig. 1 The location of FBG sensors |
将电阻导线按照一定的缠绕角度
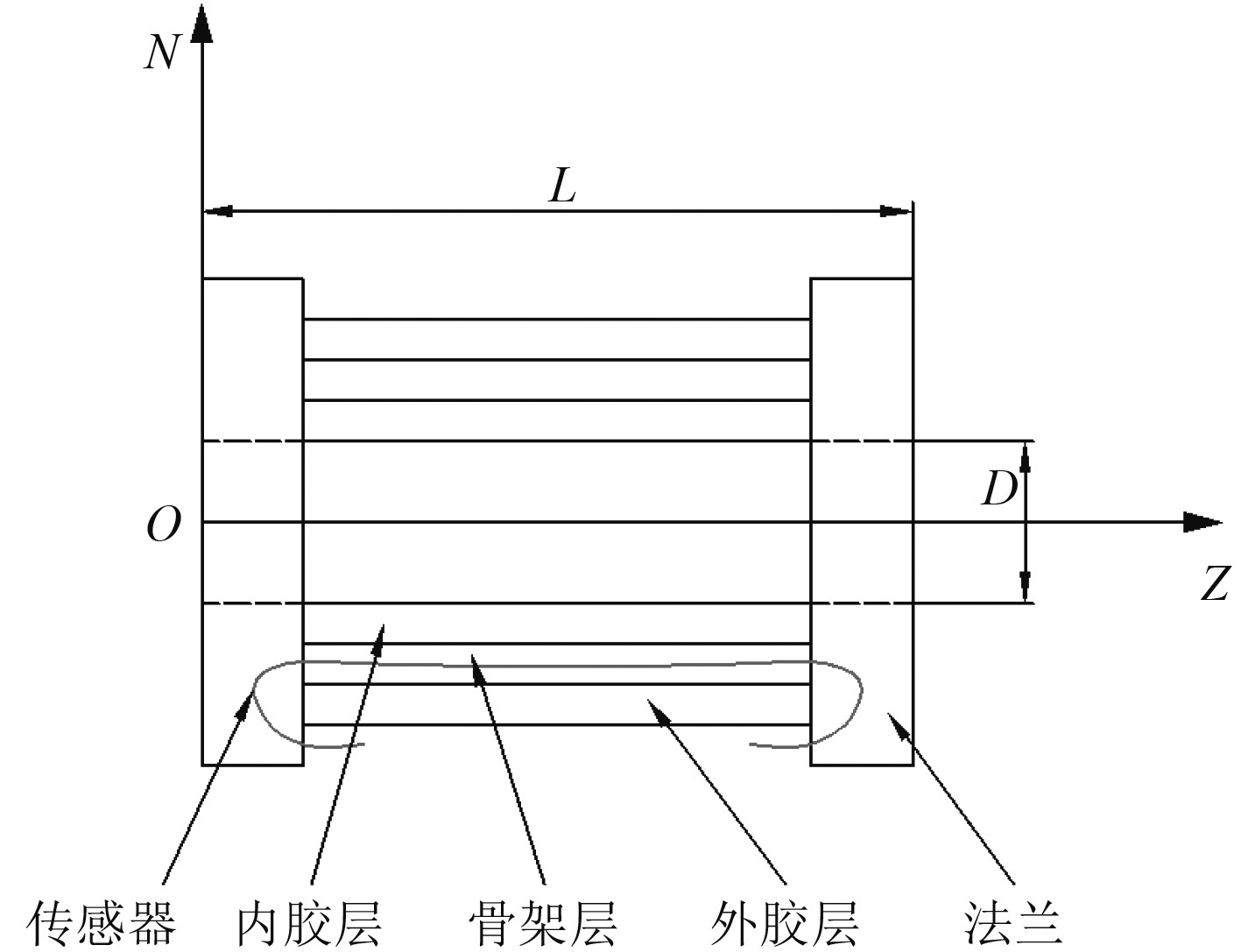
图2为管体变形监测模型,以一侧法兰的中心为原点建立坐标系,图中传感器表示电阻导线或者光纤。
|
图 2 管体变形监测模型 Fig. 2 Deformation measurement model of the pipe |
| $ I = \frac{{U{\text{π}} {r^2}\cos \varphi }}{{\rho L + {R_x}{\text{π}} {r^2}\cos \varphi }}\text{。}$ | (4) |
式中:
管体受轴向力作用而发生轴向变形位移
| $\Delta {I_Z} = \frac{{U\rho YZ}}{{(\rho L + {R_X}Y)(\rho {L_Z} + {R_X}Y)}}\text{,}$ | (5) |
式中:
光纤上各测点的纵向变形
| $\Delta {\lambda _Z} = \frac{{{k_B}Z}}{L}\text{,}$ | (6) |
式中:
由于剪切力作用导致管体发生径向变形,假设原点一侧的法兰固定,另一端法兰产生的径向位移为
| $\Delta {I_N} = \frac{{\rho UY{N^2}}}{{{\rm{(}}\rho L + {\rm{Y}}{R_x}{\rm{)}}[\rho ({N^2} + {L^2}) + Y{R_x}L]}}\text{,}$ | (7) |
光纤各测点应变量:
| $ \Delta \varepsilon = \frac{{{L_N} - L}}{L} = \frac{{\sqrt {{N^2} + {L^2}} - L}}{L}\text{,} $ |
代入式(2)中可得光纤光栅传感器反射波中心波长漂移量
| $\Delta {\lambda _N} = \frac{{k\left( {\sqrt {{N^2} + {L^2}} - L} \right)}}{L}\text{。}$ | (8) |
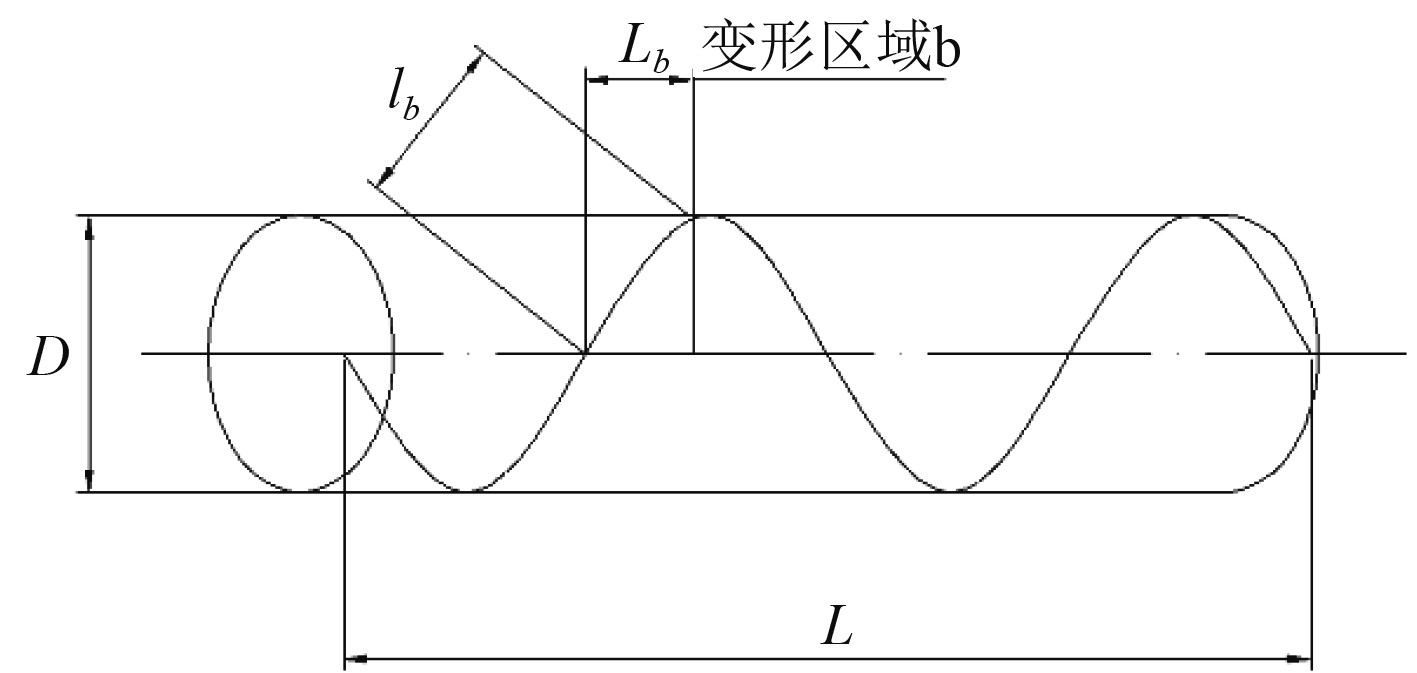
如图3所示,假定管体发生局部异常变形在管体的某一区域
|
图 3 管体局部异常变形 Fig. 3 Local abnormal deformation area of the pipe body |
| $\Delta {I_b} = \frac{{UY\rho (L - {L_b})[{r^4} - {{(r - \Delta r)}^4}]}}{{(\rho L + Y{R_x})[\rho X + Y{R_x}{{(r - \Delta r)}^4}]}}\text{,}$ | (9) |
式中:
在管体发生局部变形之后,光纤光栅传感器反射波中心波长的漂移量为
管体充压状态下,管体内部流体介质的压力作用在管体内壁,导致管体变形。在理论计算条件下,管体内壁所受的流体压力都由电阻导线和光纤承担[10],此时传感器受到的压力为极限最大值。然而在实际中,传感器布置在骨架层中,其受力变形分析还需要考虑橡胶层、芳纶纤维骨架层传递压力的影响,其受到的力要远小于理论值。通过理论计算难以满足复合材料力学的传递性,所以选用有限元软件Abaqus对管体的充压变形特性展开分析。
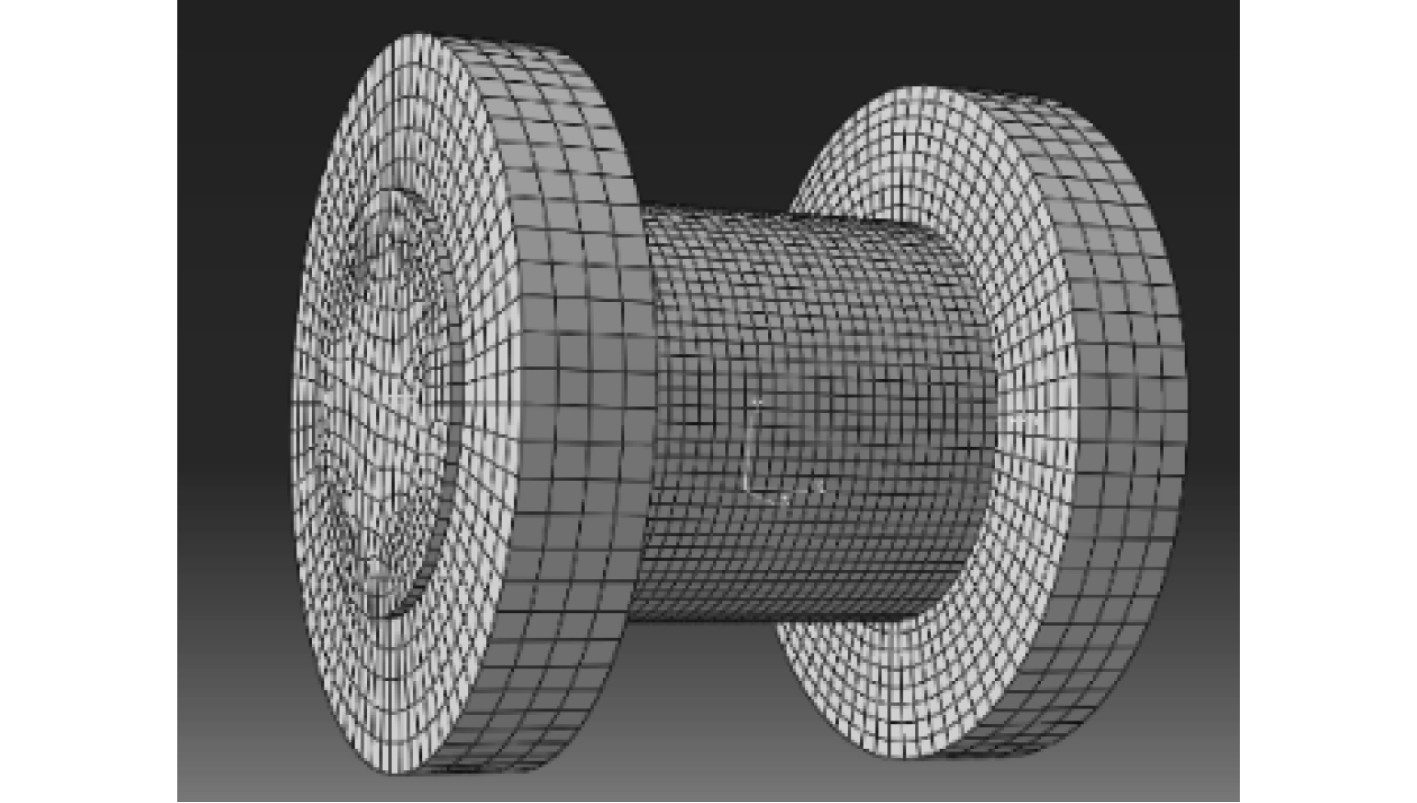
采用Mooney-Rivlin本构模型拟合橡胶材料超弹性的特性。根据弹性薄壳无矩理论[10],芳纶纤维骨架层和电阻导线层采用膜单元中的rebar层定义;法兰部分定义为刚体;通过内置命令将骨架层和电阻导线层嵌入橡胶层内,法兰与管体的接触部分采用绑定的方式进行固定;设定流体沿管体内壁的均匀压力为
|
图 4 模型划分的网格区域 Fig. 4 The mesh area of the model |
在管体充压状态下,电阻导线的轴向应变
| ${\varepsilon _l} = \frac{{{\sigma _x}}}{E} = \frac{{{\sigma _L}\sin {\varphi _0} + {\sigma _R}\cos {\varphi _0}}}{E}\text{,}$ | (10) |
式中:
| $\Delta {I_C} = \frac{{U\rho LY({\varepsilon _l}^2 + 2{\varepsilon _l})}}{{(\rho L + Y{R_x})[\rho L{{(1 + {\varepsilon _l})}^2} + Y{{\rm{R}}_{\rm{x}}}]}}\text{,}$ | (11) |
将式(10)求解的
管体中有多个光纤光栅传感器测点,通过仿真能够得到各个光纤光栅测点的纵向应变
数值计算条件:选取某型号为DN100的挠性接管进行分析,固定参数见表1。
|
|
表 1 固定参数 Tab.1 present parameters |
管体的轴向变形、径向变形、局部异常变形状态是随工况变化的,而影响这3种工况的3个参数分别为轴向位移Z、一端法兰的径向位移N、缠绕在局部异常变形区域的导线的径向变形量
|
|
表 2 参数变化范围 Tab.2 Variation range of the variable parameters |
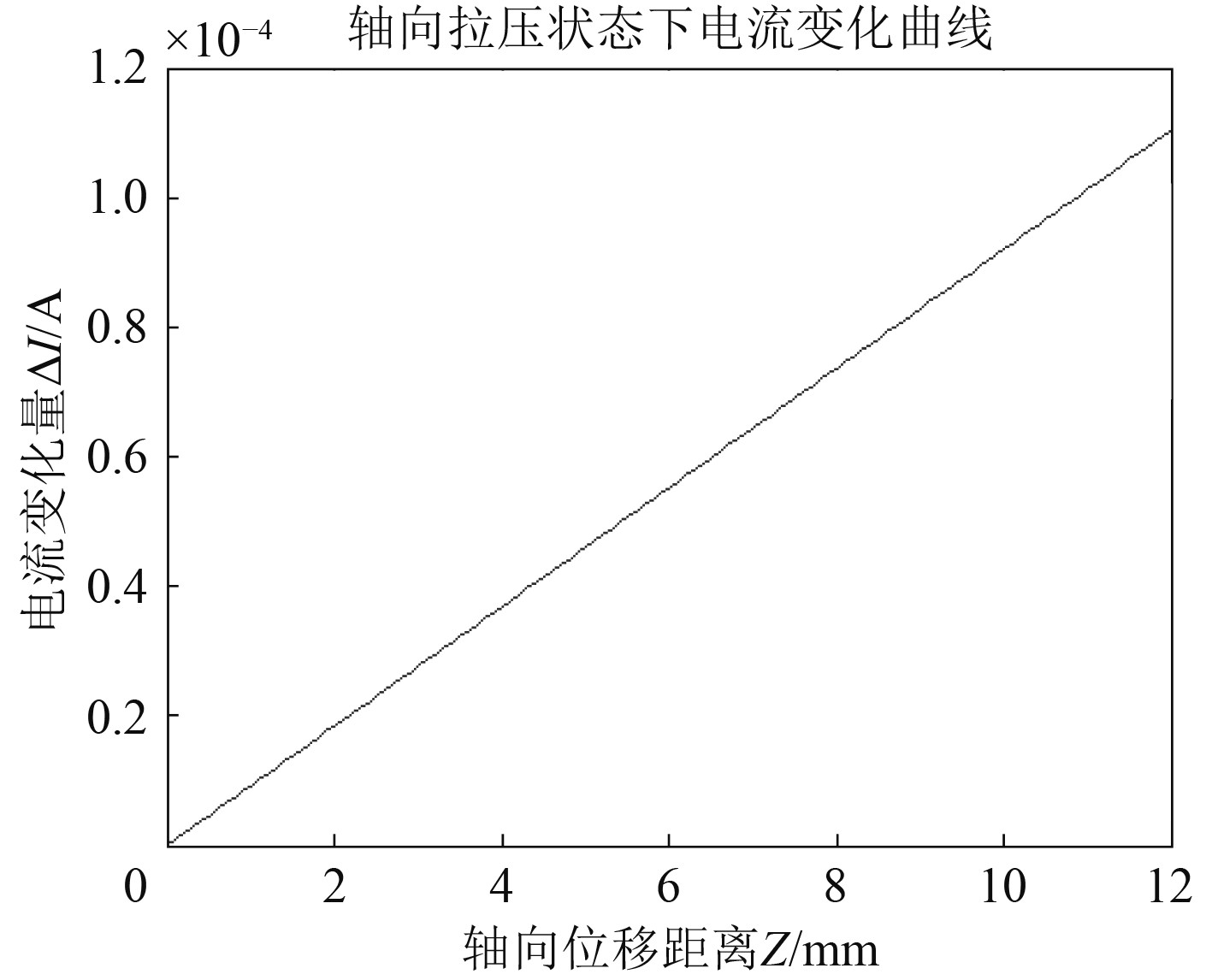
将上述参数代入计算模型,研究管体在轴向位移、径向位移、局部异常变形状态下的电流变化特性,如图5~图7所示。可知:
|
图 5 轴向变形-电流变化 Fig. 5 Axial deformation -current |
|
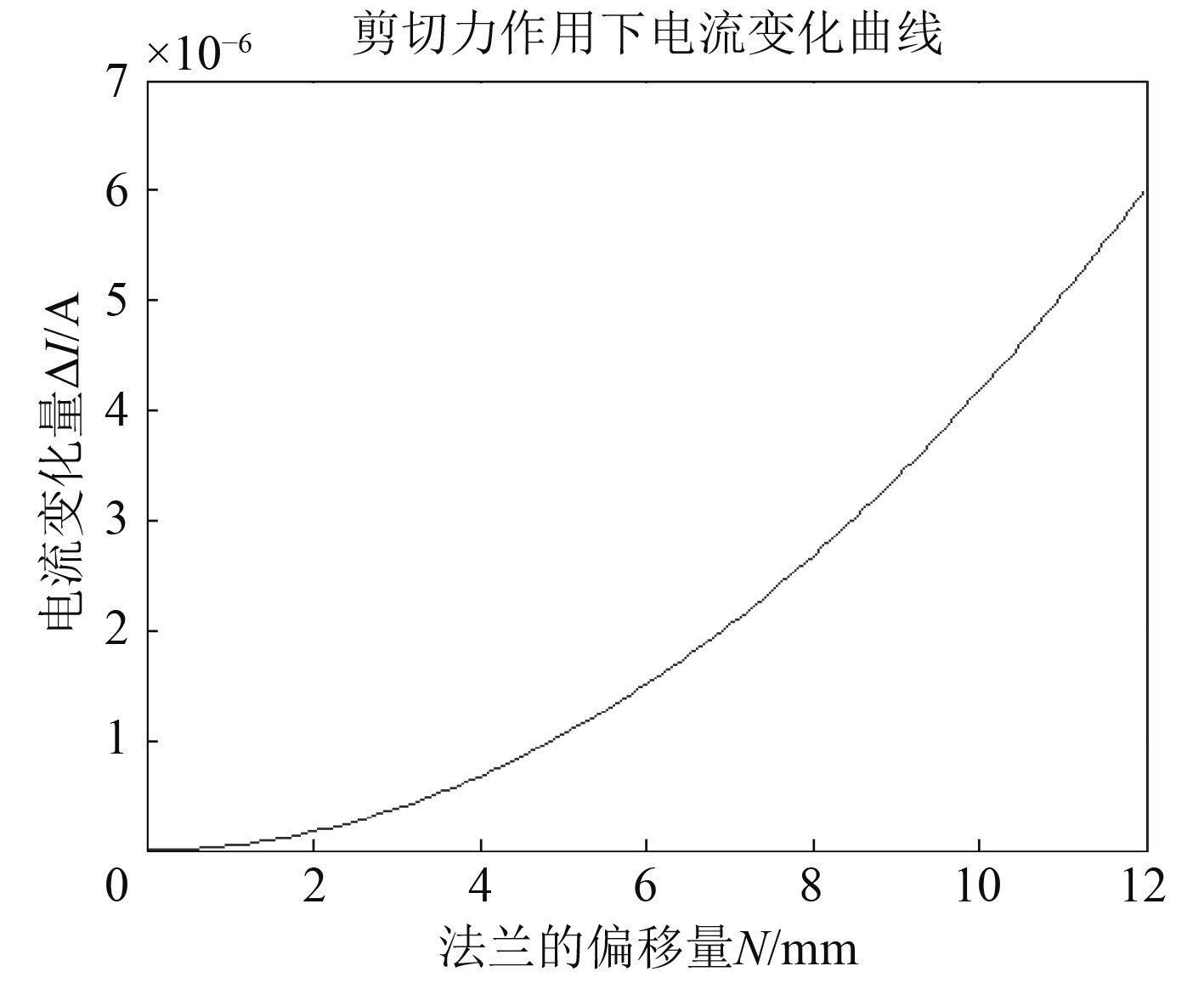
图 6 径向变形-电流变化 Fig. 6 Radial deformation -current |
|
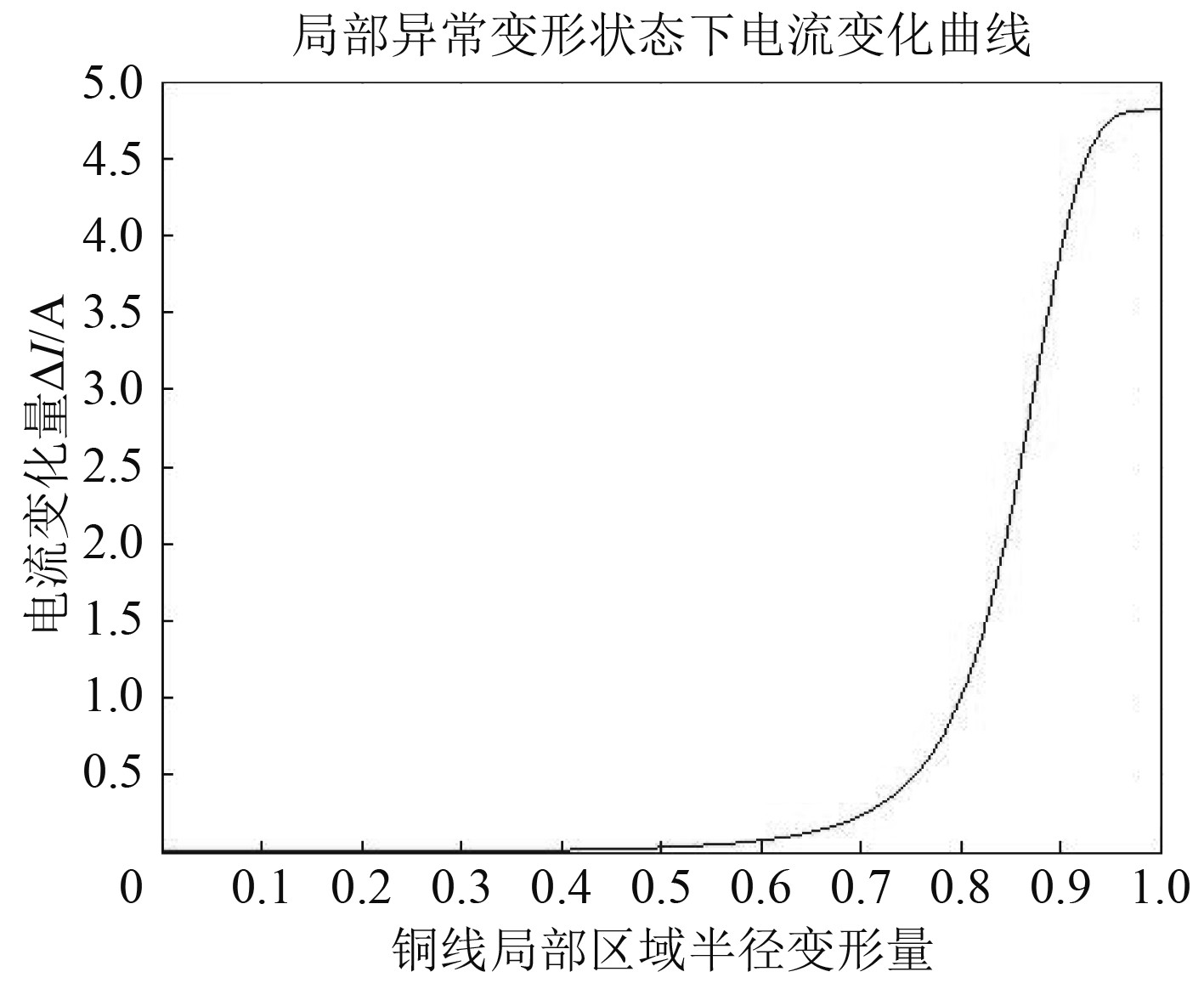
图 7 局部异常变形-电流变化曲线 Fig. 7 Local abnormal deformation- current |
1)轴向变形和径向变形引起电路电流变化很小,变化的范围分别为0~110.4 μA、0~6.022 μA,几乎可忽略不计。
2)当局部变形较大时,才能引起电流的明显变化。以该算例而言,当
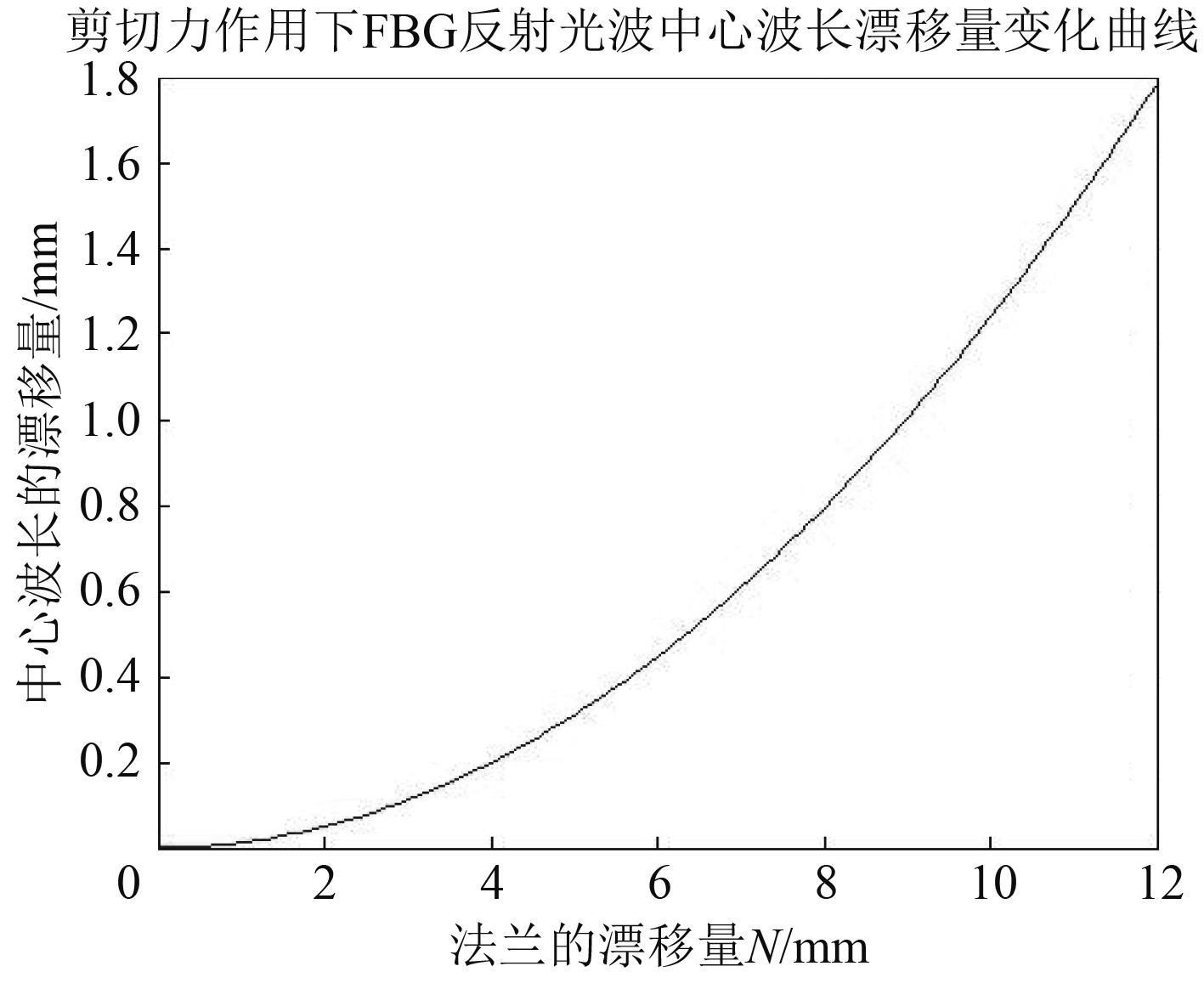
图8和图9为管体轴向变形或径向变形状态时,光纤光栅传感器反射光波的中心波长漂移量

|
图 8 轴向变形-光纤光栅波长漂移量 Fig. 8 Axial deformation -the wave length of FBG |
|
图 9 径向变形-光纤光栅测点波长漂移量 Fig. 9 Radial deformation -the wave length of FBG |
1)轴向变形引起各测点光纤光栅传感器的
2)径向变形引起各测点光纤光栅传感器
仿真参数如表3所示。
|
|
表 3 有限元仿真参数 Tab.3 Finite element simulation parameters |
将参数代入有限元模型中,图10和图11表示压力为4 MPa时,铜线的纵向应力

|
图 10 铜线纵向应力云图 Fig. 10 The longitudinal stress cloud diagram of copper wire |

|
图 11 铜线环向应力云图 Fig. 11 The circumferential stress cloud diagram of copper wire |
1)在靠近内法兰的位置,纵向应力最大,
2)在挠性管体的部分,环向应力最大,
将
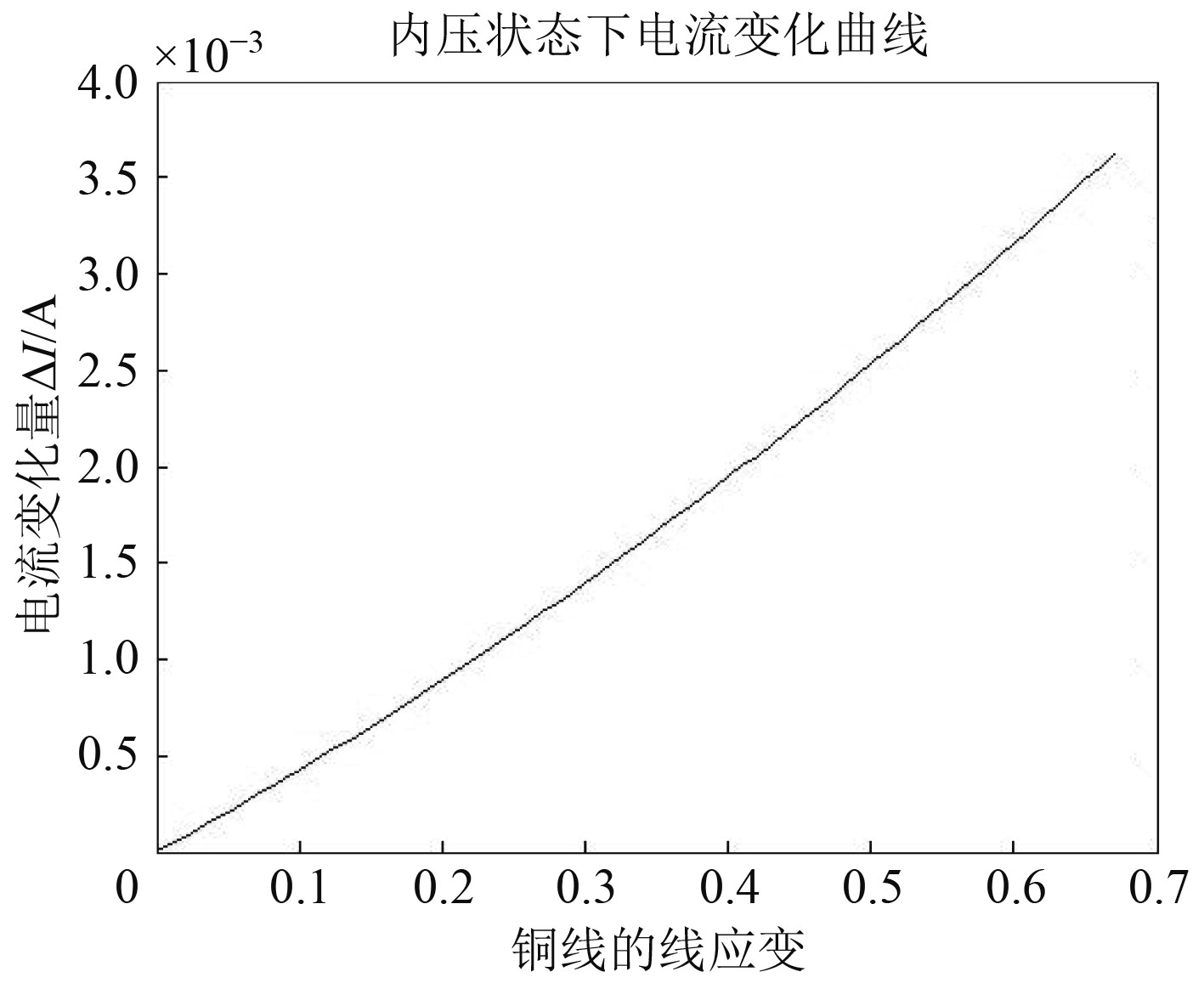
图12为管体充压状态下的电流变化曲线,可知电流变化量随铜线的线应变
|
图 12 充压状态-电流变化 Fig. 12 Pressurized state-current |
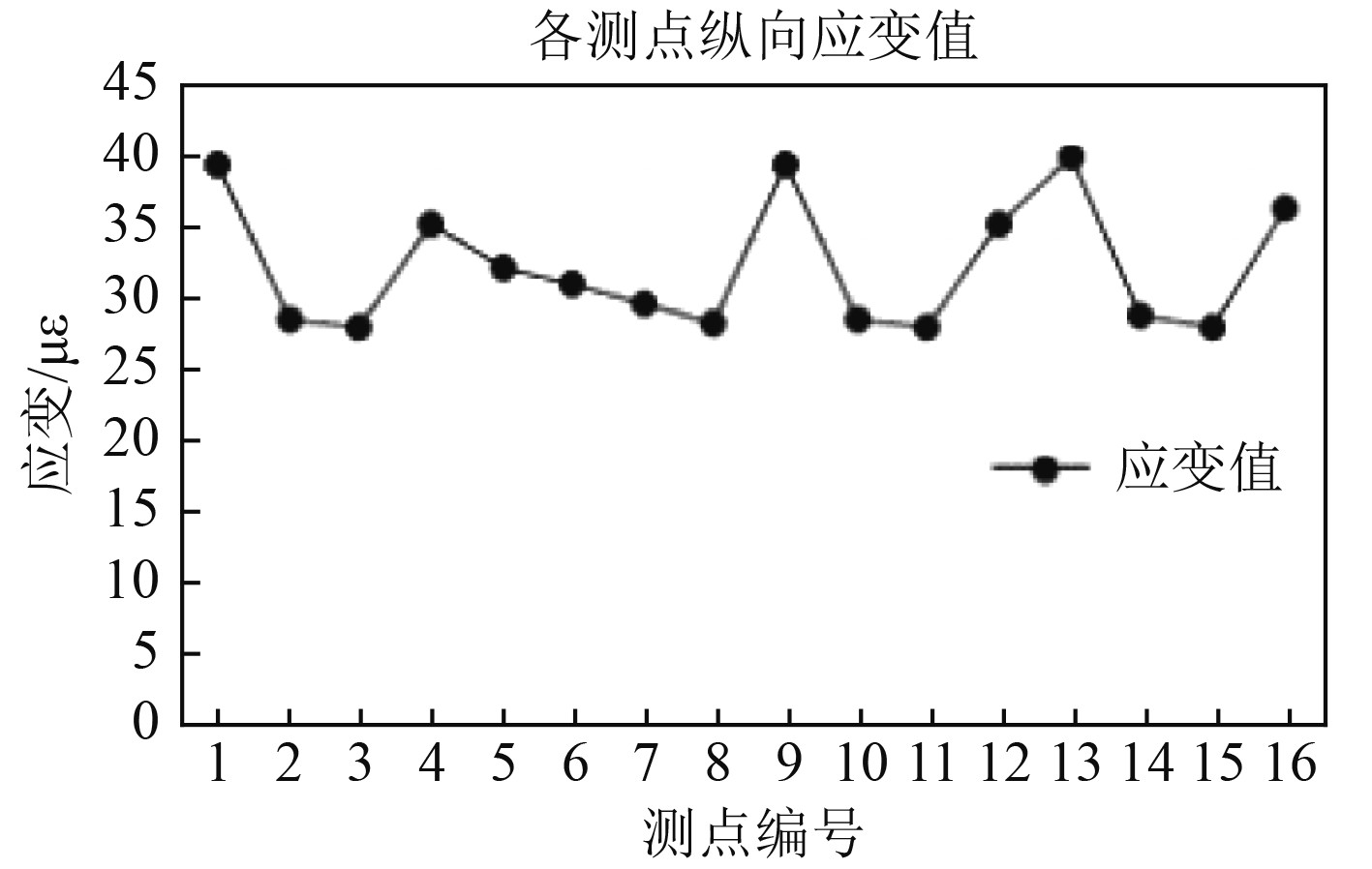
图13为光纤光栅传感器所在骨架层的纵向应变云图,可得到布置在管体各测点的纵向应变量。图14为光纤光栅传感器测点的应变分布范围。可知:在管体充压变形状态下,各测点的纵向应变的范围为

|
图 13 骨架层纵向应变 Fig. 13 The longitudinal strain of skeleton layer |
|
图 14 光纤光栅测点应变范围 Fig. 14 The Range strain of 光纤光栅 measuring points |
表4为管体4种变形特性的分析结果,针对电阻感应原理的分析如下:
|
|
表 4 挠性接管的4种变形状态特性 Tab.4 Four deformation states' characters of FW-FP |
1)轴向变形、径向变形、充压变形引起电路电流的变化量
2)局部异常变形引起
针对光纤光栅传感原理的分析如下:
1)轴向变形引起各光纤光栅传感器的
2)局部异常变形引起某一测点的
|
|
表 5 FW-FP寿命状态的判别准则 Tab.5 The criteria for determining the state of deformation |
1)当
2)当
3)当
本文提出一种基于管体变形实时监测的挠性接管寿命评估方法。采用电阻感应原理和光纤光栅传感原理,建立管体变形监测模型,对挠性接管的四种变形特性进行分析研究;针对型号DN100进行算例分析,提取出可识别管体局部异常变形的特征阈值,结论如下:
1)管体发生正常整体性变形时,电路电流变化量很小;而管体局部发生较大的异常变形时,电流变化量级很大。
2)管体在轴向变形、径向变形、充压变形状态下,各个光纤光栅传感器的反馈信号
3)通过设定电流阈值和光纤光栅传感器信号阈值,根据判别准则可实时判断管体的变形状态,对挠性接管的寿命进行评估。
| [1] |
张晓平, 何琳, 周炜. 凯夫拉纤维增强弧形体挠性接管平衡性研究[J]. 振动与冲击, 2012, 31(8): 70-73. ZHANG X P, HE L, ZHOU W. Equilibrium performance of a filament-wound flexible arc pipe[J]. Journal of Vibration and Shock, 2012, 31(8): 70-73. DOI:10.3969/j.issn.1000-3835.2012.08.014 |
| [2] |
Anon Don Deckard. Hydraulic hose with integral life-sensing capability and method therefor[P]. The United States, 7555936B2, 2009.
|
| [3] |
John Roux Phelan, Richard Stephen Pollack. Process and apparatus for monitoring a physical condition of a hose[P]. The United State, 6498991B1, 2002.
|
| [4] |
CHEVALIER et al. Abrasive material transport hose with wear detecting sensors[P]. The United States, 636237B1, 2002.
|
| [5] |
Redmond. Failure sensor hose[P]. The United States, 5969618, 1999.
|
| [6] |
EMILIO P. Neto Hose for suction and discharge of ore slurry or any other abrasive material[P]. The United States, 5634497, 1997.
|
| [7] |
孙丽. 光纤光栅传感技术与工程应用研究[D]. 大连: 大连理工大学, 2006. SUN Li. Research of fiber bragg grating sensing technology and engineering application[D]. Dalian: Dalian University Technology, 2006. |
| [8] |
周广东. 光纤光栅传感器应变传递理论研究[D]. 大连, 大连理工, 2007. ZHOU Guang-dong. Study on strain transfer characteristics of fiber bragg grating sensors[D]. Dalian: Dalian University Technology, 2007. |
| [9] |
吴永红, 邵长江, 屈文俊, 等. 大型工程长期健康监测用FBG应变传感器的研究[J]. 光电子激光, 2010, 21(4): 482-484. WU Yong-Hong, SHAO Chang-jiang, QU Wen-jun, et al. Study on FBG strain sensor for application to large engineering long term health monitoring[J]. Journal of Optoelectronics Laser, 2010, 21(4): 482-484. |
| [10] |
朱石坚, 何琳. 船舶减振降噪技术与工程设计[M]. 北京: 科学出版社, 2002.
|
 2020, Vol. 42
2020, Vol. 42
