100Cr6是一种碳含量为1%、铬含量为1.5%的轴承钢,由于自身的抗摩擦性能和高疲劳强度性能被用作轴承钢,100Cr6相当于我国的GCr15。100Cr6材料在作为传动部件的支撑时往往会产生一定程度的磨损,磨损严重会影响传动部件的性能。据不完全统计,世界能源的1/3~1/2消耗于摩擦,而机械零件80%失效原因是磨损,可见对于材料摩擦磨损的研究十分重要。
摩擦往往是一种非线性行为,一般会引起设备的稳态误差和性能下降[1],大多数摩擦磨损研究是依据宏观方程或通过多功能圆球光盘摩擦试验机进行试验研究。目前,国内外学者采用摩擦磨损试验机针对轴承的摩擦性能做了大量的研究,Liu等[2]通过销盘试验方法对尼龙(PA)/超高分子量聚乙烯(UHMWPE)复合材料在干摩擦和湿摩擦的摩擦性能进行试验研究,研究表明PA/UHMWPE复合材料的动摩擦系数随滑动距离的增大逐渐减小。Tevrüz[3,4]针对黄铜填充PTFE和碳纤维填充PTFE的摩擦性能开展试验研究,研究了摩擦因数与轴承压力、摩擦因数与滑动速度、摩擦因数与滑动距离、磨损与轴承压力、温度与滑动距离、磨损与滑动速度、磨损与滑动距离的关系,研究表明通过降低轴承温度可以减小轴承压力和滑动速度对轴承磨损的影响。Godfrey[5]通过销盘试验机研究摩擦与振动的关系,结果表明振动是由于材料表面不平和润滑不充足造成的,在没有润滑的条件下材料的滑动摩擦因数是一组波动的值而不是固定的值。黄霞等[6]通过多功能摩擦磨损试验机对酚醛树脂基水轴承材料的摩擦磨损性能进行试验研究,研究其在水介质下的摩擦性能,研究表明聚四氟乙烯和六钛酸钾晶须有利于提高酚醛树脂的摩擦学性能,而纳米氧化铝的添加会降低酚醛树脂的摩擦学性能。吴铸新等[7]采用MMW-1立式万能磨损试验机研究水润滑轴承推力瓦块的摩擦磨损性能,研究表明干摩擦时载荷与转速对材料的摩擦因数具有明显的影响,磨损量随载荷的增大而增大。
100Cr6用于机床传动轴上的轴套,此种轴套在实际运行中充分体现了其优异性能,但运行长时间后会表面发现其摩擦表面有明显的磨损痕迹。为了研究100Cr6轴承材料在干摩擦状态下的摩擦磨损性能,基于Archard磨损计算公式,通过多功能圆球光盘摩擦试验机进行试验,研究100Cr6材料的摩擦因数、磨损深度、试件温度、磨损量随法向载荷和滑动直径的变化规律。
1 摩擦磨损方法研究磨损过程一般分为3个阶段:跑合阶段,稳定磨损阶段和剧烈磨损阶段,其磨损曲线如图1所示。其中OA段为跑合阶段,AB段为稳定磨损阶段,BC段为剧烈磨损阶段。在跑合阶段机件表面被磨平,实际接触面积不断增大,表面应变硬化,形成氧化膜,磨损速率减小;在稳定磨合阶段斜率就是磨损速率,唯一稳定值;大多数机件在稳定磨损阶段服役,磨损性能是根据机件在此阶段的表现来评价的;在剧烈磨损阶段随磨损的增长,磨耗增加,表面间隙增大,表面质量恶化,机件快速失效。

|
图 1 磨损曲线图 Fig. 1 Scheme of wear curve |
在稳定磨损阶段,Archard磨损理论公式可适用,其公式如下[8-9]。
| $V = K \times F \times S\text{。}$ | (1) |
式中:
磨损系数K反映了磨损的快慢,其值并不是固定的值,而是与法向载荷、滑动距离、表面粗糙度、接触压力等有关的一个函数,其值分为7个等级(见表1),其中等级0~3为硬磨损。
|
|
表 1 磨损系数K的值 Tab.1 K value of wear coefficient |
由于磨损体积无法直接测量,但可通过磨损质量和材料密度计算得到,将Archard磨损计算公式变形如下:
| $K = \frac{V}{{F \times S}} = \frac{{\rm{m}}}{{\rho \times F \times S}}{\text{。}}$ | (2) |
式中:m为磨损量,kg;
国内外学者对于试件材料的摩擦磨损试验,往往采用球盘摩擦试验机进行,其原理如图2所示。其中可以改变滑动半径、法向载荷、滑动速度和滑动距离等参数研究材料的摩擦磨损性能。

|
图 2 摩擦试验方法 Fig. 2 Method of friction testing |
试验中,控制滑动距离和滑动表面速度不变,滑动距离取1 000 m,滑动表面速度取0.377 m/s,室温保持在23.8 ℃,空气湿度保持在34.2,改变滑动直径和法向载荷的值,接触条件为干摩擦,试验共分10组进行,研究摩擦因数、磨损深度、试件温度和磨损量随滑动直径和法向载荷的变化关系,试验输入条件见表2。
|
|
表 2 试验输入条件 Tab.2 Test input conditions |
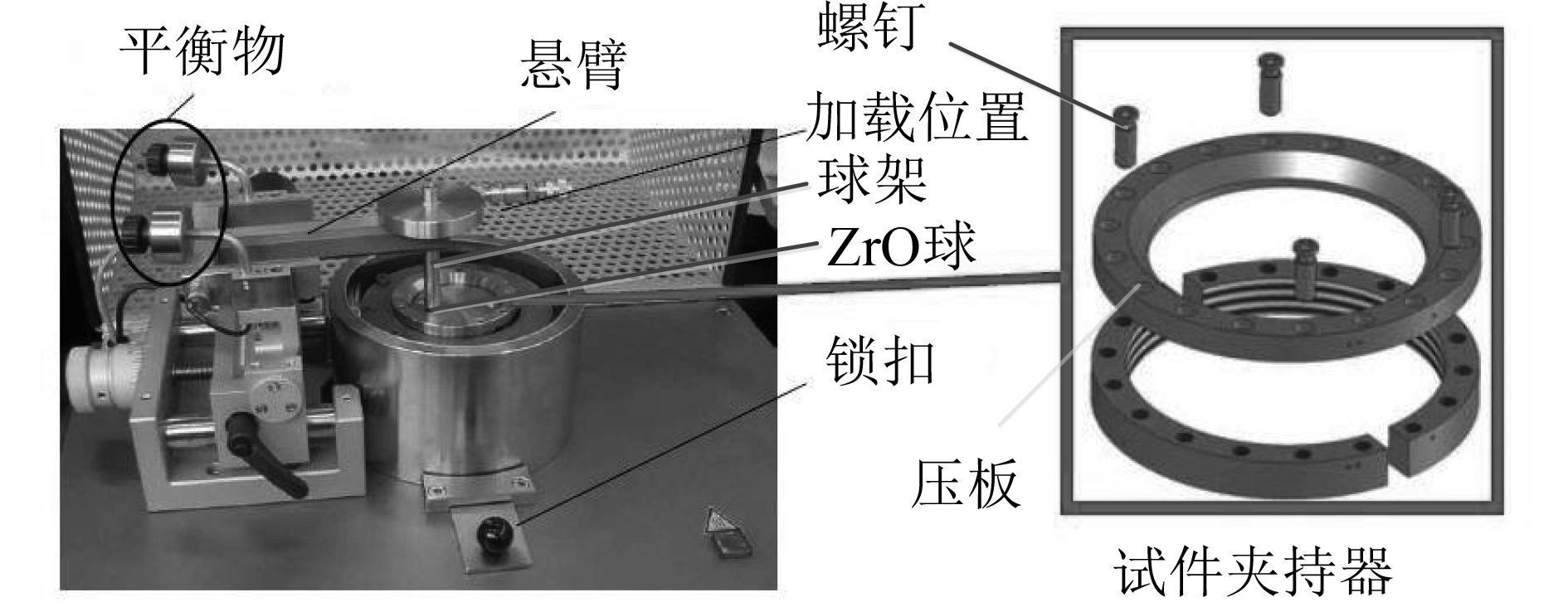
100Cr6材料的摩擦磨损试验在多功能圆球光盘摩擦试验机上进行,采用球-面摩擦形式,试验设备如图3所示。试件固定在压板的下面,压板由螺钉固定住,将ZrO球固定在球架上,球架固定在悬臂上。通过平衡物来调节悬臂的平衡以消除施加载荷的不准确性,调节完成后将法向载荷施加到悬臂上,将锁扣解锁,然后进行不同条件下的试验,通过软件设备来记录试验数据。
|
图 3 圆球光盘摩擦试验机 Fig. 3 Friction testing machine of ball-disk |
对100Cr6材料试样在测试前用丙酮进行清洗后再称重,试验结束后,将试件清洗干净烘干后进行再次称重,计算其磨损量,电子秤精度为0.000 1 g。
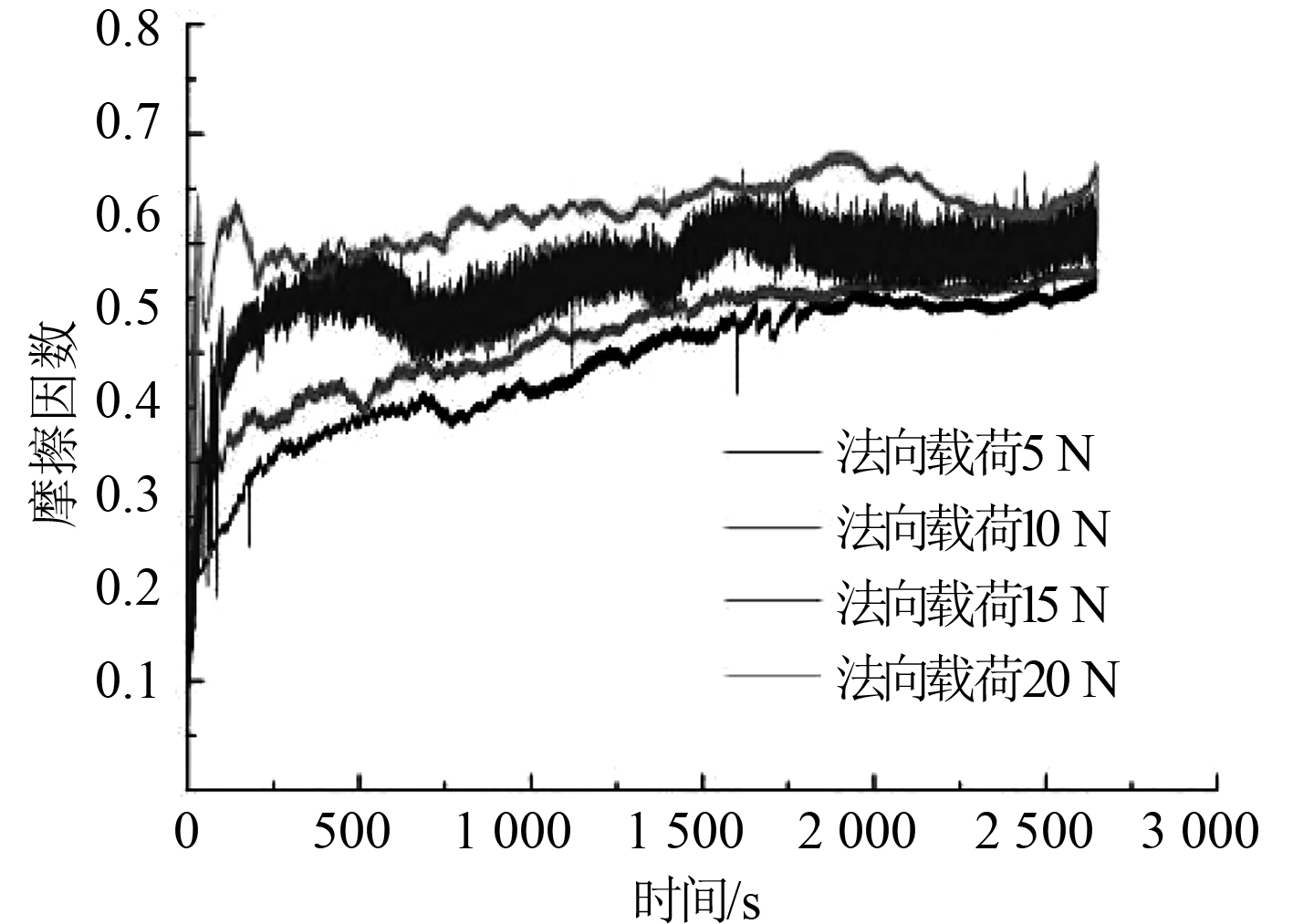
3 结果和讨论 3.1 摩擦因数选取试验编号1~8进行摩擦磨损试验,滑动直径为6 mm和12 mm,法向载荷为5 N,10 N,15 N和20 N,研究摩擦因数随法向载荷和滑动直径的关系。滑动直径为6 mm时摩擦因数随时间的变化曲线图如图4所示,滑动直径为12 mm时摩擦因数随时间的变化曲线图如图5所示,稳定状态下摩擦因数随法向载荷的变化曲线图如图6所示。
|
图 4 滑动直径为6 mm时摩擦因数随时间变化 Fig. 4 Variation of friction coefficient with time when sliding diameter is 6 mm |

|
图 5 滑动直径为12 mm时摩擦因数随时间变化 Fig. 5 Variation of friction coefficient with time when sliding diameter is 12 mm |
|
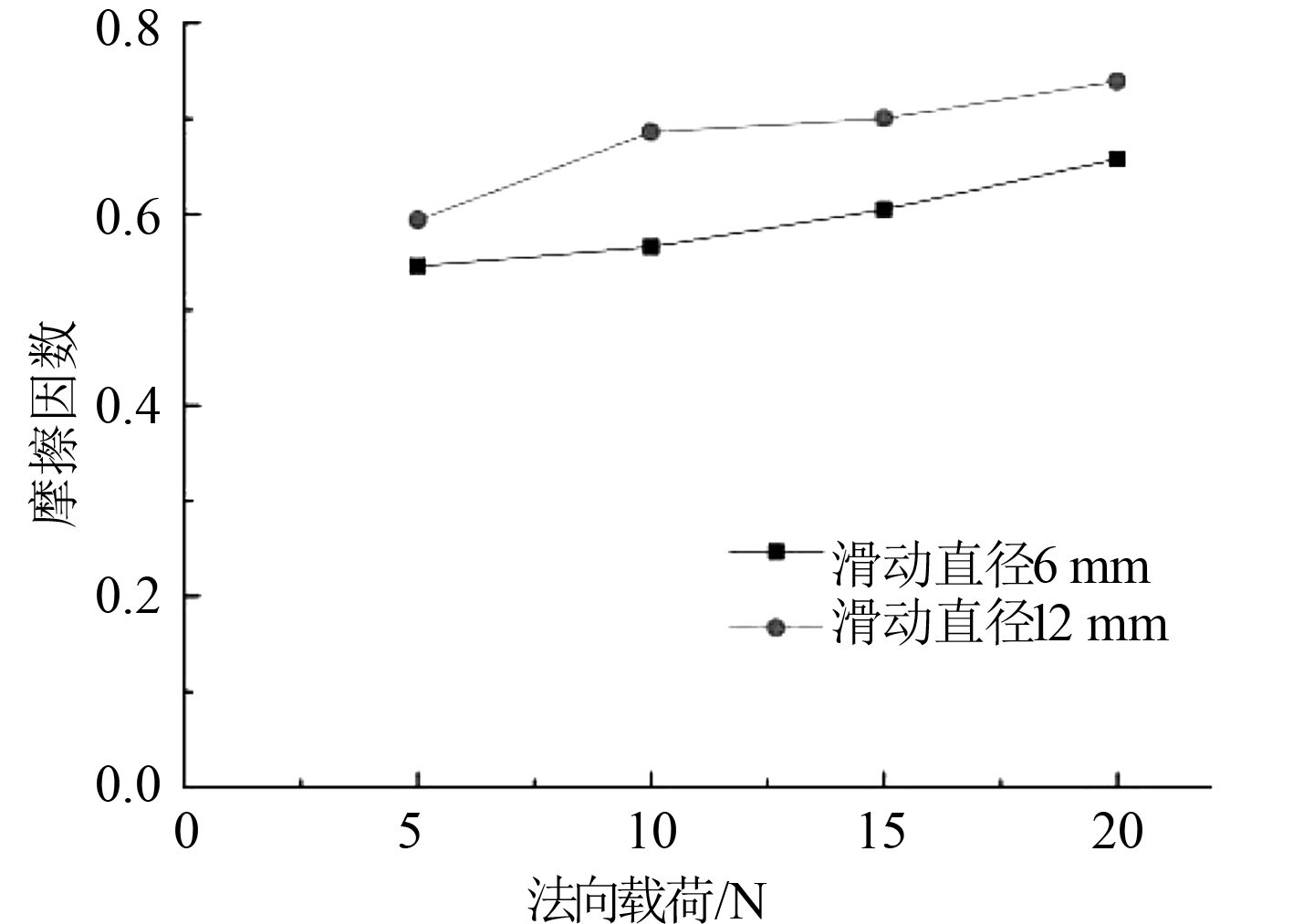
图 6 稳定状态下摩擦因数随法向载荷变化 Fig. 6 Variation of friction coefficient with normal load in stable state |
由图4可知,随着时间的变化,4种法向载荷工况下,摩擦因数在大约500 s时达到稳定值,之后处于微小的波动状态,在500 s之前摩擦因数一直处于波动状态,此阶段称为跑合阶段。由图6可知,在摩擦因数达到稳定阶段,将法向载荷由5 N增大到20 N过程中,摩擦因数随法向载荷的增大而增大,滑动直径为12 mm时的摩擦因数整体上大于滑动直径为6 mm时的摩擦因数,在法向载荷为5 N时,差值较小,法向载荷为10~20 N时,差值较大。由图5可知,滑动直径为12 mm时的摩擦因数随时间的变化规律与图4基本一致。基于以上分析可知,当法向载荷较小时,滑动直径对摩擦因数影响较小,当法向载荷较大时,影响较大。
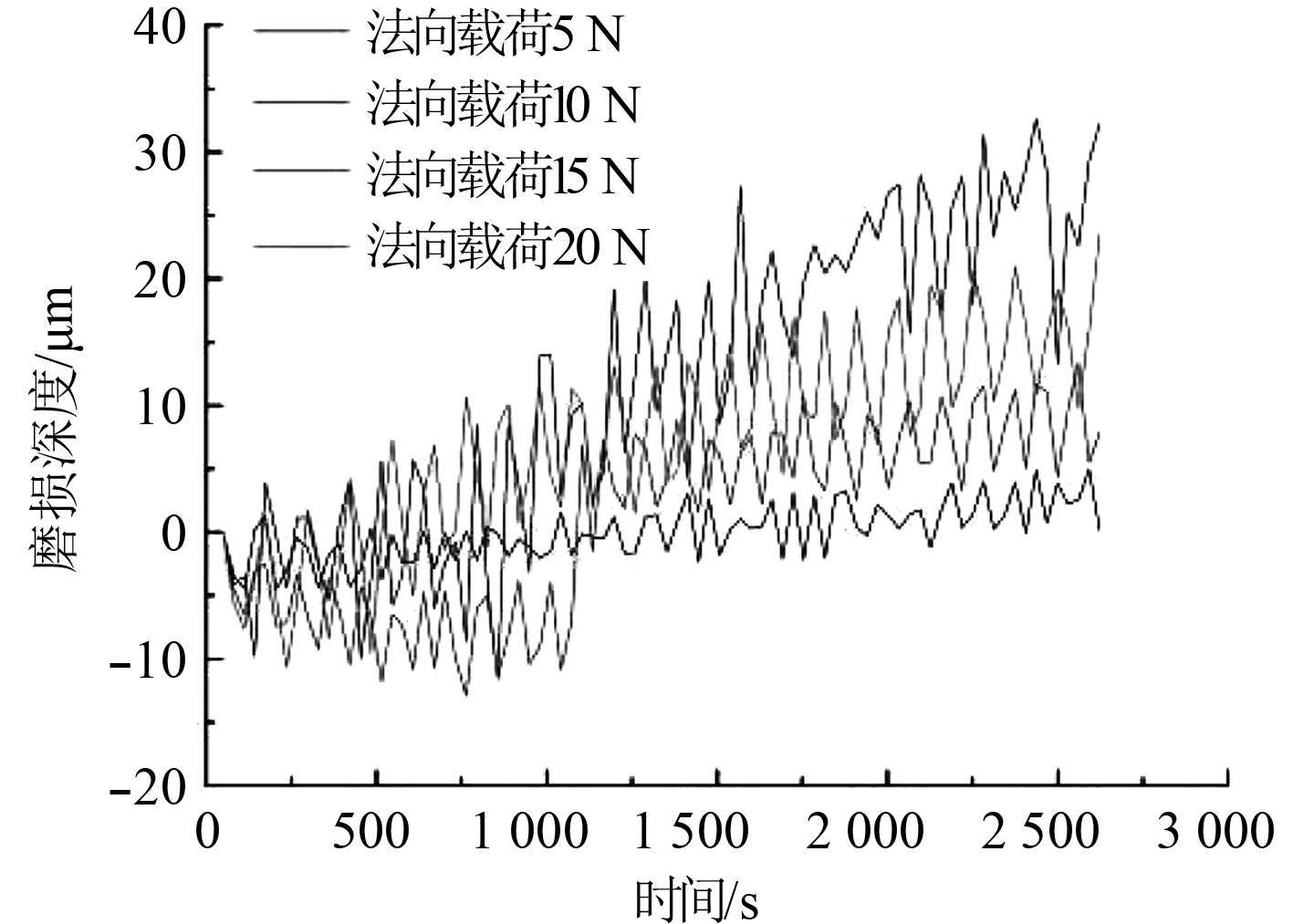
3.2 磨损深度为了避免初始的误差,在后续的试验选取50 s以后的试验数据,且后续提取的磨损深度定义为最大磨损深度减去最小磨损深度的差值,测得法向载荷为5 N,10 N,15 N和20 N,滑动直径为6 mm时的磨损深度随时间的变化关系如图7所示,滑动直径为12 mm时的磨损深度随时间的变化关系如图8所示,稳定状态下磨损深度随法向载荷的变化关系如图9所示。

|
图 7 滑动直径为6 mm时的磨损深度随时间变化 Fig. 7 Variation of penetration depth with time when sliding diameter is 6 mm |
|
图 8 滑动直径为12 mm时的磨损深度随时间变化 Fig. 8 Variation of penetration depth with time when sliding diameter is 12 mm |
|
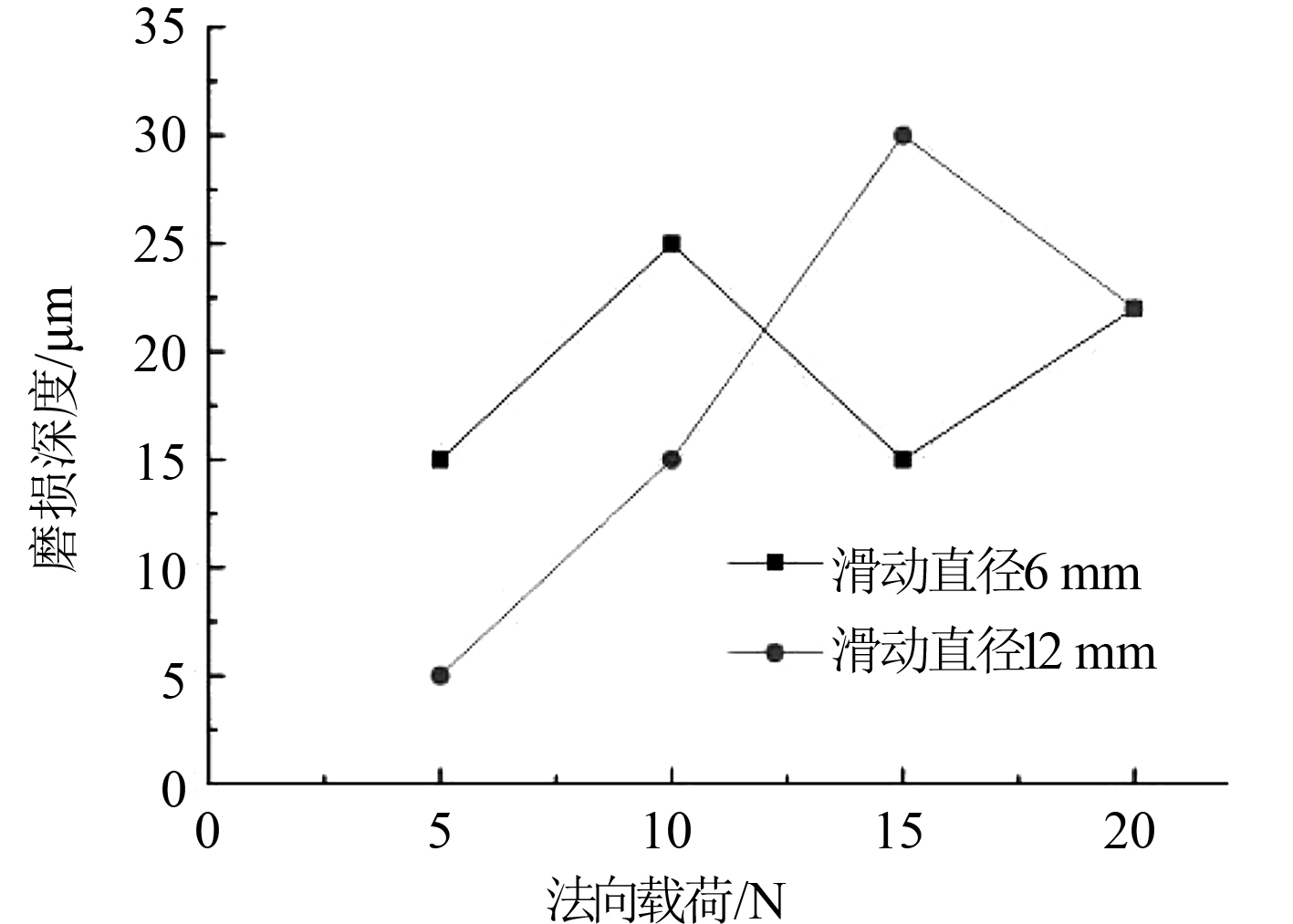
图 9 稳定状态下的磨损深度随法向载荷变化 Fig. 9 Variation of penetration depth with normal load in stable state |
由图7和图9可知,在滑动直径为6 mm时,随着法向载荷由5 N增大到10 N,磨损深度由15 μm增大到25 μm,随着法向载荷增大到15 N时,磨损深度减小到14 μm,之后法向载荷继续增大,磨损深度也随之增大,在法向载荷为15 N时,磨损深度随时间的变化波动比较明显。由图8和图9可知,在滑动直径为12 mm时,随着法向载荷由5 N增大到15 N,磨损深度由5 μm增大到30 μm,之后法向载荷继续增大,磨损深度随之减小。由图9分析可知,当法向载荷小于10 N时,滑动直径为12 mm的磨损深度小于滑动直径为6 mm的磨损深度,并且这种差值越来越小,随着法向载荷的增大,滑动直径为12 mm的磨损深度超过了滑动直径为6 mm的磨损深度。之后滑动直径为12 mm的磨损深度又随之减小,滑动直径为6 mm的磨损深度随之增大,2种工况的磨损深度最终达到相同的值,但整体上,磨损深度随法向载荷的增大而增大,随滑动直径的增大而减小。基于以上分析可知,当法向载荷较小时,滑动直径对磨损深度有显著影响,当法向载荷达到一定值时,滑动直径的变化对磨损深度的影响很小。
3.3 试件温度滑动直径为6 mm时试件温度随时间的变化关系如图10所示,滑动直径为12 mm时试件温度随时间的变化关系如图11所示,稳定状态下试件温度随法向载荷的变化关系如图13所示。

|
图 10 滑动直径为6 mm时试件温度随时间变化 Fig. 10 Variation of specimen temperature with time when sliding diameter is 6 mm |
|
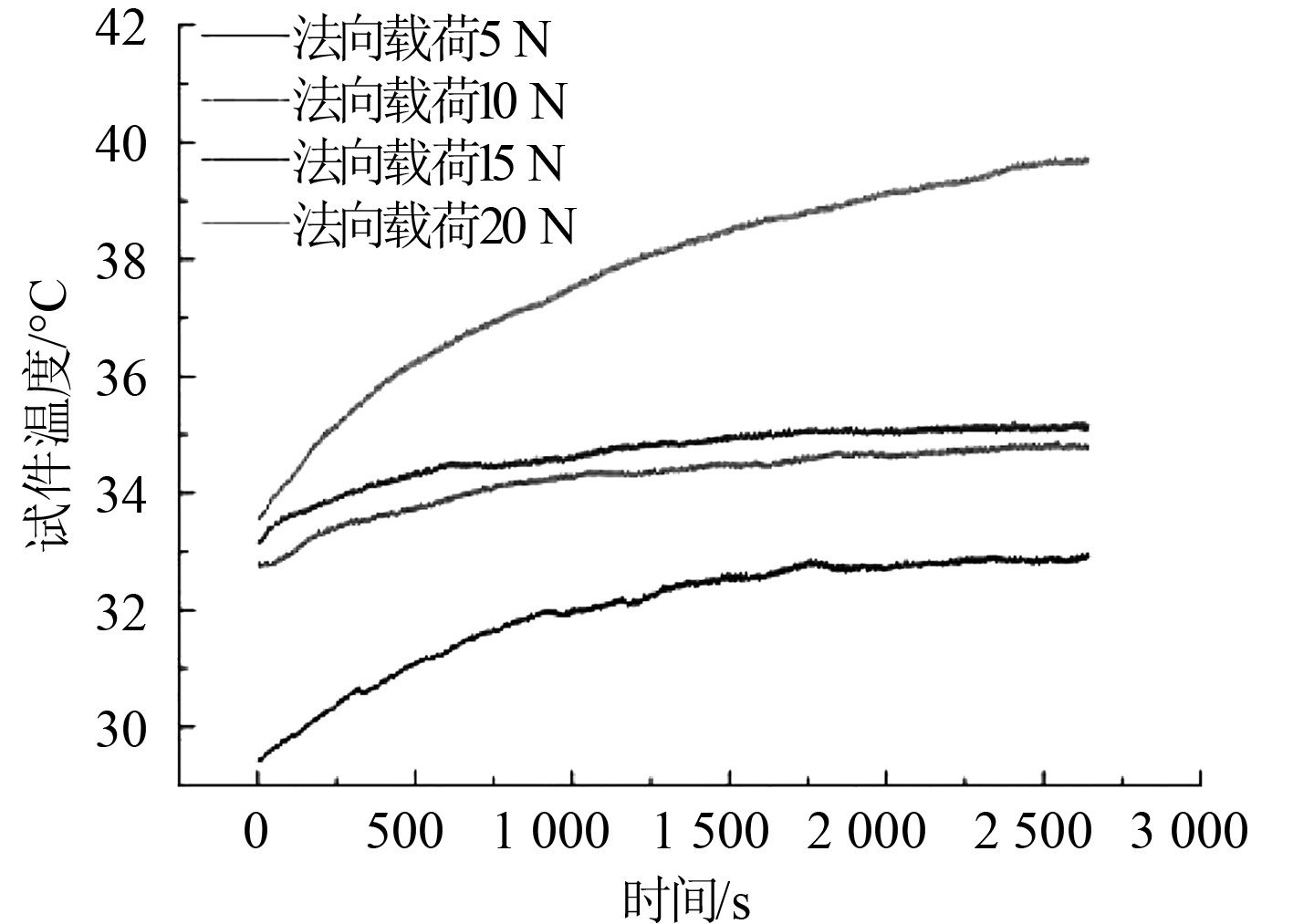
图 11 滑动直径为12 mm时试件温度随时间变化 Fig. 11 Variation of specimen temperature with time when sliding diameter is 12 mm |

|
图 13 磨损量随法向载荷变化 Fig. 13 Variation of wear loss with normal load |
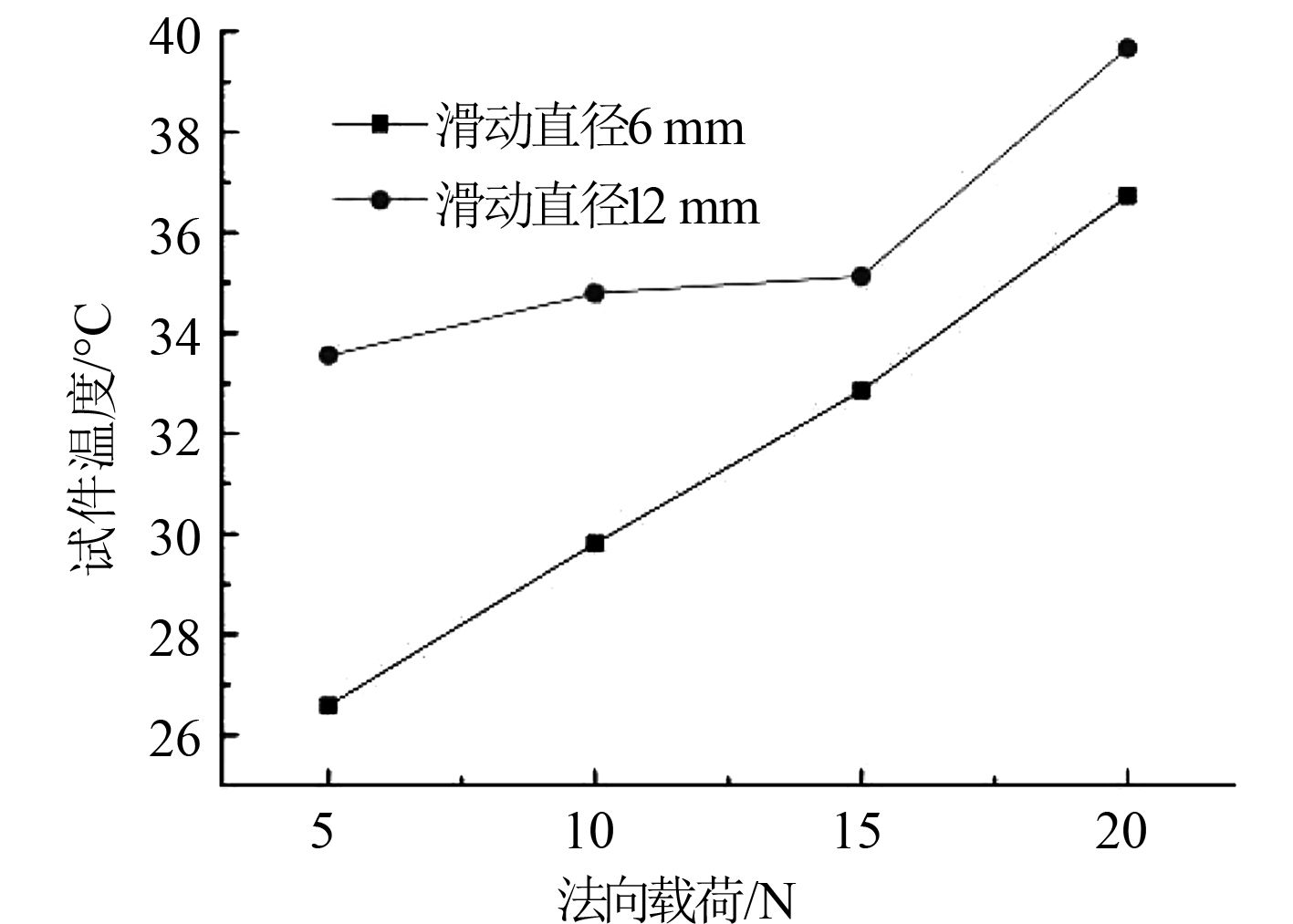
由图10可知,在法向载荷为5 N,10 N,15 N和20 N时,滑动直径为6 mm时,试件温度随时间的变化越来越高,最后趋于稳定状态。由图11可知,法向载荷为5 N,10 N,15 N和20 N时,滑动直径为12 mm时,试件温度随时间的变化规律与滑动直径为6 mm时的基本一致。由图12可知,滑动直径为6 mm和12 mm时,稳定状态下的试件温度随法向载荷的增大而增大,并且试件温度与法向载荷成一定比例的线性关系,主要是因为随着法向载荷的增大,试件表面的摩擦增大导致产生更多的热量,进而温度升高。对于统一试验条件下,滑动直径为6 mm时试件温度低于滑动直径为12 mm时的试件温度,是因为相同的滑动距离下,滑动直径为6 mm时滑动单位长度摩擦所用的时间为2倍,这样将会有更多的时间将热量带走。基于以上分析,法向载荷对试件的温度有正影响作用,滑动直径对试件的温度也有一定的影响,滑动直径越大,温度越高。
|
图 12 稳定状态下试件温度随法向载荷变化 Fig. 12 Variation of specimen temperature with normal load in stable state |
试验前后,通过电子秤来测量试件前后重量的变化,然后计算其磨损量,磨损量随法向载荷的变化关系如图13所示。
由图13可知,滑动直径为6 mm时,磨损量随法向载荷的增大稳步增大;滑动直径为12 mm时,磨损量随法向载荷的增大而增大,当增大到10 N后,磨损量保持在一个波动状态。在同等法向载荷下,滑动直径为6 mm时的磨损量大于滑动直径为12 mm时的磨损量,是因为同等滑动距离下,滑动直径为6 mm时每单位长度的摩擦时间为2倍的滑动直径为12 mm时的摩擦时间,小的滑动直径会造成更严重的磨损,因此磨损量将会更大。滑动直径较小时,法向载荷对磨损量具有显著的影响。
为了研究K值与法向载荷和滑动直径的关系,通过磨损量公式(2)将图13的数值进行变化,其曲线图如图14所示。
|
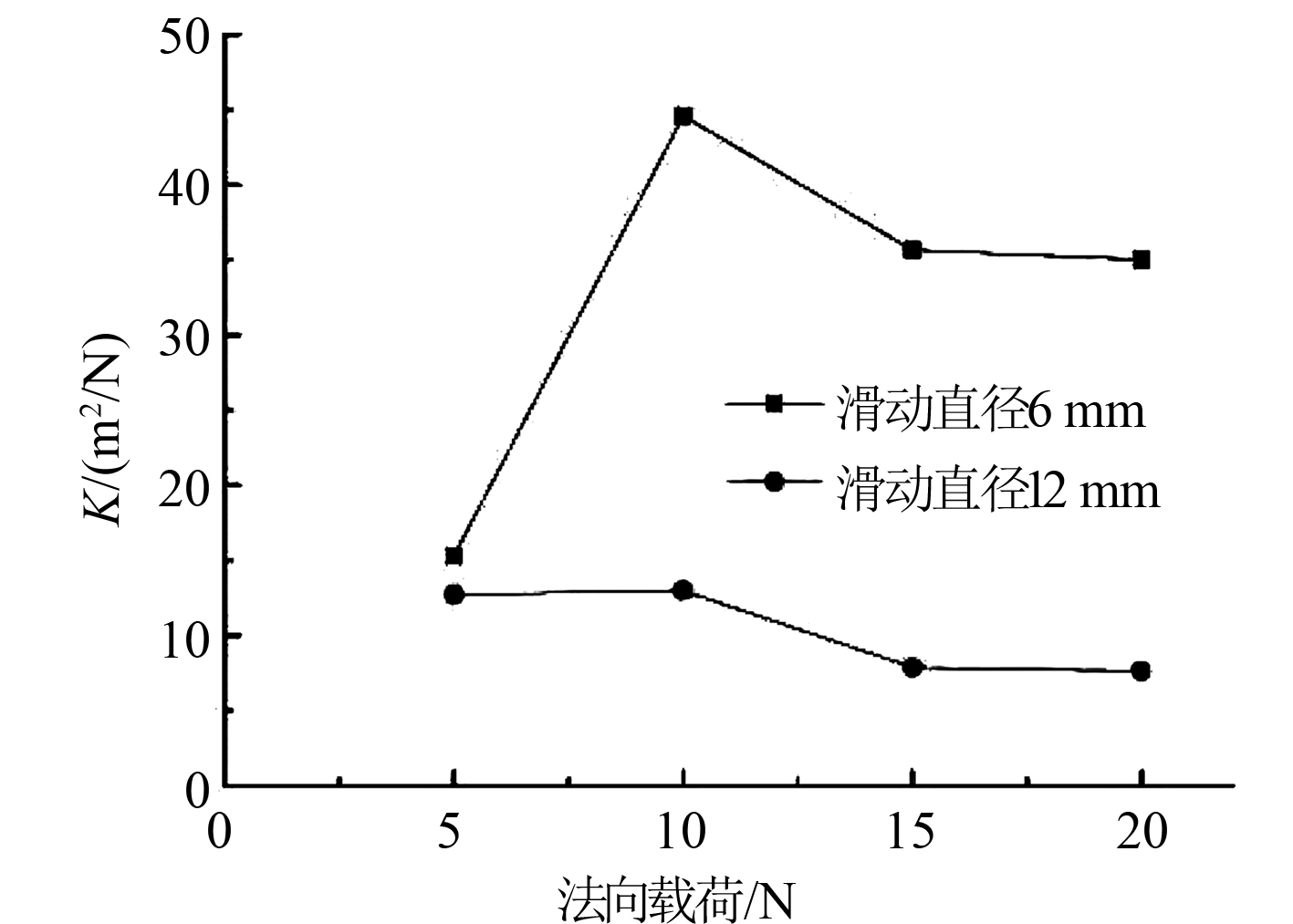
图 14 K值与法向载荷和滑动直径关系 Fig. 14 The relation of K value with normal load and sliding diameter |
由图14可知,滑动直径为6 mm时的K值明显大于滑动直径为12 mm时的K值,并且2种滑动直径下K值的变化有相似的趋势,法向载荷小于10 N时,K值随法向载荷的增大而增大,大于10 N后,随法向载荷的增大而减小。滑动距离、滑动速度和法向载荷相同时,滑动直径为6 mm时的K值比较大是因为有更严重的摩擦条件,从而表明小的滑动直径下有更严重的磨损。
4 结 语通过多功能圆球光盘摩擦试验机,基于Archard磨损理论公式,开展了100Cr6轴承材料摩擦因数、磨损深度、试件温度和磨损量等实验,主要结论如下:
1)100Cr6轴承材料摩擦因数不是一个定值,而是在初始阶段发生较大的波动,随着时间的变化达到一定的稳定值,且随着法向载荷和滑动直径的增大而增大。当法向载荷较小时,滑动直径对100Cr6轴承材料的摩擦因数影响较小,当法向载荷较大时,滑动直径对摩擦因数影响较大。
2)100Cr6轴承材料的磨损深度随法向载荷的增大而增大,随滑动直径的增大而减小。当法向载荷较小时,滑动直径对100Cr6轴承材料的磨损深度有显著的影响,当法向载荷达到一定的值后,法向载荷对100Cr6轴承材料磨损深度的影响越来越小。
3)100Cr6轴承材料的试件温度随法向载荷和滑动直径的增大而增大,且试件温度随时间缓慢增大,并不会出现很大波动。在一定的滑动直径下,试件温度与法向载荷成一定比例的线性关系。
4)100Cr6轴承材料在法向载荷和滑动距离相同时,滑动直径对磨损量有明显的影响,滑动直径越大,磨损量越小,当滑动直径较小时,法向载荷对磨损量有明显的影响;滑动距离、滑动速度和法向载荷相同时,滑动直径为6 mm的K值大于滑动直径为12 mm时的K值。
| [1] |
DE WIT C. C., OLSSON H., ASTROM K. J., et al.. A new model for control of systems with friction[J]. IEEE Transactions on Automatic Control, 1995, 40(3): 419-425. DOI:10.1109/9.376053 |
| [2] |
LIU C. Z., WU J. Q., LI J. Q., et al.. Tribological behaviours of PA/UHMWPE blend under dry and lubricating condition[J]. Wear, 2006, 260(1): 109-115. |
| [3] |
T. TEVRÜZ. Tribological behaviours of carbon filled polytetrafluoroethylene (PTFE) dry journal bearings[J]. Wear, 1998, 221(1): 61-68. DOI:10.1016/S0043-1648(98)00258-0 |
| [4] |
TEVRUZ T.. Tribological behaviours of bronze-filled polytetrafluoroethylene dry journal bearings[J]. Wear, 1999, 230(1): 61-69. DOI:10.1016/S0043-1648(99)00091-5 |
| [5] |
GODFREY D.. Friction oscillations with a pin-on-disc tribometer[J]. Tribology International, 1995, 28(2): 119-126. DOI:10.1016/0301-679X(95)92701-6 |
| [6] |
黄霞, 郑勇翔, 尹翔, 等. 酚醛树脂基水轴承材料的摩擦磨损性能研究[J]. 粉末冶金工业, 2018, 28(2): 54-57. |
| [7] |
吴铸新, 刘正林, 王隽, 等. 水润滑轴承推力瓦块材料摩擦磨损试验研究[J]. 兵工学报, 2011, 32(1): 118-123. |
| [8] |
VANBEEK A.. Advanced engineering design: lifetime performance and reliability[J]. Delft university of technology Mechanical engineering, 2006, 232~233, 244, 263. |
| [9] |
ERIKSEN M.. The influence of die geometry on tool wear in deep drawing[J]. Wear, 1997, 207(1-2): 10-15. DOI:10.1016/S0043-1648(96)07461-3 |
 2020, Vol. 42
2020, Vol. 42
